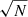| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 13 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202141915 | |
| Published online | 31 March 2022 | |
Quasars with large proper motions: A selection from the LQAC-5 catalogue combined with Gaia EDR3
Focusing on astrometric and photometric properties⋆
1
SYRTE, Observatoire de Paris – Université PSL, CNRS, Sorbonne Université, LNE, 61 avenue de l’Observatoire, 75014 Paris, France
e-mail: jean.souchay@obspm.fr
2
U.S. Naval Observatory, Washington, DC 20392-5420, USA
Received:
30
July
2021
Accepted:
8
January
2022
Context. Thanks to the cross-identification between the Gaia EDR3 (E-Data Release 3) catalogue and the quasars’ compiled catalogue LQAC-5 (Large Quasar Astrometric Catalogue-5), accurate astrometric parameters as well as photometric measurements were available for a set of 416 113 quasars.
Aims. After analysing the astrometric and photometric properties of these quasars,we concentrate our study on objects characterized by significant proper motion, which contradicts the postulate that they are fixed in the celestial sphere.
Methods. We derived statistical properties of the positions, parallaxes, and proper motions of the quasars cross-matched with Gaia EDR3. We carried out a specific investigation of quasars with a proper motion larger than 10 mas yr−1, and used colour–colour diagrams in mid-infrared to discriminate these quasars from stellar contamination. We discuss, in detail, a few cases where the abnormal proper motion could be caused by misidentifications.
Results. We note that 43% of LQAC-5 quasars were not detected by Gaia EDR3, mainly because of the cut-off magnitude at G = 21. The comparison between r(G) (Gaia) and r (SDSS) shows a normal distribution. The normalized distributions of parallaxes and proper motions are identical to that of the Gaia CRF2, as well as the distribution of the GBP − GRP colour index. We have identified 937 LQAC-5 objects (0.27% of the sample) with Gaia EDR3 proper motion which is significant at the 5σ level. We have clearly shown that below z = 0.35, the integrated magnitude G(r) obtained from SDSS spectra is smaller than G (Gaia), leading to the statement that the quasars are generally resolved under this threshold, which should lead to a bad determination of proper motion. Moreover, to discriminate quasars from stellar contamination, we have plotted them in a mid-infrared colour–colour diagram. Finally, we have made a final selection of 41 objects with μ > 10 mas yr−1, satisfying drastic constraints, which makes them potential candidates for considering their proper motion as real.
Conclusions. In this paper we carried out a complete analysis of the quasars of the LQAC-5 which were cross-identified with Gaia EDR3 ; this serves as an alternative and complementary study with respect to Gaia CRF2, involving a different population of quasars. We selected a set of 41 quasars with a proper motion exceeding 10 mas yr−1, which can be considered as very high for objects which are a priori fixed in the celestial sphere.
Key words: astrometry / catalogs / proper motions / reference systems
Full Table A.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/660/A16
© J. Souchay et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Astrometry is the astronomical discipline concerned with the accurate measurement of the positions of celestial objects as well as with the study of their changes. As was expected during its preparation phase, the Gaia mission revolutionized this field in the optical domain (Prusti et al. 2016; Brown et al. 2016) The main goal of the mission is to determine with a high level of accuracy the positions, parallaxes, proper motions of 1.8 billion objects together with their radial velocities and some astrophysical properties. A fundamental output of the mission consists of building a celestial reference frame (CRF) at visible wavelengths, in accordance with the principles of the International Celestial Reference System (ICRS; Arias et al. 1995). With that aim, Mignard et al. (2018) constructed the Gaia-CRF2, which can be considered as the first optical realization of the non-rotating CRF at sub-milliarcsecond levels of accuracy. For this purpose, they used the complete set of astrometric measurements, that bis to say the positions, parallaxes, and proper motions for a sample of more than 550 000 sources coming from the second release of the Gaia DR2 catalogue (Brown et al. 2018). Those sources were a priori known to be extragalactic objects, and mostly (but not always) quasars.
The origin of the selection of these objects is two-fold. The first selection came from a prototype of the third realization of the International Celestial Reference Frame (ICRF3; Charlot et al. 2020), adopted at the IAU General Assembly in Vienna in August of 2018, which contained the positions, at sub-milliarcsecond accuracy, of 4262 radio-loud extragalactic objects observed with VLBI at 8.4 GHz. The second selection consists of an all-sky sample of 1.4 million active galactic nuclei (AGNs) identified by Secrest et al. (2015) using data from the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010), AllWISE release. The corresponding catalogue is referred to as the AllWISE AGN catalogue (e.g., Lindegren et al. 2018). The identification of AGNs in AllWISE is rather straightforward, by using a two-colour infrared photometric criterion (Mateos et al. 2012). About half of the AllWISE sources identified by Secrest et al. (2015) were detected by Gaia, as mentioned by Mignard et al. (2018). A total of 566 869 objects were finally included after an appropriate selection in the Gaia-CRF2. They are distributed rather homogeneously in the sky, if we exclude the Galactic plane, where Galactic extinction is an important obstacle for the detection of extragalactic sources at visual wavelengths, and where source confusion limits the number of AGNs available from WISE.
In the mean time, Souchay et al. (2019) constructed an updated version of the Large Quasar Astrometric Catalogue (LQAC; Souchay et al. 2009), LQAC-5, which consists of a compilation of all the objects duly identified as quasars by the authors of the catalogues belonging to the compilation, with criteria adapted to the different properties of the surveys involved and their observational capabilities. Readers should notice that the LQAC-5 does not consist of a mere compilation of catalogues of quasars, but it contains useful additional data such as the optimized determination of the equatorial coordinates of the objects not detected by Gaia, mainly through the Large Quasar Reference Frame LQRF (Andrei et al. 2009). Moreover, LQAC-5 provides the determination of a multi-band structure index and absolute magnitudes.
Furthermore, LQAC-5 is quantitatively dominated by the 14th release of the Sloan Digital Sky Survey (DRQ14, Pâris et al. 2017) which represents nearly 90% of the whole catalogue. In this last survey, an object was selected as a quasar with the condition that its absolute magnitude Mi is smaller than −20.5 in the frame of conventional cosmology (H0 = 70 km s−1 Mpc−1). Moreover it must display at least one emission line with a full width at half maximum larger than 500 km s−1 or present complex absorption features in its spectrum, which characterizes a quasar without ambiguity thanks to the Lyman-α forest or broad absorption line (BAL) troughs. Alternative criteria for discriminating a quasar from other similar objects, mainly based on absolute luminosity, are found for other surveys or catalogues, as those fixed by Véron-Cetty & Véron (2010) for their compilation. They are discussed in Souchay et al. (2015).
We note that LQAC-5 contains a total of 592 809 objects, an amount roughly equivalent to the number of quasars selected in Gaia-CRF2. One of the important improvements of LQAC-5 with respect to previous LQAC updates (Souchay et al. 2015; Gattano et al. 2018) concerns the cross-identification of the objects with the Gaia DR2 catalogue. This cross-identification was done with a 1″ tolerance that considerably limits the probability of contamination with a star. A total of 398 697 Gaia DR2 counterparts were found, which represents 67.3% of the whole LQAC-5 sample. For these common objects, Gaia equatorial coordinates, parallax, proper motion, as well as photometry at the G, GBP, and GRP wavelengths could be added to complete data coming from the ground-based surveys. Readers should notice that Gaia DR2 does not provide the redshift of the objects, whereas it is delivered for 99% of the sample by the LQAC-5 catalogue.
Recently, on 3 December 2020, the Gaia Early Data Release 3 (EDR3) was released, which presents a significant improvement with respect to DR2 both in terms of the quality and quantity of data (Gaia Collaboration 2021a). It contains a full astrometric solution with five basic parameters (α, δ), parallaxes, and bi-dimensional proper motions for around 1.468 billion sources, with a limiting magnitude of G ≈ 21. Taking the advantages of this new EDR3 release into account for this study, we carried out a cross-identification between LQAC-5 and EDR3, which we call LQAC-5+. It contains exactly the same objects as LQAC-5 but it includes the new values coming from EDR3 concerning the celestial coordinates, the parallax, the proper motion components, the G, GBP, and GRP photometry, together with their respective uncertainty.
In this paper, we discuss quasars in LQAC-5+ that are subject to large proper motions in Gaia EDR3. In Sect. 2, we describe the construction of LQAC-5+, along with its general properties, such as photometry, astrometry, and redshifts. In Sect. 3, after giving a general overview of the various astrophysical origins which can give birth to a proper motion of quasars, we select quasars in LQAC5+ showing significant proper motion. Morever we explain how the redshift value enables one to discriminate between extended and point-like objects, and also how we excluded outliers (stars) from colour–colour diagrams in the mid-infrared domain. Lastly, in Sect. 4 we select a list of 41 quasars with a proper motion μ > 10 mas yr−1 which satisfy conditions and we consolidate their status of extra-galactic objects. Finally, we summarize our results in Sect. 5.
2. LQAC-5+ catalogue creation and properties
2.1. Catalogue construction
We matched LQAC-5 to Gaia EDR3 using the CDS Upload X-Match service in TOPCAT, version 4.8 (Taylor 2005). This produces a Gaia counterpart for every LQAC entry within the match tolerance, but the same Gaia counterpart may be matched to multiple LQAC entries (the match is not symmetric), so a second, symmetric match must be carried out for the initial table of Gaia associations. We chose a match tolerance of 1″, producing 416 113 unique matches.
2.2. Photometric properties
Figure 1 shows the magnitude distribution of the 416 113 LQAC-5+ sources with a Gaia EDR3 G magnitude. We find 12 138 quasars with G < 18, 63 802 with G < 19 and 191 129 with G < 20. For comparison, in the original LQAC-5 catalogue, we had 398 300 sources owning a Gaia DR2 G magnitude: 12 381 quasars with G < 18, 63 488 with G < 19, and 187 025 with G < 20.
 |
Fig. 1. Distribution in G-magnitude of the 416 113 quasars in Gaia EDR3 belonging to LQAC-5 (in blue) and of the 398 300 quasars in Gaia DR2 belonging to LQAC-5 (in orange). |
The new numbers could be compared with the Gaia-CRF2 sample for which Mignard et al. (2018) found 27 000, 150 000, and 400 000 sources, respectively, for the intervals considered. As a consequence, the corresponding ratios of our number of sources with respect to Gaia-CRF2 for each interval are 0.45, 0.43, and 0.47, respectively. This demonstrates that the distribution of sources per magnitude interval is a little different. When comparing the feature of the distribution in Fig. 1 with the corresponding one in Mignard et al. (2018), we observed some significant differences. First the convex bump in the interval 19 < G < 19.5 is replaced in Gaia-CRF2 by a concave outline. Moreover the number of quasars recorded significantly increases in the interval 20 < G < 20.8 to reach the maximum of the distribution for 20.6 < G < 20.8, whereas it considerably decreases in the same interval for the CRF2 sample. The explanation for this may be found in the limitation in mid-infrared magnitude of the CRF2 quasars selected through a cross-match with the AllWISE-based AGN catalogue of Secrest et al. (2015), in comparison with the access of the SDSS survey to fainter objects. The cumulative distribution, not shown here, indicates that the number of recorded quasars steadily increases up to G = 21.2, whereas it becomes flat for the Gaia CRF2 population starting from G = 20.2, which is one magnitude brighter.
Another important topic is the completeness and the limitation of the detection of quasars by Gaia with respect to their brightness. This is a strongly varying function of the sky position, owing to the peculiar scanning pattern of Gaia (see, for example, Fig. 1 in Shu et al. 2019). In Fig. 2, we plot the sky distribution of LQAC-5+, showing a clear variation in mean Gaia G as a function of the position. This spatial variation can be greatly reduced, however, by making a cut at G < 20.7 mag, the peak of the distribution of G for the LQAC-5 sample (Fig. 1).
 |
Fig. 2. Aitoff projection, HEALPix map (Górski et al. 2005), Galactic coordinates, of the 416 113 quasars in Gaia EDR3 belonging to LQAC-5. Each sky pixel shows the mean value of Gaia G, demonstrating the variation in depth across the sky. |
We note, however, that LQAC-5 is generally deeper than Gaia, with Sloan r magnitudes and a close-in central wavelength to G (∼620 nm; Riello et al. 2021), extending to ∼23 mag. Interestingly, there is a population of LQAC-5 quasars with Sloan r magnitudes considerably brighter than 20.8 that are nonetheless not recorded in Gaia (Fig. 3). This behaviour is attributable to two factors. First, the Sloan r passband is much narrower than Gaia G, so fainter sources with steep spectral indices may ‘leak’ into and out of the two passbands. Second, the photometry present in the LQAC-5 catalogue was taken at disparate times, not overlapping with Gaia EDR3, so variability causes dispersion between r and G. The percentage of quasars not recognized by EDR3, in Fig. 3 is 42.94%. This large value is in agreement with the statement that a large number of quasars identified by ground-based observations, but not detected by Gaia EDR3, should nevertheless participate in the future in the densification of the CRF by the intermediary of differential astrometry using EDR3 objects as calibrators.
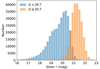 |
Fig. 3. Distribution of Sloan r magnitudes for quasars with Gaia G brighter than the nominal completeness cut for LQAC-5 (in blue); distribution of Sloan r magnitudes for quasars with G fainter than the completeness cut, or not cross-identified with Gaia DR3 (in orange). |
To explore this, we concatenated Sloan r photometry of the LQAC-5 quasars from the SDSS DR12, Pan-STARRS DR1 (Chambers et al. 2016), the Dark Energy Survey DR1 (Abbott et al. 2018), and SkyMapper DR1.1 (Wolf et al. 2018). Where photometry from multiple surveys existed, we calculated the weighted arithmetic mean magnitude for each object, and determined the intrinsic dispersion term σ such that the reduced chi-squared χ2/d.o.f. (where dof stands for degree of freedom) is equal to unity. On average, this is 0.16 mag for r. We then fitted r as a function of G for objects with G < 20.7 and redshifts greater than z ≥ 0.35, the latter cut removing objects with truncated Gaia photometry, as we discuss later. We find:
with a correlation coefficient of 0.95 and an intrinsic dispersion of 0.21 mag, similar to the per-object mean dispersion found above (Fig. 4). There is a small, higher-order variation in the relationship due to the K correction, but redshifts are not available for all objects and the variation is generally minor. An intrinsic dispersion of ∼0.2 mag is in line with expectations for AGN variability, and is sufficient to account for the scatter seen in our photometry. We note that the Gaia magnitudes are on the Vega system, while SDSS magnitudes are ∼ AB1 In performing this regression, the Vega − AB offset was implicitly subsumed in the zeroth order term.
 |
Fig. 4. Normalized distribution of the difference r(G)−r. The value of r is predicted from G minus measured r for LQAC-5 quasars cross-identified with Gaia EDR3, normalized by the formal error added in quadrature to an intrinsic dispersion term, which we find to be σintr. = 0.21 mag, consistent with expectations from AGN variability. The solid black line shows a normal distribution with mean of zero and standard deviation of unity. |
Figure 5 shows the distribution of the Gaia colour index GBP − GRP for the 415 272 EDR3 objects of LQAC-5+ that have a value for both bands. We also plot the distribution of the 370702 objects of DR2. In accordance with Mignard et al. (2018) for the Gaia-CRF2 AGNs, the distribution is rather narrow, with 90% of the sample ranging in the interval 0 < GBP − GRP < 1. We observed the same peak as these last authors, at GBP − GRP = 0.6.
 |
Fig. 5. Distribution of Gaia GBP − GRP for the quasars in EDR3 belonging to LQAC-5 (black), compared to the DR2 set (blue). |
Lastly, it should be noted that one of the great advantages of LQAC-5+ to Gaia cross-identification is to provide the value of the redshift for the near totality of common objects (roughly 99%), whereas this redshift is not given in the Gaia DR3 data itself. When we compare the distribution of the redshift of the LQAC-5-DR3 common objects with respect to the distribution of all the 589 364 quasars with a value of redshift in the LQAC-5, we remark that both distributions are rather equivalent. They are characterized by the presence of two peaks in the intervals 1.6 < z < 1.7 and 2.2 < z < 2.3, which are particularly due to the selection process in SDSS (Pâris et al. 2017). Thus we can assert that the limitation of LQAC-5 objects to the Gaia sub-sample does not significantly affect the distribution of the redshifts at all.
2.3. Astrometric properties
In the same way as Mignard et al. (2018), we investigate in this section the astrometric quality of the sample of 416 113 LQAC-5 quasars cross-identified with Gaia EDR3. This study is based on the formal uncertainties of celestial coordinates as well as of the nominal values and uncertainties of the parallaxes and proper motions given by the EDR3 catalogue.
2.3.1. Positional uncertainties
Our formula to measure the positional uncertainty of the objects is taken from Lindegren et al. (2016), who take the semi-major axis of the dispersion ellipse into account, which was computed from a combination of the standard deviation in α and δ and of a correlation coefficient, namely ρα, δ. It is given by the following straightforward relationship:
where σα⋆ = σαcos δ.
In Fig. 6 we show the distribution of σpos for the whole sample of the 416 113 LQAC-5+ quasars with a EDR3 value for the position and related standard deviations, and for the sub-sample of 63 802 objects with G < 19. We remark that the histograms for both populations are quite similar to the corresponding ones for the Gaia-CRF2 AGNs in Mignard et al. (2018) with peaks corresponding to 0.30 mas and 0.20 mas for both the whole sample and the brighter subset, respectively. It is clear from the histogram that the quality of measurement is neatly improved when limiting to the brighter subset.
 |
Fig. 6. Distribution of the positional uncertainties for the quasars in Gaia EDR3 belonging to LQAC-5 (grey), and with Gaia G < 19 mag (blue). |
2.3.2. Parallaxes
Quasars are very distant objects so they should not exhibit detectable parallaxes. As pointed out by Lindegren et al. (2018) the Gaia DR2 parallaxes had a global zero-point error of −0.029 mas, which must be taken into account because it is not corrected for in the Gaia DR2 data. We study the distribution of the set of 348 540 LQAC-5 quasars with a parallax value available in EDR3. We observed that for objects with an absolute parallax_over_error |π|/σπ of less than 4, the distribution is almost perfectly normal. However, the mean π/σπ = −0.0561 ± 0.0018, with a dispersion of 1.05956, indicates that there is still a highly significant zero-point offset and that the parallax errors are likely underestimated by about 6%. We find a zero-point offset of −0.0196 mas, with a final error correction factor of 1.0590. We show the corrected error-normalized parallaxes in Fig. 7. In the following, the debiased parallax is quoted as 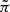 .
.
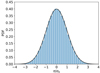 |
Fig. 7. Distribution of the uncertainty-normalized parallaxes |
After making these corrections, we find 71 objects with 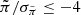 , when the expected number for a normal distribution of 348 540 objects is 11. As negative parallaxes are unphysical, this suggests that about 60 instances of objects with
, when the expected number for a normal distribution of 348 540 objects is 11. As negative parallaxes are unphysical, this suggests that about 60 instances of objects with 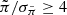 can be considered spurious, if there is no relationship between the sign of the parallax and the probability of spurious values. We find 405 LQAC5+ objects in total with
can be considered spurious, if there is no relationship between the sign of the parallax and the probability of spurious values. We find 405 LQAC5+ objects in total with 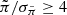 , indicating that 345 out of the 416 113 objects have real parallaxes (i.e., they are stars and not quasars), which corresponds to a contamination rate of 0.08%. In total, there are 476 objects with
, indicating that 345 out of the 416 113 objects have real parallaxes (i.e., they are stars and not quasars), which corresponds to a contamination rate of 0.08%. In total, there are 476 objects with 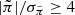 , which we removed from the sample for the proper motion analysis, leaving 348 064 objects with
, which we removed from the sample for the proper motion analysis, leaving 348 064 objects with 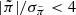 . These objects have
. These objects have 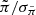 following a normal distribution with a mean of zero and standard deviation of unity, indicating that they are consistent with having been drawn from a population of objects with zero intrinsic parallax.
following a normal distribution with a mean of zero and standard deviation of unity, indicating that they are consistent with having been drawn from a population of objects with zero intrinsic parallax.
2.3.3. Proper motions
According to a well established postulate that is discussed in the next section, the proper motions μ of our sub-sample of the 348 064 LQAC-5+ quasars with available Gaia EDR3 proper motions should have intrinsic values equal to zero at the sub-mas level of precision. Before confronting this postulate with our data, we repeated the significance analysis performed in Sect. 2.3.2, finding zero-point offsets of +0.00204 mas yr−1 in right ascension (α cos δ) and −0.00017 in declination (δ), with a standard error of the mean of 0.00170 mas yr−1, indicating that these offsets are not significant. The error correction factors are 1.0456 for right ascension and 1.0519 for declination (underestimated formal uncertainties of about 5%). This is about half of the Gaia DR2-based finding of Mignard et al. (2018), who found a comparable Gaussian distribution for their set of AGNs with a zero mean and standard deviations of 1.09 in right ascension and 1.11 in declination. In Fig. 8, we show the distribution of corrected, error-normalized proper motion in right ascension.
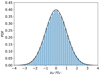 |
Fig. 8. Distribution of the normalized proper motion μα⋆ of the quasars in Gaia EDR3 belonging to LQAC-5. The black line is a Gaussian with zero mean and unity standard deviation. |
With corrected proper motion errors in α⋆ = α cos δ and δ, the joint significance of the total proper motion is expressed as follows:
For random errors in proper motion, the square-root of this expression is Rayleigh-distributed with σ = 1, and indeed this is the case for LQAC-5 objects with χμ < 4 (Fig. 9), where we plotted χμ with ρ = 0.
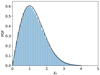 |
Fig. 9. Distribution of the normalized total proper motion χμ of the quasars in Gaia EDR3 belonging to the LQAC-5 with χμ < 5. The black line denotes a Rayleigh distribution with σ = 1. |
3. Selection of quasars with large values of proper motion
In this section, after enumerating and explaining the various possible phenomena leading to a significant proper motion of quasars, we concentrate our study on the topic of the resolution of the objects. In particular, we show how colour–colour diagrams enable one to avoid stellar contamination in our selection.
3.1. About the possible origins of proper motions of quasars
Quasars are located at cosmological distances and are characterized by extremely compact and bright emission, so that they are expected to show negligible transverse motion. For example, a quasar at z = 1 with a transverse motion of 100 km s−1 has a proper motion of ∼10 nanoarcsec yr−1 which is several orders of magnitude below the limits of current technology (i.e., Gaia). Nevertheless, recent observations as well as theoretical studies related to AGNs indicate that large-scale modifications in the accretion disk and the dusty torus surrounding the central black hole can cause shifts of the photocentre (Bachchan et al. 2016). Titov et al. (2010) noted additional causes of apparent proper motions in AGNs. They were studied in some detail by Bachchan et al. (2016) who presented them sequentially. Among them, the acceleration of the solar system assumed to be towards the Galactic centre leads to patterns of proper motion, as it has been shown by Gaia Collaboration (2021b). Primordial gravitational waves can produce systematic proper motions over the sky as well. Another cause can be a temporal shift of the angular separation of distant sources related to an anisotropic expansion of the Universe. Additionally, a peculiar proper motion might be due to the transverse acceleration produced by the local gravitational field surrounding the quasar. Finally, weak microlensing could induce apparent proper motions. Nevertheless, the expected amplitude of all these motions as listed by Bachchan et al. (2016) and taken separately is considerably small, that is to say of the order of 1 to 10 μas yr−1 or less. In comparison, Perryman et al. (2014) mention that the most important effect on quasar apparent proper motions should be by far the optical photo-centric motion, related to instabilities in the internal structure of the AGN, which should lead to typical variability of 60 μas but up to 100 μas in some cases, as was suggested by Taris et al. (2011). Simulations confirm the value of 100 μas, in a typical timescale of 3–15 years, with a peak at 6–9 years (Smith et al. 1993; Taris et al. 2011).
A natural explanation for apparent proper motion in quasars is that Gaia is detecting superluminal motion or differential brightening in the jets of distant AGNs. We briefly explore this scenario here. The FIRST survey helpfully includes an RMS coverage map for both the northern and southern sky portions, which we used to restrict to LQAC-5+ objects with valid FIRST observations. We then calculated the fraction of proper motion objects with FIRST detections and compared it to a set of matched controls. The controls are LQAC-5+ without significant proper motions that are matched to within 0.1 mag in Gaia G and 0.1 in redshift, requiring ten controls per proper motion object. By doing this, the sample and control distributions of Gaia G and redshift are consistent with K-S test p-values of approximatively unity. This rules out preferential detection based on object brightness or distance. We find no statistically significant difference (p-value = 0.37) between the FIRST detection rate of the proper motion objects and their controls, with an overall FIRST detection rate of 10%. This indicates that radio jet activity is not likely to be a major contributing factor to apparent proper motions in quasars.
Lastly, the variability of quasars’ brightness reveals astrophysical processes that could modify the inner structure of these objects. These modifications could have an impact onto the position and motion of the photocentre (Popovic et al. 2012). Indeed, the variability of quasars is regarded as a stochastic process (e.g. Kelly et al. 2009) which is well described by a random-walk-phase noise model (Markov chain process). In the optical domain, all AGNs are variable at different magnitudes and timescales. These flux variations reveal astrophysical processes as shocks in the jet, dust clouds, instabilities in the accretion disk, stellar activity close to the core, and the presence of super massive binary black holes. Some AGNs also exhibit periodic or pseudo-periodic flux variations (due, for example, to a prominent hot spot on anaccretion disk). Blazars are a sub-class of radio-loud AGNs with relativistic jets pointing at small angles to the line of sight. Their rapid variability is detected on a timescale down to hours or even minutes, characterizing an intra-day variability (IDV) but also on short (days to weeks) or long (month to several years) timescales. For example, the long term R magnitude variability of PKS0537−441 (BL Lac) shows an amplitude of 3 mag. in less than one year (Sandrinelli et al. 2014). Periodic oscillations of 15 mn in the optical light curve of the BL Lac S5 0716+714 were reported by Rani et al. (2010). They could be due to the action of turbulence behind a shock in the relativistic jet. Another sub-class of AGNs are the radio-Loud quasars (RLQs). They constitute roughly 10% of the total of the QSOs, and in consequence the remaining 90% are classified as radio-quiet quasars (RQQs). Gu & Ai (2012) studied the optical variability of a sample of 62 RLQs in the SDSS stripe 82 region. Multi-epoch data covering nine years was used. Variabilities were clearly detected in each source with an amplitude in r band, from 0.18 to 3.46 mag. Radio-loud AGNs are then highly variable objects at all timescales.
3.2. Primary selection of candidates with large proper motion
Even with the careful consideration of the statistical properties of LQAC-5+ astrometry, picking out quasars with legitimate apparent proper motions is nonetheless challenging, as the a priori chance of a quasar having an apparent proper motion can be assumed to be extremely small, so quasars with apparent proper motions must be carefully vetted. For example, while in general the purity of LQAC-5+ is extremely high in that the vast majority of objects are indeed AGNs and quasars, selecting on proper motion may preferentially select the otherwise negligible fraction of stellar contaminants misidentified as quasars.
With the astrometric properties of the LQAC-5+ catalogue understood and corrected for underestimated errors, we are in a position to search for quasars with apparent proper motions. As the parallaxes of LQAC-5+ quasars are normally distributed below a (corrected) absolute parallax_over_error < 4, we required this as an initial cut to remove likely stellar contaminants. This removed 476 out of the 348 507 quasars with a parallax value (0.14%). As the normalized total proper motion χ follows the expected Rayleigh distribution below a value of ∼4 (Fig. 9), we conservatively required χμ ≥ 5, which selected 937 objects (0.27%). For that purpose, χμ was calculated according to (3) by neglecting correlation (ρ = 0). We show the distribution of normalized proper motions in α and δ in Fig. 10. We found several systematic issues, which we explore in the following subsections.
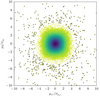 |
Fig. 10. Distribution of the proper motion significance values for LQAC-5/EDR3 matches (Sect. 3), with |
3.3. Resolved objects
While producing generally exquisite astrometry for the vast majority of objects, Gaia is nonetheless optimized only for compact and unresolved objects. Extended objects that fill the scanning window exhibit additional astrometric variance not accounted for in the formal catalogue errors. To demonstrate this, we matched the LQAC-5+ Gaia EDR3 coordinates to the specObj table for SDSS DR162 within 1″, using only spectra with ZWARNING==0 or ZWARNING==43 where a value of 0 indicates no known issues and a value of 4 may be present when broad lines are present in the spectrum, as is typical of quasars. This yields spectra for 377 175 of 416 113 objects (91%). Interestingly, however, only 300 out of the 937 proper motion objects were matched (32%).
To understand this, we explored the membership of the 937 proper motion objects to the original quasar catalogues that comprise LQAC-5. We tabulate this information in Table 1. There are significant (p < 0.05) differences between source catalogue membership for objects with apparent proper motions, versus their parent sample, for all catalogues except 2QZ (Croom et al. 2004) and FIRST (White et al. 1997). Generally, proper motion objects are over-represented in all input catalogues except for SDSS (from which 92% of the parent sample is derived) and 2dF-SDSS, for which they are under-represented. As the latter two are optical spectroscopy-based catalogues, while the other catalogues are heavily weighted to radio AGNs, this suggests that radio AGNs make up the majority of objects with apparent proper motions.
LQAC-5 source quasar catalogue membership of the 937 objects with apparent proper motions versus the parent sample of 348 031 objects.
While this might suggest a radio jet origin of proper motion, radio AGNs are also predominantly found in large elliptical galaxies, which are preferentially detected at a lower redshift owing to the relative faintness of the stellar emission compared to the accretion emission of a bolometrically dominant quasar. Large elliptical galaxies tend to fill Gaia’s scanning window, leading to under-photometered objects and likely degraded astrometric performance. In Fig. 11, we show the ‘total’ G minus measured G versus redshift for the objects with proper motions and their parent sample, where the ‘total’ G was estimated using the Kron or Petrosian r magnitude and inverting Eq. (1). Below a redshift of ∼0.35, the measured G is systematically and often dramatically fainter than the total, raising concerns about the accuracy of the astrometry for these objects. Indeed, while only 4.3% of the full parent sample is below a redshift of 0.35, this is the case for 29% of the 875 objects with a proper motion and measured redshift. We therefore require that our sample of proper motion objects have redshifts greater than 0.35, producing 619 objects.
 |
Fig. 11. Total G minus measured G versus redshift, where the total G was estimated using the Kron or Petrosian r magnitude and inverting Eq. (1). Gaia clearly under-photometers galaxies in the local Universe, making it likely that the astrometric performance is degraded for these objects. The vertical line is at a redshift cut of 0.35. |
3.4. Filtering of quasars with large proper motions from colour–colour diagrams
In contrast with all the small amplitudes of proper motions expected due to various effects mentioned in Sect. 3.1, our cross-identification between LQAC-5 and Gaia EDR3 leads to a significant number of objects with μ > 10 mas yr−1, as shown in Fig. 12. There is a correlation between the number of objects with these large proper motion values regardless of wether or not they have WISE photometry, and whether or not their WISE photometry is consistent with a bolometrically luminous AGN (w1 − w2 ≥ 0.5) or more stellar-like mid-IR emission (w1 − w2 < 0.5). We found that of the 619 objects with significant proper motions, only 399 of them have AllWISE photometry (64%). This is significantly less than the overall number of LQAC-5 objects with AllWISE photometry (82%), and this warrants an explanation.
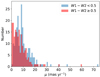 |
Fig. 12. Distribution of total proper motions of the initial sample of 399 quasars above a redshift of z > 0.35 identified by WISE, with significant apparent proper motions. |
We cross-matched the proper motion sample to the SDSS specObj table for DR16 using a tolerance of 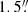 We classified spectra as stars if the CLASS value is ‘STAR’ and the difference between the best-fit reduced
We classified spectra as stars if the CLASS value is ‘STAR’ and the difference between the best-fit reduced 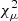 and next best-fit reduced χ2RCHI2DIFF is at least 0.1. We classified spectra with RCHI2DIFF less than 0.1 as ambiguous. These spectra can be either very low signal-to-noise, blazars with featureless power-law spectra, or very early-type stellar contaminants. We find that of the 131 objects with WISE data, 18 (14%) are classified as stars, while 42 (32%) are ambiguous. Of the 45 objects without WISE, three (7%) are classified as stars while 38 (84%) are classified as ambiguous. The apparently higher fraction of stars in the objects with WISE photometry is therefore likely due to the higher overall signal-to-noise of the SDSS spectra. Despite objects with stellar-like mid-IR colour (w1 − w2 < 0.5) comprising 31% of the objects with WISE data, they make up half of the objects with star spectral classifications, suggesting that it is worthwhile to require AGN-like mid-IR color to reduce the frequency of stellar contaminants in the proper motion sample. For the objects without WISE photometry, we do not have enough information to be certain as to their nature, so we decided to leave them out of the sample from here on out.
and next best-fit reduced χ2RCHI2DIFF is at least 0.1. We classified spectra with RCHI2DIFF less than 0.1 as ambiguous. These spectra can be either very low signal-to-noise, blazars with featureless power-law spectra, or very early-type stellar contaminants. We find that of the 131 objects with WISE data, 18 (14%) are classified as stars, while 42 (32%) are ambiguous. Of the 45 objects without WISE, three (7%) are classified as stars while 38 (84%) are classified as ambiguous. The apparently higher fraction of stars in the objects with WISE photometry is therefore likely due to the higher overall signal-to-noise of the SDSS spectra. Despite objects with stellar-like mid-IR colour (w1 − w2 < 0.5) comprising 31% of the objects with WISE data, they make up half of the objects with star spectral classifications, suggesting that it is worthwhile to require AGN-like mid-IR color to reduce the frequency of stellar contaminants in the proper motion sample. For the objects without WISE photometry, we do not have enough information to be certain as to their nature, so we decided to leave them out of the sample from here on out.
Many WISE AGN selection criteria can be found in the literature, some of them being based on WISE one colour criterion (Stern et al. 2012) or two-colour criteria (Jarrett et al. 2011). More recently, Secrest et al. (2015) used a two-colour criteria for the identification of 1.4 million AGNs when using the mid-infrared WISE data. Their algorithm was very efficient, because they tested the AGN selection criteria against a large sample of optically identified stars and found that the probability of a star being detected as a quasar is smaller than 4.0 × 10−5.
Fortunately, LQAC-5+ already contains cross-identifications of objects with the WISE catalogue, when available. Therefore it is possible to use the same method of quasar versus star discrimination as Secrest et al. (2015). It is based on the work of Mateos et al. (2012) consisting of defining an IR selection of luminous AGNs using the Bright Ultrahard XMM-Newton survey as a starting point. Thus we used the w1, w2 and w3 mid-infrared magnitudes of the WISE survey, with wavelengths at 3.4 μm, 4.6 μm and 12 μm respectively, in order to exhibit the colour–colour diagram w1 − w2 versus w2 − w3 in Fig. 13. We plotted two samples separately. One concerns 61914 LQAC-5+ objects cross-identified with WISE verifying the two following constraints : μ < 0.5 mas yr−1 and χμ < 1, which means that they can be considered as reliable fixed objects with respect to the ICRF3. At the other extremity, we plotted the 239 objects of LQAC5+ crossed with WISE verifying μ > 10 mas yr−1 and χμ > 5, which means that they show a significant proper motion at more than the 99% confidence level. For the first sample, we expectedly found the same kind of configuration as Secrest et al. (2015) when using LQAC-2 (Souchay et al. 2012). As explained in Secrest et al. (2015) most extragalactic sources that do not meet the selection criteria materialized by the dense central zone are bluer in their w1 − w2 colours, which can be explained by two effects. One is the existence of objects with rather low AGN/host galaxy luminosities ratios. The other one concerns quasars with high redshifts (z > 2) for which the spectral energy distribution (SED) of even pure AGNs begins to move out of the mid-UR colour–colour space defined by the selection criterion. For the second limited sample of 239 objects, we noticed two kinds of populations : one with w1 − w2 < 0.5 is neatly out of the criterion and has a high probability of containing a majority of stars. On the other hand, a large majority of objects of the complementary zone with w1 − w2 > 0.5 satisfy the criterion pf being a quasar.
 |
Fig. 13. Colour–colour diagram w1 − w2 versus w2 − w3 for LQAC-5+ objects with μ > 10 mas yr−1 and χμ ≥ 5. The rectangular zone delimited in red corresponds to 0.5 < w1 − w2 < 1.6 and 2.1 < w2 − w3 < 4.2. |
4. A final set of quasars with very large proper motions
To go deeper in our selection, we isolated what we call a ‘quasar zone’ characterized by 0.5 < w1 − w2 < 1.6 and 2.1 < w2 − w3 < 4.2 which corresponds, more or less, to the highest probability for an object to be a quasar. Moreover, we selected two additional zones neatly separated from the central dense cloud. One is located on the left of the diagram and is characterized by w2 − w3 < 2.0 and w1 − w2 < 0.3. Another is located on the right and is characterized by w2 − w3 > 3.6 and w1 − w2 < −0.1. A priori these two zones should contain a high proportion of stellar contaminants. In order to assert or invalidate this hypothesis we can rely on the EDR3 determination of the parallax of the objects in the three given zones. In Fig. 14 we show that the left zone is characterized in a big proportion by relatively large values of the parallax π accompanied by a large value of π/σπ. Therefore it is clear that the corresponding objects are stellar contaminants and should be deleted from the LQAC5 catalogue. By contrast, and as this could be expected, the quasar zone is characterized by relatively small parallax values, in comparison with their respective uncertainty, which insures their status as extragalactic candidates. Lastly, the objects from the right zone are questionable, because of their relative large distance from the quasar zone and their relatively small parallax value.
 |
Fig. 14. Parallax π of the objects with μ > 10 mas yr−1 and χμ > 5 selected in Fig. 13, with respect to their uncertainty σπ. The red circles correspond to the objects of the quasar zone, whereas black squares and blue triangles correspond to the left and right zones of Fig. 13, respectively. The full and dashed lines delimit the areas with |π|/σπ < 1 and |π|/σπ < 2, respectively. |
Finally we present our final selection of 41 quasars with large values of proper motion in Table A.1. They all follow the set of hard constraints already explored above, that is to say:
-
μ > 10 mas yr−1
-
χμ > 5
-
π/σπ < 4
-
0.5 < w1 − w2 < 1.6 and 2.1 < w2 − w3 < 4.2.
It is important to notice that inside Table A.1 we find for each quasar the value of two important parameters coming from the EDR3 data. The first one is the ASTROMETRIC − GOF − AL, named P1 for the sake of simplicity, which represents the goodness of fit statistic of the model with respect to along-scan obervations. For good fits it should follow a normal distribution with zero mean value and unit standard deviation. A value exceeding 3 indicates a rather bad fit. The second parameter, called P2, represents the ASTROMETRIC − EXCESS − NOISE. A small value of 0 signifies that the residuals of the fit statistically agree with the assumed observational noise.
Several important remarks can be given in view of Table A.1. First, only two objects have a redshift smaller than z = 0.35, which corresponds to the threshold under which objects seem to be resolvable, according to the discussion in Sect. 3.3. Nevertheless their value is very close to this conventional threshold. So we can conclude that most of the objects are expected to be really point-like. Second, eight quasars have a proper motion μ larger than 20 mas yr−1, and all of those have a ratio μ/σμ > 13. Third, only four objects have a Gaia magnitude larger than G = 20.5, and the only four other objects satisfy the condition 20.0 < G < 20.5, which makes the sample statistically relatively bright, in comparison with the global LQAC5+ histogram of G in Fig. 2, where the large majority of quasars are found in the interval 20.0 < G < 21.0.
Furthermore, we carried out a specific test to evaluate the coherence between the values of proper motion given by Gaia EDR3 with respect to the Gaia DR2 releases for the quasars selected in Table A.1. The results are shown in Fig. 15. We would like to point out a relatively good agreement within 1mas yr−1 with the exception of a few objects for which the difference can reach a few mas yr−1. In Fig. 16 we show the correspondence between the uncertainty σμ as given by the two catalogues. The improvement of EDR3 with respect to the DR2 in the quality of determination appears clearly, with globally a factor 2 improvement.
 |
Fig. 15. Gaia EDR3 value of the proper motion μ of the quasars with μ > 10 mas yr−1 with respect to the value given by Gaia DR2. |
 |
Fig. 16. Gaia EDR3 value of the proper motion uncertainty σμ of the quasars with μ > 10 mas yr−1 with respect to the value given by Gaia DR2. The σμ was computed as the quadrature sum of the uncertainties in μα⋆ and μδ. |
A visual inspection from a ground-based survey represents an ultimate check of the 41 selected objects. We show 34 out of the 41 objects with Pan-STARRS data in Fig. 17. We remark that although a majority of candidates present a round and compact feature, 11 among them, that is roughly one-third of the sample, are surrounded by a second companion object, likely a star located in the same line of sight. Therefore, there is a high probability of the centroid of the quasar being displaced by the companion, whose proper motion should affect the determination of that of the quasar.
 |
Fig. 17. Pan-STARRS giy images of our final selection of quasars exhibiting proper motion. Each cutout is 12″ × 12″ and in the standard orientation (north is up, and east is to the left). The RA and Dec given are the Gaia EDR3 coordinates. |
In addition, we carried out a more precise and systematic analysis by searching for each of the selected objects a companion in EDR3 data, within a radius of 1″. We found six cases of binary objects, with angular distances ranging from between 0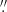 42 and 0
42 and 0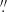 99.
99.
As examples of apparently isolated, relatively bright and compact objects we can mention [13.11195; 0.59409] and [36.85004; −1.10657] with values of G = 18.14 and G = 18.74, respectively, and a proper motion of μ = 22.407 mas yr−1 and μ = 27.598 mas yr−1, respectively. Similarly, the two brightest objects of the list, with magnitudes smaller than G = 18, that is to say G = 16.42 and G = 17.91, respectively, have good astrometric characteristics, with π/σπ < 1, μ/σμ > 10, as well as round-like and compact corresponding images.
On the other hand, the object named [227.89642; 49.99957] with the largest value of μ = 59.035 mas yr−1 is one of the six binary objects detected above. It shows a low signal/noise ratio, a somewhat ambiguous SDSS spectrum, and it is flagged by the SDSS pipeline as being a K7 star, despite broad features being present. The angular distance between the two components belonging to EDR3 is 0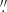 845. The probable quasar is the bluish object in the south-eastern direction from the central selected one, which is also established by EDR3, with a magnitude G = 20.78, but it has neither a parallax, nor a proper motion value.
845. The probable quasar is the bluish object in the south-eastern direction from the central selected one, which is also established by EDR3, with a magnitude G = 20.78, but it has neither a parallax, nor a proper motion value.
The object named [321.83456; −11,81565], with a magnitude G = 20.31, has the second largest proper motion of μ = 40.702 mas yr−1. In the Pan-STARRS image, we found another EDR3 source with a closer separation from the AllWISE source (0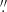 77) than for the selected one (1
77) than for the selected one (1 88) It has a magnitude G = 19.80, a parallax value π = −1.00, and a proper motion value μ = 0.485 mas yr−1. It is very likely that this second object is the quasar, corresponding to the bluer object at the botton left in the Pan-STARRS image. It is important to notice that there is a high probability that the mismatch originates from the poor astrometric quality of the Hewitt & Burbidge (1993) catalogue from which the quasar was picked up in LQAC-5: this is explained in the following.
88) It has a magnitude G = 19.80, a parallax value π = −1.00, and a proper motion value μ = 0.485 mas yr−1. It is very likely that this second object is the quasar, corresponding to the bluer object at the botton left in the Pan-STARRS image. It is important to notice that there is a high probability that the mismatch originates from the poor astrometric quality of the Hewitt & Burbidge (1993) catalogue from which the quasar was picked up in LQAC-5: this is explained in the following.
The object named [145.03068; 33.76924] with a magnitude G = 19.71 has the third largest proper motion of μ = 28.13 mas yr−1. The nearest AllWISE-AGN source source is at separation 0 42. Again, there is another EDR3 source at a 0
42. Again, there is another EDR3 source at a 0 712 angular distance, closer (0
712 angular distance, closer (0 29) to the AllWISE counterpart. It has G = 19.59 with a parallax 5.95 mas and a proper motion μ = 32.76 mas yr−1. The SDSS spectrum is unambiguously a quasar, so that there is a probability that the object is in fact a dual AGN.
29) to the AllWISE counterpart. It has G = 19.59 with a parallax 5.95 mas and a proper motion μ = 32.76 mas yr−1. The SDSS spectrum is unambiguously a quasar, so that there is a probability that the object is in fact a dual AGN.
Moreover, the astrometric quality of the quasar catalogue from which each of the 41 sources was selected and inserted in LQAC-5 appears to be a crucial point to avoid a mismatch. In total we found five catalogues, all of which are flagged with a symbol in Table A.1. Furthermore, 25 objects were taken form SDSS (Pâris et al. 2018); 11 of them were taken from Hewitt & Burbidge (1993); two of them were taken from the 2dF survey (Croom et al. 2004); two were taken from Véron-Cetty & Véron (2010); and one was in the VLBA database. Indeed, the astrometric uncertainty of the SDSS and 2dF surveys is much better than 1″, which is the adopted value of the search radius for cross-identification in LQAC-5. It is typically 0 05 in right ascension and in declination, as it can be seen in Fig. 8 of Souchay et al. (2009). On the other hand, the same figure shows that the positional uncertainty for the catalogue of Hewitt & Burbidge (1993) is comparatively very large, at the level of ±2″. This can be the cause of mismatches. Therefore we can conclude that the objects which come from SDSS and 2dF have a very small probability of being subject to mismatch, which is not the case of the objects coming from Hewitt & Burbidge (1993).
05 in right ascension and in declination, as it can be seen in Fig. 8 of Souchay et al. (2009). On the other hand, the same figure shows that the positional uncertainty for the catalogue of Hewitt & Burbidge (1993) is comparatively very large, at the level of ±2″. This can be the cause of mismatches. Therefore we can conclude that the objects which come from SDSS and 2dF have a very small probability of being subject to mismatch, which is not the case of the objects coming from Hewitt & Burbidge (1993).
This analysis clearly indicates that for each of the 41 selected sources, a complementary check is necessary, before asserting the reality of the quasars’ proper motions presented in Table A.1. In other words, a dedicated individual campaign of observations should be of primary interest to validate the existence of a real displacement of these point-like extra-galactic sources. In particular, for the six cases of binary objects found in EDR3, there is a high probability that the displacement is either due to a mismatch between the two objects, one being a quasar and the other being a star, or to the deterioration of the quasar’s proper motion as a result of the presence of the neighbouring star. For the other cases, we can involve a shift in the photocentre between the host galaxy and the variable nucleus. An appropriate observational programme involving differential astrometry, for instance with techniques of interferometry, could clarify the case.
5. Summary and conclusion
In this paper we have constructed an improved version of the LQAC5 catalogue (Souchay et al. 2019), which we called LQAC5+, by matching its total sample of 592 809 quasars with the Gaia EDR3 catalogue (Brown et al. 2018) This process, with a search radius of 1″, led to 416 113 cross-matched objects, which correspond to 70.2% of the totality. A lack of cross-matches in the vast majority involve objects too faint to be detected by the satellite, whose magnitude threshold is G = 21. This raises the opportunity in the future to carry out differential astrometric reductions in order to densify the optical reference system by taking, as calibrators, the Gaia EDR3 or upcoming DR3 objects, from which we could determine the celestial coordinates of the quasars not identified by Gaia. We have subsequently performed the analysis of the distributions of the astrometric parameters of the global set of common LQAC5+-EDR3 cross-matched objects. In particular we have shown that the normalized distributions of both parallaxes and proper motions follow a normal law, in conformity with the results obtained by Mignard et al. (2018) when constructing the Gaia CRF2 from a sample of 566 869 objects either coming from the ICRF3 (Charlot et al. 2020) or from the AGNs identified by Secrest et al. (2015). Furthermore we noticed a very similar distribution of the colour index GBP − GRP, characterized by a narrow feature, with 90% of the sample in the interval 0 < GBP − GRP < 1.
Then we directed our study towards objects with large proper motions. For that purpose, we found 937 objects satisfying the double condition χμ > 5 and |π|/σπ < 4. Moreover we have analysed, when avaiable, the difference between the integrated G magnitude calculated from SDSS spectra and the Gaia G magnitude. We arrived at the significant conclusion that this difference is particularly large when the redshift is below the value z = 0.35 and it disappears above this value. We conclude that this redshift threshold probably separates the resolved objects from the point-like ones, which are a priori less subject to proper motion uncertainty.
Lastly, we established a mid-infrared colour–colour diagramm w1 − w2 with respect to w2 − w3 coming from the WISE experiment to eliminate stellar contamination and to adopt a specific central rectangular zone, characterized in particular by w1 − w2 > 0.5, where the status of an object as a quasar is manifest. Finally we could isolate a sample of 41 quasars satisfying constraints previously mentioned concerning their parallax and with a proper motion larger than 10 mas yr−1. For six cases, we found an EDR3 companion within 1″, which should explain the abnormal value of proper motion as determined by EDR3. For the other candidates,as given the postulate that quasars are quasi-inertial objects with a priori proper motions of the order of 1 to 10 μas yr−1, the large value above can be considered as very unusual. This could bring new insight on the physical properties of the objects involved. That fact encourages one to conduct specific observational campaigns possibly based on past data to confirm the reality of the relatively large proper motions detected.
Acknowledgments
The authors are very grateful to the anonymous reviewer who made a deep and complete analysis of this paper with very judicious suggestions. The authors used TOPCAT (Taylor 2005) and Astropy (Astropy Collaboration 2013; Abbott et al. 2018) throughout this work. This research made use of APLpy, an open-source plotting package for Python (Robitaille & Bressert 2012). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. The Pan-STARRS1 Surveys (PS1) and the PS1 public science archive have been made possible through contributions by the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, the Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration under Grant No. NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation Grant No. AST-1238877, the University of Maryland, Eotvos Lorand University (ELTE), the Los Alamos National Laboratory, and the Gordon and Betty Moore Foundation. The national facility capability for SkyMapper has been funded through ARC LIEF grant LE130100104 from the Australian Research Council, awarded to the University of Sydney, the Australian National University, Swinburne University of Technology, the University of Queensland, the University of Western Australia, the University of Melbourne, Curtin University of Technology, Monash University and the Australian Astronomical Observatory. SkyMapper is owned and operated by The Australian National University’s Research School of Astronomy and Astrophysics. The survey data were processed and provided by the SkyMapper Team at ANU. The SkyMapper node of the All-Sky Virtual Observatory (ASVO) is hosted at the National Computational Infrastructure (NCI). Development and support of the SkyMapper node of the ASVO has been funded in part by Astronomy Australia Limited (AAL) and the Australian Government through the Commonwealth’s Education Investment Fund (EIF) and National Collaborative Research Infrastructure Strategy (NCRIS), particularly the National eResearch Collaboration Tools and Resources (NeCTAR) and the Australian National Data Service Projects (ANDS). Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High Performance Computing at the University of Utah. The SDSS website is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, Center for Astrophysics | Harvard & Smithsonian, the Chilean Participation Group, the French Participation Group, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatório Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
References
- Abbott, T. M. C., Abdalla, F. B., Allam, S., et al. 2018, ApJS, 239, 18 [Google Scholar]
- Andrei, A. H., Souchay, J., Zacharias, N., et al. 2009, A&A, 505, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arias, E. F., Charlot, P., Feissel, M., & Lestrade, J.-F. 1995, A&A, 303, 604 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bachchan, R. K., Hobbs, D., & Lindegren, L. 2016, A&A, 589, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beasley, A. J., Gordon, D., Peck, A. B., et al. 2002, ApJS, 141, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A. G. A., Vallenari, A., Prusti, T., et al. 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, A. G. A., Vallenari, A., Prusti, T., et al. 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, P., Jacobs, C. S., Gordon, D., et al. 2020, A&A, 644, A159 [EDP Sciences] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Croom, S. M., Smith, R. J., Boyle, B. J., et al. 2004, MNRAS, 349, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- da Ångela, J., Shanks, T., Croom, S. M., et al. 2008, MNRAS, 383, 565 [Google Scholar]
- Fomalont, E. B., Petrov, L., MacMillan, D. S., et al. 2003, AJ, 126, 2562 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2021a, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Klioner, S. A., et al.) 2021b, A&A, 649, A9 [EDP Sciences] [Google Scholar]
- Gattano, C., Andrei, A. H., Coelho, B., et al. 2018, A&A, 614, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
- Gu, M., & Ai, Y. L. 2012, Proc. Int. Astron. Union, 8, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Hewitt, A., & Burbidge, G. 1993, ApJS, 87, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [Google Scholar]
- Kelly, B. C., Bechtold, J., & Siemiginowska, A. 2009, ApJ, 698, 895 [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernandez, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ma, C., Arias, E. F., Bianco, G., et al. 2009, IERS Techn. Note, 35, 1 [NASA ADS] [Google Scholar]
- Mateos, S., Alonso-Herrero, A., Carrera, F. J., et al. 2012, MNRAS, 426, 3271 [Google Scholar]
- Mignard, F., Klioner, S. A., Lindegren, L., et al. 2018, A&A, 616, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Ross, N. P., et al. 2017, A&A, 597, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, E., et al. 2018, A&A, 613, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patnaik, A. R., Browne, I. W. A., Wilkinson, P. N., et al. 1992, MNRAS, 254, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M., Spergel, D. N., & Lindegren, L. 2014, ApJ, 789, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Petrov, L., Kovalev, Y. Y., Fomalont, E., et al. 2005, AJ, 129, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Petrov, L., Kovalev, Y. Y., Fomalont, E. B., et al. 2006, AJ, 131, 1872 [NASA ADS] [CrossRef] [Google Scholar]
- Popovic, L. C., Jovanovic, P., Stalevski, M., et al. 2012, A&A, 538, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prusti, T., de Bruijne, J. H. J., Brown, A. G. A., et al. 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, B., Gupta, A. C., Joshi, U. C., Ganesh, S., & Wiita, P. J. 2010, ApJ, 719, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, Astrophysics Source Code Library [record ascl:1208.017] [Google Scholar]
- Sandrinelli, A., Covino, S., & Treves, A. 2014, A&A, 562, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Secrest, N. J., Dudik, R. P., Dorland, B. N., et al. 2015, ApJ, 221, 12 [NASA ADS] [Google Scholar]
- Shu, Y., Koposov, S. E., Evans, N. W., et al. 2019, MNRAS, 489, 4741 [Google Scholar]
- Smith, A. G., Nair, A. D., Leacock, R. J., & Clements, S. D. 1993, AJ, 105, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Souchay, J., Andrei, A. H., Barache, C., et al. 2009, A&A, 494, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Souchay, J., Andrei, A. H., Barache, C., et al. 2012, A&A, 537, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Souchay, J., Andrei, A. H., Barache, C., et al. 2015, A&A, 583, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Souchay, J., Gattano, C., Andrei, A. H., et al. 2019, A&A, 624, A145 [EDP Sciences] [Google Scholar]
- Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 30 [Google Scholar]
- Taris, F., Souchay, J., Andrei, A. H., et al. 2011, A&A, 526, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, M. B. 2005, Astronomical Data Analysis Software and Systems XIV, 347, 29 [NASA ADS] [Google Scholar]
- Titov, O. 2010, in Sixth International VLBI Service for Geodesy and Astronomy, eds. R. Navarro, S. Rogstad, C. E. Goodhart, et al., Proc. 2010 General Meeting, 60 [Google Scholar]
- Véron-Cetty, M.-P., & Véron, P. 2010, A&A, 518, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. L., Becker, R. H., Helfand, D. J., et al. 1997, ApJ, 475, 479 [Google Scholar]
- Wolf, C., Onken, C. A., Luvaul, L. C., et al. 2018, PASA, 35, e010 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
Appendix A: Additional table
Sample of the 41 LQAC-5 quasars selected from Gaia EDR3 data with μ > 10 mas yr−1, χμ > 5, π/σπ < 4 and located in the quasars central zone (see text). π stands for the parallax, μ for the total proper motion. z is the redshift, and N the number of observations in EDR3. P1 and P2 stand respectively for the ASTROMETRIC-GOF-AL parameter and the ASTROMETRIC-EXCESS-NOISE parameter in the Gaia EDR3 release. The symbols for the cross-identifications are : ⋄ for (Hewitt and Burbridge, 1993); ⋆ for SDSS (Pâris et al., 2018); ⊔ for (Véron and Véron, 2010); ∓ for 2QZ (Croom et al., 2004); • for VLBA. The “double” column gives the angular separation of any secondary Gaia sources than 1″. The last column indicates the angular distance between the 6 detected EDR3 binary commponents (see text).
All Tables
LQAC-5 source quasar catalogue membership of the 937 objects with apparent proper motions versus the parent sample of 348 031 objects.
Sample of the 41 LQAC-5 quasars selected from Gaia EDR3 data with μ > 10 mas yr−1, χμ > 5, π/σπ < 4 and located in the quasars central zone (see text). π stands for the parallax, μ for the total proper motion. z is the redshift, and N the number of observations in EDR3. P1 and P2 stand respectively for the ASTROMETRIC-GOF-AL parameter and the ASTROMETRIC-EXCESS-NOISE parameter in the Gaia EDR3 release. The symbols for the cross-identifications are : ⋄ for (Hewitt and Burbridge, 1993); ⋆ for SDSS (Pâris et al., 2018); ⊔ for (Véron and Véron, 2010); ∓ for 2QZ (Croom et al., 2004); • for VLBA. The “double” column gives the angular separation of any secondary Gaia sources than 1″. The last column indicates the angular distance between the 6 detected EDR3 binary commponents (see text).
All Figures
 |
Fig. 1. Distribution in G-magnitude of the 416 113 quasars in Gaia EDR3 belonging to LQAC-5 (in blue) and of the 398 300 quasars in Gaia DR2 belonging to LQAC-5 (in orange). |
| In the text | |
 |
Fig. 2. Aitoff projection, HEALPix map (Górski et al. 2005), Galactic coordinates, of the 416 113 quasars in Gaia EDR3 belonging to LQAC-5. Each sky pixel shows the mean value of Gaia G, demonstrating the variation in depth across the sky. |
| In the text | |
 |
Fig. 3. Distribution of Sloan r magnitudes for quasars with Gaia G brighter than the nominal completeness cut for LQAC-5 (in blue); distribution of Sloan r magnitudes for quasars with G fainter than the completeness cut, or not cross-identified with Gaia DR3 (in orange). |
| In the text | |
 |
Fig. 4. Normalized distribution of the difference r(G)−r. The value of r is predicted from G minus measured r for LQAC-5 quasars cross-identified with Gaia EDR3, normalized by the formal error added in quadrature to an intrinsic dispersion term, which we find to be σintr. = 0.21 mag, consistent with expectations from AGN variability. The solid black line shows a normal distribution with mean of zero and standard deviation of unity. |
| In the text | |
 |
Fig. 5. Distribution of Gaia GBP − GRP for the quasars in EDR3 belonging to LQAC-5 (black), compared to the DR2 set (blue). |
| In the text | |
 |
Fig. 6. Distribution of the positional uncertainties for the quasars in Gaia EDR3 belonging to LQAC-5 (grey), and with Gaia G < 19 mag (blue). |
| In the text | |
 |
Fig. 7. Distribution of the uncertainty-normalized parallaxes |
| In the text | |
 |
Fig. 8. Distribution of the normalized proper motion μα⋆ of the quasars in Gaia EDR3 belonging to LQAC-5. The black line is a Gaussian with zero mean and unity standard deviation. |
| In the text | |
 |
Fig. 9. Distribution of the normalized total proper motion χμ of the quasars in Gaia EDR3 belonging to the LQAC-5 with χμ < 5. The black line denotes a Rayleigh distribution with σ = 1. |
| In the text | |
 |
Fig. 10. Distribution of the proper motion significance values for LQAC-5/EDR3 matches (Sect. 3), with |
| In the text | |
 |
Fig. 11. Total G minus measured G versus redshift, where the total G was estimated using the Kron or Petrosian r magnitude and inverting Eq. (1). Gaia clearly under-photometers galaxies in the local Universe, making it likely that the astrometric performance is degraded for these objects. The vertical line is at a redshift cut of 0.35. |
| In the text | |
 |
Fig. 12. Distribution of total proper motions of the initial sample of 399 quasars above a redshift of z > 0.35 identified by WISE, with significant apparent proper motions. |
| In the text | |
 |
Fig. 13. Colour–colour diagram w1 − w2 versus w2 − w3 for LQAC-5+ objects with μ > 10 mas yr−1 and χμ ≥ 5. The rectangular zone delimited in red corresponds to 0.5 < w1 − w2 < 1.6 and 2.1 < w2 − w3 < 4.2. |
| In the text | |
 |
Fig. 14. Parallax π of the objects with μ > 10 mas yr−1 and χμ > 5 selected in Fig. 13, with respect to their uncertainty σπ. The red circles correspond to the objects of the quasar zone, whereas black squares and blue triangles correspond to the left and right zones of Fig. 13, respectively. The full and dashed lines delimit the areas with |π|/σπ < 1 and |π|/σπ < 2, respectively. |
| In the text | |
 |
Fig. 15. Gaia EDR3 value of the proper motion μ of the quasars with μ > 10 mas yr−1 with respect to the value given by Gaia DR2. |
| In the text | |
 |
Fig. 16. Gaia EDR3 value of the proper motion uncertainty σμ of the quasars with μ > 10 mas yr−1 with respect to the value given by Gaia DR2. The σμ was computed as the quadrature sum of the uncertainties in μα⋆ and μδ. |
| In the text | |
 |
Fig. 17. Pan-STARRS giy images of our final selection of quasars exhibiting proper motion. Each cutout is 12″ × 12″ and in the standard orientation (north is up, and east is to the left). The RA and Dec given are the Gaia EDR3 coordinates. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



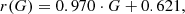
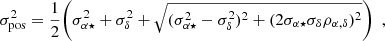
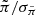
![$$ \begin{aligned} \chi _{\mu }^2 = \frac{1}{1 - \rho ^2} \times \left[\left( \frac{\mu _{\alpha \star }}{ \sigma _{\mu _{\alpha \star }}} \right)^2 + \left( \frac{\mu _{\delta }}{\sigma _{\mu _{\delta }}}\right)^2 - 2 \rho \frac{\mu _{\alpha \star } \mu _{\delta }}{\sigma _{\mu _{\alpha \star }}\sigma _{\mu _{\delta }}} \right], \end{aligned} $$](/articles/aa/full_html/2022/04/aa41915-21/aa41915-21-eq11.gif)