EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 658 (February 2022) A&A, 658 (2022) L6 Full HTML
Free Access
Issue
A&A
Volume 658, February 2022
Article Number L6
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202142123
Published online 04 February 2022

© ESO 2022

1. Introduction

The origin of high-energy astrophysical neutrinos is still a mystery despite their discovery by the IceCube experiment almost a decade ago (Aartsen et al. 2013). The detection of IC-170922A in spatial and temporal coincidence with the blazar TXS 0506+056 has therefore led to speculations that blazars contribute to the diffuse neutrino flux detected by IceCube (Aartsen et al. 2018a,b). This was the first detected blazar-neutrino association; the source was found to be flaring in GeV γ rays when the high-energy νμ (Eν ∼ 0.3 PeV) created a “track-like” event in the South Pole ice. A chance correlation was disfavored at the 3σ confidence level. A few weeks after the neutrino alert, the Major Atmospheric Imaging Cherenkov (MAGIC) telescope detected γ rays above 100 GeV from this source for the first time (Ansoldi et al. 2018). Prompted by this observation, a search for a time-dependent neutrino signal in the archival data revealed an excess of high-energy neutrino events between September 2014 and March 2015 at 3.5σ statistical significance. However, the 160-day window was not accompanied by a γ-ray flare.

Detection of the IC-170922A event reaffirms the extragalactic origin of the most IceCube astrophysical neutrinos, which is evident from their near-isotropic sky distribution. Since the detection of sub-PeV neutrinos directly indicates cosmic-ray acceleration to at least PeV energies, they are ideal messengers of hadronic processes in astrophysical sources. Blazars, a subclass of radio-loud active galactic nuclei (AGNs), have their relativistic jets pointed toward Earth. They have been long considered as the accelerators of ultra-high-energy cosmic rays (UHECRs; Dermer et al. 2009; Dermer & Razzaque 2010; Murase et al. 2012; Tavecchio 2014; Oikonomou et al. 2014; Resconi et al. 2017; Rodrigues et al. 2018). Statistical analysis with early IceCube data indicated a weak correlation between the neutrinos, UHECRs, and AGNs (Moharana & Razzaque 2015).

Other neutrino events, of lower statistical significance, have also been identified in spatial coincidence with blazars (Franckowiak et al. 2020; Giommi et al. 2020a), for example IC-190730A and IC-200107A, coincident with the direction of blazars PKS 1502+106 and 3HSP J095507.9+355101, respectively. An analysis of archival neutrino events that satisfies the IceCube real-time alert criteria revealed a correlation of IC-141209A with the blazar GB6 J1040+0617.

The neutrino flux predicted from the IceCube observation of TXS 0506+056 can be produced inside the jet emission region. The multiwavelength spectral energy distribution (SED) is explained well with a synchrotron self-Compton (SSC) model, with neutrinos produced by a radiatively subdominant hadronic component (Keivani et al. 2018; Cerruti et al. 2019; Gao et al. 2019). While the SED of most blazars can be well explained by leptonic models alone, a hadronic component is required to explain the observed neutrinos. Moreover, if blazars are capable of accelerating UHECRs, a cosmogenic neutrino flux is expected to be observed along their direction for a sufficiently small intergalactic magnetic field. The secondary γ rays produced may contribute to the SED at the highest energies, leading to an unattenuated spectrum. Thus, there exists a degeneracy in explaining the blazar SED, which can be lifted by future multi-messenger observations. Ultra-high-energy (UHE) protons, if accelerated, can escape the jet when the escape timescale is shorter than the acceleration time (see, e.g., Das et al. 2020). These UHECRs can interact with photons from the cosmic microwave background (CMB) and extragalactic background light (EBL) to produce secondary neutrinos and γ rays with a hard spectrum along the line-of-sight (Essey & Kusenko 2010; Essey et al. 2010; Kalashev et al. 2013; Das et al. 2021). In some cases, the line-of-sight γ-ray flux has shown to improve fits to the very high-energy (VHE; Eγ ≳ 30 GeV) spectra of BL Lacs (Das et al. 2020). However, the luminosity requirement in the UHECR spectrum may be challenging for a super-massive black hole (Razzaque et al. 2012).

Cosmic-ray protons with energy ≲10 PeV must interact inside the blazar jets in order to produce the sub-PeV neutrinos detected by IceCube. The rate for pγ interactions in the jet can be smaller than the escape rate, however, and a large fraction of the protons can escape the jet (see, e.g., Das et al. 2020). These cosmic-ray protons with energy ≳1 EeV can interact with the CMB and EBL photons to produce photopions. The corresponding pγ opacity is ≫1 at energies larger than a few tens of EeV for the distances of the blazars associated with the IceCube events (cf. solid line in Fig. 1). In this work, we predict the line-of-sight cosmogenic neutrino flux from a simple scaling relation between the neutrino luminosity inferred from the IceCube event and the injected UHECR luminosity.

thumbnail Fig. 1.

Optical depth of photopion production inside and outside the source emission region for TXS 0506+056. The target photons for pγ interactions inside the jet are leptonic synchrotron and SSC radiation, as shown in Fig. 3 of Gao et al. (2019) for their favored hybrid model. The parameter values given in their supplementary Table 1 for the flare state are used to calculate the photon flux in the comoving jet frame.

Protons with energy ≳10 PeV also interact in the blazar jets; however, the typical pγ opacity is ≪1 in the jets (cf. dashed line in Fig. 1; see caption for details). Therefore, at energies higher than a few tens of EeV, UHECR protons dominantly interact with the CMB photons, and the corresponding neutrino flux, peaking at ∼1 EeV, dominates over any neutrino flux from the jet. Upcoming neutrino detectors, such as IceCube-Gen2 and the Giant Radio Array for Neutrino Detection (GRAND), are also most sensitive in the ∼1 EeV range. Hence, we only consider the cosmogenic components for neutrino flux predictions in the UHE range for the blazars considered in this study. At lower energies the jet component can be important, depending on the flux of cosmic rays that interact inside the jet.

Observations of the EeV neutrinos by next-generation telescopes with improved sensitivity will set the course for precise modeling of the emission region in the jet. The production of cosmogenic neutrinos will be accompanied by a γ-ray flux resulting from the electromagnetic cascade of high-energy secondary e± and γ photons. Future observations by γ-ray missions, such as the Cherenkov Telescope Array (CTA) and the Large High Altitude Air Shower Observatory (LHAASO), can constrain the flux models and the magnitude of the extragalactic magnetic field (EGMF).

We present the results of our study and discuss them in Sect. 2. We summarize our results and present an outlook in Sect. 3.

2. Results and discussions

The UHECRs that escape from the blazar jets are deflected by the EGMF from our line of sight. Therefore, only a fraction of the secondary neutrinos and γ rays, produced by interactions of UHECRs with the CMB and EBL, will be propagating within a narrow cone around the line-of-sight. We calculated this fraction from the distribution of angular deflection of UHECRs upon arrival at the Earth from the blazars associated with IceCube events. We assumed the UHECR injection spectrum of the form dN/dE ∝ E−2.2 in the energy range 10 PeV to Ep, max and simulated their propagation using CRPropa 3 (Alves Batista et al. 2016), including all relevant energy loss processes. The observer, in this case, was considered to be a sphere of Robs = lc to increase the number of observed events in the simulation. We incorporated a random turbulent EGMF with a Kolmogorov power spectrum of magnitude Brms = 10−15 − 10−17 G and a turbulence correlation length lc = 0.1 Mpc for the extragalactic propagation. The choice of the Brms range is consistent with the lower bound obtained by Neronov & Vovk (2010) from observations of γ-ray blazars by the Fermi Large Area Telescope (Fermi-LAT).

Figure 2 shows the distribution of UHECR deflection in the EGMF, binned over 1° intervals, for TXS 0506+056 at a redshift of z = 0.3365 and various Brms values. A conservative limit to the flux of γ rays and neutrinos arriving at Earth can be obtained by multiplying the total flux with the UHECR survival fraction within 1° of the jet emission direction. For track-like events in IceCube, the angular resolution is 0.5° for a neutrino of energy Eν ∼ 30 TeV. We denote this survival fraction within 0 − 1° by ξB (i.e., the fraction observable at Earth). The value of ξB is fairly constant for Ep, max = 1, 10, and 100 EeV when all other parameters are kept fixed.

thumbnail Fig. 2.

Distribution of angular deflection of cosmic rays, over a sphere of radius 100 kpc centered at the observer position, resulting from the propagation through extragalactic space for z = 0.3365.

2.1. TXS 0506+056

The all-flavor neutrino luminosity, Lν, is three times the 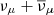ν μ + ν ¯ μ $ \nu_\mu+\overline{\nu}_\mu $ flux reported in the case of TXS 0506+056 for ΔT = 0.5 yrs and 7.5 yrs (Aartsen et al. 2018a). The factor of three corresponds to an initial production of neutrino flavors νe, νμ, ντ in the ratio 1 : 2 : 0 from pion decay. In the top-left panel of Fig. 3 we show the all-flavor neutrino fluxes with the solid and dashed black data points. We calculated the luminosity of UHECRs by assuming LUHECR = αLν, where α is a scaling factor that takes into account the escaping UHECR luminosity due to various physical effects. At E ≲ 10 PeV, 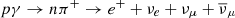p γ → n π + → e + + ν e + ν μ + ν ¯ μ $ p\gamma\to n\pi^+ \to e^+ + \nu_e + \nu_\mu + \overline{\nu}_\mu $ interactions inside the jet produce IceCube neutrinos, and the neutron escapes as a cosmic ray with ≈80% of the proton’s energy. The three ν carry 15% of the parent proton energy, and hence α ≈ 16/3. In the UHE range, a higher value is possible as protons can escape dominantly, but we considered the conservative lower bound for this study.

thumbnail Fig. 3.

Line-of-sight cosmogenic neutrino and γ-ray fluxes from TXS 0506+056 (top left) and other blazars (see legend) associated with the IceCube neutrino events. To calculate the cosmogenic fluxes, we assume that UHECRs with energies from 10 PeV to Ep, max escape from the blazars, where the lower range is consistent with the proton energy required to produce neutrinos observed by IceCube via pγ interactions inside the jet. The solid, dashed, and dotted lines corresponds to Ep, max = 1, 10, and 100 EeV. We assume the UHECR luminosity of the associated blazar is LUHECR = αLν, where Lν is the all-flavor neutrino luminosity inferred from the track-like events observed by IceCube. The filled and open green circles correspond to γ-ray flux data points from Fermi-LAT, and open magenta squares are MAGIC data points. Also shown in the plots are the sensitivities of the current and upcoming γ-ray and neutrino telescopes, as well as the limit on cosmogenic neutrinos by IceCube.

We used CRPropa 3 and the EBL model of Gilmore et al. (2012) to calculate cosmogenic photon and neutrino fluxes. The secondary electron and photons are propagated via the DINT code, which solves the transport equation to yield the respective spectra after taking the electromagnetic cascade into account (Lee 1998; Heiter et al. 2018). For ΔT = 0.5 yrs, Lν = 6.2 × 1046 erg s−1, and for ΔT = 7.5 yrs, Lν = 4.3 × 1045 erg s−1. We show the cosmogenic fluxes for ΔT = 0.5 yrs in Fig. 3, with α = 16/3 and ξB = 0.7 for Brms = 10−16 G (see Fig. 2). The data points shown with green filled circles represent the γ-ray flux in the quiescent state as reported in the Fermi-LAT third source catalog 3FGL (Acero et al. 2015).

In Fig. 3 we also show the sensitivities of currently operating and upcoming neutrino telescopes, as well as the flux upper limit from 9 years of IceCube observations (Aartsen et al. 2018c). The projected sensitivity from 5 years of observation by the IceCube Gen2 radio upgrade is the shaded region corresponding to the uncertainties in the extrapolation (Aartsen et al. 2019a). The projected sensitivity of the full 200k radio antenna configuration of the GRAND detector is for 3 years of observation (Álvarez-Muñiz 2020). Assuming the telescopes have the same sensitivity within a zenith angle of θz, the solid angle they cover is Ωz = 2π(1 − cos θz)∼0.38 − 3.14 sr for θz = 20 − 60 degree, which is of the order 1. Hence, we plot the actual neutrino flux sensitivity curves reported by the current and upcoming telescope collaborations in units of erg cm−2 s−1 sr−1.

The CTA is a ground-based imaging telescope that observes γ rays at very high energies, from 20 GeV to hundreds of TeV. A northern and a southern array are currently under construction. In Fig. 3 we show the predicted differential point-source sensitivity as a function of reconstructed energy in the northern array site of the CTA, assuming a 50 h observation time and pointing to 20 degrees zenith (Gueta 2021). The LHAASO is another air shower observatory that aims to detect γ rays up to PeV energies. We show the LHAASO 1-year sensitivity to Crab-like γ-ray point sources (Vernetto 2016). The sensitivity of the MAGIC telescope corresponding to 50 hrs of observation is displayed (Aleksić et al. 2016).

It can be seen from Fig. 3 that for Ep, max > 10 EeV the cosmogenic γ-ray flux exceeds the MAGIC observation (Ansoldi et al. 2018) of the TXS 0506+056 post-IceCube detection in the enhanced VHE γ-ray emission state (data points shown by open violet squares in the top-left panel) if the IceCube neutrino flux is at the ΔT = 0.5 yr level. The MAGIC data points, therefore, serve as upper limits to the line-of-sight γ-ray flux contribution in the sub-TeV energy band if emission from the jet also contributes to the observed flux, which does not show any significant variability in the MAGIC data. If the CTA detects γ-ray variability in the multi-TeV energy band, then the cosmogenic origin will be disfavored. The spectral index of the VHE emission in the TeV range will be crucial to understanding the origin. If it matches with the synchrotron, one can expect the yield to be leptonic, whereas gamma rays of hadronic origin are expected to have more cascade interactions inside the jet due to their higher energy. In any case, the jet component is expected to give a softer γ-ray spectrum after EBL correction compared to the cosmogenic component. For the cosmogenic component, a hard spectrum is expected at a few TeV energies, as shown in Fig. 3. IceCube Gen-2 will be able to detect cosmogenic neutrino flux for α ≳ 10, Ep, max = 1020 eV at the ΔT = 0.5 yr flux level, whereas α ≳ 30 will be required for detection at the ΔT = 7.5 yr flux level.

2.2. PKS 1502+106, 3HSP J095507.9+355101, and GB6 J1040+0617

We conducted a similar study for a few other IceCube neutrino events that are significantly associated with blazars. The number of muon neutrino and antineutrino events observed at IceCube in a given operational time, ΔT, is given by

N ν μ = Δ T ∫ ϵ ν , min ϵ ν , max d ϵ ν d Φ ν μ d ϵ ν ⟨ A eff ( ϵ ν ) ⟩ θ , $$ \begin{aligned} N_{\nu _\mu } = \Delta T \int _{\epsilon _{\nu , \mathrm {min}}}^{\epsilon _{\nu , \mathrm{max}}} \mathrm{d}\epsilon _\nu \frac{\mathrm{d}\Phi _{\nu _\mu }}{\mathrm{d}\epsilon _\nu } \langle A_{\rm eff}(\epsilon _\nu )\rangle _\theta , \end{aligned} $$(1)

where ⟨Aeff(ϵν)⟩θ is the effective detector area averaged over the zenith angle bin concerned (Aartsen et al. 2019b). For neutrino flux calculations, we used an updated effective area for event selection as a function of neutrino energy from Stettner (2020). We assumed a muon neutrino flux of the form 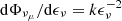d Φ ν μ /d ϵ ν =k ϵ ν −2 $ {\rm d}\Phi_{\nu_\mu}/{\rm d}\epsilon_\nu = k\epsilon_\nu^{-2} $ and an operation time ΔT = 10 years (i.e., from when IceCube became fully operational in 2010 up until 2020). The all-flavor neutrino flux can be approximated as three times the 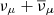ν μ + ν ¯ μ $ \nu_\mu+\overline{\nu}_\mu $ flux.

The high-energy astrophysical muon neutrino candidate IC-190730A was detected by IceCube with energy ϵν ≈ 300 TeV. The Fermi catalog source 4FGL J1504.4+1029, associated with the flat-spectrum radio quasar PKS 1502+106 at z = 1.84, was found to be within the 50% uncertainty region, at an offset of 0.31 degrees from the best-fit neutrino direction (IceCube Collaboration 2019). Assuming this to be the only event from this source in 10 yrs, the estimated all-flavor neutrino flux using Eq. (1) is ≈4.1 × 10−10 erg cm−2 s−1, and hence Lν ≈ 1049 erg s−1. We find the survival fraction of UHECRs, ξB = 0.25, within 1° of the initial emission direction toward the Earth.

IC-200107A has been associated with the γ-ray blazar 3HSP J095507.9+355101, a BL Lac at z = 0.557, which is listed in the Fermi-LAT 4FGL catalog (IceCube Collaboration 2020). It is an extreme blazar with a peak synchrotron frequency νs > 1017 Hz located at an angular separation of 0.63 degrees from the best-fit neutrino direction. There is another source, 4FGL J0957.8+3423, within the 90% localization region but 1.5 degrees from the neutrino event. The integrated all-flavor neutrino flux needed to produce the single event of ϵν = 0.33 PeV in 10 years is found to be 3 × 10−11 erg cm−2 s−1 (Giommi et al. 2020b). The corresponding all-flavor neutrino luminosity is Lν = 4.1 × 1046 erg s−1. For a source at this redshift, we find ξB = 0.52.

An archival neutrino event, IC-141209A, which satisfies the IceCube real-time trigger criteria, was found to be spatially coincident with the γ-ray source GB6 J1040+0617 (Garrappa et al. 2019). The chance probability of this coincidence was found to be 30% after trial correction. The source is listed in the Fermi-LAT 3FGL catalog at z = 0.7351 and lies within the 90% uncertainty region of the best-fit neutrino direction. The event deposited 97.4 TeV energy in the IceCube detector. We calculated the survival fraction to be ξB = 0.4 and the all-flavor neutrino flux to be 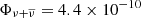Φ ν + ν ¯ = 4.4 × 10 − 10 $ \Phi_{\nu+\overline{\nu}}=4.4\times10^{-10} $ erg cm−2 s−1, and thus Lν = 1.1 × 1048 erg s−1.

In Fig. 3 we show the line-of-sight cosmogenic fluxes for the three blazars discussed above, with α = 16/3 and the respective UHECR survival fraction ξB and three values of Ep, max, namely 1, 10, and 100 EeV. Also shown are the γ-ray flux data from Fermi-LAT as well as the sensitivities of different telescopes. The inferred neutrino luminosities from the associated IceCube events in the case of PKS 1502+106 and GB6 J1040+0617 are much higher than the Eddington luminosity of a super-massive black hole, LEdd = 1.3 × 1047(Mbh/109 M⊙) erg s−1. Therefore, it is unlikely that these are the source of the detected IceCube neutrinos. Because of its high redshift, the cosmogenic γ-ray flux from PKS 1502+106 is very low. However, CTA-North will be able to constrain the cosmogenic γ-ray flux from GB6 J1040+0617. The cosmogenic neutrino flux for both blazars can be tested with IceCube Gen-2 for such an extreme blazar luminosity. The case of 3HSP J095507.9+355101 is the most compelling among these three blazars as a plausible IceCube neutrino source. The hard γ-ray spectrum observed by Fermi-LAT could be explained as cosmogenic γ rays for Ep, max ≈ 10 EeV. If a hard spectrum is also detected at a few TeV energies by the CTA, it may be the signature of cosmogenic origin because such hardening may not be seen for intrinsic emission from the jet due to EBL attenuation resulting in a soft spectrum. The sensitivity of CTA-North is comparable to the plotted flux level in Fig. 3 and will be in a position to constrain the parameter α. Detection of cosmogenic neutrinos from 3HSP J095507.9+355101 by IceCube Gen-2 will require α ≳ 10.

3. Summary and outlook

In the last few years, there has been growing evidence of blazar candidates for several high-energy IceCube events (Franckowiak et al. 2020). With observations of several well-reconstructed track events by the new Gold-alert system and the electromagnetic follow-up observations, the detection of neutrino events associated with transient phenomena is now possible. The IceCube events considered here have been studied in the past for self-consistent modeling of the blazar SED and emission of neutrinos from the jets (Banik et al. 2020; Petropoulou et al. 2020; Rodrigues et al. 2021a). In some scenarios, a significant fraction of neutrinos at EeV energies can be attributed to that produced from inside the sources (Rodrigues et al. 2021b).

We have presented cosmogenic neutrino and γ-ray fluxes from these blazars along the line-of-sight, assuming that UHECRs with energies from 1016 − 1020 eV can be accelerated and can escape from the jets. We used a suitable value of the injection spectral index in the aforementioned energy range, in the absence of an unequivocal choice. The neutrino flux may vary moderately for other values, while the cosmogenic γ-ray spectrum depends more on the cosmic background photons. For comparison, we also show the neutrino flux for lower values of Ep, max = 1 and 10 EeV while keeping the value of α = 16/3. In these cases, the cosmogenic neutrino fluxes are practically undetectable.

We used a realistic value of 10−16 G for the intergalactic magnetic field for deflection of UHECRs from the line-of-sight. The normalization of the cosmogenic fluxes was set by assuming that the UHECR luminosity of the source is a factor α times the sub-PeV neutrino luminosity inferred from the respective IceCube event. The line-of-sight cosmogenic fluxes appear with harder spectra compared to the fluxes directly from the jets and can be identified by the neutrino and γ-ray telescopes. In cases where the cosmic rays are not accelerated to 1020 eV, the cosmogenic neutrino fluxes will be lower than we estimate here. Both higher luminosity in UHECRs and a higher value of Ep, max can aid in the detection of cosmogenic neutrinos. But given the sensitivity of future detectors, an observation of a cosmogenic neutrino event at ≈1 EeV is more likely if the maximum rigidity of cosmic-ray injection is near the Greisen-Zatsepin-Kuzmin limit.

We find that the inferred sub-PeV neutrino luminosities of PKS 1502+106 and GB6 J1040+0617 are already above the Eddington luminosity because of their relatively high redshifts, and a further requirement of a factor ≳5 times this luminosity in UHECRs for cosmogenic neutrino detection by IceCube Gen-2 is unrealistic. Because of the high redshift, cosmogenic γ-ray flux from PKS 1502+106 is very low. In the case of GB6 J1040+0617, the CTA will be able to constrain the cosmogenic γ-ray flux.

We also find that the blazars TXS 0506+056 and 3HSP J095507.9+355101 are very promising sources for the detection of cosmogenic neutrino and γ-ray fluxes. The required luminosities in UHECRs are ∼10–100 times (for Ep, max ≈ 1020 eV) the sub-PeV neutrino luminosities inferred from ∼10 years of IceCube data but are consistent with the Eddington luminosity. The upcoming CTA will be able to detect or constrain the cosmogenic γ-ray fluxes and shed light on the question of whether sub-PeV neutrino sources are also the sources of UHECRs.

Acknowledgments

S.D. thanks Kumiko Kotera and Matteo Cerruti for helpful discussions. The work of S.R. was partially supported by the National Research Foundation (South Africa) and by a University of Johannesburg Research Council grant.

References

  1. Aartsen, M. G., Abbasi, R., Abdou, Y., et al. 2013, Science, 342, 1242856 [Google Scholar]
  2. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2018a, Science, 361, eaat1378 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2018b, Science, 361, 147 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2018c, Phys. Rev. D, 98, 062003 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2019a, ArXiv eprints [arXiv:1911.02561] [Google Scholar]
  6. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2019b, Eur. Phys. J. C, 79, 234 [NASA ADS] [CrossRef] [Google Scholar]
  7. Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJ, 218, 23 [NASA ADS] [Google Scholar]
  8. Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2016, Astropart. Phys., 72, 76 [Google Scholar]
  9. Álvarez-Muñiz, J., et al. 2020, Sci. China Phys. Mech. Astron., 63, 219501 [CrossRef] [Google Scholar]
  10. Alves Batista, R., Dundovic, A., Erdmann, M., et al. 2016, J. Cosmol. Astropart. Phys., 2016, 038 [Google Scholar]
  11. Ansoldi, S., Antonelli, L. A., Arcaro, C., et al. 2018, ApJ, 863, L10 [Google Scholar]
  12. Banik, P., Bhadra, A., Pandey, M., & Majumdar, D. 2020, Phys. Rev. D, 101, 063024 [CrossRef] [Google Scholar]
  13. Cerruti, M., Zech, A., Boisson, C., et al. 2019, MNRAS, 483, L12 [NASA ADS] [CrossRef] [Google Scholar]
  14. Das, S., Gupta, N., & Razzaque, S. 2020, ApJ, 889, 149 [NASA ADS] [CrossRef] [Google Scholar]
  15. Das, S., Gupta, N., & Razzaque, S. 2021, ApJ, 910, 100 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dermer, C. D., & Razzaque, S. 2010, ApJ, 724, 1366 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dermer, C. D., Razzaque, S., Finke, J. D., & Atoyan, A. 2009, New J. Phys., 11, 065016 [NASA ADS] [CrossRef] [Google Scholar]
  18. Essey, W., & Kusenko, A. 2010, Astropart. Phys., 33, 81 [Google Scholar]
  19. Essey, W., Kalashev, O. E., Kusenko, A., & Beacom, J. F. 2010, Phys. Rev. Lett., 104, 141102 [NASA ADS] [CrossRef] [Google Scholar]
  20. Franckowiak, A., Garrappa, S., Paliya, V., et al. 2020, ApJ, 893, 162 [Google Scholar]
  21. Gao, S., Fedynitch, A., Winter, W., & Pohl, M. 2019, Nature Astron., 3, 88 [CrossRef] [Google Scholar]
  22. Garrappa, S., Buson, S., Franckowiak, A., et al. 2019, ApJ, 880, 103 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gilmore, R. C., Somerville, R. S., Primack, J. R., & Domínguez, A. 2012, MNRAS, 422, 3189 [NASA ADS] [CrossRef] [Google Scholar]
  24. Giommi, P., Glauch, T., Padovani, P., et al. 2020a, MNRAS, 497, 865 [Google Scholar]
  25. Giommi, P., Padovani, P., Oikonomou, F., et al. 2020b, A&A, 640, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Gueta, O. 2021, in Proceedings of 37th International Cosmic Ray Conference – PoS(ICRC2021), 395, 885 [CrossRef] [Google Scholar]
  27. Heiter, C., Kuempel, D., Walz, D., & Erdmann, M. 2018, Astropart. Phys., 102, 39 [NASA ADS] [CrossRef] [Google Scholar]
  28. IceCube Collaboration 2019, GRB Coordinates Network, 25225, 1 [Google Scholar]
  29. IceCube Collaboration 2020, GRB Coordinates Network, 26655, 1 [Google Scholar]
  30. Kalashev, O. E., Kusenko, A., & Essey, W. 2013, Phys. Rev. Lett., 111, 041103 [NASA ADS] [CrossRef] [Google Scholar]
  31. Keivani, A., Murase, K., Petropoulou, M., et al. 2018, ApJ, 864, 84 [Google Scholar]
  32. Lee, S. 1998, Phys. Rev. D, 58, 043004 [NASA ADS] [CrossRef] [Google Scholar]
  33. Moharana, R., & Razzaque, S. 2015, J. Cosmol. Astropart. Phys., 2015, 014 [Google Scholar]
  34. Murase, K., Dermer, C. D., Takami, H., & Migliori, G. 2012, ApJ, 749, 63 [Google Scholar]
  35. Neronov, A., & Vovk, I. 2010, Science, 328, 73 [NASA ADS] [CrossRef] [Google Scholar]
  36. Oikonomou, F., Murase, K., & Kotera, K. 2014, A&A, 568, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Petropoulou, M., Oikonomou, F., Mastichiadis, A., et al. 2020, ApJ, 899, 113 [NASA ADS] [CrossRef] [Google Scholar]
  38. Razzaque, S., Dermer, C. D., & Finke, J. D. 2012, ApJ, 745, 196 [NASA ADS] [CrossRef] [Google Scholar]
  39. Resconi, E., Coenders, S., Padovani, P., Giommi, P., & Caccianiga, L. 2017, MNRAS, 468, 597 [NASA ADS] [CrossRef] [Google Scholar]
  40. Rodrigues, X., Fedynitch, A., Gao, S., Boncioli, D., & Winter, W. 2018, ApJ, 854, 54 [NASA ADS] [CrossRef] [Google Scholar]
  41. Rodrigues, X., Garrappa, S., Gao, S., et al. 2021a, ApJ, 912, 54 [NASA ADS] [CrossRef] [Google Scholar]
  42. Rodrigues, X., Heinze, J., Palladino, A., van Vliet, A., & Winter, W. 2021b, Phys. Rev. Lett., 126, 191101 [NASA ADS] [CrossRef] [Google Scholar]
  43. Stettner, J. 2020, PoS, ICRC2019, 1017 [Google Scholar]
  44. Tavecchio, F. 2014, MNRAS, 438, 3255 [Google Scholar]
  45. Vernetto, S. 2016, J. Phys. Conf. Ser., 718 [Google Scholar]

All Figures

thumbnail Fig. 1.

Optical depth of photopion production inside and outside the source emission region for TXS 0506+056. The target photons for pγ interactions inside the jet are leptonic synchrotron and SSC radiation, as shown in Fig. 3 of Gao et al. (2019) for their favored hybrid model. The parameter values given in their supplementary Table 1 for the flare state are used to calculate the photon flux in the comoving jet frame.
In the text
thumbnail Fig. 2.

Distribution of angular deflection of cosmic rays, over a sphere of radius 100 kpc centered at the observer position, resulting from the propagation through extragalactic space for z = 0.3365.
In the text
thumbnail Fig. 3.

Line-of-sight cosmogenic neutrino and γ-ray fluxes from TXS 0506+056 (top left) and other blazars (see legend) associated with the IceCube neutrino events. To calculate the cosmogenic fluxes, we assume that UHECRs with energies from 10 PeV to Ep, max escape from the blazars, where the lower range is consistent with the proton energy required to produce neutrinos observed by IceCube via pγ interactions inside the jet. The solid, dashed, and dotted lines corresponds to Ep, max = 1, 10, and 100 EeV. We assume the UHECR luminosity of the associated blazar is LUHECR = αLν, where Lν is the all-flavor neutrino luminosity inferred from the track-like events observed by IceCube. The filled and open green circles correspond to γ-ray flux data points from Fermi-LAT, and open magenta squares are MAGIC data points. Also shown in the plots are the sensitivities of the current and upcoming γ-ray and neutrino telescopes, as well as the limit on cosmogenic neutrinos by IceCube.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.