| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 4 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202141896 | |
| Published online | 03 December 2021 | |
The Tensor-Core Correlator
ASTRON, Netherlands Institute for Radio Astronomy, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
e-mail: romein@astron.nl
Received:
28
July
2021
Accepted:
18
August
2021
Correlators are key components of radio telescopes as they combine the data from all receivers. They are characterized by high data rates, impressive compute loads, and the necessity to process data in real time. Often, these instruments use graphics processing units (GPUs) to correlate the incoming data streams as GPUs are fast, energy efficient, flexible, and programmable with a reasonable programming effort. Recent GPUs are equipped with a new technology, called “tensor cores”, to perform specific (typically artificial intelligence) workloads an order of magnitude more efficiently than regular GPU cores. This paper introduces the Tensor-Core Correlator, a GPU library that exploits this technology for signal processing and allows a GPU to correlate signals five to ten times faster and more energy efficiently than traditional state-of-the-art GPU correlators. The library hides the complexity of the use of tensor cores and can be easily integrated into the GPU pipelines of existing and future instruments, leading to a significant reduction in costs and energy consumption.
Key words: instrumentation: interferometers
© ESO 2021
1. Introduction
Radio telescopes often use multiple, geographically distributed receivers to obtain high sensitivity and angular resolution. The data from all receivers are centrally combined by a “correlator” in real time. Often, both the data rates and the computational requirements of a correlator are challenging, especially when the number of receivers is large.
Graphics processing units (GPUs) have become a popular alternative to ASIC- and FPGA-based correlators, due to their flexibility, easier programming model, performance, and energy efficiency. Major facilities like the Canadian Hydrogen Intensity Mapping Experiment (CHIME; Denman et al. 2020), the Low Frequency Array (LOFAR; Broekema et al. 2018), and the Murchison Widefield Array (MWA; Ord et al. 2015) use GPU clusters to combine the signals from their receivers.
NVIDIA added new technology, called “tensor cores”, to their latest generations of GPUs (Choquette et al. 2021). Tensor cores are special-purpose matrix-matrix multiplication units that operate on limited-precision (e.g., 16-, 8-, or 4-bit) input data. Tensor cores perform such matrix multiplications an order of magnitude faster and more energy efficiently than the regular GPU cores. They were designed to speed up training and inference in deep-learning applications. However, as they can be programmed directly, they can be used for other purposes, provided that the algorithm can be expressed as matrix-matrix multiplications and operates on limited-precision input data. Recently, the first non-artificial-intelligence applications that profit from tensor cores have appeared in the literature, for example for iterative solving (Haidar et al. 2018, 2020), adaptive optics (Doucet et al. 2019), and reduction and scan operations (Dakkak et al. 2019). For processing signals from radio telescopes, there are (at least) two important use cases: (i) a correlator and (ii) a beam former that creates many beams simultaneously.
This paper introduces the Tensor-Core Correlator, an open-source GPU library1 that performs correlations at unprecedented speed and energy efficiency. The library is intended for use in an FX correlator (an FX correlator filters (F) the data into frequency channels before computing the cross correlations (X)). The library can be integrated in the processing pipelines of current and future instruments. It is not a full correlator application: The library only performs the computationally challenging correlations; other tasks, such as filtering and handling input and output, should still be implemented by the application programmer.
The remainder of this paper describes the use, implementation, and optimization challenges of the Tensor-Core Correlator library. We compare performance and energy efficiency to the widely used xGPU library (Clark et al. 2013) and show that the tensor-core technology has a disruptive impact.
2. Library use and implementation challenges
The Tensor-Core Correlator library can be used by a correlator application that is implemented in the CUDA or OpenCL programming language. The library exports two functions. The first function dynamically compiles and links a GPU kernel for a given number of receivers, channels, integration times, and bits per sample. By compiling the GPU code at runtime, a GPU kernel is instantiated that is optimized specifically for the given parameters. The second function launches the GPU kernel to correlate a memory block with 16-, 8-, or 4-bit samples and must be invoked for each new set of samples. The application itself is responsible for storing the samples in GPU memory prior to launching the correlator kernel.
For each observed frequency channel, the correlator multiplies a matrix with filtered samples S by its own Hermition, where S has size number of receives times the number of samples over which the correlations are integrated. Hence, the resulting product with visibilities is Hermitian as well (i.e., 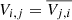 ). To reduce the amount of computations and memory use, only one side of the diagonal is computed and stored.
). To reduce the amount of computations and memory use, only one side of the diagonal is computed and stored.
Essentially, tensor cores perform the operation D = A * B + C in one go, where A, B, C, and D are fixed-size matrices (typically 16 by 16). The A and B matrices contain limited-precision values (the supported integer and floating-point types depend on the tensor-core generation), while C and D normally contain 32-bit values. Large matrices can be multiplied efficiently by decomposing the multiplication into tensor-core-sized multiplications.
The Tensor-Core Correlator library itself is implemented in CUDA and uses NVIDIA’s Warp Matrix Multiply Accumulate (WMMA) interface2 to access the GPU’s tensor cores. While implementing the library, we identified three optimization challenges: the missing support for complex numbers by the tensor-core hardware, the triangular output data structure, and the ability to feed the tensor cores fast enough with data from memory. Below, we discuss these in more detail.
2.1. Complex numbers support
Tensor cores can only operate on real-valued matrices and do not support complex-valued samples and visibilities natively. In particular, they can neither swizzle real and imaginary parts nor perform fused multiply-sub operations, which are both necessary for multiplying complex numbers. Hence, we used the GPU’s regular cores to prepare the input data for use by the tensor cores, as illustrated by Fig. 1. The left and middle matrices store the real and imaginary parts of a complex value in two consecutive memory locations. The data in the right-hand side matrix are reordered before being loaded into the tensor cores. Each row from the original input is copied into the right-hand side matrix twice: first a literal copy, and then a copy with all real and imaginary parts swapped and all real parts negated. This way, a real value in the left matrix (the red “r”) becomes the dot product of the indicated row in the middle matrix and the left row in the right matrix, while an imaginary number on the left (the blue “i”) becomes the dot product of the same row with the right column – exactly what the tensor cores compute.
 |
Fig. 1. Multiplication of complex-valued matrices with tensor cores. |
2.2. Triangular output data
The second challenge is the missing support for triangular data structures. As the computed visibilities are Hermitian, the results are stored in a triangular data structure. However, both the tensor-core hardware and the WMMA programming interface only operate on rectangular data structures, and this leads to several complications. First, it is difficult to balance the work evenly over the GPU’s compute resources (see Fig. 2 for an illustration). At the coarsest level, the work is decomposed into rectangles of 64 × 32 receivers and triangles of 64 × 64 receivers, which are processed by different thread blocks. Alternative block sizes (48 × 48 and 32 × 32; not shown in the figure) are supported as well and perform better in specific use cases.
 |
Fig. 2. Hierarchical work decomposition over thread blocks (thick red lines), warps (thinner blue lines), and units that fit a tensor-core matrix (dashed black lines). The dark green area is computed redundantly. |
Second, some matrix entries on the “wrong” side of the diagonal are computed redundantly since dynamic checks to avoid redundant computations take more time than simply performing them and discarding the result. The same is true for some entries beyond the right edge if the number of receivers is not a multiple of 48 or 64.
Third, the implementation bypasses the WMMA interface to write computed tensor core results (visibilities) directly from registers into the triangular data structure in GPU memory. The mapping between threads, tensor cores, registers, and device-memory addresses is highly complicated and depends on the tensor-core hardware generation. The library recognizes all current GPU compute models (SM 70, 72, 75, 80, and 86) and has a slower but portable fallback for unrecognized GPUs. Fortunately, all this complexity is totally hidden from the user of the library.
2.3. Fast data provision
The third challenge was to provide the tensor cores with data fast enough. For this, the Tensor-Core Correlator decomposes the work in such a way that data are cached efficiently at all levels in the memory hierarchy (including shared memory and the register file). The work-distribution scheme shown in Fig. 2 helps in achieving high cache hit rates. Additionally, the data format in which the application must provide the input data is chosen so that the library can load the input data without bank conflicts in order to fully utilize the memory bandwidth.
3. Performance and energy efficiency
We compared the performance of the Tensor-Core Correlator to xGPU (Clark et al. 2013), commonly regarded as the fastest GPU correlator for regular GPU cores. The values are obtained on an NVIDIA A100 PCIe GPU. PCIe transfers are excluded in these measurements since in realistic scenarios the GPU will perform other operations as well (e.g., filtering, source tracking, bandpass correction, and Doppler correction) while intermediate data remain in GPU memory. The reported performance can be sustained by the GPU and are not the result of short-time turbos. Only “useful” operations are counted; redundant calculations and overhead (such as address calculations or loop-counter increments) are not counted.
The top three curves in Fig. 3 show the performance of the Tensor-Core Correlator as a function of the number of (dual-polarized) receivers, for 4-bit integer, 8-bit integer, and 16-bit floating-point input data, respectively. The sawtooth patterns are caused by work-distribution imbalances and redundant computations for non-multiples of 48 or 64 receivers. The bottom two curves show the performance of xGPU on regular GPU cores (xGPU supports 32-bit float and 8-bit integer data). The Tensor-Core Correlator is typically five to ten times faster than xGPU. Especially for large numbers of receivers, the tensor cores are much more efficient than the regular GPU cores.
 |
Fig. 3. Performance of the Tensor-Core Correlator on an A100 GPU, compared to an xGPU on the A100’s regular GPU cores. |
Except for small numbers of receivers, the performance is limited by power consumption as the GPU clock speed is reduced to not exceed the 250 W board power limit. Figure 4 compares the energy efficiency of the Tensor-Core Correlator and xGPU, which we measured through the NVIDIA Management Library (NVML)3. The figure shows that the tensor cores also perform five to ten times more operations per joule than the regular GPU cores. On 8-bit and 4-bit data, the energy efficiency exceeds the teraops (1012 operations) per joule milestone.
 |
Fig. 4. Energy efficiency of the Tensor-Core Correlator on an A100 GPU, compared to an xGPU on the A100’s regular GPU cores. |
4. Discussion
A decade ago, the introduction of GPUs was a disruptive innovation that allowed an enormous performance jump over regular CPU computing. However, the bottom blue curve in Fig. 5 illustrates that the performance growth over successive GPU generations is no longer exponential, due to the deceleration of Moore’s law. The introduction of tensor cores is yet another innovation that makes disruptive performance improvements possible, at least for correlator applications.
 |
Fig. 5. Historical best-case correlator performance on the six latest generations of NVIDIA GPUs. |
5. Conclusion
This paper introduces the Tensor-Core Correlator: a GPU library that uses new tensor-core technology to correlate signals at unprecedented speed and energy efficiency. The library hides the complexity of using tensor cores and addresses several optimization challenges, such as the missing hardware support for complex numbers. Measurements show that the performance and energy efficiency is typically a factor of five to ten higher than a state-of-the-art correlator that runs on regular GPU cores. The library can be employed in a variety of radio-astronomical instruments, leading to significant savings in costs and energy use.
Acknowledgments
This work received funding from the European Commission through the H2020-FETHPC DEEP-EST grant (Grant Agreement nr. 754304), from the Netherlands eScience Center/SURF through the PADRE and RECRUIT grants, and from the Netherlands Organization for Scientific Research (NWO) through the DAS-5 and DAS-6 grants (Bal et al. 2016). We kindly thank NVIDIA for providing us with an A100 GPU.
References
- Bal, H., Epema, D., de Laat, C., et al. 2016, IEEE Comput., 49, 54 [CrossRef] [Google Scholar]
- Broekema, P. C., Mol, J. J. D., Nijboer, R., et al. 2018, Astron. Comput., 23, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Choquette, J., Gandhi, W., Giroux, O., Stam, N., & Krashinsky, R. 2021, IEEE Micro, 41, 29 [CrossRef] [Google Scholar]
- Clark, M., Plante, P., & Greenhill, L. 2013, Int. J. High Perform. Comput. Appl., 27, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Dakkak, A., Li, C., Xiong, J., Gelado, I., & Wen-mei, H. 2019, ACM International Conference on Supercomputing (ICS’19), Phoenix, AZ, 46 [CrossRef] [Google Scholar]
- Denman, N., Renard, A., Vanderlinde, K., et al. 2020, J. Astron. Instrum., 9, 2050014 [CrossRef] [Google Scholar]
- Doucet, N., Ltaief, H., Gratadour, D., & Keyes, D. 2019, IEEE/ACM Workshop on Irregular Applications: Architectures and Algorithms (IA3’19), Denver, CO, 31 [Google Scholar]
- Haidar, A., Tomov, S., Dongarra, J., & Higham, N. J. 2018, SuperComputing (SC’18), Dallas, TX [Google Scholar]
- Haidar, A., Bayraktar, H., Tomov, S., Dongarra, J., & Higham, N. J. 2020, Proc. R. Soc. A, 476 [Google Scholar]
- Ord, S. M., Crosse, B., Emrich, D., et al. 2015, PASA, 32, e006 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Multiplication of complex-valued matrices with tensor cores. |
| In the text | |
 |
Fig. 2. Hierarchical work decomposition over thread blocks (thick red lines), warps (thinner blue lines), and units that fit a tensor-core matrix (dashed black lines). The dark green area is computed redundantly. |
| In the text | |
 |
Fig. 3. Performance of the Tensor-Core Correlator on an A100 GPU, compared to an xGPU on the A100’s regular GPU cores. |
| In the text | |
 |
Fig. 4. Energy efficiency of the Tensor-Core Correlator on an A100 GPU, compared to an xGPU on the A100’s regular GPU cores. |
| In the text | |
 |
Fig. 5. Historical best-case correlator performance on the six latest generations of NVIDIA GPUs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


