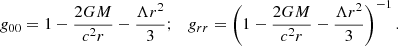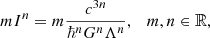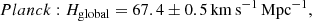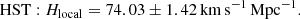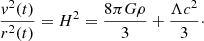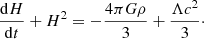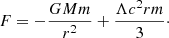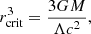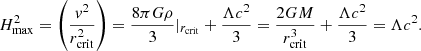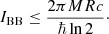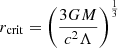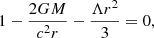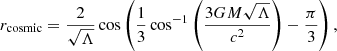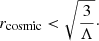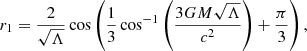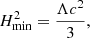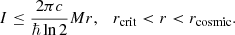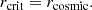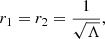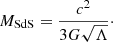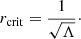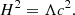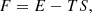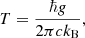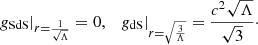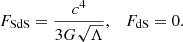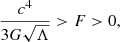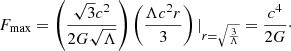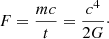| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 4 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202141736 | |
| Published online | 24 September 2021 | |
Hubble tension and absolute constraints on the local Hubble parameter
1
Center for Cosmology and Astrophysics, Alikhanian National Laboratory and Yerevan State University, Yerevan, Armenia
e-mail: gurzadyan@yerphi.am
2
SIA, Sapienza University of Rome, Rome, Italy
Received:
7
July
2021
Accepted:
14
August
2021
It is shown, from the two independent approaches of McCrea-Milne and of Zeldovich, that one can fully recover the set equations corresponding to the relativistic equations of the expanding universe of Friedmann-Lemaitre-Robertson-Walker geometry. Although similar, the Newtonian and relativistic set of equations have a principal difference in the content and hence define two flows, local and global ones, thus naturally exposing the Hubble tension at the presence of the cosmological constant Λ. From this, we obtain absolute constraints on the lower and upper values for the local Hubble parameter, √(Λc2/3) ≃ 56.2 and √(Λc2) ≃ 97.3 (km s−1 Mpc−1), respectively. The link to the so-called maximum force–tension issue in cosmological models is revealed.
Key words: distance scale
© ESO 2021
1. Introduction
Non-relativistic cosmological schemes, developed a long time ago (Milne 1934; McCrea & Milne 1934), are considered certainly efficient, such as the Newtonian limit of General Relativity, which has a limited scale for application. Moreover, according to Zeldovich (1981), the Newtonian approach would have enabled us to predict the expansion of the Universe far earlier, and he considered it “paradoxical that the Newtonian theory of expansion was discovered only after the achievement of Friedmann”.
Non-relativistic cosmology as mentioned in textbooks (e.g., Misner et al. 1973), had no link to the cosmological constant, which had been typically considered negligible or zero for many decades. In Gurzadyan (1985) it was shown that the cosmological constant Λ can be naturally introduced in the non-relativistic cosmology (i.e., in the McCrea-Milne scheme). We note that Gurzadyan (1985) appeared before the discovery of the accelerated expansion of the Universe, and hence the emergence of the role of the cosmological constant. The generalized function satisfying Newton’s basic principle of the equivalency of the gravity of a sphere and point mass was derived in Gurzadyan (1985), which contains one more term, exactly of the cosmological constant form (see discussion in Chardin et al. 2021). The emerged metric for the weak-field General Relativity (GR) at spherical symmetry is (Gurzadyan & Stepanian 2018; Gurzadyan 2019)
This metric is of Schwarzschild–de Sitter form, and as a weak-field limit of GR can be applied to the dynamics of groups and clusters of galaxies (Gurzadyan & Stepanian 2018, 2019a; Gurzadyan 2019). In Eq. (1) the cosmological constant Λ acts as a second fundamental constant (Gurzadyan & Stepanian 2018) to describe gravity, along with Newton’s gravitational constant G.
Consideration of Λ as the fourth fundamental constant, along with c, ℏ, and G, enables us to construct a class of dimensionless quantities as (Gurzadyan & Stepanian 2019b)
which at certain values of n and m leads to an information scaling (Gurzadyan & Stepanian 2019b, 2021a) and is linked to the Bekenstein bound (Bekenstein 1981).
This approach, the weak-field modified GR with Eq. (1), provides an explanation to the Hubble tension (Verde et al. 2019; Riess 2020; Di Valentino et al. 2021), the discrepancy between the local and global values of the Hubble parameter, without any free parameter (Gurzadyan & Stepanian 2019c, 2021b). Among the approaches dealing with the Hubble tension (see the extensive references in Di Valentino et al. 2021), we mention that of Capozziello et al. (2020), again without a free parameter, which deals with the basic physical principles. Clearly, the further revealing of the systematics in the different observational techniques is required when clarifying the Hubble tension issue and its possible link to basic physics.
In our approach we deal with two different flows: global and local. The global flow is related to the Friedmann-Lemaitre-Robertson-Walker (FLRW) geometry, while the local flow occurring at the non-relativistic regime is a result of the repulsive nature of the Λ term in the equations of gravity according to Eq. (1). Accordingly, the data of the Planck satellite Planck Collaboration VI (2020) refer to the measurements of the global Hubble parameter, while those obtained via the local distance indicators (e.g., Riess et al. 2019) are assigned to the local flow as
It should be noted, on the one hand, that the modified gravity is among the approaches used to describe dark matter and large-scale matter distribution; on the other hand, observations are efficiently used to constrain the deviations from GR (see, e.g., Kopeikin et al. 2001; Gurzadyan & Kocharyan 2009; Eingorn 2016; Capozziello et al. 2018; Chardin et al. 2021).
In this paper we show that energy (McCrea-Milne) and force (Zeldovich) approaches together enable us to define the complete set of non-relativistic equations corresponding to the Friedmann equations. Then, each set of equations defines a flow, however with different content and Hubble parameters. We show that the local Hubble flow defined by Eq. (1) leads to principal constraints on the upper and lower values of the Hubble parameter defining that flow. It is remarkable that these constraints are determined by Λ as of the second constant of gravity entering Eq. (1). The same approach enables us to address the maximum force–tension issue in cosmology and to show the consistency of relativistic and non-relativistic definitions.
2. Non-relativistic cosmology
The non-relativistic cosmology as given in textbooks (Misner et al. 1973), also known as the McCrea-Milne cosmology (Milne 1934; McCrea & Milne 1934), is based on the conservation of energy of a test particle on an expanding sphere with density ρ and radius r(t). In the context of Λ-gravity, the evolution of a non-relativistic universe in this cosmological model is governed by
Thus, this approach is based on the energy relation, which coincides with the first Friedmann equation of the FLRW metric in relativistic cosmology.
On the other hand, in his less known note Zeldovich (1981) proposed his own approach for non-relativistic cosmology which is based on the notion of gravitational force. Similarly, in the context of Λ-gravity, his approach yields
We can see that this momentum equation provides the second Friedmann equation of FLRW cosmology for pressureless dust ∇P = 0.
Then, considering both approaches, energy and force, we obtain the full set of equations of the non-relativistic cosmology, which are similar to the relativistic FLRW equations. However, and it is of principal importance, the nature of the local Hubble constant H(t) obtained in Eqs. ((5) and (6)), is drastically different from the global H(t) obtained from the relativistic FLRW equations. If so, we might predict the Hubble tension (i.e., the difference in the values of the local and global Hubble flows). In the next section we show that the local flow enables us to obtain strict theoretical upper and lower limits for the value of the local Hubble parameter.
3. Constraints on the local Hubble flow
In Gurzadyan & Stepanian (2019c, 2021b) it is proposed that the local Hubble flow is not due to the expansion of the Universe, but to the presence of the repulsive Λ term in the equations of weak-field limit of GR (cf. Chardin et al. 2021). Considering a test body of mass m in the vicinity of a central body of mass M, the gravitational force acting on the test body in the context of this Λ-gravity Eq. (1) is written as
Then a critical radius rcrit can be introduced as
which determines the scale of dominance of the Λ term. When the distance between two bodies is larger than rcrit, the test body starts to move away from the central object, which causes the local Hubble flow. So, in order to observe the local flow, the system under consideration should have a radius larger than rcrit. Therefore, the absolute value for the upper limit of H for any system will be obtained at its rcrit as
The local Hubble flow can be determined based on Eq. (2) as information (entropy) of the system undergone by the local Hubble flow due to presence of the central object mass, where M is given by the Bekenstein bound (Bekenstein 1981) as (Gurzadyan & Stepanian 2019a)
Here, similar to the case of black holes (BHs) in the presence of Λ (Gurzadyan & Stepanian 2021a), we have to ask the following question: What is (are) the characteristic radius (radii) R of the system?
Clearly, in this case R should be the corresponding radius or distance where the outgoing flow is analyzed.
Analyzing the dynamics of objects in the context of Λ-gravity we get two characteristic radii. The critical radius
is the absolute minimum radius at which the flow can occur.
Then the largest event horizon (the cosmological horizon) of the object is obtained by solving the equation
and can be regarded as the limit where the weak-field limit is not valid anymore, and at larger radii should be considered relativistic effects. Specifically, that radius is
which is smaller than the horizon of de Sitter (dS) spacetime:
Here the essential conceptual point is that the notion of horizon obtained in Eq. (13) is valid for all objects and is not restricted to the BHs. On the other hand, for (non-extreme) Schwarzschild–de Sitter (SdS) BHs, in addition to the rcosmic, we have another solution for Eq. (12) which is defined as
and is slightly larger than 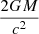 . These two radii can be illustrated via the Penrose diagram, Fig. 1, where the zigzag lines denote the spacelike singularity regarding the SdS BH.
. These two radii can be illustrated via the Penrose diagram, Fig. 1, where the zigzag lines denote the spacelike singularity regarding the SdS BH.
 |
Fig. 1. Penrose diagram for SdS BH. |
Consequently, for the local Hubble flow we have
which defines the absolute lowest value for H of the outgoing flow.
Thus, for any local flow we have
Now a natural question arises: What will happen when these two limits coincide:
This condition occurs for an extreme SdS BH where the two (positive) event horizons r1 and r2 become identical,
and the mass of the BH is a combination of fundamental constants as
The following radius is critical for such a BH (Stepanian et al. 2021):
Hence, since the event horizon and the critical radius of an extreme SdS BH coincide, the local flow for such system starts immediately outside the BH.
In addition, the information (or entropy) of an extreme SdS BH is 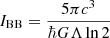 (Gurzadyan & Stepanian 2021a), which means that its formation via any astrophysical process is forbidden, as it would violate the second law of thermodynamics. Thus, by considering this and Eqs. ((18)–(20)), we can conclude that the extreme SdS BH is the absolute upper theoretical limit for all possible systems with the maximum value for the local Hubble flow:
(Gurzadyan & Stepanian 2021a), which means that its formation via any astrophysical process is forbidden, as it would violate the second law of thermodynamics. Thus, by considering this and Eqs. ((18)–(20)), we can conclude that the extreme SdS BH is the absolute upper theoretical limit for all possible systems with the maximum value for the local Hubble flow:
On the other hand, we can perform the same analysis for the theoretical lower limit. Specifically, by taking Eqs. (13) and (16) into account, it becomes clear that the dS solution is the absolute lower limit for the local flow.
Thus, considering all the above points, we can state that the extreme SdS BH and dS are the theoretical upper and lower limits for the local Hubble flow. In the next section we study these two limits in order to obtain the evolutionary process of the local Hubble flow.
4. Free energy and maximum force–tension
In this section we obtain the free energy of the extreme SdS and dS as a criterion to show the direction of evolution during the local Hubble flow. The free energy of a system is defined as
where E is the total energy of the system, T is the temperature, and S is the entropy. For both cases, SdS and dS, the temperature according to Gibbons & Hawking (1977) is
where g is the surface gravity, and for extreme SdS at rcrit and dS at 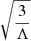 is
is
Taking all the above points into account we can obtain the free energy:
Table 1 shows the corresponding quantities as well as the value of the Hubble constant for these two limits.
Physical quantities for the theoretical upper and lower limits of the local H-flow.
Thus, the free energy of any system where the local Hubble flow occurs is
which, as can be easily checked, is in exact agreement with the notion of decrease in the amount of free energy in thermodynamics.
The maximum force–tension Barrow-Gibbons conjecture (Gibbons 2002; Barrow & Gibbons 2014) states that the maximum achievable force (or tension) in the Universe is equal to
The argument is based on the fact that by considering the combination of three fundamental constants (c, ℏ, G) the obtained unit of the force (sometimes also called the Planck force) is free of ℏ: 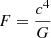 . We also note that the notion of force is not defined in GR.
. We also note that the notion of force is not defined in GR.
In the context of Λ-gravity the situation changes. Specifically, as stated above the presence of Λ in the weak-field limit according to Eq. (7) defines another limit for the weak- to strong-field transition. Consequently, in this new limit the self-gravitational force of the vacuum at 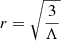 will be
will be
The obtained value is the maximum force and is two times larger than the previously conjectured value in Eq. (27). The important point is that this new limit is obtained based on the notion of force in the upper non-relativistic weak-field limit for de Sitter.
At the same time, since the limit in Eq. (28) is also the transition limit to relativistic de Sitter regimes, it is possible to show that the same value can be obtained based on the relativistic notion of tension, which is defined as
It should be noted that, generally in the Planck unit system (c, ℏ, G), the notion of maximum force or Planck force is attributed to small scales and high energies, thus leading to the yet unknown quantum theory of gravity. However, regarding the linear nature of the Λ-term in Eq. (7), it turns out that the gravitational force (and energy) grows at very far distances and consequently another weak- to strong-field transition happens. Therefore, at the upper limit of non-relativistic regimes we obtain the notion of maximum force, which in contrast to other approaches does not have any conceptual problem. In addition, by transitioning to the relativistic regimes we can also obtain the 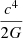 , but this time according to standard definition of tension established in relativistic physics.
, but this time according to standard definition of tension established in relativistic physics.
For both cases it is clear that no quantum effect has a role. However, at the same time we arrive at the highest possible achievable force–tension in non-relativistic and relativistic limits. So from the conceptual point of view, the reason why there is no ℏ in the definition of Planck force is that it is reached in the non-quantum regimes, based on the first principles.
This notion of maximum tension is valid for all epochs of cosmological evolution (Gurzadyan & Stepanian 2019b, 2021a); for the characteristic mass and radius 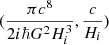 the maximum value of tension remains constant and is equal to
the maximum value of tension remains constant and is equal to 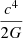 .
.
5. Conclusions
In this paper we studied the non-relativistic cosmology based on two different approaches by McCrea-Milne and by Zeldovich. The essential difference of these two approaches is that the former is based on the energy notion, while the latter deals with the notion of force. As a result, considering the two approaches plus the cosmological constant in weak-field GR, we obtained the full set of equations of non-relativistic cosmology, which are similar to FLRW equations in their form.
The two sets of equations, Friedmann and non-relativistic with Λ as a constant of gravitational interaction, define two flows (global and local) with different Hubble parameters. The latter can appear as the Hubble tension.
For the local Hubble flow we found the theoretical upper and lower limiting values for the Hubble parameter (i.e., for the extreme SdS and dS BHs). Then, we obtained the corresponding quantities for these limits and calculated the free energy for both of them. We concluded that for any system where the local flow has taken place the free energy must be between zero and 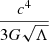 . We analyzed the Barrow-Gibbons maximum force–tension conjecture and obtained a new limit that is two times larger than the previously conjectured value and that is conceptually self-consistent with classical and relativistic notions of force and tension.
. We analyzed the Barrow-Gibbons maximum force–tension conjecture and obtained a new limit that is two times larger than the previously conjectured value and that is conceptually self-consistent with classical and relativistic notions of force and tension.
References
- Barrow, J. D., & Gibbons, G. W. 2014, MNRAS, 446, 3874 [Google Scholar]
- Bekenstein, J. D. 1981, Phys. Rev. D, 23, 287 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Capozziello, S., Faizal, M., Hameeda, M., et al. 2018, MNRAS, 474, 2430 [NASA ADS] [CrossRef] [Google Scholar]
- Capozziello, S., Benetti, M., & Spallicci, A. D. A. M. 2020, Found. Phys., 50, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Chardin, G., Dubois, Y., Manfredi, G., et al. 2021, A&A, 652, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Valentino, E., Mena, O., Pan, S., et al. 2021, Class. Quant. Grav., 38, 153001 [NASA ADS] [CrossRef] [Google Scholar]
- Eingorn, M. 2016, ApJ, 825, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Gibbons, G. W. 2002, Found. Phys., 32, 1891 [Google Scholar]
- Gibbons, G. W., & Hawking, S. W. 1977, Phys. Rev. D, 15, 2738 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gurzadyan, V. G. 1985, Observatory, 105, 42 [NASA ADS] [Google Scholar]
- Gurzadyan, V. G. 2019, Eur. Phys. J. Plus, 134, 14 [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Kocharyan, A. A. 2009, A&A, 493, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2018, Eur. Phys. J. C, 78, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2019a, Eur. Phys. J. C, 79, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2019b, Eur. Phys. J. Plus, 134, 98 [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2019c, Eur. Phys. J. C, 79, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2021a, Eur. Phys. J. Plus, 136, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2021b, Eur. Phys. J. Plus, 136, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Kopeikin, S., Efroimsky, M., & Kaplan, G. 2001, Relativistic Celestial Mechanics of the Solar System (New Jersey: Wiley) [Google Scholar]
- McCrea, W. H., & Milne, E. A. 1934, Quart. J. Math., 5, 73 [CrossRef] [Google Scholar]
- Milne, E. A. 1934, Quart. J. Math., 5, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Misner, C., Thorne, K., & Wheeler, J. A. 1973, Gravitation (San Francisco: W.H. Freeman and Co) [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stepanian, A., Khlghatyan, Sh., & Gurzadyan, V. G. 2021, Eur. Phys. J. Plus, 136, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G. 2020, Nat. Rev. Phys., 2, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2019, ApJ, 876, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Verde, L., Treu, T., & Riess, A. G. 2019, Nat. Astron., 3, 891 [Google Scholar]
- Zeldovich, Ya. B. 1981, Non-relativistic Cosmology, Editor’s appendix 1, 181, to Russian edition of S. Weinberg, The First Three Minutes, Energoizdat, Moscow (in Russian) [Google Scholar]
All Tables
Physical quantities for the theoretical upper and lower limits of the local H-flow.
All Figures
 |
Fig. 1. Penrose diagram for SdS BH. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.