| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A168 | |
| Number of page(s) | 6 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202141323 | |
| Published online | 28 September 2021 | |
Chi-squared test for planetary orbits after the impact of a single flyby and multiple stellar flybys
1
Hamburger Sternwarte,
Gojenbergsweg 112,
21029
Hamburg, Germany
2
Yatsukaho Research Center, Kanazawa Institute of Technology,
Hakusan,
Ishikawa
924-0838, Japan
e-mail: JuanJzTorres@gmail.com
Received:
16
May
2021
Accepted:
4
August
2021
Aims. In this work, I present the cumulative effects of passing stars on planetary disks and I explore the orbital modification of their components as a consequence of multiple stellar encounters. I analyze the effects of masses of the passing stars and look for differences between the effects of four encounters with low masses of 0.1 M⊙, as well as a single 0.4 M⊙ stellar encounter on a 100 a.u. planetary disk.
Methods. I applied the chi-squared (χ2) test to estimate the correlation between the resulting parameters of orbits after single and multiple impacts. I found that the χ2 value is equal to 0.666 and the probability index is equal to 0.955.
Results. This first approach suggests that three or four low-mass multiple encounters can produce comparable orbits of planets as produced by a single massive encounter.
Key words: planets and satellites: dynamical evolution and stability / planet-star interactions / protoplanetary disks / Kuiper belt: general / stars: kinematics and dynamics
© ESO 2021
1 Introduction
The effects of stellar encounters on planetary disks can significantly modify the orbital structure of their elements. The stellar dynamics of different galactic environments can determine the orbital morphology of planetary systems (Jiménez-Torres et al. 2013). For instance, in star formation clusters, the gravitational interactions between their members play a prominent role in the structure or evolution of the orbital structures (e.g., Jiménez-Torres 2021; Malmberg et al. 2007; Spurzem et al. 2009; Craig & Krumholz 2013; Breslau et al. 2014; Vincke et al. 2015). One of the most widely accepted theories for explaining the origin of the observed orbital structures in the outer Solar System, such as the Kuiper belt and distant objects, invokes the gravitational effect of a close encounter in the early Solar System (e.g., Ida et al. 2000; Pfalzner et al. 2018).
Adams et al. (2006) analyzed the dynamical evolution of stellar clusters and found that clusters with 100–1000 members in forming planetary systems produce a modest effect. They argue that the interaction rates between members are low and the planetary systems are not substantially perturbed by their environment. They conclude that the protoplanetary disks can survive their birth cluster with low perturbations. Jiménez-Torres (2020) proposes an analysis of mass densities as a function of time and found that densities from 3 × 103 M⊙ pc−3 to 1.4 × 104 M⊙ pc−3 can produce from one up to three stellar encounters on a cross-sectional area with a radius of 400 a.u. containing a 100 a.u. planetary disk in a period of 1 Myr. Adams & Laughlin (2001) calculated cross-sectional areas for planets in the outer planetary disk experiencing orbital modifications as a consequence of interactions with star systems. These authors found that cross-sectional areas with a radius of 400 a.u. can increase the orbital eccentricities and inclinations of disk particles and that areas with a radius of 130 a.u. can produce planetary ejection. They also found that Kuiper belt objects with semimajor axes of 30–70 a.u. can be scattered or affected by interactions with cross-sectional areas with a radius of 350 a.u.
Dukes & Krumholz (2012) argue that any encounter able to perturb the outer Kuiper belt would also perturb the orbit of Neptune. They believe that it is unlikely that a single encounter is capable of perturbing the outer Kuiper belt, while leaving both the orbit of Neptune and the inner Kuiper belt unperturbed. Instead of that scenario with a single encounter (e.g., Picogna & Marzari 2014; Cuello et al. 2019; Pfalzner et al. 2018; Jiménez-Torres et al. 2011, 2013), they argue that multiple encounters would be invoked and the number of encounters required would be enough to make it likely that one encounter between any of them would be close enough to modify the orbit of Neptune. This may be possible, particularly when considering that Pfalzner (2013) shows that at approximately 1 Myr, the Solar System had a probability of 15% of experiencing a close stellar encounter with an approach distance less than 100 a.u. Furthermore, Jiménez-Torres (2020) estimated a probability of 18.2% of having stellar encounters with approach distances that are smaller than 100 a.u.
Single encounters with strong effects on planetary orbits can modify the orbits of planets in the inner disk. However, a subsequent close passing star will again modify this perturbed orbit. The resulting orbit could be a similar orbit to the initial conditions before stellar impacts. Every encounter within a simulation of multiple encounters produces a specific disk dissolution and orbital modifications of disk particles, which implies that multiple encounters can produce shapes of disks that are different from those produced by a single perturbing star; that is, subsequent stellar encounters can increase or reduce the orbital modification induced by the prior encounters. Subsequent impacts may be able to slightly or dramatically modify the orbits of a previously perturbed disk. The magnitude of these subsequent modifications will depend on the masses, approach distances, impact angles, and trajectories of the perturbing stars.
In this context, I present models aimed at producing orbital structures of planetary disks by invoking multiple encounters with low-mass passing stars. This scenario fits in with the initial mass function analysis from Salpeter (1955) and Kroupa (2002), which argues that most of the newly born stars are low-mass stars.
On the other hand, we know that protoplanetary disks in birth clusters of stars are not only subject to the effects of gravitational interactions, but also the radiation fields induced by stars in the cluster. The radiation fields in star formation clusters alsoplay a prominent role in the structure and evolution of protoplanetary systems. For instance, Adams (2010) argues that radiation fields from ultraviolet radiation can produce the dissipation of the early protoplanetary system. Lee et al. (2008) argue that this ultraviolet radiation produces photodissociation of the CO in the collapsing protostars. Adams & Myers (2001) argue that crowded star formation clusters can generate environments with abundant ionizing photons to the star formation nebula. These factors can lead to an obstruction of planetary formation. Stronger radiation fields, such as those from X-ray radiation, can also alter the evolution of the circumstellar disk. In this context, Adams (2010) argue that the radiation backgrounds must not be high enough to dissipate gases in the early birth nebula of protoplanetary systems. This suggests that the protoplanetary Solar System may have formedin a moderate radiation field background. In this work, the effect of radiation on planetary disks is not taken into account. This work is only focused on a dynamical point of view. The host star and the flyby stars are assumed to be dimensionless objects. Their effective temperatures are not taken into account in the simulations.
2 Methodology
I followed the same methodology and background presented in Jiménez-Torres et al. (2013, 2011) and Jiménez-Torres (2021, 2020). In this way, I assume that planetary disks are a representation of the Solar System and that they are made of test particles distributed in orbits and phases. The sampling of disk particles follows a ∝ n−3∕2, where a is the initial radius of a particle orbit and n is the number of the orbit (e.g., Hayashi 1981).
The model assumes that the effects of disk particles are negligible and cannot significantly compete with the effects of stellar encounters. It is assumed that disk particles are affected by the gravitational forces of both the central star and the hyperbolic passing stars. The equations of motion are solved in the noninertial frame of reference centered on the host star. The model considers that the parent star, the Sun, experiences the gravitational effect of the perturbing star. The effect of the force induced by the passing star exerted on the central star produces an immediate effect on the orbits of the particles. The model considers that disk particles experience the direct force of the passing star, plus the direct force by the central star, minus the force exerted by the passing star on the Sun. The passing star experiences the force by Sun, but this is just a very low-order effect on the orbits compared to the maximum approach itself or compared to the effect of the passing star on the Sun.
To calculate the effects of multiple stellar encounters on a disk, I first modeled a single encounter on a disk with a radius of 100 a.u., whereby any resulting unbound orbits with eccentricities greater than or equal to 1 are dismissed. Then I designated the resulting positions and space velocities as initial conditions of the target disk that will be perturbed by the second encounter. The model exempts simultaneous or overlap multiple encounters and the integration time for every encounter is 104 yr.
I present the results for four 0.1 M⊙ encounters on a 100 a.u. planetary disk in a systematic way. These results are compared to the model of a single 0.4 M⊙ encounter on the disk. All of these encounters assume an approach distance of 120 a.u., impact angles α, θ, and ϕ of 45 degrees, flyby velocities of 3 km s−1, and disks with 4000 particles.
In galactic environments such as open clusters and star formation clusters, stellar densities are enough to produce up to four multiple encounters on a cross sectional area with a radius of 200 a.u. containing a 100 a.u. disk (e.g., Jiménez-Torres et al. 2013). In this way, the number of encounters equal to four is conservative.
Regarding the velocity dispersions of members in young clusters of stars, we know that some of them do not have prominent uncertainties and that they are within a small interval of uncertainties (e.g., Foster et al. 2015; Cottaar et al. 2015). Foster et al. (2015) showed that the velocity dispersion of young members (1-2 Myr) in the cluster NGC 1333 is in the order of 0.92 ± 0.12 km s−1. They find this value of velocity dispersion for members in an embedded low-mass cluster, where they can be compared to velocities of members or objects in dense and embedded star formation cores. On their part, Cottaar et al. (2015) show that members in the cluster IC 348 have velocity dispersion in the order of 0.6–0.7 km s−1. In the Orion Nebula Cluster, the velocity dispersion of their members is in the order of 3–4 km s−1 (Fűrész et al. 2006, 2008; Tobin et al. 2009). In this context, we can see that velocity dispersions of young cluster members reside within a small interval of uncertainties.
In terms of numerical realizations, the results of single stellar encounters on a planetary disk with similar flyby velocities show similar results. Thisis shown in Fig. 1, where I present resulting orbits of disk particles under the effect of five different flyby velocities from 1 km s−1 to 10 km s−1. As can be seen in Fig. 1, results from simulations with 1.5 km s−1, 2 km s−1, or 3 km s−1 velocities show similarresulting eccentricities and inclinations; that is, no significant differences for numerical models with similar flyby velocities between 1 km s−1 and 3 km s−1 are found. In this way, the assumption of constant velocities of 3 km s−1 for all members in a cluster can also be feasible as a first approach.
 |
Fig. 1 Results of single encounters on a 100 a.u. disk perturbed by a 1 M⊙ passing star for different velocities from 1.5 km s−1 to 10 km s−1. These systematic models assume an approach distance of 100 a.u., and impact angles of ϕ = 45 degrees, θ = 45 degrees, and α = 45 degrees. |
3 Results
Figure 2 shows a diagram of a single passing star over a planetary disk and a subsequent passing star over the perturbed disk. In this section, the orbits and parameters of the disk particles are presented before and after stellar impacts. The code calculates the shapes and disk dissolutions of disks under the effect of multiple encounters.
Frames in the first column in Fig. 3 show the initial conditions of disks prior to any stellar impact. Initial eccentricities and inclinations of particles are equal to zero. Orbits of disk particles are presented in X–Y and Y–Z perspectives in the first and second rows. Columns 2 to 5 correspond to the results from the four encounters with low masses (0.1 M⊙), and the last column with results from the single encounter (0.4 M⊙). The frames in Fig. 3 show the remaining disk percentage after every impact.
I carried out an additional realization of the above described numerical experiment to confirm the results seen in Fig. 3. This is because it can be expected that any single encounter can produce some unusual orbital configurations. Figure 4 shows the results from this additional realization, where the number of disk particles is set to 8000. Results presented in Fig. 4 assume the same conditions as applied in Fig. 3, but with 8000 disk particles.
The results in Figs. 3 and 4 show that the planetary disk survived under the gravitational effect of four multiple stellar encounters with low-mass stars. These results are similar to each other, however, the following analysis takes the results from Fig. 4 into account.
I find that the cumulative effects induced by the encounters produce a total disk dissolution of 17.6%. The biggest perturbation is produced by the first encounter. This is a consequence of the fragility of unperturbed disks with particles in circular orbits. The disk dissolution under multiple impacts goes from 6.2% up to 17.6%. For the 0.4 M⊙ single encounter, the disk dissolution is 11.7%.
The first encounter causes a truncation radius at 40 a.u. and eccentricities up to 0.2 in the 40–100 a.u. semimajor axis range. Inclinations exhibit a similar tendency, where they go from 0 up to 15 degrees in the 35–100 a.u. semimajor axis range. The second encounter bumps up eccentricities up to 0.35. We can see that the disk truncation happens at a semimajor axis of 40 a.u. This distance is in agreement with estimations calculated in Clarke & Pringle (1993), where they estimated that the truncation happens at a distance of one third of the approach distance of the flyby star. We see that the third, and fourth impacts resolve the most prominent orbital modification of particles in the disk from 40 a.u. to 100 a.u.
The results show that the cumulative effects of three encounters can lead to eccentricities and inclinations up to 0.4 and 30 degrees in the 80–100 a.u. semimajor range. For the 0.4 M⊙ single encounter, we can see that it produces eccentricities and inclinations up to 0.45 and 35 degrees in the outer disk. This can show that three or four low-mass passing stars could produce comparable structures as generated by a single encounter. The effect of the fourth encounter is slightly different from the effect of the third impact.
 |
Fig. 2 Diagram of a single and a subsequent stellar encounter on a planetary disk. Details are presented in Sect. 2. |
3.1 Tracking of disk particles under the effect of single and multiple encounters
As seen in Fig. 4, the third or fourth impact can produce comparable orbits to those produced by the 0.4 M⊙ single encounter. However, in the figure, we cannot see the effects induced by the encounters on specific orbits; instead, we see the total amount of orbits of disk particles after the effects of the stellar encounters.
Here, I chose five specific orbits and tracked their resulting orbital parameters, such as eccentricities and inclinations, under the gravitational effects of the single and multiple stellar encounters. The initial conditions of eccentricities and inclinations of these specific orbits are set to zero, and semimajor axes to 40 a.u. (in pink), 55 a.u. (in green), 69 a.u. (in blue), 86 a.u. (in red), and 98 a.u (in black). These particles are part of the outer planetary disk. I assumed that the inner planetary disk, particles with semimajor axes less than 30 a.u., is slightly perturbed by the stellar encounters with approach distances of 120 a.u. Therefore, it is not considered in this subsection.
The first column in Fig. 5 corresponds to the resulting eccentricities (upper frame) and inclinations (lower frame) for these specific particles under the effect of the first encounter; the second column with resulting orbits under the effect of the second encounter; the third column with resulting orbits under the effect of the third encounter; and the fourth column with resulting orbits under the effect of the fourth encounter. The last column shows results for disk particles perturbed by the single massive encounter.
As seen in Fig. 5, the eccentricities and inclinations as a consequence of four encounters progressively go from 0.15 and 10 degrees up to 0.5 and 15 degrees, respectively. This is, results show that the cumulative effect of four encounters can increaseorbital eccentricities and inclinations up to 0.5 and 15 degrees in the outer disk. For its part, the 0.4 M⊙ passing star produces eccentricities and inclinations up to 0.45 and 25 degrees in the outer disk.
These results can suggest that many of the observed orbital structures in the Solar System or planetary systems could be produced bythe effect of multiple stellar impacts in their early birth clusters, instead of a single encounter on the planetary disk.
3.2 Correlation between the resulting planetary orbits from single and multiple stellar encounters
Here, I analyzed the χ2 test to estimate the correlation between the resulting planetary orbits after the 0.4 M⊙ single encounter and orbits after the fourth impact. In particular, I compare the resulting total effect of four 0.1 M⊙ encounters and the effect of a single 0.4 M⊙ encounter on a planetary disk. Table 1 shows the final orbital parameters after the fourth impact and parameters after the single stellar encounter. Absolute errors are shown in the fifth column of Table 1.
Then I defined intervals for absolute errors with a reasonable reliability. For semimajor axes, the reliable interval is defined to 10 a.u.; the reliable interval for eccentricities is defined to 0.1, and the reliable interval for inclinations is defined to 10 degrees. Ideally, we would expect that the fifteen absolute errors in Table 1 fit these conditions well. However, we can see that two absolute error data points do not fulfill these conditions; that is, two data points cannot be accepted for this reliability assumption, while the rest can be accepted.
I defined five categories with three data points each. The five categories correspond to the five parameters shown in the second column in Table 1. According to the absolute errors shown in the fifth column in Table 1, I decided whether they are acceptable or not. This is shown in the sixth column in Table 1. Furthermore, Table 2 shows these categories, their number of accepted data, and their number of expected data.
In this context, I can determine a χ2 test to estimate the correlation between results from multiple encounters and a single encounter. The χ2 is calculated as follows:
![\[ {\chi}^2=\sum_{1}^{5} {\frac{({{\nu}_{a}} - {{\nu}_{e}}){^2}}{{\nu}_{e}}}, \]](/articles/aa/full_html/2021/09/aa41323-21/aa41323-21-eq1.png)
where νe and νa correspond to the expected frequencies and accepted frequencies, respectively. By replacing the values of Table 2, I found
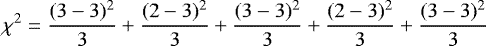
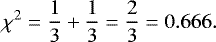
The number of degrees of freedom is (number of rows - 1)(number of columns - 1) = (5 - 1)(2 - 1) = 4. These results imply that the probability level is equal to 0.955.
 |
Fig. 3 Orbits, eccentricities and inclinations of disk particles before and after stellar impacts. First column shows the initial conditions for all experiments. Frames in Cols. 2–5 correspond to resulting orbital parameters under the effect of a single 0.4 M⊙ and four 0.1 M⊙ encounters on a planetary disk with a radius of 100 a.u. The number of disk particles is equal to 4000. |
Absolute errors between the resulting planetary orbits under the effect of single and multiple stellar impacts.
 |
Fig. 4 Orbits, eccentricities and inclinations of disk particles before and after stellar impacts. First column shows the initial conditions for all experiments. Frames in Cols. 2–5 correspond to resulting orbital parameters under the effect of a single 0.4 M⊙ and four 0.1 M⊙ encounters on a planetary disk with a radius of 100 a.u. The number of disk particles is equal to 8000. |
 |
Fig. 5 Tracking of five selected orbits after the impact of single and multiple encounters. Parameters of the perturbing stars are shown in Figs. 3 and 4. |
Total number of accepted and expected frequencies for the five categories.
4 Conclusions
The first approach employed in this work suggests that there is a fitting comparison of the results from multiple encounters and a single encounter under a reasonable assumption of reliability. Furthermore, the most prominent effects induced by a single perturbing star could be modeled with the cumulative effect induced by multiple low-mass stellar encounters.
In this work, I conclude that that the effect of multiple encounters with 0.1 M⊙ stars can reproduce similar orbital eccentricities and inclinations as produced by a 0.4 M⊙ single stellar encounter. Even though the effect of a single low-mass star could not be so disruptive, the total effect of multiple encounters plays an important role to shape and determinate the structure and orbital dynamics of planetary disks.
The disk dissolution and orbital modification of particles mainly depend on the mass, velocity, and approach distances of the passing stars. The number of encounters also plays a role in the detailed structure of the planetary disk. Every encounter contributes and plays a particular role in the final orbital structure of the planetary disk. The total effect of multiple encounters can create a different orbital shape for a planetary system to the orbital shape induced by a single stellar encounter. The modeling of the effect of multiple encounters with low-mass stars on planetary disks corresponds to a realistic scenario of a birth cluster of stars where low-mass stars represent the majority of the newly born stars.
For a future work, a more extended collection of orbits must be tracked after the impact of single and multiple flybys in order to conduct an improved analysis of the results and their correlations.
Acknowledgements
Author thanks the Hamburger Sternwarte in Germany, the Kanazawa Institute of Technology in Japan and the Instituto de Astronomía UNAM in México, where this work got started.
References
- Adams, F. C. 2010, ARA&A, 48, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., & Laughlin, G. 2001, Icarus, 150, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., & Myers, P. C. 2001, ApJ, 553, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., Proszkow, E. M., Fatuzzo, M., & Myers, P. C. 2006, ApJ, 641, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Breslau, A., Steinhausen, M., Vincke, K., & Pfalzner, S. 2014, A&A, 565, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clarke, C. J., & Pringle, J. E. 1993, MNRAS, 261, 190 [Google Scholar]
- Cottaar, M., Covey, K. R., Foster, J. B., et al. 2015, ApJ, 807, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, J., & Krumholz, M. R. 2013, ApJ, 769, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Cuello, N., Dipierro, G., Mentiplay, D., et al. 2019, MNRAS, 483, 4114 [Google Scholar]
- Dukes, D., & Krumholz, M. R. 2012, ApJ, 754, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Fűrész, G., Hartmann, L. W., Szentgyorgyi, A. H., et al. 2006, ApJ, 648, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Fűrész, G., Hartmann, L. W., Megeath, S. T., Szentgyorgyi, A. H., & Hamden, E. T. 2008, ApJ, 676, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, J. B., Cottaar, M., Covey, K. R., et al. 2015, ApJ, 799, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
- Ida, S., Larwood, J., & Burkert, A. 2000, ApJ, 528, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Torres, J. J. 2020, Acta Astron., 70, 53 [Google Scholar]
- Jiménez-Torres, J. J. 2021, Res. Notes Am. Astron. Soc., 5, 10 [Google Scholar]
- Jiménez-Torres, J. J., Pichardo, B., Lake, G., & Throop, H. 2011, MNRAS, 418, 1272 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Torres, J. J., Pichardo, B., Lake, G., & Segura, A. 2013, Astrobiology, 13, 491 [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [Google Scholar]
- Lee, J.-E., Bergin, E. A., & Lyons, J. R. 2008, Meteor. Planet. Sci., 43, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Malmberg, D., de Angeli, F., Davies, M. B., et al. 2007, MNRAS, 378, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Pfalzner, S. 2013, A&A, 549, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S., Bhandare, A., Vincke, K., & Lacerda, P. 2018, ApJ, 863, 45 [Google Scholar]
- Picogna, G., & Marzari, F. 2014, A&A, 564, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Spurzem, R., Giersz, M., Heggie, D. C., & Lin, D. N. C. 2009, ApJ, 697, 458 [Google Scholar]
- Tobin, J. J., Hartmann, L., Furesz, G., Mateo, M., & Megeath, S. T. 2009, ApJ, 697, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Vincke, K., Breslau, A., & Pfalzner, S. 2015, A&A, 577, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Absolute errors between the resulting planetary orbits under the effect of single and multiple stellar impacts.
All Figures
 |
Fig. 1 Results of single encounters on a 100 a.u. disk perturbed by a 1 M⊙ passing star for different velocities from 1.5 km s−1 to 10 km s−1. These systematic models assume an approach distance of 100 a.u., and impact angles of ϕ = 45 degrees, θ = 45 degrees, and α = 45 degrees. |
| In the text | |
 |
Fig. 2 Diagram of a single and a subsequent stellar encounter on a planetary disk. Details are presented in Sect. 2. |
| In the text | |
 |
Fig. 3 Orbits, eccentricities and inclinations of disk particles before and after stellar impacts. First column shows the initial conditions for all experiments. Frames in Cols. 2–5 correspond to resulting orbital parameters under the effect of a single 0.4 M⊙ and four 0.1 M⊙ encounters on a planetary disk with a radius of 100 a.u. The number of disk particles is equal to 4000. |
| In the text | |
 |
Fig. 4 Orbits, eccentricities and inclinations of disk particles before and after stellar impacts. First column shows the initial conditions for all experiments. Frames in Cols. 2–5 correspond to resulting orbital parameters under the effect of a single 0.4 M⊙ and four 0.1 M⊙ encounters on a planetary disk with a radius of 100 a.u. The number of disk particles is equal to 8000. |
| In the text | |
 |
Fig. 5 Tracking of five selected orbits after the impact of single and multiple encounters. Parameters of the perturbing stars are shown in Figs. 3 and 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


