EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 653 (September 2021) A&A, 653 (2021) A59 Full HTML
Open Access
Issue
A&A
Volume 653, September 2021
Article Number A59
Number of page(s) 16
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202140798
Published online 07 September 2021

© A. Bouquet et al. 2021

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

While carbonaceous chondrites (CC) are some of the most pristine materials available for studying of the origin of our solar system, they have still undergone alteration in their parent bodies as a result of exposure to fluids (Brearley 2006; Krot et al. 2015) or elevated temperatures (Huss et al. 2006). An important feature of CI, CM, and most CV chondrites is their relatively oxidized state (Brearley & Jones 1998); another feature is the presence of oxidized secondary phases in the CM and CI chondrites, attained despite the overall reducing conditions inferred from models of their geochemical evolution during aqueous alteration (Zolensky et al. 1989; Rosenberg et al. 2001). A notable example of this oxidized state in CI and CM chondrites is the presence of sulfates, in which sulfur is in the fully oxidized (+VI) form. The exact cause of the formation of these sulfates has not yet been determined. CV chondrites, on the other hand, do not feature any noticeable amount of sulfates (Gao & Thiemens 1993; Brearley 2006; Bose et al. 2017). Oxygen isotopic ratios in CM sulfates point to a pre-terrestrial origin via aqueous processes (Airieau et al. 2005). Reports in the literature change through time with regard to the presence of sulfate veins in the CI chondrite falls, suggesting that hypothetical pre-terrestrial sulfates present on the parent body were mobilized and altered once in terrestrial environments (Gounelle & Zolensky 2001). This interpretation is consistent with their oxygen isotopic composition, with a Δ17O that matches terrestrial values (Airieau et al. 2005). Formation of sulfates by disproportionation of elemental sulfur with water is unlikely; experiments indicate it would increase the δ34S (Oana & Ishikawa 1966), whereas meteoritic sulfates are depleted in 34S (Monster et al. 1965; Gao & Thiemens 1993; Labidi et al. 2017), supporting formation via oxidation of sulfides rather than S0. Pre-accretionary formation of sulfates has been suggested in Murchison (Bose et al. 2017) via irradiation of H2S and SO2 ices (Moore et al. 2007), based on slow kinetics for formation of sulfate from oxidation of HS− by water (Ohmoto & Lasaga 1982) in low-temperature environments consistent with parent body conditions.

In this study, we investigate endogenous radiolysis as a source of reactive oxidants in CC parent bodies (Cody & Alexander 2005), offering an alternate pathway to aqueous oxidation of sulfides. The source of endogenous radiolysis is the presence of radionuclides such as 26Al in the rock; the decay of these radionuclides irradiates the surrounding water and induces radiation chemistry with the potential to form products such as H2, OH, H2O2, and HO2 (Spinks & Woods 1990). The effect of this process as a source of H2 has been studied on Earth (Lin et al. 2005a,b; Blair et al. 2007; Sherwood Lollar et al. 2014) and for various planetary environments (Bouquet et al. 2017; Dzaugis et al. 2018; Ray et al. 2021). The irradiation of liquid water offers higher yields of HOx products than the irradiation of water ice (Spinks & Woods 1990), as illustrated by the modest potential for chemical modification of cometary ices by this process (Bouquet et al. 2018). The period of early aqueous alteration in CC parent bodies is correlated with intense radiation output by short-lived radionuclides 26Al and 60Fe, whose energy caused the melting of the ice in the first place. This period of aqueous alteration is thought to have begun shortly after the accretion of the parent bodies, a few million years after the formation of calcium-aluminum inclusions (CAI) (Jilly et al. 2014).

As a proxy for the oxidizing potential of endogenous radiolysis in this context, we focus on the possibility of oxidizing the CC sulfides to form sulfates. This process is known to happen in terrestrial environments (Li et al. 2016). Oxidation of pyrite into sulfates in the context of acid mine drainage is a common phenomenon and an environmental problem here on Earth (Belzile et al. 1997). The H2O2 produced byradiolysis of water has been observed to efficiently oxidize sulfur in the form of troilite (Lewis 1967), and production of sulfates from γ-irradiation of pyrite-water has been experimentally demonstrated (Lefticariu et al. 2010). Oxidation of pyrrhotite in aqueous solution has also been shown to produce sulfates (Belzile et al. 2004). To our knowledge the isotopic effect of sulfide oxidation through radiolysis has only been investigated for pyrite oxidation (Lefticariu et al. 2010; Li et al. 2016), while pyrrhotite is the most common sulfide in chondrites; this means that the isotopic composition of chondritic sulfates (with results differing between studies; see Monster et al. 1965; Gao & Thiemens 1993; Bullock et al. 2010) neither supports nor excludes a radiolytic origin. We constrain the amount of sulfates that can be formed with the calculated production of oxidants in conditions relevant to CI, CM, and CV parent bodies and compare it to the total amount of sulfur present (measured in pulverized samples, and therefore including all forms of sulfur; see Dreibus et al. 1995 for an example of the measurement methods).

In Sect. 2, we present the model of radiolytic production and the set of assumptions adopted for conditions in the CI, CM, and CV parent bodies. Section 3 is dedicated to the calculation results, and Sect. 4 discusses the implications of our findings, and examines the possibility of accreted O2 as an alternative means of production for sulfate.

2 Model and assumptions

2.1 Model of radiolytic production

To assess the potential production of oxidants and subsequently sulfates in the CC parent bodies, we use a model of radiolytic production developed for Earth and planetary applications (Hoffman 1992; Lin et al. 2005a; Blair et al. 2007; Bouquet et al. 2017, 2018). We refer the reader to these works for a more detailed explanation of the model, and we reproduce here only the main equations resulting in Yp (in molecules per unit of time per unit of volume of material) of a given product p, 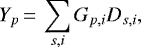(1)

where Gp,i is the experimental yield of product p due to radiation type i (e.g., 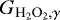is the yield of hydrogen peroxide from the irradiation of water by γ rays) in molecules per unit of energy and Ds,i is the amount of energy deposited into water by radionuclide type s emitting radiation type i, calculated as 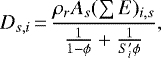(2)

where ρr is the grain density, As is the radiation activity of species s (decays per unit of time per unit of mass of rock; this is a notion separate from the thermodynamic activity), is the energy emitted by species s as radiation type i over one chain of decay (energy, we use the values tabulated in Bouquet et al. 2018), ϕ is the ratio of the volume occupied by water to the total volume (water + rock), and 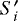is the ratio of stopping powers of radiation i (stopping power in water to stopping power in rock).

We calculate the production of the two most abundant oxidants OH and H2O2, with the following yields (all in molecules/100 eV) (Spinks & Woods 1990): GOH,β = GOH,γ = 2.72, GOH,α = 0.5, 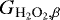= = 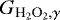0.68, 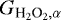= 1.45. Due to its much lower yields, we neglect the production of HO2. While O2 appears in water radiolysis experiments, it is not a primary product (Spinks & Woods 1990) and counting its yield would be redundant.

The quantity of sulfates produced is based on the amount of oxygen atoms in the oxidants produced (two H2O2 or four OH are required to form one sulfate). Ideally, the quantity of sulfates produced would be determined through a known reaction mechanism. In this section we discuss oxidation of iron monosulfides (Fe(1−x)S, for x = 0 to 0.125), since pyrrhotite is the most common sulfide in CC chondrites as indicated by recent Position Sensitive Detector-X-Ray Diffraction (PSD-XRD)studies (Bland et al. 2004; King et al. 2015; Donaldson Hanna et al. 2019). We include the discussion of oxidation involving O2. While not directly applicable to the context of endogenous radiolysis, it should be considered when assuming that significant amounts of O2 were initially present, which is the hypothesis we present in Sect. 4.2. Moreover, this is the most widelystudied sulfide oxidation process (Belzile et al. 2004), and the literature is much sparser when it comes to anoxic conditions. Significant sulfate production was observed when immersing pyrrhotite (x = 0.11) into a hydrogen peroxide solution for as little as 5 min (Buckley et al. 1985). The same study also determined that sulfates were the main product of oxidation of pyrrhotite by O2 in an ammonia solution. In the case of aqueous solutions rich in O2 (see Belzile et al. 2004 and references therein), oxidative dissolution of pyrrhotite occurs and produces sulfates, but at low pH acidic dissolution becomes important. Experiments at low pH with O2 show that a large part of the sulfides are oxidized into an elemental sulfur form, a product observed in most experimentsof pyrrhotite oxidation. Through mass balance calculation (rather than direct measurement of S0), Janzen et al. (2000) evaluate that up to 86% of the oxidized sulfides in their experiments ended up as elemental sulfur. Oxidation of CV chondrite samples in an O2 rich aqueous solution (Jones & Brearley 2006) led to the production of sulfates, with the pyrrhotite oxidation net reaction described as 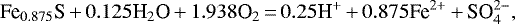(3)

which is described in more general terms by Janzen et al. (2000) for the low pH oxidation of pyrrhotite. No elemental sulfur is mentioned in the results of Jones & Brearley (2006).

While sulfate-producing oxidation of troilite (FeS) by H2O2 in aqueous, alkaline solutions has been experimentally observed (Lewis 1967), to our knowledge an exact mechanism has not been determined. Baikova et al. (2009), performing H2O2 oxidation of troilite, observed primarily the formation of elemental sulfur, sulfide ions, and thiosulfate, and hypothesized the production of sulfoxylate ions HSO, but did not discuss sulfate formation. Chiriţǎ & Descostes (2006) determined a mechanism for troilite oxidation in acidic conditions, where acidic dissolution of troilite is a key first step. The conditions of hydrothermal alteration in CC parent bodies are generally thought to be alkaline as a result of the interaction with rocks, but early acidic conditions are possible (Zolotov & Mironenko 2007). It is possible to obtain an upper bound to the amount of sulfates that can be produced by considering the net reactions to amount to 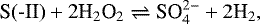(4) (5)

We also do not take into account the likely competition for oxidants from other species (Ray et al. 2021). In the case of pyrrhotite oxidation it seems inevitable that iron would get oxidized as well, and Baikova et al. (2009) observed the formation of ferric hydroxide when large amounts of H2O2 were added to their solutions. Similarly, Hamilton & Woods (1981) observed that the oxidation of pyrrhotite in alkaline solutions was strongly inhibited by the precipitation of ferric oxide onto the mineral surface; the experiments of Jones & Brearley (2006) also produced large quantities of ferric oxides. In the context of the alteration of CC parent bodies, some of the iron may have been incorporated into magnetite, which is found in large quantities in particular in CI chondrites (Hyman & Rowe 1983; Hua & Buseck 1998). In acidic conditions, ferric ions stay in solution and oxidize more pyrrhotite (Belzile et al. 2004), and the oxidation of pyrrhotite by Fe3+ at low pH actually proceeds faster than by O2 (Janzen et al. 2000). The Belzile et al. (2004) review also indicates that in numerous experiments large amounts of elemental sulfur were produced, which is at odds with its relatively low abundance in CI and CM chondrites related to sulfates and sulfides (DuFresne & Anders 1962; Kaplan & Hulston 1966; Fredriksson & Kerridge 1988; Burgess et al. 1991; Labidi et al. 2017). However, the measurements yield a wide range of different results, from 0.1 wt% (Fredriksson & Kerridge 1988) to 1.44 wt% (Kaplan & Hulston 1966); the highest values may be consistent with sulfate production being accompanied by elemental sulfur production. We therefore note that the values we obtain with our assumptions are upper limits.

2.2 Assumptions on parent bodies

The model described in Sect. 2.1 requires several inputs discussed below.

Grain density ρr

We note that the grain density values measured in CM and CI chondrites are representative of the material after alteration; the value of ρr at the onset of aqueous alteration, which is the time period to be modeled, is likely to be different and generally higher. We consider two bounds for ρr : the contemporary measured values, and 3.5 g cm−3, which corresponds to CV chondrites (anhydrous and therefore the closest direct indication available of the density of the original material).

Activity As of each species s (decays s−1 g−1)

The main input to determine is the initial amount of radionuclide type s present per unit of mass of rock; the number of decays per unit of time is a straightforward function of the half-life of s. Radionuclide abundances are determined using measurements on chondritic meteorites. The initial amount (at t = CAI) of long-lived radionuclides is determined through the present-day amount and their decay rate; the initial amount of short-lived radionuclides is a function of the present-day amount of the main stable isotope and canonical ratios: 26Al/27Al = 5.23 × 10−5 (Jacobsen et al. 2008) and 60Fe/56Fe = 1.01 × 10−8 (Tang & Dauphas 2015). While variability in the accreted 26Al/27Al ratio has been inferred from 26Al-26Mg systematics of primitive materials (Larsen et al. 2011; Nagashima et al. 2017), leading to lower 26Al abundance in CI chondrites, this variability is contested (e.g., Kita et al. 2013). We use the canonical values to provide an upper limit on oxidant production. The abundance values obtained are presented in Table 1.

Ratio ϕ

As defined in Sect. 2.1, Eq. (2), it is the ratio of the volume occupied by water to the total volume (water + rock). The initial water ice content of chondrite parent bodies is usually described using the water to rock ratio (W/R), either as a mass ratio or volume ratio. The value of ϕ can be directly derived from this value if one assumes a rock component density (value discussed below) and a liquid water density of 1.0 g cm−3.

On contemporary chondrites, in which the only water left is bound to the mineral structure, the measurement that is most closely connected to ϕ or W/R is porosity (volume of pore space divided by total volume). However the connection is not direct; the rocky component is aqueously altered, thus less dense, and simply assuming the pores are filled with water (i.e., considering ϕ = porosity) yields a W/R below the values inferred at accretion (Krot et al. 2015). As an example, the W/R of up to 1.2 (maximum derived from elemental solar ratios; Lodders 2003) inferred for CI, assuming a “dry” ρr of 3.5 g cm−3, translates into a ϕ of 0.81, considerably higher than the measured porosity of 0.35 in Orgueil (Macke et al. 2011). We also note that some of the pores seen in contemporary chondrites may have been filled with volatiles like H2 resulting from aqueous alteration (Rosenberg et al. 2001).

To bound our calculations, we adopt two end member cases: (1) the estimated W/R with ρr = 3.5 g cm−3 (dry rock case) to represent the situation at the onset of alteration more closely, and (2) contemporary values of ρr (wet rock case) along with ϕ = measured porosity to represent the end of the alteration process. Below we elaborate on our choice of values to cover case 1).

  • CI chondrites. We consider a maximum W/R (mass) of 1.2, which is the highest value allowed by solar abundances (Lodders 2003) and leads to an extreme ϕ value of 0.81. Maximum estimates are generally about three times lower. Brearley (2006) gives a W/R (mass) of 1.1–1.2, that Alexander (2019) converts into a 0.4–0.43 W/R (mass). The analysis of Alexander (2019) supports a somewhat lower W/R (mass) of 0.38 (which would translate into ϕ = 0.57). We also consider a W/R value for CI material based on the data of the Rosetta mission on comet 67P/Churyumov-Gerasimenko (hereafter 67P/C-G). Comets, as relatively unprocessed bodies, may be more representative of the early solar system material that led to CI chondrites. We consider a W/R value based on the dust-to-ice ratio measured in comet 67P/C-G; assuming a grain density of 3.5 g cm−3, the 4 ± 2 dust-to-ice mass ratio (Rotundi et al. 2015) translates into a ϕ value of 0.37–0.64. By performing our calculations with ϕ = 0.81 (maximum W/R allowed by solar system abundances) and ϕ = 0.37 (lowest value for CI-like material suggested by the data acquired at comet 67P/C-G) we cover the range of supported water content for the early solar system material that led to CI chondrites.

  • CM chondrites. We consider the range proposed by Brearley (2006): W/R (vol) = 0.3 to 0.6. This range is supported by the later analysis of Alexander (2019). It translates into ϕ = 0.22 to 0.36.

  • CV chondrites. The upper value of W/R (vol) suggested for the CV parent bodies is 1.1 (Brearley 2006) (ϕ = 0.51), on par with estimates for CI chondrites. We use this value as an upper limit, but it should be considered with caution; CV chondrites are believed to have undergone alteration at very low W/R (Krot et al. 2015). The model of Alexander (2019) yields a W/R (mass) of 0.09 (ϕ = 0.26) to explain the bulk elemental and isotopic composition of CV chondrites. We use this value as the lower bound for our calculation.

Table 1

Concentration of radionuclides used for the model (at CAI formation), and content in water, sulfur, and fraction of sulfur present as sulfates in contemporary carbonaceous chondrites.

Table 2

W/R, ϕ ratio, grain density, and accretion time used in the calculations above you use 67P/C-G; see also Fig. 1.

Ratio of stopping powers

We use as a basis the values of 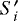considered in Bouquet et al. (2017), adapted to take into account the different ρr when needed.

In summary, we consider two families of cases. The first uses estimated W/R at accretion and assumes ρr = 3.5 g cm−3. The second case considers contemporary chondrites, but with pores filled with water, based on measurement of their properties. The set of values considered is presented in Table 2.

Accretion time–onset of aqueous alteration

The amount of short-lived radionuclides decreases sharply on the timescale of a few million years after CAI formation; therefore, the time of onset of aqueous activity in the parent body, when liquid water is available for radiolysis, is a critical factor for the total production of oxidants. A later onset translates into a smaller cumulative production. To obtain an upper bound on this production, we consider aqueous alteration to start immediately after accretion, and we neglect the smaller amounts of H2O2 and O2 that are produced by endogenous radiolysis of the ice before it melts (Bouquet et al. 2018). The most commonly supported value for the accretion of the CI and CM parent bodies is 3.0 to 4.0 Myr after CAI (see review of the literature in Desch et al. (2018); the estimates for CI and CM come mostly from Sugiura & Fujiya (2014)). To obtain an upper limit on radiolytic production, we elect to consider the earliest time of accretion (when radionuclides are more abundant); therefore, we consider 3.0 Myr after CAI formation the nominal value for CI and CM chondrites. As far as CV chondrites are concerned, while 3.0 Myr is also a supported accretion time, an earlier value of 2.5 Myr after CAI may be considered for them (Doyle et al. 2015), which we include in the “maximum porosity” cases for an estimate of the upper bound of production (see the last column of Table 2).

Sulfur content

We seek to assess what fraction of the total sulfur present in the original material can be oxidized into sulfates by radiolytically produced oxidants. We consider a total initial amount of sulfur based on chondritic values (presented in Table 1 and covering all the forms of sulfur).

The output of our model is the fraction of the initial sulfur content converted into sulfates. We then compare this value to the fraction of sulfur present in sulfate form in carbonaceous chondrites; hereafter this quantity is denoted . The study of Labidi et al. (2017) finds that 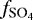= 25% for CM chondrites; since they only recovered 64% of the bulk S, Alexander (2019) suggested decreasing this value to 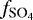= 16%. In the case of CI chondrites, studies are in close agreement on the total sulfate content: 2.1–2.6 wt% for Orgueil (DuFresne & Anders 1962; Boström & Fredriksson 1966; Kaplan & Hulston 1966; Monster et al. 1965; Fredriksson & Kerridge 1988; Burgess et al. 1991). Depending on the estimate of total sulfur content, this can translate to very different 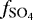values; Burgess et al. (1991) obtains a value of 74% for Orgueil, but from Fredriksson & Kerridge (1988) we deduce = 39%, with their S total value being more in line with the general literature as reviewed by Lodders et al. (1998). The value of 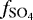is not a parameter of our calculations, but matters for interpreting the results.

3 Results

The results of calculations based on initial W/R estimates are presented in Fig. 1, and those based on contemporary measured chondritic values in Fig. 2. The maximum sulfate production (as a fraction of the available sulfur) is reached for maximum W/R. The amount of radiation emitted and the amount of available sulfur are intertwined (as both are tied to the rock component of the material) and higher W/R ensures most of the radiation energy is deposited into water and contributes to oxidant production. Therefore, the calculations based on the initial highest W/R estimates (Fig. 1) yield the larger sulfate production values.

It is apparent that none of the cases we have considered for CI and CM chondrites allow for a production that would explain the amount of sulfates observed in these chondrite types. At most 1.1% of the sulfur can be oxidized into sulfates for CM, assuming the most favorable case (lowest sulfur content, highest W/R): this would form less than 5% of the observed sulfates. The relatively flat profile of the cumulative production more than 6 Myr after CAI formation shows that the production due to long-lived radionuclides is negligible compared to the production induced by short-lived radionuclides. Considering a longer or shorter (but still >2 Myr) duration of aqueous alteration therefore does not change our results significantly. In the CI case, no more than 1.1% of the available sulfur can be converted into sulfates, an amount considerably lower than even the lowest estimate (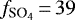%) discussed earlier. Early onset of aqueous alteration, which we considered in the CV case (2.5 Myr instead of 3 Myr) drastically increases production of oxidants compared to the nominal onset time. Even so, no more than 3.2% of the sulfur content of CVs can be oxidized into sulfate this way. We further explored the effect of an early onset of alteration (calculations not displayed), and find it is possible for the CM chondrites to match the observed 16% 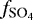if the alteration starts at 0.1 Myr after CAI, an unrealistically early time (Jilly et al. 2014).

thumbnail Fig. 1

Maximum fraction of sulfur that can be converted to sulfates through oxidation by radiolytically produced OH and H2O2, for each chondrite type, using an initial grain density of 3.5 g cm−3, assuming W/R values of 1.2 (CI), 0.4 (CI-67P), 0.1–0.6 (CM), and 0.1–0.2 (CV). The W/R = 0.2 case for CV was run assuming the earliest age of accretion of the parent body (CAI + 2.5 Myr) to obtain a maximum production; all other cases assume an accretion at CAI + 3.0 Myr (Doyle et al. 2015; Krot et al. 2015; Desch et al. 2018).
thumbnail Fig. 2

Maximum fraction of sulfur that can be converted to sulfates through oxidation by radiolytically produced OH and H2O2, for each chondrite type, using contemporary (measured) values of grain density and porosity. All the pores are assumed to be filled with water in the parent body. The high-porosity case for CV was run assuming the earliest age of accretion of the parent body (CAI + 2.5 Myr) to obtain a maximum production; all other cases assume an accretion at CAI + 3.0 Myr (Doyle et al. 2015; Krot et al. 2015; Desch et al. 2018).

4 Discussion

4.1 The role of endogenous radiolysis

Our estimates of sulfate production constitute an upper bound as they assume that all the radiolytically produced oxidants are consumed inthe production of sulfates, without taking into account other sinks for these oxidants (such as oxidation of reduced forms of iron or organic materials). We find that the radiolytic oxidants are not sufficient to explain a significant fraction of the observed sulfates in CM chondrites. If a significant part of the sulfates in CI meteorites is assumed to be extraterrestrial in origin (as opposed to being produced by oxidation while in curation), the same conclusion holds: radiolytic production can only contribute a minor amount compared to what is observed. Our calculations for CV chondrites result in an amount of sulfate representing between 0.1% and 3.3% of the total sulfur (by mole). Since no sulfate has been reported in CV meteoritic samples (Brearley 2006), it is likely that the set of assumptions leading to the lowest sulfate production (i.e., low water content and late aqueous alteration) is the closest to reality. High temperatures experienced by CV chondrites have also been proposed as a cause for the reduction of potential sulfates to sulfides or elemental sulfur (Bose et al. 2017).

4.2 Effect of accreted O2

We consider the possibility of oxidation of sulfur-bearing minerals (to include sulfides and all S-bearing phases; hereafter sulfur) by O2 contained inaccreted ice. This possibility is debatable depending on the type of CC considered. The parallel between CI chondrites and cometary bodies (specifically, between Jupiter-family comets and Orgueil) has been made before through trajectory calculation (Gounelle et al. 2006). However, the differences in isotopic ratios (see discussion below) between CI chondrites and comets point to different reservoirs and formation conditions, so this possibility should be considered cautiously. It is difficult to retain O2, a very volatile species, in solid phase in large amounts. The inferred zone of formation of CI chondrites has been estimated to be as far as 15 AU (Desch et al. 2018) at a temperature of 46 K at 3 Myr after CAI. This temperature, within the range of pressures expected in the disk, would not allow pure O2 condensation, but a CO-dominated clathrate including O2 can remain stable (Mousis et al. 2016), as can a pure O2 clathrate (calculation based on constants given in Kuhs et al. 2000). Another possibility is that mixing within the disk allowed materials that formed in the outer, colder section of the disk to be included in the formation of CC parent bodies. To retain at least a part of their molecular oxygen, these materials should be included in planetesimals large enough (kilometer size or more) to not equilibrate with the disk within the time frame of their migration and inclusion in CC parent bodies. In the case of CM chondrites, this is the most likely way to include O2 since either pure O2 ice or clathrate would be unstable at the inferred range of forming temperature of CM parent bodies, about 100 K (Desch et al. 2018).

We calculate, as a function of W/R, how much O2 in the ice is necessary to oxidize a target fraction of sulfur into sulfates (39% for CI, 25% for CM; see Table 1). This assumes that all the O2 thus accreted goes toward the oxidation of sulfur. For CI and CM, this calculation is performed for their minimum and maximum sulfur content (see Table 1; the calculation results are displayed in Fig. 3). We display the O2 content of comet 67P/C-G, with the 3.1 ± 1.1% of O2 (by number with respect to water) identified by the ROSINA mass spectrometer aboard the Rosetta mission (Bieler et al. 2015; Rubin et al. 2019), as a reference range for the possible O2 abundance in ice representative of the early solar system. Other measurements by the ALICE far-UV spectrograph also on board the Rosetta mission point toward a much higher O2 /H2O value, typically on the order of 50% (Feldman et al. 2016). However, this value is linked to outburst events, so the ROSINA values are more likely to represent the bulk O2 /H2O of the comet. Since sulfates are not observed in CV chondrites, we plot a curve with an arbitrary target sulfate fraction of 1% as a possible upper limit for the amount of O2 present in the ice accreted by CV parent bodies.

In the case of CI chondrites, Fig. 3 indicates that with W/R values within the upper range of estimates (W/R(mass) > 0.6), an O2 content comparable to the one measured in 67P/C-G by the ROSINA instrument, allows for the production of a large amount of sulfates. These numbers are compatible with accreted O2 playing a key role in forming sulfates in the CI chondrites parent body.

Calculations with values pertaining to CM chondrites similarly indicate that with W/R values compatible with literature estimates (0.3–0.6 per volume, Brearley 2006, translated into 0.09 to 0.17 per mass), it is possible their parent body accreted enough O2 to create the amount of sulfates observed now. However, the ice mixture accreted by CM parent bodies was likely not entirely unprocessed, and therefore had lost part of its most volatile compounds, which would include O2 devolatilized (Marrocchi et al. 2018). Alexander et al. (2017) propose that only 5–10% of the material would be pristine interstellar material. When considering this amount of volatile-rich ice mixture (with an O2 content comparable to comet 67P/C-G), and assuming that the rest is devoid of species more volatile than water, there would not be sufficient O2 to oxidize enough sulfur into sulfates to match the observations. This would require a much higher content of O2 in the pristine portion of the accreted ice; we calculate that the O2 content of the 10% of pristine material should be 35% for a 0.6 W/R (volume) ratio. On the other hand, this number is still below the O2 /H2O ratio measured by the ALICE far-UV spectrograph in the coma of comet 67P/C-G. However, there is no known chemical scheme that can explain such a high O2 abundance in the protosolar nebula.

The calculation for CV chondrites indicates that a low O2 content (O2 /H2O < 0.3% by numbers) is required to limit the amount of sulfate formed, which is compatible with CV parent bodies forming closer to the Sun andaccreting an ice mixture poor in the most volatile molecules, and in smaller quantity (Marrocchi et al. 2018).

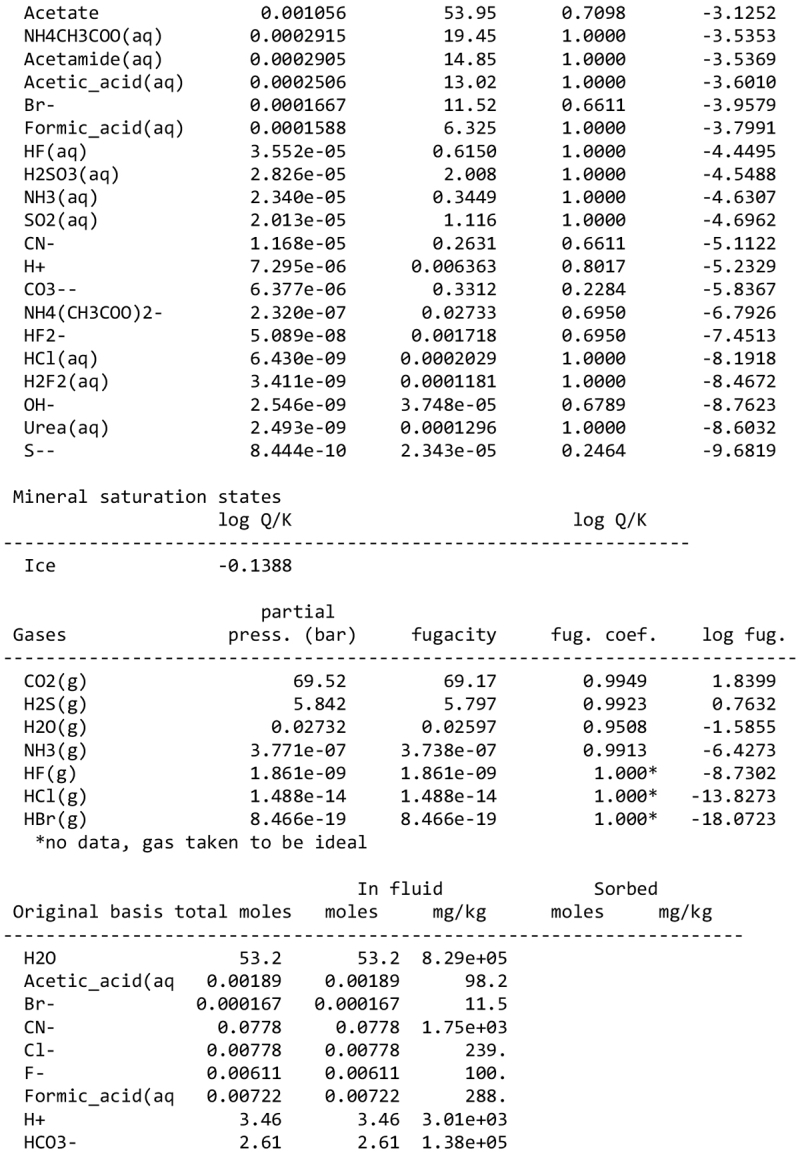
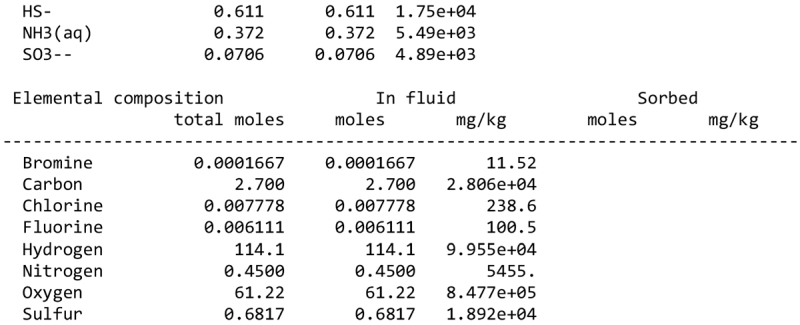
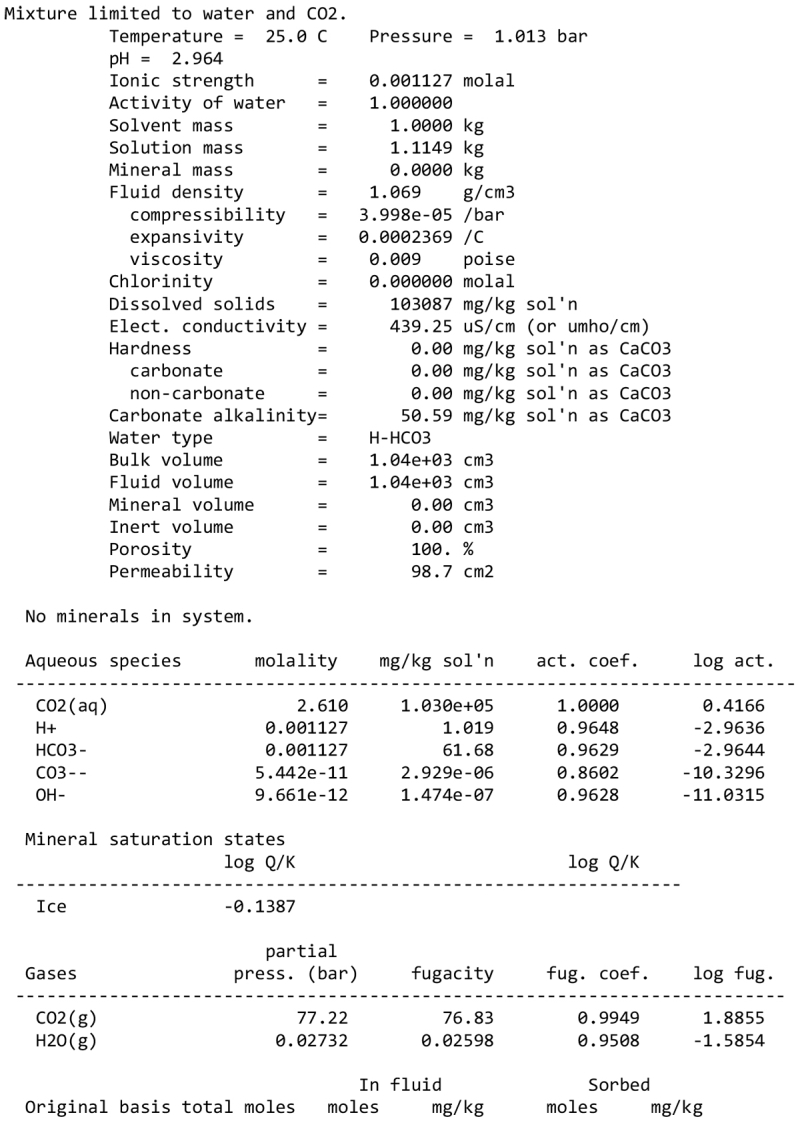
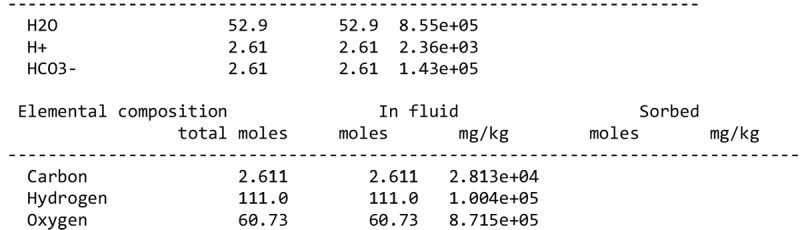
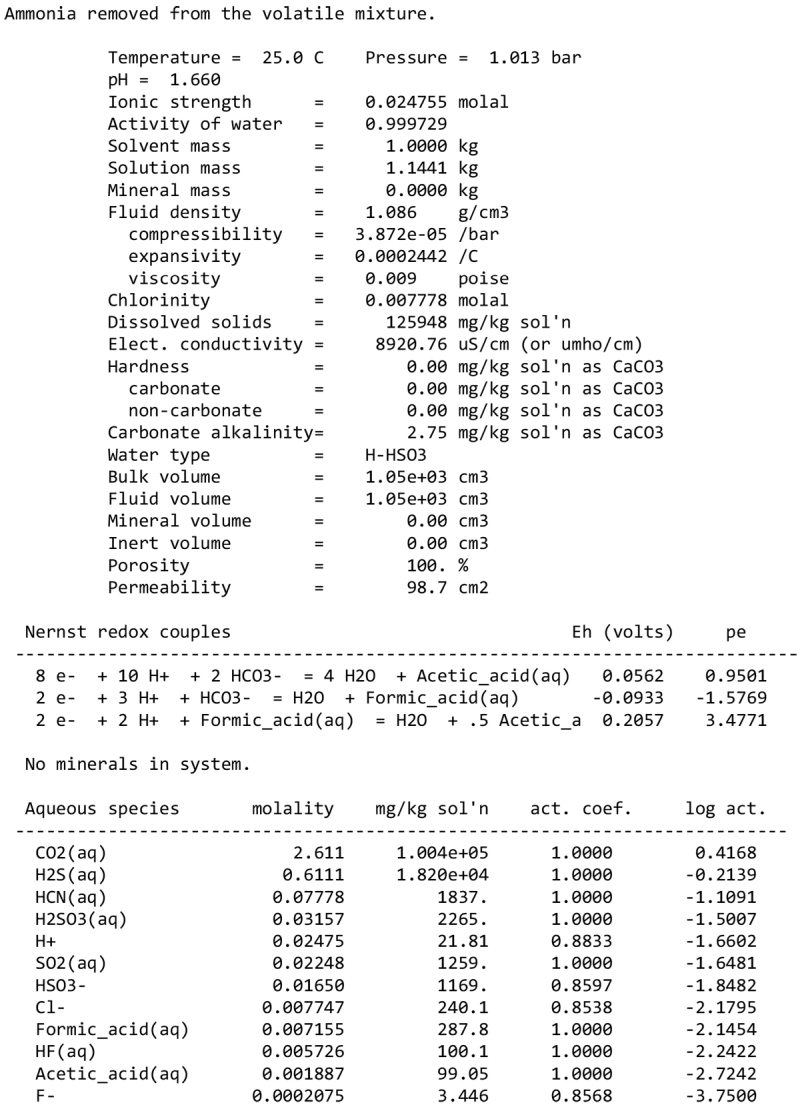
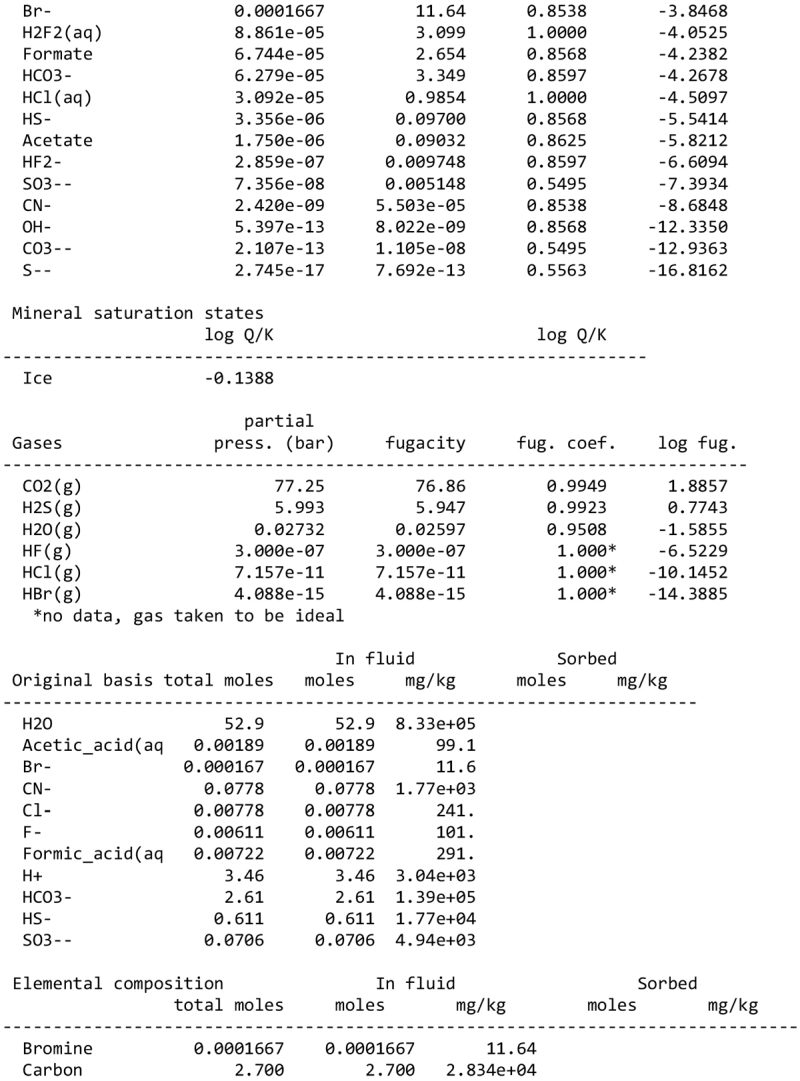
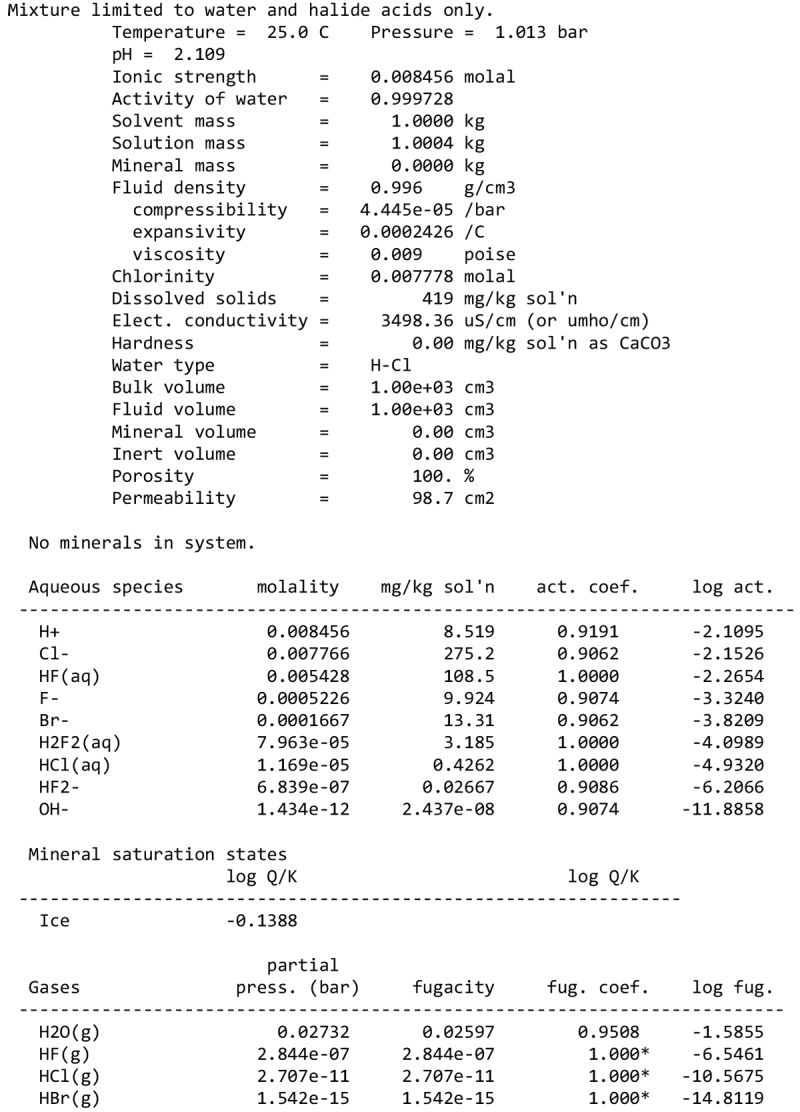
We note, however, that none of our calculations takes into account any possible competition for oxidants (see discussion in Sect. 2.1). This competition would partly depend on the pH and the fate of Fe2+ ions. Considering a scenario where the aqueous alteration comes from the melting of cometary-like ices, could the pH be initially acidic before rock–water interaction drives it toward alkaline values? We calculated the pH of an aqueous solution resulting from melting an ice with the volatile composition of comet 67P/C-G, as assessed by the ROSINA instrument (Rubin et al. 2019). We considered species that can participate in acid–base chemistry, using the SpecE8 app of the Geochemist Workbench 2021 software with the thermo.com.V8.R6+ database. No mineral or redox reactions were included and the temperature is assumed to be 25°C. The species that could be taken into account include H2O, CO2, HCOOH, CH3COOH, NH3, HCN, H2S, SO2, HF, HCl, and HBr; the species that were not included for lack of thermodynamic data all have abundances below 0.1%. The abundances of the species considered and the Geochemist Workbench outputs can be found in Appendix A. We find that the pH of this mixture is mildly acidic (~5). NH3 plays a large role in limiting the acidity; a calculation without NH3 yields a pH below 2. Calculations with only halide acids and only CO2 yield pH values of 2 and 3, respectively. Halide acids, mainly HCl, (Zolotov & Mironenko 2007) appear as the main drivers of the acidification of the solution. This indicates that variations in the amount of NH3 accreted may have allowed an initially acidic solution, letting Fe3+ act as an oxidizer of pyrrhotite in the early stages of alteration.

We now consider whether isotopic evidence matches the hypothesis of sulfate formation from accreted O2. The oxidation of sulfides into sulfates by O2 in aqueous solution is known to favor 32S (Fry et al. 1988; Eldridge & Farquhar 2018), consistent with the depletion in heavy S isotopes in chondritic sulfates compared to sulfides (Gao & Thiemens 1993; Labidi et al. 2017). Isotope exchanges of 18 O between sulfates and water are kinetically inhibited in most conditions (Lloyd 1968; Chiba & Sakai 1985; Van Stempvoort & Krouse 1994), but the fastest exchange rates observed would still allow equilibration in 103 to 105 year (Lloyd 1968). This is well within the time frame of aqueous alteration in CC parent bodies, where hotter temperatures may also have promoted faster equilibration. Exchanges between H2O and SO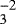, which Lloyd (1968) proposes as an intermediate in sulfate production, are also found to be much faster (on a timescale of hours). The likely outcome is that δ18 O in sulfates would mostly be a function of the δ18O of the water present. Another factor is that even in the presence of O2 the sulfates resulting from oxidation of sulfides derive their oxygen mostly (but variably) from water rather than O2 (Taylor et al. 1984; Toran & Harris 1989; Balci et al. 2007). Isotopic equilibrium between sulfate and water favors the integration of 18 O in sulfates (Lloyd 1968) to a varying degree depending on the experimental conditions. This is true for dissolved sulfates and minerals.

Isotopic ratios in cometary oxygen (in water and in molecular oxygen) are available only for comet 67P/C-G. The measured 16 O/18O = 345 ± 40 for O2 shows a very significant enrichment in 18O (Altwegg et al. 2020) compared to the terrestrial values, leading to δ18 O = +295 to +635o. Even with the rather low fraction of sulfate oxygen coming from O2, such a high value would likely be reflected in the sulfates before isotopic exchanges with water. The water ice of comet 67P/C-G also seems rich in heavy isotopes (Schroeder et al. 2019) with δ18 O between 39 to 216o. However the large error bars on this value make it statistically compatible, within 1.5 σ, with terrestrial values; therefore, no firm constraint can be derived from it.

CI chondrite sulfates are impoverished in 18 O compared to the bulk oxygen: δ18 Osulfates = +4.8o (Ivuna) and +5.4o (Orgueil) (Airieau et al. 2005) versus a bulk δ18 O of +16o (Clayton & Mayeda 1999). If sulfates were the products of oxidation driven by O2, and possibly had isotopically equilibrated with water (presumably more 18 O-rich than the bulk O content), their δ18O value should be larger than the bulk. Along with the Δ17O of CI sulfates (sitting on the terrestrial fractionation line) this could support a terrestrial origin of these sulfates.

CM chondrites show a less marked trend (Clayton & Mayeda 1999; Airieau et al. 2005), with δ18 Osulfates = +9.5o, compared tobulk values between 5 and 12 o. The primordial water in CM chondrite parent bodies has been inferred by Fujiya (2018) at δ18 O = 55 ± 13o, compatible with the range found in previous studies (Alexander et al. 2015; Guo & Eiler 2007). A scenario of production of sulfate by O2 -driven oxidation is compatible with these values, if we consider that the lower end of the bulk δ18 O value range represents the δ18O of water at the end of the alteration process, and that sulfates isotopically equilibrated with water at this late stage.

thumbnail Fig. 3

Mole fraction of O2 in accreted ice vs the W/R ratio assumed in the parent body. The plots show, for a given W/R, how much accreted O2 is necessary to oxidize enough of the total sulfur content into a quantity of sulfates consistent with contemporary measurements (see last two columns of Table 1: 16% for the CM case, 39% for the CIcase). The green part of the diagram covers the estimated range of W/R in CM parent bodies, the blue part covers the estimated W/R for CI parent bodies. The CV curve corresponds to the quantity of O2 that would lead to the oxidation of 1% of sulfur into sulfates. The red overlay represents the range of O2 abundance in the ice of comet 67P/C-G (3.1 ± 1.1%) as observed by the Rosetta mission (Rubin et al. 2019).

4.3 Conclusion

We showed that for a variety of scenarios, endogenous radiolysis can only deliver a very small contribution to the oxidation of the parent bodies of carbonaceous chondrites, as indicated by the very modest amount of sulfates that could be created through this process. Variation of key parameters such as the W/R ratio or the time for starting aqueous alteration cannot raise this contribution to a significant level unless some unrealistic values are assumed. Recent experimental evidence using Earth sediments indicates radiolysis yields may be considerably larger than those used in the present work (Sauvage et al. 2021). Considering the maximum enhanced yields, the oxidant production by endogenous radiolysis may become a larger contributor to sulfate formation (up to 11% of sulfur can be converted into sulfates in the CM case; see Appendix B) and generally to the evolution of the parent body redox state. However, this effect is highly dependent on the type of sediment considered, and its applicability to early CC parent bodies is not straightforward. Sauvage et al. (2021) suggest the catalytic effect might be due to zeolites, which to our knowledge are not expected in CC parent bodies, and calcite, which is present in CC chondrites. Experiments using the protocol of Sauvage et al. (2021) with chondritic materials would be needed to clarify this question. In the meantime, endogenous radiolysis should be considered a likely minor contributor. By contrast, solid O2 accreted with ice could account for a large proportion or even all of the sulfates formed on the parent body. The pre-accretionary origin of O2 in comet 67P/C-G is one of the best supported scenarios to date (Mousis et al. 2016; Taquet et al. 2016, 2017; Luspay-Kuti et al. 2018; Altwegg et al. 2020), allowing for its presence in ice accreted by the CC parent bodies. However, experimental evidence and reaction pathways indicate that this process would have also likely produced large amounts of elemental sulfur, but CC chondrites possess only minor amounts of it.

In the asteroid main belt, Ceres presents an interesting case of a body having undergone extensive aqueous alteration with a very high W/R ratio (Castillo-Rogez et al. 2019) that could have hosted the production of sulfates. Sulfate salts are expected to be mobile, and salt deposits on the surface would give insights into the interior. However, sulfates have not yet been firmly identified in the recent deposits of aqueously altered material on the surface of Ceres, nor can their presence be excluded (Hendrix et al. 2016; Bu et al. 2018). Modeling studies regarding Ceres indicate their formation to be highly model dependent (Neveu et al. 2017; Castillo-Rogez et al. 2018). A future mission to Ceres might be able to test for sulfates on the surface and to inform further interpretations about the process of sulfate formation in CC parent bodies. The sample return from asteroid Bennu by the OSIRIS-REx (Lauretta et al. 2017) mission may allow further exploration of this question. Bennu was chosen as the mission target for its spectral similarity to CC meteorites, and observationsby the spacecraft have confirmed the presence of aqueously altered material (Kaplan et al. 2020). The presence and amount (or absence) of sulfates in the sample to be returned will offer new insights to interpret the available data on chondrites, in particular regarding whether sulfates in CI chondrites find their origin in terrestrial alteration.

Acknowledgements

A.B. and O.M. acknowledge support by CNES. C.R.G. and K.E.M. acknowledge support from SwRI. Figures drawn with Matplotlib (Hunter 2007).

Appendix A The Geochemist’s Workbench calculation inputs

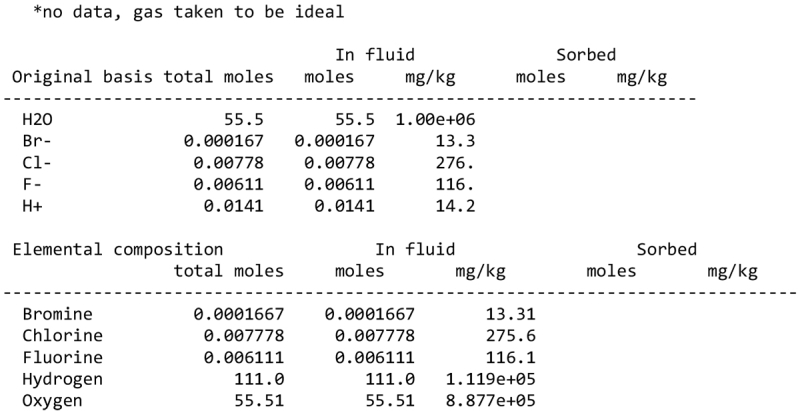
We detail inTable A.1 the volatile composition we used to assess the pH of a melt of cometary ices, based on measurements by the Rosetta mission at comet 67P/C-G.

Table A.1

Composition of cometary ices used as reference in the pH calculation of Sect. 4.2, based on Rubin et al. (2019).

The input of the GWB calculations are detailed below.

Appendix B Effect of enhanced yields in sedimentary environments

Recent experimental work (Sauvage et al. 2021) indicates that the yield of endogenous radiolysis can be greatly enhanced depending on the mineral matrix present compared with yields obtained with pure water. H2 yields can be enhanced by a factor of 27 (compared to values in pure water) in pelagic clays for α-particles

and 8.16 for γ rays in siliceous ooze. We assumed these factors also applied to oxidant yields to perform a recalculation of the results displayed in Figs. 1 and 2. As in Sauvage et al. (2021), we assumed that electron yields are enhanced by the same 8.16 factor as γ rays; however, calculations with the original electron yields (not displayed) show that the effect is not significant. Results are detailed in Figs. B.1 and B.2. We note that we applied both yield enhancements even though theypertain to different types of sediments; however, the dominant effect is the increase of yields from γ rays.

thumbnail Fig. B.1

Same calculation as Fig. 1, but using yields derived from the maximum values of Sauvage et al. (2021). The α-particle yield is enhanced by a factor of 27, and the γ-ray and electronyields by a factor of 8.16.
thumbnail Fig. B.2

Same calculation as Fig. 2, but using yields derived from the maximum values of Sauvage et al. (2021). The α-particle yield is enhanced by a factor of 27, and the γ-ray and electronyields by a factor of 8.16.

References

  1. Airieau, S., Farquhar, J., Thiemens, M., et al. 2005, Geochim. Cosmochim. Acta, 69, 4167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Alexander, C. M. 2019, Geochim. Cosmochim. Acta, 254, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Alexander, C. O., Bowden, R., Fogel, M., & Howard, K. 2015, Meteor. Planet. Sci., 50, 810 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Alexander, C. M. O., Nittler, L. R., Davidson, J., & Ciesla, F. J. 2017, Meteor. Planet. Sci., 52, 1797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Altwegg, K., Balsiger, H., Combi, M., et al. 2020, MNRAS, 498, 5855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Baikova, I., Shtamm, E., Vichutinskaya, E., & Skurlatov, Y. I. 2009, Russ. J. Phys. Chem. B, 3, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Balci, N., Shanks III, W. C., Mayer, B., & Mandernack, K. W. 2007, Geochim. Cosmochim. Acta, 71, 3796 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Belzile, N., Goldsack, D., Maki, S., & McDonald, A. 1997, in Environmental Geology of Urban Areas (Geological Association of Canada St. John’s, Canada), 223 [Google Scholar]
  9. Belzile, N., Chen, Y.-W., Cai, M.-F., & Li, Y. 2004, J. Geochem. Explor., 84, 65 [Google Scholar]
  10. Bieler, A., Altwegg, K., Balsiger, H., et al. 2015, Nature, 526, 678 [Google Scholar]
  11. Blair, C. C., D’Hondt, S., Spivack, A. J., & Kingsley, R. H. 2007, Astrobiology, 7, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bland, P. A., Cressey, G., & Menzies, O. N. 2004, Meteor. Planet. Sci., 39, 3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bose, M., Root, R., & Pizzarello, S. 2017, Meteor. Planet. Sci., 52, 546 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Boström, K., & Fredriksson, K. 1966, Smithsonian Miscellaneous Collections [Google Scholar]
  15. Bouquet, A., Glein, C. R., Wyrick, D., & Waite, J. H. 2017, ApJ, 840, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bouquet, A., Mousis, O., Teolis, B., et al. 2018, ApJ, 864, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Brearley, A. J. 2006, Meteor. Early Solar Syst. II, 943, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Brearley, A., & Jones, C. 1998, “Chondritic meteorites”, in Planetary materials, ed J. Papike, 36 (Mineralogical Society of America) [Google Scholar]
  19. Bu, C., Rodriguez Lopez, G., Dukes, C., et al. 2018, Meteor. Planet. Sci., 53, 1946 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Buckley, A.,, & Woods, R. 1985, Appl. Surf. Sci., 22, 280 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Bullock, E. S., McKeegan, K. D., Gounelle, M., Grady, M. M., & Russell, S. S. 2010, Meteor. Planet. Sci., 45, 885 [NASA ADS] [CrossRef] [Google Scholar]
  22. Burgess, R., Wright, I., & Pillinger, C. 1991, Meteoritics, 26, 55 [NASA ADS] [CrossRef] [Google Scholar]
  23. Castillo-Rogez, J., Neveu, M., McSween, H. Y., et al. 2018, Meteor. Planet. Sci., 53, 1820 [NASA ADS] [CrossRef] [Google Scholar]
  24. Castillo-Rogez, J. C., Hesse, M., Formisano, M., et al. 2019, Geophys. Res. Lett., 46, 1963 [NASA ADS] [CrossRef] [Google Scholar]
  25. Chiba, H., & Sakai, H. 1985, Geochim. Cosmochim. Acta, 49, 993 [NASA ADS] [CrossRef] [Google Scholar]
  26. Chiriţǎ, P., & Descostes, M. 2006, J. Colloid Interface Sci., 299, 260 [CrossRef] [Google Scholar]
  27. Clayton, R. N., & Mayeda, T. K. 1999, Geochim. Cosmochim. Acta, 63, 2089 [NASA ADS] [CrossRef] [Google Scholar]
  28. Cody, G. D., & Alexander, C. M. 2005, Geochim. Cosmochim. Acta, 69, 1085 [NASA ADS] [CrossRef] [Google Scholar]
  29. Desch, S. J., Kalyaan, A., & Alexander, C. M. 2018, ApJS, 238, 11 [NASA ADS] [CrossRef] [Google Scholar]
  30. Donaldson Hanna, K., Schrader, D., Cloutis, E., et al. 2019, Icarus, 319, 701 [NASA ADS] [CrossRef] [Google Scholar]
  31. Doyle, P. M., Jogo, K., Nagashima, K., et al. 2015, Nat. Commun., 6, 7444 [NASA ADS] [CrossRef] [Google Scholar]
  32. Dreibus, G., Palme, H., Spettel, B., Zipfel, J., & Wänke, H. 1995, Meteoritics, 30, 439 [NASA ADS] [CrossRef] [Google Scholar]
  33. DuFresne, E. R., & Anders, E. 1962, Geochim. Cosmochim. Acta, 26, 1085 [NASA ADS] [CrossRef] [Google Scholar]
  34. Dzaugis, M., Spivack, A. J., & D’Hondt, S. 2018, Astrobiology [Google Scholar]
  35. Eldridge, D. L., & Farquhar, J. 2018, Geochim. Cosmochim. Acta, 237, 240 [NASA ADS] [CrossRef] [Google Scholar]
  36. Feldman, P. D., A’hearn, M. F., Feaga, L. M., et al. 2016, ApJ, 825, L8 [NASA ADS] [CrossRef] [Google Scholar]
  37. Fredriksson, K., & Kerridge, J. F. 1988, Meteoritics, 23, 35 [NASA ADS] [CrossRef] [Google Scholar]
  38. Fry, B., Ruf, W., Gest, H., & Hayes, J. 1988, Chem. Geol.: Isotope Geosci. Sect., 73, 205 [CrossRef] [Google Scholar]
  39. Fujiya, W. 2018, Earth Planet. Sci. Lett., 481, 264 [Google Scholar]
  40. Gao, X., & Thiemens, M. H. 1993, Geochim. Cosmochim. Acta, 57, 3159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Gounelle, M., & Zolensky, M. E. 2001, Meteor. Planet. Sci., 36, 1321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Gounelle, M., Spurnỳ, P., & Bland, P. A. 2006, Meteor. Planet. Sci., 41, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Guo, W., & Eiler, J. M. 2007, Geochim. Cosmochim. Acta, 71, 5565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Hamilton, I., & Woods, R. 1981, J. Electroanal. Chem. Interfacial Electrochem., 118, 327 [Google Scholar]
  45. Hendrix, A. R., Vilas, F., & Li, J.-Y. 2016, Geophys. Res. Lett., 43, 8920 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Hoffman, B. 1992, in Proceedings of the 7th International Symposium on Water–Rock Interaction, 503 [Google Scholar]
  47. Hua, X., & Buseck, P. R. 1998, Meteor. Planet. Sci., 33, A215 [Google Scholar]
  48. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  49. Huss, G. R., Rubin, A. E., & Grossman, J. N. 2006, Meteor. Early Solar Syst. II, 943, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Hyman, M., & Rowe, M. 1983, J. Geophys. Res.: Solid Earth, 88, A736 [Google Scholar]
  51. Jacobsen, B., Yin, Q.-z., Moynier, F., et al. 2008, Earth Planet. Sci. Lett., 272, 353 [Google Scholar]
  52. Janzen, M. P., Nicholson, R. V., & Scharer, J. M. 2000, Geochim. Cosmochim. Acta, 64, 1511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Jarosewich, E. 1990, Meteoritics, 25, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Jilly, C. E., Huss, G. R., Krot, A. N., et al. 2014, Meteor. Planet. Sci., 49, 2104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Jones, C. L., & Brearley, A. J. 2006, Geochim. Cosmochim. Acta, 70, 1040 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Kaplan, I. R., & Hulston, J. R. 1966, Geochim. Cosmochim. Acta, 30, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Kaplan, H., Lauretta, D., Simon, A., et al. 2020, Science, 370 [Google Scholar]
  58. King, A., Schofield, P., Howard, K., & Russell, S. 2015, Geochim. Cosmochim. Acta, 165, 148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Kita, N. T., Yin, Q.-Z., MacPherson, G. J., et al. 2013, Meteor. Planet. Sci., 48, 1383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Krot, A., Nagashima, K., Alexander, C., et al. 2015, Asteroids IV, 635 [Google Scholar]
  61. Kuhs, W. F., Klapproth, A., & Chazallon, B. 2000, in Physics of Ice Core Records (Hokkaido University Press), 373 [Google Scholar]
  62. Labidi, J., Farquhar, J., Alexander, C. O., Eldridge, D., & Oduro, H. 2017, Geochim. Cosmochim. Acta, 196, 326 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Larsen, K. K., Trinquier, A., Paton, C., et al. 2011, ApJ, 735, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Lauretta, D., Balram-Knutson, S., Beshore, E., et al. 2017, Space Sci. Rev., 212, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Lefticariu, L., Pratt, L. A., LaVerne, J. A., & Schimmelmann, A. 2010, Earth Planet. Sci. Lett., 292, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Lewis, J. S. 1967, Earth Planet. Sci. Lett., 2, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Li, L., Wing, B., Bui, T., et al. 2016, Nat. Commun., 7, 13252 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Lin, L.-H., Hall, J., Lippmann-Pipke, J., et al. 2005a, Geochem. Geophys. Geosyst., 6 [Google Scholar]
  69. Lin, L.-H., Slater, G. F., Lollar, B. S., Lacrampe-Couloume, G., & Onstott, T. 2005b, Geochim. Cosmochim. Acta, 69, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Lloyd, R. 1968, J. Geophys. Res., 73, 6099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Lodders, K. 2003, ApJ, 591, 1220 [Google Scholar]
  72. Lodders, K., Fegley, B., Lodders, F., et al. 1998, The Planetary Scientist’s Companion (Oxford University Press on Demand) [Google Scholar]
  73. Luspay-Kuti, A., Mousis, O., Lunine, J. I., et al. 2018, Space Sci. Rev., 214, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Macke, R. J., Consolmagno, G. J., & Britt, D. T. 2011, Meteor. Planet. Sci., 46, 1842 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Marrocchi, Y., Bekaert, D. V., & Piani, L. 2018, Earth Planet. Sci. Lett., 482, 23 [Google Scholar]
  76. Monster, J., Anders, E., & Thode, H. 1965, Geochim. Cosmochim. Acta, 29, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Moore, M., Hudson, R., & Carlson, R. 2007, Icarus, 189, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Mousis, O., Ronnet, T., Brugger, B., et al. 2016, ApJ, 823, L41 [Google Scholar]
  79. Nagashima, K., Krot, A. N., & Komatsu, M. 2017, Geochim. Cosmochim. Acta, 201, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Neveu, M., Desch, S. J., & Castillo-Rogez, J. C. 2017, Geochim. Cosmochim. Acta, 212, 324 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Oana, S., & Ishikawa, H. 1966, Geochem. J., 1, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Ohmoto, H., & Lasaga, A. C. 1982, Geochim. Cosmochim. Acta, 46, 1727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Ray, C., Glein, C. R., Waite, J. H., et al. 2021, Icarus, 114 248 [Google Scholar]
  84. Rosenberg, N. D., Browning, L., & Bourcier, W. L. 2001, Meteor. Planet. Sci., 36, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Rotundi, A., Sierks, H., Della Corte, V., et al. 2015, Science, 347, aaa3905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Rubin, M., Altwegg, K., Balsiger, H., et al. 2019, MNRAS, 489, 594 [Google Scholar]
  87. Sauvage, J. F., Flinders, A., Spivack, A. J., et al. 2021, Nat. Comm., 12, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Schroeder, I. R., Altwegg, K., Balsiger, H., et al. 2019, A&A, 630, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Sherwood Lollar, B., Onstott, T., Lacrampe-Couloume, G., & Ballentine, C. 2014, Nature, 516, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Spinks, J. W. T., & Woods, R. J. 1990, An introduction to radiation chemistry (New York, NY, USA: John Wiley and Sons Inc) [Google Scholar]
  91. Sugiura, N., & Fujiya, W. 2014, Meteor. Planet. Sci., 49, 772 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Tang, H., & Dauphas, N. 2015, ApJ, 802, 22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Taquet, V., Furuya, K., Walsh, C., & van Dishoeck, E. F. 2016, MNRAS, 462, S99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Taquet, V., Furuya, K., Walsh, C., & van Dishoeck, E. F. 2017, Proc. Int. Astron. Union, 13, 187 [Google Scholar]
  95. Taylor, B. E., Wheeler, M. C., & Nordstrom, D. K. 1984, Geochim. Cosmochim. Acta, 48, 2669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Toran, L., & Harris, R. F. 1989, Geochim. Cosmochim. Acta, 53, 2341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Van Stempvoort, D., & Krouse, H. 1994, Environmental Geochemistry of Sulfide Oxidation (ACS Publications), 446 [Google Scholar]
  98. Zolensky, M. E., Bourcier, W. L., & Gooding, J. L. 1989, Icarus, 78, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Zolotov, M. Y., & Mironenko, M. 2007, in Lunar and Planetary Science Conference No. 1338, 2340 [Google Scholar]

All Tables

Table 1

Concentration of radionuclides used for the model (at CAI formation), and content in water, sulfur, and fraction of sulfur present as sulfates in contemporary carbonaceous chondrites.

In the text
Table 2

W/R, ϕ ratio, grain density, and accretion time used in the calculations above you use 67P/C-G; see also Fig. 1.

In the text
Table A.1

Composition of cometary ices used as reference in the pH calculation of Sect. 4.2, based on Rubin et al. (2019).

In the text

All Figures

thumbnail Fig. 1

Maximum fraction of sulfur that can be converted to sulfates through oxidation by radiolytically produced OH and H2O2, for each chondrite type, using an initial grain density of 3.5 g cm−3, assuming W/R values of 1.2 (CI), 0.4 (CI-67P), 0.1–0.6 (CM), and 0.1–0.2 (CV). The W/R = 0.2 case for CV was run assuming the earliest age of accretion of the parent body (CAI + 2.5 Myr) to obtain a maximum production; all other cases assume an accretion at CAI + 3.0 Myr (Doyle et al. 2015; Krot et al. 2015; Desch et al. 2018).
In the text
thumbnail Fig. 2

Maximum fraction of sulfur that can be converted to sulfates through oxidation by radiolytically produced OH and H2O2, for each chondrite type, using contemporary (measured) values of grain density and porosity. All the pores are assumed to be filled with water in the parent body. The high-porosity case for CV was run assuming the earliest age of accretion of the parent body (CAI + 2.5 Myr) to obtain a maximum production; all other cases assume an accretion at CAI + 3.0 Myr (Doyle et al. 2015; Krot et al. 2015; Desch et al. 2018).
In the text
thumbnail Fig. 3

Mole fraction of O2 in accreted ice vs the W/R ratio assumed in the parent body. The plots show, for a given W/R, how much accreted O2 is necessary to oxidize enough of the total sulfur content into a quantity of sulfates consistent with contemporary measurements (see last two columns of Table 1: 16% for the CM case, 39% for the CIcase). The green part of the diagram covers the estimated range of W/R in CM parent bodies, the blue part covers the estimated W/R for CI parent bodies. The CV curve corresponds to the quantity of O2 that would lead to the oxidation of 1% of sulfur into sulfates. The red overlay represents the range of O2 abundance in the ice of comet 67P/C-G (3.1 ± 1.1%) as observed by the Rosetta mission (Rubin et al. 2019).
In the text
thumbnail Fig. B.1

Same calculation as Fig. 1, but using yields derived from the maximum values of Sauvage et al. (2021). The α-particle yield is enhanced by a factor of 27, and the γ-ray and electronyields by a factor of 8.16.
In the text
thumbnail Fig. B.2

Same calculation as Fig. 2, but using yields derived from the maximum values of Sauvage et al. (2021). The α-particle yield is enhanced by a factor of 27, and the γ-ray and electronyields by a factor of 8.16.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.