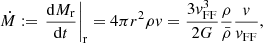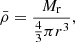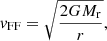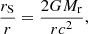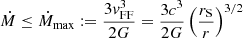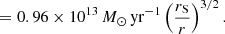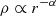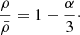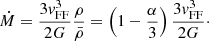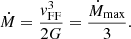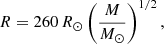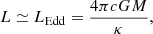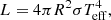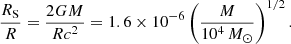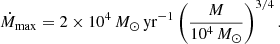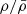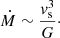| Issue |
A&A
Volume 652, August 2021
|
|
|---|---|---|
| Article Number | L7 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202141376 | |
| Published online | 06 August 2021 | |
Letter to the Editor
Maximum accretion rate of supermassive stars
1
Département d’Astronomie, Université de Genève, Chemin des Maillettes 51, 1290 Versoix, Switzerland
e-mail: lionel.haemmerle@unige.ch
2
Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
3
Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen, Im Neuenheimer Feld 205, 69120 Heidelberg, Germany
4
Center for Theoretical Astrophysics and Cosmology, Institute for Computational Science, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland
Received:
25
May
2021
Accepted:
20
July
2021
Context. The formation of the most massive quasars observed at high redshifts requires extreme inflows of gas down to the length scales of the central compact object.
Aims. Here we estimate the maximum inflow rate allowed by gravity down to the surface of supermassive stars, the possible progenitors of these supermassive black holes.
Methods. We use the continuity equation and the assumption of spherical symmetry and free fall to derive the maximum allowed inflow rates for various density profiles. We apply our approach to the mass–radius relation of rapidly accreting supermassive stars to estimate an upper limit to the accretion rates allowed during the formation of these objects.
Results. We find that, as long as the density of the accreted gas is smaller than or equal to the average density of the accretor, the maximum allowed rate, Ṁmax, is given uniquely by the compactness of the accretor. We argue that a density inversion between accreting matter and the accretor is inconsistent with gravitational collapse. For the compactness of rapidly accreting supermassive stars, Ṁmax is related to the stellar mass, M, by a power law, Ṁmax ∝ M3/4. The rates of atomically cooled halos (0.1−10 M⊙ yr−1) are allowed as soon as M ≳ 1 M⊙. The largest rates expected in galaxy mergers (104 − 105 M⊙ yr−1) become accessible once the accretor is supermassive (M ≳ 104 M⊙).
Conclusions. These results suggest that supermassive stars can accrete up to masses > 106 M⊙ before they collapse via the general-relativistic instability. At such masses, the collapse is expected to lead to the direct formation of a supermassive black hole, even within metal-rich gas, resulting in a black hole seed that is significantly heavier than in conventional direct collapse models for atomic cooling halos.
Key words: stars: massive / stars: formation / gravitation
© ESO 2021
1. Introduction
The existence of quasars at redshift ∼7 that host supermassive black holes (SMBHs) with masses ≳109 M⊙ (Mortlock et al. 2011; Bañados et al. 2018; Wang et al. 2018, 2021; Yang et al. 2020) implies extreme inflow rates down to small length scales at the centre of the host galaxy during the early stages of galaxy formation. The age of the Universe at redshift 7 is about half a billion years, so these black holes must have gained mass at an average rate exceeding ∼1 M⊙ yr−1. Only few astrophysical scenarios can lead to such high accretion rates. In scenarios relying on seed black holes of only tens to hundreds of solar masses formed by the collapse of metal-free Population III stars at z > 20, this cannot be sustained due to the ionising bubbles that easily stifle accretion (Haemmerlé et al. 2020). In direct collapse scenarios, a significantly more massive black hole seed results from the collapse of a precursor object assembled via high inflow rates (e.g. Woods et al. 2019; Haemmerlé et al. 2020). The most studied of these scenarios relies on inflows driven by the gravitational collapse of protogalaxies hosted in primordial, atomically cooled halos, reaching temperatures of ∼104 K (e.g. Bromm & Loeb 2003; Dijkstra et al. 2008; Latif et al. 2013; Regan et al. 2016, 2017), at which the ratio of the Jeans mass to the free-fall time gives typical inflow rates of 1 M⊙ yr−1. These rates are found down to 0.01 − 0.1 pc in hydrodynamical simulations (Latif et al. 2013; Chon et al. 2018; Patrick et al. 2020). This scenario requires efficient dissociation of molecular hydrogen to avoid widespread fragmentation, which would suppress the gas inflow; this in turn demands rather special environmental conditions (Woods et al. 2019). More recently, another scenario has been found that does not need the same restrictive conditions. Hydrodynamical simulations have shown that the merger of massive, gas-rich galaxies at redshifts 8−10 can trigger gas inflow as high as 104 − 105 M⊙ yr−1 down to the resolution limit of 0.1 pc (Mayer et al. 2010, 2015; Mayer & Bonoli 2019).
The formation of the black hole seed represents a critical step in the formation of the earliest SMBHs (e.g. Woods et al. 2019; Haemmerlé et al. 2020). The most important parameter is its mass, which is key for the efficiency of further accretion (e.g. Rees 1978, 1984; Volonteri & Begelman 2010; Volonteri 2010; Valiante et al. 2017; Zhu et al. 2020). It also determines the possible observational signatures of SMBH formation (Liu et al. 2007; Shibata et al. 2016; Uchida et al. 2017; Sun et al. 2017, 2018; Li et al. 2018). The direct progenitor of SMBHs in the abovementioned scenarios is thought to be a supermassive star (SMS) that grows by accretion up to masses ≳105 M⊙ (Hosokawa et al. 2012, 2013; Sakurai et al. 2015; Umeda et al. 2016; Woods et al. 2017; Haemmerlé et al. 2018a,b, 2019) and eventually collapses through the general-relativistic (GR) instability (Chandrasekhar 1964). Its mass at collapse depends sensitively on the accretion rate (Haemmerlé 2020, 2021a,b). In particular, rates ≳100 − 1000 M⊙ yr−1 are required for final masses ≳106 M⊙. This mass threshold allows a supernova explosion to be avoided even with a significant abundance of metals (Montero et al. 2012), which might be present in massive galaxies at redshifts 8−10.
The hydrodynamical simulations of atomically cooled halos and galaxy mergers are limited to a resolution of 0.01−0.1 pc. In contrast, the radius of rapidly accreting SMSs is expected to be of the order of hundreds of AU (Hosokawa et al. 2012, 2013; Schleicher et al. 2013; Haemmerlé et al. 2018a), which is one to two orders of magnitude smaller. The detailed properties of the accretion flow in the gap between the resolution limit and the accretion shock rely on complex non-axisymmetric hydrodynamics and depend on the thermal properties of the inflowing gas. However, we show in the present work that an upper limit for the accretion rate, given uniquely by the compactness of the accretor, arises from the fact that purely gravitational collapse cannot exceed free fall and always proceeds from lower- to higher-density regions. The uniqueness of this accretion rate reflects Newton’s theorem, according to which the gravitational acceleration in a spherical field is independent of the surrounding mass. When spherical symmetry is broken, torques are known to facilitate the collapse by removing angular momentum. This process decreases the outwards centrifugal acceleration, but the inwards acceleration is always ensured by the gravity of the central mass only. Moreover, strong departures from spherical symmetry are generally associated with radial velocities significantly below free fall since part of the momentum is locked in orbital motion. Thus, we can consider the spherically symmetric case as the optimal case for rapid accretion. When combined with the mass–radius relation of rapidly accreting SMSs, this maximum accretion rate is given uniquely by the mass of the SMS and implies an upper limit for this mass, as a consequence of the GR instability. The method relies on a simple application of the equation of continuity and is detailed in Sect. 2. The numerical estimates of the maximum accretion rates are presented in Sect. 3. The implications of these results are discussed in Sect. 4, and we summarise our conclusions in Sect. 5.
2. Method
According to the equation of continuity, the spherical inflow of mass in a sphere of radius r is given by the density of the material ρ and its inwards radial velocity v evaluated at r:
where Mr is the mass enclosed inside r. In Eq. (1) we have expressed the density and the velocity in dimensionless form, as fractions of the average density inside r and the free-fall velocity in r:
where G is the gravitational constant. The free-fall velocity vFF is the speed that the layer with mass coordinate Mr would have at r if it collapsed from infinity without facing a pressure gradient. Thus, it is the maximum velocity that pure gravitational attraction can produce. It is given uniquely by the compactness of the mass, Mr, defined by
where rS = 2GMr/c2 is the local Schwarzschild radius and c the speed of light.
Equation (1) shows that, without density inversion (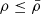 ), the inflow rate triggered by gravity (v ≤ vFF) has an upper limit, given uniquely by the free-fall velocity (Eq. (3)) at radius r, that is, by the compactness (Eq. (4)) of the mass Mr:
), the inflow rate triggered by gravity (v ≤ vFF) has an upper limit, given uniquely by the free-fall velocity (Eq. (3)) at radius r, that is, by the compactness (Eq. (4)) of the mass Mr:
Only a density inversion large enough to ensure 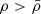 would allow this limit to be exceeded. This condition requires more than local density inversion, dρ/dr > 0, and is inconsistent with gravitational collapse, in which matter flows from low-density to high-density regions. If at a given point
would allow this limit to be exceeded. This condition requires more than local density inversion, dρ/dr > 0, and is inconsistent with gravitational collapse, in which matter flows from low-density to high-density regions. If at a given point 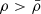 , it implies that the local free-fall time,
, it implies that the local free-fall time, 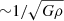 , is shorter than the global one,
, is shorter than the global one, 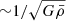 , such that the gas collapses locally faster than towards the centre. In this case, the higher-density material will fragment. The result is the formation of a stellar cluster, and the limit of Eq. (5) should hold for each star of the cluster. The conditions
, such that the gas collapses locally faster than towards the centre. In this case, the higher-density material will fragment. The result is the formation of a stellar cluster, and the limit of Eq. (5) should hold for each star of the cluster. The conditions 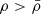 and v > vFF might be met only with an external trigger, such as an implosion or highly supersonic convergent flows. While these processes play a significant role in building the initial conditions for pre-stellar collapses (Mac Low & Klessen 2004; Klessen & Glover 2016; Girichidis et al. 2020), in all the existing scenarios of star formation the collapse is driven by gravity because an attractive force is required for the convergence of the flows to be maintained down to the small length scales of protostars.
and v > vFF might be met only with an external trigger, such as an implosion or highly supersonic convergent flows. While these processes play a significant role in building the initial conditions for pre-stellar collapses (Mac Low & Klessen 2004; Klessen & Glover 2016; Girichidis et al. 2020), in all the existing scenarios of star formation the collapse is driven by gravity because an attractive force is required for the convergence of the flows to be maintained down to the small length scales of protostars.
The maximum rate (Eq. (5)) is reached for free fall with homogeneous density ρ = cst. This last assumption is easily replaced by any power law
with α < 3. The limit α → 3 corresponds to infinite mass concentration Mr = cst. The models of isothermal collapse suggest density profiles with α ≃ 2 (Larson 1969; Penston 1969; Shu 1977; Whitworth & Summers 1985; Mac Low & Klessen 2004). For a given α, the ratio 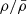 is constant:
is constant:
Inserting Eq. (8) into Eq. (1), we find a free-fall rate (v = vFF) of
In the limit α → 3, the rate goes to zero, reflecting the infinitesimal amount of mass near r compared to the central mass for such centralised distribution. For α = 2, we obtain a correction factor of 1/3 compared to the homogeneous case:
The maximum accretion rates of Eqs. (5) or (9) are given uniquely by the compactness of the accretor, that is, by its mass and its radius (Eq. (4)). It can be reduced to a M − Ṁ relation, provided we also have a mass–radius relation for the accretor. The mass–radius relation of rapidly accreting SMSs can be approximated by a power law (Hosokawa et al. 2012),
which reproduces the numerical models well for any accretion rate Ṁ ≳ 0.01 M⊙ yr−1 and for masses ≲105 M⊙ (Hosokawa et al. 2012, 2013; Haemmerlé et al. 2018a, 2019). The fact that the mass–radius relation reduces to a unique power law, independent of the accretion rate, results from the evolution along the Eddington and Hayashi limits. High accretion rates favour large radii, so rapidly accreting SMSs evolve as ‘red supergiant protostars’ (Hosokawa et al. 2013), with a nearly constant effective temperature. On the other hand, the luminosity of SMSs is always close to the Eddington limit,
where κ = cst is the opacity, dominated by electron scattering. By definition, the effective temperature is related to the luminosity and the radius by
where σ is the Stefan-Boltzmann constant. Thus, a constant Teff and L ∝ M implies R ∝ M1/2. Relation (11) is found for κ = 0.35 cm2 g−1 and Teff = 5000 K, which is typical for red supergiants. Inserting this relation with r = R and Mr = M into expressions (5) or (9), we obtain the maximum accretion rates of SMSs consistent with gravity (i.e. the rates of free fall as a function of the mass of the accretor) for different density profiles.
3. Results
The mass–radius relation (Eq. (11)) gives the following compactness for maximally accreting SMSs:
Inserting Eq. (14) into Eq. (5), we obtain
This limit is shown as a solid black line in Fig. 1. The maximum rate obtained for a density profile with α = 2 (Eq. (10)) is shown as a dashed black line, and that for 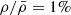 (Eq. (9)) as a dotted black line. A profile with α = 2 reduces the rate by 1/3 only compared to the homogeneous case, following Eq. (10). Obviously, the rate is decreased by two orders of magnitude for
(Eq. (9)) as a dotted black line. A profile with α = 2 reduces the rate by 1/3 only compared to the homogeneous case, following Eq. (10). Obviously, the rate is decreased by two orders of magnitude for 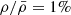 . We see that rates ≳100 M⊙ yr−1 always need masses ≳10 M⊙, even in the most favourable situation of a homogeneous density profile. For very steep density profiles, the minimum mass rapidly increases, reaching ∼104 M⊙ for
. We see that rates ≳100 M⊙ yr−1 always need masses ≳10 M⊙, even in the most favourable situation of a homogeneous density profile. For very steep density profiles, the minimum mass rapidly increases, reaching ∼104 M⊙ for 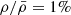 . Rates as high as 104 − 105 M⊙ yr−1 require a supermassive accretor even for homogeneous density, whereas for
. Rates as high as 104 − 105 M⊙ yr−1 require a supermassive accretor even for homogeneous density, whereas for 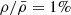 the minimum mass exceeds 106 M⊙.
the minimum mass exceeds 106 M⊙.
 |
Fig. 1. Maximum accretion rates of SMSs following the mass-radius relation (Eq. (11)), as a function of their mass, for different ratios |
4. Discussion
4.1. Impact of the mass–radius relation
While the maximum rate of expression (5), as a function of the compactness (Eq. (4)), relies only on the assumptions v ≪ vFF and 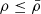 , the maximum rate (Eq. (15)), expressed as a function of the mass only, also depends on the choice of the mass–radius relation (Eq. (11)). This assumption represents the main caveat of our approach. The models of rapidly accreting SMSs (Hosokawa et al. 2012, 2013; Haemmerlé et al. 2018a, 2019), which reproduce this mass–radius relation well for M ≲ 105 M⊙, are based on several assumptions that might not be satisfied in the case of extreme accretion. In particular, the ram pressure from the accretion flow, which is neglected in these models, might lead to compressed, more compact SMSs. As a consequence of their higher compactness, such SMSs could accrete at larger rates than those following the relation in Eq. (11). From Eq. (5), the maximum rate scales with (M/R)3/2, so allowing for a rate ten times higher requires a compression by a factor of ∼5. This is a significant factor, but, because of the large density contrasts in SMSs, it requires only the outer percent of the stellar mass to be compressed. The study of such compressed SMSs is beyond the scope of the present work, but the results of Sect. 3 do show that rates above the limit of Eq. (15) might only be reached by a new class of SMSs, while rates below this limit remain consistent with existing models.
, the maximum rate (Eq. (15)), expressed as a function of the mass only, also depends on the choice of the mass–radius relation (Eq. (11)). This assumption represents the main caveat of our approach. The models of rapidly accreting SMSs (Hosokawa et al. 2012, 2013; Haemmerlé et al. 2018a, 2019), which reproduce this mass–radius relation well for M ≲ 105 M⊙, are based on several assumptions that might not be satisfied in the case of extreme accretion. In particular, the ram pressure from the accretion flow, which is neglected in these models, might lead to compressed, more compact SMSs. As a consequence of their higher compactness, such SMSs could accrete at larger rates than those following the relation in Eq. (11). From Eq. (5), the maximum rate scales with (M/R)3/2, so allowing for a rate ten times higher requires a compression by a factor of ∼5. This is a significant factor, but, because of the large density contrasts in SMSs, it requires only the outer percent of the stellar mass to be compressed. The study of such compressed SMSs is beyond the scope of the present work, but the results of Sect. 3 do show that rates above the limit of Eq. (15) might only be reached by a new class of SMSs, while rates below this limit remain consistent with existing models.
4.2. Accretion rates of direct collapse
Two channels of direct collapse have been studied in the literature: the gravitational collapse of primordial, atomically cooled halos (e.g. Bromm & Loeb 2003; Dijkstra et al. 2008; Latif et al. 2013; Regan et al. 2016, 2017) and the merger of two equal-mass gas-rich galaxies (Mayer et al. 2010, 2015; Mayer & Bonoli 2019). In the first scenario, metal-free gas is found to collapse with mass inflow rates 0.1−10 M⊙ yr−1 down to at least 0.01−0.1 pc (Latif et al. 2013; Chon et al. 2018; Patrick et al. 2020). The collapse proceeds nearly isothermally for most of the halo, which results in density profiles of ρ ∼ r−2. But in the inner ∼105 M⊙, the density profile is found to be approximately flat (Latif et al. 2013). In this case, the inflows of 0.1−10 M⊙ yr−1 appear fully consistent with accretion down to the radius of an SMS. Indeed, Fig. 1 shows that for both profiles, flat or ρ ∼ r−2, these rates are consistent with free fall as soon as M ≳ 1 M⊙.
Much larger rates are found in the case of galaxy mergers. The deep potential well resulting from the merger leads to the formation of a supermassive disc of ∼109 M⊙, which accretes at rates of 104 − 105 M⊙ yr−1 (Mayer et al. 2010, 2015; Mayer & Bonoli 2019). The disc has a radius of a fraction of a parsec, which corresponds to a compactness of ∼10−4. Inserting this value into Eq. (5), we obtain a maximum allowed accretion rate of ∼107 M⊙ yr−1 for homogeneous density. The hydrodynamical simulations show local fluctuations in the density profiles due to instabilities and inhomogeneities in the disc, but on average it follow the relation ρ ∼ r−2 down to the resolution limit of 0.1 pc. As seen in Eq. (10), the maximum rates in this case are decreased by a factor of three compared to the homogeneous case (i.e. it remains in the same order of magnitude). We see that the rates found in the hydrodynamical simulations, ranging up to 105 M⊙ yr−1, represent only about one percent of the maximum accretion rate allowed by gravity. Equation (5) indicates that a compactness rS/r ≳ 10−6 is a prerequisite for such inflows. A star that obeys the mass–radius relation (Eq. (11)) must already be supermassive (≳104 − 105 M⊙) in order to accrete at rates ∼104 − 105 M⊙ yr−1 (Eq. (15)). On the other hand, rates above the upper limit for atomically cooled halos (≳10 − 100 M⊙ yr−1) are consistent with pure gravitational attraction as soon as the mass of the accretor is ≳10 M⊙.
4.3. Maximally accreting SMSs
The properties of stars accreting at rates ≥100 M⊙ yr−1 have been studied in Haemmerlé et al. (2019). For such accretion rates, the evolutionary timescales are so short that entropy losses remain negligible, and the evolution is governed by accretion. The star contracts adiabatically, as a result of the mass increase at the surface, which implies a growing pressure in the centre. The response of the core to the changes at the surface requires the pressure excess to be communicated inwards by sound waves. If the characteristic time for accretion is shorter than the sound-crossing time, hydrostatic equilibrium is not ensured. The evolution proceeds dynamically and depends on the properties of the accretion flow. We call this regime ‘dynamical accretion’. In Haemmerlé et al. (2019), we estimate the limit of this regime on the basis of hydrostatic stellar models at constant accretion rates, corrected by accounting for the finite sound speed.
The limits of dynamical accretion in the whole star and in the envelope only are shown in Fig. 1 as solid and dashed grey lines, respectively. An object of given mass M formed at a given constant rate Ṁ can be in equilibrium only if the values of M and Ṁ are below these curves. Between the two limits, the core is expected to have reached equilibrium, while the envelope remains dynamical due to the slow sound speed in the coldest layers. Above the upper limit, even the core has not converged to local equilibrium. We see that these limits correspond approximately to the maximum accretion rates obtained in Sect. 3. The regime of full dynamical evolution can only be marginally reached with maximal accretion. It should be noted, however, that these limits have been derived under the assumption of constant accretion rates that are above Ṁmax of Eq. (15) at the beginning of the run, when M is small. Interestingly, we see that the limit of dynamical accretion in the envelope corresponds approximately to the maximum rates for density profiles with 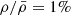 . This density contrast is typical of the outer layers of rapidly accreting SMSs (Haemmerlé et al. 2018a). Thus, dynamical evolution in the envelope would require a larger
. This density contrast is typical of the outer layers of rapidly accreting SMSs (Haemmerlé et al. 2018a). Thus, dynamical evolution in the envelope would require a larger 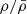 outside of the accretion shock than in the envelope (i.e. a local density inversion near the stellar surface). The coincidence between these various limits shows that inflow rates, which would prevent SMSs from evolving in equilibrium, are not produced by gravitational collapse alone. Reaching the regime of dynamical accretion necessarily implies a strong ram pressure at the accretion shock.
outside of the accretion shock than in the envelope (i.e. a local density inversion near the stellar surface). The coincidence between these various limits shows that inflow rates, which would prevent SMSs from evolving in equilibrium, are not produced by gravitational collapse alone. Reaching the regime of dynamical accretion necessarily implies a strong ram pressure at the accretion shock.
4.4. GR instability and the maximum mass of SMSs
Figure 1 also indicates the limit to equilibrium arising from GR instability in the case of spherical, non-rotating SMSs accreting at constant rates. This constraint was derived in Haemmerlé (2020); Haemmerlé (2021a) from the hydrostatic GENEC models of Haemmerlé et al. (2018a, 2019), which follow the evolution up to the instability only for rates 1−10 M⊙ yr−1. The final mass for the other rates is estimated by extrapolation of the tracks (Haemmerlé 2020). The intersection between the limit in M given by the GR instability and that in Ṁ obtained in the present work gives a maximum value for both quantities. In the absence of models at the largest rates, this intersection can be estimated only by extrapolation in M. Figure 1 suggests an upper limit for the rate of around 106 M⊙ yr−1 and a maximum mass of 106 − 107 M⊙ in the optimal cases of homogeneous or ρ ∝ r−2 profiles. For a density contrast 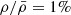 , the maximum permitted rate remains below 104 M⊙ yr−1, and the mass very rarely exceeds 106 M⊙.
, the maximum permitted rate remains below 104 M⊙ yr−1, and the mass very rarely exceeds 106 M⊙.
The impact of rotation on the GR instability in rapidly accreting SMSs has been addressed in Haemmerlé (2021b). Supermassive stars accreting at rates of atomically cooled halos are expected to increase their final mass by a factor of a few because of rotation and to always remain < 106 M⊙. Rates ≳100 M⊙ yr−1 are required to exceed this threshold, and in this case final masses as high as 108 − 109 M⊙ could be reached. Figure 1 shows that these rates are accessible before the GR instability is reached, even without rotation and even for the steep density profile 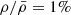 . It should be noted that the rotation velocities required to reach masses of ∼109 M⊙ always represent < 2% of the Keplerian velocity. Thus, even in this case the assumption of spherical symmetry, used to derive the maximum rate (Eq. (15)), remains relevant, and the centrifugal barrier only weakly influences our estimates.
. It should be noted that the rotation velocities required to reach masses of ∼109 M⊙ always represent < 2% of the Keplerian velocity. Thus, even in this case the assumption of spherical symmetry, used to derive the maximum rate (Eq. (15)), remains relevant, and the centrifugal barrier only weakly influences our estimates.
4.5. Jeans instability and maximum accretion rate
The expression of the maximum rate in Eq. (5), as a function of the free-fall velocity, takes a similar form as the isothermal rate of Shu (1977), given instead by the sound speed 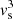 as
as
This rate follows naturally from the free fall of isolated Jeans masses Ṁ ∼ Mj/tFF. For systems with M ≫ MJ, larger rates are found, which scale roughly linearly with the number of Jeans masses contained in the cloud (Girichidis et al. 2011). The collapse of atomically cooled halos is set by the Jeans instability, and the typical inflows found in hydrodynamical simulations are consistent with the thermal rate of Eq. (16). In the absence of molecular hydrogen, primordial gas is thought to reach temperatures of ∼104 K, which corresponds to a sound speed of ∼10 km s−1 and a typical rate of 1 M⊙ yr−1 (Latif et al. 2013). In contrast, the large inflows found in simulations of galaxy mergers (Mayer et al. 2010, 2015; Mayer & Bonoli 2019) rely on the dynamics of the merger and are not set by the Jeans instability. The most massive galaxies at redshift 8−10 (∼1012 M⊙) are typically four to five orders of magnitude more massive than primordial mini-halos (∼107 − 8 M⊙) but have similar Jeans masses, MJ. If the rate scales linearly with MJ, we naturally obtain accretion rates of 104 M⊙ yr−1 and above. This shows that these rates are a natural outcome of self-gravitating systems of these masses and temperatures. The hydrodynamical simulations show highly supersonic inflows at the centre of the potential well during the merger, which illustrates the fact that vFF ≫ vs and implies that the free-fall rate (Eq. (5)) of such configurations exceeds the thermal rate (Eq. (16)). However, the fact that the rates of Eq. (5) are not exceeded shows that the supersonic inflows are driven by the self-gravity of the system and that they do not rely on departures from spherical symmetry. Asymmetries are key for removing the angular momentum, but this only allows the centrifugal barrier that itself arises from departures from spherical symmetry to be alleviated. The sound speed reflects the thermal content of the collapsing gas, which sets the Jeans mass, while the maximum rate of Eq. (5) is expressed only in terms of gravitational quantities, without any assumption on the thermodynamics. Thus, it represents an absolute limit that cannot be exceeded by gravity.
5. Summary and conclusions
We have used the equation of continuity to derive the maximum accretion rates allowed by pure gravitational collapse for which the conditions v ≤ vFF and 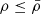 are always satisfied. Our limits assume spherical symmetry, which we consider as the optimal case for rapid accretion. These maximum allowed accretion rates are uniquely determined by the compactness (Eq. (4)) of the accretor. If the mass-radius relation of the accretor is known, this maximum accretion rate is directly given by the mass of the accretor.
are always satisfied. Our limits assume spherical symmetry, which we consider as the optimal case for rapid accretion. These maximum allowed accretion rates are uniquely determined by the compactness (Eq. (4)) of the accretor. If the mass-radius relation of the accretor is known, this maximum accretion rate is directly given by the mass of the accretor.
With the mass–radius relation (Eq. (11)) of rapidly accreting SMSs, we estimated the maximum permitted accretion rates as a function of their mass, M (Ṁ ∝ M3/4; see Eq. (15)). The accretion rates 0.1−10 M⊙ yr−1 of atomically cooled halos are consistent with gravitational infall once the central mass exceeds 1 M⊙. Larger rates can be reached only once the star is massive (M ≳ 10 M⊙). Rates as large as 104 − 105 M⊙ yr−1 can only be achieved once the accretor has become supermassive (M ≳ 104 M⊙). For stars following such maximal accretion, we estimate the GR instability to be reached at masses M ∼ 106 − 107 M⊙ in the non-rotating case, and up to M ∼ 108 − 109 M⊙ with rotation. At these masses, the instability is expected to lead to the direct formation of a SMBH even in the case of metal-rich chemical composition, in agreement with the galaxy merger scenario for direct collapse.
Acknowledgments
LH has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 833925, project STAREX). RSK acknowledges financial support from the German Research Foundation (DFG) via the collaborative research center (SFB 881, Project-ID 138713538) “The Milky Way System” (subprojects A1, B1, B2, and B8), from the Heidelberg Cluster of Excellence “STRUCTURES” in the framework of Germany’s Excellence Strategy (grant EXC-2181/1, Project-ID 390900948), and from the ERC via the ERC Synergy Grant “ECOGAL” (grant 855130).
References
- Bañados, E., Venemans, B. P., Mazzucchelli, C., et al. 2018, Nature, 553, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Bromm, V., & Loeb, A. 2003, ApJ, 596, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1964, ApJ, 140, 417 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chon, S., Hosokawa, T., & Yoshida, N. 2018, MNRAS, 475, 4104 [CrossRef] [Google Scholar]
- Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Federrath, C., Banerjee, R., & Klessen, R. S. 2011, MNRAS, 413, 2741 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Offner, S. S. R., Kritsuk, A. G., et al. 2020, Space Sci. Rev., 216, 68 [CrossRef] [Google Scholar]
- Haemmerlé, L. 2020, A&A, 644, A154 [CrossRef] [EDP Sciences] [Google Scholar]
- Haemmerlé, L. 2021a, A&A, 647, A83 [CrossRef] [EDP Sciences] [Google Scholar]
- Haemmerlé, L. 2021b, A&A, 650, A204 [CrossRef] [EDP Sciences] [Google Scholar]
- Haemmerlé, L., Woods, T. E., Klessen, R. S., Heger, A., & Whalen, D. J. 2018a, MNRAS, 474, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Haemmerlé, L., Woods, T. E., Klessen, R. S., Heger, A., & Whalen, D. J. 2018b, ApJ, 853, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Haemmerlé, L., Meynet, G., Mayer, L., et al. 2019, A&A, 632, L2 [CrossRef] [EDP Sciences] [Google Scholar]
- Haemmerlé, L., Mayer, L., Klessen, R. S., et al. 2020, Space Sci. Rev., 216, 48 [CrossRef] [Google Scholar]
- Hosokawa, T., Omukai, K., & Yorke, H. W. 2012, ApJ, 756, 93 [Google Scholar]
- Hosokawa, T., Yorke, H. W., Inayoshi, K., Omukai, K., & Yoshida, N. 2013, ApJ, 778, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Glover, S. C. O. 2016, Saas-Fee Advanced Course, 43, 85 [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. C. 2013, MNRAS, 436, 2989 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J.-T., Fuller, G. M., & Kishimoto, C. T. 2018, Phys. Rev. D, 98, 023002 [Google Scholar]
- Liu, Y. T., Shapiro, S. L., & Stephens, B. C. 2007, Phys. Rev. D, 76, 084017 [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L., & Bonoli, S. 2019, Rep. Progr. Phys., 82, 016901 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L., Kazantzidis, S., Escala, A., & Callegari, S. 2010, Nature, 466, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L., Fiacconi, D., Bonoli, S., et al. 2015, ApJ, 810, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Montero, P. J., Janka, H.-T., & Müller, E. 2012, ApJ, 749, 37 [CrossRef] [Google Scholar]
- Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Patrick, S. J., Whalen, D. J., Elford, J. S., & Latif, M. A. 2020, MNRAS, submitted [arXiv:2012.11612] [Google Scholar]
- Penston, M. V. 1969, MNRAS, 144, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J. 1978, The Observatory, 98, 210 [NASA ADS] [Google Scholar]
- Rees, M. J. 1984, ARA&A, 22, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, J. A., Johansson, P. H., & Wise, J. H. 2016, MNRAS, 459, 3377 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, J. A., Visbal, E., Wise, J. H., et al. 2017, Nat. Astron., 1, 0075 [CrossRef] [Google Scholar]
- Sakurai, Y., Hosokawa, T., Yoshida, N., & Yorke, H. W. 2015, MNRAS, 452, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., Palla, F., Ferrara, A., Galli, D., & Latif, M. 2013, A&A, 558, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibata, M., Sekiguchi, Y., Uchida, H., & Umeda, H. 2016, Phys. Rev. D, 94, 021501 [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [Google Scholar]
- Sun, L., Paschalidis, V., Ruiz, M., & Shapiro, S. L. 2017, Phys. Rev. D, 96, 043006 [Google Scholar]
- Sun, L., Ruiz, M., & Shapiro, S. L. 2018, Phys. Rev. D, 98, 103008 [Google Scholar]
- Uchida, H., Shibata, M., Yoshida, T., Sekiguchi, Y., & Umeda, H. 2017, Phys. Rev. D, 96, 083016 [CrossRef] [Google Scholar]
- Umeda, H., Hosokawa, T., Omukai, K., & Yoshida, N. 2016, ApJ, 830, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Agarwal, B., Habouzit, M., & Pezzulli, E. 2017, PASA, 34, e031 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M. 2010, A&ARv, 18, 279 [Google Scholar]
- Volonteri, M., & Begelman, M. C. 2010, MNRAS, 409, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F., Yang, J., Fan, X., et al. 2018, ApJ, 869, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F., Yang, J., Fan, X., et al. 2021, ApJ, 907, L1 [Google Scholar]
- Whitworth, A., & Summers, D. 1985, MNRAS, 214, 1 [Google Scholar]
- Woods, T. E., Heger, A., Whalen, D. J., Haemmerlé, L., & Klessen, R. S. 2017, ApJ, 842, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. E., Agarwal, B., Bromm, V., et al. 2019, PASA, 36, e027 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, J., Wang, F., Fan, X., et al. 2020, ApJ, 897, L14 [Google Scholar]
- Zhu, Q., Li, Y., Li, Y., et al. 2020, ArXiv e-prints [arXiv:2012.01458] [Google Scholar]
All Figures
 |
Fig. 1. Maximum accretion rates of SMSs following the mass-radius relation (Eq. (11)), as a function of their mass, for different ratios |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.