| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | L13 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202141394 | |
| Published online | 30 July 2021 | |
Letter to the Editor
On negative mass cosmology in General Relativity
Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Circuito Exterior CU, AP 70-543, México DF 04510, Mexico
e-mail: najera.sebastian@ciencias.unam.mx, aldojavier@ciencias.unam.mx, celia.escamilla@nucleares.unam.mx
Received:
26
May
2021
Accepted:
1
July
2021
In this Letter we present strong arguments in favour of thoroughly revising the negative mass cosmology (NMC), which has been proposed as a simple alternative explanation of dark energy and dark matter effects, within the framework of general relativity. We show that there are various physical predictions of this model which require fine-tuning in order to make them compatible with current cosmological surveys. In this way, the original motivation of the NMC model becomes obscured due to the imposition of fine-tuned unknown variables. We conclude that a more rigorous theoretical treatment is needed in order to make the NMC a viable cosmological model.
Key words: cosmology: theory / dark energy / dark matter / cosmology: observations / cosmology: miscellaneous
© ESO 2021
1. Introduction
A wide variety of observations currently favour the standard model of cosmology Λ cold dark matter (ΛCDM), for which one of its intrinsic theoretical problems is the nature of the dark sector of the Universe. Through the years, several proposals that span from theoretical and observational points of view have treated this issue successfully, in fact too many that giving fair references in this introduction would be an extensive task. In this Letter, we focus our discussion on one particular proposal: a physical model involving continuously created negative masses in cosmology (Farnes 2018), which we denote as negative mass cosmology (NMC). This proposal is presented as an alternative explanation to the dark sector of the Universe in a unified framework based on a Robertson-Walker (RW) geometry.
The existence of negative masses is not a new idea (Bondi 1957; Bonnor 1989). Moreover, problems with theorems of energy conditions naturally occur (see e.g. Schon & Yau 1979; Witten 1981). Nevertheless, the existence of physical phenomena, which violate some of these theorems, led one to question their validity (see e.g. Barcelo & Visser 2002 for a review on violations of various energy conditions). Thus, despite its peculiarity, the proposal of negative masses has been used in several physical scenarios. For example, it has been used to replace dark energy by a negative matter action (Petit & d’Agostini 2014), and, in a Schwarzschild space–time, it has been found that there is no direct connection between the regions settled by the negative and positive masses (Bondarenko 2019).
Both positive and negative masses can coexist in the Universe under the framework of general relativity (GR), which assumes the validity of the weak equivalence principle. This assumption naturally leads to the conclusion that positive mass particles attract all massive particles, and negative mass particles repel all massive particles (Bondi 1957). However, the coexistence of negative and positive masses triggers a peculiar phenomenon known as runaway motion, where two particles of equal and opposite mass produce a constant acceleration of the system towards the positive mass particle. This effect could have serious implications on structure formation and the expansion of the Universe. Therefore, we believe that a serious and rigorous analysis of this effect is pertinent and should be performed.
Before starting this analysis, we should mention that the NMC model presented by Farnes (2018) has received some strong criticism, for example Socas-Navarro (2019) identified several inconsistencies of this model with cosmological observations, such as incorrect galactic halo masses, runaway galactic motions, or a different rate of cosmological structure formation. Also, Stepanian (2019) carried out a heuristic analysis of the NMC model considering energy conditions and observations from the early Universe, resulting in a mismatch. However, our analysis discussed in this Letter goes beyond these ideas.
This Letter is structured as follows. In Sect. 2, we present a brief review of the NMC model, as well as some problems that arise in this proposal. Section 3 shows a rigorous treatment of the runaway motion present in the NMC model. Finally, in Sect. 4, we discuss the obtained results.
2. Negative mass cosmology
In the NMC model, the total density parameter can be written as the contribution of each component of the Universe as
where ΩM+, ΩM−, and ΩΛ are the critical density parameters of positive mass, negative mass, and cosmological constant, respectively, and Ωk = 1 − Ω is the curvature critical density parameter.
In this Universe, we can have the following three different scenarios: (i) a positive-mass dominated Universe, |ΩM+| > |ΩM−|; (ii) a massless cosmology, |ΩM+| = |ΩM−|, in which there is an equal number of positive and negative particles; and (iii) a negative-mass dominated Universe, |ΩM+| < |ΩM−|, with special attention given to the latter scenario as it deals with a possible cosmological constant effect produced by the continuously created negative masses and thus there is no need for a cosmological constant (Λ = 0).
As it is standard in a RW space-time, the Friedmann equation is given by1
where H is the Hubble parameter, κ = 8π, a is the scale factor, k is the curvature parameter, ρ+ is the positive mass density, and ρ− is the negative mass density associated with a pressure p− through an equation of state w− = p−/ρ− for the negative masses. Throughout this Letter, we leave w− general, unless specifically stated. According to the NMC model presented by Farnes (2018), in the case where Λ ≠ 0, there is a degeneracy between ΩM− and ΩΛ, which is given by Ωdegen = ΩM− + ΩΛ, and it is claimed that in a conventional ΛCDM cosmology, we are measuring this degeneracy. Thus, by considering ΩM− to be zero, we are falsely inferring a Λ instead of a negative mass density parameter.
The degeneracy previously shown can be discriminated by the equation of state w− of the negative masses, which yields w− = 0 for non-relativistic matter. To resolve this degeneracy, the NMC model considers that negative matter is constantly created by adding a matter creation term to the Einstein field equations with Λ. This results in an effective equation of state for the negative mass fluid in which weff ≠ 0. By adding the creation term, the Einstein field equations,
where Gab is the Einstein’s tensor and gab is the RW metric, are modified so that the energy-momentum tensor Tab is
with ρ being the total mass density, p being the total pressure, and
an effective pressure caused by the creation of negative mass particles, where Γ is the creation rate which, in principle, could depend on space and/or time. The associated continuity equation for the negative masses is
See, for example, Pan et al. (2016) for additional details on the background creation of particles in cosmology. We note that the NMC model with Γ = 0 refers to the conventional negative mass cosmology within GR without the creation of negative mass particles.
The effective equation of state parameter for a Universe in which matter is constantly created resembles that of a cosmological constant when Γ = 3H. Therefore, this NMC toy model has what appears to be an effective cosmological constant Λ− := 8πGρ− < 0. If we consider ρ+ = Λ = 0 in this toy model, we can obtain the evolution of the scale factor in a negative mass-dominated cosmology from Eq. (2). The solution corresponds to an anti-de Sitter (AdS) Universe that undergoes a cycle of expansion and contraction with a timescale of 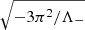 . This cyclic cosmology does not match with our current observations, however Farnes (2018) argues that there are two possible explanations for this: (i) either the Universe is so large that the local geometry appears to be flat, or (ii) the presence of negative matter and its creation would modify the CMB anisotropies. Both arguments would make the NMC toy model compatible with early time observations. A few examples that employ this NMC toy model are included in formation simulations for dark matter halos, structure formation simulations, and also in galaxy rotation curves by means of cosmological N-body simulations. Aside from this toy model, more research is needed in order to understand the origin, the properties, and the value of the creation rate Γ.
. This cyclic cosmology does not match with our current observations, however Farnes (2018) argues that there are two possible explanations for this: (i) either the Universe is so large that the local geometry appears to be flat, or (ii) the presence of negative matter and its creation would modify the CMB anisotropies. Both arguments would make the NMC toy model compatible with early time observations. A few examples that employ this NMC toy model are included in formation simulations for dark matter halos, structure formation simulations, and also in galaxy rotation curves by means of cosmological N-body simulations. Aside from this toy model, more research is needed in order to understand the origin, the properties, and the value of the creation rate Γ.
Going a step forward and without assuming a specific form of Γ, we can say more about this NMC model by analysing the deceleration parameter defined by 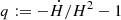 . Thus, using Eq. (2), the deceleration parameter for this model is given by
. Thus, using Eq. (2), the deceleration parameter for this model is given by
which is independent of the curvature parameter k. Current observations (Riess et al. 1998; Perlmutter et al. 1999) support the idea that the Universe goes through a late cosmic acceleration expansion, so we must have the correct combination of variables in Eq. (7) to get q(z = 0) < 0. For the NMC toy model, with Λ = 0 and Γ = 3H, Eq. (7) gives
which is independent of w−. We notice here that q > 0 is preserved; therefore, the NMC toy model does not allow for an accelerated expansion. This result leads us to reject this toy model as a viable cosmological scenario, since several observations apart from supernovae Type Ia as baryon acoustic oscillations (Bassett & Hlozek 2009), clusters of galaxies (Astier & Pain 2012), and gravitational waves as standard sirens (Abbott et al. 2017) along with the standard cosmography approach at low redshifts (Escamilla-Rivera & Capozziello 2019) confirm this cosmic acceleration.
Moreover, it is always possible to choose different values for Γ, ΩΛ, and even w− (if we try to give a more exotic nature to the negative masses) to get the required accelerated expansion. Nevertheless, the choices for these values might be non-physical and they would significantly increase the complexity of the problem and would erase the initial motivation of a NMC model as a simple alternative explanation of the dark sector.
Following the above general ideas, a final comment can be made for a negative-mass dominated cosmology (i.e. |ρ−| ≫ ρ+) with Λ = 0. From Eq. (1), these assumptions imply k = −1 and thus it is not always possible to have physical solutions compatible with observations (see comments below), since H2 could take negative values. In particular, in a negative dust Universe without the creation of particles (w− = 0, Γ = 0), H2 changes sign in
with Ωi, 0 = Ωi|t = 0, where the subindex i denotes each fluid component. The same pathology occurs in the case Λ > 0, where once again H2 could become negative for a value of a > 0. Using similar arguments, H2 could still be negative when considering radiation and the creation of negative mass particles because ρ− < 0 independently of w− and Γ, as can be shown from Eq. (6). Therefore, within the NMC model, we have a Universe which could begin with a finite size. Nevertheless, we know from estimations of the early Universe in the standard ΛCDM model that the Universe must begin from a very compact and dense state (Weinberg 2008; Ellis et al. 2012) to be able to predict cosmological observables, such as the abundances of primordial nuclei (Cyburt et al. 2016; Steigman 2007; Iocco et al. 2009) and other early universe observations (Aghanim et al. 2020; Cruz & Escamilla-Rivera 2021). In this way, we must fine-tune the nature of ρ− and Γ in order to make the NMC scale factor compatible with these observables.
3. Runaway motion
Considering co-moving coordinates and a smooth one-parameter family of geodesics γs(t), we denote the unit time-like tangent vector field to the family of geodesics as 𝒯a = (∂/∂t)a, such that 𝒯a𝒯a = −1, and the separation vector between nearby geodesics as Xa = (∂/∂r)a, which satisfies the orthogonality property 𝒯aXa = 0. In this way, the geodesic deviation equation is
where Aa = 𝒯c∇cva = 𝒯c∇c(𝒯b∇bXa) is the relative acceleration between nearby geodesics and  is the Riemann tensor. In particular, it is well known that for fundamental observers in RW space–times, Aa = −qH2(∂/∂r)a. Since q = q(t) and H = H(t), the relative acceleration must be common to all observers, and due to the symmetries of the RW metric we must deal with other geometries in order to estimate the effects of runaway motion.
is the Riemann tensor. In particular, it is well known that for fundamental observers in RW space–times, Aa = −qH2(∂/∂r)a. Since q = q(t) and H = H(t), the relative acceleration must be common to all observers, and due to the symmetries of the RW metric we must deal with other geometries in order to estimate the effects of runaway motion.
We now consider the particular case of negative and positive particles in an arbitrary space–time. Using the expansion of the Riemann tensor
where Cabcd is the Weyl tensor and Rab is the Ricci tensor, we can rewrite Eq. (10) as
Since the Weyl tensor is related to free space and the Ricci scalar is related to the energy–momentum tensor through the Einstein field equations, we can divide the geodesic deviation equation into acceleration due to free space 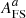 and acceleration due to matter
and acceleration due to matter  , defined by
, defined by
If we consider that the acceleration is solely due to matter and use the Einstein field equations  and R = −κT, then Eq. (14) reads as
and R = −κT, then Eq. (14) reads as
where we have used T = gabTab = −ρ + 3p, with the energy density ρ = uaubTab, the isotropic pressure p = (gab + uaub)Tab, and the definition of the spatial energy flux vector 𝒬a := −𝒯bTab.
So far, the matter content has been completely general. We restrict it to a special case. We consider the matter content as two compact fluids, the first composed of matter with positive density and the second with negative density. These fluids are separated such that we can neglect gravitational effects due to the opposite fluid and thus we can consider both as co-moving. With these assumptions, we can rewrite the energy-momentum tensor as
and from Eq. (15), we get
These results can be corroborated with Ellis & Van Elst (1999) for positive masses and a FRW geometry. Thus, observers near positive particles will be attracted, while observers in a neighbourhood of the negative particles will be repelled. Physically, this represents the so-called runaway motion. Moreover, using the NMC’s effective energy–momentum tensor in Eq. (4), 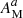 reads as
reads as
and considering w− = 0, the latter equation can be reduced to
therefore, we obtain analogous results to the dust case. We notice that, unlike the fundamental observers in RW space–times, the relative acceleration in Eqs. (17)–(19) is not homogeneous nor isotropic, hence in a NMC model with  , we have a positive relative acceleration between nearby geodesics, which could cause non-linear effects in the velocity perturbations. Thus, structure formation in this kind of cosmology becomes a fine-tuning problem.
, we have a positive relative acceleration between nearby geodesics, which could cause non-linear effects in the velocity perturbations. Thus, structure formation in this kind of cosmology becomes a fine-tuning problem.
4. Concluding remarks
In this Letter we thoroughly analysed a NMC model which arise as an alternative, simpler, and unified explanation of the dark sector of the Universe, within the context of general relativity, and with a possible background of continuously created negative mass particles. We found that this model requires fine-tuning in order to predict a late cosmological accelerated expansion, to have a Hubble parameter defined in the whole cosmic redshift range expected from early Universe observations, and to allow structure formation. Moreover, we discarded the reviewed model with a negative mass creation rate of Γ = 3H because it does not predict late accelerated expansion; this particular choice of Γ had been used to explain and numerically model the effects of dark energy and dark matter. In its current state, the NMC model requires a more concise theoretical formulation before being considered as a viable model of the Universe which can be tested with cosmological surveys.
Acknowledgments
AA, AG and SN acknowledge financial support from CONACYT postgraduate grants program. CE-R acknowledges the Royal Astronomical Society as FRAS 10147 and by DGAPA-PAPIIT-UNAM Project IA100220. This article is also based upon work from COST action CA18108, supported by COST (European Cooperation in Science and Technology). The ideas treated in this Letter were derived from a discussion in the lecture entitled “Aplicaciones Astrofísicas y Cosmológicas de la Relatividad General” at ICN-UNAM.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Nature, 551, 85 [Google Scholar]
- Aghanim, N., Akrami, Y., Ashdown, M., et al. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astier, P., & Pain, R. 2012, C. R. Phys., 13, 521 [CrossRef] [Google Scholar]
- Barcelo, C., & Visser, M. 2002, Int. J. Mod. Phys. D, 11, 1553 [CrossRef] [Google Scholar]
- Bassett, B. A., & Hlozek, R. 2009, ArXiv e-prints [arXiv: 0910.5224] [Google Scholar]
- Bondarenko, S. 2019, Mod. Phys. Lett. A, 34, 1950084 [CrossRef] [Google Scholar]
- Bondi, H. 1957, Rev. Mod. Phys., 29, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnor, W. B. 1989, Gen. Relat. Gravit., 21, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz, N. J., & Escamilla-Rivera, C. 2021, Eur. Phys. J. Plus, 136, 1 [CrossRef] [Google Scholar]
- Cyburt, R. H., Fields, B. D., Olive, K. A., & Yeh, T.-H. 2016, Rev. Mod. Phys., 88, 015004 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, G. F., & Van Elst, H. 1999, On Einstein’s Path (Springer), 203 [CrossRef] [Google Scholar]
- Ellis, G. F., Maartens, R., & MacCallum, M. A. 2012, Relativistic Cosmology (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Escamilla-Rivera, C., & Capozziello, S. 2019, Int. J. Mod. Phys. D, 28, 1950154 [NASA ADS] [CrossRef] [Google Scholar]
- Farnes, J. S. 2018, A&A, 620, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iocco, F., Mangano, G., Miele, G., Pisanti, O., & Serpico, P. D. 2009, Phys. Rep., 472, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, S., Haro, J. D., Paliathanasis, A., & Slagter, R. J. 2016, MNRAS, 460, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, J. P., & d’Agostini, G. 2014, Astrophys. Space Sci., 354, 2106 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Schon, R., & Yau, S.-T. 1979, Commun. Math. Phys., 65, 45 [CrossRef] [Google Scholar]
- Socas-Navarro, H. 2019, A&A, 626, A5 [CrossRef] [EDP Sciences] [Google Scholar]
- Steigman, G. 2007, Annu. Rev. Nucl. Part. Sci., 57, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanian, A. 2019, Mod. Phys. Lett. A, 34, 1975002 [CrossRef] [Google Scholar]
- Weinberg, S. 2008, Cosmology (Oxford University Press) [Google Scholar]
- Witten, E. 1981, Commun. Math. Phys., 80, 381 [NASA ADS] [CrossRef] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



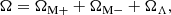
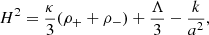
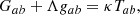
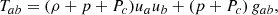

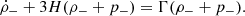
![$$ \begin{aligned} q = \frac{\Omega _{\rm M+}}{2} + \frac{|\Omega _{\rm M-}|}{2}\left[ \left(\frac{\Gamma }{H} -3\right)(1 + w_-) + 2 \right] - \Omega _\Lambda , \end{aligned} $$](/articles/aa/full_html/2021/07/aa41394-21/aa41394-21-eq9.gif)

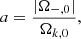
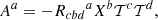
![$$ \begin{aligned} R_{abcd}=C_{abcd}+ \left(g_{a[c}R_{d]b}-g_{b[c}R_{d]a}\right)-\frac{1}{3} Rg_{a[c}g_{d]b}, \end{aligned} $$](/articles/aa/full_html/2021/07/aa41394-21/aa41394-21-eq14.gif)
![$$ \begin{aligned} A^a=-\left[C_{cbde}+\left(g_{c[d}R_{e]b}-g_{b[d}R_{e]c}\right)-\frac{1}{3} Rg_{c[d}g_{e]b}\right]g^{ea}X^b \mathcal{T} ^c \mathcal{T} ^d. \end{aligned} $$](/articles/aa/full_html/2021/07/aa41394-21/aa41394-21-eq15.gif)

![$$ \begin{aligned}&A^a_{\mathrm{M}} := -\left[\left(g_{c[d}R_{e]b}-g_{b[d}R_{e]c}\right)-\frac{1}{3} Rg_{c[d}g_{e]b}\right] g^{ea}X^b \mathcal{T} ^c \mathcal{T} ^d. \end{aligned} $$](/articles/aa/full_html/2021/07/aa41394-21/aa41394-21-eq19.gif)
![$$ \begin{aligned} A^a_{\mathrm{M}} = \frac{\kappa }{2} \left[ {T^{a}}_{b}X^b - \mathcal{Q} _b X^b \mathcal{T} ^a - \left(\frac{\rho }{3} + 2 p\right) X^a \right], \end{aligned} $$](/articles/aa/full_html/2021/07/aa41394-21/aa41394-21-eq21.gif)

![$$ \begin{aligned} A^a_{\rm M}=\frac{\kappa }{6} \left[-\rho _{+} + |\rho _{-}|\right] X^a. \end{aligned} $$](/articles/aa/full_html/2021/07/aa41394-21/aa41394-21-eq23.gif)
![$$ \begin{aligned} A^a_{\mathrm{M}} = \frac{\kappa }{6} \left\{ -\rho _+ + |\rho _-| \left[ \frac{\Gamma }{H}(1 + w_-) + 3 w_- +1 \right] \right\} X^a, \end{aligned} $$](/articles/aa/full_html/2021/07/aa41394-21/aa41394-21-eq25.gif)
![$$ \begin{aligned} A^a_{\rm M} = \frac{\kappa }{6} \left[-\rho _+ + |\rho _-| \left( \frac{\Gamma }{H} +1 \right) \right] X^a, \end{aligned} $$](/articles/aa/full_html/2021/07/aa41394-21/aa41394-21-eq26.gif)