EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 650 (June 2021) A&A, 650 (2021) L4 Full HTML
Issue
A&A
Volume 650, June 2021
Parker Solar Probe: Ushering a new frontier in space exploration
Article Number L4
Number of page(s) 6
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202039800
Published online 02 June 2021

© ESO 2021

1 Introduction

As Parker Solar Probe (PSP) descends deeper into the solar corona on its succeeding orbits, its measurements reveal features of the heliospheric plasma that will significantly increase our fundamental understanding of the workings of the solar corona, the origins of the solar wind, and the behavior of heliospheric energetic particle populations (Fox et al. 2016). In the first several orbits, PSP approached progressively nearer to the range of altitudes at which the accelerating solar wind speed exceeds the Alfvén speed. This critical zone is not a simple surface, but a more irregularly defined region above which (incompressive) magnetohydrodynamic signals, such as Alfvén waves, can no longer return to the lower altitude corona. In this very region, the analysis of heliospheric imaging (HI; DeForest et al. 2016) has described a transition from striated images that appear to be highly collimated due to a structured magnetic field and lower plasma beta to higher altitude images that appeared to be more disordered and isotropic, a condition described as “flocculation.” A number of interesting features have been reported from observations in the region, including periods of near-corotation and, notably, the appearance of magnetic reversals or “switchbacks” (Bale et al. 2019) and accompanying plasma jets (Kasper et al. 2019). Switchbacks have received considerable attention, with a focus on understanding how various plasma properties respond in and near them (Bale et al. 2019; Kasper et al. 2019; Dudok de Wit et al. 2020; McManus et al. 2020; Mozer et al. 2020; Whittlesey et al. 2019). Their origin is also a subject of active discussion, with ideas ranging from distant generation in the lower corona via interchange reconnection (Axford et al. 1999; Fisk & Kasper 2020; Zank et al. 2020) to a roll-up of the magnetic field by vortices in shear-driven turbulence (Ruffolo et al. 2020). Here we examine another important set of PSP observations and their behavior near switchbacks, namely the behavior of energetic particles as measured on PSP by the integrated Science Investigation of the Sun (IS⊙IS) instrument suite (McComas et al. 2016, 2019).

Strahl electrons are observed to reverse directionality at the switchback sites, so it makes sense to inquire whether higher energy energetic particles reverse at the switchbacks as well (Verscharen 2019). However, this has not been tested to date. Several factors may cause directional change in the energetic particle flux. It is the main goal of this Letter to investigate whether energetic particle propagation reversals occur concurrently with the magnetic field reversals (i.e., switchbacks).

From a theoretical perspective, one expects the energetic particles to follow the “S-shaped bent lines” if the gyroradii of the energetic particles are similar to or smaller than the radius of the curvature of the field-line bends. This provides us with an opportunity to explore the curvature of the switchbacks, which is otherwise difficult, from single-spacecraft measurements.

Examination of the magnetic field switchbacks and the radial reversals of the energetic particle anisotropy from the first five PSP orbits reveals a consistent picture of the statistical correlations: both magnetic field and energetic particle fluxes reverse, but magnetic reversals are typically not preferentially accompanied by energetic particle flux reversals.

In the following section we briefly review some detailed properties of switchbacks. We then describe the data and our methodology, followed by our main results. A final section provides our interpretation and a discussion emphasizing how the energetic particles provide constraints on the structure of switchbacks, as well as a likely interpretation of the energetic particle polarity reversals.

2 Properties of magnetic switchbacks

Polarity reversals of the interplanetary magnetic field have been observed at Helios orbit and beyond in the ecliptic plane (Horbury et al. 2018)as well as in Ulysses orbit at higher latitudes (Balogh et al. 1999; Borovsky 2016). They are observed relatively frequently near the heliospheric current sheet (Kahler et al. 1996). There is also some evidence that polarity reversals can occur deep in the corona (Samanta et al. 2019). In the early orbits of PSP near perihelion, reversals are observed as well. In this region, in which the prevalent magnetic field is greater and mainly radial, the observed reversals, known as switchbacks, are quite dramatic (Bale et al. 2019; Kasper et al. 2019). The associated plasma flow deflections have sometimes been referred to as “jets.” The simultaneous reversal of the magnetic and velocity field fluctuations tends to render most of these switchbacks Alfvénic in nature (Horbury et al. 2018; Dudok de Wit et al. 2020), although some recent studies hint that the switchback intervals might be less Alfvénic compared to the “pristine” solar wind samples (Bourouaine et al. 2020; Larosa et al. 2021). A conclusive definition of a switchback has not yet been settled on.

Physical explanations for polarity reversals or switchbacks (hereafter, simply switchbacks) have varied widely but fall into two main categories. The first, mostly applied at lower coronal altitudes, is that interchange reconnection between open and closed regions of opposite magnetic field polarity can result in kinks that propagate upward as large-amplitude Alfvén waves (Axford et al. 1999; Fisk & Kasper 2020). It is generally thought that such waves may propagate over a finite range before being assimilated into the surrounding fluctuations (Landi et al. 2006; Tenerani et al. 2020). A simple geometric model, based on the predictions of the Super-Parker Spiral (Schwadron & McComas 2005), has been able to explain the large, one-sided tangential flows and Alfvénicity observed in switchbacks (Schwadron & McComas 2021). The second potential source of polarity reversals is the higher turbulence levels expected at and above the Alfvén critical point (Lotova 1988; Lotova et al. 2011; Chhiber et al. 2019; Squire et al. 2020), a phenomenon that can be understood in part based on wave steepening in WKB theory (Hollweg 1974). There is also a general trend observed in STEREO imaging in approximately the same region: a transition between highly collimated striations to a more isotropic flocculation. In each of these cases, sufficiently large amplitude fluctuations would naturally lead to episodic magnetic field polarity reversals.

Moving farther outward in the heliosphere, observed switchbacks have also been attributed to local dynamics (Borovsky 2016; Horbury et al. 2018). The specific suggestion that velocity shears can induce Kelvin-Helmholtz-like roll-ups and subsequent polarity reversals has been put forward as a cause of switchbacks at greater heliocentric distances (Landi et al. 2005, 2006), as well as those in PSP observations approaching the Alfvén critical point (Ruffolo et al. 2020). Indeed, while reconnection-induced switchbacks, originating deeper in the corona, may decrease in number moving outward, switchbacks induced by shear may extend to large distances, causing an increase in the frequency of observed polarity inversions (Owens et al. 2018, 2020). It is therefore possible that switchbacks may decrease in number moving outward in the middle corona, and then begin to increase in the region outside the Alfvén critical point where turbulence amplitudes are large and shear effects become important (Ruffolo et al. 2020).

Recognizing that switchbacks cause reversals of the magnetic field (Bale et al. 2019), as well as reversals in the direction of Alfvén wave propagation (McManus et al. 2020) and electron strahl streaming (Whittlesey et al. 2019), paints an emerging picture of the geometry of switchbacks as envisioned many years ago by McCracken & Ness (1966) and which more recently has been used by Verscharen (2019) to describe early PSP results. Absent from this picture is observational evidence that would establish whether energetic particles propagate along these reversals. We examine this question here.

3 PSP data

PSP has completed six orbits since its launch on 2018 August 12. The first, second, and third solar perihelia reached a heliocentric distance of 36 R⊙, and the fourth and fifth reached a heliocentric distance of 28 R⊙. During these passages, the IS⊙IS instrument suite (McComas et al. 2016) performed detailed measurements of various kinds of energetic particles (McComas et al. 2019; Allen et al. 2020; Bandyopadhyay et al. 2020; Cohen et al. 2020; Desai et al. 2020; Giacalone et al. 2020; Joyce et al. 2020; Leske et al. 2020; Mitchell et al. 2020; Schwadron et al. 2020; Wiedenbeck et al. 2020). The fluxgate magnetometer in the FIELDS instrument suite (Bale et al. 2016) made high cadence measurements of the vector magnetic field (Bale et al. 2019). We analyzed the energetic particle data from the IS⊙IS suite, particularly the Energetic Particle Instrument-Low energy (EPI-Lo) total ion flux, from ~80–200 keV nuc−1 with no mass discrimination, but likely dominated by protons. The energies higher than 200 keV are mostly dominated by cosmic rays, so we eliminated those in our calculation (Hill et al. 2020). To avoid the background caused by photon accidentals, we removed thesignal below 80 keV and further removed look directions 25, 31, 34, 35, and 44, which are most affected by photon contamination from our analysis. The magnetic field data were obtained at 1 min cadence and resampled to the EPI-Lo flux. Proton density and velocity data were obtained from the Level 3 (L3i) Solar Probe Cup (SPC) data in the Solar Wind Electron, Alpha, and Proton (SWEAP) suite (Kasper et al. 2016). Specifically, we use the “fits” data set, which estimates the speed, temperature, and density of the solar wind proton population by fitting each spectrum to a single Maxwellian or a set of Maxwellian ion populations (Kasper et al. 2019). Only data points that resulted in a good fit quality were used in this study.

4 Results

The two principle diagnostics we examined are measures of radial anisotropy in the energetic particle flux, designated by the parameter r, and a measure of magnetic angular deflections, indicated by z. The particle anisotropy parameter is defined as 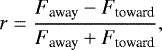(1)

where “away” and “toward” refer to the direction of the measured radial particle fluxes (F) in the selected energy range. We calculated the flux from the Sun (i.e., the away flux) by summing up the flux from look directions 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 32, 33, 36, 37, 38, 39, 40, 41, 42, 43, 45, 46, 47, 48, and 49; we calculated the toward Sun flux by summing 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, and 79. Thus, a net outward flux occurs when 0 < r < 1, and particles stream inward for − 1 < r < 0.

Magnetic deflections are quantified following Dudok de Wit et al. (2020), defining 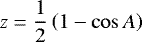(2)

with (3)

Here the angle brackets indicate a time average to assess the dominant regional polarity. Although we varied this averaging time, the results shown use an average of 6 hours, which was also used by Dudok de Wit et al. (2020). In terms of z, the magnetic polarity is “normal” when 0 < z < 1∕2, and the field is in a polarity-reversed state (i.e., a switchback) when 1∕2 < z < 1.

Some definitions of switchbacks specify a specific type of field reversal where fluctuations are Alfvénic in nature. Alfvénicity may be quantified by the cross helicity (Belcher & Davis 1971; Matthaeus & Goldstein 1982): 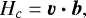(4)

where 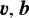are the velocity and magnetic field fluctuations. A convenient measure is obtained by normalizing Hc by the incompressible fluctuation energy per unit mass, 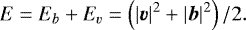(5)

The dimensionless normalized cross helicity is 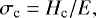(6)

where − 1 ≤ σc ≤ 1. Fluctuations with large values of (|σc|≈ 1) are sometimes called Alfvénic. The magnetic fluctuation b is measured here in Alfvén speed units 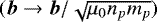. Alfvén waves have 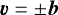and consequently σc = ±1. We followed the procedure from Parashar et al. (2020) to calculate the Alfvén speed and cross helicity.

We computed particle anisotropy from toward and away fluxes as well as the parameter r, along with the magnetic deflection parameter z for the first five PSP encounters, using EPI-Lo data and FIELDS magnetic data, as described in the previous section. An example of the relevant time series is shown in Fig. 1. Shown are the 30-min smoothed EPI-Lo toward and away ion fluxes for the energy range 80–200 keV nuc−1, the radial magnetic field BR, the normalized cross helicity σc, the magnetic deflection measure z, and the particle anisotropy measure r, as a function of time for the fourth encounter: from 2020 January 23 (day of year, DOY, 23) 14:00:55 UTC to 2020 February 04 (DOY 35) 05:14:40 UTC.

The values of z cross 0.5 at the magnetic polarity reversal regions. However, a large value of z alone may not necessarily indicate a localized reversal of the magnetic field. For example, as seen in Fig. 1, the field reversal from around 2020 February 01 04:00:00 to 04:20:00 UTC corresponds to a change of the global magnetic field polarity due to the spacecraft crossing the heliospheric current sheet, rather than an impulsive polarity reversal relative to the nearby dominant polarity. We note that some older texts also included these types of large-scale polarity reversals as switchbacks, using a broader definition (see Borovsky 2016, and references therein). However, to be consistent with the recent nomenclatures, we computed the cross helicity to select intervals containing Alfvénic wind. The third panel of Fig. 1 plots the normalized cross helicity for the fourth encounter. Some cross helicity data points are missing due to the absence of good SWEAP data, for example near the perihelion of the fourth encounter (see Fig. 1). We proceeded to select Alfvénic periods where field reversals are due to switchbacks only. To show the distinction, we focused on two intervals, as highlighted in Fig. 1. The selected intervals are later shown enlarged in Fig. 2. The first interval, highlighted in orange, shows a discrete magnetic field impulse with a sharp reversal of polarity. The cross helicity is enhanced in the switchback region, indicating an Alfvénic fluctuation. The energetic particle directions do not show any variation. However, the second event does not exhibit an increase in Alfvénicity, and the energetic particle fluxes again do not change direction. We proceeded to calculate the r and z variables, as well as σc where available, for all five of the encounters sampled by PSP to date.

The main results of the paper are shown in Fig. 3. This figure plots the values of z and r for all the solar encounters combined. As a condition for Alfvénicity, we set the threshold as |σc | ≥ 0.5, that is, we only selected the intervalswith z ≥ 1∕2 and |σc | > 0.5 as switchbacks. Imposing this constraint eliminates ~5% of data points, which had z > 1∕2 but |σc| < 0.5. The four quadrants of possible switchback versus particle flows are separated by the solid lines. Importantly, the (z > 0.5, r < 0) quadrant is very sparsely populated (~4%), while the other quadrants are relatively well populated. This observation suggests that 80–200 keV energetic ions almost never reverse direction when the magnetic field polarity reverses in switchbacks. Accordingly, there are also quite a few samples (6%) in the (z > 0.5, r > 0) quadrant, meaning that often, at themagnetic field switchbacks, the particle streaming remains radially outward. As such, the fraction of particles streaming anti-Sunward (i.e., r < 0) in a switchback region (i.e., z > 0.5) is 4∕(4 + 6) ≈ 40%

Not surprisingly, the (z < 0.5, r > 0) quadrant is the most populated, indicating the usual condition of outward propagating energetic particles and a “non-switchback” magnetic field. However, there is a significant population in the (z < 0.5, r < 0) quadrant, meaning that the particles sometimes reverse in the absence of magnetic field reversal. This may indicate scattering effects or particle flux arriving from a distant source.

In Table 1, we report the percentage of the total number of points in the different quadrants of Fig 3: the ratio of the number of points with r > 0 to r < 0 values for z < 0.5 is 65.43%∕24.47% = 2.67, while the ratio of the number of points with r > 0 to r < 0 values for z > 0.5 is 6.06%∕4.04% = 1.5. As these numbers are not too far from each other, we suggest that the distribution of r values does not depend much on whether z < 0.5 or z > 0.5. This suggests that the switchbacks do not have any special effects on the direction of propagation of the energetic particles, that is, the particles do not follow the magnetic field lines at the switchback regions.

As noted in Sect. 3, there are various backgrounds that might affect some of these data comparisons, including UV light effects, especially near perihelion. To control for them, we adjusted both the lower energy threshold and the upper energy ceiling used for the energy-integrated EPI-Lo data product. We repeated the analysis shown in Fig. 3 for each of these adjustments on the energetic particle data set. In all cases the result is qualitatively the same, inthat there are always only very rare polarity reversals of the energetic particles during magnetic switchbacks.

We note that although we considered the magnetic polarity reversals with moderate to high cross helicity (|σc | ≥ 1∕2), the qualitative conclusions remain the same even if we consider all the magnetic polarity reversals, regardless of their Alfvénicity. For the sake of general interest, we also report the statistics for all the magnetic polarity reversals in Table 2.

thumbnail Fig. 1

Encounter 4. From the top we show EPI-Lo ion flux in two look directions, the radial component of the magnetic field, the absolute value of the normalized cross helicity, the normalized deflection, and the anisotropy parameter for the EPI-Lo ions. Two high-z value regions are highlighted and later shown in more detail in Fig. 2. Many instances of polarity reversals of BR are located outside these regions, but we selected these two in particular for a detailed discussion.
thumbnail Fig. 2

Two intervals, those highlighted in Fig 1, magnified here for comparison. The radial magnetic field, the absolute value of the normalized cross helicity, the deflection parameter z, and the anisotropy parameter r for the energetic particles are shown.
thumbnail Fig. 3

Scatter plot of the solar energetic particle flux anisotropy parameter r and the normalized deflection z.
Table 1

Percentage of the population in the quadrants of Fig. 3, indicating the energetic particle (EP) direction of radial streaming and the normal vs. switchback magnetic polarity.

Table 2

Same as Table 1, but reached without regard to the presence of Alfvénicity.

5 Discussion

Kasper et al. (2019) used the electron strahl to study the geometry and configuration of large-amplitude magnetic field reversals and interpreted the magnetic field reversals as traveling S-shaped bends in the field lines coming from the Sun. However, from single-point in situ observations, it is difficult to assess the radius of the curvature of these field-line bends. As we show in this paper, the 80–200 keV energetic ions generally do not follow the field lines through the switchbacks. This result can be used to gauge an upper limit on the curvature of the S-shaped field-line bends.

The result that the EPI-Lo ions do not follow the bend of magnetic field lines in switchbacks suggests that, on average, the gyroradius of these particles is comparable to or larger than the radius of the curvature of the S-shaped field-line bends. Taking the energy of the ions to be typically ~100 keV and using a magnetic field strength of B ~ 50 nT, the gyroradius of the particles is approximately rg = mv∕qB ~ 4000 km. Therefore, the radius of the curvature of the magnetic field in the observed switchbacks is probably, on average, not much larger than 4000 km in the heliocentric distances considered here.

As a point of comparison, Dudok de Wit et al. (2020) computed residence times in switchbacks for PSP in its first orbit. In Fig. 6 of that paper, the strongest angular deflections, using the same z-parameter employed above, show a power law distribution for time durations up to about 10 seconds, after which the distribution falls rapidly. Therefore, more than half of the residence times are less than 10 seconds. Using a typical wind speed in that period of about 400 km s−1, this corresponds to 4000 km as the thickness of the frequently occurring thinner switchbacks. Although single spacecraft motion is not guaranteed to sample the S-shaped field-line bends exactly perpendicularly, and the actual duration depends on the angle of traverse, this close coincidence with the estimation of the smallest gyroradius of EPI-Lo particle energies can be used to roughly corroborate the curvature of the bends.

These arguments support the main conclusion of this paper – that energetic particles cannot follow typically observed magnetic field switchbacks because the curvature of the magnetic field in switchbacks is too abrupt for these particles to follow the field lines. Consequently, in these apparently very sharp magnetic deflections, the energetic particles do not typically reverse their streaming polarity. The energetic particle streaming reversals that are observed are due to other causes, a subject that is yet to be explored.

Acknowledgements

Parker Solar Probe was designed, built, and is now operated by the Johns Hopkins Applied Physics Laboratory as part of NASA’s Living with a Star (LWS) program (contract NNN06AA01C). Support from the LWS management and technical team has played a critical role in the success of the Parker Solar Probe mission. We are deeply indebted to everyone who helped make the PSP mission possible. In particular, we thank all of the outstanding scientists, engineers, technicians, and administrative support people across all of the IS⊙IS institutions that produced and supported the IS⊙IS instrument suite and support its operations and the scientific analysis of its data. We also thank the FIELDS and SWEAP teams for cooperation. The IS⊙IS data and visualization tools are available to the community at: https://spacephysics.princeton.edu/missions-instruments/isois; data are also available via the NASA Space Physics Data Facility (https://spdf.gsfc.nasa.gov/). This research is partially supported by the Parker Solar Probe mission and the IS⊙IS project (contract NNN06AA01C) and a subcontract to University of Delaware from Princeton University (SUB0000165). Additional support is acknowledged from the NASA LWS program (NNX17AB79G) and the HSR program (80NSSC18K1210 and 80NSSC18K1648).

References

  1. Allen, R. C., Lario, D., Odstrcil, D., et al. 2020, ApJS, 246, 36 [Google Scholar]
  2. Axford, W. I., McKenzie, J. F., Sukhorukova, G. V., et al. 1999, Space Sci. Rev., 87, 25 [Google Scholar]
  3. Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
  4. Bale, S., Badman, S., Bonnell, J., et al. 2019, Nature, 576, 237 [Google Scholar]
  5. Balogh, A., Forsyth, R. J., Lucek, E. A., Horbury, T. S., & Smith, E. J. 1999, Geophys. Res. Lett. 26, 631 [Google Scholar]
  6. Bandyopadhyay, R., Matthaeus, W. H., Parashar, T. N., et al. 2020, ApJS, 246, 61 [Google Scholar]
  7. Belcher, J., & Davis, Jr. L. 1971, J. Geophys. Res., 76, 3534 [Google Scholar]
  8. Borovsky, J. E. 2016, J. Geophys. Res. Space Phys., 121, 5055 [Google Scholar]
  9. Bourouaine, S., Perez, J. C., Klein, K. G., et al. 2020, ApJ, 904, L30 [Google Scholar]
  10. Chhiber, R., Usmanov, A. V., Matthaeus, W. H., Parashar, T. N., & Goldstein, M. L. 2019, ApJS, 242, 12 [Google Scholar]
  11. Cohen, C. M. S., Christian, E. R., Cummings, A. C., et al. 2020, ApJS, 246, 20 [Google Scholar]
  12. DeForest, C. E., Matthaeus, W. H., Viall, N. M., & Cranmer, S. R. 2016, ApJ, 828, 66 [Google Scholar]
  13. Desai, M. I., Mitchell, D. G., Szalay, J. R., et al. 2020, ApJS, 246, 56 [Google Scholar]
  14. Dudok de Wit, T., Krasnoselskikh, V. V., Bale, S. D., et al. 2020, ApJS, 246, 39 [Google Scholar]
  15. Fisk, L. A., & Kasper, J. C. 2020, ApJ, 894, L4 [Google Scholar]
  16. Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [NASA ADS] [CrossRef] [Google Scholar]
  17. Giacalone, J., Mitchell, D. G., Allen, R. C., et al. 2020, ApJS, 246, 29 [Google Scholar]
  18. Hill, M. E., Mitchell, D. G., Allen, R. C., et al. 2020, ApJS, 246, 65 [Google Scholar]
  19. Hollweg, J. V. 1974, J. Geophys. Res., 79, 1539 [Google Scholar]
  20. Horbury, T. S., Matteini, L., & Stansby, D. 2018, MNRAS, 478, 1980 [Google Scholar]
  21. Joyce, C. J., McComas, D. J., Christian, E. R., et al. 2020, ApJS, 246, 41 [Google Scholar]
  22. Kahler, S. W., Crooker, N. U., & Gosling, J. T. 1996, J. Geophys. Res. Space Phys., 101, 24373 [Google Scholar]
  23. Kasper, J. C., Abiad, R., Austin, G., et al. 2016, Space Sci. Rev., 204, 131 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kasper, J., Bale, S., Belcher, J., et al. 2019, Nature, 576, 228 [Google Scholar]
  25. Landi, S., Velli, M., & Einaudi, G. 2005, ApJ, 624, 392 [Google Scholar]
  26. Landi, S., Hellinger, P., & Velli, M. 2006, Geophys. Res. Lett., 33, L14101 [Google Scholar]
  27. Larosa, A., Krasnoselskikh, V., Dudok de Wit, T., et al. 2021, A&A, 650, A3 (PSP SI) [EDP Sciences] [Google Scholar]
  28. Leske, R. A., Christian, E. R., Cohen, C. M. S., et al. 2020, ApJS, 246, 35 [Google Scholar]
  29. Lotova, N. A. 1988, Sol. Phys., 117, 399 [Google Scholar]
  30. Lotova, N. A., Vladimirskii, K. V., & Obridko, V. N. 2011, Sol. Phys., 269, 129 [Google Scholar]
  31. Matthaeus, W. H., & Goldstein, M. L. 1982, J. Geophys. Res. Space Phys., 87, 6011 [Google Scholar]
  32. McComas, D. J., Alexander, N., Angold, N., et al. 2016, Space Sci. Rev., 204, 187 [Google Scholar]
  33. McComas, D., Christian, E., Cohen, C., et al. 2019, Nature, 576, 223 [Google Scholar]
  34. McCracken, K., & Ness, N. 1966, J. Geophys. Res., 71, 3315 [Google Scholar]
  35. McManus, M. D., Bowen, T. A., Mallet, A., et al. 2020, ApJS, 246, 67 [Google Scholar]
  36. Mitchell, D. G., Giacalone, J., Allen, R. C., et al. 2020, ApJS, 246, 59 [Google Scholar]
  37. Mozer, F. S., Agapitov, O. V., Bale, S. D., et al. 2020, ApJS, 246, 68 [Google Scholar]
  38. Owens, M. J., Lockwood, M., Barnard, L. A., & MacNeil, A. R. 2018, ApJ, 868, L14 [Google Scholar]
  39. Owens, M., Lockwood, M., Macneil, A., & Stansby, D. 2020, Sol. Phys., 295, 37 [Google Scholar]
  40. Parashar, T. N., Goldstein, M. L., Maruca, B. A., et al. 2020, ApJS, 246, 58 [Google Scholar]
  41. Ruffolo, D., Matthaeus, W. H., Chhiber, R., et al. 2020, ApJ, 902, 94 [Google Scholar]
  42. Samanta, T., Tian, H., Yurchyshyn, V., et al. 2019, Science, 366, 890 [Google Scholar]
  43. Schwadron, N. A., & McComas, D. J. 2005, Geophys. Res. Lett., 32 [Google Scholar]
  44. Schwadron, N. A., & McComas, D. J. 2021, ApJ, 909, 95 [Google Scholar]
  45. Schwadron, N. A., Bale, S., Bonnell, J., et al. 2020, ApJS, 246, 33 [Google Scholar]
  46. Squire, J., Chandran, B. D. G., & Meyrand, R. 2020, ApJ, 891, L2 [Google Scholar]
  47. Tenerani, A., Velli, M., Matteini, L., et al. 2020, ApJS, 246, 32 [Google Scholar]
  48. Verscharen, D. 2019, Nature, 576, 219 [Google Scholar]
  49. Whittlesey, P. L., Larson, D. E., Kasper, J. C., et al. 2019, in AGU Fall Meeting Abstracts, Vol. 2019, SH11A–06 [Google Scholar]
  50. Wiedenbeck, M. E., Bučík, R., Mason, G. M., et al. 2020, ApJS, 246, 42 [Google Scholar]
  51. Zank, G. P., Nakanotani, M., Zhao, L.-L., Adhikari, L., & Kasper, J. 2020, ApJ, 903, 1 [Google Scholar]

All Tables

Table 1

Percentage of the population in the quadrants of Fig. 3, indicating the energetic particle (EP) direction of radial streaming and the normal vs. switchback magnetic polarity.

In the text
Table 2

Same as Table 1, but reached without regard to the presence of Alfvénicity.

In the text

All Figures

thumbnail Fig. 1

Encounter 4. From the top we show EPI-Lo ion flux in two look directions, the radial component of the magnetic field, the absolute value of the normalized cross helicity, the normalized deflection, and the anisotropy parameter for the EPI-Lo ions. Two high-z value regions are highlighted and later shown in more detail in Fig. 2. Many instances of polarity reversals of BR are located outside these regions, but we selected these two in particular for a detailed discussion.
In the text
thumbnail Fig. 2

Two intervals, those highlighted in Fig 1, magnified here for comparison. The radial magnetic field, the absolute value of the normalized cross helicity, the deflection parameter z, and the anisotropy parameter r for the energetic particles are shown.
In the text
thumbnail Fig. 3

Scatter plot of the solar energetic particle flux anisotropy parameter r and the normalized deflection z.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.