| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202140358 | |
| Published online | 28 May 2021 | |
Phase-resolved spectrum of the Crab pulsar from NICER
No. 24, NTI Layout 1st Stage,
3rd Main, 1st Cross,
Nagasettyhalli,
Bangalore
560094,
India
e-mail: viv.maddali@gmail.com
Received:
15
January
2021
Accepted:
31
March
2021
Context. Studies of the high-energy emission regions of rotation-powered pulsars are typically based on folded light curves (FLCs) and phase-resolved spectra (PRS).
Aims. This work uses the NICER observatory to obtain the highest resolution FLC and PRS of the Crab pulsar at soft X-ray energies.
Methods. NICER has accumulated about 347 ksec of data on the Crab pulsar. The data were processed using the standard analysis pipeline. Stringent filtering was done for spectral analysis. The individual detectors are calibrated in terms of the long-time light curve (LTLC), raw spectrum, and deadtime. The arrival times of the photons are established in reference to the Solar System barycenter, while the rotation frequency ν and its time derivative ν˙ are used to derive the rotation phase of each photon.
Results. The LTLCs, raw spectra, and deadtimes of the individual detectors are statistically similar; the latter two show no evolution with epoch and the detector deadtime is independent of photon energy. The deadtime for the Crab pulsar, taking into account the two types of deadtime, is only ≈7–8% larger than that obtained using the cleaned events. Detector 00 behaves slightly differently from the rest, but can be used for spectral work. The PRS of the two peaks of the Crab pulsar are obtained at a resolution that is better than 1∕512 in rotation phase. The FLC very close to the first peak rises slowly and falls faster. The spectral index of the PRS is almost constant very close to the first peak.
Conclusions. The high-resolution FLC and PRS of the peaks of the Crab pulsar provide important constraints for the formation of caustics in the emission zone.
Key words: stars: neutron / pulsars: general / pulsars: individual: PSR J0534+2200 / X-rays: general
© ESO 2021
1 Introduction
While rotation-powered pulsars (RPPs) were first discovered at radio wavelengths, they mainly exhibit emission at the much higher X-ray and γ-ray energies. Thus, observations at these high energies are required to understand their emission mechanism. Furthermore, the radio emission of RPPs is believed to be due to a coherent radiation mechanism, which is relatively difficult to study. In contrast, the high-energy emission is relatively simple – ultra relativistic charges traveling along magnetic field lines and emitting very narrow beams of radiation along the direction of their momentum. Therefore, a realistic magnetic field line geometry (e.g., dipole field with swept back field lines close to the light cylinder) is sufficient to qualitatively reproduce the observed folded light curve (FLC) of RPPs. Such studies gained speed after the launch of the Fermi Gamma-ray Space Telescope in 2008 (Atwood et al. 2007); see also Harding (2016).
The earliest magnetic field geometry used for modeling was the static dipole. More realistic magnetic fields were explored as time progressed – the vacuum-retarded dipole, as well as the aligned force-free magnetosphere, in which the magnetic and rotation axes are parallel, and the oblique force-free magnetosphere, in which they are not parallel. The force-free magnetospheres do not have any particle acceleration by definition. Therefore, dissipative magnetospheres were invoked, which had a finite conductivity and allowed for some acceleration. However, the dissipative models did not self-consistently model the source of particles that provide the conductivity. This led to modeling of pulsar magnetospheres using particle-in-cell codes, which are still in their infancy (see Harding 2016 and references therein).
The magnetospheric models were coupled with different sites of particle acceleration, known as “gaps,” in which space charge deficiency leads to residual electric fields and, thus, to particle acceleration. The popular gaps are the polar cap gap (PC), the outer gap (OG), the slot gap (SG), and its associated two pole caustic (TPC) model and the separatrix layer (SL) model (see Harding 2016 and references therein).
Most of the above work was done at γ-ray energies. While each model was able to qualitatively explain the FLCs of some RPPs, none of them explained the FLCs of all Fermi RPPs (Bai & Spitkovsky 2010; Romani & Watters 2010; Kalapotharakos et al. 2014; Harding 2016; Pierbattista et al. 2016). Furthermore, quantitative comparisons of the observed and modeled FLCs (in terms of χ2) were often quite poor in quality (Harding 2016). However, several of the above models were able to reproduce the typical double peaked FLC even from a single magnetic pole of the RPP. They were able to reproduce the sharp peaks in terms of caustics, in which photons from different parts of the emission region arrived at the same rotation phase simultaneously due to a combination of light travel time and special relativistic aberration (Cheng et al. 1986). However, analyses of the phase resolved spectrum (PRS) have lagged behind the analysis of the FLC in most of these models, until recently (Cheng et al. 2000; Brambilla et al. 2014).
The most popular RPP for such work is the Crab pulsar. It is a very luminous source, so it has been observed all the way from radio to γ-ray energies. Furthermore, it is probably the only RPP for which the FLCs at most energies are not only similar in appearance, but are also aligned in the rotation phase (except for the radio precursor; Abdo et al. 2010). This implies that the geometry of the emission region is common for most energies in the Crab pulsar. Therefore, modeling its FLC at X-ray energies may prove as useful as modeling it at γ-ray energies. This work obtains the high phase resolution (large number of bins per rotation period) FLC and PRS of the Crab pulsar at soft X-ray energies (1−10 keV) using the Neutron star Interior Composition Explorer (NICER) satellite observatory (Arzoumanian et al. 2014; Gendreau et al. 2016), which is the main aim of this work, with a focus mainly on the formation of caustics or cusps in the FLC of the Crab pulsar at soft X-ray energies.
Cheng et al. (1986) and Romani & Yadigaroglu (1995) were among the earliest theorists to demonstrate the formation of sharp peaks in the γ ray FLC of RPPs. Using a static dipole magnetic field, Cheng et al. (1986) showed that sharp peaks can form in the FLC due to photons from a large portion of the outer gap (OG) arriving at a common rotation phase (see their Fig. 11). These so called “caustics” or “cusps” form when we take into account the combined effect of the special relativistic aberration and light travel time on a photon. Romani & Yadigaroglu (1995) demonstrated the same using the more sophisticated vacuum retarded dipole (VRD) magnetic field. Clearly, the sweep-back of the magnetic field lines in a VRD did not affect the process of caustic formation. These developments enabled the explanation of the well separated double peaks in γ ray FLCs in terms of emission from a single magnetic pole of the RPP.
Then there was the Fermi Gamma-Ray Space Telescope, which obtained high-quality γ ray FLCs of several RPPs, enabling statistical testing of more refined theoretical models of the formation of FLC. Romani & Watters (2010) tested three types of magnetospheric structures and two locations of the emission zone. The three magnetospheric structures were static magnetic field, modified VRD which they labeled the “atlas” field and “pseudo force free” (PFF) magnetosphere, which contains charges, but no currents. The two locations were the two pole caustic (TPC) and the outer gap (OG). They concluded that statistically the OG was preferable to TPC. However, their best-fit values of α, the angle between rotation and magnetic axis, and ζ, the angle between rotation axis and line of sight all differ significantly from independently known values for some RPPs. In the work of Romani & Watters (2010), caustics are caused by piling up in phase of emission from different regions (altitudes) of the magnetosphere.
Bai & Spitkovsky (2010) used only the three dimensional force free magnetosphere (FF), which, by definition, has no particle acceleration, and they explored the TPC and OG locations. The FF magnetosphere has a conducting plasma and the charges and currents are solved self-consistently. They conclude that both the TPC and OG models are unsuitable, but favor a modified version of OG which they call the “separatrix layer” (SL) gap. In this model caustics form by an entirely different process – that of radiation from the same magnetic field line piling up in phase. This is possible because outside the light cylinder the magnetic field lines are almost radial, in terms of so-called “split monopolar” geometry. They named this kind of caustic formation the “sky map stagnation” (SMS) effect. These caustics form in the outer magnetosphere. Each magnetic pole gives rise to one peak in the FLC and the rise of flux to the peak as a function of rotation phase is usually faster than its drop after the peak.
There are two important aspects of caustic formation. First, it is sensitive to the geometry of the magnetic field lines since that determines the amount of aberration and light travel time (Bai & Spitkovsky 2010). Second, as emphasized by Bai & Spitkovsky (2010), the magnetic field structure at the light cylinder determines the shape of the polar cap on the surface of the neutron star, which, in turn, determines the shape and extent of the region of emission of photons, which affects the formation of caustics.
Kalapotharakos et al. (2014) use a dissipative magnetosphere, using different values of conductivity σ; when σ = 0, the situation is similar to the VRD magnetosphere, while σ = ∞ implies the FF magnetosphere. For small values of σ, they find that the emission is mainly from the inner magnetosphere and the peaks in the FLC are not sharp. For large values of σ, the emission is mainly from the outer magnetosphere and the peaks can be sharp. For very large values of σ the emission is entirely from the outer magnetosphere and is very non-uniform, so complex FLCs are obtained. They favor a hybrid model that is FF inside the light cylinder and dissipative outside (FIDO). In terms of caustic formation, the FIDO model essentially has two poles, as in the SG model, but without emission at low altitudes or at off peak phases, as in the OG model.
The above is a brief summary of the mechanism of caustic formation in high-energy FLCs of RPPs. The results of this work may also address some questions regarding caustic formation. To achieve this, two aspects must be kept in mind. First, NICER consists of 56 co-aligned detectors, each of which is essentially a small X-ray telescope. This clever design avoids (for most sources) two of the difficulties commonly faced by X-ray observatories – pile-up of photons and detector deadtime. Correspondingly, this design requires the calibration of 56 detectors in terms of their long-time light curves (LTLCs) and their spectral properties. This has been done in this work for the 49 useful detectors of NICER.
Second, to obtain FLC and PRS at high phase resolution, we need highly accurate rotation frequency ν and its time derivative 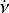 as a function of epoch since these parameters of the Crab pulsar change significantly with time and since the NICER observations of the Crab pulsar occurred over a duration of about 2.35 yr. The ν and
as a function of epoch since these parameters of the Crab pulsar change significantly with time and since the NICER observations of the Crab pulsar occurred over a duration of about 2.35 yr. The ν and 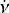 have been obtained self consistently from the NICER data itself and only the data for which the error in the derived rotational phase of each photon is less than 1∕2048 of a period has been used. This allows for the FLC and PRS of the Crab pulsar at a resolution of 1024 bins per period to be obtained, in any case, certainly better than 512 bins per period. The details of how these ν and
have been obtained self consistently from the NICER data itself and only the data for which the error in the derived rotational phase of each photon is less than 1∕2048 of a period has been used. This allows for the FLC and PRS of the Crab pulsar at a resolution of 1024 bins per period to be obtained, in any case, certainly better than 512 bins per period. The details of how these ν and 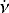 are obtained, the treatment of the Crab pulsar glitch of 2017 November, and the consistency with the radio ephemeris are explained in Vivekanand (2020). Typically, the accuracy of ν obtained by NICER is 0.0009 μHz, with a standard deviation of 0.0006 μHz. The typical accuracy of the
are obtained, the treatment of the Crab pulsar glitch of 2017 November, and the consistency with the radio ephemeris are explained in Vivekanand (2020). Typically, the accuracy of ν obtained by NICER is 0.0009 μHz, with a standard deviation of 0.0006 μHz. The typical accuracy of the 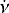 is 4 × 10−14 Hz s−1, with a standard deviation of 3 × 10−14 Hz s−1.
is 4 × 10−14 Hz s−1, with a standard deviation of 3 × 10−14 Hz s−1.
In Sect. 2, we discuss the observations and analysis carried out in this work. The next three sections describe the calibration of the 49 useful detectors of NICER. Sections 6 and 7 present the spectrum for the Crab pulsar. The last section discusses the implications of this work.
2 Observations and analysis
NICER consists of 56 co-aligned detectors (Arzoumanian et al. 2014; Gendreau et al. 2016; Prigozhin et al. 2016). Its operating range is 0.2− 12 keV, with a peak collecting area of 1900 cm2 at 1.5 keV and below. The time resolution is 0.1 microsecond (μs). At the time of this work, NICER had observed the Crab pulsar on 72 different days, starting from 2017 Aug. 5 to 2020 Apr. 27, which is a duration of 2.73 yr, with multiple observations on eight of those days, resulting in 80 observation identity numbers (ObsID). Ten of these ObsIDs had live times of less than 100 sec, so they were not analyzed. Four of them were ignored for reasons specified in Vivekanand (2020), which gives details of the earlier observations spanning 1.72 yr and their analysis. The analysis carried out in this work is slightly different because of the enhanced sensitivity requirement for spectral work.
The data were analyzed using the NICER version 2020-04-23_V007a software, which is included in the HEAsoft distribution 6.27.2. The calibration setup comes from CALDB version XTI(20200722). The analysis for each ObsID begins with the pipeline tool nicerl2 with the following parameters: angle between pointing and earth limb ELV = 30° and angle between pointing and bright earth BR_EARTH = 40° (Stevens et al. 2019; Bogdanov et al. 2019; Guillot et al. 2019; Miller et al. 2019; Trakhtenbrot et al. 2019); magnetic cut off rigidity COR_RANGE ≥ 4.0 (Bogdanov et al. 2019; Guillot et al. 2019; Malacaria et al. 2019; Riley et al. 2019; Trakhtenbrot et al. 2019; van den Eijnden et al. 2020); and undershoot count rate UNDERONLY_RANGE = 0–50; the rest of the parameters have default values (Stevens et al. 2019; Bogdanov et al. 2019). Next, the tool nimaketime is used to create good time intervals (GTI), using additionally the following two criterion: angle between pointing and sun SUN_ANGLE > 90° (Bogdanov et al. 2019); and observations must be done when NICER in not in sun light, SUNSHINE = 0 (Hare et al. 2020).
Next, the tool fselect is used to exclude data of detectors 14, 34, and 54, whose data is known to be problematic (Bogdanov et al. 2019; Ray et al. 2019). Coupled with the detectors 11, 20, 22, and 60 that are permanently switched off at NICER, this leaves 49 out of the original 56 detectors for our analysis. Then, the original GTIs of the event file are replaced by the GTIs obtained above (if required, the FITS file extension name EXTNAME has to be changed back to GTI_FILT). Then fselect is used to filter out photon events outside the GTIs, using the gtifilter option. Next the LTLC is obtained using the tool extractor with a bin size of 2.5 s. This is used to exclude durations of observations in which the mean count rate is unusually low or high; this is done by editing the GTI extension of the event file and filtering using fselect with the gtifilter option.
Then, fselect is used to extract the data of each individual detector and extractor is used to obtain its LTLC. The tool fstatistic is used on the LTLC to obtain basic statistics of the count rate of each detector – the mean value, its standard deviation, the minimum and maximum values. Unusually low or high values indicate flaring, satellite not exactly on source, or other effects, so such durations are also excluded.
High background counts are identified by extracting a LTLC of bin size 8 s in the energy range 12−15 keV and excluding those durations in which the count rate is statistically higher than 1.0 (Bult et al. 2018). Details are given in Appendix A. NICER’s background is believed to be typically less than 1 count s−1 keV−1. It is obtained by processing data from several RXTE background regions. Background region 5 of RXTE has an approximately power-law spectrum that is < 1.0 count s−1 keV−1 at 0.4 keV and < 0.1 count s−1 keV−1 above 1.4 keV (Keek et al. 2018). In the top panel of their Fig. 2, the background decreases to ≈ 0.01 count s−1 keV−1 at 10 keV, while the flux of the Crab nebula plus pulsar is 3.7 count s−1 keV−1 at that energy, which can be derived from later figures. Thus, the background is ≈ 370 times weaker than the Crab nebula plus pulsar at ≈10 keV.
A high particle background due to geomagnetic storms is accounted for by the space weather parameter Kp (Ludlam et al. 2019; Miller et al. 2019), which is required to be below the value 5. This is doneby first converting the START and STOP times in the event files from the TT timescale to UTC dates and times and then checking the Kp values during the observation in the corresponding yearly WDC files1. Details are given in Appendix B.
Finally, the event epochs that remain after the above stringent filtering are referenced to the solar system barycenter using the barycorrtool, using the JPL ephemeris DE430, with the position of the Crab pulsar at that epoch as input. The ν and 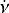 , and their reference epoch for each ObsID are then used to compute the rotation phase of each photon, which is written into the event file. Vivekanand (2020) describes most of the above analysis in a different context. Later sections of this work describe the specific analysis required for the corresponding sections.
, and their reference epoch for each ObsID are then used to compute the rotation phase of each photon, which is written into the event file. Vivekanand (2020) describes most of the above analysis in a different context. Later sections of this work describe the specific analysis required for the corresponding sections.
The filtering above reduced the total live time by ≈60%, to ≈ 139 ksec, leaving only 29 ObsIDs with sufficient data for the analysis; this data also had their ν and 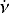 estimated by Vivekanand (2020), but without implementing this stringent filtering and thus, with many more photons at hand for obtaining ν and
estimated by Vivekanand (2020), but without implementing this stringent filtering and thus, with many more photons at hand for obtaining ν and 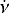 . For those groups of ObsIDs that had sufficient number of photons in spite of the stringent filtering, it was possible to estimate ν and
. For those groups of ObsIDs that had sufficient number of photons in spite of the stringent filtering, it was possible to estimate ν and 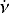 that were consistent with those derived by Vivekanand (2020).
that were consistent with those derived by Vivekanand (2020).
 |
Fig. 1 LTLC of 49 useful detectors of NICER combined, over ≈2.35 yr, with a bin size of 10 s. |
3 Long-time light curve
Figure 1 shows the LTLC of the Crab nebula plus pulsar using the 49 useful detectors of NICER, in the energy range 0.2−12 keV, for the 2.35 yr of observations used in this work,with a bin size of 10 s. This was obtained using the extractor tool. The mean count rate is 10384 per second with a standard deviation of 75, which is 0.72% of the mean. The maximum and minimum values in Fig. 1 are 10610.0 and 10173.5 counts per second, which implies that the peak-to-peak variation of the LTLC is about ≈ (10610.0−10173.5)∕10384 ≈ 4.2%. This is consistent with the recent measurement of the Crab nebula plus pulsar’s LTLC by the NuSTAR and Swift/BAT missions2. This is also consistent with the findings in the recent past, that the reported decrease in the Crab nebula’s X-ray flux by ≈ 7% over ≈ 2 yr, starting from MJD 54690 (mid 2008), as reported by Wilson-Hodge et al. (2011), is no longer observed3, 4. In fact Wilson-Hodge et al. (2011) themselves stated that they cannot predict if the flux decline will continue in the future. This result is also confirmed inFig. 1 of Kouzu et al. (2013).
Figure 2 shows the statistics of the 49 individual LTLCs. The dots with error bars show the mean count rate for each detector over the 2.35 yr duration. The crosses and the pluses represent the maximum and minimum values, respectively. All except detector 00 show statistically similar values. Detector 00 has a significantly lower mean count rate and a standard deviation slightly higher than the others. For example, the mean count rates of detectors 00 and 01 are 187.78 and 224.02, respectively, while their standard deviations are 8.15 and 5.29. The minimum values in Fig. 2 are typically − 3.8(3) standard deviations below the mean, the error in the last digit given in the parenthesis; the maximum values are typically + 3.8(3) standard deviations above the mean. Now, a Gaussian probability distribution function has 0.000145 of its area beyond the value ±3.8 standard deviations of the variable; this is obtained using the error function. This implies that half of that area, or 0.000073, lies above and below ±3.8 standard deviations, respectively. This is consistent with the fact that for our sample size of 13 454 bins for each detector, each of 10 s duration, we can expect one sample beyond 3.8 standard deviations. We note that the live time for each detector in Fig. 2 is 13 454 × 10 = 134.54 ksec and not the actual ≈139 ksec because the extractor tool ignores bins of small fractional live time.
Figure 3 compares the LTLCs of the 49 individual detectors with that of all detectors combined (shown in Fig. 1), after normalizing each LTLC with its mean count rate. The χ2 per degree of freedom is below 1.5 for 35 detectors, between 1.5 and 2 for 7 detectors and between 2 and 2.25 for 6 detectors. The value of χ2 is derived using the formula 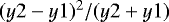 , where y1 and y2 are the counts (not count rate) in the corresponding time bins of the two LTLCs being compared. Thus, only Poisson statistical fluctuations are being accounted for in Fig. 3. In such a complicated system as NICER, it is reasonable to expect other kinds of fluctuations as well, not to mention minute source fluctuations also. Therefore, it is concluded that the LTLCs of all detectors are broadly similar.
, where y1 and y2 are the counts (not count rate) in the corresponding time bins of the two LTLCs being compared. Thus, only Poisson statistical fluctuations are being accounted for in Fig. 3. In such a complicated system as NICER, it is reasonable to expect other kinds of fluctuations as well, not to mention minute source fluctuations also. Therefore, it is concluded that the LTLCs of all detectors are broadly similar.
Thus, normalizing each LTLC with its mean count rate is justified because the variations of the latter in Fig. 2 do not merely represent statistical fluctuations, but something closer to, say, differences in effective area. The error bar on the mean counts in that figure is the standard deviation and not the error on the mean; this was done to better compare the mean value with the maximum and minimum values. For 49 detectors there are 49 × 48∕2 = 1176 distinct pairs, of which only 10, 24 and 43 pairs have count rates differing by less than 3, 5 and 10σ, respectively.So, the mean count rate of each detector is statistically distinct from that of another detector and most probably represents the difference in their effective areas.
 |
Fig. 2 Statistics of the LTLCs of the 49 individual detectors of NICER. The black dots, red crosses, and blue pluses are the mean count rate, the maximum and the minimum values, respectively. The error bars represent the standard deviation and not the error on the mean. |
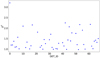 |
Fig. 3 Normalized χ2 between the LTLCs of the 49 individual detectors and their combined LTLC shown in Fig. 1. |
 |
Fig. 4 Raw spectrum of the 49 detectors combined, from channels 20 to 1200 (0.2− 12 keV). |
4 Raw spectrum
Figure 4 shows the combined raw spectrum (uncalibrated) of the 49 detectors, consisting of ≈ 139 ksec of data from 29 ObsIDs, from energy 0.2−12 keV. The sharp dip in spectrum at around 2.2 keV is due to thegold (Au) edge5; the gold coats the reflective surface of the X-ray concentrators (XRC).
Figure 5 shows the comparison between Fig. 4 and the corresponding spectrum of each detector, in terms of the χ2 per degree of freedom obtained over 1100 channels in the energy range 1−12 keV, obtained using the same formula as in Fig. 3. The lower energy range was ignored because here the χ2 was very high, mostly due to the carbon, nitrogen and oxygen edges at ≈ 0.3−0.5 keV, and also due to the fact that our analysis is done with data beyond 1 keV. 41 of the 49 χ2 values are below 2.0; the extreme value of 3.9 belongs to detector 61. Once again,we expect non-Poisson fluctuations to exist in the data. The spread in χ2 is much larger than their formal statistical errors. However, most of the χ2 gets contribution from the 2.2 keV gold edge. Therefore, we should not expect a better agreement than this. Thus, we may conclude that the raw spectra of the 49 detectors are statistically similar.
Figure 5 is not merely Fig. 2 plotted in a different way as each is sensitive to different physical parameters. The latter is sensitive to time variations of effective area, deadtime, etc., while the former is sensitive to the optical loading of the detectors as well as a calibration of the gain of the receivers that assigns an energy channel to each photon event, etc.
Figure 6 explores whether the spectrum of each detector changes as a function of time. It displays the χ2 between data earlier to and later than the date 2018 Nov 10, which roughly divides the data into two halves. The χ2 is estimated using the same formula as in Fig. 3, after scaling the two spectra with their respective live times, because the cut-off date does not divide the data into exactly two equal halves. Just as in the previous figure, the χ2 values in Fig. 6 are reasonable. We may, therefore, conclude that the raw spectrum of each detector does not change as a function of time during the 2.35 yr of observations.
In both Figs. 5 and 6, most of the estimated χ2 are larger than their formal errors. An extreme position to take would be to conclude that no detector behaves like any other. However, the acceptance or rejection of a hypothesis based on χ2 depends upon the confidence level, which can be subjective in some contexts. In complicated systems such as NICER, we would expect large χ2 due to unknown or immeasurable factors. In principle, we can choose, for further analysis, only those detectors whose χ2 is less than, say, 2.0, and live with the corresponding reduced sensitivity. Here statistics cannot be of much use; rather it is only experience, intuition, and the context that serve us best. To cite an example, in the good old days radio astronomersconsidered the detection of a point source as positive if it was detected at a signal to noise ratio (S/N) of 5. We might ask how they came to decide on 5, and not 6 or 4, for instance.The answer is that this number was arrived at through common experience and not pure statistics.
 |
Fig. 5 χ2 per degree of freedom between the raw spectrum of each detector and their combined spectrum in Fig. 4. |
 |
Fig. 6 Normalized χ2 between the raw spectra of earlier and later halves (durations) of the data for each detector. |
5 Deadtime
Wilson-Hodge et al. (2018) describe the procedure for estimating the dead time for NICER. There are two sources of deadtime. First, after reception of an event, the detector is unable to process further events for some time, during which it processes the previous event. This duration is recorded in the DEADTIME column of the event files. Second, if the source is bright, or the background is flaring, data buffers may saturate in the measurement/power units (MPUs), which may stall recording of further events until the MPUs are reset. This causes loss of GTI, or equivalently, deadtime on the source. In this work the former will be called detector deadtime while the latter will be called GTI deadtime. The detector deadtime is contributed by all events, and not just the X-ray events. In Vivekanand (2020), only the detector deadtime was taken into account and only for X-ray events.
The procedure established by Wilson-Hodge et al. (2018) was repeated almost exactly for four ObsIDs – 1013010113 and 1013010147, having the shortest (120) and longest (23364 s) live times, respectively, and 1011010201 and 1013010122 having intermediate live times (1841 and 3850 s, respectively). While Wilson-Hodge et al. (2018) used 100 phase bins per period, and 1000 phase bins for estimating GTI deadtime, here, the corresponding numbers are 256 and 1000. The results are similar for all four ObsIds, so the detailed results for ObsID 1013010147 alone will be presented here.
The top panel of Fig. 7 shows the mean X-ray counts per detector as a function of phase for ObsID 1 013 010 147 (i.e., the FLC), obtained using cleaned events (Wilson-Hodge et al. 2018). The middle panel shows the mean GTI per phase bin after subtracting the expected mean value of 91.263 s, which is obtained by dividing the live time by the number of phase bins, obtained from the GTIs of the individual MPUs. The last panel shows the mean deadtime per detector, obtained using all events (Wilson-Hodge et al. 2018). In each panel of Fig. 7, the results are first obtained per MPU and then averaged.
Two points are noteworthy in Fig. 7. First, in the middle panel, the difference in GTI per phase bin, between the observed and the expected values, has a mean value of − 0.1 ms, and an rms of 0.8 ms; the peak to peak variation is 4.25 ms. The mean value of GTI differs from the expectedvalue by − 0.0001∕91.263 ≈−0.0001%, while the peak to peakvariation corresponds to 0.00425∕91.263 ≈ 0.005% variation. This implies that the GTI per phase bin is almost constant across the FLC and that its observed value is very close to the expected value; and so there is no significant loss of GTI due to MPU buffer overflows. This is further supported by the fact that had there been GTI losses, it would have been anti-correlated with the FLC in the top panel – however, this does not appear to be the case.
Second, the detector deadtime fraction in the last panel of Fig. 7 in the off-pulse region (phase < 0.2) is 0.50%, while at the pulse peak it is 0.77%. The corresponding numbers in Fig. 1 of Vivekanand (2020) are 0.46% and 0.73%. Thus the detector deadtime fraction obtained using all events is only ≈ 5−9% larger than that obtained using only X-ray events. However, these numbers are approximations. The correct method of estimating the deadtime fraction or count rate is to first estimate them per MPU, and then average (Wilson-Hodge et al. 2018) since the GTI per MPU as well as the number of detectors per MPU could differ across the MPUs.
The correct method for carrying out this estimation is displayed in Fig. 8. The mean off-pulse deadtime fraction is 0.497(1)%, while at the pulse peak, it is 0.772(7)%; these numbers are very similar to the approximate values above. The results of Figs. 7 and 8hold for data of the other three ObsIDs also, except for lower statistical significance on account of lower live times.
Therefore, if the GTI deadtime is non-existent for the Crab pulsar, the difference between detector deadtime obtained using all events and that obtained using only X-ray events must depend upon the difference in the number of these two event types. This is demonstrated in Table 1, which contains event statistics from the filter file of that ObsID; for example the filter file for ObsID 1013010113 would be “ni1013010113.mkf” found in thedirectory AUXIL. The filter file contains the numbers of various kinds of events registered by NICER, logged once every second in time. In particular, it contains two columns labeled TOT_ALL_CNTS and TOT_XRAY_CNTS. The former contains the number of all types of events, while the latter contains the number of what are deemed to be X-ray events, but are not guaranteed to be so6. The second and third columns of Table 1 contain the sum of TOT_ALL_CNTS and TOT_XRAY_CNTS, respectively, for the duration within the GTI of the corresponding event file, for 49 useful detectors. For example, the number of TOT_ALL_CNTS and TOT_XRAY_CNTS for ObsID 1013010113 registered within the GTI are actually 1114762 and 1094359, respectively, for 52 detectors; after deleting the contributionof detectors 14, 34, and 54, found in the columns MPU_ALL_COUNT and MPU_XRAY_COUNT in the filter file, the numbers become 1049364 and 1030023, respectively.
The fourth column of Table 1 gives the ratio of the number of events of column 3 that were eventually classified as X-ray events, obtained in the keyword NAXIS2 in the corresponding event file, and TOT_ALL_CNTS. Table 1 has been made for all 29 ObsIDs used in this work, and the mean value of the above ratio is 0.922(5). This demonstrates that the difference between actual X-ray counts and all counts for the Crab pulsar data of NICER is typically about 7.8(5)%, which is a small number.
There are two conclusions so far in this section. First, the difference between the number of all events and the number of X-ray events for the NICER data of the Crab pulsar is quite small (≈ 8%). This is not surprising since the event rate for the Crab pulsar is dominated by events from the source; for much less luminous sources, the event rate would be dominated by particle events, etc. Second, the GTI deadtime is negligible for the Crab data of NICER. This is also not surprising, since source count rates of about 18846 per second (for 49 detectors) begin to show such effects7, and the Crab pulsar’s peak count rate is only about ≈17 000 counts per second. Further, MPU buffer overflow depends upon the product of the count rate and the duration for which it is maintained; for the Crab pulsar the peak count rate is maintained only for a few ms, so the probability of buffer overflow is small. Furthermore, the stringent filtering of this work might have ensured that high particle durations are excluded, which reduces the probability of buffer overflow in the remaining data.
Figure 9 compares the detector deadtime fraction of each of the 49 detectors with the combined detector deadtime fraction of all 49 detectors, across 256 phase bins in a period. It estimates the 256 differences of the two curves and computes their mean and standard deviation. Ideally, the mean should be zero for each detector and the standard deviation should reflect the average measurement error of the detector deadtime fraction across a period. Figure 9shows the ratio of mean and standard deviation for each detector. The mean value of this ratio in Fig. 9 is − 1.6 ± 2.0. If we ignore the extreme value of 5.6 of detector 62, the results are − 1.7 ± 1.7. Thus, the mean value of this ratio is consistent with a result of zero.
In Fig. 9, the relatively large values of standard deviations (not standard deviation of the ratio mean/rms) for each detector are due to two factors – the reduced number of photons in each phase bin for a single detector and, to a lesser extent, the intrinsic distribution of detector deadtimes in the column DEADTIME in the event files. It should be recalled that the quantity being estimated here (detector deadtime fraction) is very small, on the order of 0.5–0.8%; the difference of two such quantities is typically on the order of ≈ 0.05–0.005%. Now, the mean number of events in a phase bin for a single detector is 1570142182∕49∕256 ≈ 125171; the Poisson fluctuation in this quantity is of the order of 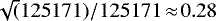 %; over 256 phase bins, the accuracy of the estimated mean (due to the Poisson process alone) would be 0.28∕16 ≈ 0.02%, which is comparable to the quantity being estimated. Similarly, the mean detector deadtime for ObsID 1013010147 is 23.1 ± 4.2μs (Vivekanand 2020). The fractional error is 4.2∕23.1 ≈ 18.2%. The mean detector deadtime estimated using 125171 events will have an accuracy of
%; over 256 phase bins, the accuracy of the estimated mean (due to the Poisson process alone) would be 0.28∕16 ≈ 0.02%, which is comparable to the quantity being estimated. Similarly, the mean detector deadtime for ObsID 1013010147 is 23.1 ± 4.2μs (Vivekanand 2020). The fractional error is 4.2∕23.1 ≈ 18.2%. The mean detector deadtime estimated using 125171 events will have an accuracy of 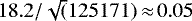 %, which is also comparable to the quantity being estimated.
%, which is also comparable to the quantity being estimated.
The time evolution of detector deadtime is studied by estimating the deadtimes of the first and second halves of the data, for all 49 detectors combined, with the cutoff date of 2018 Nov. 10 that was used in Fig. 6. The quantity plotted in Fig. 10 is (z2 − z1)∕(z2 + z1) * 2.0 as a function of phase, where z1 and z2 are the detector deadtime fractions in the first and second halves of the data, respectively. The mean value of the fractional difference is − 0.016(1); that is, the earlier and later detector deadtime fractions differ by about 1.6(1)%. It is therefore concluded that there is no evolution of detector deadtimes as a function of epoch during the 2.35 yr of observations studied here.
Finally, Fig. 11 investigates the dependence of detector deadtime upon photon energy. The combined data of all 49 detectors were divided roughly into two equal parts – one consisting of photons with energy between 1.0−1.62 keV, and the other between 1.62−10.0 keV. The FLC and deadtime fraction for each energy band is shown in the top and bottom panels of Fig. 11, respectively.The spectral evolution of the FLC with energy is evident in the top panel of Fig. 11. The deadtime fraction curves mirror this evolution in the bottom panel, so it is not possible to directly compare the two curves. However, if the detectordeadtime in a phase bin depends only upon the photon count rate in that bin and not upon the photon’s energy, then the deadtime fraction would have the same linear dependence upon the count rate for the two energy bands. So a linear fit was done to the deadtime fraction against the count rate in each energy band (see Vivekanand (2020) for justification of linear dependence), and the results are given in Table 2.
The twos lopes are almost the same, while the intercepts are negligible. This proves that the detector deadtime fraction depends only upon the count rate – and not upon the photon energy.
 |
Fig. 7 Mean values of X-ray counts per detector, GTI difference, and deadtime per detector using all counts, respectively, per phase bin for data of ObsID 1013010147, after applying the method of Wilson-Hodge et al. (2018). The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
 |
Fig. 8 Mean values of count rate per detector (deadtime corrected), and deadtime fraction per detector, respectively, per phase bin fordata of ObsID 1013010147, after applying the method of Wilson-Hodge et al. (2018). The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
Statistics of events in the four filter (MKF) files.
 |
Fig. 9 Comparison of detector deadtime fractions of the 49 detectors. |
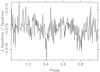 |
Fig. 10 Fractional difference in detector deadtime fraction between the first and second halves (durations) of the data. The reference epoch of phase 0.4 is MJD 58 479.425994152342. |
 |
Fig. 11 Study of detector deadtime as a function of photon energy. Top panel: FLC for data of all 49 detectors in the energy range 1.0−1.62 keV (dashed line), and in the energy range 1.62−10.0 keV (solid line). Bottom panel: deadtime fraction of the corresponding FLC in the top panel. The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
6 Calibrated phase averaged spectrum
The top panel of Fig. 12 shows the calibrated phase averaged spectrum (PAS) of the Crab nebula plus pulsar using all 49 useful detectors, for the 29 ObsIDs with a live time of ≈139 ksec. The spectrum was obtained using the extractor tool. It was analyzed using the XSPEC8 version 12.11.0, using nixti20170601_combined_v002.rmf as the main response file and nixtionaxis20170601_combined_v004.arf as the ancillary response file. These differ from the corresponding files found in the CALDB version XTI(20200722), viz. nixtiref20170601v002.rmf and nixtiaveonaxis20170601v004.arf, in that the latter two are relevant for observations using all 52 detectors ofNICER, while the former two are relevant for observations using only 49 detectors; see the relevant analysis thread9 at the NICER site. Channels 230–1000 were used (energy range 2.3−10 keV). No background spectra were used since that becomes important for the Crab pulsar only at much higher energies (Madsen et al. 2015), as mentioned in Sect. 2. Ludlam et al. (2018) state that the background fields have count rates of 0.7−2.3 counts s−1, while the Crab pulsar’s average count rate is ≈11 020 counts s−1, for 52 detectors. The default photo ionization cross-sections and solar abundances were used (vern and angr). An absorbed power law model was fit to the data of Fig. 12; the parameters of the model are the column density of absorbing hydrogen NH, the power law index Γ, and the power law normalization A. The results are: NH= 0.210(3) × 1022 cm−2, Γ =2.050(1); and A = 8.82(1); the χ2 per degree of freedom is 1.99, for 769 degrees of freedom. The errors are obtained using the error function and represent 90% confidence levels; at higher decimal places the lower and upper limits of the errors are asymmetric.
These results are consistent with the results of XMM-Newton in the 0.6−9 keV band for the overall Crab region (Kirsch et al. 2006), in their Table 2 and Fig. 6. Their values are NH = 0.260(1) × 1022 cm−2 and Γ = 2.046(3), with χ2 = 1.99 per degree of freedom.
These results also compare well with the results of NuSTAR (Madsen et al. 2015) in their Fig. 1, in the energy range 3− 78 keV. They fixed the value of NH at 0.2 × 1022 since their data are not sensitive to this parameter, and use the wilms solar abundances. Their Γ = 2.0963(4), and they do not mention the χ2. Their Γ is in the same numerical range as our result considering the fact that their energy range is much larger.
The bottom panel of Fig. 12 shows the ratio of the data to the absorbed power law model curve. As found in Fig. 1 of Madsen et al. (2015), the variations are of the order of 1%, presumably indicating the accuracy of the spectral calibration of these instruments.
As mentioned by Madsen et al. (2015), the non-piled-up instruments covering the 1− 100 keV band agree on a power law index of 2.10(2) for the PASof the Crab nebula plus pulsar, without any break or curvature in this band; see also Kirsch et al. (2005). Kouzu et al. (2013) also confirm this result using the HXD detector aboard Suzaku. Our result is consistent with this statement. Moreover, the more important result is the variation of Γ across the rotation phase, and not its absolute value, since that is correlated with NH (see Fig. 2 of Massaro et al. 2000; see also XSPEC manual). We may therefore conclude that the PAS of the Crab pulsar and nebula in Fig. 12 is consistent with that of earlier studies.
Figure 13 is similar to Fig. 12, except that lower energy limit is 1.0 keV. The ratio of the data to the model in its lower panel has variations of the order of 1%, the same as in the latter figure. The fit parameter values are: NH = 0.2943(1) × 1022 cm−2, Γ =2.0651(2); and A =9.095(2). These are consistent with the values obtained above for Fig. 12, but the errors are unreliably smaller because the χ2 per degree of freedom is 44.4, contributed mainly by the channels between energies 1.0−2.3 keV. This appears to be due to the very high photon counts in the lower energy channels. This problem disappears when the PRS is computed inthe next section since the number of photons in each energy channel is now lower in proportion to the number of phases in the period.
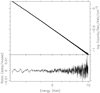 |
Fig. 12 Soft X-ray spectrum of the Crab nebula and its pulsar. Top panel: phase-averaged spectrum of the Crab nebula plus pulsar. Bottom panel: ratio of data and model. Channel-dependent effective area normalization is done using the “setplot area” command of XSPEC. |
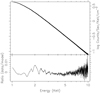 |
Fig. 13 Soft X-ray spectrum of the Crab nebula and its pulsar. The same as in Fig. 12, with a wider energy range. |
7 Calibrated phase resolved spectrum
The PRS of the Crab pulsar has been studied over the last two and half decades in a number of studies at both the soft and the hard X-ray energies, using different X-ray observatories (RXTE, BeppoSAX, XMM-Newton, Chandra, NuSTAR and Insight-HXMT; Pravdo et al. 1997; Massaro et al. 2000, 2006; Kirsch et al. 2006; Weisskopf et al. 2011; Ge et al. 2012; Madsen et al. 2015; Tuo et al. 2019). The highest phase resolution achieved so far has been typically ≈ 1∕100 in phase; even though BeppoSAX (Massaro et al. 2000, 2006) and RXTE (Ge et al. 2012) start with 300 and 1000 phase bins for the FLC, respectively, they had to estimate the PRS over ≈100 phase bins to maintain statistical significance. The following subsection presents the PRS of the Crab pulsar obtained by NICER over 128 phase bins. The next subsection obtains the PRS over 1024 bins, although the number of independent phase bins is probably 512 or better.
The 29 ObsIds used in this work already have their ν and 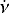 (each at its reference epoch) estimated by Vivekanand (2020), along with their formal errors. These were verified in those cases where the event files had sufficient number of photons in spite of the stringent filtering of this work. For each ObsID, using its start and stop times available in the corresponding event file, a phase error was calculated, that would result if the ν and
(each at its reference epoch) estimated by Vivekanand (2020), along with their formal errors. These were verified in those cases where the event files had sufficient number of photons in spite of the stringent filtering of this work. For each ObsID, using its start and stop times available in the corresponding event file, a phase error was calculated, that would result if the ν and 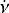 used were different by twice their formal errors. Only those ObsIDs were retained that had the phase error less than 1∕2048. This eliminated the ObsIDs 1011010201 and 1013010119, leaving 27 ObsIDs for further analysis. Next, FLCs were formed for each of the 27 ObsID in 1024 phase bins. These were then cross-correlated with the FLC of ObsID 1013010147, after shifting it in phase so that the first peak of its FLC lies at phase 0.4. The 26 phase offsets thus obtained had a typical error of ≈10−4 or better. These phase offsets were then used along with the corresponding ν and
used were different by twice their formal errors. Only those ObsIDs were retained that had the phase error less than 1∕2048. This eliminated the ObsIDs 1011010201 and 1013010119, leaving 27 ObsIDs for further analysis. Next, FLCs were formed for each of the 27 ObsID in 1024 phase bins. These were then cross-correlated with the FLC of ObsID 1013010147, after shifting it in phase so that the first peak of its FLC lies at phase 0.4. The 26 phase offsets thus obtained had a typical error of ≈10−4 or better. These phase offsets were then used along with the corresponding ν and 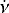 to compute the phase of each photon event in the 27 ObsIDs (see Vivekanand 2020 for details).
to compute the phase of each photon event in the 27 ObsIDs (see Vivekanand 2020 for details).
7.1 Low phase-resolution PRS
Figure 14 shows the calibrated PRS of the Crab pulsar using all 49 useful detectors (27 ObsIDs, live time ≈ 136 ksec), over the energy range 1−10 keV. The spectra were obtained with 128 phase bins per cycle, using the extractor tool, and were analyzed using XSPEC. The background spectrum was extracted from the phase range 0.0–0.2. The response and ancillary response files used are those mentioned earlier. Spectral channels below 100 and above 1000 were ignored. The default photo ionization cross-sections and solar abundances were used. Details are given in Appendix C.
It is generally known that while the PAS of the Crab pulsar fits well to a single power law model over the energy range ≈ 1−100 keV, the PRS requires either a break in power law at around 11−13 keV (Madsen et al. 2015) or a curved spectrum (Massaro et al. 2000, 2006). The NICER energy range justifies the use of a single power law. So in Fig. 14, a single absorbed power law was fit to each of the 78 phase resolved spectra, The phase ranges 0.2−0.3 and 0.9−1.0 do not have sufficient number of photons for a reasonable fit, after background subtraction.
For the fit, the spectra at all phases must have the same absorbing column density NH. As mentioned earlier, the power law index Γ is correlated with NH; and the absolute value of Γ is not as important as its variation with rotation phase. Therefore NH was fixed at the value 0.36 × 1022 cm−2 in Fig. 14 (Massaro et al. 2006; see also Table 2 of Weisskopf et al. 2011, and references in Ge et al. 2012). As before, the errors in Fig. 14 represent the 90% confidence level.
The qualitative variation of Γ with phase in Fig. 14 is consistent with the results obtained with the BeppoSAX detector MECS, in the energy range 1.6−10 keV (Fig. 3b of Massaro et al. 2000 and Fig. 1 of Massaro et al. 2006). It is also consistent with the results of RXTE in the energy range 5− 60 keV (Fig. 1 of Pravdo et al. 1997, and Fig. 12 of Ge et al. 2012). However, the RXTE results are obtained by fitting only a single power law over the much larger energy range. It is also consistent with the results of XMM-Newton in the energy range of 0.6−6.5 keV, although their phase resolution is relatively poor (see Fig. 11 of Kirsch et al. 2006). It is also consistent with the results of NuSTAR, who fit a broken power law in the energy range 3− 78 keV (bottom panel of Fig. 3 of Madsen et al. (2015)). It appears to also be consistent with the results of Insight-HXMT, although their energy range is much larger, 11−250 keV, and they appear to fit a single power law in this entire energy range; see Table 3 and Fig. 5 of Tuo et al. (2019). Chandra’s energy range was much smaller, namely, 0.3−3.8 keV, and it had relatively much fewer photons, so a comparison with this work is not straightforward. We may, therefore, conclude that the results of Fig. 14 are qualitatively consistent with previous results. Next, we go on to some quantitative comparisons.
The PRS of NuSTAR (Madsen et al. 2015) that can be compared with this work is given in the 50″ extraction region section of their Table 2. The peak of their FLC appears to be at phase 0.1 in the bottom panel of their Fig. 3, which corresponds to phase 0.4 in Fig. 14 above. So their three bins straddling the peak, with phase boundaries 0.0−0.07, 0.07−0.14 and 0.14−0.21, correspond to the phase boundaries 0.30−0.37, 0.37−0.44 and 0.44−0.51, respectively, shown in Fig. 14 above. These three bins were chosen for comparison since they contain the highest number of photons in the PRS. Their background spectrum is extracted from their phase range 0.63−0.90, which corresponds to the phase range of 0.93−0.20 in Fig. 14 above. Madsen et al. (2015) fix the value of NH at 0.2 × 1022 and use the wilm photo ionization cross-sections and vern solar abundances.
Doing the same with the NICER data in the corresponding phase bins, we obtain Γ that is compared with their Γ1 in Table 2, which is the first of the two spectral indices for a broken power law model that they use over the 3− 78 keV range, the break occurring at 13.1(4) keV. The Γ1 of Madsen et al. (2015) differs from the corresponding Γ of this work by − 1.3, + 3.6 and − 1.0 standard deviations, in the three phase bins; the corresponding reduced χ2 of the fits are 0.99, 1.04, and 0.88, respectively.It is therefore concluded that there is reasonable quantitative agreement between the results of NuSTAR and that of this work. There are three aspects of NuSTAR data analysis which might explain the + 3.6σ difference. First, Madsen et al. (2015) do not specify where exactly the peak of the main pulse lies and we are left to assume, based on visual inspection, that it is at phase 0.1 in their Fig. 3. Any small difference in this value is likely to mix up the spectrum from the adjacent bins. Second, NuSTAR data is very severely affected by deadtime, as seen in their Fig. 3. If Madsen et al. (2015) have used this for correcting the spectrum also, then the effect would be felt most in the bin at the peak. Lastly, NuSTAR is an imaging instrument, and the data presented in their Fig. 3 has been extracted from region between 17′′ and 50′′; a slightly different region might have yielded slightly different result.
Massaro et al. (2000) obtain the PRS of the Crab pulsar using the MECS instrument on BeppoSAX at the first peak, in the phase interval 0.02667 straddling the peak. They use the phase range of 0.60−0.83 in their Fig. 1 to obtain the background spectrum, which translates to the phase range 0.0−0.23 in Fig. 14 above. They use NH = 0.323 × 1022 cm−2. They obtain Γ ≈ 1.83 in their Fig. 5 (numerical value is not given). Using the same parameters we obtain Γ = 1.818(3), which is a reasonable agreement.
Figure 14 was also produced using the energy ranges 2− 10 keV and 3− 10 keV, to check if the choice of the start of the energy range made any difference to the results. The Γ variation was similar, except for reduced statistical significance on account of reduced number of photons. Two other energy ranges were also tried, viz. 1−9 keV and 1−8 keV, but here the differences were imperceptible, as expected. We may, therefore, conclude that the results of Fig. 14 are quantitatively consistent with the results of NuSTAR and BeppoSAX.
The results of this and the following sub-section were obtained using both pairs of rmf and arf calibration files; the difference between the two sets of results is insignificant, except for the power law normalization coefficient A, which differs by about ≈6%, as expected, since that is the difference in the effective area between the two calibrations.
 |
Fig. 14 Low-resolution FLC and the corresponding PRS of the Crab pulsar. Top panel: FLC of the Crab pulsar at a resolution of 1∕128 in rotation phase, in the energy range 1−10 keV. Bottom panel: power law index Γ of the PRS of the Crab pulsar at the same resolution, over the same energy range. The background spectrum is estimated from data in the phase range 0.0–0.2. The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
Comparison of the results of NuSTAR and the corresponding results of NICER.
7.2 High phase-resolution PRS
Figure 15 shows the equivalent of Fig. 14 at the two peaks of the FLC of the Crab pulsar, at a phase resolution of1∕1024. The analysis method is the same as in Fig. 14, except that due to further reduction in photon counts per phase bin, energy bins that had less than four photons were ignored in each PRS. Ge et al. (2012) give high-resolution FLC at the two peaks, but in different energy bands and they do not display Γ at this high resolution.
In the top left panel of Fig. 15 the count rate rises from 9334.3 at phase 0.38 to 11442.1 at phase 0.40, then falls to 8758.6 at phase 0.42, indicating that at the first peak, the FLC of the Crab pulsar rises slowly and falls faster. The intermediate count rates of 10383.3 and 10101.4 at phases 0.39 and 0.41, respectively,confirm this trend. In the top right panel of Fig. 15 the count rates are 8728.8, 8999.4, 9232.1, 9022.7, and 8473.4 at phases 0.78, 0.79, 0.80, 0.81 and 0.82, respectively,not showing the same clear trend.
 |
Fig. 15 High-resolution FLC and the corresponding PRS of the Crab pulsar. Same as in Fig. 14, but at a phase resolution of 1∕1024. Left and right panels: data of the two peaks of the FLC of the Crab pulsar. The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
8 Discussion
This discussion begins with the scientific motivation for obtaining high-resolution FLC and PRS of the Crab pulsar at high energies. It was mentioned in Sect. 1 that these are required to understand the high energy emission mechanism of RPPs and it was also mentioned that the analysis of the PRS lagged far behind that of the FLC. One reason was probably the success obtained in theoretically producing the double peaked FLCs of several RPPs based only on the geometry of the magnetic field. The other reason was the relative difficulty in applying the basic radiative processes in a realistic magnetosphere of the RPPs, namely, curvature radiation (CR), inverse Compton scattering (ICS), and synchrotron radiation (SR) (Cheng et al. 1986). The availability of high-resolution PRS, and its use in conjunction with high-resolution FLC, necessitates the invocation of these basic radiative processes in addition to magnetic field line geometry and magnetospheric processes. This is complex problem. In this work, the focus is restricted to the formation and properties of caustics in FLCs using the main results of this paper (Fig. 15).
8.1 Two caustics or one
The left and right sections of Fig. 15 show the FLC (top panel) and PRS (bottom panel) of the Crab pulsar at its two peaks. Now, it is generally believed that the FLC of the first peak (left section) is a caustic, due to its narrow and luminous peak. A legitimate query considers whether the much wider and less luminous FLC of the second peak (right section) is not a caustic or whether it might be a caustic that was smoothed by some physical process. In the latter case, it would be reasonable to assume that the pre-widened caustic at the second peak had a PRS similar to that at the first peak. Then the physical process widening the second peak’s FLC would also smooth its PRS. The challenge is to come up with a physical process that can reshape the FLC at the first peak into that at the second peak, while simultaneously transforming the PRS at the first peak into that at the second peak.
At first glance, this appears difficult. By deconvolving the FLC of the second peak with the FLC of the first peak, it is possible to come up with a smoothing function that can transform the first FLC into the second. Naively, this should also widen the PRS of the first peak, which would not look anything like the monotonically increasing function of phase in the second peak of Fig. 15. So we have to invoke a functional relation between the FLC smoothing function and the corresponding PRS smoothing function to explain the data in Fig. 15. This aspect depends critically upon the specific emission mechanism, so we have to derive a functional relation each for the CR, ICS, and SR mechanisms. Although this is a challenging task, it would help to identify which of the three emission mechanisms is operating in the Crab pulsar.
In the alternate case that the second peak is not a caustic, we have to explain the significant rise and fallof X-ray flux as a function of phase, coupled with the monotonic increase in Γ as a function of phase. In either case, Fig. 15 contains important constraints for the process of caustic formation in the Crab pulsar’s X-ray FLC. The third alternative is that second peak is indeed a caustic with an entirely different PRS. This is the subject of the discussion in the next section.
8.2 Caustics with different PRS
There is some observational evidence that there is likely to be at least two kinds of caustics, each with a different PRS. DeCesar (2013) show the FLC and PRS of three RPPs that have strong double peaks at γ-ray energies, obtained from the Fermi observatory; see also Brambilla et al. (2014). In their Fig. 4.3 the shape of the FLC and PRS (Γ) of the Crab pulsar is roughly similar to that in Fig. 14 above, except for differences in phase resolution, photon statistics, etc., and a small dip in the Γ variation in the first peak. In their Fig. 4.2 the FLC of the Vela pulsar has two sharp peaks, but the variation of Γ with phase appears to be approximately a phase-reversed version of the Γ variation in Fig. 14. Specifically, Γ decreases monotonically with phase in the first peak, while it is almost constant in the second peak, which is opposite to the Γ variation in Fig. 14above. In their Fig. 4.4 the Geminga pulsar also has two sharp peaks, and the Γ decreases monotonically with phase in the first peak, just as in the Vela pulsar, while its variation is irregular in the second peak, but is not inconsistent with being constant. Both Vela and Geminga RPPs have two sharp peaks each, presumably caustics, and one of them has a roughly constant Γ with phase while the other has a monotonically decreasing Γ with phase.
Unfortunately the PRS of these RPPs have not been obtained at soft X-ray energies. Moreover, the FLC of Vela and Geminga RPPs have no sharp peak at soft X-ray energies, and Vela has only one sharp peak at hard X-ray energies (Thompson 2008). Therefore this discussion has to be done at γ-ray energies until high-resolution FLC and PRS of the Vela and Geminga RPPs is obtained at soft X-ray energies.
If the observations discussed in this section are correct, then the Vela and Geminga RPPs may have two kinds of caustics, one with a roughly constant Γ and the other with Γ varying monotonically with phase. Then the second peak of the Crab pulsar in Fig. 15 could very well be a caustic with a monotonically changing Γ with phase. However, its FLC is not at all sharp, which is a problem from the point of the definition of a caustic. Clearly, the PRS at the second peak of the Crab pulsar in Fig. 15 is an important constraint for the formation of high energy caustics in RPPs.
8.3 General formation of caustics or cusps
First, it is not clear if the sharp peak of the FLC of the Crab pulsar is on account of one or two poles. This can be studied by theoretically estimating the FLC and the PRS at the peak and comparing it with the observations in Fig. 15. In the two pole scenario, we can expect photons from the pole that is farther away from the observer to traverse a region of enhanced magnetic field and particle density, before reaching the observer, as compared to photons from the closer pole, since the trajectory of the former might pass closer to the center of the RPP for reasonable values of α and ζ. This might imply enhanced optical depth, either in terms of passage through enhanced density of plasma or in terms of scattering off enhanced density of relativistic particles and photons. If this is true, then the PRS observed from two poles would be different from that observed from one pole only; it is likely that the two pole PRS would have a curvature, or even a break, in the spectrum, instead of being a simple power law. It is also likely that such an effect, if at all it exists, may be too weak to be observed by current instruments. Furthermore, the FLC from two poles may be more luminous than that from a single pole, but it may be broader (less sharp) since it requires alignment in phase of a much larger volume of emission. Currently, the above arguments can only be tested statistically since we do not have access to a FLC and PRS from a single pole that can be used as a reference.
Second, it is not clear if the sharp peak of the FLC of the Crab pulsar is formed due to the SMS effect. If so, then photons from the same magnetic field line that is stretched radially will arrive in phase independent of the length of the field line involved, at least to first order. Now, the height of the peak is proportional to the length of the field line involved (Bai & Spitkovsky 2010), while its width may not change much since it is just one field line (or a narrow group of field lines). Thus, in caustics formed by the SMS effect, the width of the peak may be relatively narrow and independent of its height. By the same argument, the variation of the PRS as a function of phase might be minimum. In contrast, a caustic formed otherwise would get contributions from a substantial volume of the magnetosphere, possibly with different PRS and different peak widths; in this case, the width of the peak may be anti correlated with its height.
Future polarization observations should show that caustics formed by the SMS effect have a higher degree of polarization, than caustics formed otherwise, where we can expect significant de-polarization due to the coming together of emission from different magnetic field lines. This has been observed in the Crab pulsar’s optical FLC, where the degree of polarization at the optical peaks is a minimum. This occurs because radiation with different polarization angles piles up at the peaks (caustics; Smith et al. 1988; Dykes & Rudak 2013; see also Fig. 5 of Romani & Yadigaroglu 1995).
8.4 Pitch angles of radiating particles
The observed width of the sharp peak of the FLC of the Crab pulsar contains interesting information. First, it could be the natural width of the caustic, in which case it contains information about the details of the caustic formation. Alternately, the caustic itself may be much narrower and the observed width may be due to, say, the pitch angles of the radiating particles in the magnetic field. In this case, it would contain information about the details of the radiative process. A proper estimate of the width is only possible if the FLC is obtained with sufficient resolution in rotation phase. By fitting a Gaussian to the phase range 0.395–0.409 in the top left panel of Fig. 15, the approximate width of the caustic turns out to be 0.026 ± 0.011 in phase. A much more accurate width estimation requires proper modeling of the caustic in terms of more diverse functions than a Gaussian. This can also be done by complete FLC modeling at the peak.
In summary, this work derives the highest resolution PRS of the two peaks of the Crab pulsar’s FLC at soft X-ray energies. It demonstrates that observationally there could be two kinds of caustics, each with a different kind of PRS, as seen in some RPPs at γ-ray energies. Currently, It is not clear how these two may correspond to the theoretically postulated SMS and non-SMS caustics.
Acknowledgements
I thank the referee for bringing to my attention the IACHEC reports, and the referee and Sergio Campana for useful discussion and suggestions.
Appendix A High Background counts
First, a LTLC in the energy range of 12−15 keV (energy channels 1200−1500) is extracted from the event file, with a bin width of 8 s using the extractor tool. Next, those time bins in the LTLC that have count rates greater than 1.0 are identified. Let these be TTIME. These times represent the center of the time bin if the keyword TIMEPIXR = 0.5; the bin width is given in the keyword TIMEDEL. The start time of the LTLC is given in the keyword TIMEZERO, which represents the center of the first time bin. Finally the keyword of the same name, TIMEZERO, but now in the event file, contains a clock correction that is usually − 1 s; here it will be labeled CLKCOR. Therefore, the relevant time range to be excluded in the event file (in units of TT) for each TTIME is given by TIMEZERO + TTIME - CLKCOR ∓ TIMEDEL∕2, representingthe lower and upper limits of the duration to be excluded, respectively.
The above time ranges have to be excluded from the GTI in the event file, in the FITS file extension 10. There are several ways of doing this. But an elegant way is to use the algorithm given in the FORTRAN function gtimerge in the library gtilib.f10.
Appendix B Space weather parameter Kp
The official Kp web page is at the German Research Center for Geosciences (GFZ); the link is given in footnote 1 of this paper. The WDC directory contains the file wdc_fmt.txt which contains the format of the data in the four ASCII files of use here, viz., kp2017.wdc, kp2018.wdc, kp2019.wdc and kp2020.wdc, one for each year of operation of NICER, from which the Kp data has to be retrieved for each ObsID.
We begin by extracting the start and end times of the observation from the event file for each ObsID, from the keywords TSTART and TSTOP. The integer and fractional parts of the reference MJD for NICER (MJDREFI and MJDREFF) are read as well as the clock correction TIMEZERO (this is labeled CLKCOR in Appendix A). Then the start and end times are converted into MJD using the formula TT(1,2) = MJDREFI + MJDREFF + ((TSTART,TSTOP) + TIMEZERO) / 86400, where TT1 and TT2 correspond to TSTART and TSTOP, respectively. These are converted into Gregorian dates using the SOFA11 software iauTttai, iauTaiutc, iauJd2cal, which convert the start and end times of observations first from TT in MJD units to TAI in MJD, then from TAI to UTC, then from UTC in JD units to Gregorian calendar date, respectively; we note the conversion from MJD to JD before the last step. The conversion to date has been verified using the web tool xTime12, a date and time conversion utility.
Based on the year of observation, the corresponding WDC file is read, and the Kp is plotted as a function of time during the observation; Kp is given over three-hour intervals. If a Kp value is greater than 5, then that entire three hours of observation has to be excluded.
Appendix C Linux shell scripts to obtain and analyze PRS
Obtaining and analyzing manually the spectral data of Figs. 14 and 15 is difficult. So, Linux shell scripts were developed to do the tasks automatically. First, the FLC of the top panels of these figures is obtained, using a C/C++ program. The output of this is an ASCII file containing two columns, viz, the central phase and the photon counts of each bin in rotation phase; in Fig. 14, that would be 128 bins.
Next, a Linux shell script (in tcsh) reads the column of central phases, computes the phase boundaries of the corresponding bins, and invokes the extractor tool to obtain the spectrum of the data within each phase bin, using 27 ObsIDs. The output of this script are FITS files of type pha, one for each phase bin. These are the so called PRS that can be analyzed using XSPEC. Next a Linux shell script (in tcsh) writes the required XSPEC commands into an ASCII file with extension.xcm, which is invoked as “xspec - *.xcm”.
The first XSPEC command defines data groups; in Fig. 14 it would be 78 data groups, one for each pha file being analyzed. The command would be “data 1:1 y_38.pha 2:2 y_39.pha ... 78:78 y_115.pha”, the file names indicating the corresponding phase bin; in Fig. 14, phase bins 38 to 115 have been analyzed. The next two commands set the response and ancillary response files for each data group: “response 1 nixti20170601_ combined_v002.rmf 2 nixti20170601_combined_v002.rmf ... 78 nixti20170601_combined_v002.rmf” and “arf 1 nixtionaxis20170601_combined_v004.arf 2 nixtionaxis20170601_combined_v004.arf ... 78 nixtionaxis20170601_combined_v004.arf”.
Next, the background spectrum file is defined for each group, as well as the channels to ignore for each group. Next the model to fit is defined “model phabs(powerlaw)”, followed by the command “/*”. Then the initial values of the parameters to fit are defined using the “newpar” command. Since there are 78 spectra each with three parameters, there are totally 3 × 78 = 234 parameters to fit. However the first parameter of each spectrum NH is fixed at the value 0.36. So the next 78 commands are “newpar 1 0.36; newpar 4 = 1; newpar 7 = 1; ... newpar 232 = 1”. The command “freeze 1” ensures that these 78 parameters are not fit but held fixed. Each command must be on a separate line. Similarly the second and third parameters of the model (Γ and A) are given initial values, but they are not frozen. Then the following three commands result in the fitting process: “renorm; query yes; fit,” each on a separate line.
The “ignore” and “model” commands require the use of the star symbol “*”, which is easy to issue manually in XSPEC but tricky to do so in a shell script.
Finally, the command to estimate the 90% confidence errors on the parameters is: “error 2 3 5 6 8 9 ... 230 231 233 234” on one line. We note that the parameters 1, 4, 7, ..., 229, 232 do not appear in the command since they refer to the parameter NH which is not fit. To speed up the execution of this command, the command “parallel error 4” uses 4 cores of the computer’s CPU for parallel processing.
The error command requires a lot of time to execute. The whole xcm script for 128 phase bins requires ≈3.0 days of continuous running on an average laptop – Acer Aspire E5-575, Intel core i3-7100U CPU @ 2.40GHz, 2 cores, 4 threads, 12 GB DDR4 Synchronous RAM @ 2133 MHz, 64 bit Fedora core 32 operating system. The script would require ≈3.5 yr of continuous running for 1024 phase bins.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 708, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Arzoumanian, Z., Gendreau, K. C., Baker, C. L., et al. 2014, Proc. SPIE, 9144, 914420 [Google Scholar]
- Atwood, W. B., Bagagli, R., Baldini, L., et al. 2007, Astropart. Phys., 28, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X. N., & Spitkovsky, A., 2010, ApJ, 715, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanov, S., Ho, W. C. G., Enoto, T., et al. 2019, ApJ, 877, 69 [Google Scholar]
- Brambilla, G., Kalapotharakos, C., Harding, A. K., et al. 2015, ApJ, 804, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bult, P., Altamirano, D., Arzoumanian, Z., et al. 2018, ApJ, 860, L9 [Google Scholar]
- Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 500 [Google Scholar]
- Cheng, K. S., Ruderman, M., & Zhang, L. 2000, ApJ, 537, 964 [Google Scholar]
- DeCesar, M. 2013, PhD thesis, University Of Maryland, USA [Google Scholar]
- Dykes, J., & Rudak, B. 2003, ApJ, 598, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, M. Y., Lu, F. J., Qu, J. L., et al., 2012, ApJS, 199, 32 [Google Scholar]
- Gendreau, K., Arzoumanian, Z., Adkins, P. W., et al. 2016, Proc. SPIE, 9905, 99051H [Google Scholar]
- Guillot, S., Kerr, M., Ray, P. S., et al. 2019, ApJ, 887, L27 [Google Scholar]
- Harding, A. 2016, J. Plasma Phys. 82, 635820306 [Google Scholar]
- Hare, J., Tomsick, J. A., Buisson, D. J. K., et al. 2020, ApJ, 890, 57 [CrossRef] [Google Scholar]
- Kalapotharakos, C., Harding, A. K., & Kazanas, D. 2014, ApJ, 793, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Keek, L., Arzoumanian, Z., & Bult, P. 2018, ApJ, 855, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kirsch, M. G. F., Briel, U. G., Burrows, D., et al. 2005, Proc. SPIE 5898, 89803 [Google Scholar]
- Kirsch, M. G. F., Schönherr, G., Kendziorra, E., et al. 2006, A&A, 453, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kouzu, T., Tashiro, M. S., Terada, Y., et al. 2013, PASJ, 65, 74 [Google Scholar]
- Ludlam, R. M., Miller, J. M., Arzoumanian, Z., et al. 2018, ApJ, 858, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Ludlam, R. M., Shishkovsky, L., Bult, P. M., et al. 2019, ApJ, 883, 39 [Google Scholar]
- Madsen, K. K., Reynolds, S., Harrison, F., et al. 2015, ApJ, 801, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Malacaria, C., Bogdanov, S., Ho, W. C. G., et al. 2019, ApJ, 880, 74 [Google Scholar]
- Massaro, E., Cusumano, G., Litterio, M., & Mineo, T. 2000, A&A, 361, 695 [NASA ADS] [Google Scholar]
- Massaro, E., Campana, R., Cusumano, G., & Mineo, T. 2006, A&A, 459, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, J. M., Kammoun, E., Ludlam, R. M., et al. 2019, ApJ, 884, 106 [CrossRef] [Google Scholar]
- Pierbattista, M., Harding, A. K., Gonthier, P. L., et al. 2016, A&A, 588, A137 [CrossRef] [EDP Sciences] [Google Scholar]
- Pravdo, S. H., Angelini, L., & Harding, A. K. 1997, ApJ, 491, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Prigozhin, G., Gendreau, K., Doty, J. P., et al. 2016, Proc. SPIE, 9905, 99051I [Google Scholar]
- Ray, P. S., Guillot, S., Ransom, S. M., et al. 2019, ApJ, 878, L22 [Google Scholar]
- Riley, T. E., Watts, A. L., Bogdanov, S., et al. 2019, ApJ, 887, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R. W., & Watters, K. P. 2010, ApJ, 714, 810 [Google Scholar]
- Romani, R. W., & Yadigaroglu, I. A. 1995, ApJ, 438, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, F. G., Jones, D. H. P., Dick, J. S. B., et al. 1988, MNRAS, 233, 305 [Google Scholar]
- Stevens, A. L., Uttley, P., Altamirano, D., et al. 2018, ApJ, 865, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, D. J. 2008, Rep. Prog. Phys., 71, 116901 [NASA ADS] [CrossRef] [Google Scholar]
- Trakhtenbrot, B., Arcavi, I., Ricci, C., et al. 2019, Nat. Astron., 3, 187 [Google Scholar]
- Tuo, Y. L., Ge, M. Y., Song, L. M., et al. 2019, RAA, 19, 87 [Google Scholar]
- van den Eijnden, J., Degenaar, N., Ludlam, R. M., et al. 2020, MNRAS, 493, 1318 [Google Scholar]
- Vivekanand, M. 2020, A&A, 633, A57 [EDP Sciences] [Google Scholar]
- Weisskopf, M. C., Tennant, A. F., Yakovlev, D. G., et al. 2011, ApJ, 743, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson-Hodge, C. A., Cherry, M. L., Case, G. L., et al. 2011, ApJ, 727, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson-Hodge, C. A., Malacaria, C., Jenke, P. A., et al. 2018, ApJ, 863, 9 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 LTLC of 49 useful detectors of NICER combined, over ≈2.35 yr, with a bin size of 10 s. |
| In the text | |
 |
Fig. 2 Statistics of the LTLCs of the 49 individual detectors of NICER. The black dots, red crosses, and blue pluses are the mean count rate, the maximum and the minimum values, respectively. The error bars represent the standard deviation and not the error on the mean. |
| In the text | |
 |
Fig. 3 Normalized χ2 between the LTLCs of the 49 individual detectors and their combined LTLC shown in Fig. 1. |
| In the text | |
 |
Fig. 4 Raw spectrum of the 49 detectors combined, from channels 20 to 1200 (0.2− 12 keV). |
| In the text | |
 |
Fig. 5 χ2 per degree of freedom between the raw spectrum of each detector and their combined spectrum in Fig. 4. |
| In the text | |
 |
Fig. 6 Normalized χ2 between the raw spectra of earlier and later halves (durations) of the data for each detector. |
| In the text | |
 |
Fig. 7 Mean values of X-ray counts per detector, GTI difference, and deadtime per detector using all counts, respectively, per phase bin for data of ObsID 1013010147, after applying the method of Wilson-Hodge et al. (2018). The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
| In the text | |
 |
Fig. 8 Mean values of count rate per detector (deadtime corrected), and deadtime fraction per detector, respectively, per phase bin fordata of ObsID 1013010147, after applying the method of Wilson-Hodge et al. (2018). The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
| In the text | |
 |
Fig. 9 Comparison of detector deadtime fractions of the 49 detectors. |
| In the text | |
 |
Fig. 10 Fractional difference in detector deadtime fraction between the first and second halves (durations) of the data. The reference epoch of phase 0.4 is MJD 58 479.425994152342. |
| In the text | |
 |
Fig. 11 Study of detector deadtime as a function of photon energy. Top panel: FLC for data of all 49 detectors in the energy range 1.0−1.62 keV (dashed line), and in the energy range 1.62−10.0 keV (solid line). Bottom panel: deadtime fraction of the corresponding FLC in the top panel. The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
| In the text | |
 |
Fig. 12 Soft X-ray spectrum of the Crab nebula and its pulsar. Top panel: phase-averaged spectrum of the Crab nebula plus pulsar. Bottom panel: ratio of data and model. Channel-dependent effective area normalization is done using the “setplot area” command of XSPEC. |
| In the text | |
 |
Fig. 13 Soft X-ray spectrum of the Crab nebula and its pulsar. The same as in Fig. 12, with a wider energy range. |
| In the text | |
 |
Fig. 14 Low-resolution FLC and the corresponding PRS of the Crab pulsar. Top panel: FLC of the Crab pulsar at a resolution of 1∕128 in rotation phase, in the energy range 1−10 keV. Bottom panel: power law index Γ of the PRS of the Crab pulsar at the same resolution, over the same energy range. The background spectrum is estimated from data in the phase range 0.0–0.2. The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
| In the text | |
 |
Fig. 15 High-resolution FLC and the corresponding PRS of the Crab pulsar. Same as in Fig. 14, but at a phase resolution of 1∕1024. Left and right panels: data of the two peaks of the FLC of the Crab pulsar. The reference epoch of the first peak (phase 0.4) is MJD 58 479.425994152342. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


