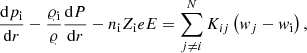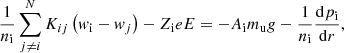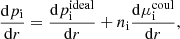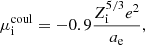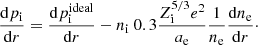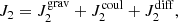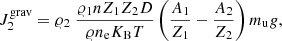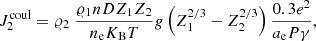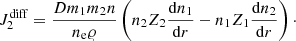EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 644 (December 2020) A&A, 644 (2020) A55 Full HTML
Free Access
Issue
A&A
Volume 644, December 2020
Article Number A55
Number of page(s) 6
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202039557
Published online 01 December 2020

© ESO 2020

1. Introduction

Element diffusion is a key physical process that may substantially modify the superficial abundances, internal chemical structure, pulsation properties, and evolution of a large variety of stars at different evolutionary stages, including our Sun (see Michaud et al. 2015). Because their gravities are extremely high, this is particularly true in the case of white dwarf (WD) stars, for which diffusion driven by gravity is responsible for the purity of the outer layers that characterizes most of these stars (see, Winget & Kepler 2008; Althaus et al. 2010; Córsico et al. 2019a for reviews). At the chemical interfaces of these stars, characterized by large composition gradients, chemical diffusion tends to dominate diffusion driven by gravity and thus strongly smoothes out the chemical profiles during WD evolution, which has consequences for the predicted pulsational properties of these stars. Earlier studies by the La Plata Group demonstrated the necessity of properly treatming element diffusion for an assessment of the adiabatic oscillation properties of pulsating WDs and the mode-trapping features produced by the outer chemical transition regions (see Córsico et al. 2002; Althaus & Córsico 2004). Diffusion processes are also at the root of the occurrence of diffusion-induced novae, that is, WDs that under certain circumstances experience a thermonuclear flash induced by chemical diffusion that carries hydrogen (H) to deeper and hotter layers (Miller Bertolami et al. 2011). Finally, gravitational settling of minor species such as 22Ne in the carbon-oxygen (CO) core of WDs releases enough energy to substantially affect the cooling times of WDs (Deloye & Bildsten 2002; García-Berro et al. 2010).

Chang et al. (2010) and Beznogov & Yakovlev (2013) have studied the diffusion process in strongly coupled Coulomb plasmas. In particular, Beznogov & Yakovlev (2013) have explored the diffusion currents for strongly coupled Coulomb mixtures of ions in dense stellar matter typical of compact stars such as WDs and neutron stars. These authors extended the work of Chang et al. (2010) to the case of nonequilibrium mixtures and showed that Coulomb separation affects the diffusion flux in WDs, driving the gravitational settling of ions with the same A/Z (mass to charge number). In such mixtures, the contribution of gravity and induced electric field to sedimentation is negligible, and the effect of Coulomb separation becomes relevant. Bezgonov and Yakovlev reported that ions with larger Z move to deeper layers and that this effect is stronger for a larger difference of Z in the mixture and for higher gravities, that is, massive WDs. In a more recent paper, Koester et al. (2020) have implemented the Coulomb corrections following Beznogov & Yakovlev (2013) to study the problem of carbon dredge-up in He-rich WDs.

Beznogov & Yakovlev (2013) suggested that the redistribution of ions due to Coulomb separation could affect the thermal evolution of WDs and their pulsational properties and thus the predictions of asteroseismology. We precisely study the effect of the Coulomb separation of ions on the evolution and pulsations of ZZ Ceti stars. These pulsating stars are H-rich (DA spectroscopic class) WDs with 10 400 K ≲ Teff ≲ 12 400 K and 7.5 ≲ log g ≲ 9.1, characterized by multiperiodic luminosity variations due to g-mode pulsations (see, Córsico et al. 2019a for a recent review). In particular, ultra-massive ZZ Ceti stars, in which Coulomb separation of ions would be more relevant and the effect on their pulsation periods could be stronger, have been reported (Kanaan et al. 2005; Castanheira et al. 2010, 2013; Hermes et al. 2013; Curd et al. 2017; Rowan et al. 2019). Specifically, we study the evolution of WD models with masses in the range 0.5 − 1.3 M⊙ derived from their progenitor history. The WD mass values cover the range of relevant stellar masses expected for these stars. We consider a time-dependent element diffusion scheme that incorporates the gravitational settling term due to Coulomb interactions at high densities. We assess the effect of Coulomb separation on the cooling times of our WD models and on their chemical profiles, Brunt–Väisälä frequency, and pulsational periods. The paper is organized as follows. In Sect. 2 we describe the input physics of our stellar models, in particular the modification to our treatment of element diffusion to include the Coulomb interaction effect. In this section we also discuss the effect of Coulomb sedimentation on the evolving chemical profiles. In Sect. 3 we describe the effect of Coulomb diffusion on the pulsational properties of DA WDs. Finally, in Sect. 4 we summarize the main findings of the paper.

2. Input physics and white dwarf models

2.1. Numerical codes

The pulsational properties of the WD models presented in this work are based on the evolutionary models provided by the LPCODE stellar evolution code. This code has been widely used and tested in numerous stellar evolution contexts of low-mass and particularly WD stars (see, Althaus et al. 2003, 2005, 2015; Salaris et al. 2013; Miller Bertolami 2016; Silva Aguirre et al. 2020; Christensen-Dalsgaard et al. 2020 for details). Specifically, LPCODE considers a full treatment of energy sources, including the energy contribution caused by phase separation of core chemical species upon crystallization. The treatment of crystallization is based on the phase diagrams of Horowitz et al. (2010) for dense CO mixtures and on that of Medin & Cumming (2010) for ONe mixtures. Relevant for this work, LPCODE computes WD evolution in a self-consistent way with the changes in the internal chemical distribution that result from the mixing of all the core chemical components induced by the mean molecular weight inversion, element diffusion (see below), and phase separation of core chemical constituents upon crystallization (and the ensuing mixing in the layers above the crystallized core). For our work, abundance changes during crystallization are a relevant issue in the case of pulsating ultra-massive ZZ Ceti stars, which are expected to be mostly crystallized. In LPCODE, these abundance changes are assessed in a self-consistent way with WD evolution. Energy release resulting from 22Ne sedimentation was not considered in this study.

For the pulsational analysis we used the LP-PUL pulsation code described in Córsico & Althaus (2006). This code employs the “hard-sphere” boundary conditions to account for the effects of crystallization on the pulsation spectrum of g modes. These conditions assume that the amplitude of the radial and horizontal eigenfunctions of g modes is null below the solid-liquid interface because of the nonshear modulus of the solid, as compared with the fluid region (see Montgomery & Winget 1999). The central boundary conditions are located at the mesh point of the crystallization front (see Córsico et al. 2004, 2005, 2019b; De Gerónimo et al. 2019). The Brunt–Väisälä frequency is computed as in Tassoul et al. (1990). The computation of the Ledoux term B includes the effects of multiple chemical species that vary in abundance.

2.2. Diffusion treatment in a strongly coupled Coulomb plasma of ions

LPCODE considers a new fully implicit treatment of time-dependent element diffusion that includes thermal and chemical diffusion and gravitational settling (Althaus et al. 2020). We follow the diffusion for the isotopes 1H,3He, 4He, 12C, 13C, 14N,15N, 16O, 17O,18O, 19F, 20Ne, 22Ne, 23Na, and 24Mg. Our treatment of diffusion is based on the formalism of Burgers (1969), which provides the diffusion velocities in a multicomponent plasma under the effect of gravity, partial pressure, and induced electric fields. Here, diffusion velocities satisfy the set of N − 1 independent equations for ions1,

d p i d r − ϱ i ϱ d P d r − n i Z i e E = ∑ j ≠ i N K ij ( w j − w i ) , $$ \begin{aligned} \frac{\mathrm{d}p_{\rm i}}{\mathrm{d}r}-\frac{\varrho _{\rm i}}{\varrho }\frac{\mathrm{d}P}{\mathrm{d}r}-n_{\rm i}Z_{\rm i}eE= \sum _{j\ne i}^NK_{ij}\left(w_j-w_{\rm i}\right), \end{aligned} $$(1)

where pi, 𝜚i, ni, Zi, and wi denote the ion partial pressure, mass density, number density, mean charge, and diffusion velocity for chemical species i, respectively. N is the number of ionic species plus electrons, e is the charge unit, and E is the electric field. Resistance coefficients Kij are taken from Paquette et al. (1986). This set of equations is solved together with the equations for no net mass flow ∑iAiniwi = 0, with Ai being the atomic mass number, and no electrical current ∑iZiniwi = 0.

Using dP/dr = −g𝜚 and 𝜚i = Ainimu, Eq. (1) can be written as

1 n i ∑ j ≠ i N K ij ( w i − w j ) − Z i e E = − A i m u g − 1 n i d p i d r , $$ \begin{aligned} \frac{1}{n_{\rm i}}\sum _{j\ne i}^NK_{ij}\left(w_{\rm i}-w_j\right) - Z_{\rm i}eE= -A_{\rm i} m_{\rm u} g -\frac{1}{n_{\rm i}} \frac{\mathrm{d}p_{\rm i}}{\mathrm{d}r}, \end{aligned} $$(2)

where g is the gravitational acceleration and mu the atomic mass. Diffusion velocities at each depth of the star are found as described in Althaus et al. (2020). To include the Coulomb interaction effect, we proceeded as in Koester et al. (2020) and Beznogov & Yakovlev (2013), and write

d p i d r = d p i ideal d r + n i d μ i coul d r , $$ \begin{aligned} \frac{\mathrm{d}p_{\rm i}}{\mathrm{d}r}= \frac{\mathrm{d}p^\mathrm{ideal}_{\rm i}}{\mathrm{d}r} + n_{\rm i} \frac{\mathrm{d}\mu ^\mathrm{coul}_{\rm i}}{\mathrm{d}r}, \end{aligned} $$(3)

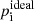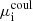where p i ideal $ p^{\mathrm{ideal}}_{\mathrm{i}} $ and μ i coul $ \mu^{\mathrm{coul}}_{\mathrm{i}} $ are the ideal pressure and the chemical potential due to Coulomb interactions of ion i. 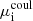μ i coul $ \mu^{\mathrm{coul}}_{\mathrm{i}} $ is given by Beznogov & Yakovlev (2013) as

μ i coul = − 0.9 Z i 5 / 3 e 2 a e , $$ \begin{aligned} \mu ^\mathrm{coul}_{\rm i}= -0.9 \frac{Z_{\rm i}^{5/3} e^2}{a_{\rm e}}, \end{aligned} $$(4)

with ae = (4πne/3)−1/3 being the electron-sphere radius. Hence,

d p i d r = d p i ideal d r − n i 0.3 Z i 5 / 3 e 2 a e 1 n e d n e d r · $$ \begin{aligned} \frac{\mathrm{d}p_{\rm i}}{\mathrm{d}r}= \frac{\mathrm{d}p^\mathrm{ideal}_{\rm i}}{\mathrm{d}r} - n_{\rm i}\ 0.3 \frac{Z_{\rm i}^{5/3} e^2}{a_{\rm e}} \frac{1}{n_{\rm e}}\frac{\mathrm{d}n_{\rm e}}{\mathrm{d}r}\cdot \end{aligned} $$(5)

This treatment is justified in the regime of strong ion coupling. Coulomb sedimentation may be relevant in a mixture of ions with the same A/Z (such as 4He, 12C, and 16O). We can illustrate this by simplifying the set of Eq. (2) to the case of two ion species (i = 1, 2). Assuming no temperature gradients and that the electron has zero mass, the diffusion flux of ion 2 (J2 = 𝜚2w2) can be expressed as the contributions from gravitational settling, Coulomb diffusion, and ordinary diffusion due to chemical gradients as

J 2 = J 2 grav + J 2 coul + J 2 diff , $$ \begin{aligned} J_2= J_2^\mathrm{grav} + J_2^\mathrm{coul} + J_2^\mathrm{diff}, \end{aligned} $$(6)

where

J 2 grav = ϱ 2 ϱ 1 n Z 1 Z 2 D ϱ n e K B T ( A 1 Z 1 − A 2 Z 2 ) m u g , $$ \begin{aligned}&J_2^\mathrm{grav} = \varrho _2\ \frac{\varrho _1 n Z_1Z_2D}{\varrho n_{\rm e} K_{\rm B}T}\left({\frac{A_1}{Z_1}} - {\frac{A_2}{Z_2}} \right)m_{\rm u} g, \end{aligned} $$(7)

J 2 coul = ϱ 2 ϱ 1 n D Z 1 Z 2 n e K B T g ( Z 1 2 / 3 − Z 2 2 / 3 ) 0.3 e 2 a e P γ , $$ \begin{aligned}&J_2^\mathrm{coul} = \varrho _2\ \frac{\varrho _1 n D Z_1Z_2}{ n_{\rm e} K_{\rm B}T}g \left(Z_1^{2/3} - Z_2^{2/3}\right) \frac{0.3 e^2}{a_{\rm e} P \gamma }, \end{aligned} $$(8)

and

J 2 diff = D m 1 m 2 n n e ϱ ( n 2 Z 2 d n 1 d r − n 1 Z 1 d n 2 d r ) · $$ \begin{aligned} J_2^\mathrm{diff} = \frac{D m_1 m_2 n}{ n_{\rm e}\varrho } \left( n_2Z_2\frac{\mathrm{d}n_1}{\mathrm{d}r} - n_1Z_1 \frac{\mathrm{d}n_2}{\mathrm{d}r}\right)\cdot \end{aligned} $$(9)

Here, D is the standard diffusion coefficient, mi = Aimu, and γ = ∂ ln P/∂ ln 𝜚2. Pressure was assumed to be provided by strongly degenerate electrons. We note that Coulomb interaction contributes to the gravitational settling in such a way that ions with larger Z move to deeper layers. We note also that for plasmas made of a mixture of 4He and 12C, 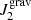J 2 grav $ J_2^{\rm grav} $ vanishes, and Coulomb separation should be important in driving gravitational settling of ions. This is particularly true in the case of more massive (and compact) WDs characterized by higher gravities (Beznogov & Yakovlev 2013). We show that Coulomb sedimentation cannot be neglected in ultra-massive WDs. In the case of a WD envelope made of 1H and 4He, 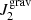J 2 grav $ J_2^{\rm grav} $ dominates and Coulomb separation constitutes a minor contribution to the settling of ions.

2.3. White dwarf models

To assess the effect of Coulomb diffusion, we computed the WD evolution with and without the Coulomb interaction term in the diffusion equations. We considered four WD models extracted from the evolution of single progenitors with final stellar masses of 0.576, 0.833, 1.159, and 1.292 M⊙. The starting 0.576 and 0.833 M⊙ WD configurations, characterized by CO cores, are H-burning post-asymptotic giant branch (AGB) star models computed by Miller Bertolami (2016) from the full evolution of their progenitor stars with metallicity Z = 0.02 and initial masses of 1.5 and 4.0 M⊙, respectively. Such starting WD models are based on detailed and improved micro- and macrophysics processes involved in AGB and thermally pulsing AGB modeling, which are relevant for the predicted internal composition of WDs. The starting 1.159 and 1.292 M⊙ ultra-massive WDs were taken from Camisassa et al. (2019). These WDs result from off-center carbon burning in the single-evolution scenario. Their progenitors experience a violent carbon-ignition phase followed by the development of an inward-propagating convective flame that transforms the CO core into a degenerate ONe one. Such WDs are composed of 16O and 20Ne, with traces of 23Na and 24Mg (see Siess 2007, 2010). All of the WD models were evolved from the beginning of the cooling track, where we performed the core mixing implied by the inversion of the mean molecular weight left by prior evolution, down to low effective temperatures, in a consistent way with abundance changes resulting from element diffusion, phase separation on crystallization, convective mixing, and residual nuclear burning in the case of CO WD models.

The chemical profiles of our initial WD models are shown in Fig. 1 for some selected isotopes. The internal composition of WDs is a crucial aspect for the determination of the pulsational properties of these stars. The WD models shown in the figure correspond at the beginning of their cooling phase prior to the onset of element diffusion and after the core mixing due to the inversion of the mean molecular weight. Their core chemical structure reflects the nuclear burning and mixing history throughout the progenitor evolution. We note that both the H and He contents of the WDs decrease with stellar mass3. Moreover, the large abundance of 14N in the He-rich buffer of the CO WD models, in particular for the 0.576 M⊙ WD model, reflects the occurrence of an appreciable third dredge-up. This model experiences a final thermal pulse at the very end of the thermally pulsing AGB phase that is responsible for higher surface carbon abundances (see Miller Bertolami 2016).

thumbnail Fig. 1.

Abundance by mass of 1H, 4He, 12C, 14N, 16O, 20Ne, 22Ne, 23Na, and 24Mg vs. the outer mass coordinate for our 0.576, 0.833, 1.159, and 1.292 M⊙ WD models at the beginning of the cooling track.

During WD cooling, element diffusion processes alter the chemical abundance distribution in the outer layers of all of the initial models. In the case of ultra-massive WDs, phase separation of the core chemical constituents upon crystallization modifies the shape of the 16O and 22Ne profiles. The resulting chemical profile by the time evolution reached the ZZ instability strip is shown in Fig. 2 at Teff = 11 000 K, which also illustrates the effect of Coulomb sedimentation on the chemical profiles. As discussed, Coulomb sedimentation is relevant for massive WDs and for mixtures of ions with equal A/Z. In this case, Coulomb separation drives gravitational settling (see Eqs. (6)–(9)), and ions with larger Z accordingly move to deeper layers. We note that the H-He interface is not affected by Coulomb diffusion because in this case the contribution due to gravity is dominant (Eq. (7)), and Coulomb diffusion represents a minor contribution to the diffusion flux. We also note that for ultra-massive WDs, Coulomb sedimentation prevents the strong inward diffusion of He toward the core, leading to the formation of a pure-He buffer with the consequent appearance of two well-separated chemical transition regions, one located at the base and the other at the top of that buffer. The neglect of Coulomb diffusion in ultra-massive WDs, in contrast, causes chemical diffusion, which in this case is dominant (see Eq. (9)), to virtually erode the initial pure He buffer, as illustrated by the figure. We consider, for example, the case of the 1.292 M⊙ model (upper panel of Fig. 2). When Coulomb diffusion is taken into account, the C-He interface is located at log(1 − mr/M⋆)∼ − 5, and the He-H interface is located at log(1 − mr/M⋆)∼ − 5.8. In contrast, for this model there is a single chemical transition region at log(1 − mr/M⋆)∼ − 5.8 of 16O, 12C, 4He, and 1H when Coulomb diffusion is neglected. Finally, we note that when we consider Coulomb diffusion, there is an internal chemical transition (located in the fluid part of the star, at log(1 − mr/M⋆)∼ − 3) due to the variation of chemical abundances of 24Mg, 20Ne, 16O, and 12C. This chemical transition is virtually absent when Coulomb diffusion is neglected. We show that all these differences affect the theoretical pulsational spectrum of these stars to some extent.

thumbnail Fig. 2.

Same as Fig. 1, but at an effective temperature of Teff = 11 000 K, corresponding to the domain of pulsating ZZ Ceti stars. Thick (thin) lines correspond to the case when Coulomb sedimentation of ions is considered (disregarded) in the diffusion equations. The gray area marks the domain of core crystallization.

We also compared the resulting WD cooling times and found that the effect of Coulomb diffusion on the cooling times is minor, except for the 1.292 M⊙ WD sequence, which evolves about 6% faster at low luminosities when Coulomb diffusion is considered. For the CO-core WD sequences, differences in the cooling times remain below 1%.

3. Pulsation results

In this section, we assess the effect of Coulomb separation of ions on the predicted pulsation periods of our WD models. We begin by illustrating in Fig. 3 the changes in the run of the Brunt–Väisälä and Lamb frequencies induced by Coulomb sedimentation for all of our WD models at Teff = 11 000 K. In particular, the 1.16 and 1.29 M⊙ models start to crystallize before the blue edge of the ZZ Ceti instability strip is reached. In these cases, the gray area marks the domain of core crystallization. Any chemical interface located within the crystallized region has no relevance to the pulsation properties of the g modes, therefore we hid them below the gray area in the plots. The Brunt–Väisälä frequency reflects any change in chemical composition in the interior of the model. Dominant bumps in the run of the Brunt–Väisälä frequency indeed exist and are associated with the various chemical transition regions, particularly the H-He interface, which produces the most dominant feature in the Brunt–Väisälä frequency. We note that in the case of the 1.292 M⊙ model computed with Coulomb diffusion, two bumps exist, one of them due to the chemical transition region of C and He, and the other associated with the He/H chemical interface (see Fig. 2). At variance with this, in the case without Coulomb diffusion, the Brunt–Väisälä frequency has a single bump that is due to the chemical interface of O, C, He, and H. On the other hand, the Brunt–Väisälä frequency has an additional bump at log(1 − mr/M⋆)∼ − 3 that is due to the multiple chemical transition region of 24Mg, 20Ne, 16O, and 12C (see also Fig. 2), which is absent in the case without Coulomb diffusion. This bump is located in the fluid part of the star, that is, within the mode-propagation zone, and therefore it has a nonzero effect on the mode-trapping properties of g modes.

thumbnail Fig. 3.

Logarithm of the squared Brunt–Vaïsälä and Lamb frequencies (red and blue lines, respectively) corresponding to the same models as analyzed in Fig. 2 at Teff = 11 000 K. Thick (thin) lines correspond to the case when Coulomb sedimentation of ions is considered (disregarded) in the diffusion equations. The gray area marks the domain of core crystallization. The Lamb frequency corresponds to dipole (ℓ = 1) modes.

The shape of the Brunt–Väisälä frequency has a strong effect on the g-mode period spectrum and mode-trapping properties of pulsating WDs. In view of the above discussion of the Brunt–Väisälä frequency, we expect that Coulomb diffusion of ions markedly changes the g-mode pulsation periods of massive ZZ Ceti stars. This is borne out by Fig. 4, which displays the relative period differences in terms of the periods of ℓ = 1 pulsation g modes resulting from including and disregarding Coulomb separation in our WD models at Teff = 11 000 K. The differences are defined as the periods calculated with Coulomb diffusion minus the periods neglecting this effect, divided by the periods computed with Coulomb diffusion. This relative difference is plotted in terms of the periods calculated with Coulomb diffusion. We note that for the ultra-massive WDs (M⋆ >  1.16 M⊙), Coulomb diffusion yields significant changes in the g-mode pulsation periods by as much as ∼15%, which is given for the lowest radial order modes (Π ≲ 600 s). This is a relevant effect and should be taken into account in detailed asteroseismological analyses of these pulsating stars. On the other hand, the effect on lower mass WDs is much less noticeable; the changes in the pulsation periods do not exceed 0.3%. Such period changes remain still above the typical uncertainties of the observed periods (≲0.01%) but are well below the period changes that result from uncertainties in convective boundary mixing and nuclear reactions during WD progenitor evolution (see De Gerónimo et al. 2017).

thumbnail Fig. 4.

Relative period differences in terms of the periods of ℓ = 1 pulsation g modes resulting from including and disregarding Coulomb separation in the same models as analyzed in Fig. 2 at Teff = 11 000 K.

4. Summary and conclusions

Motivated by the result of Beznogov & Yakovlev (2013), who suggested that the redistribution of ions due to Coulomb separation could affect the thermal evolution of WDs and their pulsational properties, we undertook this investigation to precisely assess the effect of this Coulomb separation on the WD evolution as well as on their chemical profiles, the Brunt–Väisälä frequency, and their pulsational periods at the ZZ Ceti instability strip. To this end, we followed the full evolution of WD models in the range 0.5−1.3 M⊙ derived from their progenitor history on the basis of a time-dependent element diffusion scheme that incorporates the effect of gravitational settling of ions due to Coulomb interactions at high densities.

We find that Coulomb sedimentation profoundly alters the chemical profiles of ultra-massive WDs throughout their evolution, preventing the strong inward diffusion of He toward the core, and thus leading to the formation of a pure-He buffer with two separate chemical interfaces, at variance with what occurs when Coulomb diffusion is neglected. These changes in the inner chemical distribution barely affect the cooling properties of the WDs. However, the effect on the pulsation periods is quite different. Strong changes in the g-modes pulsation periods as high as 15% are expected for ultra-massive ZZ Ceti stars. For lower mass ZZ Ceti stars, the effect of Coulomb separation is much less noticeable and causes period changes that are below the period changes that result from uncertainties in progenitor evolution, but are larger than typical uncertainties of observed periods. The process of Coulomb diffusion of ions profoundly affects the diffusion flux in massive white dwarfs, driving the gravitational settling of ions with the same A/Z (mass to charge number). We quantified the magnitude of this effect on the period spectrum of ZZ Ceti stars. The changes in the pulsational periods are sufficiently important that they should not be neglected in detailed asteroseismological analyses of massive ZZ Ceti stars.

1

For the sake of simplicity, we do not provide the equations that describe thermal diffusion.

2

Our expression for the diffusive flux is similar to that shown in Eqs. (17)−(19) of Beznogov & Yakovlev (2013).

3

For the 1.292 M⊙ WD model, the H envelope was artificially imposed, without considering nuclear burning processes.

Acknowledgments

Part of this work was supported by PICT-2017-0884 from ANPCyT, PIP 112-200801-00940 grant from CONICET, grant G149 from University of La Plata. This research has made use of NASA Astrophysics Data System.

References

  1. Althaus, L. G., & Córsico, A. H. 2004, A&A, 417, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
  5. Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Althaus, L. G., Córsico, A. H., Uzundag, M., et al. 2020, A&A, 633, A20 [CrossRef] [EDP Sciences] [Google Scholar]
  7. Beznogov, M. V., & Yakovlev, D. G. 2013, Phys. Rev. Lett., 111, 161101 [CrossRef] [Google Scholar]
  8. Burgers, J. M. 1969, Flow Equations for Composite Gases (New York: Academic Press) [Google Scholar]
  9. Camisassa, M. E., Althaus, L. G., Córsico, A. H., et al. 2019, A&A, 625, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Castanheira, B. G., Kepler, S. O., Kleinman, S. J., Nitta, A., & Fraga, L. 2010, MNRAS, 405, 2561 [NASA ADS] [Google Scholar]
  11. Castanheira, B. G., Kepler, S. O., Kleinman, S. J., Nitta, A., & Fraga, L. 2013, MNRAS, 430, 50 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chang, P., Bildsten, L., & Arras, P. 2010, ApJ, 723, 719 [NASA ADS] [CrossRef] [Google Scholar]
  13. Christensen-Dalsgaard, J., Silva Aguirre, V., Cassisi, S., et al. 2020, A&A, 635, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Córsico, A. H., & Althaus, L. G. 2006, A&A, 454, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Córsico, A. H., Althaus, L. G., Benvenuto, O. G., & Serenelli, A. M. 2002, A&A, 387, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Córsico, A. H., García-Berro, E., Althaus, L. G., & Isern, J. 2004, A&A, 427, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Córsico, A. H., Althaus, L. G., Montgomery, M. H., García-Berro, E., & Isern, J. 2005, A&A, 429, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., & Kepler, S. O. 2019a, A&ARv, 27, 7 [NASA ADS] [CrossRef] [Google Scholar]
  19. Córsico, A. H., De Gerónimo, F. C., Camisassa, M. E., & Althaus, L. G. 2019b, A&A, 632, A119 [CrossRef] [EDP Sciences] [Google Scholar]
  20. Curd, B., Gianninas, A., Bell, K. J., et al. 2017, MNRAS, 468, 239 [NASA ADS] [CrossRef] [Google Scholar]
  21. De Gerónimo, F. C., Althaus, L. G., Córsico, A. H., Romero, A. D., & Kepler, S. O. 2017, A&A, 599, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. De Gerónimo, F. C., Córsico, A. H., Althaus, L. G., Wachlin, F. C., & Camisassa, M. E. 2019, A&A, 621, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Deloye, C. J., & Bildsten, L. 2002, ApJ, 580, 1077 [NASA ADS] [CrossRef] [Google Scholar]
  24. García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  25. Hermes, J. J., Kepler, S. O., Castanheira, B. G., et al. 2013, ApJ, 771, L2 [NASA ADS] [CrossRef] [Google Scholar]
  26. Horowitz, C. J., Schneider, A. S., & Berry, D. K. 2010, Phys. Rev. Lett., 104, 231101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  27. Kanaan, A., Nitta, A., Winget, D. E., et al. 2005, A&A, 432, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Koester, D., Kepler, S. O., & Irwin, A. W. 2020, A&A, 635, A103 [CrossRef] [EDP Sciences] [Google Scholar]
  29. Medin, Z., & Cumming, A. 2010, Phys. Rev. E, 81, 036107 [NASA ADS] [CrossRef] [Google Scholar]
  30. Michaud, G., Alecian, G., & Richer, J. 2015, Atomic Diffusion in Stars (Switzerland: Springer) [CrossRef] [Google Scholar]
  31. Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Miller Bertolami, M. M., Althaus, L. G., Olano, C., & Jiménez, N. 2011, MNRAS, 415, 1396 [NASA ADS] [CrossRef] [Google Scholar]
  33. Montgomery, M. H., & Winget, D. E. 1999, ApJ, 526, 976 [NASA ADS] [CrossRef] [Google Scholar]
  34. Paquette, C., Pelletier, C., Fontaine, G., & Michaud, G. 1986, ApJS, 61, 177 [NASA ADS] [CrossRef] [Google Scholar]
  35. Rowan, D. M., Tucker, M. A., Shappee, B. J., & Hermes, J. J. 2019, MNRAS, 486, 4574 [NASA ADS] [CrossRef] [Google Scholar]
  36. Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Siess, L. 2010, A&A, 512, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Silva Aguirre, V., Christensen-Dalsgaard, J., Cassisi, S., et al. 2020, A&A, 635, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Tassoul, M., Fontaine, G., & Winget, D. E. 1990, ApJS, 72, 335 [Google Scholar]
  41. Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1.

Abundance by mass of 1H, 4He, 12C, 14N, 16O, 20Ne, 22Ne, 23Na, and 24Mg vs. the outer mass coordinate for our 0.576, 0.833, 1.159, and 1.292 M⊙ WD models at the beginning of the cooling track.
In the text
thumbnail Fig. 2.

Same as Fig. 1, but at an effective temperature of Teff = 11 000 K, corresponding to the domain of pulsating ZZ Ceti stars. Thick (thin) lines correspond to the case when Coulomb sedimentation of ions is considered (disregarded) in the diffusion equations. The gray area marks the domain of core crystallization.
In the text
thumbnail Fig. 3.

Logarithm of the squared Brunt–Vaïsälä and Lamb frequencies (red and blue lines, respectively) corresponding to the same models as analyzed in Fig. 2 at Teff = 11 000 K. Thick (thin) lines correspond to the case when Coulomb sedimentation of ions is considered (disregarded) in the diffusion equations. The gray area marks the domain of core crystallization. The Lamb frequency corresponds to dipole (ℓ = 1) modes.
In the text
thumbnail Fig. 4.

Relative period differences in terms of the periods of ℓ = 1 pulsation g modes resulting from including and disregarding Coulomb separation in the same models as analyzed in Fig. 2 at Teff = 11 000 K.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.