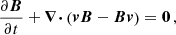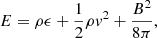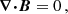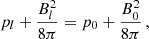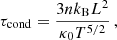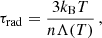| Issue |
A&A
Volume 644, December 2020
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 9 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202039023 | |
| Published online | 08 December 2020 | |
Slow and sausage loop mode excitation due to local and global spontaneous perturbations
1
Instituto de Astronomía Teórica y Experimental, CONICET-UNC, Córdoba, Argentina
e-mail: mariana.cecere@unc.edu.ar
2
Facultad de Matemática, Astronomía, Física y Computación, UNC, Córdoba, Argentina
3
Observatorio Astronómico de Córdoba, UNC, Córdoba, Argentina
4
Instituto de Estudios Avanzados en Ingeniería y Tecnología, CONICET, Córdoba, Argentina
5
Facultad de Ciencias Exactas, Físicas y Naturales, UNC, Córdoba, Argentina
6
Instituto de Física Enrique Gaviola, CONICET-UNC, Córdoba, Argentina
Received:
24
July
2020
Accepted:
21
October
2020
Aims. We analyse the capability of different types of perturbations associated with usual environment energy fluctuations of the solar corona to excite slow and sausage modes in solar flaring loops.
Methods. We performed numerical simulations of magnetohydrodynamic ideal equations with a consideration of straight plasma magnetic tubes subject to local and global energy depositions.
Results. We find that local loop energy depositions of typical microflares [∼(1027 − 1030) erg] are prone to driving slow shock waves that induce slow-mode patterns. The slow-mode features are obtained for every tested local energy deposition inside the loop. Meanwhile, in order to obtain an observable sausage mode pattern, a global perturbation that is capable of instantaneously modifying the internal loop temperature is required; specifically, the characteristic conductive heating time must be much smaller than the radiative cooling one. Experiments carried out by varying the parameter β demonstrate that the excitation of sausage modes does not significantly depend on the value of this parameter but, rather, depends on the global or local character of the energy source.
Key words: Sun: oscillations / Sun: corona / magnetohydrodynamics (MHD) / shock waves
© ESO 2020
1. Introduction
Coronal seismology is a more recent branch of solar physics that combines the measurement of temporal and spatial signatures of magnetohydrodynamic (MHD) waves and oscillations together with their theoretical modelling in different magnetic structures to infer coronal mean plasma properties. In the particular case of coronal loops, the fast sausage mode and the standing slow mode are the most commonly studied due to their compressibility, which facilitates observations (Nakariakov & Ofman 2001; Andries et al. 2005; Arregui et al. 2007; Van Doorsselaere et al. 2011a).
Sausage modes modelled as axisymmetric perturbations of magnetic cylinders are known to be compressible MHD fast modes that perturb the plasma inside the loop in the radial direction, causing a symmetric contraction and a widening of the tube without any distortion of its axis (Edwin & Roberts 1983). These modes have characteristic periods of ∼[5 − 10] s and decaying times of few periods. They are generally found associated with flaring loops in active solar regions (e.g. Zaitsev & Stepanov 1989; Asai et al. 2001; Nakariakov et al. 2003; Stepanov et al. 2004; Srivastava et al. 2008; Van Doorsselaere et al. 2011b). In fact, Aschwanden et al. (2004) showed that the existence of trapped sausage modes, prescribed by their cutoff, requires the host loop to have a high electron density, which can only occur in flaring loops. The work by Nakariakov et al. (2012) has important seismological implications for the diagnosis of plasmas in flaring loops using sausage oscillations. They showed that in the linear regime, an initial perturbation results in either a leaky or a trapped regime of sausage oscillation, depending upon whether the longitudinal wavenumber is smaller or greater than a specific cutoff value, respectively. Also, if the wave damping caused by the leakage is not high enough, the oscillations may be detectable for several cycles. This is the case particularly in dense and thick flaring loops, where the lifetime of high radial sausage harmonics could be sufficiently long and these leaky oscillations could be responsible for observed quasi-periodic pulsations (QPP, Nakariakov et al. 2005; Pascoe et al. 2007; Lim et al. 2020).
Zaitsev & Stepanov (1989) proposed that a modulation of hard X-ray and white-light emission from a loop footpoint can occur due to the change in the loop radius and the consequent change of the mirror ratio, which causes the periodic precipitation of non-thermal electrons at flaring loops. Moreover, from QPP in hard X-ray and microwave time profiles, Asai et al. (2001) proposed that a modulation can be produced by variations of macroscopic magnetic structures, for instance, the oscillations of coronal loops. In analysing a flaring loop in microwaves, Inglis et al. (2008) showed that the whole loop oscillates with the same period and almost in phase, producing either a MHD sausage mode or a periodic regime of magnetic reconnection. In addition, periodic variations of the thermal emission intensity in the extreme ultraviolet (EUV) and soft X-ray bands were associated with density perturbations and a Doppler shift of the emission lines, leading to the detection of sausage modes (Tian et al. 2016). Furthermore, Jess et al. (2010), and Nakariakov et al. (2018) presented interesting observational examples of the excitation of MHD oscillations in a coronal loop by a microflare. These observations are in line with our motivation to simulate the excitation of sausage modes by deposition of energy pulses of short duration (we call them impulsive excitations because the duration of the pulse is a small fraction of the period of oscillation).
Slow magnetoacoustic modes are more commonly excited throughout the corona. In loops, they are generally thought off as standing longitudinal modes with periods on the order of several minutes and with decaying times of few periods (e.g. Nakariakov et al. 2000, 2019; Wang et al. 2003, 2005). Numerous observations have revealed that these oscillations can be triggered by hot impulsive flares or a smaller brightening located somewhere in the loop, for instance, close to a loop footpoint or near to the apex (De Moortel et al. 2002a,b; Costa & Stenborg 2004; Mariska 2006). Numerical simulations emulate the impulsive flares by pulses of energy depositions that trigger numerical features resembling slow magnetosonic standing waves (e.g. Selwa et al. 2005, 2007; Ogrodowczyk & Murawski 2007; Fernández et al. 2009; Ogrodowczyk et al. 2009).
To study the capability of producing sausage modes, we examined different energy release scenarios that resemble the action of microflares. To that end, we began our analysis from the action of an impulsive local deposition and continued on to impulsive global energy depositions capable of exciting a pattern of coupled modes. With regard to a local deposition of energy, we refer to an energy perturbation that is initially circumscribed in a small region inside the loop and produces a disequilibrium in the loop interior. With regard to global energy depositions, consistently, we refer to an energy perturbation that initially covers the whole loop and produces its disequilibrium with the external corona. The quantitative description of these models is given below.
2. The model
The basic model starts with the ideal MHD equations that describe the macroscopic behaviour of a compressible, ideal, fully ionised plasma. The ideal MHD equations in its conservative form and in CGS units are written as:
where no gravitational terms are considered, ρ indicates the plasma density, p the thermal pressure, v the velocity, B the magnetic field, and E is the total energy (per unit volume) given by
where ϵ is the internal energy.
In addition to the MHD equations, the divergence-free condition of the magnetic field, that is,
must be fulfilled.
To complete the set of MHD equations, a closure relation among the thermodynamic variables must be imposed. We assume a calorically perfect gas for which p = 2ρkBT/mi = (γ − 1)ρϵ, where kB is the Boltzmann constant, T the plasma temperature, mi the proton mass (assuming that the plasma is fully ionised hydrogen), and γ = 5/3 is the specific heat relation.
2.1. Equilibrium configuration
The equilibrium configuration consists of a straight cylinder surrounded by the solar corona and a chromosphere at its ends. We impose an axial symmetry around r = 0 and we use a 2.5D simulation (in cylindrical coordinates), allowing us to save computational time, which could be raised to a 3D simulation by removing the azimuthal symmetry (see Fig. 1). To achieve the overall equilibrium setup, the different initial plasma parameter values are given in Table 1.
 |
Fig. 1. Scheme of the coronal loop, corona, and chromosphere in the equilibrium configuration. |
System initial equilibrium values.
In the model, the magnetic field is taken to be in the z-direction, B = (0, 0, Bz) and the environment is motionless (v = 0). Under these conditions and using Eq. (2), it can be seen that the equilibrium is obtained if
where the sub-index l states for loop parameters and the sub-index 0 for coronal parameters. The initial state variables profile can be seen in Fig. 2. The β parameter is defined by 8πp/B2. In flaring coronal loops, oscillations can occur either with β > 1 (e.g. Shibasaki 2001) or with β < 1, as reported by Nakariakov et al. (2003), which is the case that we take as reference in this work. In order to control the value of β < 1 inside the loop, appropriate temperature, magnetic fields, and density are chosen. Under this assumption, the simulated plasma structures are hotter and denser than the surrounding medium, which is consistent with the known properties of flaring coronal loops.
 |
Fig. 2. Initial parameters as a function of the transverse coordinate. The solid line is the density (g cm−3), the dashed line is the magnetic field Bz (in G), and the dot-dashed line is the temperature (MK). For clarity, the density and the magnetic field were divided by a factor 1.2 × 10−14 and 10, respectively. |
2.2. Perturbations
To analyse the modes that are capable of being excited in the loop structure, we perturb the initial equilibrium state with an axisymmetric perturbation. Firstly, we investigate the conditions that would lead to the excitation of a sausage mode. Thus, we start perturbing the equilibrium with a localised deposition of energy injected at different loop heights, emulating the energy deposition of typical microflares: 1.5 × 1027 erg and 3.5 × 1028 erg. For this purpose, we confined the energy deposition to a sphere of radius R = 1 Mm, localised in the center of the loop (r = 0 Mm, z = 17.5 Mm), with radius, Rl = 3 Mm, and length, L = 25 Mm (Nakariakov et al. 2003). These scales determine the effectiveness of the linear excitation of different harmonics, as shown in Nakariakov et al. (2005), Pascoe et al. (2007); and Lim et al. (2020).
We also modify the equilibrium, yielding a global perturbation to the system. In this case, the size of the perturbation is the size of the loop. This type of perturbation can be attributed to an energy injection at the loop bases occurring in a flaring region. When a flare occurs, a large amount of energy is released in few seconds. The heat is conducted along the whole loop and – due to the anisotropic heat conduction rate that inhibits conduction across the magnetic field lines – the loop absorbs energy beyond its environment energy content, leading to an imbalance with regard to the surrounding medium. When the conduction characteristic time is larger than the characteristic radiative cooling time, we assume that the excess of heat at the loop interior with respect to its environment can be interpreted as a global perturbation or a global deposition of energy.
The thermal conduction time is
and the radiative cooling time is
where n is the number density, L is a characteristic length, k0 ∝ 10−6 erg K−7/2 cm−1 s−1 is the heat conduction coefficient along the magnetic field and Λ(T) is the radiative loss function (10−23 erg cm−3 s−1 for T ∼ 10 MK) (Aschwanden 2005).
We note that for a flaring region with T = 40 MK and a short loop length of L = 25 Mm with a number density of n = 5 × 1010 cm−3 (Nakariakov et al. 2003), the conductive and radiative characteristic times are τcond = 20 s, and τrad = 20000 s, respectively. Thus, τcond ≪ τrad and the excess of heat content cannot be cooled down by radiation in times of the conductive time order. Therefore, a global perturbation occurs, which is associated to a short and dense loop in a flaring region where sausage loops are generally observed (Aschwanden et al. 2004).
On the other hand, in a quiet sun region, where the temperature is approximately T = 2 MK, and for the loop parameters L = 25 Mm and n = 5 × 1010 cm−3, the conductive and radiative characteristic times are τcond = 200 000 s, τrad = 40 s, respectively. Thus, τrad ≪ τcond; given a typical energy perturbation, the heat content cannot be retained along the whole loop because the radiation proceeds to cool it down. In this case, a local perturbation is responsible for the oscillating pattern.
We analyse the signatures that these perturbations produce when tube modes are excited and describe their characteristic Fourier transforms (FT). A slow, mostly longitudinal tube mode has the characteristic of having the phase where the axial velocity is increased (vz) correlated with an increase of the axial magnetic field component (Bz) and a decrease of the density, and vice versa. On the other hand, the phase where the sausage mode symmetrically contracts the tube (R is decreasing) is correlated with an increase of the axial magnetic field component (Bz; the field lines are closer) and an increase of the density, and vice versa. Hence, the FT signature of a slow tube mode is associated with a density peak at the slow frequency, correspondingly with a peak in the axial velocity (vz) and the magnetic field (Bz) components, at the same frequency. The FT signature of the sausage mode is associated with a density peak at the fast frequency correspondingly with a peak in the radial velocity (vr) and the magnetic field (Bz) components at the same frequency.
In most observations, the elementary bursts seem to arise from a single flaring loop than from several of them, resulting not from a sequence of energy-release processes but, rather, from a single deposition in a determined one (Zaitsev & Stepanov 1989). However, the perturbation could take some time, meaning that the driver could be time-dependent, which could also be important for the excitation of MHD modes (Goddard et al. 2019). In this work, we chose to trigger the numerical experiments with an instantaneous deposition of energy.
2.3. Numerical code
In order to evaluate the plasma behaviour, the MHD Eqs. (1)–(4) are numerically solved in a cylindrical grid of co-located finite volumes. We perform 2.5D simulations, considering axial symmetry of the model with the z-direction parallel to the axis of the magnetic loop and neglecting the loop curvature. The simulations are carried out using the FLASH Code (Fryxell et al. 2000), an open-source, publicly available suite of high-performance simulation tools developed at the Center for Astrophysical Thermonuclear Flashes (Flash Center) of the University of Chicago. This code, currently in its fourth version, uses the finite volume method with Godunov-type schemes to solve the high energy compressible MHD equations on regular grids. For our simulations, we chose the unsplit staggered mesh (USM) solver available in FLASH, which uses a second-order directionally unsplit scheme with a MUSCL-type reconstruction. This solver implements a more consistent treatment of the magnetic field since its formulation is based on the constrained transport method and the corner transport upwind method, which avoids the generation of non-physical magnetic field divergence (Lee & Deane 2009). To solve the interface Riemann problems, we set the HLLD solver among the available options.
Cylindrical 2D square grids are used to represent the physical domain of [0, 35] Mm × [0, 35] Mm with a discretisation of 350 × 350 cells, obtaining a resolution of ∼[0.1 × 0.1] Mm2. Boundary conditions are set as follows: at the right lateral end outflow, conditions (zero-gradient) are applied for all the variables allowing waves to leave the domain without reflection. At the left lateral (r = 0 Mm), a mirroring boundary condition is set for the vector fields in order to represent the cylindrical symmetry in the ϕ variable. At the bottom (z = 0 Mm) and at the top (z = 35 Mm) of the simulation, we implement line-tied boundary conditions to emulate the behaviour of the dense chromosphere, which extends 5 Mm from each end.
3. Results and discussion
In this section, we present the results for the two scenarios considered in this study, namely, the localised energy depositions and the global instantaneous energy deposition, with the aim of evaluating what kind of perturbations can feasibly be developed at each of them. Furthermore, we analyse the influence of the plasma features in the dynamic of the oscillations.
3.1. Localised energy depositions
An instantaneous pulse of 1.5 × 1027 erg in a sphere of radius R = 1 Mm, temperature 8 MK and n = 1010 cm−3, resembles the energy deposition released by a typical microflare (Aschwanden 2005). This perturbation produces a spherical shock wave which becomes highly collimated in the z-direction by the action of the loop magnetic field over the period of evolution. Along the z-direction, the magnetic field plays the role of being the waveguide of a fundamentally hydrodynamic shock (Fernández et al. 2009). A pair of opposite slow shock fronts develop and when the chromosphere is reached, they are mainly reflected inside the loop.
In addition, a fast shock wave front pops out in the radial direction, reaching the coronal environment through the loop’s boundary1. In the following, we chose the apex (i.e. the middle point in the cylinder) and the base of the loop as the locations for the local energy depositions to perform numerical experiments that emulate the action of typical microflare events.
3.1.1. At the apex
In this case, the pulse is located at the center of the loop r = 0 Mm, z = 17.5 Mm. Figure 3 shows a snapshot of the numerical domain and the evolution for three different times t1 = 0.5 s, t2 = 5 s, t3 = 30 s; we note the evolution of the shock front, initiated as a sphere which becomes collimated in the z-direction due to the magnetic field orientation. We chose three loop positions to measure the space and time action of the perturbations on the plasma properties: r = (0.2, 1.5, 2.8) Mm with z = 20 Mm, indicated as p1, p2, and p3, respectively, in the right panel of the figure (see t3).
 |
Fig. 3. Density evolution at different times. The minimum and maximum values chosen highlight the shock wave fronts. The points p1, p2, and p3 mark the positions where the perturbation measure is performed. |
Figure 4 shows the density evolution at the mentioned three loop positions. In the z-direction, two symmetric slow shock wave fronts develop and travel in opposite directions, channeled by the loop magnetic structure (also seen in Fig. 3). Behind each shock wave, a rarefaction wave, travelling in the opposite direction and emptying the medium, is excited. The density behind the slow shock falls up to ∼4 × 10−14 g cm−3 near the apex location (see Fig. 3, see also Fernández et al. 2009). This is clearly seen for p1 in Fig. 4. This shock pattern is damped at later times, meaning that due to successive encounters of the fronts with the chromosphere surface, part of the shock energy is transferred to the dense chromospheric plasma. However, the density is weekly perturbed for the other point locations (p2 and p3), because the energy deposition is concentrated around the loop axis due to the magnetic field collimation (see in Fig. 3 that points p2 and p3 are not reached by the vacuum region). The stationary pattern established has a periodicity of ∼100 s.
 |
Fig. 4. Density time evolution in three different points at the loop apex for the apex energy deposition. |
To calculate the FT near the loop apex, we chose to measure the significant p1 signal and evaluate it for the MHD variables: density (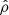 ), pressure (
), pressure (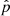 ), radial velocity (
), radial velocity (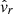 ), longitudinal velocity (
), longitudinal velocity (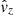 ), radial magnetic field (
), radial magnetic field (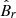 ), and longitudinal magnetic field (
), and longitudinal magnetic field (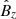 ). For reference, the slow-mode resonant cylinder frequencies are: νres, 1 = 0.00492 Hz, νres, 2 = 0.00984 Hz and νres, 3 = 0.01476 Hz (νres, n = cTn/2L, where n is an integer determining the parallel mode number, L is the cylinder’s length, and cT is the tube sound speed inside the cylinder). These frequencies are indicated with vertical lines in the FT figures (Figs. 5, 7, 9–11, and 14). Figure 5 displays the p1 FT for the different variables. Two main peaks are clearly distinguished considering all the variables: (I) ν = 0.01 Hz (period time τ = 100 s) and (II) ν = 0.075 Hz (period time τ = 13.3 s). The major peak of the density
). For reference, the slow-mode resonant cylinder frequencies are: νres, 1 = 0.00492 Hz, νres, 2 = 0.00984 Hz and νres, 3 = 0.01476 Hz (νres, n = cTn/2L, where n is an integer determining the parallel mode number, L is the cylinder’s length, and cT is the tube sound speed inside the cylinder). These frequencies are indicated with vertical lines in the FT figures (Figs. 5, 7, 9–11, and 14). Figure 5 displays the p1 FT for the different variables. Two main peaks are clearly distinguished considering all the variables: (I) ν = 0.01 Hz (period time τ = 100 s) and (II) ν = 0.075 Hz (period time τ = 13.3 s). The major peak of the density 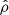 occurs at frequency I. The z-component of the velocity and the magnetic field present a peak at frequency I, which is characteristic of slow modes. Comparing the shock speed (∼379 km s−1) with the local sound speed (∼283 km s−1) and the Alfvén speed (∼499 km s−1), we can see that this shock pattern corresponds to a slow magnetosonic shock. Also, the period is of the slow-mode type (∼100 s). The r-component of the velocity has also a peak at the fast frequency II. However, the amplitude of
occurs at frequency I. The z-component of the velocity and the magnetic field present a peak at frequency I, which is characteristic of slow modes. Comparing the shock speed (∼379 km s−1) with the local sound speed (∼283 km s−1) and the Alfvén speed (∼499 km s−1), we can see that this shock pattern corresponds to a slow magnetosonic shock. Also, the period is of the slow-mode type (∼100 s). The r-component of the velocity has also a peak at the fast frequency II. However, the amplitude of 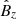 at this frequency is not intense enough to produce a fast mode. Also, the magnetic field r-component signal does not differ from the noise level. Thus, the whole picture suggests that the local pulse triggers a mode pattern of mainly two coupled frequencies that is strongly dominated by the slow one.
at this frequency is not intense enough to produce a fast mode. Also, the magnetic field r-component signal does not differ from the noise level. Thus, the whole picture suggests that the local pulse triggers a mode pattern of mainly two coupled frequencies that is strongly dominated by the slow one.
 |
Fig. 5. Fourier amplitude comparison of the different plasma parameters for the apex energy deposition measured at p1 = (0.2, 20) Mm. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
3.1.2. At the footpoint
Figure 6 shows the density evolution near the apex, that is, for p1, p2, and p3, when the pulse is located close to the chromospheric base of the loop at r = 0 Mm, z = 5.5 Mm. A similar shock pattern behaviour is obtained with a time delay in the appearance of the shock front, that is, the shock front takes some time to reach the pi apex positions from the chromospheric location, where the perturbation is triggered. As in the apex case, a shock pattern is measured for p1. When the pulse source is located at the chromospheric base, the rarefaction wave and the corresponding voided region do not initially perturb the apex and, therefore, the background density (∼8.2 × 10−14 g cm−3) is not modified.
 |
Fig. 6. Density time evolution in three different points at the loop apex for the footpoint energy deposition. |
As before, Fig. 7 shows the FT for p1, near the loop apex for the density, pressure, velocity, and magnetic field. The pulse excites a main shock that travels during 100 s from the chromospheric base into the coronal part of the loop towards the other loop end, where it rebounds. The repetition of this process produces a cycle of positive (upwards) and negative (downwards) values of the z-component of the velocity every 200 s. The other shock, which travels into the inner chromosphere, is mostly absorbed by these denser plasma layers and only a very small fraction of the wave can rebound. In the figure, we see a main peak of 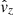 at ν = 0.005 Hz, which is associated with this principal process. The density and the magnetic field intensity Bz are enhanced every 100 s (frequency I). The coupling with its first harmonics (ν = 0.005 Hz) are also seen in the respective FTs.
at ν = 0.005 Hz, which is associated with this principal process. The density and the magnetic field intensity Bz are enhanced every 100 s (frequency I). The coupling with its first harmonics (ν = 0.005 Hz) are also seen in the respective FTs.
 |
Fig. 7. Fourier amplitude comparison for the footpoint energy deposition measured at p1 = (0.2, 20) Mm. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
We note that the r-component of the velocity and magnetic field are not distinguished from a noise signal. In this case, the whole picture suggests that the local pulse can only trigger a slow shock pattern due to its proximity to the chromosphere, where the line-tied condition is fulfilled, that is, the magnetic field tension is stronger and, thus, the r-component of the perturbation is relatively weak.
To conclude this first analysis, we remark that the increase of the pulse energy located in different positions of the loop (up to 3.7 × 1028 erg) is derived in similar signal patterns, where the enhanced fast component (for almost the entire loop) is less important than the slow one. Therefore, we find that a dominant fast mode cannot be obtained through a local deposition of energy. In other words, it is not possible to develop a sausage mode when local energy depositions are applied.
3.2. Global instantaneous energy depositions
As noted in the previous section, using a local deposition of energy resembling a typical microflare (e.g. 1.5 × 1027 erg and 3.7 × 1028 erg) is not capable of generating a significant sausage mode perturbation. In this section, taking into account the characteristic time considerations discussed in Sect. 2.2, we explore whether sausage modes can be excited in the scenario of a global instantaneous energy deposition of the same amount as in the local case. Firstly, we inject 1.5 × 1027 erg throughout the loop, producing an imbalance between the loop and the corona. This extra energy is obtained by increasing the loop temperature up to 5.4 MK. The initial disequilibrium produces a shock wave that travels out of the loop, leaking part of its energy into the corona. Then the internal loop density starts to oscillate, as can be seen in Fig. 8. A new pattern of oscillations is obtained throughout the loop, without shock waves and with a small period (13.3 s). The oscillation amplitudes at points p1 and p2 are much larger than those for p3. The perturbations are modulated by a lower frequency and are damped while they evolve over time due to the above-mentioned leakage. The initial imbalance also produces a rarefaction wave that travels radially towards the loop axis, slightly decreasing its inner density. This is stabilised in about 1000 s.
 |
Fig. 8. Density time evolution in three different points at the loop apex for the global energy deposition. |
Figure 9 displays the FT for the density (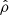 ), pressure (
), pressure (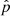 ), radial velocity (
), radial velocity (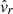 ), axial velocity (
), axial velocity (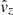 ), radial magnetic field (
), radial magnetic field (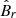 ), and axial magnetic field (
), and axial magnetic field (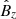 ) at p1. Contrary to the local deposition cases, in this global one, the main peak of the
) at p1. Contrary to the local deposition cases, in this global one, the main peak of the 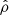 FT signal occurs at the fast frequency II and a much less intense peak occurs at the slow frequency I. We note that the fast frequency II is also the main peak for both,
FT signal occurs at the fast frequency II and a much less intense peak occurs at the slow frequency I. We note that the fast frequency II is also the main peak for both, 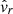 and
and 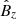 , corresponding to a fast magnetosonic mode. Thus, the global instantaneous case, for the same energy content as the local cases, excites a coupled mode pattern that is mainly determined by a dominant fast magnetosonic mode and a weak slow mode, as can be seen, for example, in the FT signal of
, corresponding to a fast magnetosonic mode. Thus, the global instantaneous case, for the same energy content as the local cases, excites a coupled mode pattern that is mainly determined by a dominant fast magnetosonic mode and a weak slow mode, as can be seen, for example, in the FT signal of 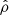 ,
, 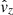 and
and 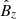 at frequency I.
at frequency I.
 |
Fig. 9. Fourier amplitude comparison for the “imbalance” at the apex for the case with energy E = 1.5 × 1027 erg and parameter β = 0.4. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
Figure 10 is the same as Fig. 9, both measuring the variables at the footpoint location r = 0.2 Mm and z = 5.2 Mm. If we compare Fig. 9 with Fig. 10, we see that due to the line-tied property, the fast mode vanishes at the chromospheric base (Nakariakov et al. 2003).
 |
Fig. 10. Fourier amplitude comparison for the “imbalance” at the foot. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
3.3. Importance of the β parameter in the excitation of sausage modes
The excitation of sausage modes requires the medium capability to regularly compress and restore the magnetic field lines. Hence, the thermal pressure must be comparable to the magnetic pressure and tension in order to balance the resistance of the magnetic field. As the β parameter measures the relative importance between thermal and magnetic energy, it seems an adequate parameter for an analysis of the capability of loop systems to excite sausage modes. Thus, we performed several numerical experiments to accomplish this task. Table 2 shows the β parameter and energy values used for the different cases. The reference case is the global case of the previous subsection.
Temperature, magnetic field, β parameter, and energy values for the different cases.
3.3.1. Case I: Enhanced β parameter (same energy)
In this experiment, we increase the β parameter from 0.4 to 0.7, keeping the same energy for the global perturbation than in the reference case (E = 1.5 × 1027 erg). In comparing Fig. 9 with Fig. 11, we observe that an increase in the β parameter leads to a notable increment in the FT amplitudes of all the MHD variables. The FT amplitudes of the density, pressure, velocity, and the longitudinal magnetic field component grow by a factor between 5 and 8 for both the slow and the fast frequencies. According to, for example, Zaitsev & Stepanov (1982), this growth could be due to the increase in the temperature or the decrease in the magnetic field (see Eq. (6) of that paper).
 |
Fig. 11. Fourier amplitude comparison for the “imbalance” at the apex for the case with energy, E = 1.5 × 1027 erg, and parameter, β = 0.7. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
To analyse the effect of the increase of β, in Fig. 12 we plot the evolution of the total energy (blue line), the magnetic energy (green line), and the internal energy (orange line) for both β cases at p1. We note that the amplitude of the oscillation is increased when β is augmented and it oscillates around the initial total energy value. Thus, different β values lead to different amplitude responses. As the reference case and case I have almost the same slow and fast frequencies, with a difference of 4%, it seems that the major amplitude response of case I is due to the smaller magnetic field value – associated with the less rigid behaviour of the magnetic field lines – and also to the larger temperature value, leading to a larger capability to bend the magnetic field lines of the loop system. The oscillatory pattern and the energy distribution between modes can also be analysed in detail from the FTs shown in Fig. 13. As seen in the figure, a similar behaviour is observed, for instance, in the FT amplitudes of the slow and the fast frequencies for the total, magnetic, and internal energies, which strongly increase when the β parameter is augmented. In addition, we can see that, as expected, the slow-mode energy content is mainly attributed to the contribution of the internal energy, almost independently of the value of the β parameter, while the energy distribution of the fast mode directly depends on the initial relation between the magnetic and the internal energy, that is, it directly depends on the β parameter. As a final result, we can say that this experiment shows that the rise in the value of the β parameter in the global case strongly increases the FT amplitudes of all the variables for both the slow and the fast modes. Hence, while β approaches one, namely, in the coronal regions of relatively high values of β, the sausage modes are more easily excited.
 |
Fig. 12. Evolution of the total, internal and magnetic energy for the “reference case” (upper panel) and “case I” (lower panel), measured at p1. |
 |
Fig. 13. Evolution of the total, internal and magnetic energy Fourier amplitude for the “reference case” (upper panel) and “case I” (lower panel), measured at p1. |
To compare the relative importance between the fast and the slow components, we show in Table 3 the rate between the fast FT peak and the slow FT peak of the density for each case. For the reference case, the rate between the fast and slow mode is 2.7, which shows a dominance of the fast mode. When the β parameter is larger, this rate is almost the same, namely: 2.2. To obtain a larger β parameter with the same initial energy we increase the temperature and decrease the magnetic field. The dynamics results more hydrodynamic favouring the slow mode. Thus, this explains the lower rate obtained in relation with the reference case seen in Table 3.
Rate between the fast FT intensity and the slow FT intensity for the density variable.
3.3.2. Case II: Enhanced energy (same β parameter)
In this experiment, the energy is increased from 1.5 × 1027 erg to 3.7 × 1028 erg, keeping the same β parameter as in the reference case (β = 0.4), see Table 2. In comparing Fig. 9 with Fig. 14, we see a notable increase in the FT components of all variables (at least by a factor of 10). The overall picture implies that the change in energy with β constant changes the proportionality between the fast and the slow FT contributions (see Table 3). When the energy increases by one order of magnitude, the rate between fast and the slow modes is twice the rate of the reference case.
 |
Fig. 14. Fourier amplitude comparison for the “imbalance” at the apex for the case with energy E = 3.7 × 1028 erg and parameter β = 0.4. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
In summary, the numerical experiments given in Table 3 with a consideration of a global deposition of energy that resembles the action of typical microflares, indicating that these perturbations lead to mode patterns where the fast sausage mode is dominant almost across the entire loop2.
4. Conclusions
In this work, we study the oscillatory modes that can be excited by microflare depositions of energy in the interior of coronal loops. Based on evidence demonstrating that the elementary bursts seem to arise from a single flaring loop than from various of them, we designed a set of numerical experiments in which the motion is triggered by an instantaneous deposition of energy. Considering different relations between the thermal conduction time and the radiative cooling time, we defined two situations that could excite an oscillatory pattern in the loop interior, namely, a “local deposition of energy” when the radiative cooling effect is dominant and a “global deposition of energy” when the heat conduction prevails.
In the local energy deposition analysis, we found that for energy levels on the order of typical microflares, the local pulse triggers a mode pattern mainly of two coupled frequencies that is strongly dominated by the slowest one. A pair of two opposite slow shocks are detected travelling along the magnetic field lines due to the strong collimation until it reaches the chromospheric surface, where the shocks rebound producing the oscillatory motion. This is in agreement with Fernández et al. (2009), who suggested that in order to detect an internal loop slow mode, a density contrast produced by a shock wave is required. This shock pattern, strongly collimated along the loop axis, is the main feature (of typical slow speeds and slow periods) that characterises every local energy deposition where fast mode signatures are weak enough; this indicates that sausage modes are not detected in this scenario.
In the analysis of the global energy deposition, we show that a pattern of coupled modes is obtained, in which the fast magnetosonic one is dominant; this indicates that the sausage mode can feasibly be developed for a global deposition of energy. These results suggest that the rarity of fast sausage modes is due to the requirement that the heat conduction effect must be dominant in this model. Such a requirement is almost exclusively achieved in active flaring regions where the temperature is high enough and the loop length is short.
Knowing that global energy deposition can produce sausage modes, we explore the influence of the β parameter and the effect of the energy level in the strength of the fast signal. For low β parameters, the magnetic forces dominate the plasma dynamics and the magnetic field resists the compression generated, for instance, by fast transverse modes, which is what happens in the corona where the sausage modes are rarely observed. For larger β parameters, which can occur when the thermal energy overcomes the magnetic field resistance, we found that the fast signal is increased almost to the same extent as the slow one. On the other hand, the increment of the energy level that keeps the β parameter constant produces a substantial rise of the fast signal over the increase in the slow one. These effects are not detected when either the β parameter or the energy level are increased in the local energy deposition scenario, which reinforces the hypothesis that a global energy deposition is needed to obtain a sausage mode.
With respect to the strong damping of sausage modes, it is clear that having used an ideal MHD model, this process is not associated with dissipation mechanisms. This is in agreement with the fact that the corona is a highly conductive medium where the resistivity can be neglected. Our experiments show that the damping of modes is due to the coupling and the transfer of energy between modes, absorption at the chromospheric bases, and leakage across the boundaries of the loops.
The loop parameters are such that linear perturbations would lead to trapped modes (Nakariakov et al. 2003) (see Eq. (5) of that paper), however, as the perturbations we are working with are nonlinear, the trapped mode condition is not valid and the energy can leak through the loop boundary.
We also performed experiments increasing the β parameter of the loop and the energy pulse in the local deposition cases. These experiments did not lead to a dominant sausage mode as those shown in Sect. 3.1.
Acknowledgments
We thank the anonymous referee for very useful comments that helped us to improve the previous version of this manuscript. HC is doctoral fellow of CONICET. MC, AC, GK and OR are members of the Carrera del Investigador Científico (CONICET). HC, MC y GK acknowledge support from ANPCyT under grant number PICT No. 2016-2480. MC also acknowledge support by SECYT-UNC grant number PC No. 33620180101147CB. Also, we thank the Centro de Cómputo de Alto Desempeño (UNC), where the simulations were carried out.
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., Andries, J., Van Doorsselaere, T., Goossens, M., & Poedts, S. 2007, A&A, 463, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asai, A., Shimojo, M., Isobe, H., et al. 2001, ApJ, 562, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J. 2005, Physics of the Solar Corona. An Introduction with Problems and Solutions, 2nd edn. [Google Scholar]
- Aschwanden, M. J., Nakariakov, V. M., & Melnikov, V. F. 2004, ApJ, 600, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, A., & Stenborg, G. 2004, Sol. Phys., 222, 229 [CrossRef] [Google Scholar]
- De Moortel, I., Hood, A. W., & Ireland, J. 2002a, A&A, 381, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., Hood, A. W., Ireland, J., & Walsh, R. W. 2002b, Sol. Phys., 209, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, C. A., Costa, A., Elaskar, S., & Schulz, W. 2009, MNRAS, 400, 1821 [NASA ADS] [CrossRef] [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Goddard, C. R., Nakariakov, V. M., & Pascoe, D. J. 2019, A&A, 624, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inglis, A. R., Nakariakov, V. M., & Melnikov, V. F. 2008, A&A, 487, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jess, D. B., Mathioudakis, M., Browning, P. K., Crockett, P. J., & Keenan, F. P. 2010, ApJ, 712, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, D., & Deane, A. E. 2009, J. Comput. Phys., 228, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, D., Nakariakov, V. M., Yu, D. J., Cho, I.-H., & Moon, Y.-J. 2020, ApJ, 893, 62 [CrossRef] [Google Scholar]
- Mariska, J. T. 2006, ApJ, 639, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Verwichte, E., Berghmans, D., & Robbrecht, E. 2000, A&A, 362, 1151 [NASA ADS] [Google Scholar]
- Nakariakov, V. M., Melnikov, V. F., & Reznikova, V. E. 2003, A&A, 412, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Pascoe, D. J., & Arber, T. D. 2005, Space Sci. Rev., 121, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Hornsey, C., & Melnikov, V. F. 2012, ApJ, 761, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Anfinogentov, S., Storozhenko, A. A., et al. 2018, ApJ, 859, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Kosak, M. K., Kolotkov, D. Y., et al. 2019, ApJ, 874, L1 [Google Scholar]
- Ogrodowczyk, R., & Murawski, K. 2007, A&A, 467, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ogrodowczyk, R., Murawski, K., & Solanki, S. K. 2009, A&A, 495, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007, A&A, 461, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selwa, M., Murawski, K., & Solanki, S. K. 2005, A&A, 436, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selwa, M., Ofman, L., & Murawski, K. 2007, ApJ, 668, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Shibasaki, K. 2001, ApJ, 557, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Srivastava, A. K., Zaqarashvili, T. V., Uddin, W., Dwivedi, B. N., & Kumar, P. 2008, MNRAS, 388, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, A. V., Kopylova, Y. G., Tsap, Y. T., et al. 2004, Astron. Lett., 30, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., Young, P. R., Reeves, K. K., et al. 2016, ApJ, 823, L16 [Google Scholar]
- Van Doorsselaere, T., Wardle, N., Del Zanna, G., et al. 2011a, ApJ, 727, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., De Groof, A., Zender, J., Berghmans, D., & Goossens, M. 2011b, ApJ, 740, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., Solanki, S. K., Curdt, W., et al. 2003, A&A, 406, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., Innes, D. E., & Curdt, W. 2005, A&A, 435, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 1982, Sov. Astron. Lett., 8, 132 [NASA ADS] [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 1989, Sov. Astron. Lett., 15, 66 [NASA ADS] [Google Scholar]
All Tables
Temperature, magnetic field, β parameter, and energy values for the different cases.
Rate between the fast FT intensity and the slow FT intensity for the density variable.
All Figures
 |
Fig. 1. Scheme of the coronal loop, corona, and chromosphere in the equilibrium configuration. |
| In the text | |
 |
Fig. 2. Initial parameters as a function of the transverse coordinate. The solid line is the density (g cm−3), the dashed line is the magnetic field Bz (in G), and the dot-dashed line is the temperature (MK). For clarity, the density and the magnetic field were divided by a factor 1.2 × 10−14 and 10, respectively. |
| In the text | |
 |
Fig. 3. Density evolution at different times. The minimum and maximum values chosen highlight the shock wave fronts. The points p1, p2, and p3 mark the positions where the perturbation measure is performed. |
| In the text | |
 |
Fig. 4. Density time evolution in three different points at the loop apex for the apex energy deposition. |
| In the text | |
 |
Fig. 5. Fourier amplitude comparison of the different plasma parameters for the apex energy deposition measured at p1 = (0.2, 20) Mm. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
| In the text | |
 |
Fig. 6. Density time evolution in three different points at the loop apex for the footpoint energy deposition. |
| In the text | |
 |
Fig. 7. Fourier amplitude comparison for the footpoint energy deposition measured at p1 = (0.2, 20) Mm. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
| In the text | |
 |
Fig. 8. Density time evolution in three different points at the loop apex for the global energy deposition. |
| In the text | |
 |
Fig. 9. Fourier amplitude comparison for the “imbalance” at the apex for the case with energy E = 1.5 × 1027 erg and parameter β = 0.4. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
| In the text | |
 |
Fig. 10. Fourier amplitude comparison for the “imbalance” at the foot. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
| In the text | |
 |
Fig. 11. Fourier amplitude comparison for the “imbalance” at the apex for the case with energy, E = 1.5 × 1027 erg, and parameter, β = 0.7. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
| In the text | |
 |
Fig. 12. Evolution of the total, internal and magnetic energy for the “reference case” (upper panel) and “case I” (lower panel), measured at p1. |
| In the text | |
 |
Fig. 13. Evolution of the total, internal and magnetic energy Fourier amplitude for the “reference case” (upper panel) and “case I” (lower panel), measured at p1. |
| In the text | |
 |
Fig. 14. Fourier amplitude comparison for the “imbalance” at the apex for the case with energy E = 3.7 × 1028 erg and parameter β = 0.4. The vertical lines correspond to the resonant frequencies: νres, 1 (solid line), νres, 2 (dashed line), and νres, 3 (dot-dashed line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



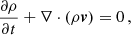
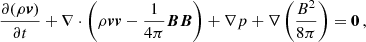
![$$ \begin{aligned} \frac{\partial E}{\partial t} + \nabla \cdot \left[\left(E + p + \frac{B^2}{8\pi }\right)\boldsymbol{v} -\frac{1}{4\pi } \left(\boldsymbol{v\cdot B}\right)\boldsymbol{B}\right] = 0 \, , \end{aligned} $$](/articles/aa/full_html/2020/12/aa39023-20/aa39023-20-eq3.gif)