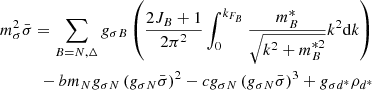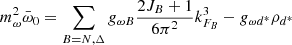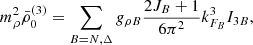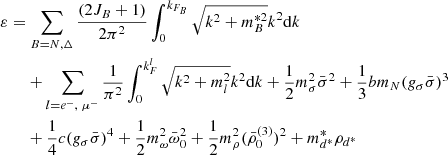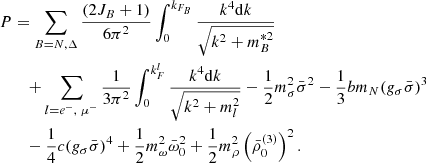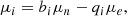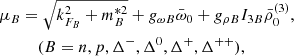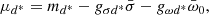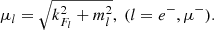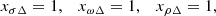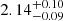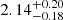| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202037749 | |
| Published online | 09 June 2020 | |
Neutron star matter equation of state including d*-hexaquark degrees of freedom
1
Department of Physics, University of York, Heslington, York Y010 5DD, UK
e-mail: alessandro.pastore@york.ac.uk
2
Department of Physics, Imperial College London, London SW7 2AZ, UK
3
INFN Sezione di Catania, Dipartimento di Fisica “Ettore Majorana”, Università di Catania, Via Santa Sofia 64, 95123 Catania, Italy
Received:
16
February
2020
Accepted:
12
April
2020
We present the extension of a previous study where, assuming a simple free bosonic gas supplemented with a relativistic mean-field model to describe the pure nucleonic part of the equation of state, we studied the consequences that the first non-trivial hexaquark d*(2380) could have on the properties of neutron stars. Compared to that exploratory work, we employ a standard non-linear Walecka model including additional terms that describe the interaction of the d*(2380) di-baryon with the other particles of the system through the exchange of σ- and ω-meson fields. Our results show that the presence of the d*(2380) leads to maximum masses compatible with recent observations of ∼2 M⊙ millisecond pulsars if the interaction of the d*(2380) is slightly repulsive or the d*(2380) does not interact at all. An attractive interaction makes the equation of state too soft to be able to support a 2 M⊙ neutron star whereas an extremely repulsive one induces the collapse of the neutron star into a black hole as soon as the d*(2380) appears.
Key words: equation of state / dense matter / stars: neutron
© ESO 2020
1. Introduction
Neutron stars are the remnants of the gravitational collapse of massive stars during a supernova event of Type-II, Ib, or Ic. Their masses and radii are typically of the order of 1−2 M⊙ (M⊙ ≃ 2 × 1033 g is the mass of the Sun) and 10−14 km, respectively. With central densities in the range of four to eight times the normal nuclear matter saturation density, ϵ0 ∼ 2.7 × 1014 g cm−3 (ρ0 ∼ 0.16 fm−3), neutron stars are most likely among the densest objects in the Universe (Shapiro & Teukolsky 2008; Glendenning 2000; Haensel et al. 2007; Rezzolla et al. 2018). These objects are therefore excellent laboratories to test our present understanding of the theory of strong interacting matter under extreme conditions, offering an interesting interplay between the physics of dense matter and astrophysical observables.
The conditions of matter inside neutron stars are very different from those encountered on Earth and cannot be probed via direct measurements. Therefore, a good theoretical knowledge of the nuclear equation of state (EoS) of dense matter is required to understand them. However, its determination is very challenging due to the wide range of densities, temperatures, and isospin asymmetries found in these objects, and constitutes nowadays one of the main problems in nuclear astrophysics. The main difficulties are associated to our lack of a precise knowledge of the behavior of the in-medium nuclear interaction, and to the very complicated resolution of the so-called nuclear many body problem (Baldo 1999).
The nuclear EoS has been thoroughly studied by many authors using both phenomenological and microscopic many-body approaches. Phenomenological approaches, either nonrelativistic or relativistic, are based on effective interactions that are frequently built to reproduce the properties of nuclei (Stone & Reinhard 2007). Skyrme interactions (Skyrme 1959; Vautherin & Brink 1972; Davesne et al. 2016; Grasso 2019) and relativistic mean-field (RMF) models (Boguta & Bodmer 1977; Serot et al. 1986; Serot & Walecka 1997) are among those most used. Many such interactions are built to describe nuclear systems close to the isospin symmetric case and therefore predictions at high isospin asymmetries should be taken with care. Most Skyrme interactions are by construction well behaved close to ρ0 and moderate values of the isospin asymmetry. However, only certain combinations of the parameters of these forces are well determined experimentally. As a consequence, there exists a large proliferation of different Skyrme interactions that produce a similar EoS for symmetric nuclear matter, but predict a very different one for pure neutron matter. A few years ago, Stone et al. (2003) performed an extensive and systematic test of the capabilities of several existing Skyrme interactions to provide good neutron star candidates, finding that only a few of these forces passed the restrictive tests imposed.
Relativistic mean-field models are based on effective Lagrangian densities where the interaction between baryons is described in terms of meson exchanges. The couplings of nucleons with mesons are usually fixed by fitting masses and radii of nuclei and the properties of nuclear bulk matter, whereas those of other baryons, like hyperons, are fixed by symmetry relations and hypernuclear observables. Recently, Dutra et al. (2014) analyzed, as in the case of Skyrme, several parametrizations of seven different types of RMF models imposing constraints from symmetric nuclear matter, pure neutron matter, symmetry energy and its derivatives finding that only a very small number of these parametrizations are consistent with all the nuclear constraints considered in that work.
Microscopic approaches on the other hand are based on realistic two- and three-body forces that describe scattering data in free space and the properties of the deuteron. These interactions are based on meson exchange (Nagels et al. 1973, 1978; Machleidt et al. 1987; Holzenkamp et al. 1989; Haidenbauer & Meißner 2005; Maessen et al. 1989; Rijken et al. 1999; Stoks & Rijken 1999; Rijken 2006; Rijken & Yamamoto 2006) or, very recently, on chiral perturbation theory (Weinberg 1990, 1991; Entem & Machleidt 2003; Epelbaum et al. 2005). To obtain the nuclear EoS, one has to solve the complicated many-body problem, the main difficulty of which lies in the treatment of the repulsive core, which dominates the short range of the interaction. Different microscopic many-body approaches have been extensively used for the study of the nuclear matter EoS. These include, among others: the Brueckner–Bethe–Goldstone (Baldo 1999; Day 1967) and the Dirac–Brueckner–Hartree–Fock (Ter Haar & Malfliet 1987a,b; Brockmann & Machleidt 1990) theories, the variational method (Akmal et al. 1998), the correlated basis function formalism (Fabrocini & Fantoni 1993), the self-consistent Green’s function technique (Kadanoff & Baym 1962; Dickhoff & Van Neck 2008), and the Vlow k approach (Bogner et al. 2003). We refer to these works for specific details.
To this day, the true nature of neutron stars remains an open question. Traditionally, the core of neutron stars has been modelled as a uniform fluid of neutron-rich nuclear matter in equilibrium with respect to the weak interaction (β-stable matter). Nevertheless, due to their high density, new degrees of freedom are expected to appear in addition to nucleons. Examples of widely studied new degrees of freedom include pion condensates (Haensel & Proszynski 1982), kaon condensates (Kaplan & Nelson 1986), hyperons (Chatterjee & Vidaña 2016; Vidaña 2018), Δ isobars (Drago et al. 2014a,b; Ribes et al. 2019), deconfined quarks (Glendenning 1992) and even di-baryonic matter (Faessler et al. 1998). The most precise and stringent neutron star constraint on the nuclear EoS comes from the recent determination of the unusually high masses of the millisecond pulsars PSR J1614−2230 (Demorest et al. 2010), PSR J0348+0432 (Antoniadis et al. 2013), and PSR J0740+6620 (Cromartie et al. 2020). These three measurements imply that any reliable model for the nuclear EoS should predict maximum masses at least larger than 2 M⊙. This observational constraint rules out many of the existent EoS models with exotic degrees of freedom, although their presence in the neutron star interior is, however, energetically favorable. This has lead to problems like the “hyperon puzzle” (Chatterjee & Vidaña 2016) or the “Δ puzzle” (Drago et al. 2014b,a), the solutions of which are not straightforward and are presently the subject of active research.
Recently, we studied the role of a new degree of freedom, namely d*(2380) (Bashkanov et al. 2019), on the nuclear EoS (Vidaña et al. 2018). The d*(2380) is a massive positively charged non-strange particle with integer spin (J = 3). It represents the first known non-trivial hexaquark for which there is experimental evidence (Adlarson et al. 2011, 2013, 2014). The importance of such a new degree of freedom resides in the fact that it has the same u, d quark composition as neutrons and protons and therefore does not involve any strangeness degrees of freedom. Moreover, it is a boson and as such it may condensate within the star. In our previous work we showed that despite its very large mass, the d*(2380) can appear in the neutron star interior at densities similar to those predicted for the appearance of other nucleon resonances, such as the Δ, or hyperons. That work was a first attempt to study the consequences that the presence of the d*(2380) could have on the properties of neutron stars where we assumed the d*(2380) as simple gas of non-interacting bosons. We have therefore decided to pursue a more detailed study which accounts for explicit interaction of d*(2380) with the surrounding medium. To this aim, we employ a standard non-linear Walecka model (Dutra et al. 2014), within the framework of a relativistic mean field theory (RMF). Starting from a well-known nucleonic Lagrangian (Glendenning 2000; Drago et al. 2014a), we employ the established d*(2380) properties to determine its interaction with other particles. In particular, we aim at providing first constraints on the sign (attractive or repulsive) for the effective interaction of such a particle.
The manuscript is organized in the following way. The Lagrangian density including the d*(2380) is shortly presented in Sect. 2. Our main results regarding the appearance and effect of d*(2380) on neutron stars are shown and discussed in Sect. 3. Finally, our concluding remarks and possible directions for future work are given in Sect. 4.
2. Lagrangian density
The total Lagrangian density of a system that is composed of nucleons (N = n, p), the four Δ isobar resonances (Δ = Δ−, Δ0, Δ+, Δ++), leptons (l = e−, μ−), scalar-isoscalar (σ), vector-isoscalar (ω) and vector-isovector (ρ) mesons, and includes in addition the d*(2380) di-baryon is simply given by
where
ΨN and 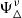 are the Dirac and Rarita–Schwinger fields for the nucleon and the Δ isobar, respectively; Ψl is the lepton Dirac field; ϕd* indicates the wave function of the d*(2380) condensate; g represents the different baryon–meson couplings; and τN and IΔ are isospin 1/2 and 3/2 operators. The field tensor of the ω and ρ mesons is denoted by Ωμν = ∂μων − ∂νωμ and Rμν = ∂μρν − ∂νρμ − gρN(ρμ × ρν), whereas the parameters b and c associated with the non-linear self-interactions of the σ field guarantee that the value of the incompressibility of nuclear matter is within the experimental range. The masses of the nucleons, Δ isobars, leptons, and the d*(2380) are denoted by mN, mΔ, ml, and md*. The main properties of the nucleons, Δs, and the d*(2380) di-baryon are summarized in Table 1. We note that the form of the di-baryon Lagrangian density, ℒd*, has been taken as analogous to the one that describes the interaction of other di-baryon species in nuclear matter, such as for instance the nonstrange ones d1(1920) and d′(2060) (Faessler et al. 1997a,b) or the long-studied strangeness −2 H-particle (Glendenning & Schaffner-Bielich 1998). We also note that a minus sign is explicitly placed in front of the gσd* coupling such that the effective mass of d*(2380) is defined similarly to that of the nucleon and that of the Δ isobar.
are the Dirac and Rarita–Schwinger fields for the nucleon and the Δ isobar, respectively; Ψl is the lepton Dirac field; ϕd* indicates the wave function of the d*(2380) condensate; g represents the different baryon–meson couplings; and τN and IΔ are isospin 1/2 and 3/2 operators. The field tensor of the ω and ρ mesons is denoted by Ωμν = ∂μων − ∂νωμ and Rμν = ∂μρν − ∂νρμ − gρN(ρμ × ρν), whereas the parameters b and c associated with the non-linear self-interactions of the σ field guarantee that the value of the incompressibility of nuclear matter is within the experimental range. The masses of the nucleons, Δ isobars, leptons, and the d*(2380) are denoted by mN, mΔ, ml, and md*. The main properties of the nucleons, Δs, and the d*(2380) di-baryon are summarized in Table 1. We note that the form of the di-baryon Lagrangian density, ℒd*, has been taken as analogous to the one that describes the interaction of other di-baryon species in nuclear matter, such as for instance the nonstrange ones d1(1920) and d′(2060) (Faessler et al. 1997a,b) or the long-studied strangeness −2 H-particle (Glendenning & Schaffner-Bielich 1998). We also note that a minus sign is explicitly placed in front of the gσd* coupling such that the effective mass of d*(2380) is defined similarly to that of the nucleon and that of the Δ isobar.
Mass (m), spin (J), isospin (I), isospin third component (I3), baryon number (b), and electric charge (q) of nucleons, Δs, and the di-baryon d*(2380).
In a RMF description of infinite nuclear matter, the meson fields are treated as classical fields. Meson field equations in the mean field approximation can be easily derived by applying the Euler–Lagrange equations to the Lagrangian density of Eq. (1) and replacing field operators by their ground-state expectation values  , ωμ → ω0,
, ωμ → ω0,  . They read simply
. They read simply
where JB is the spin of the baryon B, kFB its Fermi momentum, 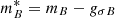 its effective mass, I3B the third component of its isospin, and
its effective mass, I3B the third component of its isospin, and 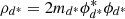 is the density of the d*(2380) di-baryon. The energy density and the pressure of the system are obtained from the energy-momentum tensor
is the density of the d*(2380) di-baryon. The energy density and the pressure of the system are obtained from the energy-momentum tensor
We note that the d*(2380) does not contribute to the total pressure of the system. Chemical equilibrium in the neutron star interior without neutrino trapping leads to the following relations between the chemical potentials of the different species:
where bi and qi are the baryon number and the electric charge of the particle i. The chemical potentials of the different particle species read
Let us finish this section with a short discussion of our choice of the different coupling constants. The nucleon couplings gσN, gωN, and gρN as well as the parameters b and c are fitted to the bulk (binding energy, density, incompressibility, symmetry energy) and single particle (nucleon effective mass) properties of symmetric nuclear matter at saturation. These couplings and parameters are taken here as being equal to those of the well-known Glendenning–Moszkowski model (Glendenning & Moszkowski 1991). In particular, we consider the parametrizations GM1 and GM3 of this model to describe the pure nucleonic part of the system. However, we should mention that these parametrizations do not fulfill the currently accepted constraints on the slope parameter L of the symmetry energy that impose it to be between 40 and 60 MeV. The values predicted by the GM1 and GM3 models are 95 and 90 MeV, respectively, significantly above the upper limit of the accepted range. However, despite this deficiency we still use them in the present work. The coupling of the Δ isobar with the different meson fields is poorly constrained due to the limited existence of experimental data. This leaves us with some freedom in the choice of these couplings. We consider two sets for the Δ–meson couplings. The first one is the so-called universal coupling (UC) scheme (Lavagno & Pigato 2012; Jin 1995) where all the Δ–meson couplings are taken as being equal to those of the nucleons:
where we have introduced the dimensionless couplings 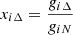 (i = σ, ω, ρ). The second set, referred to here as the stronger coupling (SC) set, corresponds to the choice xσΔ = 1.15, xωΔ = 1, xρΔ = 1. The interested reader is referred to Drago et al. (2014a,b) for more details on this second set of parameters.
(i = σ, ω, ρ). The second set, referred to here as the stronger coupling (SC) set, corresponds to the choice xσΔ = 1.15, xωΔ = 1, xρΔ = 1. The interested reader is referred to Drago et al. (2014a,b) for more details on this second set of parameters.
Being an isospin singlet, the d*(2380) di-baryon only couples with the σ and ω mesons. Unfortunately, there is currently no evidence that the interaction of d*(2380) with other particles is attractive or repulsive. In light of the lack of such information, in this work we explore a wide range of positive and negative values for the dimensionless couplings 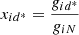 (i = σ, ω) in order to analyze the effect of both scenarios.
(i = σ, ω) in order to analyze the effect of both scenarios.
3. Results
Figure 1 shows the onset density of the d*(2380) di-baryon as a function of the dimensionless couplings xσd* and xωd* (panels a and c) and the first isospin state of the Δ isobar appearing in β-stable neutron star matter, the Δ− (panels b and d). The GM1 parametrization of the Glendenning–Moszkoski model has been used to describe the pure nucleonic part of the system. Results for the UC and SC choice of parameters for the Δ–meson couplings are shown in panels a,b and c,d, respectively. We notice that not all sets of values of xσd* and xωd* lead to physical solutions. In particular, for some sets of couplings, negative values of the pressure are obtained. These nonphysical cases correspond to the blank regions in the four panels of the figure. We observe that the onset density of the d*(2380) varies significantly as a function of the couplings xσd* and xωd*, ranging from ∼2ρ0 up to ∼7ρ0. However, the onset of the Δ− varies in a much smaller range, showing that in this particular scenario there is a very weak coupling between the two species. A similar conclusion holds using the GM3 parametrization instead of the GM1 one to describe the pure nucleonic part, as is shown in Fig. 2. However, we note that in this case the SC choice of parameters for the Δ–meson couplings leads to a later appearance of the Δ−, although this is not correlated with the appearance of the d*(2380). As a reference, we also indicate the noninteracting d*(2380) case in both figures with solid squares. The black line, defined by the relation xωd* = −0.88 xσd*, shown in the left panel of both figures indicates the case where a proper configuration of xσd* and xωd* dimensionless couplings leads to an onset density of the d*(2380) that is equal to that of the noninteracting case. We note that below this line, any combination of the xσd* and xωd* couplings predicts an onset density of the d*(2380) that is larger than that of the free case. This is an indication that the interaction of the d*(2380) is repulsive for all the values of these couplings in this region of the parameter space. Similarly, above the line xωd* = −0.88 xσd*, the predicted onset density of d*(2380) is always smaller than that of the noninteracting case, and consequently the d*(2380) is subject to attraction for any value of the couplings xσd* and xωd* sitting in this region. This is illustrated for the GM1 parametrization and the SC choice of the Δ couplings in Fig. 3 where we show the chemical equilibrium condition for the appearance of the d*(2380) for the cases in which the d*(2380) is subject to attraction (xσd* = xωd* = 0.25), repulsion (xσd* = xωd* = −0.25), or does not interact at all with the rest of the particles of the system. As seen in the plot, an attractive (repulsive) interaction leads to a decrease (increase) of the d*(2380) chemical potential, and consequently to an earlier (later) fulfillment of the equilibrium condition, μd* = 2μn − μe, signaling the appearance of the d*(2380) in matter. However, we should note that these conclusions are based on the particular models employed in the present work, and therefore they could change if other models are used or if the presence of other degrees of freedom such as hyperons or deconfined quarks are taken into account.
 |
Fig. 1. Onset density (in units of ρ0) of the d*(2380) di-baryon (panels a and c) and the Δ− isobar (panels b and d) in β-stable neutron star matter as a function of the dimensionless couplings xσd* and xωd*. Panels a and b: UC choice of parameters for the Δ–meson couplings while panels c and d: SC choice. In all cases the nucleonic part is described with the GM1 parametrization of the Glendenning–Moszkowski model. The d*(2380) noninteracting case is highlighted with squares. The black line corresponds to solutions where the onset density of the d*(2380) coincides with that of the noninteracting case. |
 |
Fig. 3. Evolution of the chemical potentials for the appearance of the d*(2380) di-baryon in β-stable matter as a function of the density of the system. Results are shown for the cases in which the d*(2380) is subject to attraction (xσd* = xωd* = 0.25) or repulsion (xσd* = xωd* = −0.25), or does not interact at all with the rest of the particles of the system. The GM1 parametrization together with the SC choice of the Δ couplings has been adopted. |
To better quantify the impact of the appearance of the d*(2380) in the medium, in Figs. 4 and 5 we show the chemical composition of β-stable matter using the GM1 (Fig. 4) and GM3 (Fig. 5) models to describe the pure nucleonic part and the UC (upper panels) or SC (lower panels) choice of parameters for the Δ–meson couplings. The interaction of d*(2380) is assumed to be either attractive, with couplings xσd* = xωd* = 0.1 (left panels), or repulsive, with couplings xσd* = xωd* = −0.1 (right panels). Results for the case in which the d*(2380) is assumed to be a free particle are also shown for comparison. We highlight the fact that the GM1 model leads in all the cases to an earlier appearance of the Δ isobar, and also, as mentioned above, that due to its negative charge the Δ− appears at much lower densities than the other members of the Δ quadruplet. We note in addition that with the UC choice for the Δ–meson couplings, no other Δ resonances appear in the range of baryonic densities considered either for the GM1 model or for the GM3 one. On the contrary, when the SC set of couplings is adopted, the Δ0 and Δ+ also appear; both appear in the case of the GM1 model and only the former in the case of the GM3 one when the d*(2380) is subject to repulsion. The Δ++ is absent in all cases. Finally, we also observe that the onset density of the Δ− is not affected by the attractive or repulsive character of the interaction of the d*(2380) with the other particles since it appears in all cases at lower densities than the d*(2380). The appearance of the d*(2380) induces an important and significant reduction of the fraction of neutrons, protons, and Δs since its baryon number is 2. In addition, as the d*(2380) is positively charged, the lepton fraction increases in order to maintain charge neutrality.
 |
Fig. 4. Particle fraction as a function of the baryon density in units of ρ0. The nucleonic part is described with the GM1 model. Results for the UC (SC) choice of parameters for the Δ–meson couplings are shown in the upper (lower) panels. Left and right panels: results for a case in which the d*(2380) feels attraction (xσd* = xωd* = 0.1) or repulsion (xσd* = xωd* = −0.1), respectively. Dashed lines show the results for the free case for comparison. |
Let us now analyze the effect of the d*(2380) on the mass–radius relation of neutron stars and, in particular, on the maximum mass. To this end, using our EoS together with that of Douchin & Haensel (2001) for the low-density stellar crust, we solved the well-known Tolmann–Oppenheimer–Volkoff (TOV) equations (Tolman 1939; Oppenheimer & Volkoff 1939) which describe the structure of nonrotating spherically symmetric stellar configurations in general relativity. In Figs. 6 and 7, we show the pressure (left panels) and the mass–radius relation (right panels) obtained using the GM1 (Fig. 6) and GM3 (Fig. 7) models to describe the pure nucleonic part of the EoS and the UC (upper panels) or SC (lower panels) choice of parameters for the Δ–meson couplings. The interaction of d*(2380) is assumed to be either attractive, with couplings (xσd*, xωd*) = (0.1, 0.1), (0.2, 0.2) and (0.3, 0.3), or repulsive, with couplings (xσd*, xωd*) = (−0.1, − 0.1),(−0.2, − 0.2) and ( − 0.3, − 0.3). Results for the case in which the presence of the d*(2380) is ignored and the case in which it is assumed to be a free particle are also shown for comparison. The first thing to be noticed when looking at the pressure of the system is that it is strongly reduced once the d*(2380) appears. This is simply due to: (i) the reduction of the neutron and proton fractions with the appearance of the d*(2380) with the consequent reduction of their partial contributions to the pressure, and (ii) the fact that the d*(2380) itself does not contributes to the pressure. We note that the pressure continues to increase slowly after the appearance of the d*(2380) in the system except for the couplings xσd* = xωd* = −0.2 and xσd* = xωd* = −0.3 in the case of the GM1 model, and xσd* = xωd* = −0.3 in the case of the GM3 one. In these cases, the gradient of the pressure becomes negative at a given density. A negative gradient of the pressure is a signal for a mechanical instability which can give rise to a possible phase transition. However, such a possibility has not been considered in the present work. Therefore, those sets of xσd* and xωd* couplings that lead to a negative gradient of the pressure at some given density represent solutions in which the appearance of the d*(2380) di-baryon induces the collapse of the neutron star into a black hole.
 |
Fig. 6. Pressure (left panels) and mass–radius relation (right panels) obtained using the GM1 model to describe the pure nucleonic part of the EoS and the UC (upper panels) or the SC (lower panels) choice of parameters for the Δ–meson couplings. The interaction of d*(2380) is assumed to be either attractive, with couplings (xσd*, xωd*) = (0.1, 0.1), (0.2, 0.2), and (0.3, 0.3), or repulsive, with couplings (xσd*, xωd*) = (−0.1, − 0.1), (-0.2, −0.2), and ( − 0.3, − 0.3). The recent measurement of the mass of the pulsar PSR J0740+6620 is shown with a 68.3% credibility interval ( |
Looking now into the mass–radius relation, one immediately notices that only the model GM1 (with both choices for the Δ–meson couplings) predicts a maximum mass that is compatible with the recent measurement of the mass of the pulsar PSR J0740+6620 (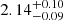 M⊙ (68.3% credibility interval) and
M⊙ (68.3% credibility interval) and 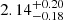 M⊙ (95.4% credibility interval) (Cromartie et al. 2020) if the d*(2380) does not interact or is subject to slight repulsion. An attractive interaction of the d*(2380) leads to values of the maximum mass smaller than the highest value observed until now. Too much repulsion on the other side leads, as mentioned above, to a negative gradient of the pressure and consequently to the collapse of the star.
M⊙ (95.4% credibility interval) (Cromartie et al. 2020) if the d*(2380) does not interact or is subject to slight repulsion. An attractive interaction of the d*(2380) leads to values of the maximum mass smaller than the highest value observed until now. Too much repulsion on the other side leads, as mentioned above, to a negative gradient of the pressure and consequently to the collapse of the star.
4. Conclusions
This work is the extension of a previous study (Vidaña et al. 2018) where, assuming a simple free bosonic gas supplemented with a RMF model to describe the pure nucleonic part of the EoS, we explored for the very first time the consequences that the presence of the d*(2380) di-baryon could have on the properties of neutron stars. Compared to that exploratory work, we have employed a standard non-linear Walecka model (Dutra et al. 2014) within the framework of a relativistic mean field theory (RMF) including additional terms that describe the interaction of the d*(2380) di-baryon with the other particles of the system through the exchange of σ- and ω-meson fields. We used the two well-know parametrizations GM1 and GM3 of the Glendenning–Moszkowski model to describe the pure nucleonic part of the EoS together with two different choices for the Δ–meson couplings, namely the universal (UC) and the strong (SC) couplings. Our results show that the presence of the d*(2380) leads to maximum masses compatible with the recent observations of ∼2 M⊙ millisecond pulsars if the interaction of the d*(2380) is slightly repulsive or the d*(2380) does not interact at all. An attractive interaction makes the EoS too soft to be able to support a 2 M⊙ neutron star whereas an extremely repulsive one induces the collapse of the neutron star into a black hole as soon as the d*(2380) appears. We conclude from our analysis that the presence of d*(2380) within a neutron star is plausible, although the exact density at which it appears and the production amount are still a matter for further scientific investigation. However, we should note that our conclusions are based on the particular models employed in the present work and therefore they could change if other models are used or if the presence of other degrees of freedom such as hyperons or deconfined quarks are taken into account. Therefore, the reader should consider the results presented here as preliminary. Finally, it is worth mentioning that the presence of d*(2380) particles in the interior of neutron stars may induce new possible cooling mechanisms as discussed by Vidaña et al. (2018).
Acknowledgments
This work was partially supported by the STFC Grants No. ST/M006433/1 and ST/P003885/1, ST/L00478X/1 and by the COST Action CA16214 “PHAROS: The multimessenger physics and astrophysics of neutron stars”.
References
- Adlarson, P., Bashkanov, M., Clement, H., et al. 2011, Phys. Rev. Lett., 106, 242302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Adlarson, P., Bashkanov, M., Clement, H., et al. 2013, Phys. Lett. B, 721, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Adlarson, P., Bashkanov, M., Clement, H., et al. 2014, Phys. Rev. Lett., 112, 202301 [NASA ADS] [CrossRef] [Google Scholar]
- Akmal, A., Pandharipande, V., & Ravenhall, D. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Annala, E., Gorda, T., Kurkela, A., & Vuorinen, A. 2018, Phys. Rev. Lett., 120, 172703 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Antoniadis, J., Freire, P. C., Wex, N., et al. 2013, Science, 340, 1233232 [Google Scholar]
- Baldo, M. 1999, Nuclear Methods and the Nuclear Equation of State (Singapore: World Scientific) [CrossRef] [Google Scholar]
- Bashkanov, M., Kay, S., Watts, D., et al. 2019, Phys. Lett. B, 789, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bogner, S., Kuo, T. T. S., & Schwenk, A. 2003, Phys. Rep., 386, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Boguta, J., & Bodmer, A. 1977, Nucl. Phys. A, 292, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Brockmann, R., & Machleidt, R. 1990, Phys. Rev. C, 42, 1965 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, D., & Vidaña, I. 2016, Eur. Phys. J. A, 52, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cromartie, H. T., Fonseca, E., Ransom, S. M., et al. 2020, Nat. Astron., 4, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Davesne, D., Becker, P., Pastore, A., & Navarro, J. 2016, Ann. Phys., 375, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Day, B. 1967, Rev. Mod. Phys., 39, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S., Roberts, M., & Hessels, J. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dickhoff, W. H., & Van Neck, D. 2008, Many-Body Theory Exposed!: Propagator Description of Quantum Mechanics in Many-Body Systems Second Edition (World Scientific Publishing Company) [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drago, A., Lavagno, A., Pagliara, G., & Pigato, D. 2014a, Phys. Rev. C, 90, 065809 [NASA ADS] [CrossRef] [Google Scholar]
- Drago, A., Lavagno, A., & Pagliara, G. 2014b, Phys. Rev. D, 89, 043014 [NASA ADS] [CrossRef] [Google Scholar]
- Dutra, M., Lourenço, O., Avancini, S., et al. 2014, Phys. Rev. C, 90, 055203 [NASA ADS] [CrossRef] [Google Scholar]
- Entem, D., & Machleidt, R. 2003, Phys. Rev. C, 68, 041001 [NASA ADS] [CrossRef] [Google Scholar]
- Epelbaum, E., Glöckle, W., & Meißner, U.-G. 2005, Nucl. Phys. A, 747, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrocini, A., & Fantoni, S. 1993, Phys. Lett. B, 298, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Faessler, A., Buchmann, A., & Krivoruchenko, M. 1997a, Phys. Rev. C, 56, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Faessler, A., Buchmann, A., Krivoruchenko, M., & Martemyanov, B. 1997b, Phys. Lett. B, 391, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Faessler, A., Buchmann, A., Krivoruchenko, M., & Martemyanov, B. 1998, J. Phys. G, 24, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K. 1992, Phys. Rev. D, 46, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K. 2000, Compact Stars: Nuclear Physics, Particle Physics and General Relativity (Berlin: Springer) [Google Scholar]
- Glendenning, N. K., & Moszkowski, S. A. 1991, Phys. Rev. Lett., 67, 2414 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Glendenning, N. K., & Schaffner-Bielich, J. 1998, Phys. Rev. C, 58, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Grasso, M. 2019, Prog. Part. Nucl. Phys., 106, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Proszynski, M. 1982, ApJ, 258, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1: Equation of State and Structure (Springer Science & Business Media), 326 [Google Scholar]
- Haidenbauer, J., & Meißner, U.-G. 2005, Phys. Rev. C, 72, 044005 [NASA ADS] [CrossRef] [Google Scholar]
- Holzenkamp, B., Holinde, K., & Speth, J. 1989, Nucl. Phys. A, 500, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, X. 1995, Phys. Rev. C, 51, 2260 [NASA ADS] [CrossRef] [Google Scholar]
- Kadanoff, L. P., & Baym, G. 1962, Quantum Statistical Mechanics (New York: Benjamin) [Google Scholar]
- Kaplan, D., & Nelson, A. 1986, Phys. Lett. B, 175, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lavagno, A., & Pigato, D. 2012, Phys. Rev. C, 86, 024917 [NASA ADS] [CrossRef] [Google Scholar]
- Machleidt, R., Holinde, K., & Elster, C. 1987, Phys. Rep., 149, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Maessen, P., Rijken, T. A., & De Swart, J. 1989, Phys. Rev. C, 40, 2226 [NASA ADS] [CrossRef] [Google Scholar]
- Nagels, M., Rijken, T. A., & De Swart, J. 1973, Phys. Rev. Lett., 31, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Nagels, M., Rijken, T. A., & De Swart, J. 1978, Phys. Rev. D, 17, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, J. R., & Volkoff, G. M. 1939, Phys. Rev., 55, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Pizzochero, P., Jones, D. I., Rea, N., & Vidaña, I. 2018, The Physics and Astrophysics of Neutron Stars (Springer) [CrossRef] [Google Scholar]
- Ribes, P., Ramos, A., Tolos, L., Gonzalez-Boquera, C., & Centelles, M. 2019, ApJ, 883, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Rijken, T. A. 2006, Phys. Rev. C, 73, 044007 [NASA ADS] [CrossRef] [Google Scholar]
- Rijken, T. A., & Yamamoto, Y. 2006, Phys. Rev. C, 73, 044008 [NASA ADS] [CrossRef] [Google Scholar]
- Rijken, T. A., Stoks, V., & Yamamoto, Y. 1999, Phys. Rev. C, 59, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Riley, T. E., Watts, A. L., Bogdanov, S., et al. 2019, ApJ, 887, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Serot, B., & Walecka, J. 1986, in Advances in Nuclear Physics, eds. J. W. Negele, & E. Vogt (New York: Plenum) [Google Scholar]
- Serot, B. D., & Walecka, J. D. 1997, Int. J. Mod. Phys. E, 6, 515 [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A. 2008, Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects (John Wiley & Sons) [Google Scholar]
- Skyrme, T. 1959, Nucl. Phys., 9, 615 [CrossRef] [Google Scholar]
- Stoks, V. J., & Rijken, T. A. 1999, Phys. Rev. C, 59, 3009 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. R., & Reinhard, P.-G. 2007, Prog. Part. Nucl. Phys., 58, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. R., Miller, J., Koncewicz, R., Stevenson, P., & Strayer, M. 2003, Phys. Rev. C, 68, 034324 [NASA ADS] [CrossRef] [Google Scholar]
- Ter Haar, B., & Malfliet, R. 1987a, Phys. Rep., 149, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Ter Haar, B., & Malfliet, R. 1987b, Phys. Rev. C, 36, 1611 [NASA ADS] [CrossRef] [Google Scholar]
- Tolman, R. C. 1939, Phys. Rev., 55, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Vautherin, D., & Brink, D. T. 1972, Phys. Rev. C, 5, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I. 2018, Proc. R. Soc. A: Math. Phys. Eng. Sci., 474, 20180145 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I., Bashkanov, M., Watts, D., & Pastore, A. 2018, Phys. Lett. B, 781, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 1990, Phys. Lett. B, 251, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 1991, Nucl. Phys. B, 363, 3 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mass (m), spin (J), isospin (I), isospin third component (I3), baryon number (b), and electric charge (q) of nucleons, Δs, and the di-baryon d*(2380).
All Figures
 |
Fig. 1. Onset density (in units of ρ0) of the d*(2380) di-baryon (panels a and c) and the Δ− isobar (panels b and d) in β-stable neutron star matter as a function of the dimensionless couplings xσd* and xωd*. Panels a and b: UC choice of parameters for the Δ–meson couplings while panels c and d: SC choice. In all cases the nucleonic part is described with the GM1 parametrization of the Glendenning–Moszkowski model. The d*(2380) noninteracting case is highlighted with squares. The black line corresponds to solutions where the onset density of the d*(2380) coincides with that of the noninteracting case. |
| In the text | |
 |
Fig. 2. Same as Fig. 1 but with the nucleonic sector described using the GM3 model. |
| In the text | |
 |
Fig. 3. Evolution of the chemical potentials for the appearance of the d*(2380) di-baryon in β-stable matter as a function of the density of the system. Results are shown for the cases in which the d*(2380) is subject to attraction (xσd* = xωd* = 0.25) or repulsion (xσd* = xωd* = −0.25), or does not interact at all with the rest of the particles of the system. The GM1 parametrization together with the SC choice of the Δ couplings has been adopted. |
| In the text | |
 |
Fig. 4. Particle fraction as a function of the baryon density in units of ρ0. The nucleonic part is described with the GM1 model. Results for the UC (SC) choice of parameters for the Δ–meson couplings are shown in the upper (lower) panels. Left and right panels: results for a case in which the d*(2380) feels attraction (xσd* = xωd* = 0.1) or repulsion (xσd* = xωd* = −0.1), respectively. Dashed lines show the results for the free case for comparison. |
| In the text | |
 |
Fig. 5. Same as Fig. 4 but with the nucleonic sector described using the GM3 model. |
| In the text | |
 |
Fig. 6. Pressure (left panels) and mass–radius relation (right panels) obtained using the GM1 model to describe the pure nucleonic part of the EoS and the UC (upper panels) or the SC (lower panels) choice of parameters for the Δ–meson couplings. The interaction of d*(2380) is assumed to be either attractive, with couplings (xσd*, xωd*) = (0.1, 0.1), (0.2, 0.2), and (0.3, 0.3), or repulsive, with couplings (xσd*, xωd*) = (−0.1, − 0.1), (-0.2, −0.2), and ( − 0.3, − 0.3). The recent measurement of the mass of the pulsar PSR J0740+6620 is shown with a 68.3% credibility interval ( |
| In the text | |
 |
Fig. 7. Same as Fig. 6 but with the nucleonic sector described using the GM3 model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



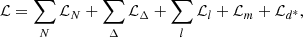
![$$ \begin{aligned}&\mathcal{L} _N=\bar{\Psi }_N\left[ i\gamma _\mu \partial ^\mu -m_N+g_{\sigma N}\sigma -g_{\omega N}\gamma _\mu \omega ^\mu -g_{\rho N}\gamma _\mu \frac{\boldsymbol{\tau _N} \cdot \boldsymbol{\rho }^\mu }{2}\right]\Psi _N, \nonumber \\&\mathcal{L} _\Delta =\bar{\Psi }_{\Delta \nu }\left[ i\gamma _\mu \partial ^\mu -m_\Delta +g_{\sigma \Delta }\sigma -g_{\omega \Delta }\gamma _\mu \omega ^\mu -g_{\rho \Delta }\gamma _\mu \boldsymbol{I}_\Delta \cdot \boldsymbol{\rho }^\mu \right]\Psi _\Delta ^\nu , \nonumber \\&\mathcal{L} _l=\bar{\Psi }_l\left[ i\gamma _\mu \partial ^\mu -m_l\right]\Psi _l, \nonumber \\&\mathcal{L} _m= \frac{1}{2}\partial _\mu \sigma \partial ^\mu \sigma -\frac{1}{2}m_\sigma ^2 \sigma ^2-\frac{1}{3}b m_N g_{\sigma N}^3 \sigma ^3-\frac{1}{4}c g_{\sigma N}^4 \sigma ^4\nonumber \\&\qquad \;+\frac{1}{2}m_\omega ^2\omega _\mu \omega ^\mu -\frac{1}{4}\Omega _{\mu \nu } \Omega ^{\mu \nu } -\frac{1}{4}{\boldsymbol{R}}_{\mu \nu }{\boldsymbol{R}}^{\mu \nu }+\frac{1}{2}m_\rho ^2 \boldsymbol{\rho }_\mu \cdot \boldsymbol{\rho }^\mu , \nonumber \\&\mathcal{L} _{d^*}=(\partial _\mu -ig_{\omega d^*} \omega _\mu )\phi ^*_{d^*}(\partial ^\mu +ig_{\omega d^*} \omega ^\mu )\phi _{d^*}-(m_{d^*}-g_{\sigma d^*}\sigma )^2\phi ^*_{d^*}\phi _{d^*}. \end{aligned} $$](/articles/aa/full_html/2020/06/aa37749-20/aa37749-20-eq2.gif)