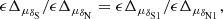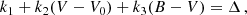| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 6 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201936541 | |
| Published online | 08 November 2019 | |
Comparison of proper motions in declination for 387 Gaia DR2 and HIPPARCOS stars from ILS observations over many decades⋆
1
Astronomical Observatory, Volgina 7, 11060 Belgrade, Serbia
e-mail: gdamljanovic@aob.rs
2
Observatoire de Paris – SYRTE, PSL Research University, CNRS/UMR 8630, Sorbonne Universités, Université Pierre et Marie Curie, LNE, 61 avenue de l’Observatoire, 75014 Paris, France
e-mail: Francois.Taris@obspm.fr
Received:
21
August
2019
Accepted:
26
September
2019
Context. The second solution of the Gaia catalog, which has been available since April 2018, plays an important role in the realization of the future Gaia reference frame. Since 1997, the reference frame has been materialized by the optical HIPPARCOS positions of about 120 000 stars. The HIPPARCOS has been compared with and linked to the International Celestial Reference Frame (ICRF). The ICRF is materialized by means of the radio positions of extragalactic sources using very large baseline interferometry observations. Both, the HIPPARCOS and Gaia missions belong to the European Space Agency, and it is important to note that the Gaia catalog is going to replace the HIPPARCOS catalog.
Aims. It has been shown that the International Latitude Service zenith telescope data pertaining to ground-based surveys that span a time baseline of about 80 yr, and which are also key when measuring proper motions, could be useful for the accurate determination of μδ for 387 ILS stars. Therefore, in this study we aim first to reduce these stars to the HIPPARCOS reference system; second, to made our original catalog of μδ, which we refer to as the ILS catalog, for these 387 bright stars; third, to present comparison results of the four catalogs by pairs (the ILS, HIPPARCOS or HIP, new HIPPARCOS or NHIP, and Gaia DR2); and fourth, to analyze the differences in μδ between pairs of catalogs to characterize the μδ errors for these catalogs with a special focus on the Gaia DR2 and ILS catalogs.
Methods. At seven ILS sites around the world at latitude 39.°1, a set of seven telescopes was used to monitor the latitude variation via observations of the same stars for about 80 yr. Here, the inverse task was applied to improve μδ values of the 387 HIPPARCOS stars using the previously mentioned observations. Due to the specific Horrebow-Talcott method of the measured star pair, it is difficult to determine μδ for each single star. However, we achieved this by developing the original method and in combination with the HIPPARCOS data. We used the previously developed least squares method and formula to determine the coefficients, which describe the systematic part of differences in μδ between the pairs of catalogs.
Results. We calculated the coefficients with the aforementioned formula (in line with the coordinates, stellar magnitude, and color index of every star) to compare ILS, HIP, NHIP, and Gaia DR2 data of μδ against each other by using the set of 387 stars. The presented differences of μδ show that the systematic errors in the four catalogs are nearly at the same level of 0.1 mas yr−1. This means that the DR2 and ILS μδ values are in good agreement with each other, and with values from the HIPPARCOS and new HIPPARCOS catalogs. Also, the random errors of differences are small ones; they are near 1 mas yr−1 for ILS-HIP and ILS-NHIP, and about 2 mas yr−1 for ILS-DR2, HIP-DR2, and NHIP-DR2. It is important to note that there is a similar level of proper motion formal errors in HIPPARCOS and new HIPPARCOS catalogs.
Key words: astrometry / catalogs / proper motions
Full Table 5 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/631/A145
© ESO 2019
1. Introduction
Gaia is a mission of the European Space Agency (ESA). It started its five-year nominal operation phase in July 2014, nearly six months after launching the Gaia satellite in December 2013 (Gaia Collaboration 2016a). The goal was to collect astronomical data (positions, proper motions, and parallaxes) for more than one billion sources brighter than 20.7 mag in G-band, and for about 500 000 quasars (Prusti 2012). There have been two releases so far, Gaia DR1 in September 2016 and DR2 in April 2018 (Gaia Collaboration 2016b; Lindegren et al. 2018). The Gaia DR1 results are based on observations collected during the first 14 months starting with July 2014, and DR2 result are from the first 22 months.
Here, we used the HIPPARCOS catalog data (ESA 1997) and the new HIPPARCOS catalog data (van Leeuwen 2007) to compare the μδ values against those from Gaia DR2 and ILS. The ILS is our original catalog of μδ for 387 ILS stars (Damljanović & Pejović 2006). The epoch of the HIPPARCOS catalog is J1991.25, and it was the first satellite catalog with about 120 000 stars. It was an ESA mission as well, and that catalog appeared in 1997 as a new reference frame (the ICRS in the optical domain).
To obtain the original ILS catalog of μδ values for 387 stars and to improve the μδH from the HIPPARCOS catalog, we took into account the latitude variations made using instruments at seven sites (see Table 1) during the period of 1899.7–1979.0. We note that approximately an 80-year-long period of ILS data is necessary to get accurate μδ values. The ILS data were included as input data into the Bureau International de l’Heure (BIH) in Paris as part of the Earth rotation programs to produce the Earth orientation parameters (EOP).
ILS stations, their geographic coordinates (longitude λW and mean latitude φ), and observed intervals.
In the following, we present information about μδ data from the ILS and the other previously mentioned catalogs. In the next section, the calculation steps necessary to obtain the proper motion in declination for 387 ILS stars are performed. The error analysis, for random and systematic errors, regarding the comparison of μδ between the four catalogs is found in Sect. 4. The Conclusion details the main results after comparing the four catalogs by pairs, and recommendations are given about useful ground-based data in the framework of the satellite Gaia mission.
2. ILS, HIPPARCOS, and Gaia DR2 data
Gaia DR2 contains results for about 1.69 billion sources in the G magnitude range from 3 to 21 and at the reference epoch J2015.5. There are about 1.33 billion sources with five astrometric parameters (coordinates, proper motions, and parallaxes) and the approximate positions for 0.36 billion faint objects. For 1.33 billion sources, the median uncertainty in position and parallax is about 0.04 mas for sources with G < 14 mag at J2015.5, and in the proper motion, the uncertainty is 0.05 mas yr−1. The Gaia DR2 optical reference frame is aligned with the ICRS via quasars (Lindegren et al. 2018). Due to calibration issues, the stars with G < 6 mag mostly have inferior astrometry; here, about one third of ILS stars are in that group (see Fig. 2). The DR1 solution (or Tycho-Gaia astrometric solution) incorporated astrometric HIPPARCOS and Tycho-2 data (Lindegren et al. 2016), but the DR2 solution is independent of HIPPARCOS and Tycho-2 catalogs. In both solutions (DR1 and DR2), the sources are treated as single stars; for unresolved binaries the presented data thus refer to the photocenter. For resolved binaries, the results are sometimes spurious due to the confusion of the components.
The HIPPARCOS catalog is the optical counterpart (Kovalevsky et al. 1997) of the ICRF. The HIPPARCOS stars (118 218 ones) are brighter than V-mag 12. Mostly, they are between 7 mag and 9 mag. The errors in position and parallax are about 1 mas at J1991.25, and in the proper motion about 1 mas yr−1, but the errors of proper motion are larger in the case of double stars than for single ones. The main reason is due to the observation period, which was less than four years (Vondrák et al. 1998). The new HIPPARCOS catalog has appeared to improve the coordinates, proper motions, and parallaxes of stars. (van Leeuwen 2007) performed a new reduction of raw HIPPARCOS observations, and the new astrometric data are better by a factor of 2.2 in total weight, and by up to a factor of four for almost all stars that are brighter than 8 mag. All ILS stars here are brighter than 8 mag (see Fig. 2). Finally, it is possible to get more accurate values, pertaining to positions and proper motions, by combining the ground-based and satellite data (such as HIPPARCOS data) with those from the HIPPARCOS catalog. This is the case for ARIHIP, the Earth Orientation Catalog (EOC; Vondrák et al. 2003), and also other catalogs.
There have been many astrometric ground-based observations of the same stars, which are found in ILS data, referred to the HIPPARCOS catalog, and made using many instruments during the last century. In the case of ILS data, 387 HIPPARCOS stars were observed at seven stations (Carloforte, Cincinnati, Gaithersburg, Kitab, Mizusawa, Tschardjui, and Ukiah), covering the period from 1899.7–1979.0 (see Table 1). Our ILS catalog of μδ (Damljanović & Pejović 2006) yields accurate data for 387 stars that are common to ILS and HIPPARCOS. To get precise μδ via ILS data, we took a reverse approach by using latitude observations and combined these ground-based data with satellite HIPPARCOS data. The original method was applied (Damljanović 2007); the corrections Δμδ of suitable HIPPARCOSμδH were calculated and applied to the corresponding μδH values. Finally, the ILS values μδ for 387 stars show a high accuracy and are in good agreement with Gaia DR2, HIPPARCOS, and new HIPPARCOS values.
3. Calculation of proper motion in declination of 387 ILS stars using latitude observations
3.1. ILS latitude observations
The error of μδ is in line with 1/Δt. Because of it, using a long ILS time interval of about 80 yr makes it possible to get a better accuracy of μδ (for 387 ILS stars) than for the HIPPARCOS stars. Even the accuracy of HIPPARCOS star positions are better than those from ground-based surveys. Also, there are many observations of the same ILS star pair (from a few to a few hundred times) per each year for the period from 1899.7 to 1979.0. Even about 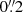 of zenith-telescope accuracy, the long time interval (from a few decades to potentially about 80 yr), and numerous observations per year are of importance for better accuracy of ILS μδ values than for the HIPPARCOS values. Plus, by combining the ILS observations with suitable HIPPARCOS data for the common stars, we can get better results than if only ground-based data are used. The point of HIPPARCOS data is done for the epoch 1991.25, and during calculation we used suitable weights for all points, which were inversely proportional to position errors (Damljanović et al. 2006). The tectonic plate motion and the mean latitude were removed from the ILS observations (Vondrák, priv. comm.); more information about ILS can be found in the publication by Yumi & Yokoyama (1980).
of zenith-telescope accuracy, the long time interval (from a few decades to potentially about 80 yr), and numerous observations per year are of importance for better accuracy of ILS μδ values than for the HIPPARCOS values. Plus, by combining the ILS observations with suitable HIPPARCOS data for the common stars, we can get better results than if only ground-based data are used. The point of HIPPARCOS data is done for the epoch 1991.25, and during calculation we used suitable weights for all points, which were inversely proportional to position errors (Damljanović et al. 2006). The tectonic plate motion and the mean latitude were removed from the ILS observations (Vondrák, priv. comm.); more information about ILS can be found in the publication by Yumi & Yokoyama (1980).
In accordance with the Horrebow-Tallcott method, the main zenith-telescope (ZT) formula to calculate latitude φP from a star pair and for the moment of measurement t is φP = (δS − δN)/2 + Δz/2. The values δS and δN are the apparent declinations of stars (south star and north star, respectively) in the star pair, and the zenith-distance difference Δz = zS − zN is from ZT observations. Values δS and δN were calculated by using the HIPPARCOS catalog. If we remove the polar motion term and systematic errors (instrumental, local, etc.) from the latitude data, the residuals are catalog errors that is of interest to us (Damljanović et al. 2006).
3.2. Proper motions in declination using latitude observations
In line with ΔφP + (dφP/dt)t ≈ (ΔδS + ΔδN)/2 + t(ΔμδS + ΔμδN)/2 (Vondrák et al. 1998), we can obtain a and b by using the least square method (LSM) and linear model resn = a + b(tn − 1991.25) on input points with weights. The values ΔδS and ΔδN are corrections of declinations, ΔμδS and ΔμδN are corrections of proper motions in declination, t is time, resn is the star pair residual, tn (in years) is the epoch of resn, a pertains to (ΔδS + ΔδN)/2, and b pertains to (ΔμδS + ΔμδN)/2. The residuals of latitude variations resn are without polar motion and the systematic terms (Damljanović 2005), a and b are in accordance with the epoch 1991.25.
There is one equation b = (ΔμδS + ΔμδN)/2, but two unknowns ΔμδS and ΔμδN. To solve that problem, we introduced one more Eq. (1), as part of our original procedure,
where μδS1 and μδN1 are from the EOC-2 catalog (Vondrák 2004), and μδS2 and μδN2 are from the HIPPARCOS catalog. About the errors, ϵΔμδS and ϵΔμδN are standard deviation of ΔμδS and ΔμδN, respectively. There is one equation 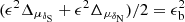 but two unknowns ϵΔμδS and ϵΔμδN. To solve that problem, we performed one more Eq. (2):
but two unknowns ϵΔμδS and ϵΔμδN. To solve that problem, we performed one more Eq. (2):
where ϵΔμδS1 and ϵΔμδN1 are from EOC-2; ϵΔμδS1 and ϵΔμδN1 are the errors of stars S (south star) and N (north star) of the ILS star pair, respectively. In that direction, it is possible to calculate corrections ΔμδS and ΔμδN (with their errors) of each star pair for common ILS and HIPPARCOS stars, to apply these corrections to corresponding HIPPARCOS values μδH, and to obtain the ILS catalog with proper motions in declination for each star separately. After which, it is of interest to compare these μδ values of 387 stars with Gaia DR2, HIPPARCOS, and new HIPPARCOS values. This is especially the case for Gaia DR2 because the ILS catalog depends of HIPPARCOS and EOC-2 data.
4. Results
In Fig. 1, the distribution of 387 stars on the celestial sphere is presented. The values of 0h < α < 24h, but 20 ° < δ < 60°; it is possible to investigate the systematics (via the comparison of four catalogs of pairs by using suitable differences of μδ) over all α (see Fig. 3), but over just a part of δ (see Fig. 4). The distribution of V magnitude is presented in Fig. 2 (4 < V < 8, mostly ILS stars are from 6 to 7 mag), and the differences as function of V magnitude are presented in Fig. 5. Suitable mean proper motion differences (as a function of α, δ, and V magnitude) are presented in Figs. 3–5.
 |
Fig. 1. Distribution of 387 stars on celestial sphere. |
 |
Fig. 2. Distribution of magnitudes of 387 stars. |
 |
Fig. 3. Mean proper motion differences as function of α: ILS-HIP (cross), ILS-NHIP (open rectangle), ILS-DR2 (open circle). |
 |
Fig. 5. Mean proper motion differences as function of magnitude; designations are the same as in Fig. 3. |
The average values of ϵμδ (mas yr−1) of 387 stars for the ILS catalog, which are also in line with V magnitude, are in Table 2. That value in the case of all HIPPARCOS stars is about ±1 mas yr−1, and it is slightly better in the case of new HIPPARCOS.
Average value of ϵμδ of catalog ILS using 387 stars.
Figures 3–5 indicate some systematic errors between the mean data values from the catalog pairs. Differences between ILS and DR2 are somewhat higher in the central part of Fig. 3 (at 12h of α), and there is a small sinusoidal curve with an amplitude of A = 0.7 ± 0.5 mas yr−1 calculated using LSM. Differences presented in Fig. 4 are mostly near zero; also, δ is just in an interval from 20° to 60°. In Fig. 5, only for stars fainter than 7 mag in the V band are the differences slightly higher than for the other stars. This means that the ILS values of μδ are in good agreement with DR2, HIPPARCOS, and new HIPPARCOS data. In Figs. 3–5, the mean error bars are from ±0.01 mas yr−1 to ±0.07 mas yr−1 for the plotted mean differences.
The μδ differences (or Δ) on α, δ, and V magnitude (in Figs. 3–5) are small, but we tried to calculate random and systematic errors of pairwise differences of 387 common stars from the catalogs using the following formula (Ivanov & Yatsenko 2003):
where V0 = 6.28 is the mean value of V magnitudes and (B − V) is the color index of a star. The unknowns k1, k2, and k3 are determined using LSM and presented in Table 3; they describe the systematic part of μδ differences. Also, in Table 3 the sum s0 of the random errors for both catalogs is found. Meaning, s0 is the random part of Δ (the unit weight error of the solution of the system). It is calculated as s0 = ![$ \left\{ \frac{1}{387-3} {\sum\nolimits_{n=1}^{387}}[\Delta_{\mathrm{n}}-(k_{1} + k_{2}(V_{n}-V_{0}) + k_{3}(B-V)_{n})]^{2}\right\}^{1/2} $](/articles/aa/full_html/2019/11/aa36541-19/aa36541-19-eq7.gif) where 1≤ n ≤ 387.
where 1≤ n ≤ 387.
Comparison of 387 μδ values from catalogs ILS, HIP, NHIP, and Gaia DR2 to calculate formal and systematic errors.
In the ILS and HIP as well as the ILS and NHIP cases, the value s0 ≈ 1 mas yr−1. However, in the case of ILS and DR2, it is close to 2 mas yr−1. The value 1 mas yr−1 is the level of errors of all HIPPARCOSμδ data. As previously mentioned, Gaia DR2 stars with G < 6 mag have inferior astrometry (Lindegren et al. 2016), and this could be the reason for s0 ≈ 2 mas yr−1 in combination for ILS and DR2. The coefficients k1, k2, and k3 (in Table 3) are small for any combination of catalogs, and their standard errors are higher than the corresponding values. As we can see, the random and systematic errors of Δ are small and mostly close to each other. The values μδ of four catalogs are with high accuracy and no significant relationship between Δ and (V − V0) (also, (B − V)) exists in any pair of catalogs. Using 387 stars here, the values μδ of Gaia DR2, which are independent and based on 22 months of Gaia observations, are in good accordance with ILS data.
There are 18 double and multiple stars in the ILS catalog (see Table 4); some information is from HIPPARCOS and the Sixth Catalog of Orbits of Visual Binary Stars. In three cases, the orbital period P < 100 yr, and the orbital motion of double and multiple stars, can influence proper motions. This depends on P. The short period of HIPPARCOS observations is negligible in comparison with most of the P values. It is not the case of ILS data because the observational period is almost 80 yr. Regarding the Gaia DR2, the published data refer to the photocenter for unresolved binaries. The ILS, HIPPARCOS, and Gaia DR2 observations are related to different positions on the orbital arc of some double or multiple stars. That time difference is more than a half century between the middle of the ILS and HIPPARCOS epochs; there is more than three quarters of a century between ILS and Gaia DR2 epochs. Here, it is of importance that μδ values of ILS are obtained from many decades of observations. Nevertheless, some HIPPARCOS and Gaia DR2 proper motions data are not reliable even with small formal errors. This is due to many unresolved binaries, the ILS and other similar data with long histories could be useful to check even satellite data, such as HIPPARCOS and Gaia data. Here, we detected two cases, H 55060 and H 117622, with big μδ (mas yr−1) differences between ILS and DR2, which are as follows: 16.32 for H 55060, and 14.02 for H 117622, respectively. Subsequently in these cases, data of ILS, HIP, and NHIP are consistent between each other, but not with DR2. We did not find any explanation for this.
Detected 18 double and multiple stars (in ILS catalog) with their HIPPARCOS/WDS number, comment, and period P (day or yr).
To add more information to the ILS catalog, we did a direct comparison between the NHIP and Gaia DR2 positions in declination (using an epoch difference of 24.25 yr) with the ILS μδ. It is μδDR2/NHIP = (δDR2 − δNHIP)/24.25 of a star. Two declinations are δDR2 and δNHIP of this star for the epochs tDR2 = 2015.5 and tNHIP = 1991.25, respectively. The error is 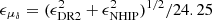 (Eichhorn 1974); ϵDR2 and ϵNHIP are the standard errors of δDR2 and δNHIP, respectively. The differences (μδILS − μδDR2/NHIP), points, and main values over 3h subintervals of α, are presented in Fig. 7. This is a different comparison as opposed to the one presented in Fig. 3, as it compares to the positional reference frames. There are three possible sources for the observed differences: a distortion in the HIPPARCOS positional reference frame, a distortion in the Gaia DR2 positional reference frame, or a distortion in the Gaia DR2 proper motions. Also, any combination of these is possible. Due to a small number of stars and limited accuracy, the ILS cannot provide a definitive answer about this. We detected one case involving substantial differences between μδILS and μδDR2/NHIP values for star H 62145 that is 13.266 mas yr−1. This is probably caused by big DR2 position error, which is ±0.723 mas yr−1 for δ.
(Eichhorn 1974); ϵDR2 and ϵNHIP are the standard errors of δDR2 and δNHIP, respectively. The differences (μδILS − μδDR2/NHIP), points, and main values over 3h subintervals of α, are presented in Fig. 7. This is a different comparison as opposed to the one presented in Fig. 3, as it compares to the positional reference frames. There are three possible sources for the observed differences: a distortion in the HIPPARCOS positional reference frame, a distortion in the Gaia DR2 positional reference frame, or a distortion in the Gaia DR2 proper motions. Also, any combination of these is possible. Due to a small number of stars and limited accuracy, the ILS cannot provide a definitive answer about this. We detected one case involving substantial differences between μδILS and μδDR2/NHIP values for star H 62145 that is 13.266 mas yr−1. This is probably caused by big DR2 position error, which is ±0.723 mas yr−1 for δ.
In Fig. 6, we show the distribution of formal uncertainties on the ILS μδ. Mostly, the formal errors are until ±0.25 mas yr−1. This is in line with NHIP and a suitable HIP value.
 |
Fig. 6. Distribution of standard errors in μδ of ILS catalog. |
 |
Fig. 7. Proper motion differences as function of α, ILS-NHIP/DR2, points (cross), and mean values (circle). |
5. Conclusion
We have presented the original ILS catalog of μδ data of 387 stars, and comparison results of the four catalogs by pairs (Gaia DR2, HIPPARCOS, new HIPPARCOS, and ILS) via μδ of these stars. The ground-based observations of about an 80-year-long interval (during the period from 1899.7–1979.0) were done with a network of seven ILS instruments. These observations provide new information about μδ of mentioned common ILS and HIPPARCOS stars. To obtain μδ of 387 stars, the original method was applied and a combination of ILS, HIPPARCOS, and EOC-2 data was used. The ILS catalog of μδ satisfies the requirements of modern astrometry, and its advantage is the large number of observations together with long observation periods (several tens per star pair per year during several decades). The HIPPARCOS period of observations is less than four years and 22 months in the case of Gaia DR2. The average value of ϵμδ of ILS is between HIPPARCOS, or new HIPPARCOS, and Gaia DR2 ones values; the Gaia DR2 is the best catalog. After comparing the four catalogs in pairs, good consistency between these catalogs was found with no significant discrepancies. The analysis of random and systematic errors via the (Ivanov & Yatsenko 2003) formula shows no significant relationship between the differences of μδ and V magnitudes, nor for the color index. Using LSM, a small sinusoidal curve with amplitude A = 0.7 ± 0.5 mas yr−1 was calculated for ILS and DR2 differences as a function of α.
We determined μδ ILS values for 387 stars by calculating corrections of HIPPARCOS suitable values. As the input, the ILS latitude data (points with epochs lasting about 80 yr ILS interval) and the HIPPARCOS point (δ for the epoch 1991.25) were used with suitable weights. Thus meaning, the ILS μδ solution is directly linked to the HIPPARCOS positions and proper motions system, but the ILS is independent of the NHIP. Therefore, there is similar behavior for the HIPPARCOS and ILS μδ values. Differences between ILS and DR2 are similar to differences between NHIP and DR2.
The systematic errors of μδ could be larger for double and multiple stars because of the influence of the orbital motion on proper motions. That effect of the orbital motion and proper motions are difficult to separate from each other; especially using short periods of satellite missions, such as HIPPARCOS and Gaia. However, ground-based data, such as ILS data, are of importance. Here, part of the random and systematic errors could be in line with orbital motions of double and multiple stars, and astrometric binaries could be a reason for some discrepancies, which are still unrecognized, between the data from the catalogs. It is necessary to continue investigating astrometric binaries. In the ILS catalog, we found 18 double and multiple stars (using HIPPARCOS and WDS data), but there could be more of them. With the ILS data, we checked over the other three catalogs, and these catalogs are consistent between each other. We hope that these investigations provide more information about the Gaia DR2 data. The presented results are in line with the activity of the IAU Working Group on Astrometry by Small Ground-Based Telescopes. The ILS catalog (see Table 5) is available at the CDS.
ILS catalog of μδ for 387 stars.
Acknowledgments
We thank the referee Dr. van Leeuwen for the very constructive comments, which helped substantially improve the manuscript. This research was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia (Project No. 176011 “Dynamics and kinematics of celestial bodies and systems”). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC; https://www.cosmos.esa.int/web/gaia/dpac/consortium).
References
- Damljanović, G. 2005, Serb. Astron. J., 170, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Damljanović, G. 2007, PhD Thesis, University of Belgrade, Serbia [Google Scholar]
- Damljanović, G., & Pejović, N. 2006, Serb. Astron. J., 173, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Damljanović, G., Pejović, N., & Jovanović, B. 2006, Serb. Astron. J., 172, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Eichhorn, H. 1974, Astronomy of Stars Positions (New York: Frederick Ungar Publishing Co.) [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 (Noordwijk: ESA Publications Division) [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016a, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A., et al.) 2016b, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanov, G., & Yatsenko, A. 2003, Kinematika i fizika nebesnykh tel, 19, 477 [NASA ADS] [Google Scholar]
- Kovalevsky, J., Lindegren, L., Perryman, M. A. C., et al. 1997, A&A, 323, 620 [NASA ADS] [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prusti, T. 2012, Astron. Nachr., 333, 453 [NASA ADS] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data (Dordrecht: Springer) [CrossRef] [Google Scholar]
- Vondrák, J. 2004, Serb. Astron. J., 168, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vondrák, J., & Ron, C. 2003, in Journées 2002 – Systèmes de Référence Spatio-Temporels, eds. N. Capitaine, & M. Stavinschi, 49 [Google Scholar]
- Vondrák, J., Pešek, I., Ron, C., & Čepek, A. 1998, Publ. Astron. Inst. Acad. Sci. Czech Republic, 87, 1 [NASA ADS] [Google Scholar]
- Yumi, S., & Yokoyama, K. 1980, Results of the International Latitude Service in a Homogeneous System 1899.9-1979.0 Central bureau IPMS, Mizusawa [Google Scholar]
All Tables
ILS stations, their geographic coordinates (longitude λW and mean latitude φ), and observed intervals.
Comparison of 387 μδ values from catalogs ILS, HIP, NHIP, and Gaia DR2 to calculate formal and systematic errors.
Detected 18 double and multiple stars (in ILS catalog) with their HIPPARCOS/WDS number, comment, and period P (day or yr).
All Figures
 |
Fig. 1. Distribution of 387 stars on celestial sphere. |
| In the text | |
 |
Fig. 2. Distribution of magnitudes of 387 stars. |
| In the text | |
 |
Fig. 3. Mean proper motion differences as function of α: ILS-HIP (cross), ILS-NHIP (open rectangle), ILS-DR2 (open circle). |
| In the text | |
 |
Fig. 4. Mean proper motion differences as function of δ; designations are the same as in Fig. 3. |
| In the text | |
 |
Fig. 5. Mean proper motion differences as function of magnitude; designations are the same as in Fig. 3. |
| In the text | |
 |
Fig. 6. Distribution of standard errors in μδ of ILS catalog. |
| In the text | |
 |
Fig. 7. Proper motion differences as function of α, ILS-NHIP/DR2, points (cross), and mean values (circle). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.