EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 631 (November 2019) A&A, 631 (2019) A112 Full HTML
Free Access
Issue
A&A
Volume 631, November 2019
Article Number A112
Number of page(s) 10
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201936407
Published online 01 November 2019

© ESO 2019

1 Introduction

Several long-period comets are known to be the parent bodies of meteoroid streams. The corresponding meteor showers are detected in the Earth’s atmosphere. The aphelion distance may exceed 100 au. The examples of such comets are C/1861 G1 (Thatcher), the parent body of April Lyrids with the aphelion distance Q = 110.4 au, and the comets that we recently studied: i.e., C/1964 N1 (Ikeya), the parent of July ξ-Arietids with Q = 106.2 au (Neslušan & Hajduková 2018a,b); and C/1975 T2 (Suzuki–Saigusa–Mori), the parent of λ-Ursae Majorids with Q = 116.0 au (Hajduková & Neslušan 2019). The orbits of the meteoroids from these comets are influenced by the objects residing beyond the orbit of Neptune. Thus, these can provide us with information about the trans-Neptunian region. This is a benefit of studying the streams of the comets with a long aphelion distance.

In this paper, we aim to increase the list of the studied comets with a large aphelion distance. We model and study a dynamical evolution of the meteoroid stream assumed to originate in the surface of the nucleus of long-period comet C/1963 A1 (Ikeya). Its aphelion distance equals 190.3 au. Comet C/1963 A1 was discovered on January 2, 1963 by Japanese observer K. Ikeya and lastly seen on October 12, 1963. The comet was closest to the Earth (0.3268 au) on February15, 1963. Seventy-six positions for this comet measured during the entire period of visibility were used for the orbit calculation by Marsden (Kronk 1999), who determined the perihelion date for this comet of March 21.47 and the orbital period equal to about 932 yr.

The search for new parent bodies of known meteor showers, or predictions of new meteor showers from known parent body, has been performed by many authors. The relationship between meteoroid streams and comets has been studied, through stream modeling, as early as the 1980s by Fox et al. (1983), and more recently, for example, by Hajdukova et al. (2015), Ishiguro et al. (2015), Kornoš et al. (2015), Rudawska et al. (2016), Abedin et al. (2015, 2017, 2018), Babadzhanov et al. (2017), Jenniskens et al. (2017), and Šegon et al. (2017). The association of streams with asteroids have been studied, for example, by Porubčan et al. (2004), Jopek & Williams (2013, 2015), Babadzhanov et al. (2015a,b), Jopek (2015), Rudawska & Vaubaillon (2015), Olech et al. (2016), Wiegert et al. (2017), Dumitru et al. (2018), Sergienko et al. (2018a,b), Ye (2018), Guennoun et al. (2019), and Ryabova et al. (2019). Some authors have attempted to work out or improve a prediction method for a particular shower, often on the basis of known parent body (Koten & Vaubaillon 2015; Ryabova 2016; Sugar et al. 2017; Vaubaillon 2017; Ryabova & Rendtel 2018a,b). All this effort is highly desirable in the current era when a number of new showers and a number of new members of known showers are reported every year (e.g., Jones 2018; Jenniskens et al. 2018; Koukal 2018; Molau et al. 2018c,a,b; Shiba et al. 2018; Toth et al. 2018; Vida et al. 2018b,a; Wisniewski et al. 2018, if we consider only the last year).

We use the term “stream” to refer to the whole structure of meteoroids released from the parent body. The stream often consists of several “filaments”, i.e., the groups of meteoroids orbiting the Sun in several common corridors. If the particles of a filament hit the Earth, they can cause a meteor “shower” corresponding to the filament.

2 Knownorbit of comet C/1963 A1

In our study, we consider the orbit of comet C/1963 A1 with the orbital elements published in the Jet Propulsion Laboratory small-body browser (Giorgini et al. 1996)1. This orbit, referring to epoch 1963 April 1.0 (JDT = 2 438 120.5), has the following elements: q = 0.632139 au, e = 0.993377, a = 95.4460214 au, ω = 336.3018°, Ω = 53.2187°, i = 160.6487°, and T = 2 438 109.9748 (1963 March 21.4748). The uncertainty of the orbit determination is unknown. Hereinafter, this orbit is referred to as the nominal orbit. The orbital period of the comet in the nominal orbit is 932 yr and its aphelion is situated in the distance of 190 au from the Sun. The comet passed its aphelion last time on August 1553 in the heliocentric distance of 175 au (aphelion of gravitationally perturbed orbit).

The variation of the orbital elements of C/1963 A1 during the last 100 kyr is shown in Fig. 1. We integrated the orbit of the comet using the RA15 integrator (Everhart 1985), which is the option of the MERCURY software package (Chambers 1999; Chambers & Murison 2000). During the followed period, the perihelion distance (Fig. 1a) frequently varies from ~ 0.5 to ~ 0.7 au. The variations of the perihelion distance and eccentricity are reflected in a large-amplitude variation of semimajor axis (Fig. 1b). This orbital element acquires values from ~ 73 to ~ 167 au during the followed period. The values of argument of perihelion (Fig. 1d) and longitude of ascending node (Fig. 1e) steadily increase.

The positions of orbital nodes in the followed period of 100 kyr are shown in Fig. 2. The ascending node (red dots in Fig. 2) was permanently situated at a vicinity of the orbit of Venus (black circle in Fig. 2) and sometimes approached the orbit of Mercury (green circle). Since the absoluteinclination of orbit of the comet to the ecliptic is low, the meteoroids can also collide with Earth, although no node is situated at its orbit. The descending node (blue dots) changed its position from the region in the interior of the orbit of Jupiter (brown arc) to the region beyond the orbit of Saturn (outer cyan arc). No collision with Earth at this node is therefore possible.

The minimum distance between the orbits of the comet and Earth was also investigated. The behavior of this distance is shown in Fig. 3 for the period of the last 100 kyr. The post-perihelion arc has been situated closer to Earth’s orbit than the pre-perihelion arc. However, the minimum distance has not decreased below ~ 0.15 au.

3 Stream modeling

3.1 Recalling the theory

We used the method of the stream modeling developed by Neslušan (1999) and later slightly modified by Tomko & Neslušan (2012). In the following, we only briefly recall its main steps. At first, the orbit of the parent body is integrated in time backward to the moment of the perihelion passage of the body, which happened closest to an arbitrarily chosen time tev. We then model a stream. In reality, the formation process of meteoroid stream is a stochastic process. For the purposes of our investigation, we filled the appropriate orbital phase with test particles representing the meteoroids. Specifically, we assumed a cloud of 10 000 test particles to be released from the parent body in the moment of the perihelion passage. All these particles, as well as the parent body itself, are then integrated in time forward, up to the present. A more detailed description of this modeling can be found in papers, for example, by Jakubík & Neslušan (2015) or Tomko & Neslušan (2019).

At the end of the integration, we select the particles that move in the orbits that approach the Earth’s orbit within 0.05 au. Their characteristics correspond to those of the expected shower and, thus, they enable us to predict the mean characteristics of the expected shower.

In our modeling, the numerical integration was performed via the integrator RA15 (Everhart 1985) within the software package MERCURY2 (Chambers 1999; Chambers & Murison 2000). We took the gravitational perturbations of eight planets, Mercury to Neptune, into account.

In the models, the dynamics of the particles is assumed to be influenced by the Poynting-Robertson (P-R, hereinafter) effect. The term P-R effect is used to refer to the action of direct solar radial electromagnetic radiation pressure and the velocity-dependent effects on the meteoroid particles. Specifically, we used the formulas published by Klačka (2014).

The strength of the P-R effect is given by parameter β, which is the ratio of the accelerations due to both the P-R effect and the gravity by the Sun. This parameter depends on the properties of particles, such as the size (geometrical cross section), density, light scattering efficiency (on albedo and light absorption ability), and mass. In the case of meteoroids, these properties are rather uncertain. Therefore, we regard β as a free parameter and search, as far as possible, for its value to achieve the best agreement between the predicted and observed characteristics of found filaments of the investigated stream related to the considered parent body.

We created a series of models for various combinations of specific values of evolutionary time tev and parameter β. In reality, parameter β ranges in a wider interval of values since the stream consists of the particles of various sizes and densities. In addition, the particles are released at various times, therefore their evolutionary time must be different and can also acquire the values from a wider interval. Hence, the particular model we created does not represent a whole stream. The model of a whole stream is a composition of partial models, which give a good prediction of the corresponding real showers.

In greater detail, we created the models for all combinations of values tev = 10, 20, 40, 60, and 80 kyr and β = 10−11 (this value practically implies no P-R effect), 0.0001, 0.001, 0.003, and 0.005. For β = 0.005, no shower was predicted. Therefore, we also created models for β = 0.004 and all considered values of tev. No shower was predicted in two of these additional models.

thumbnail Fig. 1

Behavior of perihelion distance (panel a), semimajor axis (panel b), eccentricity (panel c), argument of perihelion (panel d), longitude of ascending node (panel e), and inclination to the ecliptic (panel f) of the initially nominal orbit of comet C/1963 A1 (Ikeya). The evolution is reconstructed backward for 100 000 yr. A nongravitational force is ignored.
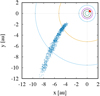thumbnail Fig. 2

Positions of ascending (red points) and descending (blue points) nodes of the orbit of comet C/1963 A1 during the last 100 000 yr. The green, black, violet, cyan, brown, and cyan circles/arcs indicate the orbits of Mercury, Venus, Earth, Mars, Jupiter, and Saturn, respectively.
thumbnail Fig. 3

Evolution of the minimum distance between the orbital arcs of comet C/1963 A1 and Earth’s orbit from 100 000 yr ago to the present. The minimum distance of post-perihelion (pre-perihelion) arc is shown by the red (blue) curve.

3.2 Results

It appears that the stream of C/1963 A1 splits up to five filaments that cross the orbit of our planet. Hence, five showers are predicted. The mean geophysical characteristics of these showers are given in Table 1 and the orbital elements of their mean orbits in Table 2. The distributions of the radiants of theoretical particles in the individual filaments and the radiants of corresponding real showers are shown in Fig. 4. The overall positions of the radiant areas on sky can be seen in the Hammer projection of the celestial sphere in Fig. 5.

In panels b and d of Fig. 4 and panel b of Fig. 5, the positions of radiants are shown in the ecliptical coordinate system centered on the apex of the motion of Earth around the Sun. This coordinate system differs from the common ecliptical coordinate system by its longitude, λ2, which is related to the longitude of the common ecliptical coordinates, λ, as λ2 = λ − (λ⊙ + 270°); λ⊙ is the solar longitude of meteor. The latitude of the apex-centered system is the same as that in the common system.

We note that some authors prefer to use the Sun-centered ecliptical coordinate system with the longitude λ′ = λ − λ⊙. We see that there is the constant difference of 270° between λ2 and λ′; therefore the relative positions of radiants and sizes of the radiant areas are exactly the same in both Sun-centered and apex-centered coordinate systems. We prefer to use the apex-centered system since the symmetry of radiant areas can better be seen in this frame.

In Figs. 4b,d and 5b, we see a grouping of the radiants around the apex of Earth’s motion around the Sun. This grouping is obviously a consequence of low-inclined, but retrograde orbits of meteoroids and suitable geometry leading to the collision of meteoroids with our planet just when their velocity vector is almost opposite from the velocity vector of Earth. As a consequence of this circumstance, the geocentric velocity of meteoroids is close to the maximum collisional velocity of two solar system objects (~ 72 km s−1). We note that the grouping of the radiants around Earth’s apex and high geocentric velocity were also observed for the filaments and corresponding showers of long-period comet C/1964 N1 (Ikeya) (Neslušan & Hajduková 2018a,b). The showers of C/1964 N1 are active in other periods of year than the showers of C/1963 A1.

In the case of the showers of comet C/1963 A1, there is also a symmetry of the radiant areas of filaments (of corresponding showers) with respect to the Earth apex: the area of filament F1 is symmetrical with that of filament F4 (Figs. 4b,d). An analogous symmetry between the areas of filaments F2 and F3 is not as clear. Nevertheless, we can state a symmetry in the sense that the area of F2 is situated in the upper left quarter of the celestial sphere (when the apex-centered coordinate frame is considered) and area of F3 in the lower right quarter.

Comets C/1964 N1 and C/1963 A1, as the parent bodies, are also similar in that in both cases, after a long time (> 50 kyr), the fifth filament of their streams emerged. This filament has the radiant area situated below the ecliptic and between the radiant areas of filaments F3 and F4. We can speculate that filament F5 occurs, in both comets, owing to a secular resonance. Proving this hypothesis, however, exceeds the scope of this work.

Table 1

Geophysical parameters of the parts of predicted showers.

Table 2

Mean orbital elements of the parts of predicted showers.

thumbnail Fig. 4

Positions of predicted radiants in the constructed models (panels a and b) and radiants of corresponding real meteors (panels c and d). The positions are shown in the equatorial (panels a and c) and the Earth apex centered ecliptical coordinate (panels b and d) frames. Panels a and c: the sinusoid-like curve is the ecliptic. The positions of the radiants of various filaments and showers are distinguished by various symbols and colors. Panels c and d: positions of meteor radiants separated from the C, S, and E catalogs are also distinguished by black, blue, and yellow, respectively.
thumbnail Fig. 5

Overall positions on sky of predicted radiants in the constructed models and radiants of corresponding real meteors. The positions are shown in the Hammer projection of the celestial sphere. Panel a: equatorial coordinate system is used. The sinusoid-like curve is the ecliptic. Panel b: Earth apex centered ecliptical coordinate frame is used. The positions of the radiants of theoretical particles are shown with black full circles. The position of the radiants of real meteors separated from the C, S, and E catalogs are shown with blue asterisks, red crosses, and green empty squares, respectively.

4 Identification of the predicted showers with real showers

The mean dynamical characteristics of the predicted shower were used to search for the corresponding real shower. We searched for the real shower in the International Astronomical Union Meteor Data Center (IAU MDC) list of all showers and in the databases ofmeteor orbits.

4.1 Identification with the showers in the IAU MDC list

The real counterparts of the predicted showers can be expected to be recorded in the IAU MDC list of all showers3 (Jopek & Kaňuchová 2014). Since only the mean characteristics of the showers are available in the list, we identified our predictions, by the individual models, to the shower in the list using the Southworth-Hawkins discriminant, DSH (Southworth & Hawkins 1963). We calculated the value of DSH for every pair of orbits, where the first component of the pair was the mean orbit of predicted shower and the second component was the orbit in the list.

In our experience, the dispersion of the meteors in the major showers, characterized by the limiting value of the DSH, ranges from 0.07 to 0.20 (see, e.g., Neslušan et al. 1995). The extraordinary numerous Perseids had Dlim = 0.32 when separated from the photographic IAU MDC database. Hence, we accepted the upper limit for the identification of predicted shower to its real counterpart equal ~ 0.20. This value is, of course, not strict.

We found an excellent agreement between the predicted mean orbit of filament F4 in the model for (tev, β) = (80 kyr, 0.001) and π-Hydrids #101, as determined by (Jenniskens 2006). In this case, DSH = 0.083. The identification of the F4 with this shower was also successful for several other models for tev = 60 and 80 kyr; the value of DSH varied up to 0.115. π-Hydrids is a minor shower, which was reported for the first time in (Jenniskens 2006). This shower was confirmed by Molau & Rendtel (2009) and Molau et al. (2017).

In the IAU MDC list, the π-Hydrid shower is given in three variants. Aside from the above-mentioned mean orbits by Jenniskens (2006) and Molau & Rendtel (2009), who provided only the geophysical parameters (orbital elements are missing), the mean parameters of this shower were also determined by Jenniskens et al. (2018). This last variant is largely different from the two previous variants and does not practically match any predicted shower; we give its mean parameters in Tables 3 and 4 in the parentheses to demonstrate the large differences. Most likely, this variant of π-Hydrids is contaminated by meteors of other showers.

Our prediction of filament F5 in the model for (tev, β) = (80 kyr, 10−11) could be identified with δ-Corvids #729, as derived by Jenniskens et al. (2016c). These authors already stated that the parent body is probably a long-period comet. The difference between both mean orbits predicted and given by Jenniskens et al. was characterized by DSH = 0.169. However, this was the single successful identification of filament F5. For the other models the value of DSH was larger than 0.4. The same is valid for all predicted models and the variant of the shower in the IAU MDC list presented by Jenniskens et al. (2018).

Finally,we discuss a vague similarity between filament F3 and November α-Sextantids #483. When calculating DSH between each of 1185 variants of 792 showers in the IAU MDC list of all showers and each of the predicted variants of filament F3, the value of DSH is lower than 0.4 only for November α-Sextantids. For a few predicted variants, DSH = 0.310 or DSH is higher but also lower than 0.4 for α-Sextantids #439. Comparing the mean characteristics of both showers #483 and #439, it seems that #439 is a substructure of #483 detected at the end of activity of the latter. It is, thus, a duplicate naming of the same shower and should likely be deleted from the list. This is why we suspect that there could be a relationship between the filament and shower #483, even though this shower has a large DSH, which significantly exceeds the adopted upper limit of ~ 0.20.

Specifically, in the IAU MDC list, the real shower is given in two variants with the mean characteristics derived by Rudawska & Jenniskens (2014), who found the shower in both Cameras for Allsky Meteor Surveillance (CAMS) and SonotaCo databases. The value of DSH between the mean orbit of the shower and that in every model for tev = 10 kyr listed in Tables 1 and 2 equals 0.279. If we consider the models for tev = 20 kyr (40, 60, and 80 kyr), then DSH = 0.285 or 0.283 in a single case (0.292 to 0.295, 0.317 to 0.329, and 0.313 to 0.336). The value of DSH for any predicted mean orbit of filament F3 and that of the November α-Sextantids, as determined by Jenniskens et al. (2016a), varies from 0.303 to 0.356. Such the high values cannot be an evidence of relationship between the shower and its parent body. However, we newly separated the variants of the November α-Sextantids from three video databases that are much more similar to filament F3 (see Sect. 4.2); therefore the relationship still seems to be real.

Filament F3 was predicted to be the most numerous of all five predicted filaments (see the second last column, labeled as n, in Table 1). The fact that a shower that would match the prediction well is missing in the observational data can be caused by worse observational conditions. The angular distance, ⟨γ⟩, of mean radiant of filament F4 from the Sun (see the third last column in Table 1) is ⟨γ⟩ ≥ 101° (and of filament F5 ⟨γ⟩ ≥ 89°), therefore a prevailing part of π-Hydrids (and δ-Corvids) can be seen on the January night sky; the angular distance of mean radiant of filament F3 from the Sun is ⟨γ⟩ ≤ 80°. Therefore, a relatively large portion of meteors corresponding to F3 can be seen on the daily November sky.

The predicted filaments F1 and F2 were not identified with any IAU MDC shower. The values of DSH were larger than 0.377 for F1 and larger than 0.4 for F2. A shower corresponding to F1, if it exists, is predicted to be an order of magnitude less numerous than the showers corresponding to filaments F3 and F4. The observational conditions to observe F1 meteors are similarly bad as those of F3. In the case of F1, ⟨γ⟩ = 74° − 77° (Table 1, the second last column).

On the contrary, the best conditions in the discussed context are those at observations of meteors related to F2, where ⟨γ⟩ ~ 109° in the first half of February. However, the shower corresponding to filament F2 is predicted to be low in numbers. This shower is “indicated” rather than “predicted” because it was predicted only in two models, i.e., for (tev,  β) = (60 kyr, 10−4) and (tev,  β) = (80 kyr, 10−4), and only with the help of four and five particles, respectively. This is obviously the reason of why no observational counterpart of F2 was found. We note that none of the identified showers at filaments F3–F5 were classified as established.

4.2 Separation of real showers from databases

We searched for a corresponding shower in the following meteor databases: (1) the IAU MDC photographic database, version-2013 (Porubčan et al. 2011; Neslušan et al. 2014); (2) the IAU MDC CAMS video database (Gural 2011; Jenniskens et al. 2011, 2016a,b,c; Jenniskens & Nénon 2016); (3) the 2007−2015 SonotaCo video (SonotaCo 2009, 2016); the European viDeo MeteOr Network Database (EDMOND) video (Kornoš et al. 2014a,b); and (5) the radio-meteor database (Hawkins 1963; Sekanina & Southworth 1975; Lindblad, priv. comm.). These databases contain 4873, 110 521, 208 826, 145 830, and 62 907 records on meteor orbits and geophysical data, respectively. We briefly refer to these databases with the capital letters F, C, S, E, and R, respectively.

To select the meteors of searched shower from the given database, we used the “break-point method” (Neslušan et al. 1995, 2013). We briefly describe the main steps of this method, which is based on an analysis of the dependence of the number of selected shower meteors on the limiting value of the Southworth-Hawkins (Southworth & Hawkins 1963) DSH discriminant, Dlim.

In the first step, we calculate the values DSH between the mean orbit of predicted shower and every meteor in the database considered. If DSH is smaller than a chosen limiting value, Dlim, then the meteor is regarded as the member of the shower. Then, we calculate the mean orbit of the separated group of shower meteors and, in the second step, calculate DSH between this new mean orbit and every meteor in the database. And, considering the meteors separated in this step, we again calculate their mean orbit, which is again the reference orbit for the new selection, etc. We terminate this iteration procedure, when the difference between two successive mean orbits is negligible. In the final separation, we obtain N shower meteors.

The above sketched iteration procedure is performed for a series of limiting values Dlim, usually 0.01, 0.02, 0.03,..., 0.50. Having the corresponding numbers of separated meteors, we can construct the dependence N = N(Dlim). If the corresponding real shower was recorded in the database, the dependence exhibits a convex behavior followed by a constant or only moderately increasing behavior, known as a plateau. The value of Dlim corresponding to the beginning of the plateau is the most appropriate to separate the densest core of the shower from the database. In other words, the actual members of the shower in our search are the meteors separated within the iteration procedure using this critical Dlim.

The iteration procedure might sometimes significantly change the mean orbit of the separated shower from its prediction. After the separation, it is therefore necessary to evaluate a measure of relationship between the theoretically predicted and separated real shower. We did this evaluation suggesting and performing the following empirical procedure. We calculated the mean value of the Southworth-Hawkins D-discriminant, ⟨Dmj⟩, between the mean orbit of real shower and each orbit of its members and its statistical uncertainty, σD. We suppose that, when the diversity is evaluated with the help of the DSH criterion, the orbit of any member of the predicted shower should not differ from the orbit of at least one meteor of real shower more than about ⟨Dmj⟩ + σD. We added σD, since some meteors of the shower itself at the border of its orbital phase space would not differ within ⟨Dmj⟩ alone.

Subsequently, we calculated DSH between every pair of the orbits of both theoretical particle and meteor of real shower. If DSH ≤ (⟨Dmj⟩ + σD) at least once, then the particle of predicted shower is regarded as matching the real shower. The values of ⟨Dmj⟩ with their sigmasfor the separated real showers are given in the last column of Table 3.

Let us denote the number of the matching particles as nyes and the number of the other particles as nno, where the sum nyes + nno equals the total number of the particles of predicted shower. The measure of the agreement of corresponding predicted and real showers is then defined as 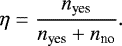η= n yes n yes + n no . \begin{equation*}\eta = \frac{n_{\textrm{yes}}}{n_{\textrm{yes}} + n_{\textrm{no}}}. \end{equation*}(1)

The mean characteristics of the successfully separated real showers, corresponding with the filaments F1, F3, F4, and F5, are given in Tables 3 and 4 together with the measure of the best agreement, ηb. We speak about the best agreement since the agreement is different for the real shower and shower predicted in various models.

As seen in Tables 3 and 4, the real counterpart of predicted filament F1 was separated only from S catalog. The shower related to F3 was separated from C, S, and E catalogs; that related to F4 from S and E catalogs; and F5-related shower only from S catalog.

The minimum and often also maximum values of DSH between the mean predicted and separated-shower orbits (see the second column in Table 3) are lower than such values between the mean predicted and IAU MDC shower orbits. Likely, the quality of the separation of a shower from the database can be better if the shower is predicted and, hence, its approximate mean orbit (entering the iteration procedure as initial orbit)is known.

When we compare the mean parameters of the separated showers with those of corresponding showers in the IAU MDC list (Tables 3 and 4), both groups are consistent and, hence, the showers separated by us can be regarded as further variants of π-Hydrids #101 and δ-Corvids #729. It also seems that our separations from C, S, and E catalogs of the shower corresponding to filament F3 can be regarded as variants of November α-Sextantids #483. Especially in the case of separations from S and C catalogs, the agreement between the prediction and these variants of a real shower is ordinarily good enough to identify the predicted filament F3 with November α-Sextantids.

It is well-known that the SonotaCo team often performs the observations of meteors during daytime as well. It is therefore not surprising that a shower, corresponding to filament F1 with the predicted daytime prevailingly activity, was separated just from the SonotaCo catalog. The separated shower is again in good agreement with the corresponding prediction. No relevant shower was found in the IAU MDC list, therefore it is a new shower. Its mean radiant is situated in the constellation of Leo, close to stars ρ Leonis and ϑ Leonis. Since the shower named ρ-Leonids already exists and it is a different shower, we suggest the new shower, originating in comet C/1963 A1 and corresponding to the predicted filament F1, be named ϑ-Leonids.

Table 3

Mean geophysical parameters of the real meteor showers related to the predicted filaments of comet C/1963 A1.

Table 4

Mean orbital elements of the real meteor showers related to the stream of comet C/1963 A1.

5 Summary

We modeled the theoretical stream originating from the long-period comet C/1963 A1 (Ikeya). It appears that the stream has a filamentary structure; we determined five filaments intersecting the orbit of the Earth.

Since the comet moves around the Sun in a low-inclined, but retrograde orbit, its geocentric velocity and the geocentric velocity of its meteoroid stream in a trajectory near the Earth’s orbit is high, i.e., ~ 70 km s−1. Consequently, the radiant areas of all filaments are situated near the apex of the Earth’s heliocentric motion. The radiant areas of the filament that we refer to as F1 is symmetrical to that of the filament referred to as F4 with respect to the apex of the Earth’s motion around the Sun. A certain symmetry of the radiant areas of filaments F2 and F3 can also be stated.

Two mostly night-time filaments, F4 and F5, were identified with the real showers in the IAU MDC list of showers and also separated from one or two considered video catalogs. Specifically, the filament F4 corresponds well to π-Hydrids #101 and F5 corresponds to δ-Corvids #729. We successfully separated π-Hydrids from S and E catalogs and δ-Corvids from the S catalog.

The characteristics of filament F3 are vaguely similar to those of the shower November α-Sextantids #483 in the IAU MDC list. The corresponding real shower was also separated from the C, S, and E catalogs. Interestingly, the separated variants of the shower match the predicted shower better than the shower in the IAU MDC list. We guess that at least a rough knowledge of the mean orbit of shower, which is going to be separated from a data set, results in a more perfect separation. This circumstance will deserve special attention in future research.

The real counterpart of filament F1 was not found in the IAU MDC list, but a shower that agreed well was separated from the S catalog. We named this new shower, originating from C/1963 A1, ϑ-Leonids.

Filament F2 was predicted to be low numerous. Hence, it is not surprising that no similar shower can be found in the IAU MDC list of all shower or separated from any considered catalog.

None of the identified real showers are classified as established.

In conclusion, comet C/1963 A1 is the parent body of several, probably four, meteor showers observable in the Earth’s atmosphere.

Acknowledgements

This article was supported by the realization of the Project ITMS No. 26220120029, based on the supporting operational Research and Development Program financed from the European Regional Development Fund (ERDF). The essential calculations were performed using the computing resources provided by the project SIVVP, ITMS 26230120002, supported by the Research and Development Operational Program funded by the ERDF. In addition, the work was supported, in part, by the VEGA – the Slovak Grant Agency for Science, grant No. 2/0037/18, and by the Slovak Research and Development Agency under the contract No. APVV-16-0148.

References

  1. Abedin, A., Spurný, P., Wiegert, P., et al. 2015, Icarus, 261, 100 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abedin, A., Wiegert, P., Pokorný, P., & Brown, P. 2017, Icarus, 281, 417 [NASA ADS] [CrossRef] [Google Scholar]
  3. Abedin, A., Wiegert, P., Janches, D., et al. 2018, Icarus, 300, 360 [NASA ADS] [CrossRef] [Google Scholar]
  4. Babadzhanov, P. B., Kokhirova, G. I., & Obrubov, Y. V. 2015a, Sol. Syst. Res., 49, 165 [NASA ADS] [CrossRef] [Google Scholar]
  5. Babadzhanov, P. B., Kokhirova, G. I., & Khamroev, U. K. 2015b, Adv. Space Res., 55, 1784 [NASA ADS] [CrossRef] [Google Scholar]
  6. Babadzhanov, P. B., Kokhirova, G. I., Williams, I. P., & Obrubov, Y. V. 2017, A&A, 598, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  8. Chambers, J. E., & Murison, M. A. 2000, AJ, 119, 425 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dumitru, B. A., Birlan, M., & Nedelcu, D. A. 2018, RoAJ, 28, 167 [NASA ADS] [Google Scholar]
  10. Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proc. IAU Colloq. 83, held in Rome, Italy, June 11–15, 1984, eds. A. Carusi, & G. B. Valsecchi (Dordrecht: Reidel, Astrophysics and Space Science Library), 115, 185 [NASA ADS] [Google Scholar]
  11. Fox, K., Williams, I. P., & Hughes, D. W. 1983, MNRAS, 205, 1155 [NASA ADS] [Google Scholar]
  12. Giorgini, J. D., Yeomans, D. K., Chamberlin, A. B., et al. 1996, BAAS, 28, 1158 [NASA ADS] [Google Scholar]
  13. Guennoun, M., Vaubaillon, J., Čapek, D., Koten, P., & Benkhaldoun, Z. 2019, A&A, 622, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Gural, P. S. 2011, in Proc. International Meteor Conference, 29th IMC, Armagh, Northern Ireland, 2010, 28 [Google Scholar]
  15. Hajduková, M., & Neslušan, L. 2019, A&A, 627, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Hajdukova, M., Rudawska, R., Kornos, L., & Toth, J. 2015, Planet. Space Sci., 118, 28 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hawkins, G. S. 1963, Smithson. Contrib. Astrophys., 7, 53 [NASA ADS] [Google Scholar]
  18. Ishiguro, M., Kuroda, D., Hanayama, H., et al. 2015, ApJ, 798, L34 [NASA ADS] [CrossRef] [Google Scholar]
  19. Jakubík, M., & Neslušan L. 2015, MNRAS, 453, 1186 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jenniskens, P. 2006, Meteor Showers and their Parent Comets (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
  21. Jenniskens, P., & Nénon, Q. 2016, Icarus, 266, 371 [NASA ADS] [CrossRef] [Google Scholar]
  22. Jenniskens, P., Gural, P. S., Dynneson, L., et al. 2011, Icarus, 216, 40 [NASA ADS] [CrossRef] [Google Scholar]
  23. Jenniskens, P., Nénon, Q., Albers, J., et al. 2016a, Icarus, 266, 331 [NASA ADS] [CrossRef] [Google Scholar]
  24. Jenniskens, P., Nénon, Q., Gural, P. S., et al. 2016b, Icarus, 266, 355 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jenniskens, P., Nénon, Q., Gural, P. S., et al. 2016c, Icarus, 266, 384 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jenniskens, P., Lyytinen, E., & Williams, G. V. 2017, CBET, 4403 [Google Scholar]
  27. Jenniskens, P., Baggaley, J., Crumpton, I., et al. 2018, Planet. Space Sci., 154, 21 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jones, P. 2018, Meteor News, 3, 38 [NASA ADS] [Google Scholar]
  29. Jopek, T. J. 2015, Highlights of Astronomy (Cambridge: Cambridge University Press), 16, 474 [NASA ADS] [Google Scholar]
  30. Jopek, T. J., & Kaňuchová, Z. 2014, Meteoroids 2013, 353 [Google Scholar]
  31. Jopek, T. J., & Williams, I. P. 2013, MNRAS, 430, 2377 [NASA ADS] [CrossRef] [Google Scholar]
  32. Jopek, T. J., & Williams, I. P. 2015, Highlights of Astronomy (Cambridge: Cambridge University Press), 16, 143 [NASA ADS] [Google Scholar]
  33. Klačka, J. 2014, MNRAS, 443, 213 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kornoš, L., Koukal, J., Piffl, R., & Tóth, J. 2014a, in Proc. International Meteor Conference, Poznan, Poland, 22 August 2013, ed. M. Gyssens, P. Roggemans, & P. Zoladek, 23 [Google Scholar]
  35. Kornoš, L., Matlovič, P., Rudawska, R., et al. 2014b, Meteoroids 2013, 225 [NASA ADS] [Google Scholar]
  36. Kornoš, L., Tóth, J., Porubčan, V., et al. 2015, Planet. Space Sci., 118, 48 [NASA ADS] [CrossRef] [Google Scholar]
  37. Koten, P., & Vaubaillon, J. 2015, Eur. Planet. Sci. Cong., 10, EPSC2015 [Google Scholar]
  38. Koukal, J. 2018, Meteor News, 3, 1 [NASA ADS] [Google Scholar]
  39. Kronk, G. W. 1999, Cometography: A Catalog of Comets (Cambridge: Cambridge University Press), 1 1799 [NASA ADS] [Google Scholar]
  40. Molau, S., & Rendtel, J. 2009, WGN, J. Int. Meteor Organ., 37, 98 [NASA ADS] [Google Scholar]
  41. Molau, S., Crivello, S., Goncalves, R., et al. 2017, WGN, J. Int. Meteor Org., 45, 82 [NASA ADS] [Google Scholar]
  42. Molau, S., Crivello, S., Goncalves, R., et al. 2018a, WGN, J. Int. Meteor Organ., 46, 166 [NASA ADS] [Google Scholar]
  43. Molau, S., Crivello, S., Goncalves, R., et al. 2018b, WGN, J. Int. Meteor Organ., 46, 205 [NASA ADS] [Google Scholar]
  44. Molau, S., Crivello, S., Goncalves, R., et al. 2018c, WGN, J. Int. Meteor Organ., 46, 142 [NASA ADS] [Google Scholar]
  45. Neslušan, L. 1999, A&A, 351, 752 [Google Scholar]
  46. Neslušan, L., & Hajduková, M. 2018a, A&A, 616, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Neslušan, L., & Hajduková, M. 2018b, Contrib. Astron. Observ. Skalnate Pleso, 48, 554 [NASA ADS] [Google Scholar]
  48. Neslušan, L., Svoreň, J., & Porubčan, V. 1995, Earth Moon Planets, 68, 427 [NASA ADS] [CrossRef] [Google Scholar]
  49. Neslušan, L., Svoreň, J., & Porubčan, V., 2013, Earth Moon Planets, 110, 41 [NASA ADS] [CrossRef] [Google Scholar]
  50. Neslušan, L., Porubčan, V., & Svoreň, J. 2014, Earth Moon Planets, 111, 105 [NASA ADS] [CrossRef] [Google Scholar]
  51. Olech, A., Żoła̧dek, P., Wiśniewski, M., et al. 2016, MNRAS, 461, 674 [NASA ADS] [CrossRef] [Google Scholar]
  52. Porubčan, V., Williams, I. P., & Kornoš, L. 2004, Earth Moon Planets, 95, 697 [NASA ADS] [CrossRef] [Google Scholar]
  53. Porubčan, V., Svoreň, J., Neslušan, L., & Schunová, E. 2011, in Meteoroids: The Smallest Solar System Bodies (Washington, D.C.: NASA), eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, 338 [Google Scholar]
  54. Rudawska, R., & Jenniskens, P. 2014, Meteoroids 2013, 217 [Google Scholar]
  55. Rudawska, R., & Vaubaillon, J. 2015, Planet. Space Sci., 118, 25 [NASA ADS] [CrossRef] [Google Scholar]
  56. Rudawska, R., Vaubaillon, J., Tóth, J., & Raetz, S. 2016, AAS/Division Planet. Sci. Meeting Abstr., 48, 218.01 [NASA ADS] [Google Scholar]
  57. Ryabova, G. O. 2016, MNRAS, 456, 78 [NASA ADS] [CrossRef] [Google Scholar]
  58. Ryabova, G., & Rendtel, J. 2018a, Eur. Planet. Sci. Cong., 12, EPSC2018 [Google Scholar]
  59. Ryabova, G. O., & Rendtel, J. 2018b, MNRAS, 475, L77 [NASA ADS] [CrossRef] [Google Scholar]
  60. Ryabova, G. O., Avdyushev, V. A., & Williams, I. P. 2019, MNRAS, 485, 3378 [NASA ADS] [CrossRef] [Google Scholar]
  61. Sekanina, Z., & Southworth, R. B. 1975, Physical and dynamical studies of meteors. Meteor-fragmentation and stream-distribution studies, Tech. rep [Google Scholar]
  62. Sergienko, M. V., Sokolova, M. G., Andreev, A. O., & Nefedyev, Y. A. 2018a, LPI Contrib., 2067, 6162 [NASA ADS] [Google Scholar]
  63. Sergienko, M. V., Sokolova, M. G., Andreev, A. O., & Nefedyev, Y. A. 2018b, LPI Contributions, 2067, 6165 [NASA ADS] [Google Scholar]
  64. Shiba, Y., Shimoda, C., Maeda, K., et al. 2018, WGN, J. Int. Meteor Organ., 46, 79 [NASA ADS] [Google Scholar]
  65. SonotaCo 2009, WGN, J. Int. Meteor Organ., 37, 55 [Google Scholar]
  66. SonotaCo 2016, WGN, J. Int. Meteor Organ., 44, 42 [NASA ADS] [Google Scholar]
  67. Southworth, R. B., & Hawkins, G. S. 1963, Smithson. Contrib. Astrophys., 7, 261 [Google Scholar]
  68. Sugar, G., Moorhead, A., Brown, P., & Cooke, W. 2017, Meteorit. Planet. Sci., 52, 1048 [NASA ADS] [CrossRef] [Google Scholar]
  69. Tomko, D., & Neslušan, L. 2012, Earth Moon Planets, 108, 123 [NASA ADS] [CrossRef] [Google Scholar]
  70. Tomko, D., & Neslušan, L. 2019, A&A, 623, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Toth, J., Kornos, L., Matlovic, P., et al. 2018, Eur. Planet. Sci. Cong., 12, EPSC2018 [Google Scholar]
  72. Šegon, D., Vaubaillon, J., Gural, P. S., et al. 2017, A&A, 598, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Vaubaillon, J. 2017, Planet. Space Sci., 143, 78 [NASA ADS] [CrossRef] [Google Scholar]
  74. Vida, D., Merlak, A., & Šegon, D. 2018a, Meteor News, 3, 298 [NASA ADS] [Google Scholar]
  75. Vida, D., Merlak, A., & Šegon, D. 2018b, Meteor News, 3, 276 [NASA ADS] [Google Scholar]
  76. Wiegert, P., Clark, D., Campbell-Brown, M., & Brown, P. 2017, CBET, 4415 [Google Scholar]
  77. Wisniewski, M., Zoladek, P., Olech, A., & Jonderko, W. 2018, WGN, J. Int. Meteor Org., 46, 30 [NASA ADS] [Google Scholar]
  78. Ye, Q.-Z. 2018, Planet. Space Sci., 164, 7 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Geophysical parameters of the parts of predicted showers.

In the text
Table 2

Mean orbital elements of the parts of predicted showers.

In the text
Table 3

Mean geophysical parameters of the real meteor showers related to the predicted filaments of comet C/1963 A1.

In the text
Table 4

Mean orbital elements of the real meteor showers related to the stream of comet C/1963 A1.

In the text

All Figures

thumbnail Fig. 1

Behavior of perihelion distance (panel a), semimajor axis (panel b), eccentricity (panel c), argument of perihelion (panel d), longitude of ascending node (panel e), and inclination to the ecliptic (panel f) of the initially nominal orbit of comet C/1963 A1 (Ikeya). The evolution is reconstructed backward for 100 000 yr. A nongravitational force is ignored.
In the text
thumbnail Fig. 2

Positions of ascending (red points) and descending (blue points) nodes of the orbit of comet C/1963 A1 during the last 100 000 yr. The green, black, violet, cyan, brown, and cyan circles/arcs indicate the orbits of Mercury, Venus, Earth, Mars, Jupiter, and Saturn, respectively.
In the text
thumbnail Fig. 3

Evolution of the minimum distance between the orbital arcs of comet C/1963 A1 and Earth’s orbit from 100 000 yr ago to the present. The minimum distance of post-perihelion (pre-perihelion) arc is shown by the red (blue) curve.
In the text
thumbnail Fig. 4

Positions of predicted radiants in the constructed models (panels a and b) and radiants of corresponding real meteors (panels c and d). The positions are shown in the equatorial (panels a and c) and the Earth apex centered ecliptical coordinate (panels b and d) frames. Panels a and c: the sinusoid-like curve is the ecliptic. The positions of the radiants of various filaments and showers are distinguished by various symbols and colors. Panels c and d: positions of meteor radiants separated from the C, S, and E catalogs are also distinguished by black, blue, and yellow, respectively.
In the text
thumbnail Fig. 5

Overall positions on sky of predicted radiants in the constructed models and radiants of corresponding real meteors. The positions are shown in the Hammer projection of the celestial sphere. Panel a: equatorial coordinate system is used. The sinusoid-like curve is the ecliptic. Panel b: Earth apex centered ecliptical coordinate frame is used. The positions of the radiants of theoretical particles are shown with black full circles. The position of the radiants of real meteors separated from the C, S, and E catalogs are shown with blue asterisks, red crosses, and green empty squares, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.