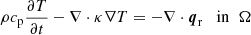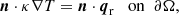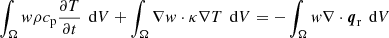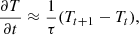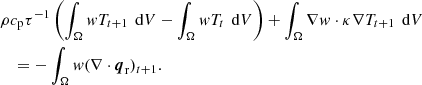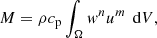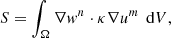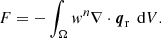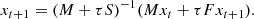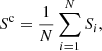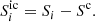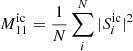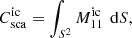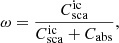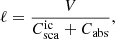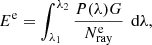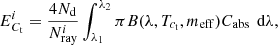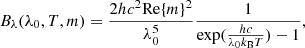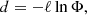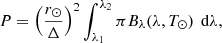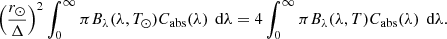| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A164 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201936235 | |
| Published online | 15 November 2019 | |
Scattering, absorption, and thermal emission by large cometary dust particles: Synoptic numerical solution
Max Planck Institute for Solar System Research, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: markkanen@mps.mpg.de
Received:
4
July
2019
Accepted:
25
September
2019
Context. Remote light scattering and thermal infrared observations provide clues about the physical properties of cometary and interplanetary dust particles. Identifying these properties will lead to a better understanding of the formation and evolution of the Solar System.
Aims. We present a numerical solution for the radiative and conductive heat transport in a random particulate medium enclosed by an arbitrarily shaped surface. The method will be applied to study thermal properties of cometary dust particles.
Methods. The recently introduced incoherent Monte Carlo radiative transfer method developed for scattering, absorption, and propagation of electromagnetic waves in dense discrete random media is extended for radiative heat transfer and thermal emission. The solution is coupled with the conductive Fourier transport equation that is solved with the finite-element method.
Results. The proposed method allows the synoptic analysis of light scattering and thermal emission by large cometary dust particles consisting of submicrometer-sized grains. In particular, we show that these particles can sustain significant temperature gradients resulting in the superheating factor phase function observed for the coma of comet 67P/Churyumov–Gerasimenko.
Key words: radiative transfer / methods: numerical / comets: individual: 67P/Churyumov–Gerasimenko
© J. Markkanen and J. Agarwal 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
The physical properties of cosmic dust particles, which include size, shape, porosity, and composition, can be constrained from remote light scattering and thermal emission observations. Observations of scattered solar and thermally emitted light have mostly been interpreted separately using different particle models and numerical methods (Kolokolova et al. 2004; Kimura et al. 2016). This may lead to contradictions in the retrieved particle properties as the interpretation procedure is not self-consistent. Using the same numerical method and the same particle model for scattered solar and thermally emitted light (i.e., synoptic modeling) results in more reliable estimates for the physical properties of dust particles. Such modeling, however, introduces various numerical challenges due to the multiscale nature of the problem. The solution is needed from ultraviolet to thermal infrared. In addition, cometary dust particles contain multiscale structures. They are thought to be large aggregates consisting of submicrometer-sized grains (Güttler et al. 2019).
Numerically exact electromagnetic techniques allow for analyses of scattering and radiative heat transfer properties of small aggregated particles. Combining the standard electromagnetic methods with the statistical fluctuation driven electrodynamic solvers, the radiative heat transfer problem can be solved directly from Maxwell’s equations (Jin et al. 2017). This approach is computationally heavy, and consequently it is not applicable to particles that are much larger than the optical wavelengths or that contain a large number of individual grains. For sufficiently large objects such as asteroids and comet nuclei, a typical approach is to localize absorption and emission sources on the surfaces of the object using a proper boundary condition. Then, by introducing the effective conductive and radiative heat transfer coefficient, heat transport inside the object can be modeled (Huebner et al. 2006; Delbo et al. 2015). This simple model is a valid approximation only for one-dimensional problems, and it introduces significant errors when the object has locally three-dimensional features (on length scales on the order of the mean free path length). Thus, large objects with small details cannot be treated rigorously with the existing computational techniques, due to the large computational time and memory requirement or inadequate approximations.
It is also possible to use the radiative transfer equation (RTE) in combination with the Fourier heat transport equation to deal with heat transfer in participating media (Howell et al. 2010; Modest 2013). A large number of different solution techniques to solve the RTE exist, for example the discrete ordinates (Hardy et al. 2016), finite-volume (Coelho 2014), finite-element methods (Richling et al. 2001), and Monte Carlo ray tracing methods (Howell 1998). Nonetheless, the standard RTE is only applicable to sparse discrete random media where the grains are in each other’s far zone. Recently, a numerical framework for electromagnetic scattering, absorption, and propagation in dense discrete random media was introduced which extends the applicability range of the standard RTE (Muinonen et al. 2018; Markkanen et al. 2018a; Väisänen et al. 2019). Furthermore, Markkanen et al. (2018b) augmented the method with the coherent field contribution to account for surface reflections and refractions allowing the scattering analysis of millimeter-sized cometary dust particles consisting of submicrometer-sized grains.
In this paper we extend the numerical method developed in Markkanen et al. (2018b) for the radiative heat transfer problems. The radiative heat transfer solution is coupled with the transient conductive heat transfer equation, which is solved by the finite-element method (FEM). The presented approach allows us to analyze the scattering and thermal properties of particles consisting of aggregates of small grains over a wide wavelength range. Finally, we show that large cometary dust particles can hold significant temperature gradients, which explains the superheating phase function of the coma of comet 67P/Churyumov–Gerasimenko (67P) measured by the Rosetta/VIRTIS (Visible and Infrared Thermal Imaging Spectrometer) instrument.
2. Methods
In this section, we present our numerical framework for solving radiative and conductive heat transfer in a particulate random medium enclosed by an arbitrarily shaped boundary. We neglect heat convection and assume that external radiation and thermal fluctuations are the only heat sources. We also assume that the radiative heat transport is much faster than the conductive heat transport. Thus, we consider the radiative part as instantaneous time harmonic radiation.
2.1. Energy equation
Let us consider a finite body Ω ∈ ℝ3 characterized by the position r dependent density ρ, specific heat capacity cp, and conductivity κ in free space. Our goal is to solve the time t dependent temperature T under the influence of the external radiation source. The energy balance equation in Ω for the combined conductive and radiative heat transfer reads as
with the boundary condition
where qr denotes the total radiative flux, ∂Ω is the boundary of Ω, and n is the inward pointing normal vector on ∂Ω.
2.2. Finite-element solution for the energy equation
To solve the energy balance Eqs. (1) and (2), we apply the standard finite-element method to discretize the spatial component of the energy equation. Taking the inner product with the testing functions w and integrating by parts, the weak formulation reads as follows:
Find T ∈ H1(Ω) such that
is valid for all w ∈ H1(Ω). Here H1(Ω) denotes the space of square integrable functions whose derivatives are also square integrable. We note that Eq. (3) automatically satisfies the Neumann boundary condition (2).
Next we discretize the time derivative using the finite-difference formula
where the subscript t indicates the time step and τ is its size. Substituting (4) into (3) and using the implicit backward Euler time integration scheme, we obtain
We discretize the domain Ω with linear tetrahedral elements and expand the unknown temperature T into the linear nodal basis functions um as T ≈ ∑mxmum, where xm are the unknown coefficients. Using Galerkin’s method, in which the testing functions and basis functions are identical wm = um, we can write the mass and stiffness matrices as
and the force vector as
Finally, we arrive at the expression for the temperature coefficient vector x given by
The force vector is strongly nonlinear with respect to temperature (F ∼ T4). Hence, estimating τFxt + 1 with τFxt would require using a very small time step τ to reach a converging numerical solution. Therefore, we solve Eq. (9) for xt + 1 by using an iterative method. In the next section we discuss how to compute the force vector F in a densly packed particulate random medium enclosed by an arbitrarily shaped boundary ∂Ω with the Monte Carlo radiative transfer approach.
2.3. Radiative transfer solution
To calculate the absorbed and thermally emitted power (i.e., the force vector F in Eq. (9)), we employ an approximate version of the recently introduced radiative transfer with the reciprocal transactions (R2T2) method for electromagnetic scattering and propagation in dense discrete random media (Muinonen et al. 2018; Markkanen et al. 2018a; Väisänen et al. 2019). R2T2 is based on the Monte Carlo ray tracing of the order-of-scattering interactions in which the fundamental scatterers are volume elements containing a large number of small grains. Incoherent electromagnetic interactions within the volume elements and the order-of-scattering interactions between the volume elements are computed via the exact electromagnetic solver, namely the fast superposition T-matrix method (FaSTMM; Markkanen & Yuffa 2017).
Here we use the far-field approximation to compute the order-of-scattering interactions. Yet, the interactions within the volume elements are computed exactly. We also neglect the reciprocal scattering diagrams (i.e., those responsible for the coherent backscattering effect). This allows us to include the coherent field contribution in terms of reflections and refractions on the surfaces of a particle using geometric optics (Markkanen et al. 2018b; Muinonen et al. 2019).
Computations proceed as follows. First, we compute scattering properties for volume elements, as described in Sect. 2.3.1. This step is done separately for each wavelength and for each material region, but it does not depend on the shape and size of the entire particle. Second, the computed scattering properties from the first step are used as input parameters in the combined Monte Carlo geometric optics radiative transfer solver, as discussed in Sect. 2.3.2. This step is computationally independent of the first step for different particle shapes and sizes.
2.3.1. Scattering properties of volume elements
Input parameters for our radiative transfer algorithm are the incoherent scattering phase function  , incoherent albedo ω, incoherent mean free path ℓ, coherent effective refractive index meff, and absorption cross section of the ensemble averaged volume element Cabs.
, incoherent albedo ω, incoherent mean free path ℓ, coherent effective refractive index meff, and absorption cross section of the ensemble averaged volume element Cabs.
We compute these parameters for spherical ensemble-averaged volume elements that contain a large number of small spherical monomers. The radius of the volume element R0 should be large enough to capture the statistics of the random medium. First, we generate a sample medium into a periodic box by randomly depositing monomers into the box until the target volumetric filling factor v is reached. Second, we draw a sample spherical volume element from the box, as explained in detail by Väisänen et al. (2019). Third, we apply FaSTMM to compute the Jones matrix Si of such a volume element i. Repeating the process N times (N = 512 is used in this work), we compute the coherent Jones scattering matrix as
and the incoherent Jones scattering matrix for the ith state as
Averaging the square of the incoherent Jones matrix over the ensemble of all N sample volume elements, we obtain the ensemble-averaged one-one element of the Mueller matrix, composed of the incoherent scattering phase function
and the incoherent scattering cross section
where S2 is the surface of the unit sphere. The incoherent albedo is defined as
where Cabs is the ensemble-average absorption cross section, and the incoherent mean free path length as
in which V is the volume of the volume element.
Finally, we solve the coherent effective medium parameter meff. This is done by matching the coherent scattering cross section 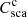 to the Csca of the equal-sized sphere using the Mie solution.
to the Csca of the equal-sized sphere using the Mie solution. 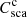 is defined as in (13), but the incoherent Mueller matrix is replaced with the coherent matrix.
is defined as in (13), but the incoherent Mueller matrix is replaced with the coherent matrix.
2.3.2. Monte Carlo ray tracing
We trace the rays in the same tetrahedral mesh as is used in the FEM. This makes it trivial to couple the radiative transfer solution (i.e., ∇ ⋅ qr) to the FEM solution. We decompose the divergence of the total flux into two parts ∇ ⋅ qr = qsol + qem in which qsol is the absorption rate due to the solar radiation, and qem is the absorption plus emission rate due to the thermally fluctuating sources.
To compute qsol, we launch 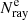 rays for a given wavelength band Δλ from outside Ω. The power of each incident ray is given by
rays for a given wavelength band Δλ from outside Ω. The power of each incident ray is given by
where P(λ) is the flux density of the incident radiation and G is the geometric cross section of the particle. Each ray has a specific position r and propagation direction 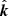 depending on the source.
depending on the source.
For thermally emitted radiation, to compute qem, 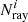 rays are launched from each tetrahedron Ct with a random position and direction. The emitted power per ray for a given wavelength is given by
rays are launched from each tetrahedron Ct with a random position and direction. The emitted power per ray for a given wavelength is given by
where Tct is the average temperature of the tetrahedron Ct and Nd is the number density of the volume elements in the tetrahedron Ct. The Planck function in a medium with the refractive index m written in terms of the free space wavelength λ0 reads as
where h is the Planck constant, c is the speed of light in vacuum, and kB is the Stefan-Boltzmann constant.
Once we have the initial position r, direction 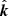 , and power of the ray E, we start tracing. If the ray hits the boundary ∂Ω, it reflects and refracts according to Snel’s law and the power is updated from Fresnel’s coefficients which are calculated using the effective refractive index meff. The position and direction of the reflected and refracted rays are updated.
, and power of the ray E, we start tracing. If the ray hits the boundary ∂Ω, it reflects and refracts according to Snel’s law and the power is updated from Fresnel’s coefficients which are calculated using the effective refractive index meff. The position and direction of the reflected and refracted rays are updated.
If the ray is in Ω, the distance to the next scattering event is generated as
where Φ is a uniform random number within [0, 1]. The scattering event happens if the ray does not cross the boundary ∂Ω. Absorbed power Eabs = E(1 − ω) in the scattering event is added into the total energy of the tetrahedron where the scattering event occurs, and the ray’s power is updated (E = Eω). A new propagation direction 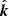 is drawn from the cumulative distribution function generated from the phase function of the ensemble averaged incoherent volume element
is drawn from the cumulative distribution function generated from the phase function of the ensemble averaged incoherent volume element 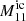 . Finally, if the ray does not scatter and it does not cross the boundary ∂Ω, intensity is collected and added to the total scattering phase function. This process is repeated until the ray’s power has decreased under the predefined threshold.
. Finally, if the ray does not scatter and it does not cross the boundary ∂Ω, intensity is collected and added to the total scattering phase function. This process is repeated until the ray’s power has decreased under the predefined threshold.
The radiative transfer computation gives us ∫Ct∇⋅qr dV for each tetrahedron, which is then used to compute the force vector F using (8). In addition, since the escaped rays are recorded, the total scattering and thermal emission phase functions and cross sections are obtained for each wavelength.
3. Numerical results
In this section, we present some numerical results. To validate the method, we compare our solution with the known approximate solution for small loosely packed grains computed by employing the effective medium approximation (EMA) and the Mie theory. Then, we apply the method to explain the superheating factor phase function measured for the coma of comet 67P.
3.1. Comparison to the effective medium approximation
Let us first consider a spherical medium consisting of small spherical silicate grains of radius r = 20 nm. The grains are randomly positioned in a spherical domain Ω with radius R. The volumetric filling factor is ν = 0.05. The wavelength dependent refractive index for magnesium-iron silicate, from Dorschner et al. (1995), is plotted in Fig. 1. Here we assume that the refractive index is independent of temperature in the studied temperature range.
 |
Fig. 1. Real and imaginary parts of the complex refractive index for magnesium-iron silicate. |
The external radiation source is the Sun, which is assumed to radiate as a perfect blackbody of temperature T⊙ = 5777 K. The solar flux P in the given wavelength band (λ1 − λ2) at the distance Δ = 1.3 AU from the Sun is given by
where r⊙ is the radius of the Sun.
Since the grain size is small, we can calculate a reference solution at the equilibrium temperature using the steady-state energy balance equation, EMA, and the Mie theory. To compute the absorption cross section Cabs, we use the Maxwell-Garnett mixing rule (Sihvola 2000) and the Mie theory. For an isothermal spherical particle, the steady-state energy balance equation reads as
To compare the proposed method to the steady-state analysis with EMA (21), we ran the transient simulation until the equilibrium was reached. Figure 2 shows the total absorbed solar radiation and thermally emitted power as a function of wavelength calculated by the proposed method and EMA for three different particle sizes R = 0.01, 0.1, and 1.0 mm. We observed excellent agreement between the two methods; however, we expect a decrease in the accuracy of our method as the particle size becomes smaller. This is evident as we used geometric optics to approximate the coherent reflections and refractions on the surface of a particle.
 |
Fig. 2. Total absorbed power of solar radiation (top) and thermally emitted power (bottom) by particles with radii 10 μm, 100 μm, and 1.0 mm as a function of wavelength computed by the proposed method and the effective medium approximation (EMA) are shown. Grain size is 20 nm and the volumetric filling factor v = 0.05. |
In the computations the volume element radius is r0 = 0.5 μm and the time step is τ = 0.1 s, τ = 1.0 s, and τ = 10 s for 0.01 mm, 0.1 mm, and 1.0 mm particles, respectively. We also assumed high thermal conductivity κ = 100 W m−1 K−1 to remove possible temperature gradients inside the body. Although it is not a realistic assumption for real dust, it serves as a validation by simplifying the problem. It is worth noting that the density ρ = 1000 kg m−3 and the specific heat capacity cp = 500 J kg−1 K−1 do not affect the equilibrium temperature as 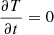 in (1) for the steady-state solution; they only affect the time it takes to reach equilibrium. Figure 3 shows the temperature evolution of the particles when the initial temperature T0 = 200 K. We see that the transient temperature reaches the equilibrium temperature computed by using the steady-state approach with EMA.
in (1) for the steady-state solution; they only affect the time it takes to reach equilibrium. Figure 3 shows the temperature evolution of the particles when the initial temperature T0 = 200 K. We see that the transient temperature reaches the equilibrium temperature computed by using the steady-state approach with EMA.
 |
Fig. 3. Temperature time evolution for porous (v = 0.05) aggregates of 20 nm silicate grains, with initial temperature T0 = 200 K. The unit on the time axis is scaled by the radii of the particles R. |
Next we studied larger grains with r = 100 nm and increased the filling factor to v = 0.3. These values are commonly used to model cometary dust (Kolokolova et al. 2004). It is evident from Figs. 4 and 5 that EMA leads to a different absorption rate, which consequently affects the equilibrium temperature and thermal emission; the EMA is no longer a valid approximation at shorter wavelengths as the grain size is approximately the same as the wavelength. Thus, care should be taken when applying EMAs to interpret infrared observations of cometary dust particles consisting of 100 nm-sized grains.
3.2. Application to the coma of 67P
We recently introduced a particle model that explains the scattering phase functions of the coma of comet 67P measured by the Rosetta/OSIRIS (Optical, Spectrocopic and Infrared Remote Imaging System) instrument (Markkanen et al. 2018b). The particle model consists of aggregated submicrometer-sized organic grains and micrometer-sized silicate grains. The shapes of the aggregates are Gaussian random spheres. It is thus interesting to study whether the same model can also explain the thermal infrared observations of the same comet. Since there is no refractive index available for cometary organic material over a wide wavelength range, we used the refractive index of carbonaceous dust analogues (Jäger et al. 1998). For silicates, we used the refractive index presented in Fig. 1 that corresponds to magnesium-iron silicate mineral (Dorschner et al. 1995).
We concentrate on the superheating factor phase function reported by Bockelée-Morvan et al. (2019) for the coma of the comet 67P. The superheating factor is defined as the ratio of the color temperature Tc to the equilibrium temperature of an ideal blackbody Tb = 278/Δ2 [K] (i.e., S = Tc/Tb). To obtain the color temperature Tc for a given phase angle, Bockelée-Morvan et al. (2019) fitted the Planck function to the Rosetta/VIRTIS near-infrared spectra (3 − 5 μm). They found that the superheating factor phase function has a phase dependence indicating that the particles can hold temperature gradients if the particles are assumed to be randomly oriented.
Computed superheating factors for different particle sizes together with the measured values (Fig. 8 in Bockelée-Morvan et al. 2019) as a function of phase angle are presented in Fig. 6. We see that only large particles can sustain temperature gradients resulting in the phase functions with significant slopes. The difference between the maximum and minimum temperature inside the particle with respect to the particle size is plotted in Fig. 7. It is evident that in order to model the measured superheating factor phase function slopes, the dust particles must sustain significant temperature gradients. Large temperature gradients, in turn, may have interesting effects on the dust dynamics in the inner coma via rocket forces caused by the asymmetrical sublimation of ices. Thermal break-down of particles may also play a role as the dust is transported from the inner to outer coma. Nevertheless, these interesting topics are beyond of the scope of this paper and are left for future research.
 |
Fig. 6. Computed superheating factors as a function of phase angle for different particle sizes. The heat conduction coefficient is κ = 0.00025 W m−1 K−1. Also shown are the measured values. |
 |
Fig. 7. Difference between the maximum and minimum temperature inside the particle as a function of particle radius for an example particle. |
In our computations, the heat conduction coefficient is assumed to be κ = 0.00025 W m−1 K−1, which corresponds to a realistic value for a porous dust aggregate (Krause et al. 2011; Arakawa et al. 2017; Sakatani et al. 2017). The heat conduction coefficient depends on porosity, grain size, and composition. Increasing the heat conduction coefficient flattens the superheating phase functions. Decreasing κ increases the slope until the radiative heat transport becomes more dominant. We also assumed that the angular velocities of the particles in the direction perpendicular to the Sun are slow (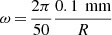 rad s−1), hence the contribution of rotation to the temperature gradients is negligible. The slow rotation rate was introduced in order to speed up numerical convergence. Higher angular velocities decrease temperature gradients and flatten the superheating factor phase functions. However, it is important to note that if the rotation axis points towards the Sun, it does not affect the temperature gradients.
rad s−1), hence the contribution of rotation to the temperature gradients is negligible. The slow rotation rate was introduced in order to speed up numerical convergence. Higher angular velocities decrease temperature gradients and flatten the superheating factor phase functions. However, it is important to note that if the rotation axis points towards the Sun, it does not affect the temperature gradients.
Finally, we averaged the modeled superheating phase functions over a differential power-law size distribution of index −3. The averaging results in a superheating factor phase function that is consistent with the measured value if the conductive heat coefficient κ = 0.00025 W m−1 K−1, as demonstrated in Fig. 8. Such a low κ value suggests that the particles must be porous. The superheating factor phase function also indicates that the dust particles in the inner coma must be large. The dominating particle size range is around 10–100 μm. Smaller particles would show flatter superheating factor phase functions with higher absolute values whereas larger particles would result in a steeper slope and smaller absolute values. The size range is also consistent with other dust models explaining the intensity phase functions measured by Rosetta/OSIRIS (Moreno et al. 2018; Markkanen et al. 2018b).
 |
Fig. 8. Modeled superheating factor phase function for different conductive heat transfer coefficients κ averaged over the differential power-law size distribution of index −3. The minimum cutoff is 10 μm and the maximum 100 μm. |
4. Conclusions
We presented a synoptic numerical solution for scattering, absorption, and thermal emission by large aggregated dust particles consisting of submicrometer-sized grains. The numerical solution is self-consistent and allows for analysis of multi-instrument data sets. We solved the transient energy equation using the finite-element method in which the radiative heat transfer part is included as an additional forcing term. We developed a new algorithm, based on the Monte Carlo radiative transfer with reciprocal transactions framework, to compute the forcing term in the dense discrete random medium enclosed by an arbitrarily shaped surface. The method explicitly computes the radiative heat transfer part in contrast to the standard thermal models in cometary science where it is included in the heat conduction coefficient by assuming that heat transport is one dimensional. Thus, the developed method provides a full three-dimensional solution for radiative heat transfer problems.
We compared the solution of the proposed method to that obtained by employing the effective medium approximation and Mie theory. The solutions match if the grains are small and loosely packed, but deviate for grain sizes and packing densities that are typically assumed to form cometary dust particles. This implies that using EMAs to interpret thermal infrared observations of cometary dust may lead to unreliable results. Finally, we showed that particles 10 − 100 μm in size can reproduce the superheating factor phase function of the coma of comet 67P if the dust particles hold significant temperature gradients. This means that the heat conduction coefficient must be very low, hence particles must be porous. The presented analysis also suggests that the visible phase functions measured by Rosetta/OSIRIS and the superheating phase function from Rosetta/VIRTIS are consistent with each other.
Acknowledgments
This work has been funded by the ERC Starting Grant No. 757390 Comet and Asteroid Re-Shaping through Activity (CAstRA). Computational resources have been provided by Gesellschaft für Wissenschaftliche Datenverarbeitung mbH Göttingen (GWDG).
References
- Arakawa, S., Tanaka, H., Kataoka, A., & Nakamoto, T. 2017, A&A, 608, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D., Leyrat, C., Erard, S., et al. 2019, A&A, 630, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coelho, P. J. 2014, J. Quant. Spectrosc. Radiat. Transf., 145, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., Mueller, M., Emery, J. P., Rozitis, B., & Capria, M. T. 2015, Asteroids IV (Tucson: Univ. of Arizona Press), 107 [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [Google Scholar]
- Güttler, C., Mannel, T., Rotundi, A., et al. 2019, A&A, 630, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hardy, D. L., Favennec, Y., Domingues, G., & Rousseau, B. 2016, J. Appl. Math. Phys., 4, 1488 [CrossRef] [Google Scholar]
- Howell, J. R. 1998, J. Heat Trans., 120, 547 [CrossRef] [Google Scholar]
- Howell, J., Siegel, R., & Mengüc, M. P. 2010, Thermal Radiation Heat Transfer (Boca Raton: CRC Press) [CrossRef] [Google Scholar]
- Huebner, W. F., Benkhoff, J., Capria, M.-T., et al. 2006, in Heat and Gas Diffusion in Comet Nuclei (Noordwijk: ESA Publications Division) [Google Scholar]
- Jäger, C., Mutschke, H., & Henning, T. 1998, A&A, 332, 291 [NASA ADS] [Google Scholar]
- Jin, W., Messina, R., & Rodriguez, A. W. 2017, Phys. Rev. B, 95, 161409 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., Kolokolova, L., Li, A., & Lebreton, J. 2016, in Light Scattering and Thermal Emission by Primitive Dust Particles in Planetary Systems, ed. A. Kokhanovsky (Berlin, Heidelberg: Springer), 363 [Google Scholar]
- Kolokolova, L., Hanner, M. S., Levasseur-Regourd, A. C., & Gustafson, B. S. 2004, in Physical Properties of Cometary Dust from Light Scattering and Thermal Emission, eds. M. C. Festou, H. U. Keller, & H. A. Weaver, 577 [Google Scholar]
- Krause, M., Blum, J., Skorov, Y. V., & Trieloff, M. 2011, Icarus, 214, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Markkanen, J., & Yuffa, A. J. 2017, J. Quant. Spectrosc. Radiat. Transf., 189, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Markkanen, J., Väisänen, T., Penttilä, A., & Muinonen, K. 2018a, Opt. Lett., 43, 2925 [NASA ADS] [CrossRef] [Google Scholar]
- Markkanen, J., Agarwal, J., Väisänen, T., Penttilä, A., & Muinonen, K. 2018b, ApJ, 868, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Modest, M. F. 2013, Radiative Heat Transfer, 3rd edn. (Boston: Academic Press), 279 [CrossRef] [Google Scholar]
- Moreno, F., Guirado, D., Muñoz, O., et al. 2018, AJ, 156, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Markkanen, J., Väisänen, T., Peltoniemi, J., & Penttilä, A. 2018, Opt. Lett., 43, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Väisänen, T., Martikainen, J., et al. 2019, J. Vis. Exp., 149, e59607 [Google Scholar]
- Richling, S., Meinköhn, E., Kryzhevoi, N., & Kanschat, G. 2001, A&A, 380, 776 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakatani, N., Ogawa, K., Iijima, Y., et al. 2017, AIP Adv., 7, 015310 [NASA ADS] [CrossRef] [Google Scholar]
- Sihvola, A. 2000, Subsurf. Sens. Technol. Appl., 1, 393 [CrossRef] [Google Scholar]
- Väisänen, T., Markkanen, J., Penttilä, A., & Muinonen, K. 2019, PLOS ONE, 14, 1 [Google Scholar]
All Figures
 |
Fig. 1. Real and imaginary parts of the complex refractive index for magnesium-iron silicate. |
| In the text | |
 |
Fig. 2. Total absorbed power of solar radiation (top) and thermally emitted power (bottom) by particles with radii 10 μm, 100 μm, and 1.0 mm as a function of wavelength computed by the proposed method and the effective medium approximation (EMA) are shown. Grain size is 20 nm and the volumetric filling factor v = 0.05. |
| In the text | |
 |
Fig. 3. Temperature time evolution for porous (v = 0.05) aggregates of 20 nm silicate grains, with initial temperature T0 = 200 K. The unit on the time axis is scaled by the radii of the particles R. |
| In the text | |
 |
Fig. 4. As in Fig. 2, but for grain size of 100 nm and filling factor v = 0.3. |
| In the text | |
 |
Fig. 5. As in Fig. 3, but for grain size of 100 nm and filling factor v = 0.3. |
| In the text | |
 |
Fig. 6. Computed superheating factors as a function of phase angle for different particle sizes. The heat conduction coefficient is κ = 0.00025 W m−1 K−1. Also shown are the measured values. |
| In the text | |
 |
Fig. 7. Difference between the maximum and minimum temperature inside the particle as a function of particle radius for an example particle. |
| In the text | |
 |
Fig. 8. Modeled superheating factor phase function for different conductive heat transfer coefficients κ averaged over the differential power-law size distribution of index −3. The minimum cutoff is 10 μm and the maximum 100 μm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.