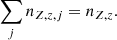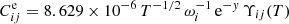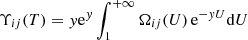| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201935337 | |
| Published online | 17 October 2019 | |
Relativistic electron impact ionization cross sections of carbon ions and application to an optically thin plasma
1
Department of Mathematics, University of Évora, R. Romão Ramalho 59, 7000 Évora, Portugal
e-mail: mavillez@galaxy.lca.uevora.pt
2
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstrasse 36, 10623 Berlin, Germany
3
Laboratory of Instrumentation, Biomedical Engineering and Radiation Physics (LIBPhys-UNL), Department of Physics, Faculty of Sciences and Technology, New University of Lisbon, 2829-516 Caparica, Portugal
Received:
22
February
2019
Accepted:
8
September
2019
Context. Ionization through electron impact is a fundamental process associated with the evolution of the ionic structure and emissivity of astrophysical plasmas. Over several decades substantial efforts have been made to measure and calculate the ionization cross sections of ionization through electron impact of different ions shell by shell, in particular, of carbon ions. Spectral emission codes use electron-impact ionization cross sections and/or rates taken from different experimental and theoretical sources. The theoretical cross sections are determined numerically and include a diversity of quantum mechanical methods. The electron-impact ionization database therefore is not uniform in the methods, which makes it hard to determine the reason for the deviations with regard to experimental data. In many cases only total ionization rates for Maxwell–Boltzmann plasmas are available, which makes calculating inner-shell ionization in collisional-radiative models using thermal and nonthermal electron distribution functions difficult. A solution of this problem is the capability of generating the cross sections with an analytical method using the minimum number of atomic parameters. In this way, uniformity in the database is guaranteed, and thus deviations from experiments are easily identified and traced to the root of the method.
Aims. The modified relativistic binary encounter Bethe (MRBEB) method is such a simple analytical scheme based on one atomic parameter that allows determining electron-impact ionization cross sections. This work aims the determination of K- and L-shell cross sections of the carbon atom and ions using the MRBEB method and show their quality by: (i) comparing them with those obtained with the general ionization processes in the presence of electrons and radiation (GIPPER) code and the flexible atomic code (FAC), and (ii) determining their effects on the ionic structure and cooling of an optically thin plasma.
Methods. The MRBEB method was used to calculate the inner-shells cross sections, while the plasma calculations were carried out with the collisional+photo ionization plasma emission software (CPIPES). The mathematical methods used in this work comprise a modified version of the double-exponential over a semi-finite interval method for numerical integrations, Gauss-elimination method with scaled partial pivoting for the solution of systems of linear equations, and an iterative least-squares method to determine the fits of ionization cross sections.
Results. The three sets of cross sections show deviations among each other in different energy regions. The largest deviations occur near and in the peak maximum. Ion fractions and plasma emissivities of an optically thin plasma that evolves under collisional ionization equilibrium, derived using each set of cross sections, show deviations that decrease with increase in temperature and ionization degree. In spite of these differences, the calculations using the three sets of cross sections agree overall.
Conclusions. A simple model like the MRBEB is capable of providing cross sections similar to those calculated with more sophisticated quantum mechanical methods in the GIPPER and FAC codes.
Key words: atomic data / atomic processes / radiation mechanisms: thermal / plasmas
© ESO 2019
1. Introduction
Carbon is the fourth most abundant element in nature after H, He, and O. It has a solar abundance of log[C/H] = −3.57 (Asplund et al. 2009) and thus contributes much to the emissivity of a plasma. Jointly with He, carbon contributes to the second peak maximum observed in the radiative cooling function of a plasma that evolves under collisional ionization equilibrium (see, e.g., Shapiro & Moore 1976; Boehringer & Hensler 1989; Schmutzler & Tscharnuter 1993; Sutherland & Dopita 1993; Gnat & Sternberg 2007; de Avillez et al. 2010). In addition, C I and C II ions (through fine-structure and metastable transitions) are the main contributors to radiative cooling at temperatures below 103 K. The other contributors are O I, Si I, Si II, S I, Fe I, and Fe II through fine-structure lines and O I, O II, Si I, Si II, Si I, S II, Fe I, and Fe II through metastable transitions (see, e.g., Dalgarno & McCray 1972; Wolfire et al. 1995, 2003). Furthermore, carbon plays an important role in the chemistry of molecular clouds (see, e.g., Larson 1981; Pavlovski et al. 2002; Glover 2007) as well as in shocks (see, e.g., Hollenbach & McKee 1989).
The cross sections of the electron-impact ionization of carbon ions have been extensively studied by means of theoretical calculations and experimental measurements. Since the seminal work of Bethe (1930), who derived the correct form of the cross section at high electron energies, much effort has been invested to calculate the cross sections using empirical and semi-empirical methods or more sophisticated quantum mechanical numerical calculations. Compilations comprising theoretical and experimental ionization cross sections for the carbon atom and ions, including the best fits to these, that have been popular in the Atomic Physics and Astrophysics communities, were published over the years by Lotz (1967, 1968), Bell et al. (1983; hereafter BL83), Arnaud & Rothenflug (1985, AR85), Lennon et al. (1988, L88), Suno & Kato (2006, SK06), Mattioli et al. (2007, M07), Dere (2007, D2007), to name only a few.
The recommended total (BL83; L88; SK06, and M07) and partial (AR85) cross sections are parametrized using the Younger (1981) formula:
where u = E/IZ, z, IZ, z is the ionization potential (in eV) of the ion with atomic number Z and ionic state z, E is the incident electron kinetic energy (in eV); nmax = 2 in Younger (1981) and AR85 and 5 in BL83, SK06 and M07. The coefficient B (the Bethe constant) is determined from the photoionization cross section, σph, through
where df/dϵ is the optical differential oscillator strength. At high energies, the cross section tends to the Bethe limit (see, e.g., Younger 1981; Pradhan & Nahar 2011),
When B is known, the coefficients Ai and C are determined directly from a least-squares fitting procedure. Hence, the fit to the cross section has the correct asymptote at high energies. In AR85, the ionization potential IZ, z and the coefficients Ai, B, and C refer to the subshell j of the initial ion. The total direct ionization cross section is then obtained by summing over all the subshells.
Bell et al. (1983) and Lennon et al. (1988) adopted the experimental data of Brook et al. (1978) for C I and extrapolated the data beyond 1 keV using a fitting equation to the Born approximation. The recommended curve for the C II ionization cross section follows the cross-beam measurements of Aitken et al. (1971) and at high energies the Coulomb-Born calculations of Moores (1972). For C III and C IV ionization, Bell and collaborators adopted the Coulomb-Born calculations of Jakubowicz & Moores (1981). In the case of C III ionization, a small contribution from inner-shell ionization was included. The cross section for ionization of C V was obtained by scaling the ionization cross section of B IV along the isosequence. For C VI the calculations by Younger (1980) have been adopted.
Arnaud & Rothenflug (1985) considered the ionization cross sections of the different subshells. The C VI cross-section (shell 1s) parameters were determined from the distorted wave-exchange approximation calculations of Younger (1981). For C V (shell 1s2) a fit to the measured cross section available at the Electron-Impact Ionization Data of Multicharged Ions database (EIIDMI; Crandall et al. 1979a)1 was carried out. The theoretical values of Younger (1981) for the direct ionization from shell 1s2 of the Li-like ion C IV were adopted, while for the 2s shell ionization, the Crandall et al. (1979b) data were kept. Excitation-autoiozation contributions to the C IV ion were taken into account; the derived formulae are presented in Appendix A of AR85. For C III (shells 1s2 and 2s2), AR85 adopted the calculations by Younger (1981) along the sequence. The fitting parameters for the C II and C I ionization of shell 2s2 were deduced by extrapolation from higher-z elements. The fit to the C II 2p shell ionization cross section is based on the measurements of Aitken et al. (1971), and those of C I were derived from the measurements by Brook et al. (1978). The parameter B was derived from the photoionization cross section of Reilman & Manson (1979).
Suno & Kato (2006) adopted for C VI and C V the cross sections calculated using the distorted-wave method with exchange (Pattard & Rost 1999) and the distorted-wave Born method (Fang et al. 1995), respectively. For C IV, the experimental data of Knopp et al. (2001) were selected. Because of excitation-autoionization, the cross section has two peaks. For C III, the experimental data of Woodruff et al. (1978) were chosen, and for C II and C I, the experimental data of Yamada et al. (1989) and Brook et al. (1978) were used, respectively.
Mattioli et al. (2007) adopted cross sections from theoretical and experimental data: the C VI and C V cross sections were taken from Arnaud & Rothenflug (1985). For C IV, the Crandall et al. (1979b) data were complemented with those available at the EIIDMI database. For C III, the data of Falk et al. (1983) for low metastable contributions and that of Loch et al. (2005) were adopted. Similarly to SK06, the cross sections of C II and C I were taken from Yamada et al. (1989) and Brook et al. (1978), respectively.
The Dere (2007) compilation combines experimental cross sections with those obtained with the flexible atomic code (FAC)2 (Gu 2002, 2008). For C VI, D2007 favored the parametric fit of Fontes et al. (1999) to their relativistic distorted -wave approximation cross-section calculations for ionization from the 1s shell; the C V cross section is determined with the FAC. For C IV and C III, direct ionization and excitation-autoionization cross sections calculated with the FAC were adopted; for C III, the 1s and 2s subshells were taken into account for the direct ionization cross sections, while for EA the 1s2l3 and 1s2l23l′ transitions were considered. The Yamada et al. (1989) and Brook et al. (1978) cross-section measurements were adopted for C II and C I, respectively. The total cross sections, available in version 8.0.7 of the CHIANTI atomic database3 (Del Zanna et al. 2015), are provided as spline nodes for a scaled energy U and cross section ΣZ, z given by
and
respectively. In these expressions f = 2 is an adjustable parameter, σZ, z is the unscaled cross section, and u, and IZ, z have the meanings related in previous paragraphs.
Further calculations using sophisticated quantum mechanical methods have been carried out in the last two decades by Bote et al. (2009), Abdel-Naby et al. (2013), and Wang et al. (2013) for C I, Ludlow et al. (2008), Ballance et al. (2011), Pindzola et al. (2012), and Lecointre et al. (2013) for C II, Fogle et al. (2008) for C III, Pindzola et al. (2012) for C IV, and Fontes et al. (1999) for C VI. Some of these authors also reported experimental measurements that were used to compare with the theoretical cross sections, for instance, Wang et al. (2013) for C I, Lecointre et al. (2013) for C II, and Fogle et al. (2008) for C III.
Empirical classical and semiclassical analytical methods have also been adopted over the years to calculate ionization cross sections of different ions. These include the binary-encounter-Bethe (BEB; Kim & Rudd 1994) model4 and its derivatives, for example, the relativistic BEB (Kim et al. 2000) and the modified relativistic BEB (Guerra et al. 2012, MRBEB) models. The advantage of these models is their simple analytical expressions and the small number of adopted parameters that depend on the binding energy, on the energy of the impacting electron, and on the shielding by inner electrons, for instance. The MRBEB model has been applied to calculate the K-, L- and M-shell ionization cross sections of several atoms, with Z varying between 6 and 83 (Guerra et al. 2012), and for several ionization stages of Ar, Fe, and Kr (Guerra et al. 2013), and U (Guerra et al. 2015). The model provides reliable direct ionization cross sections, and the relative differences to experimental data are smaller than 10% for the inner shells of neutral atoms and 20% for highly charged ions (Guerra et al. 2012, 2013). For a review of these models, see Llovet et al. (2014), for example.
We here use the MRBEB method to calculate the K- and L-shell cross sections of the carbon ions and convolve them with the Maxwell–Boltzmann electron distribution function in order to obtain the corresponding ionization rates. A further application is made to the evolution of an optically thin plasma in order to obtain the radiative losses due to electron-impact ionization, bremsstrahlung, and line emission. The structure of this paper is as follows. Section 2 describes the MRBEB model and the calculation of the K- and L-shell ionization cross sections of the carbon atom and ions. Section 3 describes the use of the calculated cross sections in determining the ionization structure and radiative losses of an optically thin plasma that evolves under collisional ionization equilibrium. Section 4 closes the paper with a discussion and final remarks.
2. Modified relativistic binary encounter Bethe model cross sections
2.1. The MRBEB model
The MRBEB model uses an analytical approach containing a single atomic parameter (the binding energy of the electron to be ionized) and takes into account the energy of the impacting electron and the shielding of the nuclear charge by the bound electrons of the target ion. Therefore, the number of electrons in the inner shells up to the subshell that is ionized acts as a screening of the nuclear potential as seen by the primary electron. In contrast to the MRBEB, the other binary encounter Bethe and relativistic binary encounter Bethe models require two input parameters (the binding energy and the kinetic energy of the bound electron).
The MRBEB cross section, denoted by σnlj, LS, refers to the ionization of an nlj electron in an atom or ion in a given initial state LS. The cross section takes into account the relativistic interactions between the incident and target electrons during inner-shell ionization of heavy atoms or ions. The determination of the cross section requires knowledge of one single parameter: the binding energy of the target electron. The cross section is given by (Guerra et al. 2012)
with
and
with
In these equations, E denotes the kinetic energy of the impacting electron, B is the binding energy of the target electron, and c stands for the speed of light, while me is the electron mass; ao and α are the Bohr radius and the fine-structure constant, respectively. The scaling 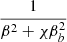 includes the effects of the shielding of the nucleus by the target-bound electron through the parameter χ, which is therefore related to the shielding coefficient Cnlj(Z) and the binding energy B of the target electron through the relation χ = 2 Ry Cnlj(Z)/B (Ry is the Rydberg energy). The shielding of the nucleus is described by
includes the effects of the shielding of the nucleus by the target-bound electron through the parameter χ, which is therefore related to the shielding coefficient Cnlj(Z) and the binding energy B of the target electron through the relation χ = 2 Ry Cnlj(Z)/B (Ry is the Rydberg energy). The shielding of the nucleus is described by
where n′l′j′ stands for the next subshell after subshell nlj, ordered in energy, and Zeff is the screening effect (Guerra et al. 2017).
2.2. Cross-section calculations
Using the MRBEB model, we calculated the K- and L-shell ionization cross sections for carbon and its ions. The binding energies of each target electron were calculated using the multi-configuration Dirac-Fock (MCDF) theoretical framework with the multi configuration Dirac-Fock and general matrix element (MCDFGME) code (Indelicato & Desclaux 1990), which evaluates level energies, including correlation and first- and second-order quantum electrodynamics corrections. Table 1 displays the binding energies obtained with the MCDF method without electronic correlation beyond the intermediate coupling using the Rodrigues et al. (2004) ground-state configurations for the different ions. First-order retardation terms of the Breit operator and the Uelhing contribution to the vacuum polarization terms were included self-consistently. The Wichmann-Kroll and Kallen-Sabry contributions, as well as higher-order Breit retardation terms and other QED effects, such as self-energy, were included as perturbations.
Binding energies (eV) calculated with the MDFGME code for the ground-state configurations of C I–C VI.
Figure 1 displays the inner shell (dashed black lines) and total (solid black lines) cross sections of the carbon ions calculated with the MRBEB model. In addition, the figure also shows the total cross sections of Arnaud & Rothenflug (1985, blue lines), Dere (2007, red lines), and those calculated with the GIPPER code5 (Fontes et al. 2015, green lines). In general, the total MRBEB, GIPPER, and D2007 cross sections have a similar distribution for C II, C III, and C IV ions. Small deviations occur during the approach to the peak maximum (C II), in the peak maximum (C III ans C IV), and after the peak maximum (C III and C IV). The total MRBEB cross sections for C II–C VI ions dominate the others for T > 108 K because of the relativistic effects, which are taken into account in the calculations.
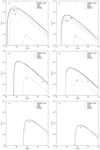 |
Fig. 1. K- and L-shell (dashed black lines) and total (solid black lines) ionization cross sections of the carbon atom and ions calculated with the MRBEB model and total cross sections in AR85 (blue lines) and D2007 (red lines) calculated with the GIPPER code (green lines). |
The MRBEB and GIPPER cross sections have small deviations for C I, C II, C III, and C IV near and at the peak maximum. The largest deviations between the MRBEB and GIPPER cross sections occur for C V and C VI ions starting at the approach to the peak maximum. The GIPPER cross sections overlap those discussed in AR85. The cross sections in D2007 have the highest values for C V and C VI ions at peak maximum and at high energies up to 108 K when the MRBEB cross section takes over. Clearly, a simple analytical method depending on a single atomic parameter gives similar results to those provided by the more sophisticated GIPPER and FAC methods.
2.3. Fits to the cross sections
The MRBEB cross sections were fit (for C I see Fig. 2) with the functional (Bote et al. 2009)
 |
Fig. 2. Fit (dotted lines) to the electron-impact ionization cross sections (solid lines) of C I using Eqs. (10) and (11). |
for U = E/Enlj ≤ 16, while for higher energies a variation of their Eq. (5) was used,
with χ = 2lnP − β2, and where 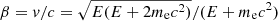 and
and 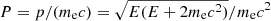 are the velocity and momentum of the impacting electron, respectively, a0 is the Bohr radius and the parameters a1 − a5 and b1 − b5 (displayed in Tables 2 and 3) are characteristic of each element and electron shell. These parameters were calculated using a least-squares fit. The two right columns in the tables represent the maximum relative differences below and above 0, respectively. The absolute relative difference is the largest of the absolute of these two maxima. The relative difference is given by
are the velocity and momentum of the impacting electron, respectively, a0 is the Bohr radius and the parameters a1 − a5 and b1 − b5 (displayed in Tables 2 and 3) are characteristic of each element and electron shell. These parameters were calculated using a least-squares fit. The two right columns in the tables represent the maximum relative differences below and above 0, respectively. The absolute relative difference is the largest of the absolute of these two maxima. The relative difference is given by
The maximum relative differences above and below zero are labeled Δσ− and Δσ+, respectively. The maximum absolute relative differences occur for U = E/Enlj ≤ 16, that is, with the fitting of Eq. (10). The maximum error is found to be 1.315% and occurs for the cross section associated with shell 2p1/2 of C I. This is followed for absolute relative differences of 0.915% and 0.81% for the fit of the EII cross sections of the 2s shell of C I and C III. For the fits associated with energies of U = E/Enlj > 16, the maximum absolute relative difference is lower than 0.07%.
3. Application to an optically thin plasma
We discussed different sets of cross sections for the ionization of the carbon atom and ions and now compare their effects on the ionization structure and on the cooling of an optically thin plasma characterized by a Maxwell–Boltzmann (MB) electron distribution function. The determination of the ionic state of the plasma as well as its emissivity is important for theoretical models as well as observations of absorption features in the diffuse medium where Li-like ions (C IV, N V, and O VI) are important to distinguish between different ionization mechanisms, such as turbulent mixing layers (Slavin et al. 1993), shock ionization (Dopita & Sutherland 1996), conduction interfaces (Borkowski et al. 1990), and radiative cooling (Edgar & Chevalier 1986). These processes in turn are used to study high-velocity clouds (see, e.g., Indebetouw & Shull 2004) or gas in the Local Bubble (de Avillez & Breitschwerdt 2009). In addition, the emission caused by C V and C VI is important to understand the spectra associated with the processes described above, as well as with that of ionizing (Masai 1984) or recombining (de Avillez & Breitschwerdt 2012) plasmas or in the soft X-ray spectra that are observed in supernova remnants. Spectral fitting codes for X-ray emitting space plasmas are often used to determine the temperature and ionization state of a plasma. Orbiting X-ray observatories such as Chandra and XMM-Newton have chip-based X-ray detectors that can barely resolve individual lines for diffuse low surface brightness plasmas like the hot interstellar medium. Therefore it is important to quantify as well as possible the contribution of various ions such as carbon to the total spectrum.
For each set of cross sections we followed the evolution of a gas parcel cooling under collisional ionization equilibrium conditions from an initial temperature of 109 K where it is completely ionized. The plasma was composed of hydrogen and carbon with solar abundances (Asplund et al. 2009) and a hydrogen particle density, nH, of 1 cm−3. These calculations are referred to as the MRBEB, GIPPER, and D2007 models.
The processes we took into account are electron-impact ionization, radiative recombination including cascades into the ground state, dielectronic recombination, bremsstrahlung, and line emission. No charge-exchange reactions were considered. Hence, and because the evolution is in collisional ionization equilibrium, the ionization structure of each element (composed of atoms and ions) can be treated independently of the other elements. Thus, the evolution of the carbon atom and ions is the same whether the plasma is composed only of carbon or of any set of elements including carbon.
3.1. Thermal model
The ionization structure and emission properties of the gas parcel were followed using the thermal model described in de Avillez et al. (2018; for further details, see de Avillez in prep.). We therefore present a summary of this model in this subsection.
The density nZ, z (cm−3) of an ion with atomic number Z and charge state z (z = 0, …, Z) is determined from the populations of the neighboring charge states z − 1, z, and z + 1 through recombination (αZ, z, which includes radiative and dielectronic recombination) and collisional ionization (SZ, z) rates from state z to z − 1 and z + 1, respectively. Hence, nZ, z is given by the system of equations
where ne is the electron density (cm−3), which is obtained from
By multiplying both sides of Eq. (13) by 1/nZ (nZ is the number density (cm−3) of the species of atomic number Z) and factorizing ne, the system of equations simplifies to
where xZ, z = nZ, z/nZ is the ion fraction (which varies between 0 and 1). This system of equations may be cast into the matrix form
where X is a vector comprising all ion fractions xZ, z and A is a tridiagonal matrix with elements SZ, z − 1, −(SZ, z + αZ, z), and αZ, z + 1 at each row populating the diagonal band. The solution of this system of equations is straightforward using any Gauss-elimination method with or without pivoting. The final solution is then transformed into the ion density through
where A(Z)=nZ/nH is the abundance of the species and nH is the hydrogen number density (cm−3).
The ionization rates, SZ, z, are determined by convolving σ(E)v with the MB electron distribution function,
and are given by
where me is the electron mass (g), Φz, z is the ionization threshold (eV), and σ(E) is the electron-impact ionization cross section (cm2).
Radiative and dielectronic recombination rates used in these calculations are based on calculations with the AUTOSTRUCTURE code6 (Badnell 2011) and are taken from Badnell (2006a) for H II and C II through C VII recombining to H I and C I through C VI, respectively. The radiative recombination rates have the functional
where A (cm3 s−1), T0, 1 (K), and b (dimensionless) are fit coefficients. The latter is replaced by b + Cexp(T2/T) (C is dimensionless and T2 is given in K) for low-ionization stages. The dielectronic recombination rates are given by the Burgess (1965) general formula
whose coefficients are taken from Badnell (2006b) for H II and C VI, Bautista & Badnell (2007) for C V, Colgan et al. (2004, 2003) for C IV and C III, respectively, and Altun et al. (2004) for C II.
The cooling due to electron-impact ionization (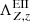 ), bremsstrahlung (
), bremsstrahlung (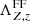 ), and line (permitted, forbidden, and semi-forbidden) emission (
), and line (permitted, forbidden, and semi-forbidden) emission (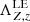 ) shown in Fig. 4 are given by
) shown in Fig. 4 are given by
with SZ, z denoting the ionization rate (cm3 s−1) and ΦZ, z is the ionization threshold (erg) of the ionizing ion,
where C = 1.4256 × 10−27 erg cm3 s−1 K−1/2, T is the temperature (K), γ2 = z2Ry/kBT (Ry is the Rydberg energy) is the normalized temperature, and ⟨gff(γ2)⟩ is the total free-free Gaunt factor (see the details of its calculation in, e.g., de Avillez & Breitschwerdt 2015), and
where nZ, z, j is the population density of level j of the ion, Aji is the spontaneous decay rate from level j to level i (i < j), and Eij is the excitation energy between the two levels.
The level populations were calculated as described in de Avillez et al. (2018) by assuming that there is an equilibrium between excitation by electron impact and de-excitation by electron impact and spontaneous decay. Hence, the population of level j is obtained from the equation
coupled to the equation of mass conservation
In these equations 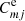 and
and 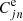 denote the excitation rates (cm3 s−1) from levels m to j (m < j) and j to n (j < n), respectively, while
denote the excitation rates (cm3 s−1) from levels m to j (m < j) and j to n (j < n), respectively, while 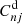 and
and 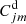 denote the de-excitation rates (cm3 s−1) from levels n to j and j to m, respectively; Anj and Ajm are the Einstein spontaneous decay coefficients (s−1) from levels n to j and j to m, respectively; and nZ, z, m and nZ, z, n are the population densities (cm−3) of levels m and n, respectively. The excitation and de-excitation rates are given by
denote the de-excitation rates (cm3 s−1) from levels n to j and j to m, respectively; Anj and Ajm are the Einstein spontaneous decay coefficients (s−1) from levels n to j and j to m, respectively; and nZ, z, m and nZ, z, n are the population densities (cm−3) of levels m and n, respectively. The excitation and de-excitation rates are given by
and
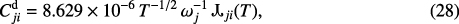
where y = Eij/kBT, U = Ee/Eij is the reduced electron energy (Ee is the energy of the impacting electron), ωi and ωj are the statistical weights of levels i and j, respectively, and T is the temperature (K). The forms of the effective collision strength, Υij(T), and of 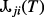 relate to the collision strengths and are given by
relate to the collision strengths and are given by
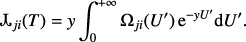
The wavelengths, coefficients of spontaneous transitions, and the effective collision strengths were taken from version 8.0.7 of the CHIANTI atomic database.
3.2. Calculations and methods
The evolution of a gas parcel is calculated as follows: (i) at each temperature calculate first the ionization and recombination rates and solve the system of equations (15) to obtain the ion fractions, (ii) determine the ions and the electron densities from Eqs. (17) and (14), respectively, and (iii) obtain the emissivity due to the different processes using Eqs. (22)–(24).
The numerical methods used in these calculations are the same as in de Avillez et al. (2018), that is, (i) numerical integrations in semi-finite intervals, such as the ionization rates, were calculated with a precision of 10−15 using the double-exponential transformation method of Takahasi & Mori (1974), Mori & Sugihara (2001), and (ii) the system of equations (15) is solved using a Gauss-elimination method with scaled partial pivoting (Cheney & Kincaid 2008) and a tolerance of 10−15.
3.3. Results
The carbon-ion fraction variations with temperature calculated with the MRBEB, GIPPER, and D2007 ionization cross sections are displayed in Fig. 3. Although there are some differences between the location of the ion profiles, the ionic structure shows similar properties in the three models: the same profiles for all the ions that are characterized with the dominance of C VII above 106 K, the dominance of C I below 104 K, and the classic C V plateau resulting from the K-shell ionization potential. The differences between the three models are reflected in the small deviation to the right for the MRBEB model with regard to the others, while the GIPPER model shows profiles that in some cases are to the left of the D2007 profiles and in other cases to the right, but always to the left of the MRBEB profiles. The reason is that the threshold ionization energies in the MRBEB model are higher than those of the GIPPER and D2007 models, which leads to a delayed ionization of the carbon ions in comparison to the other cases.
 |
Fig. 3. Carbon ionic fraction variation with temperature evolving under collisional ionization equilibrium calculated with the MRBEB, GIPPER, and D2007 cross sections. |
Figure 4 displays the cooling (erg cm3 s−1), normalized to nenH, due to electron-impact ionization (EII), bremsstrahlung (FF) using the total Gaunt factors calculated in de Avillez & Breitschwerdt (2017), for instance, and line (allowed, forbidden, and semi-forbidden) emission (LE) calculated with the three models (MRBEB, GIPPER, and D2007). Emissivities associated with different processes in different ranges in temperature overlap. For instance, above 105 K, the bremsstrahlung in the three models overlaps, except around 106. A complete overlap is visible above 2 × 106 K in electron-impact ionization and bremsstrahlung. In the latter the overlap extends to 105 K, except around 106 K. Deviations among the three models are seen in electron-impact ionization below 106 K and in line emission above 105 K, where the second peak maximum noticeably increases. For lower temperatures the line emission seems to be the same for all the models. The excess in emissivity in the MRBEB model is similar to that seen in the ionization structure (i.e., the deviation to the right). Although there are deviations in the models, they predict in general the same behavior and profile for the emissivities due to the different processes.
 |
Fig. 4. Comparison of the cooling (erg cm3 s−1), normalized to nenH, due to electron-impact ionization (EII), bremsstrahlung (FF), and line emission (LE)) in a gas parcel evolving under collisional ionization equilibrium and calculated with MRBEB, GIPPER, and D2007 electron-impact ionization cross sections. |
4. Discussion and final remarks
We applied the modified relativistic binary encounter Bethe model to calculate the K- and L-shell ionization cross sections of the carbon atom and ions and compare their variation with energy of the impacting electron with those calculated using the GIPPER code and those published by Dere (2007), which includes cross sections calculated with the flexible atomic code and the relativistic distorted wave approximation of Fontes et al. (1999), and experimental data.
In general, the three sets of cross sections have a similar profile for C II, C III, and C IV ions, and small deviations occur during the approach to the peak (C II), in the peak (C III and C IV), and after the peak (C III and C IV) maximum. The total MRBEB cross sections for C II–C VI ions dominate the others for T > 108 K because of the relativistic effects. The MRBEB and GIPPER cross sections have small deviations for C I, C II, C III, and C IV near and at the peak maximum, while the largest deviations occur in the approach to the peak maximum for C V and C VI. The D2007 cross sections have the highest values for C V and C VI ions at peak maximum and at high energies up to 108 K when the MRBEB cross sections take over. Although the FAC and GIPPER code use the distorted-wave method for the electron-impact ionization, the D2007 and GIPPER cross sections still show differences that can stem from the different numerical methods and the adopted atomic model.
We further explored the effects of the three sets of cross sections on the ion fractions of the carbon ions and on the cooling due to electron-impact ionization, bremsstrahlung, and line emission by an optically thin plasma that evolves under collisional ionization equilibrium and cooling from a temperature of 109 K. The three calculations, using the MRBEB, GIPPER, and D2007 cross sections, show deviations in the ion fractions of the same ion that decrease with increase in ionization degree: the strongest deviations occur in the lowest ionization states (C I–C III), and the smallest deviations in the highest ionization states. These differences in the ion fractions propagate to the emissivities. At high temperatures the emissivities are similar in the three calculations, while in other temperature regimes noticeable differences are observed, for instance, in the second peak maximum of the line emission around 106 K. The agreement between the emissivities calculated with the three sets of cross sections is nevertheless good overall.
The results show that a simple analytical model that only depends on one atomic parameter (the electron binding energy) is capable of providing electron-impact ionization cross sections similar to those calculated with the more sophisticated quantum mechanical methods in GIPPER and FAC. This shows that it is possible to build a database of cross sections associated with the atoms and ions of the ten most abundant elements in nature with the MRBEB method that can be used by any spectral emission code.
Acknowledgments
This research was supported by the projects “Enabling Green E-science for the SKA Research Infrastructure (ENGAGE SKA)” (M. A.; reference POCI-01-0145-FEDER-022217, funded by COMPETE 2020 and FCT) and “Ultra-high-accuracy X-ray spectroscopy of transition metal oxides and rare earths” (M. G.; reference PTDC/FIS-AQM/31969/2017, and SFRH/BPD/92455/2013 funded by FCT), and by the project UID/FIS/04559/2013 (LIBPhys). Partial support for M. A. and D. B. was provided by the Deutsche Forschungsgemeinschaft, DFG project ISM-SPP 1573. The calculations were carried out at the ISM – Xeon Phi cluster of the Computational Astrophysics Group, University of Évora, acquired under project “Hybrid computing using accelerators & coprocessors – modelling nature with a novell approach” (M. A.), InAlentejo program, CCDRA, Portugal.
References
- Abdel-Naby, S. A., Ballance, C. P., Lee, T. G., Loch, S. D., & Pindzola, M. S. 2013, Phys. Rev. A, 87, 022708 [NASA ADS] [CrossRef] [Google Scholar]
- Aitken, K. L., Harrison, M. F. A., & Rundel, R. D. 1971, J. Phys. B At. Mol. Phys., 4, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Altun, Z., Yumak, A., Badnell, N. R., Colgan, J., & Pindzola, M. S. 2004, A&A, 420, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., & Rothenflug, R. 1985, A&AS, 60, 425 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2006a, ApJS, 167, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2006b, A&A, 447, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R. 2011, Comput. Phys. Commun., 182, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Ballance, C. P., Loch, S. D., Ludlow, J. A., Abdel-Naby, S. A., & Pindzola, M. S. 2011, Phys. Rev. A, 84, 062713 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, M. A., & Badnell, N. R. 2007, A&A, 466, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, K. L., Gilbody, H. B., Hughes, J. G., Kingston, A. E., & Smith, F. J. 1983, J. Phys. Chem. Ref. Data, 12, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Bethe, H. 1930, Ann. Phys., 397, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Boehringer, H., & Hensler, G. 1989, A&A, 215, 147 [NASA ADS] [Google Scholar]
- Borkowski, K. J., Balbus, S. A., & Fristrom, C. C. 1990, ApJ, 355, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Bote, D., Salvat, F., Jablonski, A., & Powell, C. J. 2009, At. Data Nucl. Data Tables, 95, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, E., Harrison, M. F. A., & Smith, A. C. H. 1978, J. Phys. B At. Mol. Phys., 11, 3115 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A. 1965, ApJ, 141, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Cheney, W., & Kincaid, D. 2008, Numerical Mathematics and Computing, 6th edn. (Belmont: Thomson Brooks/Cole) [Google Scholar]
- Colgan, J., Pindzola, M. S., Whiteford, A. D., & Badnell, N. R. 2003, A&A, 412, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colgan, J., Pindzola, M. S., & Badnell, N. R. 2004, A&A, 417, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crandall, D. H., Gregory, D. C., & Phaneuf, R. A. 1979a, Electron Impact Ionization of Multicharged Ions, Tech. rep. [CrossRef] [Google Scholar]
- Crandall, D. H., Phaneuf, R. A., Hasselquist, B. E., & Gregory, D. C. 1979b, J. Phys. B At. Mol. Phys., 12, L249 [CrossRef] [Google Scholar]
- Dalgarno, A., & McCray, R. A. 1972, ARA&A, 10, 375 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2009, ApJ, 697, L158 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2010, in The Dynamic Interstellar Medium: A Celebration of the Canadian Galactic Plane Survey, eds. R. Kothes, T. L. Landecker, & A. G. Willis, ASP Conf. Ser., 438, 313 [NASA ADS] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2012, ApJ, 756, L3 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2015, A&A, 580, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2017, ApJS, 232, 12 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., Anela, G. J., & Breitschwerdt, D. 2018, A&A, 616, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Dere, K. P., Young, P. R., Landi, E., & Mason, H. E. 2015, A&A, 582, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P. 2007, A&A, 466, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dopita, M. A., & Sutherland, R. S. 1996, ApJS, 102, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Edgar, R. J., & Chevalier, R. A. 1986, ApJ, 310, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, D., Hu, W., Chen, C., et al. 1995, At. Data Nucl. Data Tables, 61, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Falk, R. A., Stefani, G., Camilloni, R., et al. 1983, Phys. Rev. A, 28, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fogle, M., Bahati, E. M., Bannister, M. E., et al. 2008, ApJS, 175, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Fontes, C. J., Sampson, D. H., & Zhang, H. L. 1999, Phys. Rev. A, 59, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Fontes, C. J., Zhang, H. L., Abdallah, Jr., J., et al. 2015, J. Phys. B At. Mol. Phys., 48, 144014 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O. 2007, MNRAS, 379, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Gnat, O., & Sternberg, A. 2007, ApJS, 168, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. 2002, in APS Meeting Abstracts, B17.075 [Google Scholar]
- Gu, M. F. 2008, Can. J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Guerra, M., Parente, F., Indelicato, P., & Santos, J. P. 2012, Int. J. Mass Spectrom., 313, 1 [CrossRef] [Google Scholar]
- Guerra, M., Parente, F., & Santos, J. P. 2013, Int. J. Mass Spectrom., 348, 1 [CrossRef] [Google Scholar]
- Guerra, M., Stöhlker, T., Amaro, P., Machado, J., & Santos, J. P. 2015, J. Phys. B At. Mol. Phys., 48, 144027 [NASA ADS] [CrossRef] [Google Scholar]
- Guerra, M., Amaro, P., Santos, J. P., & Indelicato, P. 2017, At. Data Nucl. Data Tables, 117, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & McKee, C. F. 1989, ApJ, 342, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., & Shull, J. M. 2004, ApJ, 605, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Indelicato, P., & Desclaux, J. P. 1990, Phys. Rev. A, 42, 5139 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jakubowicz, H., & Moores, D. L. 1981, J. Phys. B At. Mol. Phys., 14, 3733 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y.-K., & Rudd, M. E. 1994, Phys. Rev. A, 50, 3954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kim, Y.-K., Santos, J. P., & Parente, F. 2000, Phys. Rev. A, 62, 052710 [NASA ADS] [CrossRef] [Google Scholar]
- Knopp, H., Teng, H., Ricz, S., Schippers, S., & Müller, A. 2001, Phys. Scr. Vol. T, 92, 379 [NASA ADS] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lecointre, J., Kouzakov, K. A., Belic, D. S., et al. 2013, J. Phys. B At. Mol. Phys., 46, 205201 [NASA ADS] [CrossRef] [Google Scholar]
- Lennon, M. A., Bell, K. L., Gilbody, H. B., et al. 1988, J. Phys. Chem. Ref. Data, 17, 1285 [NASA ADS] [CrossRef] [Google Scholar]
- Llovet, X., Powell, C. J., Salvat, F., & Jablonski, A. 2014, J. Phys. Chem. Ref. Data, 43, 013102 [NASA ADS] [CrossRef] [Google Scholar]
- Loch, S. D., Witthoeft, M., Pindzola, M. S., et al. 2005, Phys. Rev. A, 71, 012716 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, W. 1967, ApJS, 14, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, W. 1968, Z. Phys., 216, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Ludlow, J. A., Loch, S. D., Pindzola, M. S., et al. 2008, Phys. Rev. A, 78, 052708 [NASA ADS] [CrossRef] [Google Scholar]
- Masai, K. 1984, Ap&SS, 98, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Mattioli, M., Mazzitelli, G., Finkenthal, M., et al. 2007, J. Phys. B At. Mol. Phys., 40, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- Moores, D. L. 1972, J. Phys. B At. Mol. Phys., 5, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M., & Sugihara, M. 2001, J. Comput. Appl. Math., 127, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Pattard, T., & Rost, J. M. 1999, Phys. Scr. Vol. T, 80, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovski, G., Smith, M. D., Mac Low, M.-M., & Rosen, A. 2002, MNRAS, 337, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Pindzola, M. S., Ballance, C. P., & Loch, S. D. 2012, J. Phys. Conf. Ser., 388, 062016 [CrossRef] [Google Scholar]
- Pradhan, A. K., & Nahar, S. N. 2011, Atomic Astrophysics and Spectroscopy (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Reilman, R. F., & Manson, S. T. 1979, ApJS, 40, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, G. C., Indelicato, P., Santos, J. P., Patté, P., & Parente, F. 2004, At. Data Nucl. Data Tables, 86, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Schmutzler, T., & Tscharnuter, W. M. 1993, A&A, 273, 318 [NASA ADS] [Google Scholar]
- Shapiro, P. R., & Moore, R. T. 1976, ApJ, 207, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Slavin, J. D., Shull, J. M., & Begelman, M. C. 1993, ApJ, 407, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Suno, H., & Kato, T. 2006, At. Data Nucl. Data Tables, 92, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Takahasi, H., & Mori, M. 1974, Publ. Res. Inst. Math. Sci., 9, 721 [CrossRef] [Google Scholar]
- Wang, Y., Zatsarinny, O., & Bartschat, K. 2013, Phys. Rev. A, 87, 012704 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Woodruff, P. R., Hublet, M.-C., Harrison, M. F. A., & Brook, E. 1978, J. Phys. B At. Mol. Phys., 11, L679 [CrossRef] [Google Scholar]
- Yamada, I., Danjo, A., Hirayama, T., et al. 1989, J. Phys. Soc. Jpn., 58, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, S. M. 1980, Phys. Rev. A, 22, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, S. M. 1981, J. Quant. Spectrosc. Radiat. Transf., 26, 329 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Binding energies (eV) calculated with the MDFGME code for the ground-state configurations of C I–C VI.
All Figures
 |
Fig. 1. K- and L-shell (dashed black lines) and total (solid black lines) ionization cross sections of the carbon atom and ions calculated with the MRBEB model and total cross sections in AR85 (blue lines) and D2007 (red lines) calculated with the GIPPER code (green lines). |
| In the text | |
 |
Fig. 2. Fit (dotted lines) to the electron-impact ionization cross sections (solid lines) of C I using Eqs. (10) and (11). |
| In the text | |
 |
Fig. 3. Carbon ionic fraction variation with temperature evolving under collisional ionization equilibrium calculated with the MRBEB, GIPPER, and D2007 cross sections. |
| In the text | |
 |
Fig. 4. Comparison of the cooling (erg cm3 s−1), normalized to nenH, due to electron-impact ionization (EII), bremsstrahlung (FF), and line emission (LE)) in a gas parcel evolving under collisional ionization equilibrium and calculated with MRBEB, GIPPER, and D2007 electron-impact ionization cross sections. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \sigma (E)=\frac{10^{-13}}{I^{2}_{Z,z} u}\left[\sum _{i=1}^{n_{\rm max}}A_{i}\left(1-\frac{1}{u}\right)^{i}+B\ln (u)+C\frac{\log u}{u}\right]\,\mathrm{cm}^{2} , \end{aligned} $$](/articles/aa/full_html/2019/11/aa35337-19/aa35337-19-eq1.gif)
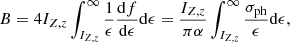
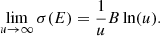
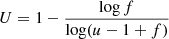
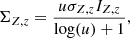
![$$ \begin{aligned} \sigma _{nlj,\,\mathrm{LS}} = \frac{4\pi a_{o}^{2}\alpha ^{4}N}{\left(\beta _{t}^{2}+\chi \beta _{b}^{2}\right)2 b^{\prime }} \left[A(\beta _{t}, t, b^{\prime })+B(t, t^{\prime },b^{\prime })\right]\,\mathrm{cm}^{2} \end{aligned} $$](/articles/aa/full_html/2019/11/aa35337-19/aa35337-19-eq6.gif)
![$$ \begin{aligned} A(\beta _{t},t,b^{\prime })= 0.5\left[\ln \left(\frac{\beta _{t}^{2}}{1-\beta _{t}^{2}}\right)-\beta _{t}^{2}-\ln (2b^{\prime })\right]\left(1-\frac{1}{t^{2}}\right) \end{aligned} $$](/articles/aa/full_html/2019/11/aa35337-19/aa35337-19-eq7.gif)
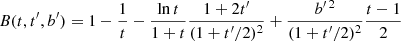
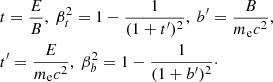
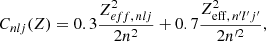
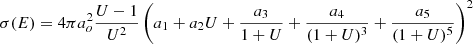
![$$ \begin{aligned} \sigma (E)=\frac{U}{U+1.513}\frac{4\pi a_{o}^{2}}{\beta ^{2}}\left[ b_{1} \chi +b_{2}\frac{\chi }{P}+b_{3}+b_{4}\left(1-\beta ^{2}\right)^{1/4}+b_{5}\frac{1}{P}\right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa35337-19/aa35337-19-eq13.gif)
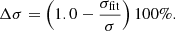
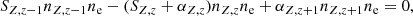
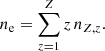
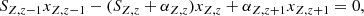
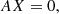
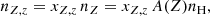
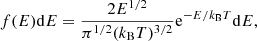
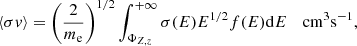
![$$ \begin{aligned} \alpha _{Z,z}^\mathrm{RR}=A\left[\left(\frac{T}{T_{0}}\right)^{1/2}\left(1+\left(\frac{T}{T_{0}}\right)^{1/2}\right)^{1-b} \left(1+\left(\frac{T}{T_{1}}\right)^{1/2}\right)^{1+b}\right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2019/11/aa35337-19/aa35337-19-eq24.gif)
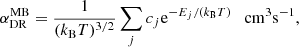
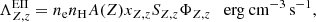
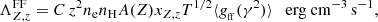
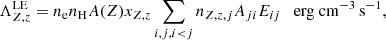
![$$ \begin{aligned}&\sum _{m<j}C_{mj}^\mathrm{e}n_{_{\rm e}}n_{Z,z,m}+\sum _{n>j}\left(A_{nj}+C_{nj}^\mathrm{d}n_{\rm e}\right)n_{Z,z,n} \nonumber \\&\quad - n_{Z,z,j}\left[\sum _{j<n}C_{jn}^\mathrm{e}n_{\rm e}+\sum _{j>m}\left(A_{jm}+C_{jm}^\mathrm{d}n_{\rm e}\right)\right] = 0, \end{aligned} $$](/articles/aa/full_html/2019/11/aa35337-19/aa35337-19-eq32.gif)