| Issue |
A&A
Volume 630, October 2019
Rosetta mission full comet phase results
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935229 | |
| Published online | 20 September 2019 | |
Outgassing-induced acceleration of comet 67P/Churyumov-Gerasimenko
1
Zuse Institute Berlin, Supercomputing Division,
Takustr. 7,
14195
Berlin,
Germany
e-mail: kramer@zib.de
2
Department of Physics, Harvard University,
17 Oxford St.,
Cambridge,
MA
02138,
USA
Received:
7
February
2019
Accepted:
18
March
2019
Context. Cometary activity affects the orbital motion and rotation state through sublimation-induced forces. The availability of precise rotation-axis orientation and position data from the Rosetta mission allows us to accurately determine the outgassing of comet Churyumov-Gerasimenko/67P (67P).
Aims. We derived the observed non-gravitational acceleration of 67P directly from the trajectory of the Rosetta spacecraft. From the non-gravitational acceleration, we recovered the diurnal outgassing variations and study a possible delay of the sublimation response with respect to the peak of the solar illumination. This allowed us to compare the non-gravitational acceleration of 67P with expectations based on empirical models and common assumptions about the sublimation process.
Methods. We used an iterative orbit refinement and Fourier decomposition of the diurnal activity to derive the outgassing-induced non-gravitational acceleration. The uncertainties of the data reduction were established by a sensitivity analysis of an ensemble of best-fit orbits for comet 67P.
Results. We find that the Marsden non-gravitational acceleration parameters reproduce part of the non-gravitational acceleration, but need to be augmented by an analysis of the nucleus geometry and surface illumination to draw conclusions about the sublimation process on the surface. The non-gravitational acceleration closely follows the subsolar latitude (seasonal illumination), with a small lag angle with respect to local noon around perihelion. The observed minor changes of the rotation axis do not favor forced precession models for the non-gravitational acceleration.
Conclusions. In contrast to the sublimation-induced torques, the non-gravitational acceleration does not place strong constraints on localized active areas on the nucleus. We find a close agreement of the orbit-deduced non-gravitational acceleration and the water production that is independently derived from Rosetta in situ measurements.
Key words: comets: general / comets: individual: 67P / celestial mechanics
© ESO 2019
1 Introduction
Studying the non-gravitational acceleration of comets provides important insights into the sublimation of cometary ices. Earth-bound astrometry allows determining the orbital corrections that arise from the sublimation of volatiles. Non-gravitational accelerations are often invoked to explain the orbital evolution of comets and even interstellar objects entering the solar system (Whipple 1950; Marsden et al. 1973; Micheli et al. 2018; Sekanina 2019).
As pointed out by Yeomans et al. (2004), it is therefore of interest to compare widely used models with the precise data returned from spacecraft missions. For comet 67P/Churyumov-Gerasimenko (67P), Krolikowska (2003) provided an assessment of the Marsden parameters within the asymmetric outgassing model of Yeomans & Chodas (1989) before the arrival of Rosetta at the comet. The determination of accurate parameters from Earth-based telescopic observations requires monitoring the position of the comet at several apparitions.
The situation is different for the orbit of 67P as observed by Rosetta. Rosetta accompanied 67P for more than two years and provided measurements of the three-dimensional position vector with an accuracy better than 100 km (see Godard et al. 2017). The discrepancy between Earth-based orbit prediction and the position where Rosetta encountered 67P 590 days before perihelion requires adjusting the Marsden-type orbit by 2000 km. From this it can be estimated that Rosetta provided an accuracy that is higher by up to 20 times compared to previous orbit determinations.
In conjunction with the precisely known rotation state of 67P, we attribute the actual orbital changes to the sublimation activity across the nucleus. Accounting for the observed gas release of 67P requires extending the non-gravitational acceleration models developed by Whipple, Marsden, and Sekanina. To this end, we introduce a Fourier decomposition of the sublimation-induced force and establish a general expression connecting the diurnal variations of the sublimation rate with the orbital evolution. This formalism simplifies the analysis by eliminating intermediate angles and emphasizes the lack of proportionality between total production rate and non-gravitational acceleration.
2 Orbit changes by non-gravitational acceleration
The equation of motion for the position vector r of the cometary nucleus is described by contributions of the solar system gravitational acceleration aG and the additional non-gravitational acceleration aNG (see, e.g., Yeomans et al. 2004),
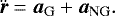 (1)
(1)
In general, this equation holds in any inertial system, but we considered it in the Earth’s equatorial system. The gravitational part aG = aG(r, t) is evaluated atthe momentary position vector and takes into account the acceleration due to all solar system planets and the Earth, Moon, Pluto, Vesta, and Ceres. Additional corrections for relativistic effects are ignored here because they only play a minor role for 67P. Relativistic corrections could be added for other objects that move faster around the Sun. The non-gravitational part is affected by the sublimation of volatiles on the nucleus across the surface. For given initial conditions r(t0), 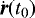 and a suitable model of the non-gravitational acceleration, the orbit of a comet can be integrated with high precision.
and a suitable model of the non-gravitational acceleration, the orbit of a comet can be integrated with high precision.
2.1 Marsden-type orbits
To understand the origin of the non-gravitational acceleration aNG, it is helpful to consider different reference frames. Starting from the icy snowball model introduced by Whipple (1950, 1951) to account for sublimation processes, Marsden and co-authors developed a powerful parameterization for the non-gravitational acceleration in a series of papers (Marsden 1968, 1969, 1972, 1970; Marsden & Sekanina 1971; Marsden et al. 1973). Marsden expressed aNG with respect to three right-handed orthogonal unit vectors with er pointing from the Sun to the nucleus, en directed along the orbital angular momentum perpendicular to the orbital plane, and et being orthogonal to both er and en. By comparing 14 cometary orbits, Marsden et al. (1973) derived the following model for the non-gravitational acceleration:
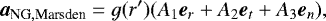 (2)
(2)
with the constant parameters A1, A2, and A3 and the empirical activity function
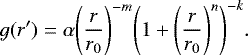 (3)
(3)
The solar distance r′ = r(t − Δt) includes a time-shift Δt introduced by Yeomans & Chodas (1989) to account for activity asymmetries with respect to perihelion, as studied by Sekanina (1988). As we discuss later, g(r) is not directly proportional to the sublimation flux, as originally stated by Marsden et al. (1973), Eq. (4). The Marsden parameters provide an excellent albeit empirical description of the non-gravitational acceleration. The integration of a Marsden-type orbit proceeds by solving Eq. (1) with the non-gravitational acceleration Eq. (2).
2.2 Orbit determination based on spacecraft data
Moving beyond the Marsden model requires more detailed data from spacecraft missions or radar observations about the magnitude and direction of the observed non-gravitational acceleration in space. For 67P, the Rosetta mission provides a two-year data set for the rotation-axis orientation (see Kramer et al. 2019) and the orbital evolution, but an iterative process was required to obtain the three-dimensional non-gravitational acceleration with high precision. We started with the multi-arc orbital solution from the flight dynamics team at ESOC, which is available as SPICE kernel (CORB_DV_257_03___T19_00345.BSP) and is returned from the Horizons system as the position for 67P during the Rosetta mission. In the following we refer to it as rESOC(t). Before and after the Rosetta mission, Horizons returns the solution 67P/K154/2 based on Marsden parameters with a discontinuous jump by 2000 km into the Rosetta period. In addition to this discontinuity in Horizons, further discontinuities in the ESOC position vector rESOC(t) during the Rosetta mission exist, which do not allow us to obtain the acceleration by a second derivative of the position vector (see the discussion by Attree et al. 2019).
An accurate estimate of the non-gravitational acceleration is tied to finding the best possible initial condition during a time with negligible cometary activity. We iteratively refined the orbit to identify the initial conditions that minimize the error norm with respect to the ESOC data in the time period (−400, −200) days from perihelion (see Table 1). During this initial search only the gravitational acceleration was considered, thus we evaluated the cometary orbits with Eq. (1) with the setup aNG = 0.
In the next step we added Marsden-type non-gravitational accelerations with the parameters used by Horizons (see Table 2 and the parameter estimation by Krolikowska 2003), and we solved Eqs. (1) and (2) to obtain rMarsden(t). We extended the integration to the years 1959–2022 (limited by two Jupiter encounters) and verified that our initial conditions lead to orbital solutions within 4400 km with respectto the Horizons solution. We compared our results with those obtained by submitting the corresponding osculating elements to the Advanced Horizons Asteroid & Comet SPK web interface (Horizons 2019). For the given initial conditions our Marsden-type solution (Fig. 1) is considerably closer to rESOC than the Marsden solution given by Attree et al. (2019). Attree et al. (2019) reported a Marsden solution with a difference in Earth-bound range |rESOC −rEarth|−|rMarsden −rEarth| of 1500 km 400 days after perihelion, while our Marsden solution at that time only differs by 50 km. This highlights the necessity of performing a thorough statistical ensemble analysis of initial conditions to validate the non-gravitational part of the orbital acceleration. In the final iteration we fit the remaining difference vector Δr(t) = rESOC −rMarsden to a combinationof exponentials and polynomials up to fourth order, which provided (upon adding it to the Marsden solution) a differentiable representation of the observed orbit,
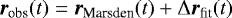
(see Fig. 1). Only after these iterative steps was the non-gravitational acceleration obtained from
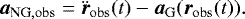 (4)
(4)
The validation of the second-order derivative of the initially noisy position vector required a careful analysis of errors introduced by the fit. We repeated the entire analysis by applying the smoothing and differentiation filter introduced by Savitzky & Golay (1964) with the corrections by Steinier et al. (1972) to the larger difference vector rESOC −r0, where r0 includes only gravitational forces. The distance is ten times larger and increases the fit uncertainties, but leads to qualitatively similar results in the period ±100 days from perihelion. The remaining systematic errors are discussed in Sect. 4. The resulting non-gravitational acceleration is shown in Fig. 2. In combination with the initial condition (Table 1), the retrieved aNG,obs reproduced the multi-arc solution rESOC for ± 400 days around perihelion with a meanerror of 21 km, mainly caused by the nonphysical jumps (see black curve in Fig. 1). At most times, the error is around 10 km (≈ 5 cometary radii). To test the sensitivity of the orbit with respect to the initial conditions, we investigated an ensemble of 1000 nearby initial conditions and verified that no further improvement is obtained. In the 1000 initial conditions, we identified 31 orbits with a mean error <22 km in the ±400-day interval around perihelion. These orbits all originate from a phase space volume extending about 3 km around the initial position listed in Table 1 and have <10−5 variations in the velocities. In the following we show results for this set of 31 solutions in the form of shaded bands to estimate the uncertainties of the derived quantities from the orbits.
Representative initial conditions for the orbit integration at JDB 2 456 897.71970 (≈ −350 days from perihelion), mean equator, and equinox of the terrestrial J2000 frame.
 |
Fig. 1 Upper panel: Euclidean error norm of various orbital solutions with respect to the multi-arc ESOC reference. Lower panel: residuals with respect to the Earth-bound range of the orbital solutions. r0 is the purely gravitational solution, rMarsden a Marsden-type orbit, and robs the best-fit reconstructed orbit for the non-gravitational acceleration shown in Fig. 2. The shaded band indicates thevariation across 31 initial positions for the Marsden solution. |
 |
Fig. 2 Non-gravitational acceleration of 67P in the terrestrial equatorial frame. Upper panel: observed aNG,obs. The shaded band indicates the variation across the set of initial conditions. Lower panel: Marsden model aNG,Marsden. The parameters are from Tables 1 and 2. |
3 Transformation of the non-gravitational acceleration to the cometary body
Next we connected the observed non-gravitational acceleration to the cometary activity on the surface. We assumed that the nucleus is not in tumbling rotation and that the rotation period and axis orientation are fixed during a single cometary rotation. For 67P this is an excellent approximation because the orientation over 800 days changed only by 0.5° and the cometary rotation period Trot decreased by 21 min from 12.4 h 300 days before the 2015 perihelion (see Godard et al. 2017; Kramer et al. 2019).
The Marsden non-gravitational acceleration given by Eq. (2) is restricted to the direction dictated by the time-independent linear combination A1, A2, and A3 of the comoving basis. This rigid link ignores the physical properties of the nucleus, in particular, the rotation axis orientation and rotation period that are encoded in the angular velocity vector ω. For cometary activity driven by the solar illumination on the nucleus, the A1, A2, and A3 components are no longer time independent. Sekanina (1967) studied the arising temporal variation of the Marsden parameters under the assumption of a fixed orientation of the rotation axis. Sekanina introduced a coordinate system that takes into account the obliquity of the comet equatorial plane with the orbital plane to study the illumination conditions of the subsolar point during the orbital motion. This approach was further extended by Whipple & Sekanina (1979), Sekanina (1984), and Sitarski (1990) to time-dependent Marsden parameters, including precession models with a changing rotation axis and associated oblateness of the nucleus. Before the rotation state of 67P was known, Krolikowska (2003) applied different models to 67P, including forced precession solutions.
For 67P a detailed shape model is available from Preusker et al. (2017), and the changes of the rotation state are known (see Jorda et al. 2016; Kramer et al. 2019). 67P showed a highly repetitive diurnal pattern of gas and dust in the coma across the entire illuminated nucleus, indicating a very regular and periodically repeating outgassing (Kramer & Noack 2016; Kramer et al. 2017, 2018; Läuter et al. 2019). Of particular interest is the surface activity with respect to the subsolar point in the body frame. For a given rotation vector ω and position vector r of the nucleus, the rotation matrix Rcom→equ is the transformation from the cometary equatorial frame (without nucleus rotation) to the terrestrial equatorial frame,
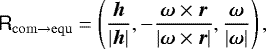 (5)
(5)
with h = − (ω ×r) ×ω. This places the Sun at a fixed subsolar longitude. This construction is very similar to Sekanina’s system (both share the basis vector ω∕|ω|). Any arising force (observed or modeled) from cometary activity Fequ = Rcom→equRz(−ωt)Fbf is expanded in a Fourier series with respect to the subsolar longitude,
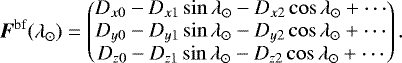 (6)
(6)
The Fourier coefficients D, in principle defined for each single rotation, are slowly varying functions with the orbital positions around the Sun. This expression encompasses comets with few active regions (see Jewitt 1997 for a simple model of a rectangular shaped comet) as well as globally active comets. The Fourier representation facilitates the rotational averaging across one rotation period (λ⊙ (t) = − ωt for 67P) in the inertial system
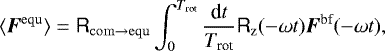 (7)
(7)
with the rotation matrix around the z axis Rz in the notation of Montenbruck & Gill (2000). The final expression for the non-gravitational acceleration acting on the orbit of a comet with mass M (1013 kg for 67P) is given by inserting Eq. (6) into Eq. (7),
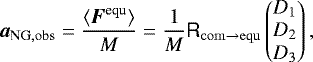 (8)
(8)
with the three linear combinations remaining from the complete Fourier expansion,
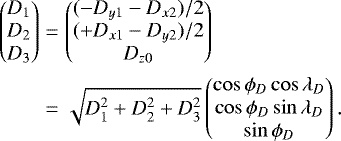 (9)
(9)
The parameters D1, D2, and D3 are the force coefficients with respect to the cometary equatorial frame (represented by the transformation in Eq. (5)). The link from Eq. (5) to the commonly used Sekanina angles is established by expressing
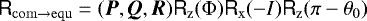 (10)
(10)
in terms of the orbital vectors P, Q, R, the obliquity I of the orbit plane to the equator of the comet, the argument of the subsolar meridian at perihelion Φ, and the longitude of the subsolar meridian from the ascending node of the orbit plane on the equator θ0. The Marsden basis vectors in Sect. 2.1 have the representation
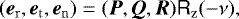 (11)
(11)
with the true anomaly ν. The vector with longitude λD and latitude ϕD in the cometary equatorial frame transforms to the components Ur, Ut, Un for the Marsden basis by the relation
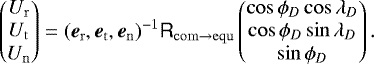 (12)
(12)
Setting θ + π = λD and ϕ = − ϕD yields Eq. (2) in Sekanina (1981). Assuming additionally − ϕD to be the latitude of the subsolar point, this relation simplifies to the classical Eq. (4) in Sekanina (1981).
4 Physical properties from non-gravitational acceleration
The parameters D1, D2, and D3, and with them, the non-gravitational acceleration, arise from the diurnally averaged activity along the spin axis and the amplitudes in the equatorial plane of the comet. This is reflected in the observed data after they are decomposed in the cometary equatorial frame in terms of spherical coordinates, see Fig. 3. The longitude λD and latitude ϕD denote the direction of the acceleration with respect to the subsolar point. Around perihelion, the observed acceleration points north, in accordance with the subsolar latitude ϕsun around − 50°, while at the two equinox crossings, the acceleration lies in the equatorial plane. Up to a shift toward more southern latitudes, the seasonal variation of the subsolar latitude is reflected in the observations. This confirms the validity of Sekanina’s approach (see Sect. 3) with respect to the seasonal component. The determination of the diurnal lag angle with respect to the solar illumination shows larger uncertainties; no lag is discernible up to perihelion. After perihelion, the acceleration vector lags behind (in time) with respect to the momentary anti-solar direction up to 50°. This lag disappears at about 140 days after perihelion, when the coma is increaslingly more strongly dominated by CO2 (see Läuter et al. 2019). The lag cannot be explained by a forced precession model because the rotation-state changes of 67P are small. In principle, a varying surface activity across the nucleus can lead to a lag angle if local surface normal directions do not point toward the sun (see Samarasinha et al. 1996 for an illustration). Davidsson & Gutiérrez (2004) studied the variations in non-gravitational force with respect to varying activity patterns across an ellipsoidal nucleus (see their Fig. 6). They found small directional changes in non-gravitational acceleration. Coma observations of 67P indicate a very repetitive gas and dust release across the entire illuminated surface, see Kramer et al. (2018). This is inline with the observation that sublimation models of 67P are not capable of reproducing the reported orbit rESOC within an Earth-bound range error <10 km. For instance, the model of Attree et al. (2019) results in a deviation of 140 km with respect to the observed Earth-bound range 150 days after perihelion. In addition to the shape of the nucleus, another possible cause of a diurnal lag angle is a delay between the maximum illumination and the highest gas release in some areas.
From the observation of sunset jets on 67P, Shi et al. (2016) obtained thermal delays of peak surface and sublimation temperatures of about 1− 2 h (corresponding to a rotation of 29°−58°) in the Ma’at region in April 2015. Their calculations are based on a thermal inertia of 50 W m−2 K−1 s1∕2. At perihelion and at other locations on the surface, the thermal delays might differ from these values, or effects can cancel each other out. Finally, the observed lag angle could be affected by an (unknown) systematic error of the ESOC orbit, which cannot be detected by the present analysis. A conclusive attribution of the observed lag angle to a physical process requires further modeling.
The initial motivation for the study of non-gravitational acceleration was to deduce the total production flux of a comet. The total sublimation flux Q(r) is approximately given by the product of the average gas velocity vgas,av with the magnitude aNG of the non-gravitational acceleration divided by the cometary mass M,
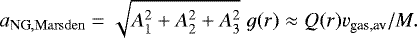 (13)
(13)
The Fourier decomposition of the total force allows us to clarify the relation between sublimation flux and non-gravitational acceleration after factoring out the average gas velocity vav :
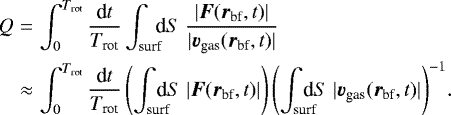 (14)
(14)
Next, we applied the triangle inequality to obtain a lower bound for the sublimation flux,
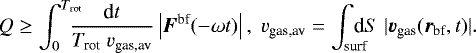 (15)
(15)
Inserting Eq. (6) for the force components and neglecting faster oscillating terms allowed us to perform the integration analytically,
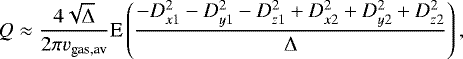 (16)
(16)
where 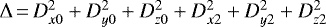 , E (x) denotes the complete elliptic integral. The result shows that the magnitude of the non-gravitational acceleration contains additional force components besides the D1, D2, D3 components, which leads to minor corrections.
, E (x) denotes the complete elliptic integral. The result shows that the magnitude of the non-gravitational acceleration contains additional force components besides the D1, D2, D3 components, which leads to minor corrections.
An entirely independent determination of the gas production for 67P has been performed by Läuter et al. (2019) by analyzing the in situ data of the Double Focusing Mass Spectrometer (DFMS) of the Rosetta Orbiter Spectrometer for Ion and Neutral Analysis (ROSINA). The non-gravitational acceleration by Eq. (13) shows a remarkable agreement to the ROSINA-derived water production QH2O(r) of 67P from Läuter et al. (2019), Fig. 3, with gas velocity vgas,av = 480 m s−1.
 |
Fig. 3 Observed non-gravitational acceleration in the cometary equatorial frame, magnitude (upper panel), and corresponding latitude and longitude of the direction of the sublimation force (lower panel). The latitude ϕD is correlated with the anti-solar latitude (− ϕsun) (black line in the lower panel), while the longitude correlates with the night terminator λD = 180°. The shaded band indicates the variation across the set of initial conditions. The red graph in the upper panel shows the ROSINA-derived water production of 67P from Läuter et al. (2019). |
5 Conclusions
The Rosetta mission to comet 67P provided the unique opportunity to retrieve the non-gravitational acceleration of a comet independently from Earth-based observations. In conjunction with the known rotation state, the position data derived from Rosetta allowed us to verify commonly invoked assumptions about the non-gravitational acceleration. We have shown that the orbit reconstruction is sensitive to the initial conditions and identified a phase-space volume 350 days before perihelion that leads to orbital solutions following the reported ESOC positions within a mean deviation of 22 km. This close match allowed us to extract the three-dimensional non-gravitational acceleration and to relate it to the activity on the nucleus.
Using a Fourier series, we have decomposed the non-gravitational acceleration into the averaged outgassing along the rotation axis and the amplitudes of the outgassing along the equatorial plane of the comet. A similar analysis and Fourier theory has been carried out by Kramer et al. (2019) for the rotation state of 67P. We provided error bounds for all derived quantities based on an extensive analysis of initial conditions for the orbital integration. Until perihelion, we find no clear signal of a lag angle between illumination and force direction, while at later times, deviations from the instantaneous illumination become apparent. The seasonal effect of the solar illumination on the non-gravitational acceleration is reflected by a strong correlation of the subsolar latitude and the direction of the sublimation force. The agreement of the observed non-gravitational acceleration with the seasonal illumination conditions demonstrates that the non-gravitational acceleration can be explained by the water-ice distribution on the entire nucleus. The derivation of the diurnal lag carries considerably larger errors at times later than 100 days after perihelion, but points to a shift toward longer delay times 50–100 days after perihelion. The non-gravitational acceleration alone is most indicative about active areas in terms of a zonal mean.
Local active areas across the surface cannot be detected because there are no longitudinal variations. This is in contrast to the torque, which affects the rotation axis orientation and rotation period: they both react sensitively to local activity variations (Kramer et al. 2019).
Finally, we have shown that based on the analysis of the Rosetta orbit alone, a close agreement with the in situ measurements of the gas coma and production of 67P exists. This connection allows us to relate Earth-based astrometry and production estimates with accurate in situ measurements and models of cometary activity, which is a prerequisite to advance non-gravitational acceleration models.
Acknowledgements
The authors acknowledge the North-German Supercomputing Alliance (HLRN) for providing computing time on the Cray XC40. We thank the anonymous referee for helpful comments.
References
- Attree, N., Jorda, L., Groussin, O., et al. 2019, A&A, 630, A18, (Rosetta 2 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davidsson, B. J., & Gutiérrez, P. J. 2004, Icarus, 168, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Godard, B., Budnik, F., Bellei, G., & Morley, T. 2017, International Symposium on Space Flight Dynamics – 26th ISSFD [Google Scholar]
- Horizons 2019, Asteroid & Comet SPK File Generation Request, https://ssd.jpl.nasa.gov/x/spk.html [Google Scholar]
- Jewitt, D. 1997, Earth Moon Planets, 79, 35 [Google Scholar]
- Jorda, L., Gaskell, R., Capanna, C., et al. 2016, Icarus, 277, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, T., & Noack, M. 2016, ApJ, 823, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, T., Läuter, M., Rubin, M., & Altwegg, K. 2017, MNRAS, 469, S20 [CrossRef] [Google Scholar]
- Kramer, T., Noack, M., Baum, D., Hege, H.-C., & Heller, E. J. 2018, Adv. Phys. X, 3, 1404436 [Google Scholar]
- Kramer, T., Läuter, M., Hviid, S., et al. 2019, A&A, 630, A3 (Rosetta 2 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krolikowska, M. 2003, Acta Astron., 53, 195 [NASA ADS] [Google Scholar]
- Läuter, M., Kramer, T., Rubin, M., & Altwegg, K. 2019, MNRAS, 483, 852 [Google Scholar]
- Marsden, B. G. 1968, ApJ, 73, 367 [Google Scholar]
- Marsden, B. G. 1969, ApJ, 74, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G. 1970, ApJ, 75, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G. 1972, IAU Symp., 45, 135 [NASA ADS] [Google Scholar]
- Marsden, B. G., & Sekanina, Z. 1971, ApJ, 76, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Yeomans, D. K. 1973, ApJ, 78, 211 [Google Scholar]
- Micheli, M., Farnocchia, D., Meech, K. J., et al. 2018, Nature, 559, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Montenbruck, O., & Gill, E. 2000, Satellite Orbits (Berlin, Heidelberg: Springer) [CrossRef] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2017, A&A, 607, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samarasinha, N. H., Mueller, B. E., & Belton, M. J. 1996, Planet. Space Sci., 44, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Savitzky, A., & Golay, M. J. E. 1964, Anal. Chem., 36, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z. 1967, Bull. Astr. Inst. Czechosl., 18, 15 [NASA ADS] [Google Scholar]
- Sekanina, Z. 1981, Ann. Rev. Earth Planet. Sci., 9, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z. 1984, ApJ, 89, 1573 [Google Scholar]
- Sekanina, Z. 1988, ApJ, 96, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z. 2019, ArXiv e-prints [arXiv:1901.08704] [Google Scholar]
- Shi, X., Hu, X., Sierks, H., et al. 2016, A&A, 586, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sitarski, G. 1990, Acta Astron., 40, 405 [NASA ADS] [Google Scholar]
- Steinier, J., Termonia, Y., & Deltour, J. 1972, Anal. Chem., 44, 1906 [CrossRef] [Google Scholar]
- Whipple, F. L. 1950, ApJ, 111, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1951, ApJ, 113, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F., & Sekanina, Z. 1979, AJ, 84, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Yeomans, D. K., & Chodas, P. W. 1989, ApJ, 98, 1083 [Google Scholar]
- Yeomans, D. K., Chodas, P. W., Sitarski, G., Szutowicz, S., & Królikowska, M. 2004, in Comets II (Tucson, AZ: The University of Arizona Press), 16 [Google Scholar]
All Tables
Representative initial conditions for the orbit integration at JDB 2 456 897.71970 (≈ −350 days from perihelion), mean equator, and equinox of the terrestrial J2000 frame.
All Figures
 |
Fig. 1 Upper panel: Euclidean error norm of various orbital solutions with respect to the multi-arc ESOC reference. Lower panel: residuals with respect to the Earth-bound range of the orbital solutions. r0 is the purely gravitational solution, rMarsden a Marsden-type orbit, and robs the best-fit reconstructed orbit for the non-gravitational acceleration shown in Fig. 2. The shaded band indicates thevariation across 31 initial positions for the Marsden solution. |
| In the text | |
 |
Fig. 2 Non-gravitational acceleration of 67P in the terrestrial equatorial frame. Upper panel: observed aNG,obs. The shaded band indicates the variation across the set of initial conditions. Lower panel: Marsden model aNG,Marsden. The parameters are from Tables 1 and 2. |
| In the text | |
 |
Fig. 3 Observed non-gravitational acceleration in the cometary equatorial frame, magnitude (upper panel), and corresponding latitude and longitude of the direction of the sublimation force (lower panel). The latitude ϕD is correlated with the anti-solar latitude (− ϕsun) (black line in the lower panel), while the longitude correlates with the night terminator λD = 180°. The shaded band indicates the variation across the set of initial conditions. The red graph in the upper panel shows the ROSINA-derived water production of 67P from Läuter et al. (2019). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


