| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834988 | |
| Published online | 26 September 2019 | |
On the recent parametric determination of an asteroseismological model for the DBV star KIC 08626021
1
Grupo de Evolución Estelar y Pulsaciones. Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
e-mail: fdegeronimo@fcaglp.unlp.edu.ar, tbattich@fcaglp.unlp.edu.ar, mmiller@fcaglp.unlp.edu.ar
2
Instituto de Astrofísica La Plata, IALP (CCT La Plata), CONICET-UNLP, La Plata, Argentina
Received:
28
December
2018
Accepted:
21
August
2019
Context. Asteroseismology of white dwarf stars is a powerful tool that allows us to reveal the hidden chemical structure of white dwarfs and infer details about their present and past evolution by comparing the observed periods with those obtained from appropriate stellar models. A recent asteroseismological study has reproduced the period spectrum of the helium-rich pulsating white dwarf KIC 08626021 with the unprecedented precision of (Pobs − Pmodel)/Pmodel < 10−8. The chemical structure derived from that asteroseismological analysis is notably different from that expected for a white dwarf according to currently accepted formation channels. It therefore poses a challenge to the theory of stellar evolution.
Aims. We explore the relevant micro- and macrophysics processes that act during the formation and evolution of KIC 08626021 and might lead to a chemical structure similar to that found through asteroseismology. We quantify to which extent it is necessary to modify the physical processes that shape the chemical structure in order to reproduce the most important features of the asteroseismic model.
Methods. We modeled the previous evolution of KIC 08626021 by exploring specific changes in the 12C(α, γ)16O reaction rate, screening processes, microscopic diffusion, and convective boundary mixing during core-He burning.
Results. We find that in order to reproduce the core chemical profile derived for KIC 0862602, the 12C+α nuclear reaction rate has to be increased by a factor of ∼10 during the helium-core burning, and reduced by a factor of ∼1000 during the following helium-shell burning as compared with the standard predictions for this rate. In addition, the main chemical structures derived for KIC 0862602, such as the very thin helium-pure envelope, the mass of the carbon-oxygen core, and the pure C buffer, cannot be reconciled with our current knowledge of white dwarf formation.
Conclusion. We find that within our current understanding of white dwarf formation and evolution, it is difficult to reproduce the most important asteroseismologically derived features of the chemical structure of KIC 08626021.
Key words: stars: oscillations / stars: interiors / stars: evolution / white dwarfs
© ESO 2019
1. Introduction
White dwarf (WD) stars constitute the most common final evolutionary stage of low- and intermediate-mass stars (up to ∼10.6 M⊙, Woosley & Heger 2015). In average-mass WDs, the chemical constitution of the core is mostly a mixture of 12C and 16O plus trace elements, of which 22Ne is expected to be the most abundant. This chemical composition is the result of the core He-burning phase (CHeB) during progenitor evolution. At advanced stages of evolution, the WD progenitor is expected to evolve to the thermally pulsing asymptotic giant branch (TP-AGB), where the chemical composition of the outer layers of the WD is built up (Althaus et al. 2010a). This critical phase affects the evolution and pulsational properties of the emerging WD (De Gerónimo et al. 2017, 2018).
White dwarfs exhibit pulsational instabilities at some point in their evolution. In particular, H-deficient (He-rich) pulsating WDs (or DBVs) are found to be unstable against pulsations in the effective temperature range 22 000 ≲ Teff ≲ 30 000 K. Their multimode photometric variations are caused by nonradial g-mode pulsations of low degree with periods between 100 and 1400 s. In the single-evolution scenario, DB WD stars are believed to be formed in the very late thermal pulse (VLTP), where the progenitor star experiences its final thermal pulse on the early cooling branch, with the result that the remaining H envelope is consumed (Herwig et al. 1999; Iben et al. 1983; Miller Bertolami et al. 2006). Alternatively, some DB WDs can be formed by mergers of two WDs, either carbon-oxygen (CO)- or helium (He)-core WDs (Saio & Jeffery 2000, 2002).
Details of the inner chemical structure of WDs can be inferred through interpreting their pulsational spectra by means of adequate representative models (asteroseismology). This procedure constitutes a key technique for understanding the evolution of the WD progenitors (Córsico et al. 2019; Fontaine & Brassard 2008; Winget & Kepler 2008; Althaus et al. 2010b). In addition, asteroseismological analyses of WD stars provide strong constraints on the stellar mass, thickness of the outer envelopes, core-chemical composition, and stellar rotation rates (e.g., Bognár et al. 2014; Romero et al. 2012; Córsico et al. 2012; Bischoff-Kim & Østensen 2011), and allow us to study physical processes such as crystallization (Montgomery & Winget 1999; Córsico et al. 2004; Romero et al. 2013; De Gerónimo et al. 2019).
Two main approaches have been adopted for the asteroseismology of pulsating WD stars. The first is based on static stellar structures with parameterized luminosity and chemical profiles (Bischoff-Kim & Østensen 2011; Bischoff-Kim et al. 2014, 2019; Giammichele et al. 2014, 2016, 2017). The second approach is based on stellar evolution models computed from the zero-age main sequence (ZAMS) to the WD stage (see Romero et al. 2012, 2013; Córsico & Althaus 2006; Córsico et al. 2006, 2009, in the case of H-rich WD, DB, and PG1159 stars, respectively). The first approach includes the construction of a very dense grid of models and the exploration of chemical structures that are not necessarily expected from our current understanding of stellar evolution. The flexibility of this method allows for extremely high-precision fits and asteroseismic models that are not necessarily accurate, however. Parameterized chemical profiles are usually mildly inspired by stellar evolution results. The second approach, on the other hand, relies on the accuracy of stellar evolution theory for a restriction of the parameter space but is usually based on coarser grids. This prevents high-precision fits, but conversely, they are expected to be more accurate as they are informed by a mature theory such as that of stellar evolution. This is particularly useful in the case of WD asteroseismology, where the number of observed independent periods is usually small. This asteroseismological approach is, however, affected by current uncertainties during the progenitor evolution. These uncertainties leave their signature on the predicted pulsation properties and asteroseismic inferences of pulsating WDs. As recently shown in De Gerónimo et al. (2017, 2018), the effect of these uncertainties can be quantified and bounded.
Based on the parametric approach, Giammichele et al. (2018) found an asteroseismic model with an unprecedented precision in their pulsation-period match for the DBV star KIC 08626021. The derived stellar parameters are MWD = 0.570 ± 0.005 M⊙, Teff = 29 968 ± 198 K, and log g = 7.92 ± 0.01 cm s−2. This pulsating star, located near the blue edge of the instability strip, has been extensively monitored by the Kepler mission, revealing eight independent modes with periods from 143.2 s to 376.1 s (Zong et al. 2016; Bischoff-Kim et al. 2014; Østensen et al. 2011). The precision of the fit is better than 1 μs (i.e., a relative period difference of Pobs − Pmodel)/Pmodel < 10−8), which is well below the observational uncertainties of ∼38 μs. However, this finding has been put into question by Timmes et al. (2018), who showed that the inclusion of neutrino emission, which is expected in young WDs and was not considered by Giammichele et al. (2018), affects the low-order g-mode frequencies up to ∼70 μHz. Additionally, the derived structure parameters, such as a large CO core, a high central O abundance, a well-defined C-pure mantle, and a thin pure-He envelope, pose a challenge to the predictions of the stellar evolution. This is particularly true for the homogeneous CO-core derived by Giammichele et al. (2018) that is much more massive (0.45 M⊙) than theoretical expectations. This disagreement between stellar evolution theory and the asteroseismological model of Giammichele et al. (2018) is surprising in view of the previous studies by Van Grootel et al. (2010a,b), Charpinet et al. (2011), and Constantino et al. (2015) about the size of the He-burning core. These asteroseismological determinations found a good agreement between the size of the He-burning convective core (0.22– 0.28 M⊙), which shapes the future homogeneous CO-core of the WD, with that coming from stellar evolution (see Constantino et al. 2015; Bossini et al. 2015).
We here show that the main features of the chemical structure derived for KIC 08626021 from asteroseismology cannot be reproduced in the frame of the standard evolutionary theory. We assess the effect of possible uncertainties during WD and progenitor evolution by computing the full evolution of initial star models from the ZAMS through the CHeB and TP-AGB phases, and finally to the WD domain. We explore several physical processes that could lead to a chemical structure that is characterized by a large CO-core with high O abundance, a C-mantle around the CO-core, and a C-rich intershell at the bottom of the very thin He envelope, as illustrated by the asteroseismic model for KIC 08626021. In particular, we explore the mixing processes that occur at the border of the convective core as well as the dependence of the 12C(α, γ)16O nuclear reaction rate on the temperature during the CHeB phase. We also analyze to what extent the evolution during the TP-AGB could affect the CHe intershell in addition to the C buffer. Finally, we assess the effect that element diffusion has on the predicted chemical profile for KIC 08626021.
This paper is organized as follows: in Sect. 2 we describe the main features found in the chemical structure of a WD and their connection with the prior evolution. In Sect. 3 we present the results of our computations, and finally, in Sect. 4 we summarize our results and conclusions.
2. Formation of the chemical structure of a WD
Figure 1 shows the typical chemical structure of a DBV model with similar parameters to those found by Giammichele et al. (2018): MWD = 0.58M⊙, Teff ∼ 29 000 K, and log g = 7.93 cm s−2, derived from the full computation of the progenitor evolution (upper panel) and the chemical-abundance profiles predicted by the asteroseismic model for the DBV KIC 08626021 (Giammichele et al. 2018, bottom panel). The abundance distribution of O, C, and He from the core to the outer layers are shown in terms of the outer mass fraction coordinate. The chemical structure of the evolutionary model bears the clear signatures of distinct processes that are operative during stellar evolution, such as the CHeB, He-shell burning during the AGB, convective mixing during the TP-AGB, and element diffusion during the WD regime. Different regions of the WD chemical profile can be tracked down to individual processes and, consequently, they can be related to specific uncertainties in stellar evolution. From center to surface, that is, from left to right in the upper panel of Fig. 1, we identify the homogeneous central CO core [−q ≲ 0.3, q = log(1 − mr/M⋆)], which is shaped during He-core burning and the very beginning of He-shell burning. The size of the homogeneous core and the O mass fraction are therefore affected by uncertainties in convective boundary mixing (CBM) and the 12C(α, γ)16O rate (Straniero et al. 2003; Constantino et al. 2015, 2017; Bossini et al. 2015). The region at 0.3 ≲ −q ≲ 1.5 follows, which is built up during the early AGB and the TP-AGB as the He-burning shell progresses outward (Salaris et al. 1997; Althaus et al. 2010a). The details of this region, in particular its C mass fraction and extension, are mostly affected by CBM during the thermal pulses and at the bottom of the convective envelope, which determine the efficiency of the third dredge-up and also the intensity of the second dredge-up in more massive stars. This affects the height of the C peak at −q ∼ 1.5, which is higher when no CBM is included. Between 1.5 ≲ −q ≲ 5 lies the He-C-O intershell, which is produced during the last thermal pulse experienced by the progenitor star. The C and O abundances in this region are very dependent on the third dredge-up history of the progenitor and therefore on CBM during the TP-AGB. The more efficient the CBM, the larger the final O abundance at the expense of C and He (Herwig 2000, 2005). The chemical transitions at −q ∼ 1.5 and −q ∼ 5 are shaped by gravitational settling, although the inner transition is far from diffusive equilibrium when it reaches the DBV instability strip (Althaus et al. 2009). In addition, the total He content of the final WD is slightly affected by details on the AGB evolution, but its order of magnitude is defined by the total mass of the final WD.
 |
Fig. 1. Upper panel: inner distribution of O, C, and He in terms of the outer mass fraction corresponding to the expectations from a typical DBV model of mass ∼0.58 M⊙ resulting from the complete progenitor evolution. Bottom panel: same as above, but for the asteroseismic model for the DBV KIC 08626021 of Giammichele et al. (2018). |
Figure 1 illustrates the profound contrast between the chemical structure predicted by stellar evolutionary theory and that predicted by the asteroseismic model for the DBV KIC 08626021. The central O abundance and, more noticeably, the extension of the CO-core are both larger than predicted by stellar evolution for stars with final masses MWD ≲ 0.6 M⊙ (Salaris et al. 1997; Althaus et al. 2010a). In addition to the properties of the CO core, other unconventional features are easily distinguishable in the asteroseismic model for the DBV KIC 08626021. The existence and location of the almost pure C buffer located at 2.5 ≲ −q ≲ 3 is very different from that predicted by stellar evolution models. While stellar evolution models (e.g., Straniero et al. 2003; Miller Bertolami & Althaus 2006; Bossini et al. 2015) show a C peak that formed during the late AGB evolution, its C mass fraction is always XC < 0.8 and it is located deeper inside the star. This last fact is connected to another unusual feature of the asteroseismic model for the DBV KIC 08626021: the low He content derived for that star (MHe = 0.0001 MWD), which is about 2 orders of magnitude lower than that predicted for WDs of average mass ∼0.6 M⊙ (Romero et al. 2012). Finally, the asteroseismologically derived pure He envelope is about 3 orders of magnitude less massive than that predicted by gravitational settling at the evolutionary stage at which KIC 08626021 is found.
3. Results
The WD evolutionary models we used were computed with the stellar evolution code LPCODE (Althaus et al. 2005; Miller Bertolami 2016). LPCODE produces detailed WD models in a consistent way with the predictions of progenitor evolutionary history, based on an updated physical description. In the following we enumerate the most relevant physical parameters we adopted: (i) Diffusive overhsooting during the evolutionary stages prior to the TP-AGB phase was allowed to occur following the description of Herwig et al. (1997). We adopted f = 0.0174 for all sequences, except when indicated otherwise. The occurrence of overshooting is relevant for the final chemical stratification of the WD (Prada Moroni & Straniero 2002; Straniero et al. 2003). (ii) Gravitational settling and thermal and chemical diffusion were taken into account during the WD stage for 1H, 3He, 4He,12C,13C, 14N, and 16O (Althaus et al. 2003). (iii) During the WD phase, chemical rehomogenization of the inner C-O profile induced by Rayleigh–Taylor (RT) instabilities was implemented following Salaris et al. (1997).
In the next sections we investigate the physical processes that act during the evolution of the progenitor and WD that might be responsible for shaping the most important features of the chemical structure of the asteroseismic model for KIC 08626021.
3.1. Convective boundary mixing during CHeB
The treatment of CBM is one of the main uncertainties that affect the stellar evolutionary models and has some influence on the chemical profile of the WD. In particular, the incorrect application of the Schwarzschild criterion during the He-core burning phase can have a strong effect on the final chemical profile of the WD (Gabriel et al. 2014; Salaris & Cassisi 2017). The mass of the homogeneous central part of the CO core of WD models results from the interplay between convection and nucleosynthesis during CHeB, the ignition of the He shell at the very beginning of the early AGB, and the late homogenization of the central parts driven by an inversion in the mean molecular weight of the stellar material (see Fig. 3 of Salaris et al. 1997).
The location of the outer boundary of the convective core is initially governed by a self-driving mechanism (Castellani et al. 1971). Any extension of the convective boundary beyond its formal value as given by the Schwarzschild criterion is expected to increase the C abundance of the neighboring layers, thus leading to an increase in their opacity, and consequently ∇rad, and thus to a larger convective core. The increase in size of the convective core moves the convective boundary, and CBM, even further. This process continues until the value of ∇rad equals the local value of the adiabatic gradient ∇ad. The self-driving nature of this mechanism means that as soon as some mixing is allowed beyond the He-burning convective core, the process develops until it reaches its stable value. Michaud et al. (2007) showed that even atomic diffusion is enough to trigger this instability, eventually increasing the size of the convective He core. Consequently, the adoption of a bare Schwarzschild criterion for the determination of the convective borders will lead to nonphysical convective He-burning cores, where neutral buoyancy is not attained at both sides of the convective border as a consequence of the chemical discontinuity. In our case, this problem can either be solved by a detailed analysis of convective stability at both sides of the convective border (Gabriel et al. 2014), or by allowing for some mixing beyond the ill-defined convective boundary. The inclusion of even a very tiny CBM already allows models to grow the convective core so that it reaches neutral buoyancy at its outer convective boundary. It is expected that the final size of the convective core is similar regardless of the nature of the additional mixing that occurs at the convective boundary because the mechanism is self-driving. A detailed account of CBM during the He-core burning stage of low-mass stars can be found in Sect. 4.2 of Salaris & Cassisi (2017).
In addition to this self-driving mechanism, the later He-core burning gives rise to the appearance of splittings in the formal (i.e., Schwarzschild criterion) convective core that can be modeled as a partially mixed region, where neutral buoyancy is attained (Castellani et al. 1985). This is referred to as semiconvection by some authors1. Again, the inclusion of some minor CBM allows the convective zone to remain connected, and although details in the final chemical profiles keep a record of the exact method that is adopted to compute mixing beyond the formal convective boundary, all algorithms lead to similar sizes of the homogeneous central part of the CO core (Bossini et al. 2015; Constantino et al. 2015). As a consequence, different treatments of convective boundary mixing during the CHeB stage do not lead to significant discrepancies in the final chemical profiles of the WD, provided that some mixing is allowed beyond the formal Schwarzschild convective boundary.
The extent of the homogeneous central part of the core in the chemical profile derived by Giammichele et al. (2018) is about 0.45 M⊙, much higher than the predicted by evolutionary computations, ∼0.32 M⊙. Giammichele et al. (2018) proposed that this could be due to more mixing during the CHeB by semiconvection or overshooting. We explored the effect of the extension of the convective core on the final size of the homogeneous central part of the WD core. In order to do this, we performed simulations starting from the same initial model (Z = 0.01, Mi = 1 M⊙) for different values of the CBM parameter f during CHeB2. In particular, we explored values of f = 0.00174, 0.0087, 0.0174, 0.0348, 0.087, and 0.174, which correspond to 1/10, 1/2, 1, 2, 5, and 10 times the standard value of f0 = 0.0174, see Miller Bertolami (2016).
Figure 2 shows the resulting chemical profiles of our models at the beginning of the thermally pulsing AGB phase, after the homogenization of the central parts driven by an inversion in the mean molecular weight of the stellar material (Salaris et al. 1997). As expected, as soon as some additional mixing is allowed at the convective boundary, the size of the homogeneous CO core is significantly enlarged. Even a very minor CBM efficiency (f = f0/10) is already enough to start the self-driving mechanism we described at the beginning of this section, which produces a homogeneous CO core of MCO ≃ 0.286 M⊙ (to be compared with the MCO ≃ 0.205 M⊙ that results in the unrealistic case in which all CBM is prevented). In comparison, further increases in the value of f by factors of 5, 10, and 20 (i.e., f = 0.0087, 0.0174, and0.03) lead to relatively minor increases in the mass of the homogeneous CO core: MCO ≃ 0.292, 0.322, and 0.322 M⊙, respectively. Based on our previous discussion, this is an expected trend because the main process that determines the size of the core only requires the existence of some additional mixing, provided that it is enough to alter the layers immediately outside the formal convective border (Castellani et al. 1971, 1985). Only when f = 0.087 is adopted does the extent of the CBM lead to a larger homogeneous core of 0.354 M⊙. This value is still far below the value of 0.45 M⊙ derived by Giammichele et al. (2018) for KIC 08626021. Considering that a value of f = 0.087 = 5 × f0 is very high in comparison with any calibration of the overshooting parameter, this rules out the possibility that CBM is the cause for the large CO core inferred for KIC 08626021. Assuming a higher value of f, that is, f = 0.174, we find the evolution of the post-CHeB star to be completely altered, with thermal pulses developing only 800 000 yr after the end of CHeB. This is more than a factor 10 shorter than in a normal evolution, and thus effectively truncates the very existence of the early AGB phase. Such a model would be incompatible with the existence of the early AGB phase and should be discarded on these grounds alone. Even with this inconsistently high value of f = 0.174, the mass of the homogeneous CO core is reduced by the first thermal pulse to 0.386 M⊙ (from a value of 0.422 M⊙ at the very end of the HeCB), which is well below the value of 0.45 M⊙ derived by Giammichele et al. (2018).
 |
Fig. 2. Oxygen chemical profiles as a function of the mass coordinate for different assumptions of the overshooting parameter. The vertical dashed line corresponds to the extent of the homogeneous central part of the core that is predicted by the asteroseismic model of KIC 8626021. |
The inability to produce homogeneous CO cores as large as those reported by Giammichele et al. (2018) is not a property of the exponentially diffusive overshooting prescription adopted here but of all studied CBM recipes. As was shown in Fig. 4 of Straniero et al. (2003) for standard-size WDs (∼0.6 M⊙), semiconvection and penetrative or mechanical overshooting, even under extreme assumptions, lead to homogeneous CO cores well below the value derived by Giammichele et al. (2018). A similar result is shown in Fig. 2 of Constantino et al. (2015), which in addition to penetrative overshooting and semiconvection also explores the CO profiles left by a moderate exponentially decaying overshooting, and in Fig. A1 of Bossini et al. (2015), which shows the final CO profiles under different assumptions of the temperature gradient for the mechanical overshooting approximation (called “overshooting” and “penetrative convection” in their work) under the extreme assumption of a 1HP overshooting zone. In addition to these experiments, Constantino et al. (2015) explored a “maximal-overshooting” scheme that avoids the splitting of the He-burning core at later stages of the CHeB phase. This recipe leads to slightly smaller homogeneous CO cores than the standard exponential and penetrative overshooting prescriptions. Finally, Constantino et al. (2017) also explored the incorporation of Spruit’s core-growth rate (Spruit 2015). Spruit (2015) described physically sound arguments regarding the maximum rate at which a convective He-burning core can grow in a steady regime based on the higher buoyancy of the material ingested. These arguments then set an upper limit on the maximum size of a He-burning core and consequently on the size of the homogeneous CO region in the core of WDs. Figure 1 of Constantino et al. (2017) shows that Spruit’s argument also leads to convective cores not larger than those obtained with the exponentially decaying overshooting approximation. All these works together show that the outer boundary of the homogeneous CO core of a low-mass star, like the progenitor of KIC 08626021, cannot exceed 0.35 M⊙ even in the most extreme situations. We conclude that CBM cannot cause the homogeneous part of the core to grow up to 0.45 M⊙ without drastically changing other parts of the stellar evolution that are well constrained, such as the existence of the early AGB phase.
3.2. Efficiency of the diffusion processes
Several processes strongly modify the chemical structure of the progenitor star during the evolution of a WD. Gravitational settling is the primary shaper of WD chemical profiles: it forms chemically pure outer layers. Here, we explore to what extent element diffusion processes that are due to gravitational settling and thermal and chemical diffusion might be responsible for the formation of a C-pure buffer at the top of the CO core. We also explore for how long a very thin He envelope can survive the effects of diffusion in the absence of competing processes. Diffusion coefficients, which determine how efficient these processes are, have been calculated by various groups (e.g., Paquette et al. 1986; Baalrud & Daligault 2013). Differences in the diffusion coefficients are at most of one order of magnitude in the regime of strong coupled plasma (Baalrud & Daligault 2013; Paxton et al. 2015).
To explore the effect of time-dependent diffusion on the chemical profile of a WD at the effective temperature and mass of KIC 8626021, we evolved a ∼0.57 M⊙ WD model from ∼200 000 K to ∼29 000 K and modified the efficiency of the diffusion processes by a multiplicative factor f, f = 0.01, 1, and 100, which covers the actual uncertainties in these processes well. Figure 3 shows the chemical profiles we obtained with our experiment. Clearly, changing the efficiency of the diffusion processes in any reasonable amount is not expected to reproduce the main remarkable features of the asteroseimological profile of KIC 8626021. In particular, we note that the peak of C at log(1 − mr/M⋆)∼ − 1.4 does not change significantly in either the peak value or in position. This means that we cannot invoke diffusion as the process responsible for creating an almost pure C buffer in the WD.
 |
Fig. 3. Chemical profiles for He, C, and O of our DBV evolutionary models (∼29 000 K) in terms of the outer mass fraction, resulting from different efficiency of element diffusion. The values of the quantity f indicates the multiplicative factor of the diffusion efficiency with respect to the standard value (f = 1). |
A difficulty also arose when we tried to reproduce the thin pure-He envelope derived by Giammichele et al. (2018). The relatively low uncertainties in the diffusion physics in the outer regions of WDs (Baalrud & Daligault 2013; Paxton et al. 2015) mean that we can estimate how long such a thin He-pure envelope can survive. To this end, we performed a set of numerical experiments with LPCODE by computing the speed of gravitational settling at the evolutionary stage and mass of KIC 8626021. The initial chemical profiles are shown in Fig. 3, but the outer He-pure envelope is located at different initial depths of −log(1 − mr/M⋆) = 7.6, 8.6 (models A and B, respectively). Our computations show that in about 100 000–200 000 yr the envelope becomes already thicker than the value found for KIC 8626021, −log(1–mr/M⋆) = 7.4 (see Fig. 4), which is beyond the range of the asteroseismical solutions. These timescales are only 1% to 2% of the time required by standard DB WD models to cool down to Teff ∼ 30 000 K, which is about 10 Myr for models in that mass range (Althaus et al. 2009). Hence, if KIC 8626021 were characterized by this thin He envelope, then the WD should have been formed by an evolutionary scenario that allowed it to cool down to its present state about 50 to 100 times faster than normal DB stars.
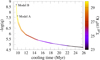 |
Fig. 4. Time evolution of the position of the bottom of the pure-He envelope (measured in terms of the outer mass fraction q) from Teff ∼ 30 000 K for models with initial −log(q)∼7.6 and 8.6 (models A and B, respectively). For model A (B), 0.08 (0.18) Myr is enough for diffusion processes to thicken the He envelope below log(q)∼7.4. |
Competing processes such as strong winds or rotation might delay the action of gravitational settling. However, the existence of strong winds in WDs is at variance with the observed action of radiative levitation in DO stars (Hoyer et al. 2018), which can only be effective if winds do not prevent the action of diffusion. The location of the DO-PG1159 transition (Werner et al. 2017) can also be reproduced (Unglaub & Bues 2000) when WD winds decay strongly with decaying luminosity, as expected from theory of radiation-driven winds (e.g., Ṁ ∝ L1.86, as proposed by Bloecker 1995). In particular, stellar winds are expected to stop as soon as metals sink below the photosphere and are not available to absorb momentum from the radiation field (Unglaub & Bues 2000). In addition, the fast drop in mass loss with stellar luminosity proposed by Bloecker (1995) is needed to provide a coherent picture of the GW Vir red edge instability domain (Quirion et al. 2012). All these concerns are reinforced by the fact that such winds would require an extremely fine tuning of its intensity to remove almost all, but not quite the entire, initial He content. Similarly, while rotational mixing could lead to a delay of gravitational settling, the slow solid-body rotation measured in KIC 0826021 by Giammichele et al. (2018) strongly argues against this possibility.
3.3. 12C(α, γ)16O nuclear reaction rate and Coulomb screening
The chemical abundances of the CO core, as well as those in the layers immediately above the core, are produced at the end of CHeB phase and at the beginning of He-shell burning. In the previous section we showed that diffusion is unable to create the C-pure buffer, even when diffusion coefficients beyond the current uncertainties are adopted. Assuming that diffusion is the only process that can modify the chemical structure during the WD stage, any chemical structure that is located so deep in the interior of the star is expected to be a fossil record of the previous evolution. The O-to-C ratio left by He burning is a consequence of the competition of the 3α reactions that create 12C and the 12C+α reaction that destroys 12C to create 16O. In particular, the 12C+α reaction is one of the most uncertain reactions in stellar evolution. In this section, we explore to which extent the temperature dependence of the 12C+α nuclear reaction rate should be altered in order to produce the high central O abundances together with the previously discussed C buffer. Recently, De Gerónimo et al. (2017) explored the implications of the current uncertainties in the 12C + α nuclear reaction rate during the CHeB phase over the chemical structure and pulsation periods of hydrogen-rich pulsating WDs. The authors found that these uncertainties have a non-negligible effect on the chemical structure, but their Fig. 7 shows that it is clear that none of their models predict the most important features of the asteroseismic model found for KIC 08626021.
In view of these findings, we computed the evolution of a progenitor star from the ZAMS to the DB WD stage by significantly altering the nuclear reaction rate for the purpose of mimicking the chemical structure of KIC 08626021. Because of the different temperatures at which CHeB and He-shell burning proceed in the progenitor evolution, it is possible to alter the 12C+α reaction rate to simultaneously reproduce the large central O abundance and the C buffer that was derived by Giammichele et al. (2018). We have been able to reproduce the high central abundance for 16O (∼82% by mass) by enhancing the 12C + α reaction rate during the CHeB phase (up to ten times higher than the highest value predicted by Kunz et al. 2002) for T ≲ 0.13 × 109 K. Beyond the core, we were able to form a C mantle at the top of the CO core by reducing the generation of O in the outward-moving He-burning shell during post-CHeB evolution. To do this, we decreased the reaction rate in the range 0.13 × 109 ≲ T by about 100 to 1000 times compared to the rate predicted by Kunz et al. (2002). A C-dominated buffer was found only in this way (∼90%), with a small amount of O. In Fig. 5 we compare the standard 12C + α reaction rate with its current uncertainties–±30% of the relative uncertainty–at the CHeB temperatures together with the altered reaction rate that is required to reproduce the asteroseismic model for KIC 8626021. It is clear that the uncertainty in the 12C + α reaction rate cannot be invoked to produce the high O abundance in the core and the almost C-pure buffer of the WD profile described in Giammichele et al. (2018).
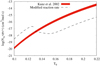 |
Fig. 5. 12C + α reaction rate at the CHeB temperatures according to Kunz et al. (2002; red thick line) together with the altered reaction rate that is required to mimic the asteroseismic model for KIC 8626021 (dashed line). |
We also explored possible uncertainties in the Coulomb screening factors that might lead to the formation of such features in the chemical structure. The screening corrections are applied as a multiplicative factor of the form expf to the nuclear reaction rates, where the factor f depends upon the charge of the nucleus taking part in the reactions. Up to now, all the recipes of screening corrections were derived within certain assumptions (Dewitt et al. 1973; Graboske et al. 1973; Wallace et al. 1982). However, we need to keep in mind that any change in the screening correction of a particular reaction will not affect only that reaction, but possibly also every nuclear reaction where one of the same nuclei is involved. This prevents us from changing the screening factors in an extreme way. In particular, as discussed in the previous paragraph, the 12C + α reaction rate is the main responsible factor for setting the interior profile of a WD during the CHeB and the He-shell burning phases. When we interpret this change to be due to the uncertainty in the screening factor, we need expf to be more than one order of magnitude higher than is calculated by our code (taken from Graboske et al. 1973 and Wallace et al. 1982) for temperatures up to T9 ∼ 0.13 and lower for temperatures T9 ≳ 0.13 (two orders of magnitude lower for T9 ≳ 0.16). These extreme changes in the screening of the 12C + α reaction rate are expected to affect other screening factors for reactions involving C, He, or both (or even other isotopes because the change depends on the temperature dependence). This most probably drastically changes other parts of the stellar evolution that are well constrained.
3.4. Thermal pulses on the AGB
Three main features in the chemical structure of the asteroseismic model can be connected with physical processes that occur at the TP-AGB phase: the CHe plateau located beyond the C buffer, the total content of He, and the size of the degenerate core. The CHe plateau is the result of the short-lived convective episodes that occur at the He-burning shell stage, which dredge up C and shape the flattened profile. The amount of O, C, and He that is left in this intershell region depends on the strength of the CBM at the border of the pulse-driven convection zone, where f ∼ 0.0075 reproduces both the initial to final mass relation and the abundances of PG1159 stars reasonably well (Miller Bertolami 2016). Particularly the intershell abundances derived for the asteroseismic model (C ∼ 80%, see lower panel of Fig. 1) disagree with the results from Herwig (2000) and our computations, as shown in Fig. 6. There we show the intershell abundances resulting from the computations of a MZAMS = 1.5 M⊙ (final CO-core mass MCO ∼ 0.58M⊙) model adopting extreme values for the overshooting parameter f = 0 and f = 0.0174 in terms of the number of thermal pulses experienced by the star on the AGB. These extreme values of f cover the current overshooting uncertainties during the TP-AGB phase well. We find that the maximum amount of 12C in the intershell region (∼50%) occurs at the very first thermal pulses of the model with f = 0.0174, and this abundance is still far below the 12C abundances derived for KIC 08626021.
 |
Fig. 6. Intershell abundances of 4He,12C, and 16O during the evolution on the thermally pulsing AGB phase. Dashed (solid) lines refer to the model in which (no) overshooting is considered in this stage. |
The low total content of He of the asteroseismological model could be explained if the star experienced a long-lasting TP-AGB phase, that is, if the star experienced very many thermal pulses. We find that it is possible to reduce the total He content of the star from 1.7 × 10−1 to 1 × 10−2 M⊙ in the course of 10 thermal pulses. A total He content of 10−4 M⊙, as found for KIC 08626021, would be possible if the star experienced more than 30 thermal pulses. In this case, however, the growth of the core would largely exceed the mass derived for the asteroseismic model. It is therefore not possible to find a model with an extremely low content of He for an average mass WD in this context. A He content like this is found for ultra-massive WDs (Camisassa et al. 2019). Similar results were reported by Lawlor & MacDonald (2006, see Figs. 9 and 10), who described a final He content of ∼6 × 10−4 M⊙ for a WD of 1.05 M⊙.
A drawback arises when we attempt to reproduce the intershell abundances and the low content of He for the same model. The inclusion of CBM during the TP-AGB phase favors the occurrence of third dredge-up episodes that prevent the core from growing and leads to the C enrichment of the surface layers. The pollution of the stellar surface with C drives strong winds, with the result of an earlier departure from the TP-AGB. This is in contrast with the long-lasting TP-AGB phase that is required for the depletion of He to values close to ∼1 × 10−4 M⊙. In light of the previous discussion, it appears difficult to assume that the physical processes that operate in the TP-AGB phase within their respective uncertainties could lead to the scenario in which an average-mass WD is formed with a C-rich intershell region simultaneously with a very low He content.
4. Summary and conclusions
Giammichele et al. (2018) have performed an extremely precise asteroseismological study of KIC 8626021 for the first time. This is a DBV star that has been extensively monitored by the Kepler mission. The authors were able to find an asteroseismic model with an unprecedented precision in their pulsation period match. This paved the way to investigating the physical processes that lead to the formation of WD stars. The chemical structure derived by Giammichele et al. (2018) from their asteroseismological analysis for KIC 8626021 contradicts what is expected for a DB WD star in terms of the widely accepted formation channels. It therefore poses a challenge to the theory of WD formation. We here explored to what extent both microphysics (diffusion processes and nuclear reaction rates) and macrophysics (convective boundary mixing and semiconvection) processes would need to be modified in order to reproduce the chemical structure that has asteroseismologically been derived for the DB pulsating WD KIC 8626021 by Giammichele et al. (2018). To this end, we computed the evolution of progenitor stars from the ZAMS to the DBV domain with final masses MWD ∼ 0.58 M⊙. As a first step, we explored the extent of the convective boundaries during the CHeB phase in order to reproduce the mass of the large central homogeneous part of the core. Based on the arguments presented by Giammichele et al. (2018), we explored the effect of extending the convective core on the final size of the homogeneous central part of the WD core by enhancing the overshooting up to five times the standard value. Even with such a large extension of the convective boundary, our models are unable to develop a homogeneous central part of the core of M ∼ 0.45 M⊙. We also explored the efficiency of the diffusion processes that act during the WD cooling path in order to mimic the C buffer at the top of the core. We evolved a ∼0.57 M⊙ WD model from ∼200 000 K to the DB phase (∼30000 K) in which we varied the efficiency of the diffusion processes from 0.01 to 100 times the standard value. We found that diffusion is unable to create the C buffer at the top of the core within a reasonable timescale. Additionally, we found that the thin He envelope that characterizes the asteroseismic model could take place if the star cooled down 50 to 100 times faster than normal DB stars.
In view of these findings and assuming that diffusion is the only process that can modify the chemical structure during the WD stage, these chemical features that are located so deep in the interior of the star need to be created during the evolution of the progenitor star during the CHeB and AGB phases. We computed the complete evolution of a progenitor star in which we altered the 12C(α, γ)16O nuclear reaction rate during the whole evolution. By modifying the nuclear reaction rate far beyond the extreme values predicted by Kunz et al. (2002), we were able to reproduce a C buffer at the top of an O-dominated core. In particular, these features were only achieved when we enhanced the nuclear reaction rate by up to 10 times for T < 0.13 × 109 K and decreased it to 100–1000 times for T > 0.13 × 109 K, which clearly lies outside the values suggested by laboratory determinations, including their uncertainties. In addition, we discarded the idea that these features in the chemical structure might be reproduced by altering the screening factors within their uncertainties. We discussed the C-rich CHe plateau and the low He content in the whole asteroseismic model. We found that a long-lasting TP-AGB phase might be scenario for the formation of a star with low He content, but we envisage that this He content will be possible for WDs with M⋆ ≈ 1.05 M⊙. This result is in contrast with the inclusion of CBM at the TP-AGB phase, a necessary ingredient for reproducing the intershell abundances.
Our results suggest that the asteroseismic model for KIC 8626021 developed by Giammichele et al. (2018) is difficult to reconcile with our current understanding of the standard evolutionary scenario for the formation of WDs. Further investigations are needed to understand the origin of this discrepancy.
In closing, it is appropriate to comment that Timmes et al. (2018) have shown that even the very feeble effect of neutrino emission on the mechanical structure of the WDs is enough to alter low-order g-mode frequencies by about 70 μHz, which has a sizeable effect on WD mass, radius, and central O mass fraction. Numerical experiments on our full evolutionary models show that the small chemical details left by previous evolution (e.g., the small O bump at −q ∼ 2, see the upper panel of Fig. 1) can alter low-order g-mode periods by ∼0.1 s (∼107 μHz).
Not to be confused with the semiconvection mechanism described in textbooks (Kippenhahn et al. 2013), which is due to overstability as a consequence of nonadiabatic effects.
The value of f relates the mixing coefficient of a layer outside the formal convective zone (DCBM) at given distance d from the formal convective boundary to the mixing coefficient close to the formal convective boundary (D0) through the relation DCBM = D0 × exp−2d/fHP, where HP is the local pressure scale height at the formal convective boundary (Herwig et al. 1997).
Acknowledgments
We wish to acknowledge the suggestions and comments of an anonymous referee that strongly improved the original version of this work. Part of this work was supported by AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR, and by the PIP 112-200801-00940 grant from CONICET. This research has made use of NASA’s Astrophysics Data System.
References
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Panei, J. A., Miller Bertolami, M. M., et al. 2009, ApJ, 704, 1605 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010a, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010b, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Baalrud, S. D., & Daligault, J. 2013, Phys. Rev. Lett., 110, 235001 [NASA ADS] [CrossRef] [Google Scholar]
- Bischoff-Kim, A., & Østensen, R. H. 2011, ApJ, 742, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Bischoff-Kim, A., Østensen, R. H., Hermes, J. J., & Provencal, J. L. 2014, ApJ, 794, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Bischoff-Kim, A., Provencal, J. L., Bradley, P. A., et al. 2019, ApJ, 871, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bloecker, T. 1995, A&A, 299, 755 [NASA ADS] [Google Scholar]
- Bognár, Z., Paparó, M., Córsico, A. H., Kepler, S. O., & Győrffy, Á. 2014, A&A, 570, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bossini, D., Miglio, A., Salaris, M., et al. 2015, MNRAS, 453, 2290 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Córsico, A. H., et al. 2019, A&A, 625, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellani, V., Giannone, P., & Renzini, A. 1971, Ap&SS, 10, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Chieffi, A., Tornambe, A., & Pulone, L. 1985, ApJ, 296, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Van Grootel, V., Fontaine, G., et al. 2011, A&A, 530, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Constantino, T., Campbell, S. W., Christensen-Dalsgaard, J., Lattanzio, J. C., & Stello, D. 2015, MNRAS, 452, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Constantino, T., Campbell, S. W., & Lattanzio, J. C. 2017, MNRAS, 472, 4900 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2006, A&A, 454, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., García-Berro, E., Althaus, L. G., & Isern, J. 2004, A&A, 427, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., & Miller Bertolami, M. M. 2006, A&A, 458, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Romero, A. D., Althaus, L. G., & García-Berro, E. 2009, A&A, 506, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., & Bischoff-Kim, A. 2012, A&A, 541, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., & Kepler, S. O. 2019, A&ARv, 27, 7 [NASA ADS] [CrossRef] [Google Scholar]
- De Gerónimo, F. C., Althaus, L. G., Córsico, A. H., Romero, A. D., & Kepler, S. O. 2017, A&A, 599, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Gerónimo, F. C., Althaus, L. G., Córsico, A. H., Romero, A. D., & Kepler, S. O. 2018, A&A, 613, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Gerónimo, F. C., Córsico, A. H., Althaus, L. G., Wachlin, F. C., & Camisassa, M. E. 2019, A&A, 621, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dewitt, H. E., Graboske, H. C., & Cooper, M. S. 1973, ApJ, 181, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, M., Noels, A., Montalbán, J., & Miglio, A. 2014, A&A, 569, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giammichele, N., Fontaine, G., Brassard, P., & Charpinet, S. 2014, in Precision Asteroseismology, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, IAU Symp., 301, 285 [NASA ADS] [Google Scholar]
- Giammichele, N., Fontaine, G., Brassard, P., & Charpinet, S. 2016, ApJS, 223, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Giammichele, N., Charpinet, S., Brassard, P., & Fontaine, G. 2017, A&A, 598, A109 [Google Scholar]
- Giammichele, N., Charpinet, S., Fontaine, G., et al. 2018, Nature, 554, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Graboske, H. C., Dewitt, H. E., Grossman, A. S., & Cooper, M. S. 1973, ApJ, 181, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Bloecker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
- Herwig, F., Blöcker, T., Langer, N., & Driebe, T. 1999, A&A, 349, L5 [NASA ADS] [Google Scholar]
- Hoyer, D., Rauch, T., Werner, K., & Kruk, J. W. 2018, A&A, 612, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, Jr., I., Kaler, J. B., Truran, J. W., & Renzini, A. 1983, ApJ, 264, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Kunz, R., Fey, M., Jaeger, M., et al. 2002, ApJ, 567, 643 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Lawlor, T. M., & MacDonald, J. 2006, MNRAS, 371, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Richer, J., & Richard, O. 2007, ApJ, 670, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., & Althaus, L. G. 2006, A&A, 454, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Serenelli, A. M., & Panei, J. A. 2006, A&A, 449, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montgomery, M. H., & Winget, D. E. 1999, ApJ, 526, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Bloemen, S., Vučković, M., et al. 2011, ApJ, 736, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Paquette, C., Pelletier, C., Fontaine, G., & Michaud, G. 1986, ApJS, 61, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Prada Moroni, P. G., & Straniero, O. 2002, ApJ, 581, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Quirion, P.-O., Fontaine, G., & Brassard, P. 2012, ApJ, 755, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, A. D., Córsico, A. H., Althaus, L. G., et al. 2012, MNRAS, 420, 1462 [Google Scholar]
- Romero, A. D., Kepler, S. O., Córsico, A. H., Althaus, L. G., & Fraga, L. 2013, ApJ, 779, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Jeffery, C. S. 2000, MNRAS, 313, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Jeffery, C. S. 2002, MNRAS, 333, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Cassisi, S. 2017, R. Soc. Open Sci., 4, 170192 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Domínguez, I., García-Berro, E., et al. 1997, ApJ, 486, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 2015, A&A, 582, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Straniero, O., Domínguez, I., Imbriani, G., & Piersanti, L. 2003, ApJ, 583, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Townsend, R. H. D., Bauer, E. B., et al. 2018, ApJ, 867, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Unglaub, K., & Bues, I. 2000, A&A, 359, 1042 [NASA ADS] [Google Scholar]
- Van Grootel, V., Charpinet, S., Fontaine, G., Green, E. M., & Brassard, P. 2010a, A&A, 524, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Grootel, V., Charpinet, S., Fontaine, G., et al. 2010b, ApJ, 718, L97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wallace, R. K., Woosley, S. E., & Weaver, T. A. 1982, ApJ, 258, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, K., Rauch, T., & Kruk, J. W. 2017, A&A, 601, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Heger, A. 2015, ApJ, 810, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Zong, W., Charpinet, S., Vauclair, G., Giammichele, N., & Van Grootel, V. 2016, A&A, 585, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Upper panel: inner distribution of O, C, and He in terms of the outer mass fraction corresponding to the expectations from a typical DBV model of mass ∼0.58 M⊙ resulting from the complete progenitor evolution. Bottom panel: same as above, but for the asteroseismic model for the DBV KIC 08626021 of Giammichele et al. (2018). |
| In the text | |
 |
Fig. 2. Oxygen chemical profiles as a function of the mass coordinate for different assumptions of the overshooting parameter. The vertical dashed line corresponds to the extent of the homogeneous central part of the core that is predicted by the asteroseismic model of KIC 8626021. |
| In the text | |
 |
Fig. 3. Chemical profiles for He, C, and O of our DBV evolutionary models (∼29 000 K) in terms of the outer mass fraction, resulting from different efficiency of element diffusion. The values of the quantity f indicates the multiplicative factor of the diffusion efficiency with respect to the standard value (f = 1). |
| In the text | |
 |
Fig. 4. Time evolution of the position of the bottom of the pure-He envelope (measured in terms of the outer mass fraction q) from Teff ∼ 30 000 K for models with initial −log(q)∼7.6 and 8.6 (models A and B, respectively). For model A (B), 0.08 (0.18) Myr is enough for diffusion processes to thicken the He envelope below log(q)∼7.4. |
| In the text | |
 |
Fig. 5. 12C + α reaction rate at the CHeB temperatures according to Kunz et al. (2002; red thick line) together with the altered reaction rate that is required to mimic the asteroseismic model for KIC 8626021 (dashed line). |
| In the text | |
 |
Fig. 6. Intershell abundances of 4He,12C, and 16O during the evolution on the thermally pulsing AGB phase. Dashed (solid) lines refer to the model in which (no) overshooting is considered in this stage. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


