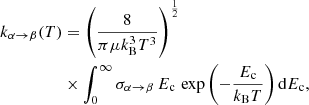| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 5 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201936170 | |
| Published online | 16 September 2019 | |
Hyperfine excitation of CH and OH radicals by He⋆
1
School of Health, Sport and Bioscience, University of East London, Stratford Campus, Water Lane, London E15 4LZ, UK
e-mail: s.marinakis@uel.ac.uk
2
Department of Chemistry and Biochemistry, School of Biological and Chemical Sciences, Queen Mary University of London, Joseph Priestley Building, Mile End Road, London E1 4NS, UK
3
Department of Optics and Spectroscopy, Tomsk State University, 36 Lenin av., Tomsk 634050, Russia
e-mail: kalugina@phys.tsu.ru
4
Institute of Spectroscopy, Russian Academy of Sciences, Fizicheskaya St. 5, 108840 Troitsk, Moscow, Russia
5
Department of Chemistry and Biochemistry, University of Maryland, College Park MD 20742, USA
e-mail: jklos@umd.edu
6
LOMC-UMR 6294, CNRS-Université du Havre, 25 rue Philippe Lebon, BP 1123, 76 063 Le Havre Cedex, France
Received:
24
June
2019
Accepted:
25
July
2019
Context. Because of their high reactivity, the CH and OH radicals are of particular interest in astrochemistry. Modeling of CH and OH molecules requires the calculation of accurate radiative Einstein coefficients and rate coefficients for (de)excitation by collisions with the most abundant species such as H2 and He.
Aims. The present paper focuses on the calculation of inelastic rate coefficients among the lowest OH/CH hyperfine levels in their ground vibrational state induced by collisions with He atoms.
Methods. Calculations of hyperfine (de)excitation of CH/OH by He were performed using the close-coupling and recoupling methods from the most recent ab initio potential energy surfaces.
Results. Cross sections for transitions among the 60 and 56 lowest hyperfine levels of CH and OH, respectively, were calculated for collision energies up to 2500 cm−1. These cross-sections were used to calculate the rate coefficients for temperatures between 10 and 300 K. A propensity rule for transitions with ΔF = Δj was observed.
Conclusions. The new rate coefficients will help significantly in interpreting the CH/OH spectroscopic data observed with current and future telescopes, and help to accurately describe the OH masers and the hyperfine anomalies in CH emission spectra.
Key words: molecular processes / ISM: molecules
The rate coefficients are available in the BASECOL database via http://basecol.vamdc.eu
© ESO 2019
1. Introduction
The past thirty years have seen an increased understanding of the role that free radicals play in astrochemistry. This has been achieved by observations of them in the interstellar medium together with advances in modeling of astrochemistry. The hydroxyl (OH) and methylidene (CH) radicals are two of the most important diatomic radicals in astrochemistry.
Indeed, the OH radical is very abundant in molecular clouds and OH fine and hyperfine transitions can be employed as a tracer of both the density (Cotten et al. 2012) and temperature (Ebisawa et al. 2015) of molecular clouds. They are also key species in the network of reactions relevant to water and other oxygen-bearing molecules (Viti et al. 2001; van Dishoeck et al. 2013; Holdship et al. 2017). Also, OH masers have been observed in many astrophysical objects and their detailed modeling is a useful probe of physical conditions. The methylidene also plays an important role in the interstellar medium (ISM). It is commonly used as a proxy for molecular hydrogen (Wiesemeyer et al. 2018).
The molecular abundances of these two radicals can be derived from interstellar spectra registered by ground- and space-based telescopes. A general property of these molecular spectra is that the populations of the energy levels are rarely at local thermodynamical equilibrium (LTE). Indeed, in space, the density is usually such that the frequency of collisions is neither negligible nor large enough to maintain LTE. In such conditions, interpreting spectra requires one to simultaneously solve the radiative transfer equation and a set of statistical equilibrium equations for the molecular energy levels. Solving the statistical equilibrium in turn necessitates the availability of the energy levels, the state-to-state rates for spontaneous radiative decay, and the state-to-state rate coefficients for collisional (de-)excitation (Roueff & Lique 2013). The predominant collision partners in the cold interstellar gas are the He atom and the molecular hydrogen (Roueff & Lique 2013).
The calculation of collisional rate coefficients for these two species has always attracted physical chemists. A brief review of the calculations of astrophysical interest can be found in Roueff & Lique (2013). Recently, we derive new collisional rotational rate coefficients for the excitation of OH and CH by He (Kalugina et al. 2014; Marinakis et al. 2015, 2016, 2019). Together with the very recent OH–H2 and CH–H2 collisional data (Kłos et al. 2017; Dagdigian 2018), these rate coefficients should enable an accurate determination of CH and OH abundance in molecular clouds. However, in these calculations as in the recent OH–H2, the hyperfine structure of the target was neglected. Indeed, the hydrogen atom possesses a non-zero nuclear spin (I = 1/2) and the coupling between I and the rotation j of the molecule results in a splitting of each level into hyperfine levels.
Resolving the hyperfine structure of a rotational transition is extremely useful. By assuming that all components have the same line width and excitation temperature, a simultaneous fit of all hyperfine components can be performed. The abundance of the molecule can be directly derived from the fit.
Then, the present paper aims to advance the above discussion by providing the necessary hyperfine resolved data to obtain accurate estimates of CH and OH abundances from observational data. After an outline of the rotational levels of CH and OH (Sect. 2), the calculation of CH–He and OH–He hyperfine resolved collisional rate coefficients is presented in Sect. 3. The results and applications of these rate coefficients are given in Sect. 4, and the main conclusions of this work are in Sect. 5.
2. Hyperfine energy levels of CH and OH molecules
Both CH and OH are open-shell molecules (radicals) in their X 2Π ground electronic state. In its lowest rovibrational levels, the CH is a Hund’s case (b) radical and the OH is a Hund’s case (a) (Brown & Carrington 2003). Because of the (electron) spin-orbit coupling, there are two spin-orbit manifolds. The 2Π1/2 spin-orbit is the lowest in CH, and the 2Π3/2 is the lowest in OH. In addition, each rotational level j is split into two Λ-doublets because of the interaction between the 2Π ground electronic state with the higher-lying Σ states. The two close lying Λ-doublet levels have opposite total parities under space-fixed inversion operator. Levels with parity ( − 1)j − 1/2 are labeled e, and levels with parity −(−1)j − 1/2 are labeled f. In addition, the hydrogen atom also possesses a non-zero nuclear spin (I = 1/2). The coupling of j and I results in a splitting of each Λ-doublet level into two hyperfine levels, which correspond to different values of the grand total angular momentum F quantum number, where F = j + I. The energies of the first CH hyperfine levels are shown graphically in Fig. 1 and for those of OH in Fig. 1 in Marinakis et al. (2016).
 |
Fig. 1. Energy level diagram of lowest 60 hyperfine levels of 12C1H. The zero reference energy is defined for the lowest CH rotational level (2Π1/2, j = 1/2). The rotational levels are drawn to scale but the Λ-doubling and the hyperfine splittings are not shown to scale for clarity reasons. It should be noted that f levels are lower than e in the F1 spin-orbit manifold but the reverse is true in the F2 spin-orbit manifold. Regarding the energy order of the hyperfine levels, higher F corresponds to higher energy in F2 but the reverse is true in F1 (with the exception for the lowest Λ-doublet shown in red). The total parity (±) is also shown. |
3. Scattering calculations
The present paper uses the most recent ab initio potential energy surface PES for CH–He (Marinakis et al. 2015) and OH–He (Kalugina et al. 2014). We refer the reader there for a discussion of previous work on these two inelastic systems. We note that there was a very good agreement between all available experimental and theoretical data validating the quality of the PESs. In the present calculations we used Alexander’s method (Alexander 1985) to study the inelastic scattering between a 2Π diatomic molecule and structureless atom. Quantum close-coupling calculations were performed using HIBRIDON program (Alexander et al. 2014) in order to obtain the nuclear-spin-free SJ(Fijεl; F′ij′ε′l′) scattering matrices between nuclear-spin-free fine structure levels of CH/OH. In this notation, Fi denotes the spin-orbit manifold, j the rotational level, ε can be either e or f, and l is the orbital angular momentum quantum number. The prime is used to denote the post-collisional levels. In the calculations, all the molecules are in the ground vibrational state, and the OH/CH rotation constants, spin-orbit coupling constants, and the Λ-doubling parameters are those from Kalugina et al. (2014) and Marinakis et al. (2015). The CH–He and OH–He and hyperfine cross-sections were obtained from the nuclear-spin-free scattering matrix using the recoupling method (Faure & Lique 2012; Marinakis et al. 2016).
The corresponding rate coefficients were computed as an average over the collision energy (Ec):
where σα → β is the cross-section from initial state α to final state β, μ is the CH/OH–He reduced mass and kB is Boltzmann’s constant. The transitions involve all levels with j up to 7.5 for temperatures ranging from 10 to 300 K for CH–He collisions, and for j up to 6.5 and for temperatures ranging from 5 to 300 K for OH–He collisions. All these rate coefficients will be available in the BASECOL (Dubernet et al. 2013) and LAMDA (Schöier et al. 2005) databases.
4. Results
State-to-state hyperfine rate coefficients for Λ-doublet changing collisions of CH/OH (X 2Π1/2, j = 0.5e) and He are shown in Figs. 2 and 3, respectively. These Λ-doublet transitions are important in astrophysics and especially for interpreting maser emission. We note that the transition F = 0 → F = 0 is forbidden. In order to examine the rotational dependence of the hyperfine Λ-doublet changing collisions, the rate coefficients between the j = 1.5 levels in the 2Π3/2 state are shown in Figs. 4 and 5. As discussed in the case of OH–He (Marinakis et al. 2016), the energy difference in these hyperfine levels is negligible and can be disregarded in the discussion on propensities at usual temperatures. Each Λ-doublet level has two hyperfine components that correspond to two different hyperfine quantum numbers Fmax and Fmin, with Fmax > Fmin. In the case of OH–He, it was shown (Marinakis et al. 2016) that the cross-sections were larger in the following order: Fmax → Fmax ≥ Fmin → Fmin > Fmin → Fmax ≥ Fmax → Fmin. This is what is observed in Fig. 6 for the rate coefficients at 100 K of CH/OH–He for all the rotational levels with the exception of j = 0.5, where as discussed one out of four transitions is forbidden. This is consistent with typical hyperfine propensity rules (Lique & Kłos 2011) that show propensity in favor of Δj = ΔF transitions, but are also proportional to the degeneracy (2F′+1) of the final hyperfine level.
 |
Fig. 2. Temperature dependence of state-to-state hyperfine rate coefficients for spin-orbit conserving collisions of CH(X 2Π1/2) and He. The initial and final levels are j = 0.5e and j = 0.5f, respectively. The initial and final F quantum numbers are shown in the graph. |
 |
Fig. 3. Temperature dependence of state-to-state hyperfine rate coefficients for spin-orbit conserving collisions of OH(X 2Π1/2) and He. The initial and final levels are j = 0.5e and j = 0.5f, respectively. The initial and final F quantum numbers are shown in the graph. |
 |
Fig. 4. Temperature dependence of state-to-state hyperfine rate coefficients for spin-orbit conserving collisions of CH(X 2Π3/2) and He. The initial and final levels are j = 1.5f and j = 1.5e, respectively. The initial and final F quantum numbers are shown in the graph. |
 |
Fig. 5. Temperature dependence of state-to-state hyperfine rate coefficients for spin-orbit conserving collisions of OH(X 2Π3/2) and He. The initial and final levels are j = 1.5f and j = 1.5e, respectively. The initial and final F quantum numbers are shown in the graph. |
 |
Fig. 6. Comparison between state-to-state Λ-doublet e → f changing hyperfine rate coefficients at 100 K for spin-orbit conserving collisions of CH/OH (X, v = 0) and He. The spin-orbit states are shown in the graph. Fmax → Fmax are shown in filled magenta circles, Fmin → Fmin transitions are shown in empty black circles, Fmin → Fmax in empty blue squares, and Fmax → Fmin in filled red squares. |
The theoretical hyperfine-resolved rate coefficients are dependent on the propensity rules observed in calculations without taking into account the nuclear spin (i.e., pure rotational data). The rate coefficients for CH(2Π1/2, j = 0.5e, F = 1 → j = 1.5−7.5, F″) collisions (some of which are shown in Fig. 7) for spin-orbit changing collisions are on average 5.45 times larger than for spin-orbit conserving transitions. On the contrary, in the OH(2Π1/2, j = 1.5e, F = 2 → j = 2.5−6.5, F′) rates (some of which are shown in Fig. 8) the spin-orbit conserving rates are on average 10.6 times larger than the corresponding spin-orbit changing rates. The difference in the rotationally-resolved spin-orbit propensities for He–CH/OH collisions has been discussed in previous work, and is due both to the difference in the spin-orbit constants (28.1468 cm−1 and −139.321 cm−1 for CH and OH, respectively) and to the different underlying PESs (Marinakis et al. 2007; Kalugina et al. 2014; Marinakis et al. 2015).
 |
Fig. 7. Comparison between state-to-state rotational-excitation hyperfine rate coefficients for spin-orbit conserving (left panel) and changing (right panel) collisions of CH (2Π1/2, v = 0, j = 0.5e, F = 1) and He. The e → e transitions are shown in the upper panel and e → f transitions are shown in the lower panel. The final j and F quantum numbers are shown next to the corresponding curves. |
 |
Fig. 8. Comparison between state-to-state rotational-excitation hyperfine rate coefficients for spin-orbit conserving (left panel) and changing (right panel) collisions of OH (2Π3/2, v = 0, j = 1.5e, F = 2) and He. The e → e transitions are shown in the upper panel and e → f transitions are shown in the lower panel. The final j and F quantum numbers are shown next to the corresponding curves. |
As discussed by Corey & Alexander (1988) in their study on hyperfine propensities in OH–H2 collisions, in the absence of external magnetic fields, the orientation of the I vector cannot be changed because the intermolecular potential is purely electrostatic. Therefore, only changes in the relative orientation of the j and I vectors can lead to a change in the magnitude of the resultant F vector (Corey & Alexander 1988). Because of the tendency for preservation of the j vector and of the general propensity for ΔF = Δj, a propensity for ΔF = 0 is often observed (Corey & Alexander 1988; Offer et al. 1994; Marinakis et al. 2016).
As discussed in previous work (Dagdigian et al. 1989; Marinakis et al. 2015), there is a propensity for transitions into antisymmetric rotational levels (Π(A″) levels, meaning F1f, F2e), in He–CH(X) upward transitions. That propensity appears in the cross-sections at various collision energies at high rotational levels but sometimes the reverse is true at low rotational levels, and this is related to the rotational dependence of the degree of electron alignment (Macdonald & Liu 1989). Also, a propensity for spin-orbit manifold conserving transitions over spin-orbit manifold changing transitions was not observed in agreement with previous work on purely rotational excitation (Marinakis et al. 2015). Although a detailed discussion of propensities is beyond the scope of this work, a visual comparison between rate coefficients for spin-orbit conserving and spin-orbit changing (left and right), and e → e versus e → f transitions for He–CH/OH collisions is shown in Figs. 7 and 8, respectively. The initial level was chosen to be the lowest e level in the lowest spin-orbit manifold with the highest F quantum number, that is j = 0.5e, F = 1 for CH, and j = 1.5e, F = 2 for OH. Different choices of the initial level can be considered in order to examine all the propensities. The final levels were from j = 2.5 to 6.5. Some of these rates are shown in Figs. 7 and 8. From these He–CH collisions, on average, the propensity is for final levels in 2Π3/2 f > 2Π1/2 f>2 Π1/2 e > 2Π3/2 e. In the case of He + OH collisions, on average, the propensity is for final levels in 2Π3/2 f > 2Π3/2 e > 2Π1/2 f > 2Π1/2 e.
In order to simplify the notation in the following discussion, let us call m and M the lowest and highest values for F, respectively, for any rotational level, j. Regarding CH(2Π1/2 → 2Π1/2), starting from j = 0.5, F = 1 for various Δj transitions, at the high j-limit, the propensity is em > eM > fM > fm. For OH(2Π1/2 → 2Π1/2), the propensity at the high j-limit is fM > fm > em > eM. For CH(2Π3/2 → 2Π3/2), we have fM > (fm, eM)> em, where the order of fm versus eM alternates with j. For OH(2Π3/2 → 2Π3/2), the propensity at the high-j limit is eM > em > fM > fm.
5. Discussion and conclusions
The newly obtained hyperfine rate coefficients for He–CH/OH collisions can be used for accurate modeling in astrophysical chemistry. CH is an important proxy for H2 especially at high column densities, and the He–CH hyperfine-resolved rate coefficients may help in more sophisticated calculations for CH in the interstellar medium. For example, using reduced mass from He to para-H2 as collision partner, Wiesemeyer et al. (2018) scaled the He–CH rotational coefficients (Marinakis et al. 2015) without taking into account the hyperfine levels.
Neither the observations of inverted lines in CH spectra nor the relative intensities of the emissions are well understood (Bouloy et al. 1984; Dagdigian 2018). Future radiative-collisional simulations may explain the anomalous hyperfine signals by taking into account the overlap of the far-infrared hyperfine lines, possible propensities in various recombination and photodissociation pathways of CH production, and turbulence.
Acknowledgments
F.L./S.M. acknowledge the support from COST Action CM1401 “Our Astrochemical History”, J.K. acknowledges financial support from the NSF Grant No CHE-1565872 to Millard Alexander. This research utilized Queen Mary’s MidPlus computational facilities, supported by QMUL Research-IT, http://doi.org/10.5281/zenodo.438045. F.L. acknowledges financial support from the Institut Universitaire de France, the Agence Nationale de la Recherche (ANR-HYDRIDES), contract ANR-12-BS05-0011-01 and the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES. Y.K. acknowledges the support of the RSF grant No. 17-12-01395.
References
- Alexander, M. H. 1985, Chem. Phys., 92, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, M. H., Manolopoulos, D. E., Werner, H.-J., & Follmeg, B. 2014, the HIBRIDON package, http://www2.chem.umd.edu/groups/alexander/ [Google Scholar]
- Bouloy, D., Nguyen-Q-Rieu, & Field, D. 1984, A&A, 130, 380 [Google Scholar]
- Brown, J. M., & Carrington, A. 2003, Rotational Spectroscopy of Diatomic Molecules (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Corey, G. C., & Alexander, M. H. 1988, J. Chem. Phys., 88, 6931 [NASA ADS] [CrossRef] [Google Scholar]
- Cotten, D. L., Magnani, L., Wennerstrom, E. A., Douglas, K. A., & Onello, J. S. 2012, AJ, 144, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Dagdigian, P. J. 2018, MNRAS, 475, 5480 [NASA ADS] [CrossRef] [Google Scholar]
- Dagdigian, P., Alexander, M., & Liu, K. 1989, J. Chem. Phys., 91, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Dubernet, M.-L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ebisawa, Y., Inokuma, H., Sakai, N., et al. 2015, ApJ, 815, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., & Lique, F. 2012, MNRAS, 425, 740 [Google Scholar]
- Holdship, J., Viti, S., Jiménez-Serra, I., Makrymallis, A., & Priestley, F. 2017, AJ, 154, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kalugina, Y., Lique, F., & Marinakis, S. 2014, Phys. Chem. Chem. Phys., 16, 13500 [CrossRef] [Google Scholar]
- Kłos, J., Ma, Q., Dagdigian, P. J., et al. 2017, MNRAS, 471, 4249 [NASA ADS] [CrossRef] [Google Scholar]
- Lique, F., & Kłos, J. 2011, MNRAS, 413, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Macdonald, R., & Liu, K. 1989, J. Chem. Phys., 91, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Marinakis, S., Paterson, G., Kłos, J., Costen, M. L., & McKendrick, K. G. 2007, Phys. Chem. Chem. Phys., 9, 4414 [CrossRef] [PubMed] [Google Scholar]
- Marinakis, S., Dean, I. L., Kłos, J., & Lique, F. 2015, Phys. Chem. Chem. Phys., 17, 21583 [CrossRef] [Google Scholar]
- Marinakis, S., Kalugina, Y., & Lique, F. 2016, Eur. Phys. J. D, 70, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marinakis, S., Kalugina, Y., & Lique, F. 2019, Eur. Phys. J. D, 73, 92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offer, A. R., van Hemert, M. C., & van Dishoeck, E. F. 1994, J. Chem. Phys., 100, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., & Lique, F. 2013, Chem. Rev., 113, 8906 [CrossRef] [PubMed] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Herbst, E., & Neufeld, D. A. 2013, Chem. Rev., 113, 9043 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Viti, S., Roueff, E., Hartquist, T. W., Pineau des Forêts, G., & Williams, D. A. 2001, A&A, 370, 557 [Google Scholar]
- Wiesemeyer, H., Güsten, R., Menten, K. M., et al. 2018, A&A, 612, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Energy level diagram of lowest 60 hyperfine levels of 12C1H. The zero reference energy is defined for the lowest CH rotational level (2Π1/2, j = 1/2). The rotational levels are drawn to scale but the Λ-doubling and the hyperfine splittings are not shown to scale for clarity reasons. It should be noted that f levels are lower than e in the F1 spin-orbit manifold but the reverse is true in the F2 spin-orbit manifold. Regarding the energy order of the hyperfine levels, higher F corresponds to higher energy in F2 but the reverse is true in F1 (with the exception for the lowest Λ-doublet shown in red). The total parity (±) is also shown. |
| In the text | |
 |
Fig. 2. Temperature dependence of state-to-state hyperfine rate coefficients for spin-orbit conserving collisions of CH(X 2Π1/2) and He. The initial and final levels are j = 0.5e and j = 0.5f, respectively. The initial and final F quantum numbers are shown in the graph. |
| In the text | |
 |
Fig. 3. Temperature dependence of state-to-state hyperfine rate coefficients for spin-orbit conserving collisions of OH(X 2Π1/2) and He. The initial and final levels are j = 0.5e and j = 0.5f, respectively. The initial and final F quantum numbers are shown in the graph. |
| In the text | |
 |
Fig. 4. Temperature dependence of state-to-state hyperfine rate coefficients for spin-orbit conserving collisions of CH(X 2Π3/2) and He. The initial and final levels are j = 1.5f and j = 1.5e, respectively. The initial and final F quantum numbers are shown in the graph. |
| In the text | |
 |
Fig. 5. Temperature dependence of state-to-state hyperfine rate coefficients for spin-orbit conserving collisions of OH(X 2Π3/2) and He. The initial and final levels are j = 1.5f and j = 1.5e, respectively. The initial and final F quantum numbers are shown in the graph. |
| In the text | |
 |
Fig. 6. Comparison between state-to-state Λ-doublet e → f changing hyperfine rate coefficients at 100 K for spin-orbit conserving collisions of CH/OH (X, v = 0) and He. The spin-orbit states are shown in the graph. Fmax → Fmax are shown in filled magenta circles, Fmin → Fmin transitions are shown in empty black circles, Fmin → Fmax in empty blue squares, and Fmax → Fmin in filled red squares. |
| In the text | |
 |
Fig. 7. Comparison between state-to-state rotational-excitation hyperfine rate coefficients for spin-orbit conserving (left panel) and changing (right panel) collisions of CH (2Π1/2, v = 0, j = 0.5e, F = 1) and He. The e → e transitions are shown in the upper panel and e → f transitions are shown in the lower panel. The final j and F quantum numbers are shown next to the corresponding curves. |
| In the text | |
 |
Fig. 8. Comparison between state-to-state rotational-excitation hyperfine rate coefficients for spin-orbit conserving (left panel) and changing (right panel) collisions of OH (2Π3/2, v = 0, j = 1.5e, F = 2) and He. The e → e transitions are shown in the upper panel and e → f transitions are shown in the lower panel. The final j and F quantum numbers are shown next to the corresponding curves. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.