| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201935614 | |
| Published online | 08 July 2019 | |
Experimental and theoretical lifetimes and transition probabilities for spectral lines in Nb II
1
Lund Observatory, Lund University, Box 43, 22100 Lund, Sweden
e-mail: hampus.nilsson@astro.lu.se
2
Department of Physics, Lund University, Box 118, 22100 Lund, Sweden
3
Materials Science and Applied Mathematics, Malmö University, 20506 Malmö, Sweden
4
Physique Atomique et Astrophysique, Université de Mons, 7000 Mons, Belgium
5
IPNAS, Université de Liège, 4000 Liège, Belgium
Received:
4
April
2019
Accepted:
30
May
2019
Aims. We have measured and calculated lifetimes of high lying levels in Nb II, and derived absolute transition probabilities by combining the lifetimes with experimental branching fractions.
Methods. The lifetimes were measured using time-resolved laser-induced fluorescence in a two-photon and two-step excitation scheme. The branching fractions were measured in intensity calibrated spectra from a hollow cathode discharge, recorded with a Fourier transform spectrometer. The calculations were performed with the relativistic Hartree–Fock method including core polarization.
Results. We report experimental lifetimes of 13 levels in the 4d3(4F)5d and 4d3(4F)6s subconfigurations, at an energy around 70 000 cm−1. By combining the lifetimes with experimental branching fractions absolute transition probabilities of 59 lines are derived. The experimental results are compared with calculated values.
Key words: atomic data / methods: laboratory: atomic / techniques: spectroscopic
© ESO 2019
1. Introduction
Niobium was discovered in 1801 by the British chemist Charles Hatchett. The element was discovered in the mineral columbite, and Hatchett gave the element the name columbium (Cb). In 1844 Heinrich Rose reported two new elements, niobium, and penopium. However, Jean-Charles de Marignac showed that the elements columbium, niobium and penopium were in fact all the same. The name columbium was in use until 1949 when niobium was adopted as the official name of element number 41. The Swedish chemist Christian Blomstrand is believed to be the first one to isolate niobium. The fascinating history of niobium, columbium, pelopium, and tantalum and Charles Hatchett can be found in Griffith & Morris (2003).
Niobium is a key element to understand and probe the slow-neutron-capture process (the s-process). Niobium is monoisotopic (93Nb) and believed to be mainly produced by β decay of 93Zr, with a half-life of τ1/2 = 1.53 × 106 yr. The probability of 93Zr capturing a neutron and producing 94Zr is larger than that of 93Zr decaying to 93Nb as long as the s-process is ongoing. Hence the niobium abundance can give the time since the s-process ended (Smith & Lambert 1984). Furthermore, by comparing the ratios 93Zr/93Nb and 99Tc/99Ru it is possible to determine the s-process temperature and the time since the s-process started (Neyskens et al. 2015).
In 1935 Meggers & Schribner (1935) published a paper reporting the term analysis of the first two spectra, CbI and CbII (arc and spark) of columbium, including 2000 lines combining 60 levels in CbII. The analysis was extended by Humpreys & Meggers (1945) who reported 183 levels in CbII. In Iglesias (1954) a study of the vacuum ultraviolet spectrum was reported, identifying 20 new energy levels and 330 spectral lines as belonging to Nb II (this is the first term analysis paper using the name niobium instead of columbium). The most recent term analysis of Nb II is reported by Ryabtsev et al. (2000), based on spectra recorded with Fourier transform spectroscopy. A total of 353 energy levels in Nb II are presently known from the work reported in these papers.
Experimental transition probabilities in Nb II have been reported by Hannaford et al. (1985), by combining radiative lifetimes of 27 levels with branching fractions (BFs) derived from the work of Corliss & Bozman (1962). Nilsson & Ivarsson (2008) reported transition probabilities for 145 lines combining BFs measured in Fourier transform spectra with the lifetimes reported by Hannaford et al. (1985). In Nilsson et al. (2010) additional transition probabilities were reported for lines from the 4d3 5p configuration derived from lifetimes combined with BFs, along with new theoretical calculations.
Niobium has one stable isotope, 93Nb, which has an odd number of nucleons. Due to the nuclear spin I = 9/2 and a large magnetic moment, μ = 6.1705 μN (Mills et al. 1988), many of the spectral lines show large hyperfine structure (hfs). Experimental measurements of hfs has been reported by Young et al. (1995) and Nilsson & Ivarsson (2008). However, none of the lines reported in the present work are noticeably affected by hfs.
In this work we report experimental transition probabilities for 59 lines originating from 13 levels in the 4d3(4F)5d and 4d3(4F)6s subconfigurations, derived by combining branching fractions and radiative lifetimes. These new data are compared with semi-empirical calculations performed using a relativistic Hartree-Fock model including core-polarization effects.
2. Laboratory measurements
2.1. Lifetimes
The spectrum and term system of Nb II have been thoroughly investigated by Ryabtsev et al. (2000). This work was essential not only to find the investigated levels but also to check for possible blending, as discussed below. The ground term in Nb II is the even 4d45D, with levels between 0 and 1200 cm−1, and the second lowest even term is 4d3(4F)5s 5F between 2300 and 4150 cm−1. To reach the investigated high lying even 5d and 6s levels, between 68 000 and 73 200 cm−1, we employed either two-photon excitations using a single laser or a two-step procedure where the first laser excited intermediate odd levels in the 4d3(4F)5p 5G term from which the second laser reached the 5d and 6s levels. Figure 1 illustrates the levels and wavelengths involved, and Table 1 gives the detailed excitation scheme for each level.
 |
Fig. 1. Schematic term system for Nb II showing the investigated levels and the typical wavelengths used for the two-photon and two-step excitations. |
Experimental details and the measured and calculated lifetimes of the levels in Nb II.
The experimental setup for two-photon and two-step measurements at the high-power laser facility at the University of Lund is described in detail in Engström et al. (2014) and Lundberg et al. (2016) and only the most important details will be given here. The setup includes three Nd:YAG lasers operating at 10 Hz. The frequency-doubled output of one of them (Continuum Surelite) is focused on a rotating niobium target in a vacuum chamber with a pressure of about 10−4 mbar to produce the niobium ions through laser ablation. Interactions with the electrons in the created plasma also excite the even 4d4 and 4d35s configurations, which contain the starting levels in our experiments.
For the two-step measurements, the second Nd:YAG (Continuum NY-82) laser pumps a dye laser (Continuum Nd-60) which, after frequency-doubling, produces a 10 ns long pulse for the first excitation to the odd 4d3(4F)5p 5G levels. A similar laser combination is used for the second step, but here the output of the Nd:YAG laser is temporally compressed using Brillouin scattering in water before pumping the dye laser. The frequency-doubled light from the dye laser is then passed through a tube with hydrogen gas where a Stokes shift of 4153 cm−1 could be added. The final length, full width at half maximum (FWHM), of the second step pulse was about 1 ns.
Both laser pulses intersected the niobium plasma from the same direction at right angles to the ablation laser a few millimeter above the niobium target. The timing between the two excitations is very important and adjusted so that the second step laser coincided in time with the maximum fluorescence from the intermediate level. Because of the difference in pulse length between the two lasers this ensures that the intermediate level population is constant during the second excitation. For the two-photon measurements only the short pulses from the second laser were used.
The fluorescence from the excited levels was observed with a small f/8 monochromator, with its 120 μm wide entrance slit parallel to the excitation lasers, in a direction perpendicular to all three laser beams. The observed line width (FWHM) was 0.5 nm in the second spectral order. The time varying signal was registered with a microchannel-plate photomultiplier (Hamamatsu R3809U) with a rise time of 0.15 ns, and digitized by a Tektronix DPO 7254 oscilloscope in time intervals of 50 ps. A second channel on the oscilloscope sampled simultaneously the temporal shape of the short-pulsed (1 ns) laser obtained from a fast photodiode. Each decay curve and pulse shape was averaged over 1000 laser shots. Between 10 and 20 decay curves were recorded for each level. The lifetimes were determined by fitting a single exponential decay, convoluted by the measured shape of the second step laser, and a constant background using the software DECFIT (Palmeri et al. 2008). In the two-photon case, the square of the measured excitation pulse was used.
In the two-step measurements some corrections of the recorded decay curves were necessary before the fitting procedure. In the case of 5d 5H6, 7 the only sufficiently intense decay channels were the same as those used for the second step excitation. This resulted in a contamination of the decay by scattered laser light. However, this effect was taken care of by recording a decay curve for the second laser either at a wavelength slightly off resonance or with the first step laser blocked. This measurement was then subtracted from the observed primary decay before the lifetime extraction. Figure 2 illustrates this problem for 5d 5H6, which was the worst case observed. Another problem was encountered in most cases because the very intense and long-lived fluorescence from the intermediate level could produce a small but noticeable contribution in the measured decay channel even at substantial wavelength differences. Similar to the previous example, this could be handled by recording and subtracting the signal from the intermediate level with the second step laser blocked. Finally, for both two-photon and two-step measurements, uncorrectable blending problem may arise from cascades, that is intermediate levels being populated from the level under investigation that in turn decay with wavelengths close to the investigated decay channel. This problem precluded for example the measurement of the 5d 5G4 level. To search for such effects, detailed spectroscopic studies, such as the one by Ryabtsev et al. (2000), are essential.
 |
Fig. 2. Measured decay curve for the 4d35d 5H6 level (+) and the recorded second step laser pulse (−). The dashed curve is a recording of the scattered light from the second step laser at a slightly detuned wavelength. This measurement is then subtracted from the real decay before the lifetime determination. The actual measurement extends to 40 ns. |
The excitation schemes employed and the final experimental lifetimes are presented in Table 1. The quoted uncertainties are based on the variations between the repeated measurements that include tests to ascertain the absence of systematic effect. Examples of the latter effects are the variations in the lifetimes with and without the small correction for the background contribution from the intermediate levels, discussed above, and the search for saturation effects by inserting a varying number of neutral density filters in the second step laser beam. Furthermore, possible flight effects (Sikström et al. 2002) were investigated by varying the delay between the ablation and excitation lasers, which results in ions with different velocities arriving in the interaction zone at a fixed distance from the target.
2.2. Branching fractions and transition probabilities
The branching fraction (BF) of a line is defined as the transition probability of the line divided by the sum of transition probabilities for all lines from the same upper level, that is the inverse of the lifetime (τ). Hence, if one can measure the intensity of all transitions from one upper level, transition probabilities can be derived by combining the BFs with radiative lifetimes according to 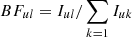 and Aul = BFul/τu. To convert the transition probabilities to oscillator strengths (f), the following relation can be used: glflu = (λ/258.27)2guAul, where gl(u) is the statistical weight of the lower (upper) level, with λ in nm and A in (ns)−1.
and Aul = BFul/τu. To convert the transition probabilities to oscillator strengths (f), the following relation can be used: glflu = (λ/258.27)2guAul, where gl(u) is the statistical weight of the lower (upper) level, with λ in nm and A in (ns)−1.
However, some lines can be too weak to be measured, but the total BF of all missing lines can be estimated from theoretical calculations. This correction is called the residual and is given in Table A.1 for each level.
The niobium spectra where produced in a hollow cathode discharge with a mixture of neon and argon as carrier gas (at a current of 0.6 A and a pressure of 1 Torr), and recorded using the Lund Observatory Chelsea Instruments FT500 UV Fourier transform spectrometer, with a resolution of 0.035 cm−1. Two spectra were used. The first, covering the wavenumber region 20 000–40 000 cm−1 (250–500 nm), was recorded with a Hamamatsu R955 optical photomultiplier tube. The second spectrum (28 000–56 000 cm−1, 180–360 nm) was recorded with a Hamamatsu R166 solar blind photomultiplier tube. The spectra were intensity calibrated using branching ratios in argon (from 20 000 to 35 000 cm−1, 290–500 nm) reported by Whaling et al. (1993), and a deuterium lamp calibrated by Physicalisch-Technische Bundesanstalt, Berlin, Germany (30 000–50 000 cm−1, 200–330 nm). The calibration procedure is further discussed in Sikström et al. (2002).
The uncertainties in the BFs include the uncertainty in the intensity measurements and the uncertainty in the intensity calibration, not only in the line itself, but also in the other lines from the same upper level, as they influence the derived value of the BF. The method to estimate uncertainties is described in detail in Sikström et al. (2002). The derived BFs and log(gf) values are given in Table A.1. The BFs are compared with theoretical values from this work and values from Kurucz (2017). In addition, we present the uncertainties both in the BFs and in the gf-values. The uncertainty in the gf-values includes the uncertainty both in the BF and the lifetime.
In most cases the lines were easy to identify thanks to the thorough analysis by Ryabtsev et al. (2000). However, we found a few lines that were blended or misidentified. The transition 4d3(4F)5p 5F3 – 4d3(4F)5d 5P3 at 34 748.346 cm−1 (287.7 nm) is blended with a weak hfs pattern, as seen in Fig. 3. The intensity of the line is corrected by measuring the intensity of the adjacent hfs components to estimate the blending contribution. The correction changed the BF of this line from 0.40 to 0.35.
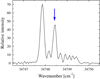 |
Fig. 3. 4d3(4F)5p 5F3 – 4d3(4F)5d 5P3 transition, marked with the arrow. The line is blended with the wide hfs pattern of an unidentified line. The blending intensity is estimated with the adjacent hfs components (see text). |
The line at 25 770.230 cm−1 (387.9 nm) is identified by Ryabtsev et al. (2000) as 4d3(2H)5p 3H4 – 4d3(4F)5d 5F5. However, as suggested by Nilsson et al. (2010), this is probably the 4d4 a1G4 – 4d3(4F)5p z3F4 transition instead, which has a Ritz wavenumber of 25 770.263 cm−1. Furthermore, this identification is strengthened by analysing the hfs pattern (as can be seen in Fig. 4) of the line, which is consistent with the splittings in the two levels, 4d4a1G4 and 4d3(4F)5p z3F4, reported by Nilsson & Ivarsson (2008).
 |
Fig. 4. 4d4 a1G4 – 4d3(4F)5p z3F4 transition. The line is wrongly assigned as 4d3(2H)5p 3H4 – 4d3(4F)5d 5F5 transition by Ryabtsev et al. (2000) (see text). |
The line at 32 554.352 cm−1 (307.1 nm) is identified by Ryabtsev et al. (2000) as 4d3(4F)5p 3F4 – 4d3(4F)5d 5F5. However, this coincides with the 4d4 a1G4 – 4d3(2H)5p 3H4 transition (with the Ritz wavenumber 32 554.359 cm−1) which, according to our calculations, has a transition probability that is orders of magnitude larger. We therefore conclude that the two lines 25 770.230 cm−1 and 32 554.352 cm−1 are misidentified by Ryabtsev et al. (2000), and we have excluded them in the analysis of the level 4d3(4F)5d 5F5 at 73 115.352 cm−1.
In most cases the residual is small (between 0.4 and 4.1%). However, for the 4d3(4F)5d 5P1 and 4d3(4F)5d 5F1 transitions, the residuals are larger 14.4 and 31.3%, respectively). This is because that the population is proportional to the statistical weight, g = 2J + 1, so lines from levels with J = 1 have a lower signal to noise ratio, and some of the lines therefore become too weak to be measured. However, the lines that are measured are in good agreement with the theoretical values, if scaled with the residual. The uncertainties for these two levels will perhaps be overestimated as the residual is given an uncertainty of 50%.
For the levels 4d3(4F)5d 5P3 and 4d3(4F)5d 5F3, both J = 3, a poor agreement between experiment and theory is seen. We find no experimental reason for this, but it can be noted that the two different calculations are not in agreement for these two levels. Because of the poor agreement between experiment and theory we have not included residuals for these levels. This may overestimate the BFs from these levels slightly.
3. Semi-empirical calculations
The experimental radiative parameters measured in the present work are compared with theoretical results obtained using the pseudo-relativistic Hartree–Fock (HFR) method of Cowan (1981) modified to take core-polarization effects (HFR+CPOL) into account, as described fore example by Quinet et al. (1999, 2002). The calculations are based on the same physical model as the one assumed to be best (referred to as HFR(B)) in our previous work on Nb II (Nilsson et al. 2010). As a reminder, in this model the intravalence interactions were considered by explicitly including the following multi-configuration expansions: 4d4 + 4d35s + 4d36s + 4d35d + 4d25s2 + 4d25p2 + 4d25s6s + 4d25s5d + 4d24f5p + 4d25p5f + 4d26s2 + 4d25d2 + 4d25d6s + 4d25p6p for the even parity, and 4d35p + 4d36p + 4d34f + 4d35f + 4d25s5p + 4d25s6p + 4d24f5s + 4d24f5d + 4d25s5f + 4d25p6s + 4d25p5d + 4d26s6p for the odd parity. Using the well-established least-squares approach that minimizes the differences between the calculated and the available experimental energy levels published by Ryabtsev et al. (2000), some radial parameters were optimized according to the methodology described in detail by Nilsson et al. (2010). The core-polarization effects were first estimated using the dipole polarizability corresponding to the ionic Nb IV core given in Fraga et al. (1976), 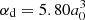 , while the cut-off radius (rc) was chosen to be the mean value ⟨r⟩ of the outermost 4d core orbital, rc = 1.85a0. Using these two parameters, we found that our calculated lifetimes were systematically a few percent longer than those measured in the present work for 4d36s and 4d35d levels. Therefore, we adjusted semi-empirically the dipole radial integrals of the 4d35p – 4d36s and 4d35p – 4d35d transitions to fit the calculations to the experimental lifetimes. This gave rise to the values ⟨5p|r|6s⟩= − 2.64 a.u. and ⟨5p|r|5d⟩= − 5.74 a.u., that being respectively 6% and 9% larger than the values obtained using the HFR(B) model considered in our previous paper (Nilsson et al. 2010).
, while the cut-off radius (rc) was chosen to be the mean value ⟨r⟩ of the outermost 4d core orbital, rc = 1.85a0. Using these two parameters, we found that our calculated lifetimes were systematically a few percent longer than those measured in the present work for 4d36s and 4d35d levels. Therefore, we adjusted semi-empirically the dipole radial integrals of the 4d35p – 4d36s and 4d35p – 4d35d transitions to fit the calculations to the experimental lifetimes. This gave rise to the values ⟨5p|r|6s⟩= − 2.64 a.u. and ⟨5p|r|5d⟩= − 5.74 a.u., that being respectively 6% and 9% larger than the values obtained using the HFR(B) model considered in our previous paper (Nilsson et al. 2010).
The calculated lifetimes are compared with the experimental measurements in Table 1. We can clearly note that our calculated values fall within the experimental uncertainties, the average ratio τCalc/τExp being equal to 0.99 ± 0.05 where the uncertainty represents the standard deviation from the mean. This agreement is similar to (but slightly better than) the one obtained when comparing the theoretical data from Kurucz (2017) with the experimental lifetimes (τKurucz/τExp = 0.98 ± 0.06). In Table A.1, the BFs calculated in the present work are compared with the experimental values and the theoretical results deduced from the work of Kurucz (2017). These comparisons are illustrated in Figs. 5 and 6. It can be seen that our computed values are generally in better agreement with the experimental values (standard deviation Δσ = 0.067) than those from Kurucz (2017) (Δσ = 0.089). However, for two upper even levels, those located at 72 125.247 and 72 183.090 cm−1, rather large discrepancies (up to two orders of magnitude) are observed when comparing the theoretical BFs with the measurements. This is mainly due to the strong mixings characterizing not only the upper but also the lower levels involved in the transitions. More precisely, according to our calculations, the main LS components of the levels at 72 125.247 and 72 183.090 cm−1 are 81% 5d 5P3 + 13% 5d 3D3 + 2% 5d 5F3 and 60% 5d 5F3 + 33% 5d 5G3 + 2% 5d 3D3, respectively. Both of them have, for example, one transition to the 5p 5F3 lower level (E = 37 376.901 cm−1), for which the theoretical and experimental BFs disagree. In fact, for this latter level, our calculations give a strongly mixed eigenvector, 53% 5p 5F3 + 25% 5p 3D3 + 7% 5p 5D3, giving rise to transition decay rates for the lines at 2876.991 and 2872.209 Å, which are very sensitive to small changes in the eigenvector compositions, both for the upper 5d and lower 5p levels. Moreover, both levels at 72 125.247 and 72 183.090 cm−1 are depopulated by quite a large number of very weak lines (contributing to the residuals given in Table A.1), which are affected by strong cancellation effects in our calculations (see Cowan 1981). This makes the determination of BFs less reliable for these two levels.
 |
Fig. 5. Comparison between our experimental BFs and theoretical values. |
 |
Fig. 6. Comparison between our experimental BFs and theoretical values from Kurucz (2017). |
4. Summary
We report experimental and theoretical radiative lifetimes for high lying even 4d3 5d and 6s levels, between 68 000 and 73 200 cm−1 in Nb II. In addition, we have measured BFs for 59 lines depopulating the levels. Combing the lifetimes with the BFs has generated absolute transition probabilities for the lines. The experimental values are compared with theoretical data, both new data reported in this work and values from the literature (Kurucz 2017).
Acknowledgments
This work was supported by the Swedish Research Council through the Linnaeus grant to the Lund Laser Centre and the Knut and Alice Wallenberg Foundation. This work was financially supported by the Integrated Initiative of Infrastructure Project LASERLAB-EUROPE, contract LLC002130. H.H acknowledges the Swedish Research Council Grant 2016-04185. P.P. and P.Q. are respectively Research Associate and Research Director of the Belgian Fund for Scientific Research F.R.S.-FNRS. Financial support from this organization is sincerely acknowledged.
References
- Corliss, C. H., & Bozman, W. R. 1962, Natl. Bur. Stand. (US) Monogr., 53 (Washington, D.C.: US Department of Commerce) [Google Scholar]
- Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra (Berkeley: Univ. California Press) [Google Scholar]
- Engström, L., Lundberg, H., Nilsson, H., Hartman, H., & Bäckström, E. 2014, A&A, 570, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraga, S., Karwowski, J., & Saxena, K. M. S. 1976, Handbook of Atomic Data (Amsterdam: Elsevier) [Google Scholar]
- Griffith, W. P., & Morris, P. J. T. 2003, Notes Rec. R. Soc. Lond., 57, 299 [CrossRef] [Google Scholar]
- Hannaford, P., Lowe, R. M., Biemont, E., & Grevesse, N. 1985, A&A, 143, 447 [NASA ADS] [Google Scholar]
- Humpreys, C. J., & Meggers, W. F. 1945, Res. Nat. Bur. Stand. (U.S.), 43, 481 [Google Scholar]
- Iglesias, L. 1954, An. Real Soc. Esp. Fys. Quim. (Madrid), 50, 135 [Google Scholar]
- Kurucz, R. L. 2017, Available at http://kurucz.harvard.edu/atoms.html [accessed June 18] [Google Scholar]
- Lundberg, H., Hartman, H., Engström, L., et al. 2016, MNRAS, 460, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Meggers, W. F., & Schribner, B. F. 1935, J. Res. Natl. Bur. Stand. (U.S.), 14, 629 [CrossRef] [Google Scholar]
- Mills, I., Cvitas, T., Homann, K., Kallay, N., & Kuchitsu, K. 1988, Quantities, Units and Symbols in Physical Chemistry (Oxford, UK: Blackwell Scientific Publications) [Copyright 1988 IUPAC] [Google Scholar]
- Nilsson, H., & Ivarsson, S. 2008, A&A, 492, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nilsson, H., Hartman, H., Engström, L., et al. 2010, A&A, 511, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neyskens, P., Van Eck, S., Jorissen, A., et al. 2015, Nature, 517, 174 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Palmeri, P., Quinet, P., Fivet, V., et al. 2008, Phys. Scr., 78, 015304 [NASA ADS] [CrossRef] [Google Scholar]
- Quinet, P., Palmeri, P., Biémont, E., et al. 1999, MNRAS, 307, 934 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quinet, P., Palmeri, P., Biémont, E., et al. 2002, J. Alloys Comp., 344, 255 [CrossRef] [Google Scholar]
- Ryabtsev, A. N., Churilov, S. S., & Litzén, U. 2000, Phys. Scr., 62, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Sikström, C. M., Nilsson, H., Litzén, U., Blom, A., & Lundberg, H. 2002, J. Quant. Spectrosc. Radiat. Transfer, 74, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., & Lambert, D. L. 1984, Publ. Astron. Soc. Pac., 96, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Whaling, W., Carle, M. T., & Pitt, M. L. 1993, J. Quant. Spec. Radiat. Transf., 50, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Young, L., Hasegawa, S., Kurtz, C., Datta, D., & Beck, D. R. 1995, Phys. Rev. A, 51, 3534 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
Experimental and theoretical branching fractions for transitions in Nb II.
All Tables
Experimental details and the measured and calculated lifetimes of the levels in Nb II.
All Figures
 |
Fig. 1. Schematic term system for Nb II showing the investigated levels and the typical wavelengths used for the two-photon and two-step excitations. |
| In the text | |
 |
Fig. 2. Measured decay curve for the 4d35d 5H6 level (+) and the recorded second step laser pulse (−). The dashed curve is a recording of the scattered light from the second step laser at a slightly detuned wavelength. This measurement is then subtracted from the real decay before the lifetime determination. The actual measurement extends to 40 ns. |
| In the text | |
 |
Fig. 3. 4d3(4F)5p 5F3 – 4d3(4F)5d 5P3 transition, marked with the arrow. The line is blended with the wide hfs pattern of an unidentified line. The blending intensity is estimated with the adjacent hfs components (see text). |
| In the text | |
 |
Fig. 4. 4d4 a1G4 – 4d3(4F)5p z3F4 transition. The line is wrongly assigned as 4d3(2H)5p 3H4 – 4d3(4F)5d 5F5 transition by Ryabtsev et al. (2000) (see text). |
| In the text | |
 |
Fig. 5. Comparison between our experimental BFs and theoretical values. |
| In the text | |
 |
Fig. 6. Comparison between our experimental BFs and theoretical values from Kurucz (2017). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


