| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201935579 | |
| Published online | 28 June 2019 | |
Rotational spectroscopy of isotopic species of methyl mercaptan at millimeter and submillimeter wavelengths: CH334SH⋆,⋆⋆
1
I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
e-mail: zakharenko@ph1.uni-koeln.de, hspm@ph1.uni-koeln.de
2
Institute of Radio Astronomy of NASU, Mystetstv 4, 61002 Kharkiv, Ukraine
3
Quantum Radiophysics Department, V. N. Karazin Kharkiv National University, Svobody Square 4, 61022 Kharkiv, Ukraine
4
Department of Physics, University of New Brunswick, Saint John, NB, Canada
5
Departments of Chemistry and Astronomy, The University of Virginia, Charlottesville, VA, USA
6
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received:
29
March
2019
Accepted:
20
May
2019
Methyl mercaptan (CH3SH) is an important sulfur-bearing species in the interstellar medium, terrestrial environment, and potentially in planetary atmospheres. The aim of the present study is to provide accurate spectroscopic parameters for the most abundant minor isotopolog CH334SH to support radio astronomical observations at millimeter and submillimeter wavelengths. The rotational spectrum of CH334SH, which is complicated by the large-amplitude internal rotation of the CH3 group versus the 34SH frame, was investigated in the 49−510 GHz and 1.1−1.5 THz frequency ranges in natural isotopic abundance. The analysis of the spectrum was performed up to the second excited torsional state, and the obtained data were modeled with the RAM36 program. A fit within experimental accuracy was obtained with a RAM Hamiltonian model that uses 72 parameters. Predictions based on this fit are used to search for CH334SH with the Atacama Large Millimeter/submillimeter Array (ALMA) toward the hot molecular core Sgr B2(N2), but blends with emission lines of other species prevent its firm identification in this source.
Key words: methods: laboratory: molecular / techniques: spectroscopic / ISM: molecules / astrochemistry / ISM: abundances / radio lines: ISM
The input and output files of the fit are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/627/A41
© ESO 2019
1. Introduction
Sulfur (S) is of importance for astrophysics as one of the constituents of interstellar dust. The studies of the interstellar grains, extracted from the interplanetary dust particles embedded in meteorites, show that sulfur is often included into interstellar silicates (Bradley et al. 1999). Astronomical silicates are one of the fundamental building blocks from which the solar system is assumed to be formed. In addition, sulfur is considered to be one of the tools to study the evolutionary stages of massive stars (Kahane et al. 1988).
The sulfur-bearing molecule methyl mercaptan, CH3SH, plays an important role in interstellar chemistry and potentially in planetary atmospheres (Vance et al. 2011). It is abundant in some astronomical sources and was first detected in Sgr B2 (Turner 1977). The molecule was observed later toward the high-mass star-forming region G327.3−0.6 (Gibb et al. 2000). Recently, methyl mercaptan was observed in molecular line surveys carried out with the Atacama Millimeter/submillimeter Array (ALMA) towards Sgr B2(N2) (Müller et al. 2016; Belloche et al. 2016) at levels that make detection of its 34S isotopic species promising. The terrestrial abundance of the second-most abundant stable sulfur isotope 34S is 4.21%. Investigation of the 34S isotopolog and its detection in the interstellar medium will provide additional information on the 32S/34S abundance ratio, which is of interest for investigation of stellar nucleosynthesis and thus Galactic chemical evolution. With the increased sensitivity and resolution of the ALMA telescope, a large number of new unknown lines is observed compared to the past. A considerable portion of the unknown lines belongs to high rotational or vibrational (including torsional) states of known molecules, as well as to their isotopologs, with CH334SH being a potential contributor.
The rotational spectrum of methyl mercaptan was investigated in the centimeter (Kojima & Nishikawa 1957; Kojima 1960), millimeter (Bettens et al. 1999; Lees & Mohammadi 1980; Sastry et al. 1986; Xu et al. 2012), and infrared wavelength regimes (Lees et al. 2018). Recently, the CH332SD isotopolog was studied in the 150−510 GHz frequency range (Zakharenko et al. 2019). This study extended the previous investigation of the CH332SD spectrum performed by Tsunekawa et al. (1989). Concerning the 34S isotopolog of methyl mercaptan, only one transition, 101 ← 000, was observed (Solimene & Dailey 1955). One additional series of the 34S isotopic species of the molecule was found around 31 GHz by Kojima (1960), but assignments were not discussed. We report a global modeling of the rotational transitions of CH334SH in the ground, the first, and the second excited torsional states. The spectrum is complicated by the large-amplitude internal rotation of the methyl group CH3 with respect to the 34SH frame. Quantum chemical calculations were performed to provide initial estimates of the rotational constants and determine the geometry of CH334SH. The aim of the present study is to obtain accurate spectroscopic parameters of the 34S isotopolog of methyl mercaptan to support astronomical observations by radio telescope arrays, in particular at millimeter and submillimeter wavelengths. The remainder of the manuscript is laid out as follows. Sections 2 and 3 provide details on our quantum chemical calculations and on our laboratory measurements, respectively. The laboratory spectroscopic analysis and discussion are given in Sect. 4. Sections 5 and 6 describe our astronomical observations and the results of our search for CH334SH, respectively, while Sect. 7 details the conclusions of our investigations.
2. Quantum chemical calculations
All calculations were performed using the Gaussian 09 (G09), Revision A.03, software package (Frisch et al. 2016). The molecular parameters and the harmonic force field of methyl mercaptan were evaluated using the Møller-Plesset second-order theory (MP2; Møller & Plesset 1934) with aug-cc-pVTZ basis set. The structural parameters were obtained in order to provide an accurate equilibrium structure. The schematic view and the main structural parameters are shown in Fig. 1.
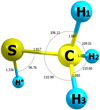 |
Fig. 1. Schematic view of 34S methyl mercaptan and equilibrium geometry calculated at MP2/aug-cc-pVTZ level of theory. The structural parameters are shown in angstroms and degrees. |
3. Experimental details
Measurements in Cologne were done in the frequency ranges of 155−510 GHz and 1.1−1.5 THz using the Cologne mm/submm wave and THz spectrometers. An Agilent E8257D synthesizer, referenced to a rubidium standard, together with VDI (Virginia Diodes, Inc.) Amplified Multiplier Chains were employed as frequency sources. The mm/submm output radiation was guided through the 5 m double-pass glass cell (the THz radiation to the 7 m glass cell) of 10 cm in diameter and then to the detectors. We used Schottky diode detectors to detect output frequencies in the 155−510 GHz frequency region and a helium-cooled bolometer (QMC Instruments Ltd.) in the 1.1−1.5 THz frequency region. The measurements were carried out at room temperature and at a pressure of 20−40 μbar. The input frequency was modulated at 47.8 kHz in the 155−510 GHz range and at 16.7 kHz in the terahertz range. The modulation amplitude and frequency steps were adjusted to optimize the signal-to-noise ratio (S/N). The output signal from the detector was detected by a lock-in amplifier in 2f mode to give second-derivative spectra, with a time constant of 20 or 50 ms. Detailed descriptions of the spectrometers may be found in Bossa et al. (2014) and Xu et al. (2012). Methyl mercaptan (purity ≥98.0%) was purchased from Sigma Aldrich and was used without further purification. The 34S isotopic species of CH3SH was measured in natural abundance.
Measurements in Kharkiv were done in the frequency range of 49−150 GHz using the automated spectrometer of the Institute of Radio Astronomy of NASU (Alekseev et al. 2012). The synthesis of the frequencies in the millimeter wave range was carried out by a two-step frequency multiplication of a reference synthesizer in two phase-lock-loop (PLL) stages. The reference synthesizer is a computer-controlled direct digital synthesizer (DDS AD9851), whose output is upconverted into the 385−430 MHz frequency range. At the first multiplication stage a klystron operating in the 3.4−5.2 GHz frequency range with a narrowband (1 kHz) PLL system was used. At the second multiplication stage, an Istok backward wave oscillator (BWO) was locked to a harmonic of the klystron. A set of BWOs was used to cover the frequency range from 49 to 149 GHz. The input frequency was modulated at 11.16 kHz and the output signal from the detector was detected by a lock-in amplifier in 1f mode to give first-derivative spectra. The measurements were carried out at room temperature and at a pressure of 10−20 μbar. The uncertainty of the measurements was estimated to be 10 kHz for a relatively strong isolated line (S/N > 10), 30 kHz for weak lines (2 < S/N < 10), and 100 kHz for very weak lines (S/N < 2). Methyl mercaptan was synthesized from a 21% water solution of sodium thiomethoxide CH3SNa (purchased from Sigma Aldrich and used without further purification). The 34S isotopic species of CH3SH was measured in natural abundance.
4. Laboratory spectroscopic analysis and discussion
Methyl mercaptan has two dipole moment components, μa = 1.312 D and μb = 0.758 D (Tsunekawa et al. 1989), thus, both a-type and b-type transitions are observed. The a axis lies almost parallel to the S−C bond at an angle of 1.67°, and the H∗ − S − C − H2 chain lies in the ab plane with the H* − S bond at an angle of 8.43° to the b axis, see Fig. 1. The ρ axis method (RAM; Kirtman 1962; Lees & Baker 1968; Hougen et al. 1994), implemented in the RAM36 code (Ilyushin et al. 2010), was used to perform the analyses of the high resolution millimeter-wave and terahertz spectra of methyl mercaptan. The initial predictions were based on a set of the rotational constants obtained from quantum chemical calculations. With the assumption that the 34S isotopic substitution does not considerably alter the molecular structure, the values of the quartic centrifugal distortion parameters and main internal rotation parameters (such as the internal rotation barrier V3, the coupling parameter ρ, and the internal rotation constant F) were fixed at the corresponding values of the CH332SH parent molecule (Xu et al. 2012).
 |
Fig. 2. Partial methyl mercaptan spectrum around 175 GHz. The aR6 rotational transitions in the ground as well as the first two excited torsional states of CH332SH are shown on the right and those of CH334SH on the left. The inset contains symmetry (A or E) and Ka labels for lines of the ground state of CH334SH. |
We started our analysis from the search of the series of intense a-type R-branch transitions with low Ka quantum numbers. The part of the spectrum of methyl mercaptan illustrated in Fig. 2 shows the relative intensities of the series of aR6 rotational transitions of CH334SH compared to the main isotopolog. The predicted lines were not in the immediate vicinity of the observed lines. Nevertheless, the assignments of the ground state lines of CH334SH were made due to the similarity in the spectral patterns of the 34S and the main isotopic species. The assigned transitions were fit, and further analyses proceeded by increasing the J and Ka quantum numbers. The process of assignment comprises gradual adding of newly measured transitions to the dataset and numerous cycles of improving of the parameter set. A large number of Q-, P-, and R-branch b-type transitions were assigned subsequently, which provided a large dataset for the detailed modeling of the rotational spectrum.
The analyses of the first and second excited states of the methyl torsion were carried out in a similar manner. The predictions for the excited torsional states were calculated based on the set of the ground state parameters of CH334SH. Finally, a number of measured transitions in the frequency range 1.1−1.5 THz were added to the dataset. These data did not pose any problem for the fitting process. Figure 3 shows an example of the agreement achieved between predicted and experimental spectra for methyl mercaptan in the THz region, with the three Q-branch series again illustrating the relative intensity ratio between the main and 34S isotopic species.
 |
Fig. 3. Partial methyl mercaptan spectrum around 1375 GHz. Series of Q branch rotational transitions in the THz frequency region are shown (K = 8 ← 7, E, vt = 0 and K = 0 ← −1, E, vt = 2 of CH332SH, and K = 8 ← 7, E, vt = 0 of CH334SH). |
In total, 3469 rotational transitions were measured for the ground, the first, and the second excited torsional states of CH334SH, which correspond to 3069 fit line frequencies due to blending. Some statistical information on the final fit is presented in Table 1. The estimated uncertainties for measured line frequencies are in the range from 10 to 100 kHz depending on the frequency range and the observed S/N. The upper limits of the J and Ka quantum numbers naturally decrease with energy progression from the ground, over the first, to the second excited torsional states. The full dataset was fit using 72 parameters with an overall weighted root mean square (rms) deviation of 0.83. The input and output files of the final fit are available on the Cologne Database for Molecular Spectroscopy (CDMS; Endres et al. 2016). The 72 parameters from the global fit of the CH334SH spectrum are listed in Table A.1. It should be noted that the final fit converged properly: the relative change in the weighted rms deviation of the fit at the last iteration was about 10−7; the corrections to the parameter values generated at the last iteration are less than 10−4 of the calculated parameter confidence intervals; the changes generated at the last iteration in the calculated frequencies are less than 1 kHz. Nevertheless, the analysis of the singular value decomposition reveals a group of highly correlated parameters, namely ρmK, ρKK, ρmm, Fmm, FmK, FKK, ρm, FK. Unfortunately, elimination of any of these correlated parameters leads to a significant worsening of the overall weighted rms deviation of the fit. The problem with the correlations listed above may be caused by small rotation-torsion-vibration interactions in the spectra, such as those discussed in Xu et al. (2012) in connection with the analysis of the main isotopolog of methyl mercaptan. Similar perturbations occur in the spectrum of the 34S isotopolog and increased rms deviations for the E type, vt = 2 group of transitions in comparison with other groups is a manifestation of such perturbations. The perturbations from the low-lying, small amplitude vibrations propagating through torsion-rotation interaction down to the low-lying torsional states require inclusion of additional terms that lead to increased correlations among parameters. An additional manifestation of such perturbations in the parameter set is the same order of magnitude of the V6 and V9 terms in the expansion of the torsional potential function.
Total number of transitions and other statistical information for the CH334SH data set.
We decided to compare our current results with the parameters of the main isotopolog (Xu et al. 2012) and of the deuterated methyl mercaptan (Zakharenko et al. 2019) in order to have a more detailed picture of what is happening with the Hamiltonian model of CH3SH upon isotopic substitution. All three fits employ slightly different sets of high-order torsion-rotational parameters, in particular due to differences in the datasets. Therefore, we limit ourselves to the comparison of parameters of only up to the fourth order in Table A.2. Compared to the H/D substitution, the 34S isotopic substitution does not lead to large changes either in the rotational constants or in the main internal rotational parameters V3, ρ, and F (the differences for the latter are about 0.1 percent and less). Furthermore, many torsion-rotation distortion parameters of the fourth order agree between the 34S and 32S isotopologs.
Nevertheless, we observe changes in sign for two parameters, namely ΔJK and DabJ, for the 34S isotopolog compared to the 32S isotopolog. At the same time, the sign of the ΔJK parameter in the 34S isotopolog coincides with the sign of the corresponding parameter in the SD isotopolog. Although these discrepancies may be caused by the difference in the datasets, it is also possible that the agreement in the sign of the ΔJK parameter between the 34SH and 32SD isotopologs speaks in favor of additional correlation issues in the CH332SH parameter set, where the number of fourth order parameters exceeds by two the number of allowed parameters for this order, as predicted by the reduction scheme proposed by Nakagawa et al. (1987).
5. Observations
We use the Exploring Molecular Complexity with ALMA (EMoCA) spectral line survey performed toward the high-mass star-forming region Sagittarius B2(N) with ALMA to search for the 34S isotopolog of methyl mercaptan. The observations, data reduction, and method used to identify the detected lines and derive column densities were described in detail in Belloche et al. (2016). In short, the survey has a median angular resolution of 1.6″. It was done with five frequency tunings that fully cover the frequency range from 84.1 GHz to 114.4 GHz with a spectral resolution of 488.3 kHz (1.7 to 1.3 km s−1). The phase center was set at 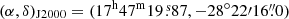 . We focus on the peak position of the hot molecular core Sgr B2(N2) at (α, δ)
. We focus on the peak position of the hot molecular core Sgr B2(N2) at (α, δ)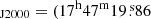 ,
, 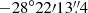 ) in the present work.
) in the present work.
6. Astronomical results
In order to search for rotational lines of the 34S isotopolog of methyl mercaptan in the EMoCA spectrum of Sgr B2(N2), we started from the best-fit radiative-transfer model we obtained for the 32S isotopolog for this source (Müller et al. 2016). We assumed the same size of the emitting region (1.4″), temperature (180 K), linewidth (5.4 km s−1), and centroid velocity (73.5 km s−1) as those derived for the main isotopolog. We followed Wilson & Rood (1994) and assumed a 32S/34S isotopic ratio of 22.5, equal to the Solar System value. Given the column density of 3.4 × 1017 cm−2 obtained for the main isotopolog, this implies a column density of 1.5 × 1016 cm−2 for the 34S isotopolog. With these parameters, we computed a synthetic spectrum of CH334SH under the local thermodynamic equilibrium approximation using Weeds (Maret et al. 2011) and compare it to the observed EMoCA spectrum in Fig. 4.
 |
Fig. 4. EMoCA survey detail. This figure shows transitions of CH334SH that are covered by the survey and that contribute significantly to the detected signal toward Sgr B2(N2). The local thermodynamic equilibrium synthetic spectrum of CH334SH is displayed in red and overlaid on the observed spectrum shown in black. The green synthetic spectrum contains the contributions of all molecules identified in our survey so far, including the species shown in red. The y-axis is labeled in brightness temperature units. The dotted line indicates the 3σ noise level. |
The synthetic spectrum of CH334SH is consistent with the spectrum of Sgr B2(N2), but most of the strongest transitions expected for CH334SH are, unfortunately, blended with emission from other molecules, which prevents their robust assignment to CH334SH. Therefore, the molecule is not securely identified in the EMoCA spectrum. Still, the agreement between the observed and synthetic spectra for the line at 99519 MHz (which is contaminated by other species, though only in its wings) suggests that the molecule is present at the level expected for the 32S/34S isotopic ratio assumed above.
7. Conclusions
A new study of the rotational spectrum of the 34S isotopolog of CH3SH was carried out in the frequency ranges of 49−510 GHz and 1.1−1.5 THz in order to provide accurate predictions for astronomical searches. The rotational transitions of the ground, the first, and the second excited torsional states were assigned up to high J and Ka quantum numbers (see Table 1) and fit using a RAM Hamiltonian within experimental accuracy. The overall weighted rms deviation of the global fit of 3469 rotational transitions of the CH334SH is 0.83, indicating that we have an appropriate set of parameters to provide reliable predictions to support astronomical observations. CH334SH was searched for with ALMA between 84 GHz and 114 GHz toward the hot molecular core Sgr B2(N2), but blends with emission lines of other species prevent its firm identification in this frequency range for this source. Nevertheless, the satisfactory agreement between observations and the astronomical model for the least contaminated CH334SH line at 99519 MHz may make a secure detection possible in future observations of this source in a wider frequency range.
A calculated line list of this isotopic species, including information on intensities and calculated uncertainties, will be provided in the catalog section1 of the Cologne Database for Molecular Spectroscopy, CDMS (Endres et al. 2016). Files containing the experimental lines or parameters along with auxiliary files are available in the data section of the CDMS2.
Acknowledgments
The present study was supported by the Deutsche Forschungsgemeinschaft (DFG) in the framework of the collaborative research grant SFB 956 (project ID 184018867), sub-project B3. O.Z. is funded by the DFG via the Gerätezentrum “Cologne Center for Terahertz Spectroscopy” (project ID SCHL 341/15-1). The research in Kharkiv was carried out under support of the Volkswagen foundation. The assistance of Science and Technology Center in Ukraine is acknowledged (STCU partner project P686). L.H.X. and R.M.L. received support from the Natural Sciences and Engineering Research Council of Canada.
References
- Alekseev, E. A., Motiyenko, R. A., & Margules, L. 2012, Radio Phys. Radio Astron., 3, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Müller, H. S. P., Garrod, R. T., & Menten, K. M. 2016, A&A, 587, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bettens, F. L., Sastry, K. V. L. N., Herbst, E., et al. 1999, ApJ, 510, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Bossa, J.-B., Ordu, M. H., Müller, H. S. P., Lewen, F., & Schlemmer, S. 2014, A&A, 570, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradley, J. P., Keller, L. P., Snow, T. P., et al. 1999, Science, 285, 1716 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., & Schlegel, H. B. 2016, Gaussian 16 Revision A.03 (Wallingford, CT, USA: Gaussian Inc.) [Google Scholar]
- Gibb, E., Nummelin, A., Irvine, W. M., Whittet, D. C. B., & Bergman, P. 2000, ApJ, 545, 309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hougen, J., Kleiner, I., & Godefroid, M. 1994, J. Mol. Spectr., 163, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Ilyushin, V. V., Kisiel, Z., Pszczółkowski, L., Mäder, H., & Hougen, J. T. 2010, J. Mol. Spectr., 259, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kahane, C., Gomez-Conzales, J., Cernicharo, J., & Guelin, M. 1988, A&A, 190, 167 [NASA ADS] [Google Scholar]
- Kirtman, B. 1962, J. Chem. Phys., 37, 2516 [NASA ADS] [CrossRef] [Google Scholar]
- Kojima, T. 1960, J. Phys. Soc. Jpn., 15, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Kojima, T., & Nishikawa, T. 1957, J. Phys. Soc. Jpn., 12, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Lees, R. M., & Baker, J. G. 1968, J. Chem. Phys., 48, 5299 [NASA ADS] [CrossRef] [Google Scholar]
- Lees, R. M., & Mohammadi, M. A. 1980, Can. J. Phys., 58, 1640 [NASA ADS] [Google Scholar]
- Lees, R. M., Xu, L.-H., Guislain, B. G., et al. 2018, J. Mol. Spectr., 343, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Hily-Blant, P., Pety, J., Bardeau, S., & Reynier, E. 2011, A&A, 526, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Belloche, A., Xu, L.-H., et al. 2016, A&A, 587, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakagawa, K., Tsunekawa, S., & Kojima, T. 1987, J. Mol. Spectr., 126, 329 [Google Scholar]
- Sastry, K. V. L. N., Herbst, E., Booker, R. A., & Lucia, F. C. D. 1986, J. Mol. Spectr., 116, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Solimene, N., & Dailey, B. P. 1955, J. Chem. Phys., 23, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Tsunekawa, S., Taniguchi, I., Tambo, A., et al. 1989, J. Mol. Spectr., 134, 63 [Google Scholar]
- Turner, B. E. 1977, ApJ, 213, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Vance, S., Christensen, L. E., Webster, C. R., & Sung, K. 2011, Planet. Space Sci., 59, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., Fisher, J., Lees, R. M., et al. 2008, J. Mol. Spectr., 251, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., Lees, R. M., Crabbe, G. T., et al. 2012, J. Chem. Phys., 137, 104313 [NASA ADS] [CrossRef] [Google Scholar]
- Zakharenko, O., Lewen, F., Ilyushin, V. V., et al. 2019, A&A, 621, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Additional tables
Parameters for CH334SH.
Comparison of the low-order parameters of CH334SH, CH332SH, and CH332SD.
All Tables
Total number of transitions and other statistical information for the CH334SH data set.
All Figures
 |
Fig. 1. Schematic view of 34S methyl mercaptan and equilibrium geometry calculated at MP2/aug-cc-pVTZ level of theory. The structural parameters are shown in angstroms and degrees. |
| In the text | |
 |
Fig. 2. Partial methyl mercaptan spectrum around 175 GHz. The aR6 rotational transitions in the ground as well as the first two excited torsional states of CH332SH are shown on the right and those of CH334SH on the left. The inset contains symmetry (A or E) and Ka labels for lines of the ground state of CH334SH. |
| In the text | |
 |
Fig. 3. Partial methyl mercaptan spectrum around 1375 GHz. Series of Q branch rotational transitions in the THz frequency region are shown (K = 8 ← 7, E, vt = 0 and K = 0 ← −1, E, vt = 2 of CH332SH, and K = 8 ← 7, E, vt = 0 of CH334SH). |
| In the text | |
 |
Fig. 4. EMoCA survey detail. This figure shows transitions of CH334SH that are covered by the survey and that contribute significantly to the detected signal toward Sgr B2(N2). The local thermodynamic equilibrium synthetic spectrum of CH334SH is displayed in red and overlaid on the observed spectrum shown in black. The green synthetic spectrum contains the contributions of all molecules identified in our survey so far, including the species shown in red. The y-axis is labeled in brightness temperature units. The dotted line indicates the 3σ noise level. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


