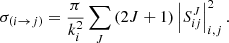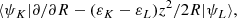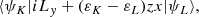| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201834922 | |
| Published online | 03 May 2019 | |
Electron capture in slow collisions of O6+ ions with atomic hydrogen⋆
1
School of Physics, Beijing Institute of Technology, Beijing 100081, PR China
2
Institute of Applied Physics and Computational Mathematics, Beijing 100088, PR China
e-mail: wu_yong@iapcm.ac.cn
3
HEDPS, Center for Applied Physics and Technology, Peking University, Beijing 100084, PR China
4
Macedonian Academy of Sciences and Arts, PO Box 428, 1000 Skopje, Macedonia
Received:
19
December
2018
Accepted:
2
March
2019
Aims. Electron capture in collisions of highly charged O6+ ions with ground-state hydrogen atoms is a very important process in solar wind X-ray studies.
Methods. In the present study, the full quantum-mechanical molecular-orbital close-coupling method is employed to study electron capture reactions in collisions of O6+ ion with ground-state atomic hydrogen in the energy region from 10−4 keV u−1 to 5 keV u−1. The ab initio multi-reference single- and double-excitation configuration interaction (MRD-CI) method is used to calculate the potential and coupling data used in the QMOCC calculations.
Results. Total and state-selective cross sections for the dominant and subdominant reaction channels are calculated and compared with the available experimental and theoretical data. The branching ratios for Lithium-like O5+ excited ions are used to calculate the contribution of cascade radiative transitions from n = 5 levels to the population of 4l states. From the calculated cross sections, reaction rate coefficients are obtained for temperatures between 1000 and 1 × 109 K and compared with other calculations.
Key words: solar wind / atomic data
Tables of the cross-sections are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/625/A29
© ESO 2019
1. Introduction
Electron capture (or charge exchange) processes between highly charged ions and neutral species have received considerable attention in studies investigating the production of X-rays and/or extreme ultraviolet photons in various astrophysical environments. The solar wind charge exchange (SWCX) mechanism, namely the charge exchange processes between solar wind ions (Cravens 1997) (H, He, C, N, O, Ne, S, Si, Fe, etc) and neutrals, has been confirmed as a primary source of the soft X-ray background (SXRB). The X-ray observation of comets and other solar-system objects can often provide a diagnostic of the composition, evolution, and velocity of the solar wind, and the distribution of the neutral gas density.
With the appearance of sophisticated X-ray observatories such as Chandra, XMM-Newton, and Suzaku observatories, X-ray emission has been observed from several solar-system objects including the Sun, the Moon, the Earth, Saturn, Mars, Venus, Jupiter, and comets (Bhardwaj et al. 2006, 2009; Bhardwaj & Gladstone 2000; Cravens 2000). The original discovery of soft X-rays from the Jupiter aurora regions are currently believed to originate from the charge-exchange collisions of multi-charged ion Oq+ and Sq+ with H, He, H2 of the neutral ambient gas (Kharchenko et al. 2008; Krasnopolsky & Mumma 2001; Hui et al. 2010); extreme ultraviolet and X-ray emission from many comets (such as Hale-Bopp, Halley, and Hyakutake) are considered to result from charge-transfer processes between highly charged solar-wind particles (O4 − 6+, C4, 5+, Ne7+) and neutral particles of the comets (Cravens 1997, 2002; Haberli et al. 1997). Similarly, the X-ray emission from the heliosphere, the geocorona, and the Martian and Venusian halo are considered to derive from charge-exchange collisions between highly charged heavy ions (Oq+, Cq+, Neq+ and Siq+) in the solar wind and gaseous neutral species in the atmosphere or exosphere of these bodies (Bhardwaj et al. 2009). In addition, in magnetic fusion plasmas, the electron capture processes of highly charged impurity ions with the neutral species are an important radiative plasma cooling mechanism. However, as the electron capture on these ions populates excited states, their radiation can be used as a plasma diagnostic tool as well (Rice et al. 1986).
The electron capture processes in O6+–H collisions have been studied in the past by many authors, both theoretically and experimentally. On the experimental side, total electron-capture measurements have been performed (Crandall et al. 1979; Phaneuf et al. 1982; Dijkkamp et al. 1985; Panov et al. 1983; Meyer et al. 1979) covering the combined energy range 0.1–100 keV u−1. The absolute single electron-capture cross sections to 4l have been measured using the emission spectroscopy in the energy range between 0.94 and 7.5 keV u−1 by Dijkkamp et al. (1985). On the theoretical side, electron capture cross-section calculations for this collision system have been performed by the semi-classical molecular orbital close-coupling (SCMOCC; Hanssen et al. 1984; Bendahman et al. 1985; Harel & Jouin 1988), atomic orbital close-coupling (AOCC; Liu et al. 2012; Wu et al. 2012), classical trajectory Monte Carlo (CTMC; Wu et al. 2012; Olson & Salop 1977; Shipsey et al. 1981), perturbed stationary states (PSS; Shipsey et al. 1981) methods, and by the full quantum-mechanical molecular-orbital close-coupling (QMOCC) method (Wu et al. 2012). The conclusion of these theoretical studies was that the electron capture process in these systems dominantly populates the n = 4 shell, and sub-dominantly populates the n = 5 shell.
The purpose of the present work is to study the electron capture in the O6++H system using the QMOCC method with a very large expansion basis, performing the calculations in the energy range 10−4–5 keV u−1. The most extensive previous QMOCC calculations for this system considered a basis of 25 molecular states of 2Σ+ and 2Π symmetries, while in the present calculations the basis contains 50 molecular states of 2Σ+, 2Π, 2Δ, 2Φ, and 2Γ symmetries. The present QMOCC calculations use ab initio adiabatic potentials and nonadiabatic radial and rotational coupling matrix elements obtained with the multi-reference single and double excitation configuration interaction (MRD-CI) approach, employing optimized atomic basis sets to describe the high-lying Rydberg states of O5+ ion.
The organization of the paper is as follows. In the following section, we briefly outline the theoretical calculation methods that are used. In Sect. 3, we present and discuss the results of our molecular structure and cross-section calculations. Finally, a brief summary is given in Sect. 4.
Atomic units are used throughout unless otherwise stated.
2. Theoretical methods
2.1. Scattering theory
The quantal molecular orbital close-coupling (QMOCC) method is described in detail elsewhere (Nolte et al. 2012; Zygelman et al. 1992); here we give only its brief outline. The total scattering wave function of the collision system is expanded in terms of adiabatic electronic wave functions ψi(R, r):
where r is the electron position vector taken with respect to the center of mass of the nuclei, and R is the internuclear distance. The Schrödinger equation is given as
where I is the unit matrix, u is the diagonal adiabatic potential matrix, and M and P are coupling matrices, defined as
Inserting the expansion (1) in Eq. (2) the following system of coupled differential equations is obtained for the expansion coefficients Fj(R),
where J is the total angular momentum, λ is the a diagonal matrix with elements λj that satisfy 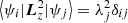 , Lz is the projection of angular momentum J on internuclear axis, and VR and VC are the radial and rotational coupling matrices, respectively,
, Lz is the projection of angular momentum J on internuclear axis, and VR and VC are the radial and rotational coupling matrices, respectively,
where ⟨i|...|j⟩ represents ⟨ψi|...|ψj⟩. Near an avoided crossing of adiabatic potentials, the radial coupling Aij(R) (Aij(R) = ⟨i|∂/∂R|j⟩) is almost singular, causing significant problems in numerical integration of coupled Eq. (4). To avoid these problems, the following diabatic transformation of fJ(R) is usually performed
where C is an orthogonal transformation matrix that satisfies the limit C(R)→I; R → ∞. Under this transformation, the coupled Eq. (4) take the form
where U and P are the diabatic radial and rotational coupling matrices, respectively. Using the multichannel log-derivative method of Johnson (1973) to solve these equations, one gets the scattering matrices K and S
The electron capture cross section from the initial channel i to the final channel j is given by
In order to include the effects of electron translational factors (important only for energies above ∼1 keV u−1), we transform the radial and rotational coupling matrix elements between the states ψK and ψL into
where εK and εL are the electronic energies of states ψK and ψL, and z2 and zx are the components of quadrupole moment tensor. This modification of the couplings is similar in form to the one resulting from the application of the common translational factor method (Errea et al. 1982).
2.2. Molecular structure calculations
Adiabatic potentials and coupling matrix elements for the O6+ + H scattering system have been obtained with the multi-reference single- and double-excitation configuration interaction (MRDCI) approach (Buenker et al. 2014; Krebs & Buenker 1995). For the O5+ ion, we have adopted a hybrid basis set, which is developed by Wu et al. (2011, 2012) and consists of two components: (i) the standard Dunning neutral atom basis and (ii) a one-electron basis of hydrogen-like orbitals. In order to produce almost exactly the hydrogen-like Rydberg ion energies, a large Gaussian basis set (19s, 13p, 10d, 6f, 3g) has been optimized and used for oxygen. A (6s, 3p, 2d, 1f) basis contracted to [4s, 3p, 2d] was employed for hydrogen (Dunning 1989). The full configuration interaction calculation was employed to compute the adiabatic potentials and coupling matrix elements of the [OH]6+ system for internuclear distances between 1.0 and 40 au Twenty 2Σ+, nine 2Δ and two 2Γ electronic states in A1 symmetry, and fourteen 2Π and five 2Φ electronic states in B1 symmetry have been obtained. The asymptotic energies of considered states in the present calculations compared with the available experimental data (Kelly 1987) are shown in Table 1. The largest error in the relative asymptotic energies of the [OH]6+ system is about 0.105 eV. This accuracy of the energies is considered to be adequate for the QMOCC scattering calculations. Given the optimized basis, the molecular wave functions are computed and the radial and rotational coupling elements are calculated by applying the finite-difference method (Buenker & Peyerimhoff 1974, 1975; Buenker & Phillips 1985; Buenker 1986).
Asymptotic separated-atom energies for the states of [OH]6+.
Since in Sect. 3.2 our cross-section results are systematically compared with the results of the previous QMOCC calculations by Wu et al. (2012), we note that in their implementation of MRDCI method a Gaussian basis set containing 17s, 15p, 9d, 6f, and 3g states was used on O5+, and a 6s, 3p, 2d, and 1f basis contracted to [4s, 3p, 2d, 1f] was used on H. The full configuration interaction calculations were performed in the internuclear distance range 1–40 au with a maximum error of 0.03 eV in the asymptotic energies of [OH]6+. The difference between the molecular structure calculations in the present work and those in Wu et al. (2012) can obviously result in differences in the distribution of positions of avoided crossings along the internuclear distance, as well as in differences in the strengths and radial extension of both radial and rotational couplings.
3. Results and discussion
3.1. Potentials and couplings
In Fig. 1a, the calculated adiabatic potential energy curves for the lowest 20 2Σ+ and 14 2Π molecular states are presented as a function of internuclear distance, where the 162Σ+ state represents the initial channel in O6+(1s2)+H(1s) collision. The potentials of 2Δ, 2Φ, and 2Γ molecular states, also included in cross-section calculations, are shown in Fig. 1b for the internuclear distances R = 1–40 au The region of avoided crossings involving the initial state and those correlating with the n = 4 and 5 atomic states are displayed in Fig. 1c. The avoided crossings are distributed in the ∼5–24 au internuclear distance range, suggesting a strong radial coupling of initial and n = 4, 5 final channels in this region. The avoided crossings of initial channel with those of n = 6 appear in the region around R = 325.00 au, but, being extremely small, the associated radial couplings do not produce any transitions.
 |
Fig. 1. Adiabatic potential energy curves of [OH]6+ as a function of internuclear distance R. Panel a: calculated adiabatic potential energy curves for the lowest 20 2Σ+ and 14 2Π molecular states for n = 3, 4, 5 and 6 channels, panel b: potentials of 2Δ, 2Φ, and 2Γ molecular states for n = 3, 4, 5, and 6 channels, and panel c: adiabatic potentials near the vicinity of the avoided crossings for n = 4 and n = 5 channels. |
In Fig. 2, we show the radial coupling matrix elements between the adjacent states for the n = 2, 3, 4, 5, 6 manifolds. It can be noted that the positions of the peaks in radial couplings are consistent with the positions of avoided crossings of adiabatic potentials shown in Fig. 1. In Fig. 3, the most important rotational coupling matrix elements within the n = 4 manifold are displayed as a function of internuclear distance. At large internuclear distances, the rotational couplings approach zero or a constant value for the states belonging to different configurations or to the same configuration, respectively.
 |
Fig. 2. Radial coupling matrix elements between the adjacent states for [OH]6+. Panels a–d: 2Σ+–2Σ+ couplings, panels e–f: 2Π–2Π couplings. |
 |
Fig. 3. Rotational coupling matrix elements for [OH]6+. Panel a: (6–9)2Σ+–(4–5)2Π couplings, panel b: (6–10)2Σ+–(6–10)2Π couplings, panel c: (11–12)2Σ+–(7–10)2Π couplings, panel d: (13–14)2Σ+–(7–10)2Π couplings. |
3.2. Cross sections
In the present work we performed two sets of QMOCC calculations for the electron capture to 4l and 5l states in O6+(1s2)+H(1s) collisions: one with 34 molecular states in the basis, involving only the 2Σ+ and 2Π states correlating with n = 2–6 atomic manifolds, and another one with 50 molecular states in the basis, involving all the states correlating with the n = 2–6 atomic manifolds. The cross sections were calculated in the energy range 10−4–5.0 keV u−1. We note that in the previous QMOCC calculations by Wu et al. (2012) a relatively modest expansion basis was used, consisting of 25 2Σ+ and 2Π states, correlating with the n = 3, 4, 5 atomic manifolds.
In Fig. 4 we show the results of present QMOCC calculations for the total electron capture cross section with the above two basis sets. A noticeable difference between the results of two calculations appears only for energies above 0.1 keV u−1. The present total cross sections are compared also with the results of previous theoretical calculations (Hanssen et al. 1984; Bendahman et al. 1985; Harel & Jouin 1988; Liu et al. 2012; Wu et al. 2012; Shipsey et al. 1981) and with experimental data of Crandall et al. (1979), Phaneuf et al. (1982), Dijkkamp et al. (1985), Panov et al. (1983). We note that only the QMOCC result of Wu et al. (2012) covers the energy range of the present work and extends up to 10 keV u−1. It can be observed that the present QMOCC results in the region below 0.2 keV u−1 differ significantly from those of Wu et al. (2012) and lie closer to the experimental data of Phaneuf et al. (1982) in this region. This is a result of the much smaller expansion basis used in Wu et al. (2012), and also due to the differences in the nonadiabatic couplings involved in the two calculations. In the energy range 0.2–5 keV u−1 our QMOCC results agree with the experimental results of Phaneuf et al. (1982), Dijkkamp et al. (1985) within their uncertainties, as well as with the PSS (Shipsey et al. 1981) and SMOCC (Hanssen et al. 1984; Bendahman et al. 1985; Harel & Jouin 1988) theoretical results, which continue to be in fair agreement with the experiment up to ∼8 keV u−1. We note that the low-energy points of Shipsey et al. (1981) are results from their PSS calculations, while those at high energies are their CTMC results.
 |
Fig. 4. Total charge transfer cross sections in O6+–H collisions. |
The cross sections for capture to n = 4 and n = 5 shells of O5+ from present QMOCC calculations are shown in Figs. 5 and 6, respectively. They are compared with the theoretical SMOCC results of Harel & Jouin (1988), the AOCC results of Liu et al. (2012) and Wu et al. (2012), the QMOCC results of Wu et al. (2012) and with the experimental data of Dijkkamp et al. (1985). In the overlapping energy range, the present QMOCC results for capture to the n = 4 shell are in good agreement with the experiment, as well as with the SMOCC (Harel & Jouin 1988) and AOCC (Liu et al. 2012; Wu et al. 2012) results. As in the case of total electron capture, the present QMOCC results in the region below ∼0.2 keV u−1 considerably disagree with those of Wu et al. (2012). For the capture to the n = 5 the situation is similar (cf. Fig. 6), except that the difference between the present and QMOCC result of Wu et al. (2012) becomes enormous (more than two orders of magnitude) in the region below ∼0.03 keV u−1 and very significant for energies above ∼1 keV u−1.
 |
Fig. 5. Cross sections for electron capture to n = 4 shell of O5+ ion in O6+–H collisions. |
 |
Fig. 6. Cross sections for electron capture to n = 5 shell of O5+ ion in O6+–H collisions. |
The present QMOCC cross sections for capture to 4l and 5l states are shown in Figs. 7 and 8, respectively. They are compared with the previous QMOCC (Wu et al. 2012), SMOCC (Harel & Jouin 1988), and AOCC (Liu et al. 2012; Wu et al. 2012) results and with the emission spectroscopy measurements of Dijkkamp et al. (1985). In Fig. 7 we also show the 4l population cross sections that include the radiative cascade contributions from the 5l levels, calculated using the Lithium-like O5+ excited ions branching ratios of Nahar (2002). As observed in Fig. 7, the cascade corrected 4l population QMOCC (with full basis) results for the 4p states are in much better agreement with experimental data in the overlapping energy range than with the uncorrected cross sections. For the 4d and 4f states, for which the disagreement of present results and experimental data is large, the cascade corrections do not bring any improvement. The cause for the observed significant differences between the present QMOCC results and those of previous QMOCC calculations (Wu et al. 2012) in the entire energy range considered is a consequence of the differences in the number of radial and rotational couplings (and of the differences in their strengths and positions on and extensions along the internuclear distance) involved in the two calculations. More specifically, we have found that the higher angular momentum molecular states 2Δ, 2Φ, 2Γ (excluded in the expansion basis of Wu et al. 2012) strongly affect the cross sections in the 0.1–5 keV u−1 energy range.
 |
Fig. 7. Cross sections for electron capture to 4l shell of O5+ ion in O6+–H collisions. Panel a: cross sections for electron capture to O5+(4s) state. Panel b: cross sections for electron capture to O5+(4p) state. Panel c: cross sections for electron capture to O5+(4d) state. Panel d: cross sections for electron capture to O5+(4f) state. |
 |
Fig. 8. Cross sections for electron capture to 5l shell of O5+ ion in O6+–H collisions. Panel a: cross sections for electron capture to O5+(5s) state. Panel b: cross sections for electron capture to O5+(5p) state. Panel c: cross sections for electron capture to O5+(5d) state. Panel d: cross sections for electron capture to O5+(5f) state. Panel e: cross sections for electron capture to O5+(5g) state. |
Our QMOCC cross sections for capture to 5l states in Fig. 8 show sharp increases in the narrow energy range ∼0.02–∼0.08 keV u−1 caused by the well localized radial couplings of the initial and 5l reaction channels in the internuclear distance range 19.5–23.5 au It should be noticed that our QMOCC 5l results (except for 5g), calculated with the basis containing only the 2Σ+ and 2Π states, are consistent with the QMOCC results of Wu et al. (2012) in the energy region below 1 keV u−1 (down to ∼0.03 keV u−1), after which they become drastically different. It should also be noted that in the overlapping energy range, the QMOCC and AOCC cross sections are consistent with each other, especially for the 5f and 5g states.
3.3. Reaction rate coefficients
The reaction rate coefficients for charge transfer process are calculated in the temperature range 1000−109 K by averaging the cross sections of Eq. (9) over a Maxwellian velocity distribution, and the results, compared with the previous results given by Wu et al. (2012), are displayed in Figs. 9 and 10. Based on the present QMOCC calculations and previous AOCC results (Liu et al. 2012; Wu et al. 2012), we have obtained the recommended total charge transfer cross sections in the energy range 10−4–100 keV u−1. In Fig. 9a, the current recommended cross sections are presented and compared with the previous recommended results (Wu et al. 2012). Using these total cross sections, the total reaction rate coefficients are shown in Fig. 9b. Good agreement between the present total charge transfer rate coefficient and that given by Wu et al. (2012) is observed only in the overlapping temperature range 6 × 104 K–2 × 108 K. For T < 6 × 104 K and T > 2 × 108 K, the present results differ significantly from those of Wu et al. (2012). The differences in the reaction rate coefficients of present calculations and those in Wu et al. (2012) are obviously consistent with the differences in the corresponding charge transfer cross sections. In Fig. 10, the present rate coefficients for all considered charge transfer processes increase with increasing temperature and attain their maximum values at T ∼ 2−3 × 107 K, while those of Wu et al. (2012) attain their maxima at T ∼ 4−5 × 107 K. It is also observed in Fig. 10 that in the temperature region T > 3 × 106 K dominant contribution to the n = 4 reaction rate in the present calculations gives the capture to 4f state, while in the calculations of Wu et al. (2012) this is the 4p state.
 |
Fig. 9. Recommended total charge transfer cross sections and rate coefficients for O6+–H collisions. Panel a: recommended total charge transfer cross sections. Panel b: total reaction rate coefficients. Black lines: present results; red lines: results of Wu et al. (2012). |
 |
Fig. 10. nl-resolved charge transfer rate coefficients for O6+–H collisions. Solid lines: present results; dashed lines: results of Wu et al. (2012). |
4. Conclusions
The charge transfer in collisions of O6++H is a very important process in solar wind X-ray studies. In the present study we employed the full quantum-mechanical molecular-orbital close-coupling (QMOCC) method to study the dynamics of this process in detail in the energy range from 10−4 keV u−1 to 5 keV u−1. The multi-reference single- and double-excitation configuration interaction, with optimized atomic basis sets to accurately describe the high-lying Rydberg states, was used to compute the adiabatic potential and coupling data needed in QMOCC calculations. The cross sections of dominant (4l) and subdominant (5l) reaction channels are calculated with two basis sets: one containing 34 (2Σ+ and 2Π symmetries only) and the other 50 (all symmetries) molecular states that correlate with the n = 2-6 atomic state manifolds. The calculated total, n-shell, and nl-state selective cross sections are compared with the available experimental and theoretical data. Large differences between the present and previous QMOCC results of Wu et al. (2012) are observed, especially for the n-shell and nl-state selective cross sections, and are attributed to the differences in the sizes of the expansion bases used in the coupled channel calculations, as well as to the differences in the strengths and radial extensions of nonadiabatic couplings. While the agreement of present QMOCC total and n = 4-shell cross sections with the experimental data in the overlapping energy range can be considered as good (within the experimental uncertainties), the agreement of cascade-corrected 4l QMOCC cross sections in the overlapping energy range can be considered as satisfactory for the 4p state. Using the cross sections for the considered charge transfer processes, we calculated the rate coefficients in the temperature range 1000–109 K and compared them with those of Wu et al. (2012).
Acknowledgments
This work was supported by the National Key Research and Development Program of China under Grants No. 2017YFA0402300 and 2017YFA0403200 and the National Natural Science Foundation of China (Grants No. 11474032, 11534011 and U1530261).
References
- Bendahman, M., Bliman, S., Dousson, S., et al. 1985, J. Phys., 46, 561 [CrossRef] [Google Scholar]
- Bhardwaj, A., & Gladstone, G. R. 2000, Rev. Geophys., 38, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Bhardwaj, A., Elsner, R. F., Gladstone, G. R., et al. 2006, J. Geophys. Res. Space Phys., 111, A11225 [NASA ADS] [CrossRef] [Google Scholar]
- Bhardwaj, A., Elsner, R. F., & Gladstone, G. R., et al. 2009, Adv. Geosci, 229 [Google Scholar]
- Buenker, R. J. 1986, Int. J. Quant. Chem., 29, 435 [CrossRef] [Google Scholar]
- Buenker, R. J., & Peyerimhoff, S. D. 1974, Theor. Chim. Acta, 35, 33 [CrossRef] [Google Scholar]
- Buenker, R. J., & Peyerimhoff, S. D. 1975, Theor. Chim. Acta, 39, 217 [CrossRef] [Google Scholar]
- Buenker, R. J., & Phillips, R. A. 1985, J. Mol. Struct. THEOCHEM, 123, 291 [CrossRef] [Google Scholar]
- Buenker, R. J., Phillips, R. A., Krebs, S., et al. 2014, Theor. Chem. Acc., 133, 1468 [CrossRef] [Google Scholar]
- Crandall, D. H., Phaneuf, R. A., & Meyer, F. W. 1979, Phys. Rev. A, 19, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T. 1997, Geophys. Res. Lett., 24, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T. E. 2000, Adv. Space Res., 26, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T. 2002, Science, 296, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkkamp, D., Ciric, D., de Boer, A., de Heer, F. J., & Vlieg, E. 1985, J. Phys. B At. Mol. Phys., 18, 4763 [NASA ADS] [CrossRef] [Google Scholar]
- Errea, L. F., Mendez, L., & Riera, A. 1982, J. Phys. B At. Mol. Phys., 15, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Haberli, R., Gombosi, T., De Zeeuw, D., Combi, M., & Powell, K. 1997, Science, 276, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Hanssen, J., Gayet, R., Harel, C., & Salin, A. 1984, J. Phys. B At. Mol. Phys., 17, L323 [CrossRef] [Google Scholar]
- Harel, C., & Jouin, H. 1988, J. Phys. B: At. Mol. Opt. Phys., 21, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, Y., Schultz, D. R., Kharchenko, V. A., et al. 2010, J. Geophys. Res, 115, A07102 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, B. 1973, J. Comput. Phys., 13, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Dunning, Jr., T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, R. L. 1987, J. Phys. Chem. Ref. Data, 16 [Google Scholar]
- Kharchenko, V., Bhardwaj, A., Dalgarno, A., Schultz, D. R., & Stancil, P. C. 2008, J. Geophys. Res. (Space Phys.), 113, A08229 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, V. A., & Mumma, M. J. 2001, ApJ, 549, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Krebs, S., & Buenker, R. J. 1995, J. Chem. Phys., 103, 5613 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, L., Wang, J. G., & Janev, R. K. 2012, J. Phys. B At. Mol. Opt. Phys., 45, 015202 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, F. W., Phaneuf, R. A., Kim, H. J., Hvelplund, P., & Stelson, P. H. 1979, Phys. Rev. A, 19, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N. 2002, A&A, 389, 716 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolte, J. L., Stancil, P. C., Liebermann, H. P., et al. 2012, J. Phys. B At. Mol. Phys., 45, 245202 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, R. E., & Salop, A. 1977, Phys. Rev. A, 16, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Panov, M. N., Basalaev, A. A., & Lozhkin, K. O. 1983, Phys. Scr. T., 124 [Google Scholar]
- Phaneuf, R. A., Alvarez, I., Meyer, F. W., & Crandall, D. H. 1982, Phys. Rev. A, 26, 1892 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, J., Marmar, E., Terry, J., Kallne, E., & Kallne, J. 1986, Phys. Rev. Lett., 56, 50 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shipsey, E. J., Browne, J. C., & Olson, R. E. 1981, J. Phys. B At. Mol. Phys., 14, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Stancil, P. C., Liebermann, H. P., et al. 2011, Phys. Rev. A, 84, 022711 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Stancil, P. C., Schultz, D. R., et al. 2012, J. Phys. B At. Mol. Phys., 45, 235201 [NASA ADS] [CrossRef] [Google Scholar]
- Zygelman, B., Cooper, D., Ford, M., et al. 1992, Phys. Rev. A At. Mol. Opt. Phy., 46, 3846 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Adiabatic potential energy curves of [OH]6+ as a function of internuclear distance R. Panel a: calculated adiabatic potential energy curves for the lowest 20 2Σ+ and 14 2Π molecular states for n = 3, 4, 5 and 6 channels, panel b: potentials of 2Δ, 2Φ, and 2Γ molecular states for n = 3, 4, 5, and 6 channels, and panel c: adiabatic potentials near the vicinity of the avoided crossings for n = 4 and n = 5 channels. |
| In the text | |
 |
Fig. 2. Radial coupling matrix elements between the adjacent states for [OH]6+. Panels a–d: 2Σ+–2Σ+ couplings, panels e–f: 2Π–2Π couplings. |
| In the text | |
 |
Fig. 3. Rotational coupling matrix elements for [OH]6+. Panel a: (6–9)2Σ+–(4–5)2Π couplings, panel b: (6–10)2Σ+–(6–10)2Π couplings, panel c: (11–12)2Σ+–(7–10)2Π couplings, panel d: (13–14)2Σ+–(7–10)2Π couplings. |
| In the text | |
 |
Fig. 4. Total charge transfer cross sections in O6+–H collisions. |
| In the text | |
 |
Fig. 5. Cross sections for electron capture to n = 4 shell of O5+ ion in O6+–H collisions. |
| In the text | |
 |
Fig. 6. Cross sections for electron capture to n = 5 shell of O5+ ion in O6+–H collisions. |
| In the text | |
 |
Fig. 7. Cross sections for electron capture to 4l shell of O5+ ion in O6+–H collisions. Panel a: cross sections for electron capture to O5+(4s) state. Panel b: cross sections for electron capture to O5+(4p) state. Panel c: cross sections for electron capture to O5+(4d) state. Panel d: cross sections for electron capture to O5+(4f) state. |
| In the text | |
 |
Fig. 8. Cross sections for electron capture to 5l shell of O5+ ion in O6+–H collisions. Panel a: cross sections for electron capture to O5+(5s) state. Panel b: cross sections for electron capture to O5+(5p) state. Panel c: cross sections for electron capture to O5+(5d) state. Panel d: cross sections for electron capture to O5+(5f) state. Panel e: cross sections for electron capture to O5+(5g) state. |
| In the text | |
 |
Fig. 9. Recommended total charge transfer cross sections and rate coefficients for O6+–H collisions. Panel a: recommended total charge transfer cross sections. Panel b: total reaction rate coefficients. Black lines: present results; red lines: results of Wu et al. (2012). |
| In the text | |
 |
Fig. 10. nl-resolved charge transfer rate coefficients for O6+–H collisions. Solid lines: present results; dashed lines: results of Wu et al. (2012). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



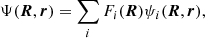
![$$ \begin{aligned} [ \nabla _R^2 \mathbf{I } - 2\mu (\boldsymbol{u} - E \mathbf{I } ) ] F( {\boldsymbol{R}} ) = ({\boldsymbol{M}} ({\boldsymbol{R}} ) + {\boldsymbol{P}} ({\boldsymbol{R}}) \bullet {\nabla _R}) F({\boldsymbol{R}}) , \end{aligned} $$](/articles/aa/full_html/2019/05/aa34922-18/aa34922-18-eq2.gif)
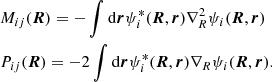
![$$ \begin{aligned} \left[\frac{{{\mathrm{d}^2}}}{{\mathrm{d}{R^2}}} - \frac{{J(J + 1) - {\lambda ^2}}}{{{R^2}}} - 2\mu (u(R) - E)\right]{f^J}(R) = ({\boldsymbol{V}^R}(R) + {\boldsymbol{V}^C}(R)){f^J}(R) , \end{aligned} $$](/articles/aa/full_html/2019/05/aa34922-18/aa34922-18-eq4.gif)
![$$ \begin{aligned} \mathbf V _{ij}^{R}(R)&=\left[ \left\langle i\left| -\frac{{{\partial }^{2}}}{\partial {{R}^{2}}}+\frac{L_{x}^{2}+L_{y}^{2}}{{{R}^{2}}} \right|j \right\rangle -2\left\langle i\left| \frac{\partial }{\partial R} \right|j \right\rangle \frac{\partial }{\partial R} \right]{{\delta }_{{{\lambda }_{i}}{{\lambda }_{j}}}} \nonumber \\ \mathbf V _{ij}^{C}(R)&=-2{{\delta }_{{{\lambda }_{i}}{{\lambda }_{j}}+1}}\frac{1}{{{R}^{2}}}\left[ {{\left[ (J-{{\lambda }_{i}})(J+{{\lambda }_{i}}+1) \right]}^{1/2}}\frac{\left\langle i\left| i{{L}_{y}} \right|j \right\rangle }{{{R}^{2}}} \right] \nonumber \\&\quad +2{{\delta }_{{{\lambda }_{i}}{{\lambda }_{j}}-1}}\frac{1}{{{R}^{2}}}\left[ {{\left[ (J+{{\lambda }_{i}})(J-{{\lambda }_{i}}+1) \right]}^{1/2}}\frac{\left\langle i\left| i{{L}_{y}} \right|j \right\rangle }{{{R}^{2}}} \right], \end{aligned} $$](/articles/aa/full_html/2019/05/aa34922-18/aa34922-18-eq6.gif)
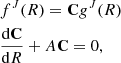
![$$ \begin{aligned}&\left[\frac{{\mathrm{d}^{2}}}{\mathrm{d}{{R}^{2}}}-\frac{J(J+1)-{{\lambda }^{2}}}{{{R}^{2}}}+2\mu E\right]g_{\gamma }^{J}-2\mu \mathop \sum \limits _{{{\gamma }^{\prime }}}{\mathbf{U _{\gamma {\gamma }^{\prime }}}(R)}g_{{{\gamma }^{\prime }}}^{J}=0 \nonumber \\&{\mathbf{U }_{\gamma {\gamma }^{\prime }}}(\textit{R})\equiv {{\left[ C(u-\mathbf P ){{C}^{-1}} \right]}_{\gamma {\gamma }^{\prime }}}, \end{aligned} $$](/articles/aa/full_html/2019/05/aa34922-18/aa34922-18-eq8.gif)
![$$ \begin{aligned} \mathbf S =[I+i\mathbf K ]{{[I-i\mathbf K ]}^{-1}}. \end{aligned} $$](/articles/aa/full_html/2019/05/aa34922-18/aa34922-18-eq9.gif)