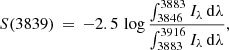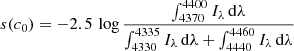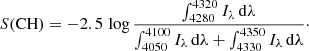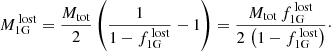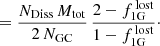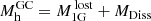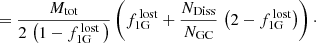| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 12 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201834825 | |
| Published online | 15 May 2019 | |
Purveyors of fine halos: Re-assessing globular cluster contributions to the Milky Way halo buildup with SDSS-IV
1
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstr. 12–14, 69120 Heidelberg, Germany
e-mail: andreas.koch@uni-heidelberg.de
2
School of Physics, University of New South Wales, Sydney, NSW 2052, Australia
3
Center of Excellence for Astrophysics in Three Dimensions (ASTRO-3D), Australia
Received:
7
December
2018
Accepted:
3
April
2019
There is ample evidence in the Milky Way for globular cluster (GC) disruption. It may therefore be expected that part of the Galactic halo field star population may also once have formed in GCs. We seek to quantify the fraction of halo stars donated by GCs by searching for stars that bear the unique chemical fingerprints typical for a subset of GC stars often dubbed “second-generation stars”. These are stars showing light-element abundance anomalies such as a pronounced CN-band strength accompanied by weak CH-bands. Based on this indicator, past studies have placed the fraction of halo stars with a GC origin between a few to up to 50%. Using low-resolution spectra from the most recent data release (DR14) of the latest extension of the Sloan Digital Sky Survey (SDSS-IV), we were able to identify 118 metal-poor (−1.8 ≤ [Fe/H] ≤ −1.3) CN-strong stars in a sample of 4470 halo giant stars out to ∼50 kpc. This increases the number of known halo stars with GC-like light-element abundances by a factor of two and results in an observed fraction of these stars of 2.6 ± 0.2%. Using an updated formalism to account for the fraction of stars lost early on in the GC evolution, we thus estimate the fraction of the Galactic halo that stems from disrupted clusters to be very low, at 11 ± 1%. This number would represent the case that stars lost from GCs were entirely from the first generation and is thus merely an upper limit. Our conclusions are sensitive to our assumptions of the mass lost early on from the first generation formed in the GCs, the ratio of first-to-second generation stars, and other GC parameters. We carefully tested the influence of varying these parameters on the final result and find that under realistic scenarios, this fraction depends on the main assumptions at less than 10 percentage points. We further recover a flat trend in this fraction with Galactocentric radius, with a marginal indication of a rise beyond 30 kpc that could reflect the ex situ origin of the outer halo as is also seen in other stellar tracers.
Key words: stars: carbon / stars: statistics / Galaxy: formation / globular clusters: general / Galaxy: halo / Galaxy: stellar content
© ESO 2019
1. Introduction
In the current picture of hierarchical structure formation, major parts of galactic halos stem from the accretion of small, presumably dark-matter-dominated, subgalactic units similar to the progenitors of today’s dwarf satellites (Searle & Zinn 1978; Dekel & Silk 1986; Bullock & Johnston 2005). This channel of halo formation is indeed seen in action in observations of satellite disruption within and outside our own Milky Way (MW; e.g., Ibata et al. 1994; Belokurov et al. 2006; McConnachie et al. 2009; Koch et al. 2012; Ludwig et al. 2012; Shipp et al. 2018; Morales et al. 2018, to name a few).
Moreover, globular clusters (GCs) are progressively gaining consideration as building blocks of so far unknown fractions of the Galactic stellar halo, which is also bolstered by their observed disruption in the tidal field of the MW through tidal tails in the Galactic halo (e.g., Odenkirchen et al. 2001; Lee et al. 2004; Lauchner et al. 2006; Chun et al. 2010; Jordi & Grebel 2010; Niederste-Ostholt et al. 2010; Sollima et al. 2011; Myeong et al. 2017; Navarrete et al. 2017; Carballo-Bello et al. 2018; Kuzma et al. 2018), the detection of extra-tidal stars with a likely GC origin based on photometric filtering techniques or stellar abundances and velocities (e.g., Jordi & Grebel 2010; Kunder et al. 2014, 2018; Anguiano et al. 2015, 2016; Navin et al. 2016; Simpson et al. 2017a), for instance, or the discovery of thin streams with possible GC progenitors (e.g., Grillmair & Dionatos 2006; Grillmair 2009; Bonaca et al. 2012; Bernard et al. 2014).
Globular clusters stand out in that they show significant light chemical element variations over a broad mass range of cluster masses, as was first noted in the 1970s. Prominent manifestations of these are significant dispersions in Na and O (e.g., Osborn 1971; Cohen 1978; Carretta et al. 2009), and bimodalities in their stellar CN abundances (e.g., Popper 1947; Harding 1962; Norris & Cottrell 1979; Kraft et al. 1982; Harbeck et al. 2003; Kayser et al. 2008; Smolinski et al. 2011). Furthermore, a clear correlation between Mg and Al is seen, stemming from the same proton-burning channels (Gratton et al. 2001). All of these lead to clear (anti-)correlations rather than generic abundance spreads alone, although not all GCs show Mg spreads, as recently reviewed by Pancino et al. (2017). To higher order, these findings are complemented by later burning stages in the first stellar generation, causing Mg, Si, and Zn to anticorrelate as well (e.g., Hanke et al. 2017). Such give-away abundance variations have to date been traced down to the low-mass GC regime (Bragaglia et al. 2017; Simpson et al. 2017b), and were also found in old GCs in external galaxies (e.g., Mucciarelli et al. 2009; Mateluna et al. 2012; Colucci et al. 2014; Larsen et al. 2018), as well as in massive, intermediate-age clusters in the Magellanic Clouds (e.g., Hollyhead et al. 2017, 2018) and down to cluster ages of ∼2 Gyr (Martocchia et al. 2018a).
It is accepted today that these variations occur along with multiple stellar populations in GCs; color-magnitude diagrams uniquely support that there are two or more populations, possibly separated in age by several ∼100 Myr1, and distinct in other tracers such as variations in He content. However, the origin of these populations is unclear so far because no model can currently explain all of the observational constraints (e.g., Bastian & Lardo 2018). In particular, it remains unresolved whether GCs did indeed experience two or more episodes of star formation that resulted in the observed abundance anomalies. Nonetheless, we follow the commonly adopted terminology of calling stars that are enhanced in O and C and that show lower Na and N abundances (in other words, “normal” stars by metal-poor GC standards) “first-generation” stars and those with higher Na and N levels “second-generation” stars. We do so for the sake of convenience and without implying that we favor a particular formation scenario such as repeated star formation. Either way, the ratio of stars in the two main populations in each cluster lies at ∼50% each, with a possible trend toward a higher fraction of the first-generation stars with decreasing cluster mass (Milone et al. 2017; cf. Bastian & Lardo 2015).
Ad hoc models of GC evolution that are designed to explain multiple populations through multiple epochs of star formation (e.g., D’Ercole et al. 2008; Bastian et al. 2013) predict that during an initial phase of cluster dissolution, a large fraction of up to 90% of the first generation of cluster stars is lost from a GC and released into the halo. Because these first generation stars bear the chemical imprint of a standard, early chemical evolution, however, they are indistinguishable from any given halo field star. More generally, several studies suggest that GCs have on average lost a considerable fraction of their stars since they formed, for example, around two-thirds according to Kruijssen (2015) or about 75–80% according to Baumgardt (2017) and Baumgardt et al. (2019).
Because first-generation stars that end up in the halo are chemically indistinguishable from normal halo stars, the second-generation stars are of particular interest because they can be traced through their peculiar chemistry. They are enhanced in N and Na and in turn depleted in C and O, a pattern that is qualitatively consistent with proton-capture reactions in a generation of polluters such as intermediate-mass asymptotic giant branch (AGB) stars (D’Ercole et al. 2008), fast-rotating massive stars (Decressin et al. 2007), massive binaries (de Mink et al. 2009), or supermassive stars (Gieles et al. 2018).
In order to assess the actual fraction of the MW halo that is made up of former GC stars, we can use the empirical fact that the light element variations described above are commonly found in GCs but not in young open clusters or dwarf galaxy field stars, and only rarely in the halo field (Pilachowski et al. 1996; Geisler et al. 2007). If any stars with second-generation-like chemistry (classified by their molecular band strengths as CN-strong and CH-weak) exist in the halo, this indicates that they most likely originated from disrupted GCs.
Large sky surveys such as the Sloan Digital Sky Survey (SDSS) have permitted statistical investigations of the fraction of the MW halo that is contributed by disrupted GCs based on the discovery of CN-strong and CH-weak field halo stars (e.g., Martell & Grebel 2010; Martell et al. 2011; Carollo et al. 2013; Tang et al. 2019), with estimates ranging from 17–50%, depending on the assumptions of the ratio of first- to second-generation stars in GCs and the statistics of GC dissolution. Likewise, Carretta et al. (2010) and Ramírez et al. (2012) found candidates with second-generation-like Na- and O-abundance ratios across the metal-poor tails of all MW components, while Lind et al. (2015) identified one potential GC escapee in the Gaia-ESO Survey (GES; Gilmore et al. 2012) of a few hundred halo stars, based on its second-generation-like Mg and Al abundances. This was extended toward a larger fraction of five out of the studied seven metal-rich field stars with Mg-Al anomalies using the SDSS-III APOGEE Survey (Majewski et al. 2017; Fernández-Trincado et al. 2016, 2017). Similarly, Martell et al. (2016) employed APOGEE to identify five halo giants enriched in N and Al. These more recent studies typically arrive at estimates of just a few percent of halo stars with GC cluster origin, suggesting that GC disruption is a minor contributor to the halo field population. On the modeling front, Schaerer & Charbonnel (2011) estimated a contribution of 5–8% of low-mass first-generation stars to the halo field population, and possibly as high as 20% if second-generation stars are also accounted for.
While the Galactic bulge is not the target of our current study, we note that in the Galactic bulge, N-rich field stars were also discovered (Schiavon et al. 2017). Schiavon et al. (2017) argued that if the N-rich stars are indeed former GC stars, then the mass in destroyed GCs exceeds the mass in surviving GCs by a factor of eight.
In our work, we seek to make use of the latest extensions to the SDSS (Blanton et al. 2017) in order to improve the number statistics of CN-strong stars in the MW halo. While previous studies detected a few tens of such stars in spectroscopic samples of several thousand (leading to a fraction of CN-strong field stars of ∼2%; Martell et al. 2011), the latest generations of massive spectroscopic surveys allow for a potential increase in the number of disrupted GC stars by factors of several. This paper is organized as follows: in Sect. 2 we describe the data set and steps taken to define the bona fide halo sample. Our spectral index measurements to determine CN- and CH-band strengths are laid out in Sect. 3, and the method to distinguish CN-strong from CN-normal stars is presented in Sect. 4. Next, Sect. 5 is dedicated to the formalism for determining the fraction of the halo that likely originated from dissolved GCs. Our results and their limitations are then discussed in Sect. 6.
2. Data and sample selection
The first statistical endeavour toward the fraction of halo stars born in GCs (Martell & Grebel 2010) was based on the seventh data release (DR7) of the SDSS, which already included the first important add-on of the Sloan Extension for Galactic Understanding and Exploration (SEGUE) with additional spectra of 240 000 stars (Yanny et al. 2009), taken with a resolving power of R ∼ 2000 over a wavelength range of 3800–9200 Å. The subsequent work of Martell et al. (2011) built upon more numerous data from the next extension within SDSS-III, that is, SEGUE-2 (with an additional 120 000 stellar spectra). After applying a number of stringent selection criteria, this yielded the discovery of 16 further CN-strong stars, adding to the 49 such objects out of ∼2000 regular halo stars from the previous study.
In our current study, we employed data from the latest phase of the SDSS-IV (Blanton et al. 2017), as drawn from its DR14 catalog (Abolfathi et al. 2018). The SDSS-IV low-resolution spectroscopy primarily targeted galaxies and quasars from the SDSS project “extended Baryon Oscillation Spectroscopic Survey” (eBOSS; Dawson et al. 2016), which contains on the order of 9% stellar spectra. Moreover, DR14 contains the previously observed spectra from the earlier phases of the SDSS. As in previous works, we relied on stellar parameter and metallicity measurements provided in the SDSS catalogs, which in turn are based on the automated Segue Stellar Parameter Pipeline (SSPP; Lee et al. 2008).
2.1. Selection criteria
In order to build a representative sample of halo red giants, we applied the same selection criteria as Martell & Grebel (2010) in our SQL query to the SDSS. That is, we preselected only stars with [Fe/H] ≤ −1 to focus on halo objects. We further demanded that the error on metallicity was σ[Fe/H] ≤ 0.5 and that at least three of the ten independent metallicity determinations within the SSPP were flagged as reliable. Furthermore, only objects with surface gravities constrained to log g ≤ 3 and respective errors below σlog g ≤ 0.5 were queried. Finally, the mean signal-to-noise ratio (S/N) was required to lie above 20 per pixel, and we employed a color cut toward cooler giants using (g − r)0 ≥ 0.2, leaving a starting sample of ∼15 000 halo giants.
Next, we required an S/N above 15 per pixel in the region of 4000–4100 Å because lower S/Ns would cloud our measurements of the respective spectral indices below. The ensuing subsample was further refined by dividing the entire sample into metallicity bins of 0.2 dex each. Within each bin, we constructed fiducial lines in diagrams of log g versus color (which transpired to yield the clearest separation) and pruned the sample from contaminating AGB, main sequence, and turn-off stars using a smoothed 3σ cut along those ridge lines. This is illustrated for each metallicity bin in Fig. 1.
 |
Fig. 1. Modified Kiel diagrams for several metallicity bins. The red 3σ envelopes were used to select bona fide halo giants. |
We also ascertained that our field star sample was not contaminated by present-day GC member stars, as they have not yet been released into the surrounding halo. To this end, we rejected stars that fell within the tidal radii of any object from the catalog of Harris (1996; 2010 version). In this way, we identified 43 giants located in M3, M13, and M15. We were thus left with 6801 halo field candidates.
Finally, in the following, we explicitly ignored the metal-rich ([Fe/H] > − 1.3 dex) tail of our distribution. This is to avoid any possible false detections of CN-strong stars that are not the progeny of actual GC dissolutions, as suggested by follow-up observations of a subsample of the CN-strong halo stars by Martell et al. (2011), which do not show any signatory Na-enhancement (Martell et al., in prep.). While it is well established that metal-rich GCs do show CN/CH anticorrelations (Harbeck et al. 2003; Kayser et al. 2008), it is strictly not required that a former GC star would need to show both enhanced N and Na-enhancement for a first identification, in particular because we are here solely concerned with low-resolution spectra without any means to constrain the Na content of our CN-strong stars. Nonetheless, imposing our additional metallicity cut will ascertain a bona fide sample for unbiased identification of the desired GC-like stars as halo stars. Furthermore, metal-poor stars below −1.8 dex were removed from the sample, as elaborated below in Sect. 2.2. This left us with a final sample of 4649 stars with halo characteristics in the metallicity range of −1.3 to −1.8. Figure 3 shows the full queried initial and the selected halo subsample.
2.2. Distances
In order to determine the distances of the stars, we first computed their r-band absolute magnitudes, Mr, where we resorted to a set of 10 Gyr old Dartmouth isochrones (Dotter et al. 2008) for a broad grid of metallicities from −1 to −2.5 dex, using no α-enhancement, because these provide the best global representation of metal-poor Galactic GCs (see also Hendricks et al. 2014). These isochrones were interpolated to the observed dereddened (g − r)0 color as provided by the SDSS. Because the isochrone spacing becomes smaller and less distinguishable toward the lowest metallicities, and with the grid limitation of the Dartmouth tracks to ≥ − 2.5 dex, we followed Martell et al. (2011) in selecting only stars more metal-rich than −1.8 dex. This selection mainly picks up halo giants that are broadly located around the peak of the halo metallicity distribution function (Schörck et al. 2009). This is further beneficial because the CN band strength loses its sensitivity to N-abundance at low metallicities (e.g., Boberg et al. 2016a), leaving CN bimodalities largely undetectable from this tracer.
3. Spectral indices
At the low resolution of the SDSS spectra, measuring band indices in the blue spectral region provides a powerful tool for identifying CN-strong and CN-weak stars. In particular, the frequently used S(3839) index, first defined and optimized by Norris et al. (1981) to measure the strength of the CN-band at 3839 Å, is ideal for tracing bimodal band strength distributions:
where Iλ refers to the observed flux in the spectrum.
The run of this CN index versus absolute magnitude (bottom panel), color (middle), and metallicity (top) is shown in Fig. 2, displaying the trademark increase in CN-band strengths with color. This increase arises because colder (thus redder) stars form progressively more (CN) molecules.
 |
Fig. 2. Kiel diagram of the full sample (contours; satisfying the initial query restrictions in log g < 3, [Fe/H] < −1, (g − r)0 > 0.2, S/N > 20, and respective cuts in the parameter errors) and the subset of halo giants (dots; after removal of metallicity-dependent CMD features and further pruning the metal-rich and -poor tails above −1.3 and below −1.8 dex) used for our statistical purposes. |
Similarly, strong bands of carbonaceous molecules such as CH and CN are seen in carbon stars, and in the metal-poor regime, in carbon-enhanced metal-poor (CEMP) stars (Beers & Christlieb 2005; Hansen et al. 2016). In this case, the strong bands are rather a result of their strong carbon-overabundance and do not reflect the light element variations that result from the early nucleosynthesis in the GCs to be engulfed into the halo. These objects can be efficiently flagged using indices encompassing the CH- (at 4350 Å) and C2-bands (at 4737 Å) that are mainly sensitive to carbon and only little affected by nitrogen features in the neighboring spectral regions. These indices read
We therefore discarded another 179 stars from further analysis because of their strong C-bands, employing the set of restrictions in s(c0), s(c1), and [Fe/H] outlined in Martell & Grebel (2010). Separating these by metallicity yields fractions of C-rich stars that are fully compatible with those found by Martell & Grebel (2010), which moreover display a metallicity distribution function that directly traces that of such objects in the Galactic halo as found in other large-scale surveys (e.g., Lucatello et al. 2006; Carollo et al. 2012). In particular, the largest fraction of C-stars is found at low metallicities, where 73% of our sample lie below −2 dex. This is the formal boundary of CEMP stars (Beers & Christlieb 2005).
Finally, in order to cross-identify the “CN-strong” nature of the stars of interest as also being “CH-weak”, we determined the strength of the CH G-band at 4300 Å through the index definition of Martell et al. (2008):
Throughout our entire work, errors on all measured parameters were determined in a Monte Carlo sense by varying the input quantities (g0, r0, [Fe/H]) by their respective uncertainty.
4. Separation of CN-weak and -strong stars
In order to identify CN-normal and CN-weak stars, several methods have been devised in the literature. For instance, Gerber et al. (2018) employed separation by spline interpolation in CN-band strength versus absolute magnitude space. However, their data have higher S/N and smaller errors on individual measurements, and the confirmed membership of their sample stars with a known GC facilitated an accurate MV determination. Furthermore, Boberg et al. (2016b) discussed an accurate treatment of the index-measurement errors, but at super-solar metallicities, which are beyond the range of our halo sample.
For our purpose, we first removed any temperature, gravity, and metallicity trend in the S(3839) measurements through a straight-line fit to the CN-weak sequence in the S(3839) versus magnitude space in Fig. 3 (bottom). Computing a vertical distance of each individual star from the best fit then yielded a “corrected” index δS(3839). Because the slope of this parameter space mildly depends on metallicity, flattening toward the metal-poor regime, we performed the calculation of the δS(3839) values in independent bins of metallicity, each 0.1 dex wide (Fig. 4).
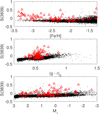 |
Fig. 3. CN index in the halo giant candidates (black dots) according to Eq. (1) vs. absolute magnitude (bottom), color (middle), and metallicity (top). Carbon- and CEMP-stars (red triangles) were rejected based on their s(c0) and s(c1) indices (Eqs. (2) and (3)). |
 |
Fig. 4. CN-band strength vs. absolute magnitude for separate metallicity bins of 0.1 dex width. The solid line shows the best fit to the CN-weak sequence, while the dashed red line delineates the separation into CN-weak and CN-strong stars. |
For each bin, we computed a generalized, that is, error-weighted, histogram of δS(3839), from which we drew the distinction into CN-weak and CN-strong stars by defining the largest separation in the histogram, aided by a Sobel edge-detection filter. As an independent test, we also applied a heteroscedastic Kayes mixture modeling algorithm (KMM; Ashman et al. 1994) to every metallicity subsample, which assigns probabilities to each star to belong to either the CN-strong or CN-weak populations. These probabilities are explicitly assumed to be Gaussian. The resulting distribution (dashed lines in Fig. 5) shows a vast overlap of CN-weak and CN-strong stars and leads to a large overall ratio of these two populations that is higher than previous estimates in the literature. Considering this overlap and the fact that our first method takes into account the more realistic error distribution of our data, we did not pursue the KMM separation any further.
 |
Fig. 5. Combined sample of CN-strong (red) and CN-normal stars. The right panel shows the generalized histogram of both populations, where the curve for the CN-strong stars has been scaled up by a factor of ten. Dotted lines show the distribution derived by Martell & Grebel (2010), and the dashed curves are the results from our KMM separation. |
To construct the final sample, we took advantage of the fact that stellar evolution in the progenitors, whether massive or not, produces the phenomenologically observed anticorrelations between CN- and CH-band strength in GC stars by efficiently converting C into N. For the present purpose, this means that strong CN-bands should be accompanied by considerably weakened CH-band strengths. Following Martell et al. (2011), we adopted the mean S(CH) of stars more metal rich than −1.3 dex as a delimiter between CH-normal and CH-weak for the low-metallicity bins that make up our present sample. This selection was again carried out in metallicity bins of 0.1 dex and is shown in Fig. 6.
 |
Fig. 6. Separation of regular halo stars that are CN-normal and CH-strong (black dots) and the bona fide CN-strong, CH-weak stars that we assume to have originated in now-dissolved GCs (red circles). In concordance with Fig. 3, this was done in separate metallicity bins. While not used in the actual statistics, we include stars above [Fe/H] = −1.3 in this figure for illustration. |
Figure 5 displays the combined sample in the corrected δS(3839) index, also accounting for its error distribution (right panel). Owing to the additional separation criterion in terms of metallicity (Fig. 4), some of the CN strong stars are also CH-strong, but we do not consider them as GC-descendants. Nonetheless, this leads to an overlap in these figures that focus on CN-strength alone (Figs. 4, 5).
A clear bimodality of CN-strong and CN-normal stars is seen, as is commonly found in Galactic and extragalactic GCs (e.g., Kayser et al. 2008; Larsen et al. 2018; Hollyhead et al. 2018). These separate populations are the base for all our subsequent statistics and number counts. Sample spectra from either group are depicted in Fig. 7, including those of some rejected metal-rich examples. This demonstrates the success in isolating the relevant stellar tracers based on our spectral index analysis.
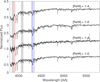 |
Fig. 7. Sample spectra for the stellar types relevant to this work. These are (from top to bottom): a metal-poor CN-strong star, a more metal-rich CN-strong star, and two CN-normal stars with the same stellar parameters as the former stars. Metal-rich stars above [Fe/H] = −1.3 were rejected from our sample because of the risk of misclassifications. The red (blue) and gray shaded areas indicate the line and continuum bandpasses for the S(3839) and S(CH) index after Norris et al. (1981) and Martell et al. (2008), see Eqs. (1) and (4). |
5. Halo fractions of globular cluster stars
We find that 118 out of our 4470 halo giant stars are CN-strong and CH-weak, thereby qualifying as second-generation progeny of dissolved GCs. We note that we recover the 65 CN-strong candidates of Martell et al. (2011) as well, which is expected because this work used the same selection criteria. This corresponds to an observed fraction of halo stars with second-generation abundance patterns of 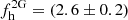 %, where the error is solely based on Poisson statistics. We also note that this number would increase to 3.7% if we were to include the entire metallicity range up to −1 dex, thereby yielding 252 CN-strong stars. This metallicity dependence of this fraction is illustrated in Fig. 8.
%, where the error is solely based on Poisson statistics. We also note that this number would increase to 3.7% if we were to include the entire metallicity range up to −1 dex, thereby yielding 252 CN-strong stars. This metallicity dependence of this fraction is illustrated in Fig. 8.
 |
Fig. 8. Dependence of the observed fraction of CN-strong halo stars on metallicity. The solid line shows our recovered overall fraction based on the sample within −1.8 ≤ [Fe/H] ≤ −1.3, whereas the dashed line also accounts for the metal-rich tail up to −1 dex. |
5.1. Formalism
Our goal is to compute the fraction of the halo that was contributed by disrupting GCs,  . This is the ratio of the total mass in former GC stars in the halo field,
. This is the ratio of the total mass in former GC stars in the halo field, 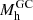 , to the total present-day stellar mass of the halo, which we adopt here as Mh, tot = 109 M⊙2. We also note that the MW GC system currently accounts for about 2–3% of the stellar halo mass (Forbes et al. 2018).
, to the total present-day stellar mass of the halo, which we adopt here as Mh, tot = 109 M⊙2. We also note that the MW GC system currently accounts for about 2–3% of the stellar halo mass (Forbes et al. 2018).
We used the following terminology and formalisms, which differ in several details from those of Martell & Grebel (2010) and Martell et al. (2011). In our work, “mass loss at early time” refers to the phase of strong loss of first-generation stars from GCs that was proposed to solve the mass budget problem, that is, the observational evidence that the current stars with primordial signatures (and the respective higher mass stars that have already perished) are insufficient to have produced the amount of light elements required to enrich the second-generation stars to the observed levels (e.g., Bastian & Lardo 2015). During this period, a fraction of 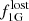 of mass in the initial GC system is lost. We discuss the implication of the exact value of this parameter in Sect. 5.1.3 below. Accordingly,
of mass in the initial GC system is lost. We discuss the implication of the exact value of this parameter in Sect. 5.1.3 below. Accordingly, 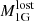 is the mass lost from the GC system at these early times. In contrast, “late mass loss” is taken as stars escaping from GCs after the second generation has formed, whether through internal or external processes.
is the mass lost from the GC system at these early times. In contrast, “late mass loss” is taken as stars escaping from GCs after the second generation has formed, whether through internal or external processes.
5.1.1. Ratio of first- to second-generation stars
For present-day GCs, the ratio of first- to second-generation stars is still debated. Early studies, observationally and theoretically, commonly assigned the GCs with an equal proportion of primordial and enriched populations (e.g., D’Ercole et al. 2008; Carretta et al. 2009). Based on their study of 33 MW CGs, Bastian & Lardo (2015) concluded that the fraction of second-generation stars is 68% and independent of cluster parameters such as mass, metallicity, or location within the Galaxy.
Conversely, Milone et al. (2017) found a clear trend of the second population with present-day GC mass in the form of a decreasing occurrence of the enriched stars with decreasing mass (see also Gerber et al. 2018). Moreover, the population fractions are expected to vary with distance from each GC center (e.g., Milone et al. 2009; Vanderbeke et al. 2015; Nardiello et al. 2018) and change during the clusters’ dynamical evolution (Vesperini et al. 2013). The influence of varying this ratio on the final derived fraction of the halo stemming from dissolved GCs is illustrated in Fig. 9. Finally, Baumgardt (2017) did not find a correlation between the first-generation fraction and the global mass function of GCs, but instead a trend of the escape velocity with the first-generation fraction, which reflects the finding of Milone et al. (2017) of a mass dependence.
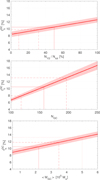 |
Fig. 9. Top panel: dependence of the final fraction of donated halo stars on the adopted fraction of first-generation stars. The solid, dashed, and dash-dotted lines are for ratios of 0.5 (Carretta et al. 2009), 0.32 (Bastian & Lardo 2015), and 0.09, the minimum value in the catalog of Milone et al. (2017). This calculation adopted a ratio of an early mass-loss fraction (Sect. 5.1.3) of 56% and an average present-day GC mass of 2.2 × 105 M⊙. Middle panel: influence of the number of present-day GCs in our analysis. Here, the solid line shows the 157 objects in the Harris (1996) catalog, while the dashed lines correspond to a variation by ±25%, e.g., due to selecting only halo GCs. Bottom panel: dependence on the adopted mean present-day GC mass. Red lines show the masses based on the Harris (1996) catalog adopted in this work (solid), the catalog of GC masses from McLaughlin & van der Marel (McLaughlin & van der Marel, dashed), and a mass of 5 × 105 M⊙ (dotted) as adopted by Martell et al. (2011). Here, the calculations adopted a ratio of first- to second-generation stars of 50:50 and an early mass-loss rate of 56%. |
In principle, a realistic distribution of GC masses might also be assumed (see Sect. 5.1.2 below) and a CN-strong fraction be attached to each mass value through the functional trend implied by Milone et al. (2017). However, as the range of resulting fractions shown in Fig. 9 is fairly small, we adopted for simplicity that the GCs consist of 50% first-generation stars and 50% second-generation stars, which is at the higher end of the values suggested in the literature, noting that this will provide an upper limit in our final results.
5.1.2. Cluster masses and number of present-day GCs
To date, NGC old GCs have been identified in the MW; this is the number of surviving clusters in the Galaxy, for which we adopt a value of 157, corresponding to the number of known GCs in the Harris (1996, 2010 edition) catalog. We here study the buildup of the stellar halo, therefore only the halo clusters should be considered, which make up ∼75% of this database. This would only mildly decrease the resulting halo fraction obtained in Sect. 5.3, from 11 to 8%. The influence of this parameter on our final result is shown in the middle panel of Fig. 9.
In order to convert this number into an overall mass of the Galactic GC system, we consulted the catalog of known MW GCs by Harris (1996) and computed cluster luminosities from their absolute magnitudes. For their stellar populations, we assumed a stellar mass-to-light ratio of M/L = 2(M/L)⊙, noting that this may vary to within a factor of about two (Illingworth 1976; Pryor & Meylan 1993; Strader et al. 2009). Summing these values results in a total mass of the GC system of Mtot = 3.5 × 107 M⊙. In turn, this yields a simplistic estimate of the mean mass of a typical present-day MW GC of ⟨MGC⟩ = Mtot/NGC = 2.2 × 105 M⊙.
Alternatively, McLaughlin & van der Marel (2005) determined dynamical masses and mass-to-light ratios of approximately half of the MW GCs and found M/L ratios that are consistent with the value of 2 adopted in our work. The average GC mass in their catalog is higher by ∼60%. However, this has only a minor influence during the propagation through our formalism below, and the final accreted halo fraction does not change by more than two percentage points. The influence of varying the present-day mean GC mass on the final derived fraction of the halo stemming from dissolved GCs is illustrated in the bottom panel of Fig. 9.
Now we designate NDiss and MDiss as the number of completely dissolved GCs and the stellar mass lost through complete cluster dissolution, respectively, which are needed to explain the observed fraction of second-generation halo stars (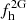 ). Thus we can first determine the mass that has been lost at early times as
). Thus we can first determine the mass that has been lost at early times as
Clusters that dissolve completely in turn contribute through their early mass loss, as well as through their final masses, thus:
This means that the total mass of GC stars in the halo field can be expressed by summing the above as
5.1.3. Mass loss from the first generation
Previous studies have adopted a large fraction for 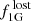 of up to 90% early cluster mass loss, preferentially if the clusters were massive. This is based, for example, on the AGB scenario (D’Ercole et al. 2008; Conroy 2012). This accounts for cluster evolutionary effects such as tidal disruption, two-body relaxation, energy input from supernovae, or residual gas loss (e.g., Gnedin & Ostriker 1997), but not for effects like “infant mortality”, that is, the disruption of young clusters already during their formation stages (cf. Bastian & Goodwin 2006). Likewise, in a scenario where fast-rotating massive stars were the main polluters of the second generation, models predict that the clusters were once more massive by up to factor of 25 (
of up to 90% early cluster mass loss, preferentially if the clusters were massive. This is based, for example, on the AGB scenario (D’Ercole et al. 2008; Conroy 2012). This accounts for cluster evolutionary effects such as tidal disruption, two-body relaxation, energy input from supernovae, or residual gas loss (e.g., Gnedin & Ostriker 1997), but not for effects like “infant mortality”, that is, the disruption of young clusters already during their formation stages (cf. Bastian & Goodwin 2006). Likewise, in a scenario where fast-rotating massive stars were the main polluters of the second generation, models predict that the clusters were once more massive by up to factor of 25 (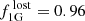 ). However, recent models and observations do not further support such a strong mass loss. For instance, observations of GC populations in dwarf galaxies (Larsen et al. 2012, 2014) and young star clusters in merging galaxies (Cabrera-Ziri et al. 2015) ascertain lower mass-loss fractions of
). However, recent models and observations do not further support such a strong mass loss. For instance, observations of GC populations in dwarf galaxies (Larsen et al. 2012, 2014) and young star clusters in merging galaxies (Cabrera-Ziri et al. 2015) ascertain lower mass-loss fractions of 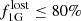 .
.
Likewise, Baumgardt & Sollima (2017) argued for a loss fraction for a typical GC of 75%, which could reach as much as 90% for the most massive objects, however, based on N-body simulations in comparison with the observed mass functions of 35 Galactic GCs. The simulations of Webb & Leigh (2015), accounting for orbital evolution, also indicated that an average cluster was initially 4.5 times more massive (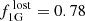 ). We also note that Kruijssen (2015) considered a two-phase model for GC evolution, according to which only the least massive and/or metal-rich clusters suffered from high mass-loss rates, whereas an average system has experienced typically
). We also note that Kruijssen (2015) considered a two-phase model for GC evolution, according to which only the least massive and/or metal-rich clusters suffered from high mass-loss rates, whereas an average system has experienced typically 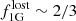 .
.
It stands to reason, furthermore, that in the mass loss considered above, only first-generation stars are lost, not those from the second generation. While originally hypothesized to solve the mass budget problem, a number of works have since shown that this heavy mass loss of only first-generation stars encounters a number of problems (see the discussion in Bastian & Lardo 2018). A strong argument for this is the result from Milone et al. (2017) that the fraction of enriched stars increases with cluster mass, whereas in the heavy mass-loss scenario the opposite trend is expected. This suggests that clusters did not undergo very strong mass loss and that the current fraction is close to the initial fraction; GCs did not preferentially lose large fractions of first-generation stars. Reina-Campos et al. (2018) found that clusters with present-day masses in excess of 105 M⊙ once were only more massive at birth (after accounting for stellar evolution) by factors of 2–4. For our purpose, this would imply that if second-generation stars are lost at a similar rate to those from the first population, then we would only need to correct for the relative population fractions (i.e., 50/50), and not for any additional factors. For completeness, we chose to follow our previous assumptions and to retain the full correction factors, referring again to Fig. 9 for a quantitative estimate of their variations. Further discussions of the initial mass function and its relevance for GC evolution can be found in Forbes et al. (2018).
5.1.4. Mass loss by stellar evolution
Many of the GC models discussed in Sect. 5.1.3 account for stellar evolution, where about a factor of two comes from stellar evolution and the other half stems from the aforementioned dynamical mass loss, that is, either two-body relaxation or tidal shocking. This equally affects stars that are part of a cluster and those that are lost from the outer regions.
Most importantly, our empirical analysis hinges on the comparison of halo stars with GCs of similar age and metallicity. If we assert that the clusters were twice as massive at birth than now as a result of stellar evolution, we must also recognize that the halo was also twice as massive because of the same channels of stellar evolution. Consequently, the mass-loss factors introduced in Sect. 5.1.3 need be lowered by a factor of two. In the following, we start with the assumption that the initial GCs were 4.5 times as massive as they are today, as argued by Webb & Leigh (2015), who did include stellar evolution. Therefore, we halve this value to 2.25 times higher initial masses, neglecting stellar evolution, which corresponds to our final adopted fraction of 56% for the mass loss from the first generation.
In Fig. 10 we show the resulting mass fraction of the halo from GC disruption (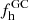 ) according to the calculations concluded in Sect. 5.2 as a function of the adopted mass-loss rate
) according to the calculations concluded in Sect. 5.2 as a function of the adopted mass-loss rate 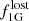 . Whether the cause lies in the details of the model or in factoring in the effect of stellar evolution is redundant in this figure, as it merely shows the dependence of our results with respect to the quantitative assumption. To this end, we rather highlight three sets of adopted model fractions, each shown for the cases of inclusion and exclusion of stellar evolution.
. Whether the cause lies in the details of the model or in factoring in the effect of stellar evolution is redundant in this figure, as it merely shows the dependence of our results with respect to the quantitative assumption. To this end, we rather highlight three sets of adopted model fractions, each shown for the cases of inclusion and exclusion of stellar evolution.
 |
Fig. 10. Dependence of the final fraction of accreted halo stars on the adopted mass-loss rate of first-generation stars. The lines indicate the fractions adopted by various works: Baumgardt & Sollima (2017, dash-dotted), Martell et al. (2011, dashed), and our study (solid). Here, red lines show the cases that neglect stellar evolution, while blue lines show values where this is accounted for. This calculation adopted a ratio of first- to second-generation stars of 50:50 and an average present-day GC mass of 2.2 × 105 M⊙. |
Even in the hypothetical absence of any such early losses (i.e., Eqs. (9),(10) with 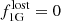 ), a theoretical lower limit of
), a theoretical lower limit of  GC contributions to the present-day stellar halo would still be found. This is due to those clusters that have by now fully dissolved and that also contributed to the halo buildup through later mass loss throughout their lives. In the MW halo, a mass-loss fraction of
GC contributions to the present-day stellar halo would still be found. This is due to those clusters that have by now fully dissolved and that also contributed to the halo buildup through later mass loss throughout their lives. In the MW halo, a mass-loss fraction of  is certainly conceivable; we note that this does not imply that there was no mass loss from any GC, but rather means that no stars of the first generation were lost, or that the fraction of first- and second-generation stars lost was roughly equal.
is certainly conceivable; we note that this does not imply that there was no mass loss from any GC, but rather means that no stars of the first generation were lost, or that the fraction of first- and second-generation stars lost was roughly equal.
5.2. Resulting halo fraction
At this point, we consider the actual number of dissolved GCs, NDiss, that are required to provide the fraction of second-generation stars, 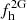 , that we found in the Galactic halo in the previous sections. As elaborated in Martell et al. (2011), this value is given as
, that we found in the Galactic halo in the previous sections. As elaborated in Martell et al. (2011), this value is given as
with the factor two stemming from the adopted similar fractions of first- and second-generation stars in the early clusters. It is this factor, which is not strongly constrained by observations, that dominates the final inferred fraction. Therefore we highlighted its influence in Fig. 9 (top); see Sect. 5.1.1. Based on our observed fraction of 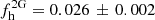 and on these assumptions, we obtain a large number of 240 ± 22 clusters to be dissolved. This is more than twice the value found by Martell et al. (2011), but their working hypothesis had been a higher average cluster mass of 5 × 105 M⊙.
and on these assumptions, we obtain a large number of 240 ± 22 clusters to be dissolved. This is more than twice the value found by Martell et al. (2011), but their working hypothesis had been a higher average cluster mass of 5 × 105 M⊙.
As a result, we find that the fraction of the stellar halo that originates from disrupted GCs, 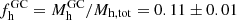 , under the assumption of a mass-loss fraction (Sect. 5.2) of 56%. The influence of different mass-loss prescriptions is shown in Fig. 10 and has been discussed before in Sects. 5.1.3 and 5.1.4. Martell & Grebel (2010) stated that a high fraction of up to 50% of the halo field must have formed in massive star clusters, constituting the CN-strong population observed today, with a further unknown contribution of CN-weak stars from now fully dissolved systems. Expanding their analysis using larger data sets, and using their finding of a lower
, under the assumption of a mass-loss fraction (Sect. 5.2) of 56%. The influence of different mass-loss prescriptions is shown in Fig. 10 and has been discussed before in Sects. 5.1.3 and 5.1.4. Martell & Grebel (2010) stated that a high fraction of up to 50% of the halo field must have formed in massive star clusters, constituting the CN-strong population observed today, with a further unknown contribution of CN-weak stars from now fully dissolved systems. Expanding their analysis using larger data sets, and using their finding of a lower 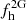 of 2.5%, Martell et al. (2011) estimated a lower limit of 17% of halo stars with both first- and second-generation element patterns, under the omission of low-mass clusters that are long gone. The observed fraction of GC-like halo stars from the latter work is consistent with the value found in our work, while our inferred value for donated halo stars is slightly lower. This is, however, chiefly due to the updated statistical treatment and different model assumptions, which we amply addressed through our Figs. 9 and 10.
of 2.5%, Martell et al. (2011) estimated a lower limit of 17% of halo stars with both first- and second-generation element patterns, under the omission of low-mass clusters that are long gone. The observed fraction of GC-like halo stars from the latter work is consistent with the value found in our work, while our inferred value for donated halo stars is slightly lower. This is, however, chiefly due to the updated statistical treatment and different model assumptions, which we amply addressed through our Figs. 9 and 10.
As a further test, as mentioned in Sect. 5.1.2, we assigned to each present-day GC mass in the compilation of McLaughlin & van der Marel (2005) a corresponding first- to second-generation fraction using the empirical trend from Milone et al. (2017) rather than adopting the generic 50/50 ratio. As a result, we would find NDiss = 100 ± 8 dissolved clusters and a donated-halo fraction of 6%. This hinges in a great part on the assumption of the present-day mass distribution. Any sophisticated treatment would need to adopt a lower mass limit above which to define a “GC”, initial population fractions according to Reina-Campos et al. (2018), and/or explicit initial mass functions, the latter being highly conjectural at this point, so that we continue our discussion with our above finding of 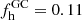 .
.
We note that all our results are upper limits because we assumed here that all halo stars with second-generation chemical imprints are the result of cluster dissolution. Alternative sources for these chemical patterns could be the effects of post-mass-transfer AGB binaries (e.g., Pols et al. 2012) or internal mixing processes during stellar evolution within the stars themselves (Spite et al. 2005; Stancliffe et al. 2009; Hansen et al. 2016).
5.3. Dependence on distance
Figure 11 shows the trend of the CN-strong stars in our sample as a function of Galactocentric distance; for the latter we adopted a distance to the Galactic center of 8.34 kpc (Reid et al. 2014). Both the observed fraction of stars with second-generation chemistry (middle panel) and the derived fraction of that portion of the halo that would stem from GCs (bottom panel) show a predominantly flat trend within ∼30 kpc, while there is an apparent rise beyond this radius, although this is hampered by the overall small-number statistics and accordingly large error bars at these large distances.
 |
Fig. 11. Top panel: distribution of CN-weak (black) and CN-strong (red) stars with Galactocentric distance. Middle and bottom panels: resulting fraction of CN-strong to CN-weak stars as function of Galactocentric distance. The error bars are based on Poisson statistics. Gray shaded areas show the radial trend of the 65 CN-strong stars found by Martell et al. (2011). |
We further caution that the conversion between these fractions, following Eqs. (5)–(10), assumes that the distribution of the formerly disrupted GCs (entering through NDiss) with Galactocentric radius was isotropic. This also presumes that the orbital history of the entire MW GC system is considered irrelevant in that we reference our formalism to the present-day total number of GCs. The MW GCs are rather distributed anisotropically and separated into the underlying Galactic components such as disks, bulge, or halo GCs. This is not crucial to the our analysis, however, because we are mainly concerned with halo GCs and halo stars following our selection criteria.
The radial trend of Fig. 11 is qualitatively reminiscent of those seen in other studies (Carollo et al. 2013) and other halo tracers such as carbon stars (Carollo et al. 2012), RR Lyrae (Medina et al. 2018), and similarly for the radial (metallicity) profiles in the neighboring Andromeda galaxy M31 (Ibata et al. 2005; Koch et al. 2008) and other external galaxies (e.g., Forbes et al. 2011), although the latter examples show generally stronger declines with radius within their inner halos.
Martell et al. (2011) found one CN-strong star beyond 30 kpc, giving rise to an apparent bump in their distance distribution of the CN-strong to CN-normal fraction. Such a feature, although not significant, is also seen in our profile at 30–35 kpc, which could indicate the presence of a real substructure in the halo at these far distances. Overall, we find 13 second-generation GC stars at distances beyond 30 kpc; the farthest CN-strong star in our sample lying at 47 ± 6 kpc.
6. Discussion
Our exploitation of the large-scale low-resolution spectroscopic surveys of the SDSS has resulted in our detection of more than one hundred stars in the halo field that show strong CN- and weak CH-bands, which are the key signatures of second-generation GC stars. We thus estimate that about one-tenth of the present-day MW halo originates from disrupted GC stars; this value lies below previous estimates that were based on SDSS data from earlier releases with smaller numbers of selected stars, which used different formalisms.
Our estimate hinges on several assumptions, some of which pose significant limitations to the extractability of a halo fraction from observations of stars with GC-like chemistry. We list some of them below.
Ratio of first to second generations (Sect. 5.1.1). The dependence of this parameter on global GC parameters such as mass (be it initial or present-day) or metallicity is still not fully settled. We have adopted here a value of 50% of first-generation stars, which is an upper limit to the values suggested by theories and observations. Our observational finding that second-generation stars make up 2.5% of the stellar halo could effectively be doubled when correcting for the population ratio. If some mechanism were only to remove the first generation, then our derived fraction would only be a lower limit, with a final number between 5% and 100% depending on the assumed mass-loss rate. However, according to our formalism, the change in this value when the respective population ratio is changed by a few tens of percent is marginal.
Mass loss at early times (Sects. 5.1.3 and 5.1.4). Here, we have adopted a mass-loss fraction of 56%. While substantially stronger mass loss is suggested by several theories of GC enrichment and evolution, this would according to our formalism imply that unrealistically, the entire MW halo or more consists of stars formerly hosted by now-disrupted GCs. This problem of “overpopulation” has also been noted for the MW bulge (Schiavon et al. 2017) in the context of mismatches in the metallicity distribution function of the GC population of the Fornax dwarf spheroidal galaxy when scaled to that of its field stars (Larsen et al. 2012), and it has been theoretically addressed by Vesperini et al. (2010). We restate that our adopted value assumes that stellar evolution is not accounted for because it affects stars regardless of their environment (read: halo and GCs), which prompted the need to halve the literature value from the model adopted in our work.
Mass loss from the second generation. Canonical models of GC evolution and disruption mainly engage mass loss at early times, as also inherent in our formalism. However, it is natural to assume that the second-generation stars escape from the GCs at an early stage, as suggested by Schaerer & Charbonnel (2011). The implication of their model (with fast-rotating massive stars as the main enrichers) is that the GCs were initially more massive by factors of ∼10 times (only first generation loss) or 25 times (also second-generation loss). In the scenario proposed by Schaerer & Charbonnel (2011), this also affects the conclusions drawn on the fraction that present-day GCs have contributed to the low-mass stars in the Galactic halo: while the former mass-loss fraction results in 5–8%, when the second generation is also accounted for, this value increases to the 20% level. Similarly, Baumgardt & Sollima (2017) expected that a typical MW GC (permitting for various mass functions) would have lost about 75% of its mass since formation, while more evolved clusters have already lost more than 90% and are expected to dissolve over the next 1–2 Gyr, which does not give us a means for distinguishing stars of the first and second generation in the field, however. In accordance with our discussion in Sect. 5.1.4, we note that these models did include the effects of stellar evolution.
Stellar halo mass. In our statistics we have explicitly adopted one single number (109 M⊙) for the mass of the stellar halo, while more sophisticated correction factors for the footprint of the employed surveys (here, SDSS) could be envisioned, which could be argued for both our target selection and the number of present-day GCs to which we scaled our formalism. Moreover, our approach ignored the orbital histories of the observed MW GCs and assumed an isotropic distribution.
Another potentially aggravating factor is the exact value for the stellar halo mass. On the other hand, many studies have attempted weighing the entire halo (i.e., dark plus stellar) from a variety of tracers (e.g., Wilkinson & Evans 1999; Sakamoto et al. 2003; Xue et al. 2008; Kafle et al. 2014; Wang et al. 2015; Elias et al. 2018), and the resulting range is less critical in our analysis. As the halo mass enters inversely in the fraction of the GC-built halo, corrections can easily be implemented.
Present-day GCs (Sect. 5.1.2). In the comparison of the number of dissolved GCs to the present-day GC population in the MW we have adopted the census of the Harris (1996) catalog. Ever since its latest revision in 2010, more GCs are being discovered toward all major Galactic components including the Galactic halo (e.g., Balbinot et al. 2013; Laevens et al. 2014; Kim et al. 2016; Koposov et al. 2017; Ryu & Lee 2018). In particular, an estimated dozen objects toward low Galactic latitudes (while not necessarily relevant to studies of the halo) are still awaiting discovery (Ivanov et al. 2005). Because a generous decrease in the number of present-day GCs (excluding disk and bulge objects) or its increase (extrapolating future discoveries) by 25% only amounts to a change of a few percentage points in our results, the exact choice of this parameter is uncritical.
Low-mass clusters. There is now observational support for a minimum mass on the order of a few 104 M⊙ for GCs to exhibit multiple populations and light element variations (Simpson et al. 2017b; Bragaglia et al. 2017; Bastian & Lardo 2018). Furthermore, some systems appear to be first-generation-only systems (Villanova et al. 2013) without any photometric or chemical evidence for the presence of a second generation, such as we searched for here. However, the lowest-mass systems and those with peculiar population mixes are also likely to have experienced destruction and contributed to the halo buildup. As a consequence, these objects would not spawn any measurable quantity of the enriched second-generation stars, while they could well have contributed first-generation (CN-weak) stars, which we generally discarded from consideration. This factor thus leads to an underestimate of our resulting fraction of the halo stars with GC origin by an unknown amount. When we assume that all star formation occurs in a clustered manner, we also miss the contributions of the early counterparts of open clusters and associations, which would not have included second-generation stars. Our current work refers to contributions by GCs with masses of at least a few times 104 M⊙, which may reasonably be assumed to have formed second-generation stars.
The final a posteriori value of the donated halo fraction 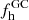 thus relies on these mainly model-dependent assumptions, which hampers a clear-cut case distinction. Conversely, according to our formalism above, in particular through Figs. 9 and 10, the parameter space of the early mass-loss fraction, GC mass, and generation ratio could be greatly constrained if models were to independently predict
thus relies on these mainly model-dependent assumptions, which hampers a clear-cut case distinction. Conversely, according to our formalism above, in particular through Figs. 9 and 10, the parameter space of the early mass-loss fraction, GC mass, and generation ratio could be greatly constrained if models were to independently predict 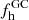 . Kruijssen (2015) used his “end-to-end (yet simple)” model to conclude that the minimum mass for the formation of multiple populations was 105 M⊙ at z ≥ 2 under the observational constraint that about 2% of the halo consists of the CN-strong (and enriched in other nucleosynthetic products of the relevant burning processes) stars targeted in this work. The conclusion of Kruijssen (2015) is now bolstered by our empirical finding that this fraction lies at the 2% level.
. Kruijssen (2015) used his “end-to-end (yet simple)” model to conclude that the minimum mass for the formation of multiple populations was 105 M⊙ at z ≥ 2 under the observational constraint that about 2% of the halo consists of the CN-strong (and enriched in other nucleosynthetic products of the relevant burning processes) stars targeted in this work. The conclusion of Kruijssen (2015) is now bolstered by our empirical finding that this fraction lies at the 2% level.
By excluding stellar evolutionary mass loss (occurring both in the halo and the GCs), we lowered the estimated halo fraction from 23% to the 10% level, which would represent the case that the stars lost from GCs were 100% from the first generation, which means that our result is clearly a mere upper limit. This also constitutes a significant difference in the interpretation with previous works, but our result it is now based on empirical relations instead of the “arbitrary” theoretical correction factor required by the scenarios invoking pollution by AGB or fast-rotating massive stars. We also reiterate that the early loss of first-generation stars is observationally unconstrained, and with a higher early mass-loss rate, the fraction could still be higher than 11%.
Our findings may provide qualitative evidence for the inner/outer halo dichotomy, which is a consequence of hierarchical galaxy formation where an outer halo is dominated by an ex situ accreted component, whereas the inner halo results from both in situ formation and the accretion of a small number of more massive satellites (Cooper et al. 2013; Pillepich et al. 2015), but we no longer see the pronounced decline in the fraction of stars with a GC origin toward the outer reaches of the inner halo found in Martell et al. (2011).
Cosmological simulations are concerned with the accretion of dark-matter-dominated sub-galactic fragments related to progenitors of present-day dwarf spheroidal and dwarf irregular galaxies (which in turn can bring in their own GC systems; e.g., Larsen et al. 2001; Law & Majewski 2010; Hendricks et al. 2016; Kruijssen et al. 2018; Myeong et al. 2018; Helmi et al. 2018). Detecting the traces of disrupted GCs (which may include both objects formed in situ and accreted GCs) as a main purveyor of the Galactic halo(s) emphasizes the complexity of disrupting satellites down to the smallest star cluster scales. We note, however, that small satellites, which make up the outer halo, are hardly exptected to have contributed any GCs, whereas massive satellites contributing to the inner halo are likely to come with more GCs. Larger and deeper spectroscopic samples are needed in order to verify the potential rise seen in the outer halo in Fig. 11.
Overall, the CN-strong stars we detected in our sample are fairly similar in many regards to their CN-weak halo mates. The latter display a mild radial metallicity gradient, as is also seen in the GC-donated component, although their small numbers frustrate a unique comparison. An important question is whether the kinematics of these second-generation stars also coincide with those of the underlying halo component, as this would provide valuable information on their accretion history and the possible orbits of the progenitor systems (e.g., Roederer et al. 2018). This will be explored in our second paper in this series (Hanke et al., in prep.), exploiting the capabilities of the new Gaia data (Gaia Collaboration 2018).
As we have argued that the CN-strong stars broadly reflect the dichotomy of an inner and outer halo, it can also be envisioned that the stars at large Galactocentric distances could originate from regular mass loss from GCs that have been accreted from satellite dwarf galaxies (cf. Kruijssen 2015; Helmi et al. 2018). This tagging is enabled by the fact that chemically, the GC-stars in dwarf galaxies closely follow the field star population of those dwarfs (Hendricks et al. 2016). In this case, further chemical tagging of the CN-strong objects as purported (accreted) dwarf galaxy GC stars to explore the full chemical abundance space is clearly warranted.
Large spectroscopic surveys are bound to find ever more former GC stars out to large distances, for instance, SDSS-V (Kollmeier et al. 2017), or 4MOST (de Jong et al. 2012; Helmi et al. 2019), as their wavelength ranges are able to capture a large number of relevant element abundance tracers (Hansen et al. 2015). This goes in line with the desirability of a broader set of abundance tracers that can ascertain a clear-cut classification as second-generation stars. Similarly, any observed radial trends in the significance of GC contributions to the buildup of the inner and outer Galactic halos will greatly benefit from the recent and future data releases of Gaia, by pinning down the proper motions and the distances to the CN-strong candidates, although Gaia’s reach is limited toward smaller distances in the outer halo.
For ancient GCs (ages > 10 Gyr), an age difference of ∼200 Myr is possible, limited by the accuracy in age dating, whereas for the ∼2 Gyr old cluster NGC 1978, Martocchia et al. (2018b) found that the two populations are coeval to within an upper limit of 20 Myr.
Strictly, this number should be scaled down by a factor of four due to the smaller footprint of the SDSS used in this work compared to the entire halo volume. Likewise, a correction factor for our limited distance coverage could be envisioned, which, however, would counteract our investigation of the distance dependence addressed in Sect. 5.3.
Acknowledgments
This work was supported by Sonderforschungsbereich SFB 881 “The MW System” (subproject A08) of the German Research Foundation (DFG). We are grateful to the referee, N. Bastian, for a very constructive report and helpful discussions. SLM acknowledges support from the Australian Research Council through Discovery Project grant DP180101791. Parts of this research were supported by the Australian Research Council Centre of Excellence for All-Sky Physics in 3 Dimensions (ASTRO 3D), through project number CE170100013. This publication has benefited from the conference on “Multiple populations in stellar clusters” held at the Sexten Center for Astrophysics (http://www.sexten-cfa.eu/). Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatório Nacional/ MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
References
- Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Anguiano, B., Zucker, D. B., Scholz, R.-D., et al. 2015, MNRAS, 451, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Anguiano, B., De Silva, G. M., Freeman, K., et al. 2016, MNRAS, 457, 2078 [NASA ADS] [CrossRef] [Google Scholar]
- Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] [Google Scholar]
- Balbinot, E., Santiago, B. X., da Costa, L., et al. 2013, ApJ, 767, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., & Goodwin, S. P. 2006, MNRAS, 369, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., & Lardo, C. 2015, MNRAS, 453, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., & Lardo, C. 2018, ARA&A, 56, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Lamers, H. J. G. L. M., de Mink, S. E., et al. 2013, MNRAS, 436, 2398 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baumgardt, H. 2017, MNRAS, 464, 2174 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Sollima, S. 2017, MNRAS, 472, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Hilker, M., Sollima, A., & Bellini, A. 2019, MNRAS, 482, 5138 [Google Scholar]
- Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2006, ApJ, 642, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Schlafly, E. F., et al. 2014, MNRAS, 443, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Boberg, O. M., Friel, E. D., & Vesperini, E. 2016a, ApJ, 824, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Boberg, O. M., Gerber, J. M., Friel, E. D., et al. 2016b, AJ, 151, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., Geha, M., & Kallivayalil, N. 2012, ApJ, 760, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Carretta, E., D’Orazi, V., et al. 2017, A&A, 607, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera-Ziri, I., Bastian, N., Longmore, S. N., et al. 2015, MNRAS, 448, 2224 [NASA ADS] [CrossRef] [Google Scholar]
- Carballo-Bello, J. A., Corral-Santana, J. M., Catelan, M., et al. 2018, MNRAS, 474, 4766 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Martell, S. L., Beers, T. C., & Freeman, K. C. 2013, ApJ, 769, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chun, S.-H., Kim, J.-W., Sohn, S. T., et al. 2010, AJ, 139, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G. 1978, ApJ, 223, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Colucci, J. E., Bernstein, R. A., & Cohen, J. G. 2014, ApJ, 797, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C. 2012, ApJ, 758, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., D’Souza, R., Kauffmann, G., et al. 2013, MNRAS, 434, 3348 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, K. S., Kneib, J.-P., Percival, W. J., et al. 2016, AJ, 151, 44 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S., Bellido-Tirado, O., Chiappini, C., et al. 2012, Ground-based and Airborne Instrumentation for Astronomy IV, 84460T, 8446 [Google Scholar]
- de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Elias, L. M., Sales, L. V., Creasey, P., et al. 2018, MNRAS, 479, 4004 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Trincado, J. G., Robin, A. C., Moreno, E., et al. 2016, ApJ, 833, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Trincado, J. G., Zamora, O., García-Hernández, D. A., et al. 2017, ApJ, 846, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., Spitler, L. R., Strader, J., et al. 2011, MNRAS, 413, 2943 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., Bastian, N., Gieles, M., et al. 2018, Proc. R. Soc. London Ser. A, 474, 20170616 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geisler, D., Wallerstein, G., Smith, V. V., & Casetti-Dinescu, D. I. 2007, PASP, 119, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Gerber, J. M., Friel, E. D., & Vesperini, E. 2018, AJ, 156, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Gieles, M., Charbonnel, C., Krause, M. G. H., et al. 2018, MNRAS, 478, 2461 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gnedin, O. Y., & Ostriker, J. P. 1997, ApJ, 474, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grillmair, C. J. 2009, ApJ, 693, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Dionatos, O. 2006, ApJ, 643, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hanke, M., Koch, A., Hansen, C. J., & McWilliam, A. 2017, A&A, 599, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Ludwig, H.-G., Seifert, W., et al. 2015, Astron. Nachr., 336, 665 [Google Scholar]
- Hansen, C. J., Nordström, B., Hansen, T. T., et al. 2016, A&A, 588, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harbeck, D., Smith, G. H., & Grebel, E. K. 2003, AJ, 125, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, G. A. 1962, The Observatory, 82, 205 [NASA ADS] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Irwin, M., Deason, A., et al. 2019, The Messenger, 175, 23 [NASA ADS] [Google Scholar]
- Hendricks, B., Koch, A., Walker, M., et al. 2014, A&A, 572, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hendricks, B., Boeche, C., Johnson, C. I., et al. 2016, A&A, 585, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollyhead, K., Kacharov, N., Lardo, C., et al. 2017, MNRAS, 465, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Hollyhead, K., Lardo, C., Kacharov, N., et al. 2018, MNRAS, 476, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Chapman, S., Ferguson, A. M. N., et al. 2005, ApJ, 634, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Illingworth, G. 1976, ApJ, 204, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, V. D., Kurtev, R., & Borissova, J. 2005, A&A, 442, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jordi, K., & Grebel, E. K. 2010, A&A, 522, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kafle, P. R., Sharma, S., Lewis, G. F., & Bland-Hawthorn, J. 2014, ApJ, 794, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Kayser, A., Hilker, M., Grebel, E. K., & Willemsen, P. G. 2008, A&A, 486, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, D., Jerjen, H., Mackey, D., Da Costa, G. S., & Milone, A. P. 2016, ApJ, 820, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Rich, R. M., Reitzel, D. B., et al. 2008, ApJ, 689, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Burkert, A., Rich, R. M., et al. 2012, ApJ, 755, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Kollmeier, J. A., Zasowski, G., Rix, H. W., et al. 2017, ArXiv e-prints [arXiv:1711.03234] [Google Scholar]
- Koposov, S. E., Belokurov, V., & Torrealba, G. 2017, MNRAS, 470, 2702 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., Suntzeff, N. B., Langer, G. E., et al. 1982, PASP, 94, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D. 2015, MNRAS, 454, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Pfeffer, J. L., Reina-Campos, M., Crain, R. A., & Bastian, N. 2018, MNRAS, 1, 22 [Google Scholar]
- Kunder, A., Bono, G., Piffl, T., et al. 2014, A&A, 572, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kunder, A., Mills, A., Edgecomb, J., et al. 2018, AJ, 155, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Kuzma, P. B., Da Costa, G. S., & Mackey, A. D. 2018, MNRAS, 473, 2881 [Google Scholar]
- Laevens, B. P. M., Martin, N. F., Sesar, B., et al. 2014, ApJ, 786, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, S. S., Brodie, J. P., Huchra, J. P., Forbes, D. A., & Grillmair, C. J. 2001, AJ, 121, 2974 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, S. S., Strader, J., & Brodie, J. P. 2012, A&A, 544, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsen, S. S., Brodie, J. P., Forbes, D. A., & Strader, J. 2014, A&A, 565, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsen, S. S., Brodie, J. P., Wasserman, A., & Strader, J. 2018, A&A, 613, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lauchner, A., Powell, Jr., W. L., & Wilhelm, R. 2006, ApJ, 651, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., & Majewski, S. R. 2010, ApJ, 718, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K. H., Lee, H. M., Fahlman, G. G., & Sung, H. 2004, AJ, 128, 2838 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Beers, T. C., Sivarani, T., et al. 2008, AJ, 136, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., Koposov, S. E., Battistini, C., et al. 2015, A&A, 575, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucatello, S., Beers, T. C., Christlieb, N., et al. 2006, ApJ, 652, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, J., Pasquali, A., Grebel, E. K., & Gallagher, III., J. S. 2012, AJ, 144, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Martell, S. L., & Grebel, E. K. 2010, A&A, 519, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martell, S. L., Smith, G. H., & Briley, M. M. 2008, PASP, 120, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Martell, S. L., Smolinski, J. P., Beers, T. C., & Grebel, E. K. 2011, A&A, 534, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martell, S. L., Shetrone, M. D., Lucatello, S., et al. 2016, ApJ, 825, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Martocchia, S., Cabrera-Ziri, I., Lardo, C., et al. 2018a, MNRAS, 473, 2688 [Google Scholar]
- Martocchia, S., Niederhofer, F., Dalessandro, E., et al. 2018b, MNRAS, 477, 4696 [NASA ADS] [CrossRef] [Google Scholar]
- Mateluna, R., Geisler, D., Villanova, S., et al. 2012, A&A, 548, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McConnachie, A. W., Irwin, M. J., Ibata, R. A., et al. 2009, Nature, 461, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Medina, G. E., Muñoz, R. R., Vivas, A. K., et al. 2018, ApJ, 855, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Stetson, P. B., Piotto, G., et al. 2009, A&A, 503, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Piotto, G., Renzini, A., et al. 2017, MNRAS, 464, 3636 [NASA ADS] [CrossRef] [Google Scholar]
- Morales, G., Martínez-Delgado, D., Grebel, E. K., et al. 2018, A&A, 614, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mucciarelli, A., Origlia, L., Ferraro, F. R., & Pancino, E. 2009, ApJ, 695, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Myeong, G. C., Jerjen, H., Mackey, D., & Da Costa, G. S. 2017, ApJ, 840, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Myeong, G. C., Evans, N. W., Belokurov, V., Sanders, J. L., & Koposov, S. E. 2018, ApJ, 863, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Nardiello, D., Milone, A. P., Piotto, G., et al. 2018, MNRAS, 477, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Navarrete, C., Belokurov, V., & Koposov, S. E. 2017, ApJ, 841, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Navin, C. A., Martell, S. L., & Zucker, D. B. 2016, ApJ, 829, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Niederste-Ostholt, M., Belokurov, V., Evans, N. W., et al. 2010, MNRAS, 408, L66 [NASA ADS] [Google Scholar]
- Norris, J., & Cottrell, P. L. 1979, ApJ, 229, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J., Cottrell, P. L., Freeman, K. C., & Da Costa, G. S. 1981, ApJ, 244, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Rockosi, C. M., et al. 2001, ApJ, 548, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Osborn, W. 1971, The Observatory, 91, 223 [NASA ADS] [Google Scholar]
- Pancino, E., Romano, D., Tang, B., et al. 2017, A&A, 601, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilachowski, C. A., Sneden, C., & Kraft, R. P. 1996, AJ, 111, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Madau, P., & Mayer, L. 2015, ApJ, 799, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Izzard, R. G., Stancliffe, R. J., & Glebbeek, E. 2012, A&A, 547, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popper, D. M. 1947, ApJ, 105, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, eds. S. G. Djorgovski, & G. Meylan, ASP Conf. Ser., 50, 357 [NASA ADS] [Google Scholar]
- Ramírez, I., Meléndez, J., & Chanamé, J. 2012, ApJ, 757, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Reina-Campos, M., Kruijssen, J. M. D., Pfeffer, J., Bastian, N., & Crain, R. A. 2018, MNRAS, 481, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Hattori, K., & Valluri, M. 2018, AJ, 156, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Ryu, J., & Lee, M. G. 2018, ApJ, 863, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Chiba, M., & Beers, T. C. 2003, A&A, 397, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., & Charbonnel, C. 2011, MNRAS, 413, 2297 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Schiavon, R. P., Zamora, O., Carrera, R., et al. 2017, MNRAS, 465, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Schörck, T., Christlieb, N., Cohen, J. G., et al. 2009, A&A, 507, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Shipp, N., Drlica-Wagner, A., Balbinot, E., et al. 2018, ApJ, 862, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. D., Martell, S. L., & Navin, C. A. 2017a, MNRAS, 465, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. D., De Silva, G., Martell, S. L., Navin, C. A., & Zucker, D. B. 2017b, MNRAS, 472, 2856 [NASA ADS] [CrossRef] [Google Scholar]
- Smolinski, J. P., Martell, S. L., Beers, T. C., & Lee, Y. S. 2011, AJ, 142, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A., Martínez-Delgado, D., Valls-Gabaud, D., & Peñarrubia, J. 2011, ApJ, 726, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stancliffe, R. J., Church, R. P., Angelou, G. C., & Lattanzio, J. C. 2009, MNRAS, 396, 2313 [Google Scholar]
- Strader, J., Smith, G. H., Larsen, S., Brodie, J. P., & Huchra, J. P. 2009, AJ, 138, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, B., Liu, C., Fernández-Trincado, J. G., et al. 2019, ApJ, 871, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderbeke, J., De Propris, R., De Rijcke, S., et al. 2015, MNRAS, 451, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Vesperini, E., McMillan, S. L. W., D’Antona, F., & D’Ercole, A. 2010, ApJ, 718, L112 [NASA ADS] [CrossRef] [Google Scholar]
- Vesperini, E., McMillan, S. L. W., D’Antona, F., & D’Ercole, A. 2013, MNRAS, 429, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Geisler, D., Carraro, G., Moni Bidin, C., & Muñoz, C. 2013, ApJ, 778, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W., Han, J., Cooper, A. P., et al. 2015, MNRAS, 453, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, J. J., & Leigh, N. W. C. 2015, MNRAS, 453, 3278 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkinson, M. I., & Evans, N. W. 1999, MNRAS, 310, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, X. X., Rix, H. W., Zhao, G., et al. 2008, ApJ, 684, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Modified Kiel diagrams for several metallicity bins. The red 3σ envelopes were used to select bona fide halo giants. |
| In the text | |
 |
Fig. 2. Kiel diagram of the full sample (contours; satisfying the initial query restrictions in log g < 3, [Fe/H] < −1, (g − r)0 > 0.2, S/N > 20, and respective cuts in the parameter errors) and the subset of halo giants (dots; after removal of metallicity-dependent CMD features and further pruning the metal-rich and -poor tails above −1.3 and below −1.8 dex) used for our statistical purposes. |
| In the text | |
 |
Fig. 3. CN index in the halo giant candidates (black dots) according to Eq. (1) vs. absolute magnitude (bottom), color (middle), and metallicity (top). Carbon- and CEMP-stars (red triangles) were rejected based on their s(c0) and s(c1) indices (Eqs. (2) and (3)). |
| In the text | |
 |
Fig. 4. CN-band strength vs. absolute magnitude for separate metallicity bins of 0.1 dex width. The solid line shows the best fit to the CN-weak sequence, while the dashed red line delineates the separation into CN-weak and CN-strong stars. |
| In the text | |
 |
Fig. 5. Combined sample of CN-strong (red) and CN-normal stars. The right panel shows the generalized histogram of both populations, where the curve for the CN-strong stars has been scaled up by a factor of ten. Dotted lines show the distribution derived by Martell & Grebel (2010), and the dashed curves are the results from our KMM separation. |
| In the text | |
 |
Fig. 6. Separation of regular halo stars that are CN-normal and CH-strong (black dots) and the bona fide CN-strong, CH-weak stars that we assume to have originated in now-dissolved GCs (red circles). In concordance with Fig. 3, this was done in separate metallicity bins. While not used in the actual statistics, we include stars above [Fe/H] = −1.3 in this figure for illustration. |
| In the text | |
 |
Fig. 7. Sample spectra for the stellar types relevant to this work. These are (from top to bottom): a metal-poor CN-strong star, a more metal-rich CN-strong star, and two CN-normal stars with the same stellar parameters as the former stars. Metal-rich stars above [Fe/H] = −1.3 were rejected from our sample because of the risk of misclassifications. The red (blue) and gray shaded areas indicate the line and continuum bandpasses for the S(3839) and S(CH) index after Norris et al. (1981) and Martell et al. (2008), see Eqs. (1) and (4). |
| In the text | |
 |
Fig. 8. Dependence of the observed fraction of CN-strong halo stars on metallicity. The solid line shows our recovered overall fraction based on the sample within −1.8 ≤ [Fe/H] ≤ −1.3, whereas the dashed line also accounts for the metal-rich tail up to −1 dex. |
| In the text | |
 |
Fig. 9. Top panel: dependence of the final fraction of donated halo stars on the adopted fraction of first-generation stars. The solid, dashed, and dash-dotted lines are for ratios of 0.5 (Carretta et al. 2009), 0.32 (Bastian & Lardo 2015), and 0.09, the minimum value in the catalog of Milone et al. (2017). This calculation adopted a ratio of an early mass-loss fraction (Sect. 5.1.3) of 56% and an average present-day GC mass of 2.2 × 105 M⊙. Middle panel: influence of the number of present-day GCs in our analysis. Here, the solid line shows the 157 objects in the Harris (1996) catalog, while the dashed lines correspond to a variation by ±25%, e.g., due to selecting only halo GCs. Bottom panel: dependence on the adopted mean present-day GC mass. Red lines show the masses based on the Harris (1996) catalog adopted in this work (solid), the catalog of GC masses from McLaughlin & van der Marel (McLaughlin & van der Marel, dashed), and a mass of 5 × 105 M⊙ (dotted) as adopted by Martell et al. (2011). Here, the calculations adopted a ratio of first- to second-generation stars of 50:50 and an early mass-loss rate of 56%. |
| In the text | |
 |
Fig. 10. Dependence of the final fraction of accreted halo stars on the adopted mass-loss rate of first-generation stars. The lines indicate the fractions adopted by various works: Baumgardt & Sollima (2017, dash-dotted), Martell et al. (2011, dashed), and our study (solid). Here, red lines show the cases that neglect stellar evolution, while blue lines show values where this is accounted for. This calculation adopted a ratio of first- to second-generation stars of 50:50 and an average present-day GC mass of 2.2 × 105 M⊙. |
| In the text | |
 |
Fig. 11. Top panel: distribution of CN-weak (black) and CN-strong (red) stars with Galactocentric distance. Middle and bottom panels: resulting fraction of CN-strong to CN-weak stars as function of Galactocentric distance. The error bars are based on Poisson statistics. Gray shaded areas show the radial trend of the 65 CN-strong stars found by Martell et al. (2011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.