| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834579 | |
| Published online | 25 April 2019 | |
The survey of planetary nebulae in Andromeda (M 31)
I. Imaging the disc and halo with MegaCam at the CFHT⋆
1
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
e-mail: sbhattac@eso.org
2
European Southern Observatory, Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago de Chile, Chile
3
Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstrasse, 85748 Garching, Germany
4
Aix Marseille Université, CNRS, LAM–Laboratoire d’Astrophysique de Marseille, 38 rue F. Joliot-Curie, 13388 Marseille, France
5
NRC Herzberg Institute of Astrophysics, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
6
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
Received:
5
November
2018
Accepted:
6
March
2019
Context. The Andromeda (M 31) galaxy subtends nearly 100 square degrees on the sky. Any study of its halo must therefore account for the severe contamination from the Milky Way halo stars whose surface density displays a steep gradient across the entire M 31 field of view.
Aims. Our goal is to identify a population of stars firmly associated with the M 31 galaxy. Planetary nebulae (PNe) are one such population that are excellent tracers of light, chemistry, and motion in galaxies. We present a 16 square degree survey of the disc and inner halo of M 31 with the MegaCam wide-field imager at the CFHT to identify PNe, and characterise the luminosity-specific PN number and PN luminosity function (PNLF) in M 31.
Methods. PNe were identified via automated detection techniques based on their bright [O III] 5007 Å emission and absence of a continuum. Subsamples of the faint PNe were independently confirmed by matching with resolved Hubble Space Telescope sources from the Panchromatic Hubble Andromeda Treasury and spectroscopic follow-up observations with HectoSpec at the MMT.
Results. The current survey reaches two magnitudes fainter than the previous most sensitive survey. We thus identify 4289 PNe, of which only 1099 were previously known. By comparing the PN number density with the surface brightness profile of M 31 out to ∼30 kpc along the minor axis, we find that the stellar population in the inner halo has a luminosity-specific PN number value that is seven times higher than that of the disc. We measure the luminosity function of the PN population and find a bright cut-off and a slope consistent with previous determinations. Interestingly, it shows a significant rise at the faint end, present in all radial bins covered by the survey. This rise in the M 31 PNLF is much steeper than that observed for the Magellanic clouds and Milky Way bulge.
Conclusions. The significant radial variation of the PN specific frequency value indicates that the stellar population at deprojected minor-axis radii larger than ∼10 kpc is different from that in the disc of M 31. The rise at the faint end of the PNLF is a property of the late phases of the stellar population. M 31 shows two major episodes of star formation and the rise at the faint end of the PNLF is possibly associated with the older stellar population. It may also be a result of varying opacity of the PNe.
Key words: galaxies: individual: M 31 / galaxies: halos / planetary nebulae: general
Based on observations obtained with MegaCam, a joint project of the CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. The observations at the CFHT were performed with care and respect from the summit of Maunakea which is a significant cultural and historic site.
© ESO 2019
1. Introduction
The Andromeda galaxy, M 31, is the closest giant spiral disc to our Milky Way (MW). It lies at a distance of ∼780 kpc with a high inclination to the line of sight (i ∼ 77 deg) making it ideally suited for studies of its halo regions. Since galaxies are believed to be formed by hierarchical mass assembly, their outskirts with long dynamical timescales are expected to have coherent debris from past accretion events for the greatest longevity (Ferguson & Mackey 2016). Through the Pan-Andromeda Archaeological Survey (PAndAS; McConnachie et al. 2009) map of the resolved stellar population number counts, we now know about the substructures present in the M 31 halo (Giant Stellar Stream, G1 and NE clump, NE and W shelves; McConnachie et al. 2018) and that the stellar halo extends out to 165 kpc.
Because of the faint surface brightness of the M 31 halo, μv > 25 outside the main disc (∼15 kpc major-axis distance), the use of discrete stellar tracers is superior to integrated absorption-line spectroscopy in providing a global mapping of the halo kinematics. Globular clusters (GCs) have been shown to efficiently trace the outer halo (outside 50 kpc) substructures of M 31 (Mackey et al. 2010; Veljanoski et al. 2014) bolstering the idea that these clusters and the substructures they trace have been accreted in various merger events. However, the inner halo substructures (within 50 kpc) are not well traced by the GCs. Some of these substructures, especially the Giant Stream, may have resulted from a single merger event ∼2 Gyr ago (Bernard et al. 2015; Hammer et al. 2018) perhaps between M 31 and the large (MM 32P ∼ 2.5 × 1010 M⊙) progenitor of M 32 (D’Souza & Bell 2018).
We can gain information on the motions of the stars in the low surface brightness regions of M 31 by studying planetary nebulae (PNe) that act as discrete tracers of stars in the halo. PNe are the glowing shells of gas and dust observed around stars that have recently left the asymptotic giant branch (AGB) and are evolving towards the white dwarf stage. They are traditionally considered the late phases of stars with masses between ∼0.7 and 8 M⊙, but have been shown to exhibit a wide variety of striking morphologies pointing towards a binary evolution in many systems (Jones & Boffin 2017). Since the timescales between the AGB and PN phases are short, the distribution and kinematics of PNe are expected to be identical to their parent population, having the same angular momentum distribution as the stellar population (e.g., Hui et al. 1995; Arnaboldi et al. 1996, 1998; Méndez et al. 2001). Studying PNe as a population provides insight into galactic structure and evolution. Because of their relatively strong [O III] 5007 Å emission, PNe can be readily identified. They have been shown to be efficient tracers of stellar light in different galaxies like M 87 (Longobardi et al. 2013), M 49 (Hartke et al. 2017), and many other early-type galaxies (Coccato et al. 2009; Cortesi et al. 2013; Pulsoni et al. 2018). The luminosity-specific PN number (α-parameter) varies slightly with B − V colour of galaxies with higher values for late-type galaxies and lower values for early-type galaxies (Buzzoni et al. 2006). Different α-parameter values point to differences in stellar populations even within the same galaxy (e.g., M 49; Hartke et al. 2017).
The characteristic [O III] 5007 Å PN luminosity function (PNLF) has proven itself to be a reliable secondary distance indicator for determining galactic distances out to ∼20 Mpc by virtue of its invariant absolute bright cut-off, M*. The faint end of the PNLF was shown by Jacoby (1980) to follow an exponential function expected from slowly evolving central stars embedded in rapidly expanding, optically thin nebulae (Henize & Westerlund 1963). The PNLF was first described by Ciardullo et al. (1989) estimated empirically from the brightest PN they found in the centre of M 31 as
The bright end exponential cut-off, supported with accurate measures of foreground extinction, is currently measured at M* = −4.54 ± 0.05 (Ciardullo et al. 2013). Apart from M* reducing in low metallicity populations (e.g., Ciardullo & Jacoby 1992; Ciardullo et al. 2002; Hernández-Martínez & Peña 2009), the PNLF cut-off has proved to be largely invariant with metallicity and age of the parent stellar population, and galaxy type.
The faint end of the PNLF has been shown to vary considerably, depending on the details of the stellar population. It is seen to be correlated with the star formation history of the parent stellar population, with steeper slopes associated with older stellar populations and conversely flatter slopes with younger populations (Ciardullo et al. 2004; Ciardullo 2010; Longobardi et al. 2013; Hartke et al. 2017). The changes in the PNLF slope can result from the superposition of multiple stellar populations, which can then be disentangled using the PNe kinematics (Longobardi et al. 2015; Hartke et al. 2018). The PNLF has also been shown to display a dip for some galaxies. The dip is seen ∼3.5 mag below the bright cut-off in the Small Magellanic Cloud (SMC; Jacoby & De Marco 2002), ∼2.5 mag below the bright cut-off for NGC 6822 (Hernández-Martínez & Peña 2009) and also slightly in the Large Magellanic Clouds (Reid & Parker 2010), and ∼1 mag below the bright cut-off in M 87 (Longobardi et al. 2015). This dip is thought to be related to the opacity of the PN and may be characterised by accounting for circumstellar extinction in the PNe. Circumstellar extinction correction indeed modifies the PNLF (Reid & Parker 2010; Davis et al. 2018), but it is difficult to estimate for the faint end of the PNLF (beyond ∼2.5 mag below the bright cut-off) to test for changes in opacity of the PN. Additionally, PNe mimics like H II regions and symbiotic stars (SySts) may be misidentified as PNe thereby affecting the PNLF.
Since the first empirical study of the PNLF by Ciardullo et al. (1989) using 104 objects in the M 31 bulge, the number of PNe known in M 31 has increased by leaps and bounds. Most notably, Merrett et al. (2006, hereafter M06) utilised the custom-built Planetary Nebula Spectrograph (PNS; Douglas et al. 2002) at the William Herschel Telescope (WHT) to identify 2615 PNe in the disc and bulge of M 31, and to simultaneously obtain their [O III] 5007 Å magnitude and line-of-sight velocity (LOSV). M06 corroborated the PNLF found by Ciardullo et al. (1989) and increased the photometric depth to ∼3.5−4 mag below the bright cut-off along with the increased uniform coverage. Since then, Martin et al. (2018) and Li et al. (2018) have identified more PNe in the central regions and circumnuclear region of M 31, respectively, adding to the large number of PNe already known in M 31.
While some of the PNe identified by M06 have been shown to be H II regions (Sanders et al. 2012; Veyette et al. 2014), the M06 PNe sample remains the largest uniform sample of PNe in any galaxy. The LOSV of the M06 PNe predicted links between the NE shelf and the giant stream substructures of M 31 which have been further explored in deep spectroscopic chemical tagging studies by Fang et al. (2015, 2018) to further establish these links. However, while some identified PNe have been associated with the halo, a uniform survey of PNe in much of the metal-poor halo of M 31 and the inner-halo substructures is necessary not only to unambiguously trace them, but also to probe the variation in the PNLF further out from the disc to corroborate the invariant nature of its bright cut-off and observe the evolutionary effects on its faint end.
In this paper, we survey the inner 16 square degrees of M 31 (corresponding to 20−30 kpc from the centre), covering the disc, parts of the inner halo, and some of the inner halo substructures. We detect PNe using the on-off-band technique to a depth further than M06. We describe the observations and data reduction in Sect. 2, and the identification of PNe in Sect. 3. In Sect. 4 we describe the identification of the PNe counterparts in a subsample of Hubble Space Telescope (HST) data. We obtain the α-parameter in Sect. 5 and analyse the PNLF in Sect. 6. We present the discussions of the results in Sect. 7, and we summarise and conclude in Sect. 8.
2. CFHT MegaCam M 31 PNe survey
2.1. Imaging and observations
The observations were carried out with the MegaCam wide-field imager (Boulade et al. 2003) mounted on the 3.6 m Canada-France-Hawaii Telescope (CFHT), located near the summit of the Mauna Kea mountain on Hawaii’s Big Island at an altitude of 4204 m. MegaCam is comprised of a mosaic of 40 individual 2048 × 4612 CCDs, resulting in a contiguous field of view of 0.96 × 0.94° with a pixel scale of 0.187″/pixel. The inner 20−30 kpc radius of the M 31 halo were observed through 16 pointings of the MegaCam imager. The fields are shown in Fig. 1. The observations were carried out, under photometric conditions, during two runs: October 9–11 and November 6–7, 2016. Over the course of the observations, seeing varied between 0.5″ and 1.1″, while the airmass varied between 1.03 and 1.48.
 |
Fig. 1. Fields observed with CFHT MegaCam (in blue, labelled with their observation ID). North is up, east is left. The background image is from SDSS obtained using the Aladin Sky Atlas (Bonnarel et al. 2000). |
M 31 is observed through a narrow-band [O III] filter (λc = 5007 Å, Δλ = 102 Å, on-band) and a broad-band g-filter (λc = 4750 Å, Δλ = 1540 Å, off-band). The photometry is calibrated with observations of spectrophotometric standard stars. Each on-band image generally consists of four dithered exposures with a total exposure time of 1044 s, and each off-band image of three dithered exposures with a total exposure time of 300 s. For some fields there are more dithered images for both on-band and off-band, leading to higher exposure times. A summary of the field positions and exposure times for the on-band and off-band exposures is presented in Table 1. The exposure time was chosen such that PNe with an apparent narrow-band magnitude of 6 mag from the bright cut-off m5007 = 20.2 mag, in the m5007 system described by Jacoby (1989), can still be detected.
Summary of the field positions, exposure times, and seeing for the narrow-band (on-band) and broad-band (off-band) images.
2.2. Data reduction
The data are pre-processed using the Elixir1 pipeline (Magnier & Cuillandre 2004), which accomplishes the bias, flat, and fringe corrections and also determines the photometric zero point of the observations. The zero points for the [O III] and g-band frames in AB magnitudes, normalised to a 1 s exposure, are Z[O III] = 23.434 and Zg = 26.5. For every observed field, a weight map is computed corresponding to each exposure using WeightWatcher2 (Marmo & Bertin 2008). This is used to assign higher weights to pixels that are more reliable compared to their local backgrounds. For each field, the exposures corresponding to the on-band image and those corresponding to the off-band image are then combined using SWARP3 (Bertin et al. 2002) to produce the respective on-band and off-band images. The exposures are combined using median-type combination in conjunction with their respective weight maps, while a background subtraction is carried out with a background mesh size of 25 pixels. The images thus obtained are used for source extraction.
3. Selection of PNe candidates and catalogue extraction
Having a bright [O III] 5007 Å and no continuum emission, extragalactic PNe can be identified as detected objects in the on-band [O III] image that are not detected in the off-band continuum images or that have an excess [O III] – g colour. Additionally, PNe are typically unresolved at extragalactic distances from ground-based observations and so we only considered point-like objects for analysis. We used the automatic selection procedure developed and validated in Arnaboldi et al. (2002, 2003), which has been optimised for large imaging surveys by Longobardi et al. (2013) and Hartke et al. (2017).
3.1. Source extraction
We used SExtractor (Bertin & Arnouts 1996), a source detection algorithm that detects and measures flux from point-like and extended sources, to detect and carry out photometry of the sources on the images. For each field, we measure the narrow-band and broad-band magnitudes, mn and mb, in dual-image mode for sources detected on the narrow-band image. The broad-band magnitudes were extracted using the same apertures as the narrow-band image. Sources were detected in the narrow-band image requiring that 25 adjacent pixels or more have flux values 1.2 × σ rms above the background. Local backgrounds were calculated for the detected sources on apertures having a width of 25 pixels. and magnitudes were measured with different apertures having widths of 15, 17, 19, and 21 pixels. Magnitudes were also measured with an aperture having a width of 5 pixels corresponding to the core of the sources mcore. Sources for which a broad-band magnitude could not be detected at the position of the [O III] detection were assigned a mb corresponding to 1 × σ rms above the background in the broad-band image, similar to Arnaboldi et al. (2002). The narrow-band magnitude, mn, in the AB system was converted to the m5007 system as m5007 = mn + 2.27 (see Appendix A.1 for details). The central part of our survey covering part of the bulge of M 31 are mostly saturated. In some observed fields, a few CCDs were noisy. Such noisy regions and CCD edges, affected by dithering and saturation, were masked as detailed in Appendix A.3. The effective survey area is shown in Fig. 2.
 |
Fig. 2. The effective survey area is shown in black. CCD edges and noisy or saturated regions have been masked. |
3.2. Limiting magnitude
In order to determine the limiting magnitude of our sample for each field, we simulated a synthetic point-like population onto the on-band image (with its corresponding exposure time and zero-point) using the Image Reduction and Analysis Facility (IRAF4) task mkobjects. The synthetic population follows a PNLF as detailed in Ciardullo et al. (1989) and the sources have a Moffat PSF profile as detailed in Appendix A.2. The sources are then extracted. The magnitude aperture most suited to recovering the simulated sources is found to be 15 pixels as detailed in Appendix A.4. The limiting magnitude is defined as the magnitude at which the recovery fraction of the simulated sources drops below 50% (Fig. 3). This limiting magnitude varies between m5007 = 25.64 for the shallowest observed field, Field# 33_4, and m5007 = 26.4 for the deepest observed field, Field# 35_4. The limiting magnitude is provided for each field in Table 1.
 |
Fig. 3. Recovery fraction of simulated sources for a single field to illustrate the limiting magnitude at the 50% completeness limit. |
3.3. Colour selection
We selected PNe candidates based on their position on the m5007 versus mn–mb colour-magnitude diagram (CMD). These are sources with a colour excess mn−mb < −1 that are brighter than the limiting magnitude. The colour excess corresponds to an equivalent width EWobs = 110 Å (Teplitz et al. 2000) and was chosen in order to limit contamination from background galaxies.
Sources that do not have an excess in mn–mb are classified as continuum sources. However, some colour excess may be seen for some of these sources during the source extraction from the images, especially for those with fainter magnitudes. We thus simulated the same synthetic point-like population onto the off-band image and checked their position on the extracted m5007 versus mn–mb CMD (Fig. 4). We calculate the 99% and 99.99% limits on their positions in the CMD, below which the probability of detecting continuum sources was reduced to the 1% and 0.01% level respectively. Sources with colour excess within the 99.99% limit are also discarded as possible PNe.
 |
Fig. 4. Colour-magnitude diagram showing the synthetic continuum sources and the 99% and 99.99% limits on their positions for a single field. The region beyond the limiting magnitude of this field is shown in grey. |
3.4. Point-like selection
Planetary nebulae are typically unresolved point-like objects at extragalactic distances, and to differentiate them from extended ones (e.g., background galaxies or other extended objects with strong [O III] emission), we analyse the light distribution of the simulated sources, as described in Sect. 3.2, on the on-band image. For each field, we use the half-light radius (Rh) of the simulated sources, which is the radius within which half of the object’s total flux is contained, to determine its upper limit (Rhmax) corresponding to 95% of the simulated population. We considered sources as point-like if they satisfied the following two criteria: (i) they have a half-light radius such that 1 < Rh < Rhmax, and (ii) they fall in the region where the difference between mn and mcore, magnitude of the source for flux within an aperture of 5 pixels, is within the 95% limit of the simulated population. The point-like selection criteria are shown in Fig. 5, as applied to the colour-selected simulated population and to the real sources.
 |
Fig. 5. Top: difference between mn and mcore for all sources in black and those within the 95% limits of the simulated population in red for the simulated population (left) and as applied to the real sources (right) for a single field. Bottom: same as the top panel, but for half-light radius, Rh. |
In order to estimate the number of continuum sources that may be misidentified as PNe in any field, we count the number of point-like continuum sources (excluded as PNe by the colour selection criteria) and multiply by 0.01%. We estimate that in each field, our identified PNe sample may be contaminated by 2−4 continuum sources that lie in the faint magnitudes >25.
3.5. PNe catalogue
For each field, the [O III] sources that are brighter than the limiting magnitude and fulfil both the point-like and colour selection criteria are considered as PNe candidates. They are shown in the CMD in Fig. 6 for a single field. Since the bandwidth of the broad-band filter also covers that of the narrow-band filter, the bright PNe are expected to show some remnant flux in the broad band as well. This remnant broad-band flux is in the ratio of the filter widths and leads to nearly a constant colour excess, ![$ m_{\mathrm{n}}{-}m_{\mathrm{b}} = 2.5 \log(\frac{\Delta\lambda_\mathrm{[{\mathrm{O}\,\textsc{iii}}]}}{\Delta\lambda_{\mathit{g}}}) =-2.95 $](/articles/aa/full_html/2019/04/aa34579-18/aa34579-18-eq2.gif) , for the bright PNe. The observed constant colour excess is slightly less negative due to the flux contributed to the broad band from the [O III] 4959 Å line which is expected to be ∼1/3 of the brightness of the [O III] 5007 Å line in PNe, as seen in Fig. 6. The final catalogue of confirmed PNe is then checked for spurious sources by eye. Regions of spurious sources, typically caused by saturated stars, are masked and the final catalogue of confirmed PNe is obtained for each field. Counting the PNe identified in the overlapping regions of adjacent fields only once, we identify an unprecedented 4289 PNe in M 31 in our survey. Their spatial distribution, overlaid on a map of RGB stars identified by the PAndAS survey, is shown in Fig. 7. Our survey is uniformly complete (in the effective survey area) down to m5007 = 25.64 which is the 50% completeness limit of the shallowest field (Field# 33_4). However photometric depth varies with fields and we find PNe down to m5007 = 26.4 for the deepest field (Field# 35_4).
, for the bright PNe. The observed constant colour excess is slightly less negative due to the flux contributed to the broad band from the [O III] 4959 Å line which is expected to be ∼1/3 of the brightness of the [O III] 5007 Å line in PNe, as seen in Fig. 6. The final catalogue of confirmed PNe is then checked for spurious sources by eye. Regions of spurious sources, typically caused by saturated stars, are masked and the final catalogue of confirmed PNe is obtained for each field. Counting the PNe identified in the overlapping regions of adjacent fields only once, we identify an unprecedented 4289 PNe in M 31 in our survey. Their spatial distribution, overlaid on a map of RGB stars identified by the PAndAS survey, is shown in Fig. 7. Our survey is uniformly complete (in the effective survey area) down to m5007 = 25.64 which is the 50% completeness limit of the shallowest field (Field# 33_4). However photometric depth varies with fields and we find PNe down to m5007 = 26.4 for the deepest field (Field# 35_4).
 |
Fig. 6. Colour-magnitude diagram for a single field showing all the detected sources (brighter than the limiting magnitude) in black, the colour-selected sources in blue, and identified PNe in red. The 99% and 99.99% limits for the continuum sources are shown in blue, while the region beyond the 50% completeness limit is shown in grey. The histogram (in logarithmic scale) shows clearly the number of PNe recovered as a function of colour with all the detected sources (brighter than the limiting magnitude) in black, the colour-selected sources in blue, and identified PNe in red. |
 |
Fig. 7. Planetary nebulae identifed by the survey are overlaid on the map of RGB stars from the PAndAS survey. PNe brighter than m5007 = 25.64 mag, which is the 50% completeness limit of the shallowest field (Field# 33_4), are shown in blue. PNe fainter than m5007 = 25.64 mag, with photometric depth varying with field, are shown in green. The M06 PNe, re-identified by our survey, are shown in yellow. North is up, east is left. |
3.6. Completeness correction
Our colour and point-like selection criteria would exclude a number of PNe that are affected by photometric errors, especially in the fields covering the bright M 31 disc. Thus, in order to determine the selection completeness of our extracted sample, we follow the procedure outlined in Longobardi et al. (2013) and Hartke et al. (2017). We simulated a population of 104 point-like sources (Sect. 3.2) on the narrow-band image. On the broad-band image, we also simulate sources at the same positions with their fluxes scaled down by the ratio of the filter widths5. We then use SExtractor in dual-mode to simultaneously extract mn and mb of these simulated sources. Figure 8 shows the CMD of the simulated population for a single field. The colour excess remains nearly constant for the bright simulated sources, as expected from the ratio of their filter widths, but many are missed at fainter magnitudes. We can thus determine the selection completeness of the simulated population at different magnitude ranges for each field. To a single candidate extracted in a given field, we assign the value of the selection completeness at that magnitude as a probability of being detected after the selection effects. We also compute the detection completeness of the simulated population at different magnitude ranges from the recovery fraction and similarly assign a detection probability to each PN candidate extracted in each field. The completeness correction is thus obtained from both the selection and the detection probability (see further details in Sect. A.5).
 |
Fig. 8. Colour-magnitude diagram for a single field showing all the simulated sources in black and those recovered as PNe in red (see Sect. 3.6). The 99% and 99.99% limits for the continuum sources are shown in blue, while the region beyond the limiting magnitude is shown in grey. The dotted black line shows the colour selection adopted to limit contamination from background galaxies. The histograms (in logarithmic scale) show the number of PNe recovered as a function of colour (right) and magnitude (top) with the simulated sources in black and those recovered as PNe in red. |
3.7. Comparison with the Merrett et al. (2006) PNe catalogue
We identify those sources in our PNe catalogue that have a counterpart in the catalogue of PNe identified by M06 by matching them spatially within a 3″ aperture (Fig. 9). The astrometry of the M06 sample is reliable up to 3″ (Veyette et al. 2014). We match 1099 such sources (in yellow in Fig. 7). The narrow-band magnitudes of the matched PNe in our survey are 0.045 mag brighter than the corresponding value in M06, well within the photometric uncertainty of the M06 sample. We thus validate the [O III] 5007 Å photometry of our PNe with the sample of M06. The photometry of the M06 PN sample is not very accurate for fainter sources because the PN.S instrument used by M06 has not been optimised for photometry measurements, but rather for the measurement of radial velocities.
 |
Fig. 9. Difference between the narrow-band magnitudes of this work and M06 obtained for the matched sources, plotted against m5007. The red dashed line corresponds to the mean offset. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
While we find most of the PNe found by M06 in the observed fields, we miss quite a few in the regions that we masked, mainly in the crowded bulge and the CCD edges. In our survey area, we recover 82.22% of the M06 PNe. Up to 25% of the M06 PNe candidates were actually H II regions in the M 31 disc (Veyette et al. 2014). The spatial resolution of MegaCam bolstered by the favourable seeing allows us to improve the image quality and obtain an accurate PSF to identify PNe in M 31. The H II regions would appear as extended objects and discarded as PNe by our point-like selection. We investigate the contamination of our PNe catalogue by H II regions in the next section and further discuss it in Sect. 7.1. Thus, the 82.22% recovery fraction of the M06 PNe is driven by the tighter morphological constraints on the light distribution of the detected [O III] sources in our survey. Since the limiting magnitude of our survey is 1.5−2 mag fainter than that of M06, we find a much larger number of new PN candidates in the overlapping area.
4. Counterparts in HST imaging
To test the image quality of our PNe survey, and to estimate the possible contamination from H II regions and other sources, we identified PNe counterparts in the HST data available from the Panchromatic Hubble Andromeda Treasury (PHAT; Dalcanton et al. 2012) covering a portion of the M 31 disc.
4.1. The Panchromatic Hubble Andromeda Treasury
The PHAT6 survey covers ∼1/3 of the star-forming disc of M 31 in six bands from the near-UV to the near-IR using the HST imaging cameras (WFC3/IR, WFC3/UVIS, and ACS/WFC cameras). It combines the wide-field coverage typical of ground-based surveys with the precision of HST observations. The overall survey strategy, initial photometry, and data quality (DQ) assessments are described in detail in Dalcanton et al. (2012). We utilise the second generation of photometric measurements of the resolved stars in the PHAT imaging (Williams et al. 2014), which takes advantage of all available information by carrying out photometry simultaneously in all six filters, resulting in a significant increase in the depth and accuracy the photometry over that presented in Dalcanton et al. (2012).
4.2. Finding PNe counterparts in PHAT
Veyette et al. (2014) conducted a search for M06 PNe counterparts in 16 of the 23 bricks in the PHAT footprint. They find that ∼25% of the PNe identified by M06 in the M 31 disc are either H II regions resolved in HST or stellar contaminants. They utilised the photometry presented in Dalcanton et al. (2012). They found a linear relation between the M06 m5007 magnitude and the PHAT F475W magnitude given by
We adopt a similar method for identifying PHAT counterparts to our PNe in the entire PHAT footprint. However, we search for our counterparts in the updated PHAT photometry from Williams et al. (2014). We only consider those sources from the v2 star files whose square of the sharpness parameter in the F475W filter is below 0.2, to avoid cosmic rays and extended objects. The selection is made on the basis of the following parameters: 1. difference between F475W mag and the F475W mag expected from the m5007 using the relation described by Veyette et al. (2014); 2. the F475W−F814W colour; 3. the positional separation between the PNe and the PHAT counterpart; and 4. the roundness of the PSF. To automatically select candidates on the basis of these parameters, we construct an initial training set with the PNe in common with Veyette et al. (2014). We calculated the average value (X̄PN) and 1σ spread (σPN) of each identification parameter. We found that the separation is within 0.7″. For every PNe, the differences between the training set (X̄PN) and the source (Xs) parameter values were normalised by the σPN of the parameter values for each source in PHAT within 1″ of our PNe location. These normalised parameters are of the form
We obtain the sum of these normalised parameters, with half the weight given to roundness, as the merit function ZPN:
For each PNe, the PHAT source with the lowest value of ZPN is considered as the counterpart. The distribution of the assigned ZPN with the m5007 of the PHAT-matched PNe is shown in Fig. 10. Thresholds in ZPN are used to classify the PNe based on the ZPN assigned to those PHAT sources which were not PNe counterparts. PNe with ZPN < 1.5 are classified as “likely”, those with 1.5 < ZPN < 2 are classified as “possible” and those with ZPN > 2 are classified as “unlikely”. The likely PHAT sources have a significantly lower ZPN than that of other PHAT sources in the search region, but those that are possible do not stand out quite so much. Those classified as unlikely may not be PNe at all as stellar PHAT sources can have ZPN ∼ 2, even though most of them have ZPN > 4. The spatial distribution of PHAT PNe counterparts is presented in Fig. 11.
 |
Fig. 10. Merit function, ZPN, of the PHAT-matched PNe plotted against m5007. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red, respectively. The PNe previously found by M06 are ringed in black. |
 |
Fig. 11. Spatial distribution of the PHAT-matched PNe in the PHAT footprint. The solid bricks are those previously analysed by Veyette et al. (2014), while the dashed ones have been analysed here for the first time. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red, respectively. The PNe previously found by M06 are ringed in black. |
4.3. Characteristics of the PHAT-matched PNe
Of the 1023 PNe in the PHAT footprint, 700 are classified as likely, 292 as possible and 31 as unlikely. True colour images of three PNe, one for each classification, is shown in Fig. 12. None of the PHAT PNe are resolved as H II regions. The 31 unlikely PNe (∼3% of the PHAT PNe) may be stellar contaminants. Of the H II regions spectroscopically identified by Sanders et al. (2012), 81 are present in the PHAT footprint. Many of these were misidentified by M06 as PNe. We misidentify only three of these H II regions (probably compact H II regions) as PNe, which is a testament to the photometric quality and improved spatial resolution of our survey.
 |
Fig. 12. True colour images of PHAT-matched PNe. F814W, F475W, and F336W were used for the red, green, and blue images, respectively. One “likely” (left), “possible” (centre), and “unlikely” (right) PN is shown. The circle denotes 0.5″ around the PN position. |
The mean positional separation of our PNe and their PHAT counterparts is 0.27″ which is a testament to the accurate astrometry of the image and the Elixir pipeline greatly benefiting our survey. Figure 13 shows the variation in separation with m5007. The separation remains largely uniform throughout the range of m5007. The correlation between m5007 and the PHAT F475W mag is also seen for our PNe (Fig. 14), although there is larger dispersion at the faint end. Similarly the variation in the PHAT F475W mag with the F475W−F814W colour (Fig. 15) shows that most of the faint sources that are classified as possible and unlikely have a higher F475W−F814W colour. The dispersion in F475W mag and the higher colour for some of the faint sources may be due to the [O III] 5007 Å line not being as prominent as the continuum flux in F475W for the fainter PNe.
 |
Fig. 13. Positional separation between the PNe and their PHAT counterparts plotted against m5007. The dashed line shows the mean positional separation. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red respectively. The PNe previously found by M06 are ringed in black. |
 |
Fig. 14. F475W mag of the PHAT-matched PNe plotted against m5007. The dashed line shows their relation described by Veyette et al. (2014). The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red respectively. The PNe previously found by M06 are ringed in black. |
 |
Fig. 15. F475W mag of the PHAT-matched PNe plotted against its F475W−F814W colour. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red respectively. The PNe previously found by M06 are ringed in black. |
5. Planetary nebula luminosity-specific frequency
The PNe population follows the sampled (bolometric) luminosity of its parent stellar population. The PN luminosity-specific frequency (α-parameter; Jacoby 1980) is the ratio of the total number of PNe, NPN, to the total bolometric luminosity of the parent stellar population, Lbol, given by
where B is the specific evolutionary flux (stars yr−1
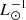 ) and τPN is the PN visibility lifetime (Buzzoni et al. 2006). The α-parameter value provides the number of PNe expected per unit bolometric light. We determine the radial PN number density profile and by comparison with the stellar surface brightness profile of M 31, derived from broad-band photometric studies, we compute the α-parameter value, similarly to the procedure followed for M 87 (Longobardi et al. 2013) and M 49 (Hartke et al. 2017).
) and τPN is the PN visibility lifetime (Buzzoni et al. 2006). The α-parameter value provides the number of PNe expected per unit bolometric light. We determine the radial PN number density profile and by comparison with the stellar surface brightness profile of M 31, derived from broad-band photometric studies, we compute the α-parameter value, similarly to the procedure followed for M 87 (Longobardi et al. 2013) and M 49 (Hartke et al. 2017).
5.1. Radial PN number density profile
Figure 16 shows the distribution of PNe on the sky together with 15 elliptical bins aligned using the known position angle, PA = 38° of M 31 and its ellipticity = 0.73 (Walterbos & Kennicutt 1988). The binning was chosen such that each bin contains the same number of PNe brighter than m5007 = 25.64, which is the 50% completeness limit of the shallowest field (Field# 33_4). These bins correspond to 0.65−26.13 kpc radial distances projected on the minor axis of M 31, Rmin. The PN logarithmic number density profile is defined as
where μ0 is a constant in order to match the PN number density profile with the stellar surface brightness profile, and ΣPN is the completeness-corrected PN number density which is in turn given by
and NPN, corr is the completeness-corrected PN number in any elliptical bin. The completeness correction accounts for both detection and colour incompleteness, detailed in Sect A.5. The parameter A(r) is the observed area in any elliptical bin. We obtain the density profile using only the PNe within 2.5 mag of the bright cut-off (m5007 < 22.56). The resulting PN density profile in each elliptical bin is matched to the V-band surface brightness profile, obtained by Irwin et al. (2005) using photometry and number counts along the minor axis of M 31. It is shown in Fig. 17. We compute μ0 = 11.085 ± 0.004. Courteau et al. (2011) decomposed the M 31 luminosity profile into the bulge, disc, and halo components finding that the halo component becomes significant from Rmin ∼ 8 kpc and it dominates the luminosity profile over the disc from Rmin ∼ 11 kpc. The PN density profile follows the surface brightness profile from Rmin ∼ 2−8 kpc, where the disc dominates the luminosity profile. The M 31 B − V colour, available out to Rmin ∼ 10 kpc, shows a gradient towards bluer colours at larger radii (Walterbos & Kennicutt 1988; Tempel et al. 2010). We find a flattening of μPN with respect to the observed surface brightness profile at larger radial distances. This correlates with the B − V colour gradient and the increasing dominance of the halo component in the light-profile. Additionally, the light from the inner-halo substructures is underestimated by the surface brightness profile obtained along the minor axis of M 31 at larger radii. This may also lead to a flattening of μPN.
 |
Fig. 16. Planetary nebulae are shown spatially divided into elliptical bins containing an equal number of PNe brighter than the 50% completeness limit of the shallowest field (Field# 33_4). |
 |
Fig. 17. Radial surface brightness profile of M 31 (Irwin et al. 2005) (in black) and the PN density using only the PNe within 2.5 mag of the bright cut-off, obtained at different elliptical bins (in blue). The Courteau et al. (2011) decomposition of the M 31 luminosity profile into the bulge, and disc and halo components scaled to the V-band surface brightness profile are also shown. The three-component photometric model for the predicted PN surface density is shown in blue. |
5.2. PN luminosity-specific number: the α-parameter
We can compute the value of α for the observed M 31 PNe from μ0 using the relation
where the K = 26.4 mag arcsec−2 is the V-band conversion factor to physical units L⊙ pc−2, BC⊙ = −0.07 is the solar bolometric correction, and s = D/206265 is a scale factor related to the galaxy distance D. A fixed value of BCV = 0.85 can be assumed with 10% accuracy based on the study of stellar population models for different galaxy types (irregular to elliptical; see Buzzoni et al. 2006).
For the PNe within 2.5 mag of the bright cut-off, we obtain α2.5 = (40.55 ± 3.74) × 10−9 PN 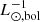 . For a PN population following the PNLF described by Ciardullo et al. (1989), this corresponds to a log α = log(α2.5/0.1) = −6.39 ± 0.04 and τPN = (22527.78 ± 207.78) yr (based on relations described in Buzzoni et al. 2006). M06 obtained α2.5 = (15 ± 2) × 10−9 PN
. For a PN population following the PNLF described by Ciardullo et al. (1989), this corresponds to a log α = log(α2.5/0.1) = −6.39 ± 0.04 and τPN = (22527.78 ± 207.78) yr (based on relations described in Buzzoni et al. 2006). M06 obtained α2.5 = (15 ± 2) × 10−9 PN 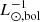 , but only within 1.8 kpc of the minor-axis radius. Scaling our PN number density profile to the surface brightness profile only within this interval, we find μ0 = 10.33 ± 0.01 corresponding to α2.5 = (20.16 ± 1.87) × 10−9 PN
, but only within 1.8 kpc of the minor-axis radius. Scaling our PN number density profile to the surface brightness profile only within this interval, we find μ0 = 10.33 ± 0.01 corresponding to α2.5 = (20.16 ± 1.87) × 10−9 PN 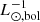 , which is closer to the value obtained by M06. This may be due to the bulge, disc, and halo components of M 31 having differing α-parameter values.
, which is closer to the value obtained by M06. This may be due to the bulge, disc, and halo components of M 31 having differing α-parameter values.
5.3. Three-component photometric model for M 31
Longobardi et al. (2013) and Hartke et al. (2017) also saw differences in the α-parameter values associated with different components of the surface brightness profile, although they looked at halo and intra-group light components. As in their procedure, we describe a photometric model for the predicted PN surface density as
where α2.5,bulge, α2.5,disk, and α2.5,halo are the α2.5 values associated with the bulge, disc, and halo components of M 31, respectively; Ibulge, Idisk, and Ihalo are the surface brightness profiles of the bulge, disc, and halo components of M 31, respectively, as per the Courteau et al. (2011) decomposition of the M 31 luminosity profile into the bulge, disc, and halo components, scaled to the V-band surface brightness profile observations by Irwin et al. (2005).
We simultaneously fit the different α-parameter values of the photometric model to the observed PN surface density to obtain α2.5,bulge = (5.28 ± 6.25) × 10−9 PN 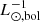 , α2.5,disk = (39.16 ± 3.33) × 10−9 PN
, α2.5,disk = (39.16 ± 3.33) × 10−9 PN 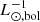 and α2.5,halo = (273.89 ± 41.31) × 10−9 PN
and α2.5,halo = (273.89 ± 41.31) × 10−9 PN 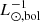 . The model is also shown in Fig. 17. While the α2.5,bulge is not very well constrained, we find the α2.5,disk is quite close to the α2.5 obtained for the whole PN sample, which is expected since the surface brightness profile of M 31 is dominated by the disc component in our survey. We also find that α2.5,halo ∼ 7α2.5,disk. The observed variation in α-parameter values in different galaxies that spans almost two orders of magnitude was studied by Buzzoni et al. (2006), who show that late-type spiral and irregular galaxies with bluer B − V colours are expected to have larger α-parameter values than the redder early-type galaxies. Their analysis is based on population synthesis models of galaxies with different ages, metallicities, and morphological types. The different stellar populations in these galaxies thus exhibit very different α-parameter values. Hartke et al. (2017) also found that α-parameter values for the intra-group light of M 49 is three times larger than that of its halo. Hartke et al. (2018) later confirmed that the halo PNe and intra-group light PNe were kinematically different, and correspond to two separate parent stellar populations. We can thus infer that the larger α-parameter value of the bluer halo of M 31 may indicate that the stellar population of the inner halo is different from that of the disc. While the bluer halo is thus expected to have a higher α2.5 than the disc, its absolute value measured for the M 31 halo is the highest observed in any galaxy.
. The model is also shown in Fig. 17. While the α2.5,bulge is not very well constrained, we find the α2.5,disk is quite close to the α2.5 obtained for the whole PN sample, which is expected since the surface brightness profile of M 31 is dominated by the disc component in our survey. We also find that α2.5,halo ∼ 7α2.5,disk. The observed variation in α-parameter values in different galaxies that spans almost two orders of magnitude was studied by Buzzoni et al. (2006), who show that late-type spiral and irregular galaxies with bluer B − V colours are expected to have larger α-parameter values than the redder early-type galaxies. Their analysis is based on population synthesis models of galaxies with different ages, metallicities, and morphological types. The different stellar populations in these galaxies thus exhibit very different α-parameter values. Hartke et al. (2017) also found that α-parameter values for the intra-group light of M 49 is three times larger than that of its halo. Hartke et al. (2018) later confirmed that the halo PNe and intra-group light PNe were kinematically different, and correspond to two separate parent stellar populations. We can thus infer that the larger α-parameter value of the bluer halo of M 31 may indicate that the stellar population of the inner halo is different from that of the disc. While the bluer halo is thus expected to have a higher α2.5 than the disc, its absolute value measured for the M 31 halo is the highest observed in any galaxy.
We also obtain the radial variation of the α-parameter values (Fig. 18) by scaling the PN number density individually in each elliptical bin, which shows an increase at larger radii. The increasing trend in the α-parameter values is a direct consequence of the flattening of μPN, given the B − V colour gradient of M 31. The radial variation of the α-parameter values found by M06 also showed an slight increasing trend within the errors at larger radii. However, for the furthest radial bin in Fig. 18, the minor-axis surface brightness profile may be underestimating the light from the known inner halo substructures of M 31 primarily found along the disc major axis. This may also be contributing to the large α2.5,halo value. More accurate surface brightness profile measurements need to be performed in order to quantify the contribution of substructures to the minor-axis surface brightness profile of M 31.
 |
Fig. 18. Values of α2.5 obtained at different elliptical bins (in blue). The dotted black line and the dashed black line show the bulge-disc transition and the disc-halo transition, respectively, from the Courteau et al. (2011) decomposition of the M 31 luminosity profile. |
6. Planetary nebula luminosity function
For different galaxies, the generalised analytical formula for the PNLF introduced by Longobardi et al. (2013) is
where c1 is a normalisation constant, c2 is the slope at the faint end, and M* is the absolute magnitude of the LF bright cut-off. The Ciardullo et al. (1989) analytical LF is then a specific case of the generalised analytical formula with c2 = 0.307 that reproduces their best fit to the PNLF of M 31. Observations suggest that the slope described by the parameter c2 is correlated with the star formation history of the parent stellar population (Ciardullo et al. 2004; Ciardullo 2010; Longobardi et al. 2013; Hartke et al. 2017). In order to ascertain the robustness of the morphology of the PNLF at magnitude ranges not reached before, we investigate the M 31 PNLF from our survey with different independent methods.
6.1. PNLF of M 31
The PNLF is corrected for detection completeness and also for selection completeness due to the colour and point-like selection, detailed in Sect. 3.6. Figure 19 shows the PNLF of M 31 for all the PNe identified by our survey, fitted by the generalised analytical formula with c2 = 0.279 ± 0.024, which agrees well with that previously found by Ciardullo et al. (1989). Only the data corresponding to m5007 < 24 are considered for the fit. The bright cut-off remains consistent with the known value of M*. The faint end of the PNLF shows a rise with respect to the fitted function. This rise is seen at m5007 > 24.5 in all the fields of the survey. This rise was not seen by M06 whose sample was photometrically complete to a brighter magnitude (m5007 = 23.5).
 |
Fig. 19. Completeness-corrected PNLF for the whole catalogue of M 31 PNe is shown fitted by both the generalised analytical formula (in orange) and the Ciardullo et al. (1989) analytical LF (in blue). The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
6.2. Cumulative PNLF
The M 31 PNe can be fitted to a cumulative luminosity function (e.g., Peña et al. 2007, for NGC 3109) to avoid potential histogram binning considerations such as the bin size, limits, or the position of the first bin. However, some important features of the canonical PNLF (such as the dip) could be lost. Rodríguez-González et al. (2015) presented the Cumulative PNLF corresponding to the analytical PNLF described by Ciardullo et al. (1989). The Cumulative PNLF for the generalised PNLF is presented as follows:
Figure 20 shows the cumulative PNLF of M 31 for all the PNe identified by our survey, fitted by the generalised analytical formula with c2 = 0.257 ± 0.011, which agrees well with that found from the canonical PNLF, thereby corroborating that the effect histogram binning considerations on the canonical PNLF is negligible. Only the data corresponding to m5007 < 24 are considered for the fit. The faint end of the cumulative PNLF also shows the rise with respect to the fitted function.
 |
Fig. 20. Completeness-corrected cumulative PNLF (binned for visual clarity) for the whole catalogue of M 31 PNe is shown fitted by both the generalised analytical formula for the cumulative PNLF (in orange) and the cumulative PNLF corresponding to the Ciardullo et al. (1989) analytical formula (in blue). The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
6.3. Two-mode PNLF
The rise at the faint end of the PNLF may be an indication that there are two PN populations, one dominating the brighter end and a second one at the fainter end. Thus, we fit the observed cumulative PNLF with two modes similar to Rodríguez-González et al. (2015). The two-mode PNLF is defined as I2m(M) = Ib(M)+If(M), where Ib(M) is the cumulative function for the generalised PNLF set to parameters found in the previous section, which accurately represents the observed PNLF before the rise at the faint end, and If(M) is a cumulative function for the generalised PNLF considered with free parameters, cf1, cf2, and 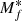 , which are the normalisation constant, slope, and bright cut-off of a possible second faint PNe population. Rodríguez-González et al. (2015) had included an additional magnitude cut-off in their definition of the two-mode PNLF where the contribution of the brighter mode was set to zero at this magnitude and only the faint-end contribution was present. We do not include this magnitude cut-off because any PN population, such as the one dominating in the brighter end, should have a contribution down to ∼8 mag below the bright cut-off (Buzzoni et al. 2006). The two-mode fit of the observed PNLF is shown in Fig. 21. For the second possible PNe population, we find cf2 = 4.4 ± 0.1 and
, which are the normalisation constant, slope, and bright cut-off of a possible second faint PNe population. Rodríguez-González et al. (2015) had included an additional magnitude cut-off in their definition of the two-mode PNLF where the contribution of the brighter mode was set to zero at this magnitude and only the faint-end contribution was present. We do not include this magnitude cut-off because any PN population, such as the one dominating in the brighter end, should have a contribution down to ∼8 mag below the bright cut-off (Buzzoni et al. 2006). The two-mode fit of the observed PNLF is shown in Fig. 21. For the second possible PNe population, we find cf2 = 4.4 ± 0.1 and 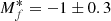 . Thus, the observed cumulative PNLF may have a second PN population with a much steeper slope and very different bright cut-off.
. Thus, the observed cumulative PNLF may have a second PN population with a much steeper slope and very different bright cut-off.
 |
Fig. 21. Completeness-corrected cumulative PNLF (binned for visual clarity) for the whole catalogue of M 31 PNe. It is fitted with two modes of the generalised analytical formula for the cumulative PNLF (in orange) with one component dominating the brighter end (in green) and another dominating the faint end (in red). The cumulative PNLF corresponding to the Ciardullo et al. (1989) analytical formula (in blue) is also shown. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
6.4. PNLF of the deepest field
The deepest field in our survey is Field# 35_4, which has a limiting magnitude at m5007 = 26.4 and is 90% complete at m5007 = 25.6. The PNLF for the PNe observed in this field is shown in Fig. 22 both before and after completeness correction. We note that the rise in the PNLF at m5007 > 25 is present in the observed PNLF within the 90% completeness limit. Thus, the rise of the PNLF is a physical property of the observed PN sample.
 |
Fig. 22. For the deepest field (Field# 35_4), the observed number of PNe in each magnitude bin (in black) and the completeness corrected number (in blue). The region beyond the limiting magnitude of this field is shown in grey. The grey dotted line indicates the 90% completeness limit of this field. |
6.5. Radial variation of PNLF
We divide the PNe spatially into five elliptical bins (Fig. 23) similar to Fig. 16. The PNLF corresponding to each bin is shown in Fig. 24. Only the data corresponding to m5007 < 24 are considered to fit each PNLF. We observe that the rise in the PNLF remains invariant as we go radially outwards indicating that the rise is ubiquitous throughout the surveyed area, and is not a function of photometry in crowded areas. Pastorello et al. (2013) identified PNe in the high metallicity nuclear region within 80 pc of the centre of M 31 with HST and SAURON data. They found a PNLF with a paucity of bright PNe within ∼1 mag of the bright cut-off. We find that the bright cut-off remains invariant as we go radially outwards, but this is expected because the median metallicity of the disc and inner halo stars is largely uniform as the metal-poor inner halo is colligated with stars associated with the more metal-rich substructures (Ibata et al. 2014). We note that the PNLF corresponding to the innermost bin, covering part of the bulge of M 31 which is mostly saturated in our survey, has a steeper fitted slope as expected from PNe corresponding to an older parent stellar population (Longobardi et al. 2013).
 |
Fig. 24. Completeness-corrected PNLF for each elliptical bin fitted by both the generalised analytical formula (in blue) and the Ciardullo et al. (1989) analytical LF (in orange). The projected major-axis elliptical radii covered by each bin is indicated along with the fitted slope of the PNLF. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
6.6. PNLF of PHAT-matched PNe
Figure 25 shows the PNLF of the PHAT-matched PNe. The faint end of the PNLF still shows a rise even for the conservatively selected “likely” PNe. This indicates that the colour and magnitude of faint PNe are consistent with those of the bright PNe.
 |
Fig. 25. Completeness-corrected PNLF for PHAT-matched PNe is shown for the “likely” (blue), “possible + likely” (yellow) and “possible + likely + unlikely” (red) cases. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
6.7. Comparison with other deep PN surveys in Local Group galaxies
We compare the shape of the M 31 PNLF with that of other surveys in different galaxies that sample similar magnitude intervals from the bright cut-off. A catalogue of PNe with m5007 down to ∼10 mag below the bright cut-off of the PNLF is available for the Large Magellanic Cloud (LMC) from Reid & Parker (2010). This catalogue is not completeness corrected as the m5007 magnitudes are estimated from spectroscopy but is expected to be largely complete to ∼6 mag below the bright cut-off, i.e. the magnitude interval covered by our survey of PNe in M 31. Another catalogue of PNe is available for the Small Magellanic Cloud (SMC) from Jacoby & De Marco (2002) with m5007 down to ∼8 mag below the bright cut-off. It is also not corrected for completeness, but has significantly fewer PNe than the LMC and may suffer from significant completeness issues ∼6 mag below the bright cut-off. A catalogue of PNe identified in the MW bulge is also available (Kovacevic et al. 2011), and assuming that all their PNe are at a constant 8 kpc distance (Majaess 2010), i.e. the average distance to the MW bulge, a PNLF may be constructed. The distance approximation may be inaccurate, and completeness information is also unavailable.
Considering the LMC, SMC, and MW bulge PNe at the distance of M 31 normalised for the number of PNe in M 31, we can compare the shape of their PNLF with that of M 31 (Fig. 26). We note that the difference in the bright cut-off is expected from the difference in metallicity between the three galaxies. The dip in the PNLF seen for both the LMC and the SMC, albeit at different magnitudes, is not seen for M 31. The MW bulge PNe seem to show a different slope, but no rise is evident. However, we cannot disregard the possibility that a dip or a rise at the faint end of the PNLF may be seen pending accurate distance determination. The rise at the faint end of the PNLF of M 31 is much steeper than any of the others.
 |
Fig. 26. Completeness-corrected PNLF for the whole catalogue of M 31 PNe (black points) is shown fitted by the Ciardullo et al. (1989) analytical LF (black dotted line). The LMC (Reid & Parker 2010), SMC (Jacoby & De Marco 2002), and MW Bulge PNe (Kovacevic et al. 2011) shifted to the distance of M 31 are shown in blue, orange, and green, respectively. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
7. Discussion
7.1. Possible sources of contamination
As discussed in Sect. 3.4, up to 50 continuum sources may contaminate our PNe catalogue, most of which should be fainter than m5007 = 25. This is also corroborated for the PHAT counterparts where ∼3% of the matched PNe may actually be stellar contaminants. The contamination from Milky Way (MW) halo and disc PNe is negligible as there are no MW halo PNe at m5007 > 20.5 (Kovacevic et al. 2011). Background galaxies at redshift z = 0.345 that are [OII]3727 Å emitters can be another source of contamination, but they are not known to have EWobs > 95 Å (Colless et al. 1990; Hammer et al. 1997; Hogg et al. 1998). Our colour selection thus renders their contamination negligible.
H II regions are also bright in the [O III] 5007 Å line and are present in the same region of the CMD as PNe. However, H II regions appear extended at the distance of M 31 and with the photometric quality of our survey, we are able to significantly limit their contamination as seen in Sect. 4. Some compact H II regions, especially in the disc of M 31, may still contaminate our survey. Of the 253 H II regions identified by Sanders et al. (2012) later from spectroscopy, M06 had classified 101 of them as PNe. We find only 15 of these in our survey as PNe, thereby corroborating the excellent photometric quality of our survey. Other [O III] 5007 Å sources like SySts may also mimic PNe and contaminate our survey. We investigate in the following whether the contribution from SySts is responsible for the two-mode PNLF investigated in Sect. 6.3.
7.2. Symbiotic star contribution to PNLF
SySts are among the longest orbital period interacting binaries, consisting of an evolved cool giant and an accreting, hot, luminous companion (usually a white dwarf) surrounded by a dense ionised nebula. Depending on the nature of the cool giant, there are two main classes of SySts: the S-types (stellar), which are normal M giants with orbital periods of the order of a few years, and the D-types (dusty), which contain Mira variable primaries surrounded by warm dust with orbital periods of a decade or longer. Mikołajewska et al. (2014) found 31 confirmed Systs in M 31, 10 of which had unambiguous PHAT counterparts. Of these, 9 were S-types and their spectra show that the continuum emission is high in the F814W filter. Mikołajewska et al. (2014) utilised this to identify the PHAT counterpart of their SySt as the PHAT source that had the brightest F814W mag in their 0.75″ search radius. It is also seen that the F475W−F814W colour of these SySt generally have a high positive value which can be used to distinguish them from PNe.
We estimate the probability that each of our PHAT-matched PN is a SySt by checking how close it was in F814W mag (F814WPN) to the brightest F814W mag source (F814Whigh) in our search radius, and also if it had a colour excess in F814W with respect to F475W. The probability, PSySt, is given by the following formula:
Here 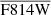 is the mean F814W mag of all sources in the search radius and Pcol is the colour excess check, which equals 1 if F475W−F814W > 1 (most of the Mikołajewska et al. 2014 SySt have this), 1/2 if 0 < F475W–F814W < 1 (some of the confirmed PNe have this), and 0 otherwise. PHAT-matched PN with F814W below the
is the mean F814W mag of all sources in the search radius and Pcol is the colour excess check, which equals 1 if F475W−F814W > 1 (most of the Mikołajewska et al. 2014 SySt have this), 1/2 if 0 < F475W–F814W < 1 (some of the confirmed PNe have this), and 0 otherwise. PHAT-matched PN with F814W below the 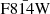 are set to have a PSySt = 0. We find that there is a systematic overestimation of PSySt since PHAT-matched PNe just above their
are set to have a PSySt = 0. We find that there is a systematic overestimation of PSySt since PHAT-matched PNe just above their 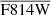 would still be assigned a small value of PSySt. We thus update the PSySt by subtracting the mean of the probability,
would still be assigned a small value of PSySt. We thus update the PSySt by subtracting the mean of the probability, 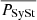 , from each source and setting those with negative values to zero. We find that most PHAT-matched PNe with a probability of being a SySt are clustered around a high F475W−F814W colour (Fig. 27). Removing the contribution of SySts from the PNLF (Fig. 28), it is evident that the rise at the faint end of the PNLF cannot be explained by SySts. Figure 28 also shows the PNLF for only those PHAT-matched PNe with F475W−F814W < 0 to show that the rise in the PNLF is not dependent on the F475W−F814W colour. Continuum stars are unlikely to have F475W−F814W < 0 and considering that we limit contamination from H II regions, the sources with F475W−F814W < 0 are most likely genuine PNe. The rise in the observed PNLF is indeed visible, even prior to completeness correction.
, from each source and setting those with negative values to zero. We find that most PHAT-matched PNe with a probability of being a SySt are clustered around a high F475W−F814W colour (Fig. 27). Removing the contribution of SySts from the PNLF (Fig. 28), it is evident that the rise at the faint end of the PNLF cannot be explained by SySts. Figure 28 also shows the PNLF for only those PHAT-matched PNe with F475W−F814W < 0 to show that the rise in the PNLF is not dependent on the F475W−F814W colour. Continuum stars are unlikely to have F475W−F814W < 0 and considering that we limit contamination from H II regions, the sources with F475W−F814W < 0 are most likely genuine PNe. The rise in the observed PNLF is indeed visible, even prior to completeness correction.
 |
Fig. 27. Histogram for PHAT-matched PNe is shown for the “likely” (blue), “possible + likely” (yellow) and “possible + likely + unlikely” (red) cases. The histogram of possible SySts are shown in black. |
 |
Fig. 28. Completeness-corrected PNLF for PHAT-matched PNe with the contribution from SySts removed is shown in black. The completeness-corrected PNLF for only those PNe with F475W–F814W < 0 is shown in blue. The PNLF for the observed PHAT-matched PNe with F475W–F814W < 0 is shown in red. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
D-type SySts do not show an excess in the F814W filter. Thus, in our analysis a D-type SySt cannot be distinguished from a PNe. Even so, their numbers are expected to be far lower than that of a S-type SySt and so there should not be any significant number of D-type SySts plaguing our data. Mikołajewska et al. (2014) had one D-type SySt in the PHAT footprint, which we indeed misidentify as a PNe in our study.
7.3. Spectroscopically confirmed PNe and the faint end of the PNLF
A spectroscopic follow-up of a complete subsample of the M 31 PNe was carried out with the Hectospec multifibre positioner and spectrograph on the Multiple Mirror Telescope (MMT; Fabricant et al. 2005). Observations were made on September 15, 2018, and October 10, 2018, with an exposure time of 9000 s each, and also on December 4, 2018, with an exposure time of 3600 s. The Hectospec 270 gpm grating was used and provided spectral coverage from 3650 to 9200 Å at a resolution of ∼5 Å. Each Hectospec fibre subtends 1.5″ on the sky. The fibres were placed on PNe candidates to maximise the observation of bright PNe, obtain their LOSV, and determine their chemical abundances. Of the 343 PNe candidates observed in M 31, 129 had confirmed detection of the [O III] 4959/5007 Å emission lines. The [O III] 5007 Å emission line was detected in all cases with a signal-to-noise ratio higher than 8. All of them also had the Hα line present. Since our original PNe sample is largely devoid of H II regions, these observed sources are expected to be PNe. Details of the spectroscopy confirming them as PNe, along with their LOSV distribution and chemical abundances will be presented in a forthcoming paper (Bhattacharya et al., in prep.). The fraction of PNe detected as a function of magnitude is shown in Fig. 29.
 |
Fig. 29. Fraction of PNe targeted with spectroscopic observations where a narrow [O III] 5007 Å emission line was detected. The uncertainty in detection fraction is the binomial proportion confidence-interval of observed PNe in any magnitude bin obtained using the Wilson score interval method (Wilson 1927). The blue dashed line shows the 50% detection limit of the spectroscopic follow-up. |
The spectroscopic follow-up shows that all the PNe candidates observed were confirmed as PNe, from the presence of [O III] 4959/5007 Å and Hα emission lines, down to 24.5 mag, but only a fraction of the targeted PNe candidates at fainter magnitudes could be confirmed. While the required emission lines may not have been detected due to a low signal-to-noise ratio in the spectra for the faint targeted PNe candidates, it is also possible that those faint sources are continuum contaminants or background galaxies instead. Making the conservative assumption that all such sources are not PNe, we can modify the PNLF to account for this behavior. Since the rise in the PNLF is seen at different radii at about the same extent, we can compute the expected PNLF for the fraction of PNe that are conservatively confirmed spectroscopically, as shown in Fig. 30. The PNLF is still consistent with the rise at the faint end of the PNLF although the uncertainty in the fraction with spectral confirmation is large.
 |
Fig. 30. Completeness-corrected PNLF for all PNe (in black) fitted by both the generalised analytical formula for the cumulative PNLF (in orange) and the cumulative PNLF corresponding to the Ciardullo et al. (1989) analytical formula (in blue). The completeness-corrected PNLF accounting for the detection fraction from spectroscopy is shown in blue. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. The blue dashed line shows the 50% detection limit of the spectroscopic follow-up. |
7.4. Summary of the observational evidence for the rise at the faint end of the PNLF
Our investigation of the morphology of the PNLF is carried out at different positions and radial distances, and considering the effects of possible contaminants. The rise at the faint end of the PNLF is observed not only in the PNLF for the whole survey but also in individual fields, including the deepest field discussed in Sect. 6.4. In this field, it is already visible for the observed PNe even before completeness correction.
The rise at the faint end of the PNLF occurs from m5007 ∼ 24.5−25 and is present at varying radial distances from the centre of M 31 (Sect. 6.5). If the rise at the faint end of the PNLF was due to compact H II regions, it would be largely present only in the disc of M 31 and not in all radial elliptical bins. In the survey region in common with HST data from PHAT, we also see the rise in the PNLF for those PNe with reliable PHAT counterparts (Sect. 6.6). The rise is especially evident when looking at the PNLF from PHAT-matched PNe with F475W−F814W < 0, a region in colour occupied almost exclusively by PNe, even prior to completeness correction (Fig. 28). The spectroscopic follow-up also shows that the rise at the faint end of the PNLF is seen in confirmed PNe, albeit with large errors.
This observational evidence means that it is reasonable to believe that the rise in the PNLF is indeed physical and associated with the PN population and their parent stars. Rodríguez-González et al. (2015) fitted the two-mode PNLF for NGC 6822 (an irregular galaxy in the local group) and from its star formation history they show that the two modes of the PNLF may correspond to PNe associated with the two episodes of star formation, with the older parent stellar population corresponding to the fainter PNe. It is possible that the second PN population in M 31 is associated with an older stellar population. With data from the PHAT survey, Williams et al. (2017) found that there was a burst of star formation ∼2−4 Gyr ago throughout the M 31 stellar disc. Bernard et al. (2015) studied individual HST fields associated with the disc and inner halo substructures of M 31 to find that all the fields show a burst of star formation ∼2 Gyr ago even though most of the stars in the M 31 outer disc formed >8 Gyr ago. Since the slope of the PNLF associated with PNe belonging to an older stellar population is seen to be steeper (Sect. 6.3), it is possible that the steep rise at the faint end of the PNLF is caused by PNe associated with the older population while the PNe associated with the ∼2 Gyr old burst of star formation populate the brighter magnitudes of the PNLF.
Another possible reason for the rise in the faint end of the PNLF could be a change in opacity of the nebula of the PNe. The PNe occupying the bright end of the PNLF could be more opaque, with the nebula more efficiently reprocessing the ionising flux of the central star into [O III] 5007 Å while the faint end may be populated by the more transparent PNe. The significant dependence of the PNLF on the considerations of the nebular transparency is also evident in the models by Gesicki et al. (2018). This scenario has previously been invoked to describe the dip in the PNLF seen in the SMC (Jacoby & De Marco 2002).
8. Conclusions
We present a 16 square degree survey in the disc and inner halo of M 31 with the MegaCam at the CFHT using the narrow-band [O III] 5007 Å filter and the broad-band g filter. We identify point-lke PNe from the colour excess between the narrow-band and broad-band images down to a limiting magnitude between m5007 = 25.64 for the shallowest observed field to m5007 = 26.4 for the deepest observed field. We obtain 4289 PNe, the largest sample outside the MW, of which 1099 were previously observed by M06. Using a simulated PN population, we are able to account for incompleteness. We find counterparts in PHAT for 1023 of our identified PNe in the PHAT footprint. We find no resolved H II regions and a very small fraction (∼3%) of PNe that could be stellar contamination. The α-parameter value obtained shows an increasing trend as we go further away from the centre of M 31, but reasonably matches the value obtained by M06 for the central regions. The high value of the obtained α2.5,halo may be attributed to the bluer halo of M 31 indicating that the stellar population in the halo, at radii larger than ∼10 kpc, may be different from that of the inner disc.
The PNLF of the whole sample is complete down to ∼5.5 mag fainter than the bright cut-off and shows a significant rise at the faint end. The generalised analytical formula fitted to the completeness corrected PNLF, for magnitudes brighter than m5007 < 24, returns parameters that are in agreement with those previously determined by Ciardullo et al. (1989). The rise at the faint end is seen at different elliptical radial distances from the centre and also in the PHAT-matched PNe implying that this rise is not associated with crowding. The rise is steeper than that seen in the LMC and the SMC. It is also not caused by contaminating sources like symbiotic stars, and seems to be a property of the parent population of the PNe, evident from the comparison with PHAT. Early findings from the spectroscopic follow-up also show that the rise in the number of PNe at faint magnitudes is physical, albeit with large uncertainty. It is possible that the PNe in M 31 associated with the population created from the burst of star formation ∼2 Gyr ago populate the brighter magnitudes of the PNLF, while those at the faint end are associated with the older population. It is also possible that the faint end is populated by PNe with more transparent nebulae7, while those with opaque nebulae populate the bright end.
Acknowledgments
SB and JH acknowledge support from the IMPRS on Astrophysics at the LMU Munich. We are grateful to the anonymous referee for the constructive comments that improved the manuscript. This research made use of IRAF, distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013); Numpy (Oliphant 2015); and Matplotlib (Hunter 2007). This research also made use of NASA’s Astrophysics Data System (ADS).
References
- Arnaboldi, M., Freeman, K. C., Mendez, R. H., et al. 1996, ApJ, 472, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Gerhard, O., et al. 1998, ApJ, 507, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Aguerri, J. A. L., Napolitano, N. R., et al. 2002, AJ, 123, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Okamura, S., et al. 2003, AJ, 125, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barmby, P., Ashby, M. L. N., Bianchi, L., et al. 2006, ApJ, 650, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Chapman, S. C., et al. 2015, MNRAS, 453, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, in Astronomical Data Analysis Software and Systems XI, eds. D. A. Bohlender, D. Durand, & T. H. Handley, 281, 228 [NASA ADS] [Google Scholar]
- Bonnarel, F., Fernique, P., Bienaymé, O., et al. 2000, A&AS, 143, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, 4841, 72 [Google Scholar]
- Buzzoni, A., Arnaboldi, M., & Corradi, R. L. M. 2006, MNRAS, 368, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R. 2010, PASA, 27, 149 [NASA ADS] [Google Scholar]
- Ciardullo, R., & Jacoby, G. H. 1992, ApJ, 388, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Jacoby, G. H., Ford, H. C., & Neill, J. D. 1989, ApJ, 339, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., et al. 2002, ApJ, 577, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Durrell, P. R., Laychak, M. B., et al. 2004, ApJ, 614, 167 [Google Scholar]
- Ciardullo, R., Gronwall, C., Adams, J. J., et al. 2013, ApJ, 769, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Ellis, R. S., Taylor, K., & Hook, R. N. 1990, MNRAS, 244, 408 [NASA ADS] [Google Scholar]
- Cortesi, A., Arnaboldi, M., Coccato, L., et al. 2013, A&A, 549, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courteau, S., Widrow, L. M., McDonald, M., et al. 2011, ApJ, 739, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Lang, D., et al. 2012, ApJS, 200, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, B. D., Ciardullo, R., Jacoby, G. H., Feldmeier, J. J., & Indahl, B. L. 2018, ApJ, 863, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, N. G., Arnaboldi, M., Freeman, K. C., et al. 2002, PASP, 114, 1234 [NASA ADS] [CrossRef] [Google Scholar]
- D’Souza, R., & Bell, E. F. 2018, Nat. Astron., 2, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D., Fata, R., Roll, J., et al. 2005, PASP, 117, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., García-Benito, R., Guerrero, M. A., et al. 2015, ApJ, 815, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., García-Benito, R., Guerrero, M. A., et al. 2018, ApJ, 853, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A. M. N., & Mackey, A. D. 2016, in Tidal Streams in the Local Group and Beyond, eds. H. J. Newberg, & J. L. Carlin, 420, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Gesicki, K., Zijlstra, A. A., & Miller Bertolami, M. M. 2018, Nat. Astron., 2, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Flores, H., Lilly, S. J., et al. 1997, ApJ, 481, 49 [CrossRef] [Google Scholar]
- Hammer, F., Yang, Y. B., Wang, J. L., et al. 2018, MNRAS, 475, 2754 [NASA ADS] [Google Scholar]
- Hartke, J., Arnaboldi, M., Longobardi, A., et al. 2017, A&A, 603, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartke, J., Arnaboldi, M., Gerhard, O., et al. 2018, A&A, 616, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henize, K. G., & Westerlund, B. E. 1963, ApJ, 137, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Martínez, L., & Peña, M. 2009, A&A, 495, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hogg, D. W., Cohen, J. G., Blandford, R., & Pahre, M. A. 1998, ApJ, 504, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, X., Ford, H. C., Freeman, K. C., & Dopita, M. A. 1995, ApJ, 449, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., McConnachie, A. W., et al. 2014, ApJ, 780, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M. J., Ferguson, A. M. N., Ibata, R. A., Lewis, G. F., & Tanvir, N. R. 2005, ApJ, 628, L105 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jacoby, G. H. 1980, ApJS, 42, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H. 1989, ApJ, 339, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., & De Marco, O. 2002, AJ, 123, 269 [Google Scholar]
- Jones, D., & Boffin, H. M. J. 2017, Nat. Astron., 1, 0117 [CrossRef] [Google Scholar]
- Kovacevic, A. V., Parker, Q. A., Jacoby, G. H., et al. 2011, MNRAS, 414, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., Li, Z., Dong, H., Fang, X., & Xu, X. 2018, Res. Astron. Astrophys., 18, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., et al. 2013, A&A, 558, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., & Hanuschik, R. 2015, A&A, 579, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, A. D., Huxor, A. P., Ferguson, A. M. N., et al. 2010, ApJ, 717, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Magnier, E. A., & Cuillandre, J. C. 2004, PASP, 116, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Majaess, D. 2010, Acta Astron., 60, 55 [NASA ADS] [Google Scholar]
- Marmo, C., & Bertin, E. 2008, in Astronomical Data Analysis Software and Systems XVII, eds. R. W. Argyle, P. S. Bunclark, & J. R. Lewis, 394, 619 [NASA ADS] [Google Scholar]
- Martin, T. B., Drissen, L., & Melchior, A.-L. 2018, MNRAS, 473, 4130 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W., Irwin, M. J., Ibata, R. A., et al. 2009, Nature, 461, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McConnachie, A. W., Ibata, R., Martin, N., et al. 2018, ApJ, 868, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez, R. H., Riffeser, A., Kudritzki, R. P., et al. 2001, ApJ, 563, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Merrett, H. R., Merrifield, M. R., Douglas, N. G., et al. 2006, MNRAS, 369, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Mikołajewska, J., Caldwell, N., & Shara, M. M. 2014, MNRAS, 444, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Oliphant, T. E. 2015, Guide to NumPy, 2nd edn. (USA: CreateSpace Independent Publishing Platform) [Google Scholar]
- Pastorello, N., Sarzi, M., Cappellari, M., et al. 2013, MNRAS, 430, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Peña, M., Richer, M. G., & Stasińska, G. 2007, A&A, 466, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pulsoni, C., Gerhard, O., Arnaboldi, M., et al. 2018, A&A, 618, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, W. A., & Parker, Q. A. 2010, MNRAS, 405, 1349 [NASA ADS] [Google Scholar]
- Rodríguez-González, A., Hernández-Martínez, L., Esquivel, A., et al. 2015, A&A, 575, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, N. E., Caldwell, N., McDowell, J., & Harding, P. 2012, ApJ, 758, 133 [Google Scholar]
- Tempel, E., Tamm, A., & Tenjes, P. 2010, A&A, 509, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teplitz, H. I., Malkan, M. A., Steidel, C. C., et al. 2000, ApJ, 542, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Veljanoski, J., Mackey, A. D., Ferguson, A. M. N., et al. 2014, MNRAS, 442, 2929 [NASA ADS] [CrossRef] [Google Scholar]
- Veyette, M. J., Williams, B. F., Dalcanton, J. J., et al. 2014, ApJ, 792, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Walterbos, R. A. M., & Kennicutt, Jr., R. C. 1988, A&A, 198, 61 [NASA ADS] [Google Scholar]
- Williams, B. F., Lang, D., Dalcanton, J. J., et al. 2014, ApJS, 215, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. F., Dolphin, A. E., Dalcanton, J. J., et al. 2017, ApJ, 846, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, E. B. 1927, J. Am. Stat. Assoc., 22, 209 [CrossRef] [Google Scholar]
Appendix A: Catalogue extraction
A.1. Flux calibration for m5007
The integrated flux, F5007, from the [O III] 5007 Å line is related to the m5007 magnitude (Jacoby 1989) as
where the flux is in units of erg cm2 s−1. The AB magnitude (Oke & Gunn 1983) relates to F5007 through the MegaCam narrow-band [O III] filter characteristics as
where λc = 5007 Å and Δλeff = Δλ × T for the on-band with Δλ = 102 Å and effective transmission, T = 0.91. The relation between the AB and m5007 mag, for this narrow-band filter, is thus determined (following Arnaboldi et al. 2003) to be
A.2. Point spread function
The point spread function (PSF) is the instrumental response to a point-like object. The degree of spreading of the PSF represents the quality of the instrument imaging. To determine the PSF, we first used the IRAF tasks daofind, daophot, and pstsel to respectively extract all the positions of detected sources, determine their magnitude, and select the brighter stars. We then used the IRAF task psf, which allowed us to select the best stars to fit the PSF, and reject bad objects (e.g., saturated or located near an another source). The confirmed stars are used to calculate the PSF. The PSF is modelled with different luminosity profiles (e.g., Gaussian, Moffat function) and the best fit is selected using χ2 minimisation (goodness of fit). The best fit is a Moffat function (parameters in Table A.1) of the form
A.3. Masking of noisy regions and CCD edges
After identifying sources on the images, the image regions that were affected by dithering or saturation are masked on the on-band and off-band images. This is carried out for each field. Dithering leads to different exposure depths at the image edges. Due to the combination of the 42 MegaCam CCDs, the same effect also affects columns at the borders of the individual CCDs. Additionally, in order to mask those regions with a high background value (e.g., due to charge transfer or saturated stars) we used the rms-background map created by SExtractor and create a pixel-mask with all values higher than three times the median background.
A.4. Choice of aperture width
After simulating sources on to the on-band, we determine the magnitude aperture most suited to recovering them. Figure A.1 shows that different SExtractor aperture widths (AW) of 15, 17, 19, and 21 pixels all recover the magnitudes well but an AW of 15 pixels can recover sources most accurately even for fainter sources.
Parameters for the best fitting PSF.
 |
Fig. A.1. Recovery of the input magnitude of simulated sources using different SExtractor aperture widths, AW, for a single field. |
A.5. Completeness correction in the survey
For the entire survey, the mean percentage total completeness is shown as a function of the m5007 magnitude in Fig. A.2 in black, while the mean percentage detection completeness and percentage selection completeness are shown in blue and orange, respectively. It is clear that the completeness correction applied is dominated by the selection completeness, correcting for the number of genuine PNe missed due to our colour and point-like selection. The percentage completeness shown is only representative in Fig. A.2; the completeness varies in each field and the completeness correction is applied to PNe in each field separately.
 |
Fig. A.2. For the entire survey the number of PNe in each magnitude bin (in black), and the completeness corrected number (in blue) for a single field. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
 |
Fig. A.3. Completeness-corrected PNLF for PHAT-matched PNe within (left) and outside (right) 0.3 deg of the centre of M 31 is shown for the “likely” (blue), “possible + likely” (yellow), and “possible + likely + unlikely” (red) cases. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
A.6. Detection check on background
For each image, as a by-product of the source extraction, we obtain a background image. In order to check for spurious sources in any image, we run SExtractor on this background image with the parameters described in Sect. 3.1. The sources detected on the background image and their distribution as a function of magnitude would give us an indication of the number of spurious sources present in our PNe catalogue. However, subjecting these sources to the PNe selection criteria described in Sects. 3.3 and 3.4, we find that even if these detected sources survive the colour selection, they would be rejected as PNe in the point-like selection as their half-light radius is much smaller than that expected from the simulated PNe population.
Appendix B: PNe counterparts in PHAT
B.1. The M06 PNe counterparts in PHAT
For each M06 PNe, Veyette et al. (2014) searched for counterparts within 3″. They expected a strong relation between the M06 m5007 mag and the PHAT F475W magnitude since the majority of F475W flux is due to the [O III] 5007 Å line, and a colour excess between the PHAT F475W and F814W filters, since PNe are not expected to show a strong continuum excess. Additionally, they utilised the separation between the M06 PNe and the PHAT counterpart, and the roundness and sharpness of its PSF. Of the 711 PNe in the M06 catalogue that overlap the PHAT images, they found that only 467 had counterparts consistent with being PNe. The rest were either H II regions or possible stellar sources with no PHAT counterpart consistent with being a PNe.
B.2. Further characteristics of the PHAT-matched PNe
We also check the PNLF for consistency both near the crowded centre (within 0.3 deg) and in the less crowded outer disc (outside 0.3 deg) as shown in Fig. A.3. The PNLF is similar in both cases, indicating again that the rise in the PNLF does not depend on crowding, but the value in the less crowded disc shows a more pronounced dip in the PNLF. This may be due to the presence of the 10 kpc star-forming ring in M 31 (Barmby et al. 2006), which may be populating the brightest 2.5 mag of the PNLF with PNe evolved from young massive stars. There are 954 PNe that have detections in the PHAT NIR filters. Figure A.4 shows the F110W mag of the PHAT-matched PNe plotted against its F110W−F160W colour. There are 644 PNe that have detections in the PHAT UV filters. Figure A.5 shows the F275W mag of the PHAT-matched PNe plotted against its F275W−F336W colour. The trends in the UV and the NIR are similar to those found by Veyette et al. (2014) for the M06 PNe.
 |
Fig. A.4. F110W mag of the PHAT-matched PNe plotted against its F110W−F160W colour. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red, respectively. The PNe previously found by M06 are ringed in black. |
 |
Fig. A.5. F275W mag of the PHAT-matched PNe plotted against its F275W−F336W colour. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red, respectively. The PNe previously found by M06 are ringed in black. |
All Tables
Summary of the field positions, exposure times, and seeing for the narrow-band (on-band) and broad-band (off-band) images.
All Figures
 |
Fig. 1. Fields observed with CFHT MegaCam (in blue, labelled with their observation ID). North is up, east is left. The background image is from SDSS obtained using the Aladin Sky Atlas (Bonnarel et al. 2000). |
| In the text | |
 |
Fig. 2. The effective survey area is shown in black. CCD edges and noisy or saturated regions have been masked. |
| In the text | |
 |
Fig. 3. Recovery fraction of simulated sources for a single field to illustrate the limiting magnitude at the 50% completeness limit. |
| In the text | |
 |
Fig. 4. Colour-magnitude diagram showing the synthetic continuum sources and the 99% and 99.99% limits on their positions for a single field. The region beyond the limiting magnitude of this field is shown in grey. |
| In the text | |
 |
Fig. 5. Top: difference between mn and mcore for all sources in black and those within the 95% limits of the simulated population in red for the simulated population (left) and as applied to the real sources (right) for a single field. Bottom: same as the top panel, but for half-light radius, Rh. |
| In the text | |
 |
Fig. 6. Colour-magnitude diagram for a single field showing all the detected sources (brighter than the limiting magnitude) in black, the colour-selected sources in blue, and identified PNe in red. The 99% and 99.99% limits for the continuum sources are shown in blue, while the region beyond the 50% completeness limit is shown in grey. The histogram (in logarithmic scale) shows clearly the number of PNe recovered as a function of colour with all the detected sources (brighter than the limiting magnitude) in black, the colour-selected sources in blue, and identified PNe in red. |
| In the text | |
 |
Fig. 7. Planetary nebulae identifed by the survey are overlaid on the map of RGB stars from the PAndAS survey. PNe brighter than m5007 = 25.64 mag, which is the 50% completeness limit of the shallowest field (Field# 33_4), are shown in blue. PNe fainter than m5007 = 25.64 mag, with photometric depth varying with field, are shown in green. The M06 PNe, re-identified by our survey, are shown in yellow. North is up, east is left. |
| In the text | |
 |
Fig. 8. Colour-magnitude diagram for a single field showing all the simulated sources in black and those recovered as PNe in red (see Sect. 3.6). The 99% and 99.99% limits for the continuum sources are shown in blue, while the region beyond the limiting magnitude is shown in grey. The dotted black line shows the colour selection adopted to limit contamination from background galaxies. The histograms (in logarithmic scale) show the number of PNe recovered as a function of colour (right) and magnitude (top) with the simulated sources in black and those recovered as PNe in red. |
| In the text | |
 |
Fig. 9. Difference between the narrow-band magnitudes of this work and M06 obtained for the matched sources, plotted against m5007. The red dashed line corresponds to the mean offset. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. 10. Merit function, ZPN, of the PHAT-matched PNe plotted against m5007. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red, respectively. The PNe previously found by M06 are ringed in black. |
| In the text | |
 |
Fig. 11. Spatial distribution of the PHAT-matched PNe in the PHAT footprint. The solid bricks are those previously analysed by Veyette et al. (2014), while the dashed ones have been analysed here for the first time. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red, respectively. The PNe previously found by M06 are ringed in black. |
| In the text | |
 |
Fig. 12. True colour images of PHAT-matched PNe. F814W, F475W, and F336W were used for the red, green, and blue images, respectively. One “likely” (left), “possible” (centre), and “unlikely” (right) PN is shown. The circle denotes 0.5″ around the PN position. |
| In the text | |
 |
Fig. 13. Positional separation between the PNe and their PHAT counterparts plotted against m5007. The dashed line shows the mean positional separation. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red respectively. The PNe previously found by M06 are ringed in black. |
| In the text | |
 |
Fig. 14. F475W mag of the PHAT-matched PNe plotted against m5007. The dashed line shows their relation described by Veyette et al. (2014). The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red respectively. The PNe previously found by M06 are ringed in black. |
| In the text | |
 |
Fig. 15. F475W mag of the PHAT-matched PNe plotted against its F475W−F814W colour. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red respectively. The PNe previously found by M06 are ringed in black. |
| In the text | |
 |
Fig. 16. Planetary nebulae are shown spatially divided into elliptical bins containing an equal number of PNe brighter than the 50% completeness limit of the shallowest field (Field# 33_4). |
| In the text | |
 |
Fig. 17. Radial surface brightness profile of M 31 (Irwin et al. 2005) (in black) and the PN density using only the PNe within 2.5 mag of the bright cut-off, obtained at different elliptical bins (in blue). The Courteau et al. (2011) decomposition of the M 31 luminosity profile into the bulge, and disc and halo components scaled to the V-band surface brightness profile are also shown. The three-component photometric model for the predicted PN surface density is shown in blue. |
| In the text | |
 |
Fig. 18. Values of α2.5 obtained at different elliptical bins (in blue). The dotted black line and the dashed black line show the bulge-disc transition and the disc-halo transition, respectively, from the Courteau et al. (2011) decomposition of the M 31 luminosity profile. |
| In the text | |
 |
Fig. 19. Completeness-corrected PNLF for the whole catalogue of M 31 PNe is shown fitted by both the generalised analytical formula (in orange) and the Ciardullo et al. (1989) analytical LF (in blue). The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. 20. Completeness-corrected cumulative PNLF (binned for visual clarity) for the whole catalogue of M 31 PNe is shown fitted by both the generalised analytical formula for the cumulative PNLF (in orange) and the cumulative PNLF corresponding to the Ciardullo et al. (1989) analytical formula (in blue). The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. 21. Completeness-corrected cumulative PNLF (binned for visual clarity) for the whole catalogue of M 31 PNe. It is fitted with two modes of the generalised analytical formula for the cumulative PNLF (in orange) with one component dominating the brighter end (in green) and another dominating the faint end (in red). The cumulative PNLF corresponding to the Ciardullo et al. (1989) analytical formula (in blue) is also shown. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. 22. For the deepest field (Field# 35_4), the observed number of PNe in each magnitude bin (in black) and the completeness corrected number (in blue). The region beyond the limiting magnitude of this field is shown in grey. The grey dotted line indicates the 90% completeness limit of this field. |
| In the text | |
 |
Fig. 23. Same as Fig. 16, but with five elliptical bins. |
| In the text | |
 |
Fig. 24. Completeness-corrected PNLF for each elliptical bin fitted by both the generalised analytical formula (in blue) and the Ciardullo et al. (1989) analytical LF (in orange). The projected major-axis elliptical radii covered by each bin is indicated along with the fitted slope of the PNLF. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. 25. Completeness-corrected PNLF for PHAT-matched PNe is shown for the “likely” (blue), “possible + likely” (yellow) and “possible + likely + unlikely” (red) cases. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. 26. Completeness-corrected PNLF for the whole catalogue of M 31 PNe (black points) is shown fitted by the Ciardullo et al. (1989) analytical LF (black dotted line). The LMC (Reid & Parker 2010), SMC (Jacoby & De Marco 2002), and MW Bulge PNe (Kovacevic et al. 2011) shifted to the distance of M 31 are shown in blue, orange, and green, respectively. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. 27. Histogram for PHAT-matched PNe is shown for the “likely” (blue), “possible + likely” (yellow) and “possible + likely + unlikely” (red) cases. The histogram of possible SySts are shown in black. |
| In the text | |
 |
Fig. 28. Completeness-corrected PNLF for PHAT-matched PNe with the contribution from SySts removed is shown in black. The completeness-corrected PNLF for only those PNe with F475W–F814W < 0 is shown in blue. The PNLF for the observed PHAT-matched PNe with F475W–F814W < 0 is shown in red. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. 29. Fraction of PNe targeted with spectroscopic observations where a narrow [O III] 5007 Å emission line was detected. The uncertainty in detection fraction is the binomial proportion confidence-interval of observed PNe in any magnitude bin obtained using the Wilson score interval method (Wilson 1927). The blue dashed line shows the 50% detection limit of the spectroscopic follow-up. |
| In the text | |
 |
Fig. 30. Completeness-corrected PNLF for all PNe (in black) fitted by both the generalised analytical formula for the cumulative PNLF (in orange) and the cumulative PNLF corresponding to the Ciardullo et al. (1989) analytical formula (in blue). The completeness-corrected PNLF accounting for the detection fraction from spectroscopy is shown in blue. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. The blue dashed line shows the 50% detection limit of the spectroscopic follow-up. |
| In the text | |
 |
Fig. A.1. Recovery of the input magnitude of simulated sources using different SExtractor aperture widths, AW, for a single field. |
| In the text | |
 |
Fig. A.2. For the entire survey the number of PNe in each magnitude bin (in black), and the completeness corrected number (in blue) for a single field. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. A.3. Completeness-corrected PNLF for PHAT-matched PNe within (left) and outside (right) 0.3 deg of the centre of M 31 is shown for the “likely” (blue), “possible + likely” (yellow), and “possible + likely + unlikely” (red) cases. The region beyond the limiting magnitude of the shallowest field (Field# 33_4) is shown in grey. The grey dotted line shows the 90% completeness limit of the shallowest field. |
| In the text | |
 |
Fig. A.4. F110W mag of the PHAT-matched PNe plotted against its F110W−F160W colour. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red, respectively. The PNe previously found by M06 are ringed in black. |
| In the text | |
 |
Fig. A.5. F275W mag of the PHAT-matched PNe plotted against its F275W−F336W colour. The “likely”, “possible”, and “unlikely” PNe are shown in blue, yellow, and red, respectively. The PNe previously found by M06 are ringed in black. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



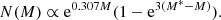
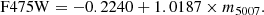
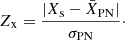
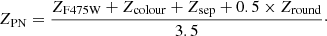
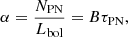
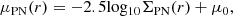
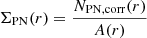
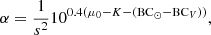
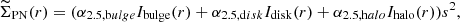
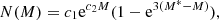
![$$ \begin{aligned} I(M)&=c_1\mathrm{e}^{c_2M}\left[\frac{1}{c_2}\mathrm{e}^{c_2M}+\frac{1}{3-c_2}\mathrm{e}^{3(M^{*}+\mu )-(3-c_2)M}\right.\nonumber \\&\left.\qquad \qquad \quad -\left(\frac{1}{c_2}+\frac{1}{3-c_2}\right)\mathrm{e}^{c_2(M^{*}+\mu )}\right]\cdot \end{aligned} $$](/articles/aa/full_html/2019/04/aa34579-18/aa34579-18-eq19.gif)
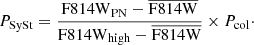
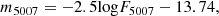
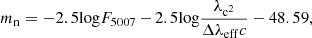
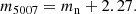
![$$ \begin{aligned} f(r,\alpha ,\beta )=\frac{\beta -1}{\pi \alpha }\left[1+\left(\frac{r}{\alpha }\right)^2\right]^{-\beta }. \end{aligned} $$](/articles/aa/full_html/2019/04/aa34579-18/aa34579-18-eq30.gif)