| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 9 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201834060 | |
| Published online | 25 February 2019 | |
Comparison of results on Neff from various Planck likelihoods
LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
e-mail: versille@lal.in2p3.fr
Received:
9
August
2018
Accepted:
29
November
2018
In this paper, we study the estimation of the effective number of relativistic species from a combination of cosmic microwave background (CMB) and baryon acoustic oscillations (BAO) data. We vary different ingredients of the analysis: the Planck high-ℓ likelihoods, the Boltzmann solvers, and the statistical approaches. The variation of the inferred values gives an indication of an additional systematic uncertainty, which is of the same order of magnitude as the error derived from each individual likelihood. We show that this systematic uncertainty is essentially associated to the assumptions made in the high-ℓ likelihood implementations, in particular for the foreground residuals modellings. We also compare a subset of likelihoods using only the TE power spectra, expected to be less sensitive to foreground residuals.
Key words: cosmological parameters
© ESO 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The expansion rate in the early universe depends on the energy density of relativistic particles, which is parameterised by Neff, the effective number of relativistic species or degrees of freedom. According to the standard model (SM) of particle physics, Neff should only receive contributions from the three neutrino species. Due to residual interactions, as the neutrinos were not completely decoupled during the electron-positron annihilation, Neff is expected to be equal to 3.045 (de Salas & Pastor 2016).
Any deviation from the SM value can be attributed to extra relativistic radiation in the early universe. This can be, for example, massless sterile neutrino species (Hamann et al. 2010), axions (Melchiorri et al. 2007; Hannestad et al. 2010), decay of non-relativistic matter (Fischler & Meyers 2011), gravitational waves (Smith et al. 2006; Henrot-Versillé et al. 2015), extra dimensions (Binetruy et al. 2000; Shiromizu et al. 2000; Flambaum & Shuryak 2006), early dark energy (Calabrese et al. 2011), asymmetric dark matter (Blennow et al. 2012), or leptonic asymmetry (Caramete & Popa 2014). Accurately measuring Neff is therefore of particular interest not only to constrain neutrino physics but also any other process that changes the expansion history.
Any variation of the expansion rate of the universe affects the cosmic microwave background (CMB) power spectra by changing the relative scales of the Silk damping relative to the sound horizon (see e.g. Abazajian et al. 2015). Therefore, the current best constraint on Neff comes from the accurate measurements of the temperature and polarisation anisotropies performed by Planck.
In this paper we discuss in detail the estimation of Neff from CMB data and quantify the dependence of the results on the choices made in the analysis. We investigate different possible sources of systematic errors. We first compare the results obtained using two Boltzmann codes: CAMB (Lewis et al. 2000) and CLASS (Blas et al. 2011). We then use three different Planck high-ℓ likelihoods. We also discuss the statistical analysis, comparing the frequentist and Bayesian approaches, to pinpoint any remaining volume effects. We show that varying the above-listed ingredients leads to a non-negligible spread of the mean Neff values.
The paper is organised as follows. In Sect. 2, we introduce the datasets, the Planck likelihoods, the Boltzmann codes, and the statistical analysis. In Sect. 3, we quantify the effect of possible sources of systematic error on Neff using the combination of temperature and polarization CMB data (TT + TE + EE) together with baryon acoustic oscillation (BAO) data. In Sect. 4, we compare the results obtained with the CMB TT and TE power spectra. The conclusions are given in Sect. 5.
2. Phenomenology and methodology
2.1. Introduction
Neff relates the radiation (Ωrad) and the photon (Ωγ) energy densities relative to the critical density through:
Under the assumption that only photons and standard light neutrinos contribute to the radiation energy density, Neff is equal to the effective number of neutrinos: Neff ≃ 3.045. This value has been derived from the number of neutrinos constrained by the measurement of the decay width of the Z boson (Beringer 2012), and takes into account residual interactions during the electron-positron annihilation.
2.2. Data sets and likelihoods
The datasets and likelihoods used in this paper are summarized together with their corresponding acronyms in Table 1. Several high-ℓ (respectively low-ℓ) likelihoods have been derived from the Planck 2015 data (Planck Collaboration XI 2016; Couchot et al. 2017a; Planck Collaboration Int. XLVII 2016) and are further described in Sect. 2.2.2 (respectively Sect. 2.2.1). The BAO data are also discussed in Sect. 2.2.3.
Summary of keywords, data, and likelihoods together with their corresponding acronyms used in this paper.
2.2.1. Low-ℓ likelihoods
At low multipoles (ℓ < 50), the Planck public likelihood is lowTEB, based on Planck Low Frequency Instrument (LFI) maps at 70 GHz for polarization and a component-separated map using all Planck frequencies for temperature (Commander Planck Collaboration XI 2016).
In the following, we also test a combination of the Lollipop likelihood (Mangilli et al. 2015) with Commander in place of lowTEB, following what has been done for the latest Planck results on the reionisation optical depth (Planck Collaboration Int. XLVII 2016).
2.2.2. High-ℓ likelihoods
At high multipoles (ℓ > 50), different likelihoods were developed within the Planck collaboration: Plik (Planck Collaboration XI 2016) being the one delivered to the community. Their implementations are further detailed in this section. Since there is no valuable reason to favour one implementation over another, we use them in the following to assess the impact of the various ingredients entering their derivation on the Neff inferred value. We consider Plik, CamSpec (Planck Collaboration XI 2016), and HiLLiPOPps.
All these likelihoods are based on pseudo-Cℓ cross-spectra between Planck High Frequency Instrument (HFI) half-mission maps at 100, 143, and 217 GHz (for more details, see Planck Collaboration XI 2016). The main differences are listed below:
Data.HiLLiPOPps makes use of all 15 cross-spectra from the six half-mission maps whereas Plik and CamSpec remove the 100 × 143 and 100 × 217 correlations together with two of the four 143 × 217 cross-spectra (for temperature data only). To avoid residual contamination from dust emission, HiLLiPOPps and CamSpec do not use the multipoles below 500 for the 143 × 217 and 217 × 217 cross-spectra.
Masks. The Galactic masks used in temperature are very similar. Still, HiLLiPOPps relies on a more refined procedure for the point-source masks that preserves Galactic compact structures and ensures the completeness level at each frequency, but with a higher detection threshold (thus leaving more extra-Galactic diffuse sources as residuals). In polarization, CamSpec uses a cut in polarization amplitude (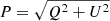 ) to define diffuse Galactic polarization masks whereas HiLLiPOPps and Plik use the same masks as in temperature.
) to define diffuse Galactic polarization masks whereas HiLLiPOPps and Plik use the same masks as in temperature.
Covariance matrix. The approximations used to calculate the covariance matrix which encompasses the ℓ-by-ℓ correlations between all the cross-power spectra are slightly different. Plik and CamSpec assume a model for signal (from cosmological and astrophysical origin) and noise (with slight differences in the methods used to estimate noise). In HiLLiPOPps, it is estimated semi-analytically with Xpol (a polarized version of the power spectrum estimator described in Tristram et al. 2005) using a smoothed version of the estimated spectra (Couchot et al. 2017a).
Galactic dust template.HiLLiPOPps uses templates for the Galactic dust emission derived from Planck measurements both for the shape of the power spectra (Planck Collaboration Int. XXX 2016) and for the spectral energy distribution (SED; Planck Collaboration Int. XXII 2015), rescaled by one amplitude for each polarisation mode (TT, EE and TE). In contrast, due to Galactic cirrus residuals that are included in their point-source masks, Plik and CamSpec have to rely on an empirical fit of the spectrum mask difference at 545 GHz and fit one amplitude for each of the cross-frequency spectra with priors on the amplitude based on a power-law (with slightly different spectral index: −2.63 for Plik and −2.7 for CamSpec). In polarization, CamSpec compresses all the frequency combinations of TE and EE spectra into single TE and EE spectra (weighted by the inverse of the diagonals of the appropriate covariance matrices), after foreground cleaning using the 353 GHz maps. As a consequence, CamSpec has no nuisance parameters describing polarized Galactic foregrounds.
SZ template. The template spectra for thermal Sunyaev-Zeldovich (SZ) effect residuals is based on a model for Plik and CamSpec; whereas it comes directly from Planck measurements in the case of HiLLiPOPps.
Point-source template.HiLLiPOPps includes a two-component point-source model (including infrared dusty galaxies and extragalactic radio sources) with one amplitude for each component and a fixed SED whereas all the other likelihoods fit one point-source amplitude for each cross-frequency. We also consider a version which fits one point-source amplitude per cross-spectrum (as what is done in Plik), labelled HiLLiPOP.
The results obtained with those high-ℓ likelihoods have been compared in Planck Collaboration XI (2016) when combined with a prior on the optical depth to reionization (τreio). It was shown that the ΛCDM parameters derived from temperature data were very compatible. Still, as described in Couchot et al. (2017b), when combining them with lowTEB, a disagreement was observed, especially on τreio and As (the initial super-horizon amplitude of curvature perturbations at k = 0.05 Mpc−1). This was shown to be related to a discrepancy on the AL fitted value: AL is a phenomenological parameter that was first introduced in Calabrese et al. (2008) to cross-check the consistency of the data with the ΛCDM model. Further studies on the impact of those differences on the measurement of the sum of the neutrino mass were also performed in Couchot et al. (2017c).
In the following we investigate the systematic effects hidden in the assumptions made for the derivation of those likelihoods. As the use of a single likelihood does not ensure the full propagation of errors, we base our analysis on a comparison of the results inferred from each of them and estimate the order of magnitude of the related errors.
2.2.3. Baryon acoustic oscillation (BAO) data
Information on the late-time evolution of the universe geometry is also included. In this work, we use the acoustic-scale distance ratio DV(z)/rdrag measurements from the 6dF Galaxy Survey at z = 0.1 (Beutler et al. 2014).
DV(z) is a combination of the comoving angular diameter distance DM(z) and Hubble parameter H(z) according to:
and rdrag is the comoving sound horizon at the end of the baryonic-drag epoch. At higher redshift, we have also included the BOSS DR12 BAO measurements (Alam et al. 2017). They consist in constraints on (DM(z),H(z),f(z)σ8(z)) in three redshift bins, which encompass both BOSS-LowZ and BOSS-CMASS DR11 results. The factor σ8(z) gives the normalization of the linear theory matter power spectrum at redhift z on 8 h−1 Mpc scales and f(z) is the derivative of the logarithmic growth rate of the linear fluctuation amplitude with respect to the logarithm of the expansion factor. The combination of those measurements is labelled BAO in the following. We note that this is an update of the BAO data with respect to those used in Planck Collaboration XIII (2016).
2.3. Statistics and Boltzmann codes
We use the CAMEL software1 (Henrot-Versillé et al. 2016) tuned to a high precision setting to perform the statistical analysis. It allows us to compare both the frequentist (profile likelihoods) and the Bayesian approaches. CAMEL includes a MCMC algorithm based on the Adaptative Metropolis method (Haario et al. 2001). It also encapsulates the CLASS Boltzmann solver (Blas et al. 2011). The CLASS and CAMB softwares have been extensively compared (Lesgourgues 2011), and lead to very close predictions in terms of CMB spectra. Still, the public Planck results are derived using CAMB: their comparison with the ones derived with CAMEL allows us to cross-check the compatibility of the theoretical predictions while fitting for Neff.
For both setups, we are using the model of Takahashi et al. (2012) extended to massive neutrinos as described in Bird et al. (2012) to include non-linear effects on the matter power spectrum evolution. We have used the big-bang nucleosynthesis (BBN) predictions calculated with the PArthENoPE code (Consiglio et al. 2018) updated to the latest observational data on nuclear rates and assuming a neutron lifetime of 880.2 s, identical to the standard assumptions made in Planck Collaboration XIII (2016).
For ΛCDM, we assume that all the neutrino mass (Σmv = 0.06 eV) is carried out by only one heavy neutrino. Considering current knowledge of the neutrino sector (Tanabashi et al. 2018), we do not yet have access to a measurement of the individual masses. Two mass hierarchy scenarios are therefore considered in the literature: the normal hierarchy with m1 < m2 ≪ m3 and the inverted hierarchy with m3 ≪ m1 < m2, where mi (i = 1; 2; 3) denotes the neutrino mass eigenstates. In this paper, we have also performed fits with three neutrinos with a mass splitting scheme derived from the normal hierarchy (keeping Σmv = 0.06 eV) and obtain identical results.
We illustrate in Fig. 1 the relative variations of the temperature spectra (ΔCℓ/Cℓ) between CAMB and CLASS. We show the impact of a negative shift of the Neff value in three cases: ΔNeff = −0.18 corresponding to the 1σ error reported by Planck, ΔNeff = −0.027 which is the forecasted uncertainty for the next generation “Stage-4” ground-based CMB experiment, CMB-S4 (Abazajian et al. 2016), and ΔNeff = −0.01 which is close to the CAMB/CLASS difference. The non-linear effects have been deliberately neglected to produce this figure.
 |
Fig. 1. Relative variations of the predicted temperature spectra between CLASS and CAMB (blue). We also compare the spectra when we shift Neff toward negative values for ΔNeff = −0.18 (red), ΔNeff = −0.027 (black), and ΔNeff = −0.01 (green) with CLASS (θ is fixed, H0 is therefore recalculated). |
3. TT+TE+EE+BAO results
In this section, we discuss the results obtained with the combination of Planck TT+TE+EE (so-called ALL) likelihoods together with BAO data. They are given in Table 2, and are classified according to various kinds of systematic errors. Each of them is further discussed in a dedicated subsection below: we first assess the impact of the choice of the Boltzmann solver, then we discuss the impact of the choice of the high-ℓ likelihood. Finally we compare the results using different statistical analysis.
Results on Neff obtained when combining PlikALL, hlpALL and hlpALLps with BAO.
All the values which are tagged with a ♯ are extracted from the PLA.
3.1. Boltzmann code and sampler effects
In this subsection, we study the impact of the choice of the Boltzmann solver that is used to infer cosmological parameters. Within our setup we cannot disentangle the impact of the Boltzmann code from the one of the sampler used for the MCMC mutiparameter space exploration, as a consequence the estimation given in this section combines both effects.
The comparison of the results using Plik are given in Table 2 (line 1 and 2): the use of CLASS combined with the CAMEL MCMC sampler tends to induce slightly smaller error bars on Neff as well as a very small shift of 0.01 toward lower values when results are compared with the public Planck results; this effect is further illustrated by the difference between the black (for the public/CAMB) and the blue (for this work/CLASS) marginal distributions on cosmological parameters shown on Fig. 2 (see following section for a full description of the figure). This shift is consistent with the difference shown on Fig. 1 between spectra predicted by both Boltzmann solvers, and is largely subdominant compared to the statistical uncertainty.
 |
Fig. 2. Cosmological parameters obtained with a combination of lowTEB, BAO, and high-ℓ likelihoods: HiLLiPOP, HiLLiPOPps, Plik/CLASS, and Plik/CAMB (the chains are the ones of the PLA using CAMB). |
We also tested the effect of changing the neutrino model. We have compared the results when attributing to each of the three neutrinos a mass derived from the Normal Hierarchy scenario expectation and found a 0.01 shift of the Neff results. Given the actual precisions on the CMB spectra, we can therefore safely assume a ΛCDM model with only one massive neutrino carrying all the mass.
3.2. Likelihood comparisons
3.2.1. Results
A possible source of systematic error to be estimated is related to the choice of the Planck high-ℓ likelihood. As discussed in Sect. 2.2, various assumptions have been made to build the likelihood. The comparison of the results from each likelihood allows for the impact of the underlying assumptions to be quantified.
A discrepancy between PlikALL and CamSpecALL is already mentioned in Planck Collaboration XIII (2016), which quotes ΔNeff ≃ 0.15. Using the HiLLiPOP likelihoods, we find differences of the same order of magnitude as quoted in Table 2 (line 1 vs. lines 3, 4, 5). This variation can reach a maximum of ΔNeff ≃ 0.17.
However, as stated in Sect. 2.2, there are more data in the HiLLiPOPps likelihoods than in Plik and CamSpec. This can affect the interpretation of the shift, as part of it might be due to statistical fluctuations. To test this effect, we have derived the results using HiLLiPOP while removing the 100 × 143, 100 × 217, and two of the four 143 × 217 cross-spectra, and reducing the ℓ range (see Sect. 2.2.2): the result is quoted on line 9 and labelled HiLLiPOPps(Plik-like). We see that a small part (up to 0.03) of the value of 0.17 may be attributed to a statistical effect (including the covariance matrix determination).
3.2.2. Correlations with other parameters
In this section we investigate the correlation between Neff and the cosmological and nuisance parameters, the definition of the latter being given in Table A.1. For hlpTTps, the model for the point-source residuals is slighly different (see Sect. 2.2.2): Aradio and Adusty are respectively the amplitudes of the radio sources and the dusty galaxies (Couchot et al. 2017a). The nuisance parameters for Plik are further defined in Planck Collaboration XV (2014) and Planck Collaboration XI (2016). The cosmological parameters we infer together with Neff are the sixth parameters of the base ΛCDM model, as defined in Planck Collaboration XVI (2014), namely:
-
Ωbh2: Today’s baryon density,
-
Ωch2: Today’s cold dark matter density,
-
H0: Current expansion rate in km s−1 Mpc−1,
-
τreio: Optical depth to reionization,
-
ns: Scalar spectrum power-law index,
-
ln(1010As): Log power of the primordial curvature perturbations.
We give on Table 3 and Fig. 2 the results of the CAMEL MCMC sampler using the CLASS Boltzmann solver with PlikALL, hlpALL, and hlpALLps (combined with lowTEB and BAO) compared to the Planck public chains for Neff, plus the six ΛCDM parameters. Similarly to what is observed on Neff, we find variations of the parameters between likelihoods of the order of one sigma or less. The error bars of the HiLLiPOPps likelihoods are slightly smaller due to the additional data that are used (see Sect. 2.2.2).
Results on MCMC chains for all cosmological parameters obtained when combining the PlikALL, hlpALL, and hlpALLpsPlanck likelihoods with lowTEB and BAO.
The correlations between Neff and the nuisance parameters are illustrated on Fig. 3 for the three likelihoods (from top to bottomml: hlpALL, hlpALLps, PlikALL). For HiLLiPOP, the highest values of the coefficients are obtained for the nuisance parameters related to foregrounds which play a role at small scales: namely the point sources (with a “PS” label in the name of the parameter) and/or the SZ sector. Neff is anti-correlated to the point source parameters when the related nuisance parameters are left free to vary (as this is the case of HiLLiPOPps). Conversely, adding information in the point source model (as done in HiLLiPOPps), this relation is broken. We also observe a correlation between Neff, AkSZ (the amplitude of the kinetic SZ effect), and ASZxCIB (the amplitude of the correlation between SZ and the cosmic infrared background - CIB) but those parameters are only very slightly constrained with Planck data. For Plik, the correlation level is lower for all nuisance parameters, but the number of parameters is higher.
 |
Fig. 3. Correlation coefficients between Neff and the nuisance parameters from top to bottom for hlpALL, hlpALLps, and PlikALL when combined with BAO and lowTEB. |
3.3. Statistical analysis systematics
3.3.1. Results
In this section, we study the impact of the choice of the statistical analysis (Bayesian vs. frequentist). The main purpose of such a comparison is to check for any volume effect that may significantly impact the results (see e.g. Hamann 2012). The Neff estimates for various Planck likelihoods using profile likelihoods are given on lines 6 to 8 of Table 2. A visual comparison of the results is shown on Fig. 4, where the profile analysis results are transformed in terms of ℒ/ℒmax and are superimposed on the MCMC posterior distributions.
 |
Fig. 4. Posterior distributions of the MCMC analysis (plain lines) and Profile likelihood ratio ℒ/ℒmax (dashed lines) for hlpALL (blue), hlpALLps (red), and PlikALL (green) combined with lowTEB+BAO. |
The profile analysis results systematically lead to smaller mean values, keeping the error bars almost similar. This effect is also present in the PLA: for example, the Neff values extracted from the best-fit procedure (which is exactly what is done in a profile analysis) quoted for the PlikALL+lowTEB+BAO combination is equal to 2.996, a value which is ≃0.04 smaller than the maximum of the MCMC posterior distributions. The variation is specific to each likelihood and not expected to be constant as it reflects its very shape in the multidimensional parameter space. The higher volume effect is observed for HiLLiPOP and does not exceed ΔNeff = 0.05.
3.3.2. Statistical and nuisance error contribution
Following the procedure described in Aad (2014), we have separately estimated the two contributions to the total error: the one coming from statistics and the one linked to the foreground and instrumental modelling (so-called nuisance error). We first built the usual profiles for each likelihood: they are shown in solid lines on Fig. 5 and the corresponding results are given in lines 6 to 8 of Table 2. In a second step, we built another set of profiles, fixing the nuisance parameters to the values of the previously obtained best-fit. The errors derived from this second fit (shown by a dashed line in Fig. 5) correspond to the ultimate error one would obtain if the precise nuisance parameters were known (and they had the values given by the best-fit). Finally the nuisance error of each individual likelihood is deduced by quadratically subtracting the statistical uncertainty from the total error. The results are given in Table 4.
 |
Fig. 5. Comparison of profile likelihoods obtained for the combination of hlpALL (blue), hlpALLps (red), and PlikALL (green) together with BAO and lowTEB. The superimposed dashed profiles were obtained when fixing the nuisance parameter values to the ones obtained for the best fit of each likelihood combination. |
From the comparison of the results of hlpALLps(Plik-like) and hlpALL, we can deduce that the additional data induce a slight shift (ΔNeff = 0.03), apart from the expected reduction of the statistical error.
From the comparison of the results of hlpALLps(Plik-like) and PlikALL, we observe that the statistical error is exactly the same: giving high confidence to the fact that the impact of the different choices made in the likelihood implementation for the covariance matrix is negligible. The remaining difference, which happens to be the bigger one, comes from the effect of the foreground modelling, which impacts both the mean value and the nuisance error. The foreground modelling (but a different one) is also tested through the comparison of the results of hlpALL and hlpALLps.
3.4. Other cosmological data
We have further tested the impact of CMB Lensing on the Neff measurement and found it to be very small, as expected (cf. Planck Collaboration XIII 2016), slightly lowering the overall results by 0.01.
We have also checked that the choice of the low-ℓ likelihood had no impact on the final results (replacing lowTEB with Lollipop+Commander as stated in Sect. 2.2.1).
It must be noted that the supernova data do not help to further constrain Neff once the BAO data are used. We therefore chose not to use them in this analysis. For completeness we note that the update of the BAO data from DR11 to DR12 does not impact the constraint on Neff (Alam et al. 2017).
3.5. Summary
The results on Neff are summarized in Fig. 6. The shift of the mean values observed when using one likelihood or another is of the same order of magnitude as the error derived from each individual likelihood (ΔNeff ≃ 0.17 vs. σ(Neff) = 0.18). This shift has been shown to be mainly driven by the assumptions made for the foreground modelling. A small part of this variation (up to 0.03) has been identified as being linked to the data considered in HiLLiPOP and not in Plik. Still, it is high enough not to be neglected when constraining theoretical models from the Neff measurement only.
 |
Fig. 6. Comparison results for the combination of Planck TT+TE+EE likelihoods, with lowTEB and BAO. |
4. Fitting TT and TE separately
In the previous sections we have shown the results of the combination of temperature and polarisation CMB data. In the following, we estimate Neff for TT and TE separately to further compare the outcome of each likelihood.
4.1. TT+lowTEB+BAO results
In this section, we consider the combination of temperature-only CMB likelihoods, together with BAO data. The results are summarized in Table 5 for various configurations. For this specific combination the CamSpec results are not public, and therefore we cannot use them in the comparison.
Results on Neff obtained when combining PlikTT, hlpTT, and hlpTTps with BAO.
From Table 5, we obtain ΔNeff ≃ 0.18 from the largest difference observed between hlpTT-Profile/CLASS and PlikTT♯-Profile/CLASS.
As in the previous section, we have checked that the impact of the neutrino settings is almost negligible, as well as the impact of supernovae data. In addition, the choice of the DR12 BAO data instead of DR11 has no effect.
4.2. TE+lowTEB+BAO results
Given the Planck noise level, the TE likelihoods lead to similar results to those obtained with TT on ΛCDM. In addition they are less sensitive to the foreground modellings (Galli et al. 2014; Couchot et al. 2017a). In this section we use the TE likelihood in place of the TT one and compare the results obtained on Neff when combined with lowTEB and BAO in Table 6.
Results on Neff obtained when combining BAO with PlikTE, and hlpTE.
The remaining ΔNeff is of the order of 0.07, which is small with respect to the total error with TE only. It may still contain some residual systematic uncertainty from temperature to polarisation leakage, the study of which is beyond the scope of this paper.
5. Conclusions
We have studied in detail the estimation of the effective number of relativistic species from CMB Planck data. We have tested different ingredients of the analysis to further quantify their impact on the results: mainly the Boltzmann codes, the high-ℓ likelihoods (Plik, HiLLiPOPps and CamSpec), and the statistical analysis.
-
The estimated variation of Neff when switching from CAMB to CLASS is negligible: of the order of ΔNeff = 0.01.
-
If we can safely neglect the impact of the covariance matrix estimation, as suggested by the obtained results, the variation linked to the assumptions on foreground residuals modelling derived from the comparison of the high-ℓ likelihoods has been estimated to be of the order of ΔNeff = 0.17, of which a small part (up to 0.03) may be attributed to a statistical effect. We have also shown that, at least for HiLLiPOP, Neff was mainly correlated with nuisance parameters linked to foregrounds playing a role at small scales (i.e. point sources and SZ).
-
We have found slight differences between the Bayesian and the frequentist inferred mean values, linked to particular likelihood volume effects. A shift between both methods has been estimated to be ΔNeff ≤ 0.05.
As an overall conclusion, we have shown that the variation of the mean Neff values is non-negligible. This foreground related systematic uncertainty is of the same order of magnitude as the error derived for each individual likelihood. In addition the results obtained with HiLLiPOP and CamSpec lead systematically to lower values than the ones derived from the public Planck likelihood.
We have cross-checked the consistency of the results when considering TT and TE separately. When considering TE only (together with BAO and lowTEB), which is less sensitive to foreground residuals, this observed variation drops down to ΔNeff = 0.05 for the likelihoods we have been able to compare.
We have shown that likelihood modelling is an important challenge for the current Planck measurements for the Neff interpretation, even for temperature data. The shift discussed in this paper is very large compared to the σ(Neff) = 0.027 statistical-only expectations for CMB-S4. However, we expect data from the next generation of CMB experiments to be more robust to such systematic error. The increase in constraining power from the TE power spectrum with respect to the TT one, as well as the better determination of the temperature power spectrum on small scales, will reduce the impact of foreground mismodelling.
References
- Aad, G., Abbott, B., Abdallah, J., et al. 2014, Phys. Rev. D, 90, 052004 [NASA ADS] [CrossRef] [Google Scholar]
- Abazajian, K. N., Arnold, K., Austermann, J., et al. 2015, Astropart. Phys., 63, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, CMB-S4 Science Book, First Edition [CrossRef] [Google Scholar]
- Alam, S., Ata, M., Bailey, S., et al. 2017, MNRAS, 470, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- Beringer, J., Arguin, J.-F., Barnett, R. M., et al. 2012, Phys. Rev. D, 86, 010001 [Google Scholar]
- Beutler, F., Saito, S., Brownstein, J. R., et al. 2014, MNRAS, 444, 3501 [NASA ADS] [CrossRef] [Google Scholar]
- Binetruy, P., Deffayet, C., Ellwanger, U., & Langlois, D. 2000, Phys. Lett. B, 477, 285 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bird, S., Viel, M., & Haehnelt, M. G. 2012, MNRAS, 420, 2551 [NASA ADS] [CrossRef] [Google Scholar]
- Blas, D., Lesgourgues, J., & Tram, T. 2011, JCAP, 7, 034 [NASA ADS] [CrossRef] [Google Scholar]
- Blennow, M., Fernandez-Martinez, E., Mena, O., Redondo, J., & Serra, P. 2012, JCAP, 1207, 022 [NASA ADS] [CrossRef] [Google Scholar]
- Calabrese, E., Slosar, A., Melchiorri, A., Smoot, G. F., & Zahn, O. 2008, Phys. Rev. D, 77, 123531 [NASA ADS] [CrossRef] [Google Scholar]
- Calabrese, E., Huterer, D., Linder, E. V., Melchiorri, A., & Pagano, L. 2011, Phys. Rev. D, 83, 123504 [NASA ADS] [CrossRef] [Google Scholar]
- Caramete, A., & Popa, L. 2014, JCAP, 1402, 012 [NASA ADS] [CrossRef] [Google Scholar]
- Consiglio, R., de Salas, P. F., Mangano, G., et al. 2018, Comput. Phys. Commun., 233, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Couchot, F., Henrot-Versillé, S., Perdereau, O., et al. 2017a, A&A, 602, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Couchot, F., Henrot-Versillé, S., Perdereau, O., et al. 2017b, A&A, 597, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Couchot, F., Henrot-Versillé, S., Perdereau, O., et al. 2017c, A&A, 606, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Salas, P. F., & Pastor, S. 2016, JCAP, 7, 051 [NASA ADS] [CrossRef] [Google Scholar]
- Fischler, W., & Meyers, J. 2011, Phys. Rev. D, 83, 063520 [NASA ADS] [CrossRef] [Google Scholar]
- Flambaum, V., & Shuryak, E. 2006, Europhys. Lett., 74, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, S., Benabed, K., Bouchet, F., et al. 2014, Phys. Rev. D, 90, 063504 [NASA ADS] [CrossRef] [Google Scholar]
- Haario, H., Saksman, E., & Tamminen, J. 2001, Bernoulli, 7, 223 [CrossRef] [MathSciNet] [Google Scholar]
- Hamann, J. 2012, JCAP, 3, 021 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, J., Hannestad, S., Raffelt, G. G., Tamborra, I., & Wong, Y. Y. Y. 2010, Phys. Rev. Lett., 105, 181301 [CrossRef] [Google Scholar]
- Hannestad, S., Mirizzi, A., Raffelt, G. G., & Wong, Y. Y. 2010, JCAP, 1008, 001 [NASA ADS] [Google Scholar]
- Henrot-Versillé, S., Perdereau, O., Plaszczynski, S., et al. 2015, Class. Quant. Grav., 32, 045003 [NASA ADS] [CrossRef] [Google Scholar]
- Henrot-Versillé, S., Perdereau, O., Plaszczynski, S., et al. 2016, ArXiv e-prints [arXiv:1607.02964] [Google Scholar]
- Lesgourgues, J. 2011, ArXiv e-prints [arXiv:1104.2934] [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [Google Scholar]
- Mangilli, A., Plaszczynski, S., & Tristram, M. 2015, MNRAS, 453, 3174 [NASA ADS] [CrossRef] [Google Scholar]
- Melchiorri, A., Mena, O., & Slosar, A. 2007, Phys. Rev. D, 76, 041303 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XV. 2014, A&A, 571, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2016, A&A, 594, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXII. 2015, A&A, 576, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXX. 2016, A&A, 586, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVII. 2016, A&A, 596, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shiromizu, T., Maeda, K.-I., & Sasaki, M. 2000, Phys. Rev. D, 62, 024012 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, T. L., Pierpaoli, E., & Kamionkowski, M. 2006, Phys. Rev. Lett., 97, 021301 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, R., Sato, M., Nishimichi, T., Taruya, A., & Oguri, M. 2012, ApJ, 761, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Tanabashi, M., Hagiwara, K., Hikasa, K., et al. 2018, Phys. Rev. D, 98, 030001 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, M., Macías-Pérez, J. F., Renault, C., & Santos, D. 2005, MNRAS, 358, 833 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Appendix on nuisance parameters
This appendix presents the nuisance parameters of the HiLLiPOPps likelihood in Table A.1.
Nuisance parameters for the HiLLiPOPps likelihood.
All Tables
Summary of keywords, data, and likelihoods together with their corresponding acronyms used in this paper.
Results on MCMC chains for all cosmological parameters obtained when combining the PlikALL, hlpALL, and hlpALLpsPlanck likelihoods with lowTEB and BAO.
All Figures
 |
Fig. 1. Relative variations of the predicted temperature spectra between CLASS and CAMB (blue). We also compare the spectra when we shift Neff toward negative values for ΔNeff = −0.18 (red), ΔNeff = −0.027 (black), and ΔNeff = −0.01 (green) with CLASS (θ is fixed, H0 is therefore recalculated). |
| In the text | |
 |
Fig. 2. Cosmological parameters obtained with a combination of lowTEB, BAO, and high-ℓ likelihoods: HiLLiPOP, HiLLiPOPps, Plik/CLASS, and Plik/CAMB (the chains are the ones of the PLA using CAMB). |
| In the text | |
 |
Fig. 3. Correlation coefficients between Neff and the nuisance parameters from top to bottom for hlpALL, hlpALLps, and PlikALL when combined with BAO and lowTEB. |
| In the text | |
 |
Fig. 4. Posterior distributions of the MCMC analysis (plain lines) and Profile likelihood ratio ℒ/ℒmax (dashed lines) for hlpALL (blue), hlpALLps (red), and PlikALL (green) combined with lowTEB+BAO. |
| In the text | |
 |
Fig. 5. Comparison of profile likelihoods obtained for the combination of hlpALL (blue), hlpALLps (red), and PlikALL (green) together with BAO and lowTEB. The superimposed dashed profiles were obtained when fixing the nuisance parameter values to the ones obtained for the best fit of each likelihood combination. |
| In the text | |
 |
Fig. 6. Comparison results for the combination of Planck TT+TE+EE likelihoods, with lowTEB and BAO. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



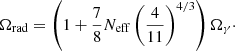
![$$ \begin{aligned} D_{\mathrm{V}}(z) = \left[D^{2}_{\mathrm{M}}(z) \frac{cz}{H(z)}\right]^{1/3}, \end{aligned} $$](/articles/aa/full_html/2019/03/aa34060-18/aa34060-18-eq3.gif)