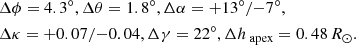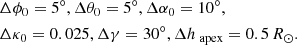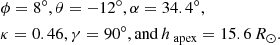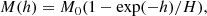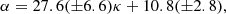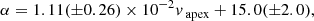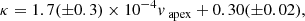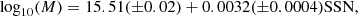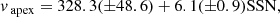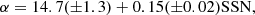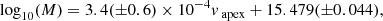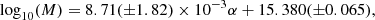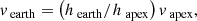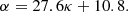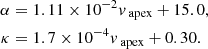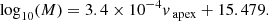EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 623 (March 2019) A&A, 623 (2019) A139 Full HTML
Free Access
Issue
A&A
Volume 623, March 2019
Article Number A139
Number of page(s) 11
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201833829
Published online 21 March 2019

© ESO 2019

1. Introduction

Coronal Mass Ejections (CMEs) are explosive large-scale outbursts of the Sun’s coronal plasma and magnetic field. They can induce strong geomagnetic storms at Earth (Tsurutani et al. 1988; Gosling et al. 1991), which pose serious threats to space systems, communications and navigation (Cherry 2002; Thomson et al. 2011; Pulkkinen et al. 2005; Burlaga et al. 1987). Therefore, precise measurements of CME kinematics are important to predict their arrival at Earth. Besides knowledge about the prevailing solar wind conditions, the performance of CME propagation models relies on accurate measurements of the CME initial geometry and CME apex speed as well as the CME mass. For example, the Drag-Based Model (DBM; Vršnak et al. 2013), which is based on the hydrodynamic analogue of the aerodynamic drag acting between the solar wind and the CME, depends on these properties. To maximise the benefit for space weather predictions, CME kinematics and geometry have to be determined as early as possibly during the CME emergence. Coronagraph observations can provide these values at CME distances within a few solar radii away from the Sun. CMEs are optically thin structures because the observed brightness arises from the Thompson scattering of the photospheric lights from the entrained electrons (Billings 1966). Hence, they are subject to projections effects due to (1) structure overlap along the line of sight, and (2) due to the viewing geometry (e.g. Vourlidas & Howard 2006). We use the term “projection effects” to refer to both effects in this paper. Projection effects are discussed often in the context of CME kinematics (Burkepile et al. 2004; Vršnak et al. 2007; Temmer et al. 2009; Liu et al. 2010a; Shen et al. 2013; Davies et al. 2013), masses (Vourlidas et al. 2010) and morphologies (Liu et al. 2010b; Savani et al. 2011a,b; Vourlidas et al. 2013; Kwon et al. 2015). The Thompson scattering projection effects can result in an overestimation of the CME size and an underestimation of the CME velocity. The effects on the mass determination depend on the chosen approach and are discussed in more detail in Sect. 3.3. These Thomson scattering effects become extreme for the so-called “halo events”. The term “halo” refers to CMEs that exhibit a circular or elliptical white-light morphology encircling the Sun (Howard et al. 1982). The halo appearance generally implies that the event is directed along the Sun-observer line and most likely arise from the CME-driven shock (Kwon et al. 2015). We adopt the term “disk events” to characterise events originating from close to an observer’s solar disk centre, propagating along the Sun-observer line towards or away to the observer. The kinematic and morphological characteristics of disk events, such as the height, width and propagation speed suffer from severe projection effects. These projection effects have been assessed via multi-viewpoint geometrical modelling (Thernisien et al. 2009; Liewer et al. 2011; Temmer et al. 2009; Lee et al. 2014).

With the launch of NASA’s Solar TErrestrial Relations Observatory (STEREO) mission in the October 2006 (Kaiser et al. 2008) long-term multi-viewpoint observations of CMEs have been made possible. The STEREO mission consists of two nearly identical spacecraft. The STEREO-A orbit is closer to the Sun than the STEREO-B orbit, which results in STEREO-A pulling further ahead of Earth and STEREO-B falling successively behind Earth at a rate of about 22.5° per year. Each spacecraft carries the Sun-Earth Connection Coronal and Heliospheric Investigation (SECCHI; Howard et al. 2008) payload that consists of one extreme ultraviolet (EUV) full disk imager, two coronagraphs – COR1 and COR2, and two heliospheric imagers – HI1 and HI2. In this work, the white-light images of the SECCHI/COR2 coronagraphs are used for the geometrical modelling as well as for the CME mass determination. The CME mass is derived from the total electron content which is estimated from the CME brightness. It requires the consideration of the CME geometry as well as the direction of propagation. Vourlidas et al. (2010, V10, hereafter) discuss extensively the methodology, caveats, and historical background of mass measurements. They specifically exclude halo events from the analysis, to avoid significant mass overestimations resulting from projection effects for single viewpoint measurements. The objective of the present study is to analyse the reliability of CME mass-determinations in the context of projection effects using multi-viewpoint measurements. To achieve this goal, we combine multi-viewpoint geometrical modelling with mass-determination and compare the mass results for disk and limb events to identify possible sources of mass overestimation. Our approach is also used to provide important CME parameter correlations between the CME mass and the initial CME speed close to the Sun. Such correlations are important to estimate CME masses in real-time, in order to make reasonable assumptions in CME prediction models, such as the DBM or WSA-ENLIL plus Cone Model (Odstrčil & Pizzo 1999; Odstrcil et al. 2004; Mays et al. 2015). For instance, in the DBM the CME deceleration increases inversely with the CME mass.

The paper is organised as follows: In Sect. 2, we present our measurement methodology in detail. This includes event selection criteria, image processing, application of geometrical forward modelling and the CME mass determination technique. We use an example event to demonstrate the methodology. In Sect. 3, we provide a statistical analysis of the data set. The results are discussed in Sect. 4 and compared to previous single-viewpoint studies. We conclude in Sect. 5.

2. Methodology

2.1. Event selection

We model 122 CME events, which occurred between January 2007 and December 2013, using data from the SECCHI/COR2 coronagraphs. The STEREO satellite geometry for the observed events is presented in Fig. 1. All events are assembled in the Coronal Mass Ejection Kinematic Database Catalogue (KinCat). As part of the more comprehensive HELCATS catalogue (Harrison et al. 2016), KinCat is cross-linked via a unique identifier (ID) to other sub-catalogues. This includes catalogues of heliospheric observations, in situ and automated coronagraphic detections as well as source regions and low coronal events. The full HELCATS catalogue1 and the KinCat catalogue2 are accessible online.

thumbnail Fig. 1.

Evolution of STEREO spacecraft separation from the first catalogue event, over the STEREO opposition phase to the last event. The shown minimal STEREO separation (MSS) angle σ is defined as the minimal angular distance between both STEREO satellites (STEREO Science Center; https://stereo-ssc.nascom.nasa.gov/where/).

In addition to kinematic, geometric and mass parameters, KinCat also provides animated fitting sequences, height-time profiles and the STEREO observing geometry for each event. It is based on the first multi-viewpoint CME catalogue, compiled at the University of Göttingen. The catalogue contains 1060 events from 2007 to 2011 and a subset of 263 events was selected based on subjective clear visibility and assembled in the “Best-of” list. From this list, 243 events were modelled (Bosman & Bothmer 2012; Bosman et al. 2012) with GCS modelling technique developed by Thernisien et al. (2006) at the point in time of their clearest visual appearance. Starting from the 243 events, we compare them with the Rutherford Appleton Laboratory Heliospheric Imager (RAL-HI) event-list which contains over 1000 entries within the relevant time period. This step ensures that our events can also be used for more comprehensive studies which follows the purpose of the HELCATS project. As a result of the comparison, 109 events out of 243 events were matched with the HI list. The list is extended by another 13 events between 2012 and 2013. These events are associated with Earth-directed CMEs and are chosen from the HELCATS linked catalogue called LINKCAT (Kilpua et al. 2017) which connects heliospheric and in-situ CME observations. All of our events are isolated, well-defined CME events and we have not observed any obvious signs of interactions with other events within the COR2 field of view.

2.2. Data processing

We start with the COR2 Level−0.5 FITS images, which are obtained from the NASA Goddard Space Flight Center3. Level−0.5 FITS images are already aligned to the ecliptic north. They are further processed to Level−1.0 FITS images via the IDL SolarSoft routine secchi_prep.pro. The resulting images are normalised by the exposure duration, the correction of on-board image processing, the subtraction of the CCD bias, the conversion to the physical units of mean solar brightness (MSB), vignetting and flat-field corrections and other optical distortion corrections (Howard et al. 2008). Then a suitable pre-event image, generally the last image prior to the appearance of the CME in the particular coronagraph’s field of view, is subtracted from the CME images to remove the background corona. In order to avoid visual signatures of coronal streamers and other CMEs, it can sometimes be reasonable to subtract an earlier image instead (see V10 for details). We then apply Thomson scattering theory to Level−1.0 FITS images to create so called “mass images”. This translation of the images from the unit of MSB to grams per pixel is realised with the make_mass_fits.pro routine of the Solarsoft library. The exact procedure is described in Savani et al. (2013). Details and issues arising in the CME mass calculations are described in V10. For completeness we provide a brief summary below.

Obviously, all CME white-light observations are projections of the 3-dimensional CME structures onto the POS of the observing instrument. Two basic geometrical approximations are traditionally applied that result in a lower limit estimate of the CME mass:

  1. All CME material is confined onto a 2-dimensional plane along the direction with the longitudinal angle ϕ away from the POS.

  2. The plane is assumed to be positioned on the POS (ϕ = 0°).

V10 analysed the consequences from both assumptions and showed that the POS assumption yields a lower limit mass estimation. The underestimation increases with the CME width and reaches a factor of two for a CME with 60° angular width. In this work, we call this approach “POS mass determination”. V10 also numerically analysed the results of the applied scattering theory for the case where ϕ is equal to the actual longitudinal CME propagation angle away from the POS. They found that this improves the accuracy of the mass measurements relative to POS mass determination up to a propagation angle of ϕ = 60°. From there on, the CME mass becomes exponentially overestimated with increasing ϕ. In the case of a CME propagating at ϕ = 80° (disk event) and possessing a width of 60°, the CME mass could be overestimated by about a factor of five. For that reason, this approach can be used to determine an upper limit of the CME mass, in particular for disk events. In this study, we call this approach “directional mass determination”. Previous stereoscopic mass studies by Colaninno & Vourlidas (2009); Bein et al. (2013) and de Koning (2017) are not combined with geometrical modelling. They use an inverse approach by comparing the mass results in dependance of the unknown propagation angle ϕ for each coronagraph and deliver the correspondent mass result to that angle. In this study ϕ is determine from geometrical modelling, which is a very established method for this purpose.

2.3. Graduated cylindrical shell model

We apply the Graduated Cylindrical Shell (GCS) model (Thernisien et al. 2009) as our geometrical modelling method to COR2 images to derive their 3D size and direction as a function of height. The model represents a simplified geometric proxy to a magnetic flux rope topology. This CME topology has been suggested by many authors (e.g. Chen et al. 1997; Vourlidas et al. 2000; Cremades & Bothmer 2004). Recently, Vourlidas et al. (2013) have shown that it applies to at least 40% of all CMEs. It was further suggested that the absence of such a structure can likely be traced back to observational effects (Gopalswamy 2013). The shape of the model is reminiscent of a hollow croissant and the basic geometry consists of two cone shaped legs, separated by twice the half angle α and the leg height h. The circular annulus in the middle of the tube section is given by a(r)=κr, where r is the distance from the solar centre to a point of the outer edge of the shape and κ is the aspect ratio. The origin of the model is rooted at the solar centre. Its main axis enters the solar surface at a point given by longitude ϕ, latitude θ. The rotation along the main axis is described with the tilt angle γ. In the full set of GCS parameters it is common to substitute the leg height h with the apex height hapex. The GCS modelling is performed with the rtsccguicloud.pro routine in the SECCHI analysis tree of the IDL SolarSoft distribution. The routine enables us to adjust the wire grid simultaneously onto the white-light CME structures in both COR2 coronagraphs. The projection of the shape is plotted over each coronagraph image with respect to the STEREO satellite configuration, as demonstrated with the sample event in Sect. 2.5.

2.4. Geometrical modelling

The GCS model is applied to the full COR2 observation sequence which later will be also used to derive CME speeds. Further, the events from the original list are fitted at the height of their individual best white-light visibility. For our analysis, we define a reference height at which the CME properties are compared to each other, in order to reduce evolutionary effects of the CME parameters. Vourlidas et al. (2000, 2010) showed that the majority of CMEs reach a steady-state above about 10R⊙. On the other hand, our observations are restricted to the FOV of the SECCHI coronagraphs (2.5 − 15 R⊙) and the 15 min cadence. This cadence diminishes the guaranteed observation range in the worst case to around 12 R⊙, for a CME which expands along the POS with a speed of 2600 km s−1. Sachdeva et al. (2017) showed that CME acceleration largely ends within 5 R⊙ for fast events (≥900 km s−1), and between 12 and 50 R⊙ for slow events (< 900 km s−1). The study of Liu et al. (2016) has even shown that the speed of slow CMEs is nearly invariant at heights above 20 − 30 R⊙. Consequently, we can maximize the comparability of our events by choosing the latest guaranteed observation height of 12 R⊙ as our reference height. In the following we present our GCS modelling:

In the first step, the six GCS parameters are iteratively adapted until a best visual fit of the data is achieved for both STEREO COR2 coronagraphs. Images from the SOHO/LASCO coronagraphs, positioned along the Sun-Earth line, are used to confirm the direction of the CME if it is seen as halo in both STEREO satellites. In the next step, we alter the fitting between the first and last COR2 image pairs for a few times. Generally, this approach is helpful to separate the main CME shape from unambiguous parts and shock features, which both are frequently observed in coronagraph white-light images of very intense events (Vourlidas et al. 2013, 2009). In the last step, the CME parameters are adapted to the reference height.

A sensitivity analysis by Thernisien et al. (2009) evaluates the average deviation of each parameter:

Δ ϕ = 4 . 3 ° , Δ θ = 1 . 8 ° , Δ α = + 13 ° / − 7 ° , Δ κ = + 0.07 / − 0.04 , Δ γ = 22 ° , Δ h apex = 0.48 R ⊙ . $$ \begin{aligned}&\Delta \phi = 4.3^{\circ }, \Delta \theta = 1.8^{\circ }, \Delta \alpha = +13^{\circ }/{-}7^{\circ },\\&\Delta \kappa = +0.07/{-}0.04, \Delta \gamma = 22^{\circ }, \Delta h_{\text{ apex}} = 0.48\,{{R}_{\odot }}. \end{aligned} $$

Equally, we have also estimated the errors of these parameters in our data set, based on the modelling result of the first and second author for a similar subset of 15 events. The averaged error Δx0 of each GCS parameter x yields:

Δ ϕ 0 = 5 ° , Δ θ 0 = 5 ° , Δ α 0 = 10 ° , Δ κ 0 = 0.025 , Δ γ = 30 ° , Δ h apex = 0.5 R ⊙ . $$ \begin{aligned}&\Delta \phi _0=5^{\circ }, \Delta \theta _0 =5^{\circ }, \Delta \alpha _0 = 10^{\circ },\\&\Delta \kappa _0 = 0.025, \Delta \gamma = 30^{\circ }, \Delta h_{\text{ apex}}=0.5\,{{R}_{\odot }}. \end{aligned} $$

These values are in good agreement with the sensitivity analysis. Nevertheless, it has to be stated that the largest uncertainties for fitted GCS parameters arise from the misidentification of the CME shape, for example by the unintentional fitting of the CME shock or not separating the CME front from other coronal features. This might produce errors on a much larger scale which are difficult to quantify.

2.5. Combined geometrical modelling and mass determination technique

We use the event of July 12, 2012 to illustrate our combined geometrical modelling and mass determination technique on a pair of SECCHI/COR2 images. On this day, the STEREO spacecraft were 125° apart, which enables a reasonable geometrical modelling of the CME white-light shape. The described GCS fitting approach is used to derive the initial geometric parameters. Figure 2 displays the projection of the geometrical grid in both SECCHI/COR2 images. The grid is created with the following fitting parameters for the reference height of 12 R⊙:

ϕ = 8 ° , θ = − 12 ° , α = 34 . 4 ° , κ = 0.46 , γ = 90 ° , and h apex = 15.6 R ⊙ . $$ \begin{aligned}&\phi = 8^{\circ }, \theta =-12^{\circ }, \alpha = 34.4^{\circ }, \\&\kappa =0.46, \gamma =90^{\circ }, \mathrm{and}\,h_{\text{ apex}}= 15.6\,{{R}_{\odot }}. \end{aligned} $$

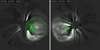thumbnail Fig. 2.

GCS model fitted onto the coronagraph images of SECCHI/COR2B (left panel) and COR2A (right panel) for the CME event on July 12, 2012 at 18.39 UT.

At this point, we create the mass images required for the directional mass determination. Savani et al. (2013) determined the CME mass density for a single event from SECCHI/COR2 images with this approach. In their study, the propagation direction in the corona was estimated by the propagation throughout the entire inner heliosphere via the fixed-ϕ J-map technique (Sheeley et al. 1999) from SECCHI/HI-1 and HI-2 observations. In our study, we can derive the CME propagation direction ϕa and ϕb in relation to the POS of STEREO A and B directly from our GCS modelling result. This step requires to transform the source region coordinates from HEE coordinate system by the respective STEREO satellite longitude. If one assumes a radial propagation of each CME from its active source region (Reiner et al. 2003; Cremades & Bothmer 2004; Kahler & Vourlidas 2005), the modelled GCS flux rope source regions can be considered as approximations of the real source regions. For the calibration of the images, we consider the positions of the GCS modelled source regions and transpose them to the correspondent SECCHI/COR2 perspectives. In Fig. 4 we give an overview of the event distribution on the solar disk observed from Earth and from both STEREO/SECCHI COR2 perspectives, determined by our GCS modelling. We want to emphasise that the absence of central backside events along the Sun-Earth line is a result of the event selection requiring the association with a SECCHI/HI CME.

Events are classified based on their minimal angular propagation distance away from the observed POS. For ϕ <  60° we classify them as limb events and for ϕ ≥ 60° as disk events.

In the following, we determine the CME masses from the STEREO images. The applicability to SECCHI/COR2 images and cross-calibration with the SOHO/LASCO mass images has been confirmed by Colaninno & Vourlidas (2009). To determine a CME mass, the region containing the CMEs white-light emission, commonly termed region of interest (ROI), has to be defined. One advantage of our method is that we can benefit from our geometrical fitting results and define the ROI by the enclosed projection of the correspondent GCS grid as shown by Savani et al. (2013). The integration over the ROI in the mass images yields a mass value. For a sequence of mass images we apply the previously modelled GCS shape and expand it self-similarly to the correspondent height (Fig. 3). The fitted height values are used for the height-time profile in Fig. 5 (top), from which we derive the apex speed at 12 R⊙. Based on the error propagation of the CME apex height, we derive that the height measurements correspond to a relative velocity error of Δv/v = 6%. In Fig. 5 (bottom) the mass-height profile of the current example is displayed. V10 suggested that the mass and energy properties of CMEs are reaching a constant plateau above ∼10 R⊙ if the POS mass determination approach is used. This is mostly, but not always the case for the directional method used in this study. Thus, we extrapolate the absolute CME mass M0 from the mass-height series. We use the fitting function from Colaninno & Vourlidas (2009), which considers that CME masses can only be detected when a CME has overcome the occulter field of above 2.5 R⊙ in COR2:

M ( h ) = M 0 ( 1 − exp ( − h ) / H ) , $$ \begin{aligned} M(h)=M_0(1-\exp (-h)/H), \end{aligned} $$(1)

thumbnail Fig. 3.

GCS fitting on a sequence of COR2A (top panel) and COR2B (bottom panel) images of the STEREO/SECCHI coronagraphs for the July 12, 2012 event from 16:54 to 18:24 UT.

thumbnail Fig. 4.

Source region distribution of all 122 KinCat events, estimated by GCS fitting and presented in the Earth-based Stonyhurst coordinate system (middle panel) as well as transposed to the perspectives of STEREO/SECCHI COR2A (right panel) and COR2B (left panel).

thumbnail Fig. 5.

GCS fitting results of the July 12, 2012 event. Top panel: height-time profile of the CME apex with the fitted apex speed v apex = 1239 km s−1 at 12 R⊙. Bottom panel: mass-height profile for both STEREO/SECCHI COR2 instruments with the extrapolated total masses Ma and Mb.

where H is a fitted normalisation height and M(h) the detected CME mass at the apex height h.

3. Results

We present the statistical results of the GCS modelling and important parameter correlations to identify projection effects. This is followed by the presentation of the CME mass results, which are further analysed in terms of mass overestimations and causes. We demonstrate that the event selection criteria created an representative data-set which can reproduce known correlations to the monthly sunspot number (SSN). Further, the correlations to SSN have a useful application when it comes to comparing different data-sets. In the last part, we regard the mutual parameter correlation and analyse if the mass of a CME can be best estimated from the CME kinematic or the CME morphology.

3.1. Morphology and kinematics

In the GCS model, the CME morphology is characterised by the aspect ratio and the half angle. We present distributions of the CME morphology together with the velocity distribution, which are derived from our data-set, in Fig. 6. All three distributions are basically reminiscent to a log-normal distribution, which is in this context also a typical parameter distribution in larger data-set (e.g. in V10). However, the CME velocities are closer to satisfy such a log-normal distribution than the two others. We obtain the averaged values of ⟨v apex⟩ = 629 km s−1, ⟨κ⟩=0.405 and ⟨α⟩=22.0° for all 122 events.

thumbnail Fig. 6.

Distribution of the GCS modelling results at 12 R⊙ for the CME apex speed (top panel), the GCS half angle (middle panel) and the GCS aspect ratio (bottom panel).

To investigate possible projection effects, we correlate all three parameters in Fig. 7 and further categorise each event based on its appearance as limb or disk event – accordingly to our previous definition. The parameter fits result in:

α = 27.6 ( ± 6.6 ) κ + 10.8 ( ± 2.8 ) , $$ \begin{aligned} \alpha&= 27.6(\pm 6.6) \kappa +10.8 (\pm 2.8) ,\end{aligned} $$(2)

α = 1.11 ( ± 0.26 ) × 10 − 2 v apex + 15.0 ( ± 2.0 ) , $$ \begin{aligned} \alpha&=1.11 (\pm 0.26)\times 10^{-2} v_{\text{ apex}}+ 15.0 ( \pm 2.0), \end{aligned} $$(3)

κ = 1.7 ( ± 0.3 ) × 10 − 4 v apex + 0.30 ( ± 0.02 ) , $$ \begin{aligned} \kappa&=1.7 (\pm 0.3)\times 10^{-4} v_{\text{ apex}}+ 0.30 ( \pm 0.02) , \end{aligned} $$(4)

thumbnail Fig. 7.

Individual results of GCS fitted aspect ratio κ and half angle α derived for all 122 catalogue events. The events are classified by their limb or disk appearance in each STEREO/SECCHI COR2 instrument.

with α in [deg], κ without dimension and vapex in [km s−1].

We notice that in Fig. 7 (top) CMEs seen as disk event in both telescopes tend to have a much large κ than the other events in the reference period. Also in Fig. 7 (bottom) all derived κ values for disk events are above the linear fitting curve. Therefore, we investigate the occurrence of projection effects by comparing the morphology of the 8 disk event, which all occurred in 2011, to all 59 events of that year. We notice that they are comparable in terms of their half angle (α2011 = 25° vs. αdisk both = 27°) but not in terms of their aspect ratio (κ2011 = 0.45 vs. κdisk both = 0.71). It appears that κ is significantly overestimated for disk events, which may be partly driven by the higher average speeds (1050 km s−1) compared to the 2011 sample (710 km s−1) in addition to projection effects.

3.2. CME mass results

In this section we show the results of our CME mass determination – averaged from both coronagraphs. In 3 out of 122 cases we have only obtained CME masses from COR2A as COR2B images were intentionally avoided, due to overlapping with coronal features, such as secondary CMEs, solar event particles or coronal streamers. At first, we present the overall distribution of the logarithmic masses in Fig. 8. According to V10, the mass distribution of CMEs should generally follow a log-normal distribution which would result in a normal distribution of the logarithmic masses.

thumbnail Fig. 8.

Distribution of the CME mass results in logarithmic units averaged from both SECCHI/COR2 measurements for 119 events and three single measurements.

In our results, we notice a departure from such a normal distribution towards larger mass values – a first indication for the mass overestimation of some events. To investigate this, we plot the logarithmic mass results of all 119 events which have been observed with both coronagraphs over the event dates in Fig. 9. The events are classified by their limb or disk appearance in each STEREO/SECCHI COR2 instrument. Further, we add the minimal STEREO separation (MSS) angle σ between both COR2 instruments.

thumbnail Fig. 9.

CME mass in logarithmic units for 119 events averaged from both coronagraphs and classified by their limb or disk appearance in each COR2 instrument together with STEREO geometry, which is characterised by the minimal STEREO separation (MSS) angle σ (dashed).

Obviously, the highest mass values are detected between 2011 and 2012. Two points are noteworthy to mention at this phase, likely explaining these high values. First, the solar activity approaches a maximum around 2011–2013, which results in generally more massive CMEs (Vourlidas et al. 2010, 2017). Second, CMEs tend to appear with redundant projection shapes in both COR2 telescopes since the spacecraft are in opposition. This configuration occurs when the MSS angle σ is close to 0° or 180°. As several of the more massive entries in Fig. 9 are from CMEs seen as disk events in both telescopes, this suggests an additional influence of projection effects leading to mass overestimations in such cases.

3.3. Mass overestimations

Since we do not know the 3-dimensional electron distribution within a specific CME, we assume that it is equivalent to its 2-dimensional projection, as stated in Sect. 2.2. However, the 2-dimensional projection changes with the observed propagation direction and as consequence also the determined mass values. We compare the propagation direction away from the POS for each coronagraph in Fig. 10 with the determined mass values to investigate if the CME masses of disk events are overestimated by such a geometrical effect. For a single spacecraft study with the SOHO/LASCO coronagraph, covering over 7000 CME non-halo events, V10 found that the majority of CMEs masses lie in the range of 1013 − 1016 g. Therefore, CME masses bigger than 1016.5 g are excluded from our further analysis, due to an expected mass overestimation. This applies to eight events. We further notice that the statistical mass overestimation of disk events at angle of ϕ = 80° away from the solar centre reaches an average factor of three. At the same time we see a clustering of the CME masses of disk events with a likely additional overestimation of about a factor of ten or more, which is way above the maximum error of a factor of five as derived by V10. Therefore, the projection effects on the CME alone are insufficient to explain such large mass values.

thumbnail Fig. 10.

Logarithmic CME masses for 122 events are measured in COR 2A (top panel) and 119 events in COR 2B (bottom panel) against the angular distance ϕ of their propagation direction away from the POS.

A possible explanation for the usually high mass values could arise from additional brightness contributions of other coronal features. We present an illustrative example for such a case with the CME event on September 22, 2011. This CME is seen as disk event in the opposing STEREO coronagraphs (Fig. 11, top). At least two intense streamers appear within our ROI, which is defined by the green GCS fit, and contribute to the overall brightness. Our mass determination yields a value of 3 × 1017 g, the highest mass value of the KinCat. We compare our obtained mass values of this event to the mass value in the SOHO/LASCO CME Catalogue. The SOHO/LASCO C3 coronagraph is positioned at ϕ = 0 and observes the event perpendicular to both COR2 coronagraphs. The C3 images (Fig. 11, bottom) suggest that a northern pre-existing streamer increases in brightness and is deflected towards the POS of COR2 coronagraphs during the eruption. Obviously, such streamers can not be removed with a difference imaging approach. For comparison – from the LASCO perspective, the northern streamer is largely outside of the ROI used in the mass calculation and contributes less to the overall brightness. The reported mass for this event is 2.1 × 1016 g, but with some uncertainty due to the presence of a shock. However, the northern streamer can not be excluded from the COR2 ROI, which results in a total mass increase of 1.4 orders of magnitude.

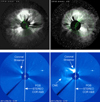thumbnail Fig. 11.

Top panel: GCS modelling of the CME event on September 22, 2011, observed with the STEREO COR 2A (left panel) and STEREO COR 2B (right panel), which are positioned at ϕb = −97° and ϕa = 104° in HEE. Bottom panel: same event observed with the LASCO C3 coronagraph. During the eruption, a pre-existing coronal streamer increases in brightness and is deflected towards solar north pole – close to the POS of both COR2 coronagraphs.

3.4. CME correlations

Before we regard the individual parameter correlation, we like to proof that our data-set can reproduce the known and more basic correlations to the solar cycle. Ivanov & Obridko (2001) have shown that the cycle variation of the average CME width and average CME velocity are associated to the cycle variation of the large-scale solar magnetic field for solar cycle 22. It was further stated, that fast CMEs make the primary contributions in these statistics. As far as the CME mass is concerned, V10 have shown their dependence to the activity of solar cycle 23. By investigating solar cycle 24, Wang & Colaninno (2014) also stated that fast, wide and massive CMEs undergo a stronger solar cycle correlation. Our data-set is biased towards bright and generally fast events, we therefore expect them to reflect the correlation to the solar cycle activity very well.

In Fig. 12, we demonstrate this by using annually averaged values of half angles, the apex velocities and CME masses of our data-set together with the activity of solar cycle 24, represented by SSN.

thumbnail Fig. 12.

Annual evolution of the average half angle, average CME speed for 122 events and the CME mass for 114 events of the KinCat. CME masses above 1016.5 g are excluded. Further, the annual event count and the total 13-month smoothed monthly sunspot numbers are displayed. The sunspot numbers are provided by WDC-SILSO, Royal Observatory of Belgium, Brussels.

For the mass analysis, we have applied the same upper CME mass limits as before to reduce influence of some questionable mass results. We derived the following linear correlations between the annual average of the monthly sunspot number and the annual averages of the CME mass, speed and GCS half angle from Fig. 13 :

log 10 ( M ) = 15.51 ( ± 0.02 ) + 0.0032 ( ± 0.0004 ) SSN , $$ \begin{aligned}&\log _{10}(M)= 15.51(\pm 0.02)+0.0032(\pm 0.0004)\mathrm{SSN}, \end{aligned} $$(5)

v apex = 328.3 ( ± 48.6 ) + 6.1 ( ± 0.9 ) SSN , $$ \begin{aligned}&v_{\text{ apex}}=328.3(\pm 48.6)+6.1(\pm 0.9)\mathrm{SSN},\end{aligned} $$(6)

α = 14.7 ( ± 1.3 ) + 0.15 ( ± 0.02 ) SSN , $$ \begin{aligned}&\alpha =14.7(\pm 1.3)+0.15(\pm 0.02)\mathrm{SSN}, \end{aligned} $$(7)

thumbnail Fig. 13.

Annual average of the GCS half angle and CME speed (122 KinCat events) as well as of the CME mass (114 KinCat events) over the total 13-month smoothed monthly sunspot numbers. CME masses above 1016.5 g are excluded. The sunspot numbers are provided by WDC-SILSO, Royal Observatory of Belgium, Brussels.

with α in [deg], vapex in [km s−1] and M in [g]. Such connections of CME event properties to the SSN may also be useful for the comparison of different CME data-sets. All three parameters largely correlate as expected with the SSN. Only in 2013 we see that the average half angle and the average CME mass descends in contrast to the CME speed. This is likely a result of the different event selection criteria for the years 2012–2013. Also, the low event count during a very active solar period makes the results of this phase likely less significant. However, these statistics are in agreement with the (Vourlidas et al. 2017) statistics, which are based on a much larger sample of COR2 events. Our higher speed average is likely a result caused by our event selection towards brighter and generally faster CMEs.

We now continue by presuming a mutual dependency of the CME speed and width to the CME mass. Since the latter is usually the most difficult to measure in near real-time, the outcome could lead to useful applications in CME forecasts. In Fig. 14 we plot the average CME masses for all 122 events from the KinCat against the CME apex speed and the CME half angle. We have applied the same upper CME mass limits as before. The two linear parameter fits result in:

log 10 ( M ) = 3.4 ( ± 0.6 ) × 10 − 4 v apex + 15.479 ( ± 0.044 ) , $$ \begin{aligned} \log _{10}(M)&= 3.4(\pm 0.6)\times 10^{-4} v_{\text{ apex}}+ 15.479 (\pm 0.044),\end{aligned} $$(8)

log 10 ( M ) = 8.71 ( ± 1.82 ) × 10 − 3 α + 15.380 ( ± 0.065 ) , $$ \begin{aligned} \log _{10}(M)&=8.71(\pm 1.82)\times 10^{-3} \alpha + 15.380 (\pm 0.065) , \end{aligned} $$(9)

thumbnail Fig. 14.

Averaged CME masses for all 122 events from the KinCat against (top panel) the CME apex speed and (bottom panel) the CME half angle. CME masses above 1016.5 g are excluded for the fitting.

with α in [deg], vapex in [km s−1] and M in [g]. As the majority of the excluded events with masses above 1016.5 g are also identical with the 8 disk events of our data-set, it is noteworthy, that we have at the same time excluded possible large uncertainties in the velocity and the half angle values caused by projection effects.

4. Discussion

First of all, we like to point out the advantages of the data-set created by our combined method. It provides the two most important CME parameters in the context of CME arrival analysis with the DBM–the CME mass and the CME speed in the direction of Earth. As the latter, is only provided indirectly, we want to explain how to derive this value from our data-set.

In Fig. 15 we expand the fitted GCS shape self-similarly in the Heliocentric Earth Ecliptic (HEE) coordinate system to 1 AU, which allows to analyse if the CME is Earth-directed and which part of it will potentially impact Earth. If only the slower flank and not the CME apex is directed towards Earth, the apex speed can be a very inaccurate proxy for the Earth-directed speed. Instead, the speed component towards Earth can be derived from the data-set by

v earth = ( h earth / h apex ) v apex , $$ \begin{aligned} v_{\text{ earth}}=\left(h_{\text{ earth}}/h_{\text{ apex}}\right) v_{\text{ apex}}, \end{aligned} $$(10)

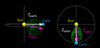thumbnail Fig. 15.

GCS-shape of the July 12, 2012 event propagated self-similarly to 1 AU in the HEE coordinate system. The height of GCS front in the main axis and in Earth-direction are included for illustration.

where hapex is the apex height, hearth is the height in Earth-direction and vapex is the initial apex speed. CME propagation models, as the DBM, can now be applied and their results can be compared to in-situ measured CME signatures at L1.

4.1. CME morphology

We have analysed the GCS morphology, represented by the values of κ and α, of our modelling results. In Sect. 3.1 we have shown that the results are consistent in the case that events are seen as pure limb event in both coronagraphs or as a combination of disk and limb event. On the other hand, we noticed an significant overestimation of κ if the event is seen as disk events in both coronagraphs. In such cases, the shape projection of disk events appears as ellipse, where the semi-minor axis is defined by κ and semi-major axis by κ and α. We want to emphasise that the fitting accuracy of κ and α also depends on the rotation of the GCS model and generally favours one or the other. The determination of the GCS model rotation can be extremely difficult for disk events, especially without considerations of the orientation of the source region. For that reasons, such overestimations of the CME morphology might also affect the determined α values. This can possibly account for some of the spread of data from the fitting line.

There are three possible explanations for the general trend of the larger measured morphology of disk events. First, if an event appears as disk event in both coronagraphs, the instrument separation needs to be very small or close to 180°. In this case the perspectives are nearly redundant and the projection effect are converging to the known effects for observations from only one vantage point. Second, for larger κ the projected GCS shapes appear more circular, rather than elliptical. The fact that all eight disk events are concerned, let us conclude that this a more general phenomenon resulting from projection effects, due to which modellers tend to overestimate κ. This overestimation generally leads to a more circular projected CME shape, rather than elliptic, which may be a hint, that disk events heavily favour unintentional additional fitting of CME shock features, which encloses the regular CME shape. It has to be evaluated how the knowledge of this effect and the shown κ to α correlation in Eq. (2) can contribute to a more accurate fitting of disk events. Last, the presence of additional coronal features might also lead to an overestimation of the morphology. Since, these results are obtained under the presence of a very active corona, the influence of coronal features could partially contribute to this results.

4.2. CME velocity

We further compared the GCS modelling result for disk and limb events to their velocity in Sect. 3.1. It was frequently discussed that projection effects of halo events generally lead to an overestimation of the CME morphology and therefore to an underestimation of the CME speed (Gopalswamy et al. 2010). In the work Yashiro et al. (2004), which is based on projected CME speeds, it was reported that fast CMEs tend to be larger. However, the correlation was described as very weak. Generally, the determined speeds of non-deprojection disk events is on average 25–50% slower as their deprojected speeds (Vršnak et al. 2007). Shen et al. (2013) compared projected and deprojected CME speeds. They have shown that most full halo CMEs, originating within 45 degree away from the Sun-Earth line and possessing a projected speed slower than 900 km s−1 suffer from large projection effect in contrast to faster ones.

In this work we regard deprojected CME speeds and the shown velocity distribution in Fig. 6 seems to follow a typical log-normal distribution. We have analysed the relation between the CME velocity and the CME morphology. Our data has shown that the CME speed correlates at least moderately with the deprojected morphology (R = 0.34 for α and R = 0.41 for κ). Even with the overestimation of the morphology, we have not noticed a significant velocity underestimation of disk events, which would be the consequence of known projection effects for observations from only one vantage point. Likely, accurate stereoscopic velocity measurements require a smaller separation of both observing instruments than accurate measurements of the morphology.

4.3. Mass determination

The mass results have been presented in Sect. 3.2. We already mentioned, that V10 found that the majority of CMEs masses lie in the range of 1013 − 1016 g, and for that reason consider masses higher than 1016.5 g as suspicious. We have detected significantly higher masses for eight CMEs – five of them were seen as disk events in both COR2 instruments and two others as disk events in COR2B. We investigated the systematical overestimation of CME masses, based on our directional mass determination method in Sect. 3.3. V10 stated that this method improves the accuracy of the mass measurements relative to the sky plane assumption to about ϕ = 60°, but decreases fast beyond that angle. At ϕ = 80°, this mass overestimation reaches about factor five, based on hypothetical CME width of 2α = 60°.

We have presented the disk-limb mass distribution for both COR2 coronagraphs and estimated the mass overestimation based on the overall geometry. The statistical mass overestimation of disk events at ϕ = 80° reaches an average factor of three for the mass range of 1015–1016.5 g. If the eight events with higher mass values are also included into the analysis, the overestimation reaches a factor of six. We conclude that geometrical effects on the CME alone can not fully explain the largest mass values of our data-set.

We have shown an example for another relevant source of mass overestimation due to the presence of a coronal streamer. In this case the mass overestimation of the directional mass determination reached a factor of fourteen. We have also discussed, that such sources of mass overestimation are most likely for disk events during phases of high solar activity. The visual inspection of the eight overestimated events with the further help of the LASCO C3 coronagraph, positioned close to Earth, confirmed that in seven cases the additional mass results from coronal streamers (see example in Fig. 11, Sect. 3.3) and in one case from the occurrence of another CME.

One can notice that an overestimation and misinterpretation of the GCS shape was caused by streamers in two cases and by a CME shock front in one case. We identified a relevant explanation for the large mass values of our disk events with the presence and brightness enhancement of overlapping coronal streamers. From this example event we deduce that overlapping structures can be a significant source of mass overestimation. Such overlapping structures occur much more likely during the solar maximum and they are also much more likely present for disk events, as these exhibit larger areas in the observers FOV compared to limb events. For that reason, we suggest to estimate the CME mass of disk events based on their relation to other CME parameter.

4.4. Empirical correlations

In Sect. 3.4 we confirmed that the kinematics, morphologies and masses of our observed CMEs correlate very well with the solar activity cycle. Hence, the question arose if the kinematics or morphology of a CME could be used to estimate the CME mass. We presented both correlations and have shown that the mass-velocity correlation coefficients of Eq. (8) is slightly superior (R = 0.41) to the one of the mass-half angle correlation in Eq. (9) (R = 0.31). Moreover, we have discussed that errors of the CME speed measurements are smaller compared to the measurement of the CME morphology. Of course both are most reliable if the CME is seen as limb event in at least one perspective. Thus, we recommend to use Eq. (8) when it comes to empirical estimations of the CME mass. The advantage of this result is that speed measurements can be used to derive the other CME properties. Once applied to a CME propagation model, as the DBM, they result in more accurate first estimations of the terrestrial arrival of intense CMEs. These results might also be valuable for setting observational constraints in space weather prediction models such as ENLIL (Odstrcil et al. 2004) and empirical models for predicting the parameters at L1 (Austin & Savani 2018).

5. Summary – conclusion

The objective of this work is to present a combined method of geometrical modelling and CME white-light mass determination. The method has been applied to a set of 122 intense events observed with STEREO COR2 roughly spanning over solar cycle 24. We determined the three-dimensional flux rope structure of these CMEs with the Graduated Cylindrical Shell (GCS) model. We further determined the mass content of each event based on the directional mass determination approach under the consideration of the CMEs propagation direction. All determined kinematic, geometric and mass parameters of the 122 events are gathered in the “KinCat” online catalogue. All results are referenced to a fixed apex height of 12 R⊙, to faciliate comparison among all events. Moreover, the annual average of all derived parameters are associated to the SSN to make them comparable to other studies. To quantify the influence of the geometry in the fitting results, we have separated our events by their appearance as limb or disk events in the COR2 coronagraphs. Within this study, we have analysed the applicability of the presented method to disk events. Further, we investigated if the CME mass can be empirically estimated from its connection to the CME kinematic. From the analysis of the catalogue parameters, we obtained the following results:

  1. The CME morphology of disk events can lead to an overestimation of the flux rope width up to a factor of two – at least if coronal features are present.

  2. The average morphology of the CMEs within our data-set can be described with the GCS half angle α and the GCS aspect ratio κ via:

    α = 27.6 κ + 10.8 . $$ \begin{aligned} \alpha = 27.6 \kappa +10.8. \nonumber \end{aligned} $$

  3. The obtained CME speeds of disk events are less affected by projection effects than the CME morphology. The latter can be estimated for disk events from the CME speed via:

    α = 1.11 × 10 − 2 v apex + 15.0 , κ = 1.7 × 10 − 4 v apex + 0.30 . $$ \begin{aligned} \alpha&=1.11 \times 10^{-2} v_{\text{ apex}}+ 15.0, \nonumber \\ \kappa&=1.7 \times 10^{-4} v_{\text{ apex}}+ 0.30. \nonumber \end{aligned} $$

  4. Projection effects lead to an average mass overestimation for our applied mass determination approach. The overestimation reaches a factor of three for disk events emerging at an angular distance of ϕ = 80° away from the POS.

  5. Mass overestimations of a factor of ten and more can result from overlapping features. Such effects are more likely present in disk events because they tend to occupy a large range of position angles due to the observed geometry.

  6. Finally, we propose that the following empirical correlation between the CME masses and the CME speeds is most suited to estimate the mass of intense CMEs from coronagraph images:

    log 10 ( M ) = 3.4 × 10 − 4 v apex + 15.479 . $$ \begin{aligned} \log _{10}(M)= 3.4\times 10^{-4} v_{\text{ apex}}+ 15.479. \nonumber \end{aligned} $$

We conclude that for stereoscopic measurements of disk events, the measurements of initial CME speed are the most reliable ones and can be used to derive the CME morphology and mass to make them quickly applicable in space weather forecasts. However, for scientific purposes, such derived values should be treated with caution.

Acknowledgments

The work in this paper was funded under the HELCATS project by the EU FP7 program. A.Vourlidas is supported by NASA grants NNX16AH70G and NNX17AC47G. Volker Bothmer acknowledges support of the CGAUSS (Coronagraphic German and US Solar Probe Plus Survey) project for WISPR on NASA PSP by the German Space Agency DLR under grant 50 OL 1601 and the support of the project Stereo/Corona by the German Bundesministerium fur Bildung und Forschung through the deutsche Zentrum fur Luft-und Raumfahrt e.V. (DLR, German Space 59 Agency). Stereo/Corona was a science and hardware contribution to the optical image package SECCHI, developed for the NASA STEREO mission. The STEREO/SECCHI data used for this study are prepared by an international consortium of NASA Goddard Space Flight Center (USA), Lockheed Martin Solar and Astrophysics Lab (USA), Naval Research Laboratory (USA), Rutherford Appleton Laboratory (UK), University of Birmingham (UK), Max-Planck-Institut für Sonnensystemforschung (Germany), Institut d’Optique Théorique et Appliquée (France), Institut d’Astrophysique Spatiale (France) and Centre Spatiale de Liège (Belgium). We further acknowledge close collaborations with the US Naval Research Laboratory (NRL), Dr. Russ A. Howard (PI of STEREO/SECCHI), Dr. Arnaud Thernisien and Dr. Jackie Davies from the Rutherford Appleton Laboratory (RAL), Dr. Eckhard Bosman, Malte Venzmer and Johannes Hinrichs from University of Göttingen (UGOE).

References

  1. Austin, H. J., & Savani, N. P. 2018, Weather, 73, 362 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bein, B. M., Temmer, M., Vourlidas, A., Veronig, A. M., & Utz, D. 2013, ApJ, 768, 31 [Google Scholar]
  3. Billings, D. E. 1966, A guide to the solar corona (New York: Academic Press), 344 [Google Scholar]
  4. Bosman, E., & Bothmer, V. 2012, in EGU Gen. Assem. Conf. Abstr., eds. A. Abbasi, & N. Giesen, 14, 11632 [Google Scholar]
  5. Bosman, E., Bothmer, V., Nisticò, G., et al. 2012, Sol. Phys., 281, 167 [NASA ADS] [Google Scholar]
  6. Burkepile, J. T., Hundhausen, A. J., Stanger, A. L., St. Cyr, O. C., & Seiden, J. A. 2004, J. Geophys. Res. (Sp. Phys.), 109, A03103 [NASA ADS] [CrossRef] [Google Scholar]
  7. Burlaga, L. F., Behannon, K. W., & Klein, L. W. 1987, Geophys. Res., 92, 5725 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chen, J., Howard, R. A., Brueckner, G. E., et al. 1997, ApJ, 490, L191 [Google Scholar]
  9. Cherry, N. 2002, Nat. Hazards J. Int. Soc. Prev. Mitig. Nat. Hazards, 26, 279 [Google Scholar]
  10. Colaninno, R. C., & Vourlidas, A. 2009, ApJ, 698, 852 [Google Scholar]
  11. Cremades, H., & Bothmer, V. 2004, A&A, 422, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Davies, J. A., Perry, C. H., Trines, R. M. G. M., et al. 2013, ApJ, 777, 167 [NASA ADS] [CrossRef] [Google Scholar]
  13. de Koning, C. A. 2017, ApJ, 844, 61 [Google Scholar]
  14. Gopalswamy, N. 2013, Astron. Soc. India Conf. Ser., 10 [Google Scholar]
  15. Gopalswamy, N., Yashiro, S., Michalek, G., et al. 2010, Sun and Geosphere, 5, 7 [NASA ADS] [Google Scholar]
  16. Gosling, J. T., McComas, D. J., Phillips, J. L., & Bame, S. 1991, J. Geophys. Res., 96, 7831 [NASA ADS] [CrossRef] [Google Scholar]
  17. Harrison, R., Davies, J., Perry, C., et al. 2016, EGU Gen. Assem. Conf. Abstr., 18, EPSC2016-10220 [Google Scholar]
  18. Howard, R. A., Michels, D. J., Sheeley, Jr., N. R., & Koomen, M. J. 1982, ApJ, 263, L101 [NASA ADS] [CrossRef] [Google Scholar]
  19. Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
  20. Ivanov, E. V., & Obridko, V. N. 2001, Sol. Phys., 198, 179 [NASA ADS] [CrossRef] [Google Scholar]
  21. Kahler, S. W., & Vourlidas, A. 2005, J. Geophys. Res. (Sp. Phys.), 110, A12S01 [Google Scholar]
  22. Kaiser, M. L., Kucera, T. A., Davila, J. M., et al. 2008, Space Sci. Rev., 136, 5 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kilpua, E., Möstl, C., Bothmer, V., et al. 2017, EGU Gen. Assem. Conf. Abstr., 19, 9051 [Google Scholar]
  24. Kwon, R.-Y., Zhang, J., & Vourlidas, A. 2015, ApJ, 799, L29 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lee, H., Moon, Y.-J., Na, H., & Jang, S. 2014, AAS Meet. Abstr., 224, 218.34 [Google Scholar]
  26. Liewer, P. C., Hall, J. R., Howard, R. A., et al. 2011, J. Atmos. Sol. Terr. Phys., 73, 1173 [Google Scholar]
  27. Liu, Y., Davies, J. A., Luhmann, J. G., et al. 2010a, ApJ, 710, L82 [Google Scholar]
  28. Liu, Y., Thernisien, A., Luhmann, J. G., et al. 2010b, ApJ, 722, 1762 [NASA ADS] [CrossRef] [Google Scholar]
  29. Liu, Y. D., Hu, H., Wang, C., et al. 2016, ApJS, 222, 23 [NASA ADS] [CrossRef] [Google Scholar]
  30. Mays, M. L., Taktakishvili, A., Pulkkinen, A., et al. 2015, Sol. Phys., 290, 1775 [CrossRef] [Google Scholar]
  31. Odstrčil, D., & Pizzo, V. 1999, J. Geophys. Res., 104, 493 [Google Scholar]
  32. Odstrcil, D., Pizzo, V. J., Linker, J. A., et al. 2004, J. Atm. Sol. Terr. Phys., 66, 1311 [Google Scholar]
  33. Pulkkinen, A., Lindahl, S., Viljanen, A., & Pirjola, R. 2005, Sp. Weather, 3, S08C03 [Google Scholar]
  34. Reiner, M. J., Vourlidas, A., Cyr, O. C. S., et al. 2003, ApJ, 590, 533 [NASA ADS] [CrossRef] [Google Scholar]
  35. Sachdeva, N., Subramanian, P., Vourlidas, A., & Bothmer, V. 2017, Sol. Phys., 292, 118 [NASA ADS] [CrossRef] [Google Scholar]
  36. Savani, N. P., Owens, M. J., Rouillard, A. P., et al. 2011a, ApJ, 731, 109 [NASA ADS] [CrossRef] [Google Scholar]
  37. Savani, N. P., Owens, M. J., Rouillard, A. P., et al. 2011b, ApJ, 732, 117 [Google Scholar]
  38. Savani, N. P., Vourlidas, A., Pulkkinen, A., et al. 2013, Sp. Weather, 11, 245 [Google Scholar]
  39. Sheeley, N. R., Walters, J. H., Wang, Y.-M., & Howard, R. A. 1999, Geophys. Res., 104, 24739 [Google Scholar]
  40. Shen, C., Wang, Y., Pan, Z., et al. 2013, J. Geophys. Res. (Sp. Phys.), 118, 6858 [Google Scholar]
  41. Temmer, M., Preiss, S., & Veronig, A. M. 2009, Sol. Phys., 256, 183 [Google Scholar]
  42. Thernisien, A. F. R., Howard, R. A., & Vourlidas, A. 2006, ApJ, 652, 763 [Google Scholar]
  43. Thernisien, A., Vourlidas, A., & Howard, R. A. 2009, Sol. Phys., 256, 111 [Google Scholar]
  44. Thomson, A. W. P., Dawson, E. B., & Reay, S. J. 2011, Sp. Weather, 9, S10001 [NASA ADS] [Google Scholar]
  45. Tsurutani, B. T., Smith, E. J., Gonzalez, W. D., Tang, F., & Akasofu, S. I. 1988, Geophys. Res., 93, 8519 [Google Scholar]
  46. Vourlidas, A., & Howard, R. A. 2006, ApJ, 642, 1216 [Google Scholar]
  47. Vourlidas, A., & Ontiveros, V. 2009, in AIP Conf. Ser., eds. X. Ao, & G. Z. R. Burrows, 1183, 139 [NASA ADS] [CrossRef] [Google Scholar]
  48. Vourlidas, A., Subramanian, P., Dere, K. P., & Howard, R. A. 2000, ApJ, 534, 456 [Google Scholar]
  49. Vourlidas, A., Howard, R. A., Esfandiari, E., et al. 2010, ApJ, 722, 1522 [NASA ADS] [CrossRef] [Google Scholar]
  50. Vourlidas, A., Lynch, B. J., Howard, R. A., & Li, Y. 2013, Sol. Phys., 284, 179 [NASA ADS] [Google Scholar]
  51. Vourlidas, A., Balmaceda, L. A., Stenborg, G., & Dal Lago, A. 2017, ApJ, 838, 141 [NASA ADS] [CrossRef] [Google Scholar]
  52. Vršnak, B., Sudar, D., Ruždjak, D., & Žic, T. 2007, A&A, 469, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Vršnak, B., Žic, T., Vrbanec, D., et al. 2013, Sol. Phys., 285, 295 [Google Scholar]
  54. Wang, Y.-M., & Colaninno, R. 2014, ApJ, 784, L27 [NASA ADS] [CrossRef] [Google Scholar]
  55. Yashiro, S., Gopalswamy, N., Michalek, G., et al. 2004, J. Geophys. Res. (Sp. Phys.), 109, A07105 [Google Scholar]

All Figures

thumbnail Fig. 1.

Evolution of STEREO spacecraft separation from the first catalogue event, over the STEREO opposition phase to the last event. The shown minimal STEREO separation (MSS) angle σ is defined as the minimal angular distance between both STEREO satellites (STEREO Science Center; https://stereo-ssc.nascom.nasa.gov/where/).
In the text
thumbnail Fig. 2.

GCS model fitted onto the coronagraph images of SECCHI/COR2B (left panel) and COR2A (right panel) for the CME event on July 12, 2012 at 18.39 UT.
In the text
thumbnail Fig. 3.

GCS fitting on a sequence of COR2A (top panel) and COR2B (bottom panel) images of the STEREO/SECCHI coronagraphs for the July 12, 2012 event from 16:54 to 18:24 UT.
In the text
thumbnail Fig. 4.

Source region distribution of all 122 KinCat events, estimated by GCS fitting and presented in the Earth-based Stonyhurst coordinate system (middle panel) as well as transposed to the perspectives of STEREO/SECCHI COR2A (right panel) and COR2B (left panel).
In the text
thumbnail Fig. 5.

GCS fitting results of the July 12, 2012 event. Top panel: height-time profile of the CME apex with the fitted apex speed v apex = 1239 km s−1 at 12 R⊙. Bottom panel: mass-height profile for both STEREO/SECCHI COR2 instruments with the extrapolated total masses Ma and Mb.
In the text
thumbnail Fig. 6.

Distribution of the GCS modelling results at 12 R⊙ for the CME apex speed (top panel), the GCS half angle (middle panel) and the GCS aspect ratio (bottom panel).
In the text
thumbnail Fig. 7.

Individual results of GCS fitted aspect ratio κ and half angle α derived for all 122 catalogue events. The events are classified by their limb or disk appearance in each STEREO/SECCHI COR2 instrument.
In the text
thumbnail Fig. 8.

Distribution of the CME mass results in logarithmic units averaged from both SECCHI/COR2 measurements for 119 events and three single measurements.
In the text
thumbnail Fig. 9.

CME mass in logarithmic units for 119 events averaged from both coronagraphs and classified by their limb or disk appearance in each COR2 instrument together with STEREO geometry, which is characterised by the minimal STEREO separation (MSS) angle σ (dashed).
In the text
thumbnail Fig. 10.

Logarithmic CME masses for 122 events are measured in COR 2A (top panel) and 119 events in COR 2B (bottom panel) against the angular distance ϕ of their propagation direction away from the POS.
In the text
thumbnail Fig. 11.

Top panel: GCS modelling of the CME event on September 22, 2011, observed with the STEREO COR 2A (left panel) and STEREO COR 2B (right panel), which are positioned at ϕb = −97° and ϕa = 104° in HEE. Bottom panel: same event observed with the LASCO C3 coronagraph. During the eruption, a pre-existing coronal streamer increases in brightness and is deflected towards solar north pole – close to the POS of both COR2 coronagraphs.
In the text
thumbnail Fig. 12.

Annual evolution of the average half angle, average CME speed for 122 events and the CME mass for 114 events of the KinCat. CME masses above 1016.5 g are excluded. Further, the annual event count and the total 13-month smoothed monthly sunspot numbers are displayed. The sunspot numbers are provided by WDC-SILSO, Royal Observatory of Belgium, Brussels.
In the text
thumbnail Fig. 13.

Annual average of the GCS half angle and CME speed (122 KinCat events) as well as of the CME mass (114 KinCat events) over the total 13-month smoothed monthly sunspot numbers. CME masses above 1016.5 g are excluded. The sunspot numbers are provided by WDC-SILSO, Royal Observatory of Belgium, Brussels.
In the text
thumbnail Fig. 14.

Averaged CME masses for all 122 events from the KinCat against (top panel) the CME apex speed and (bottom panel) the CME half angle. CME masses above 1016.5 g are excluded for the fitting.
In the text
thumbnail Fig. 15.

GCS-shape of the July 12, 2012 event propagated self-similarly to 1 AU in the HEE coordinate system. The height of GCS front in the main axis and in Earth-direction are included for illustration.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.