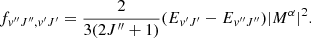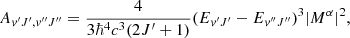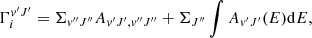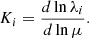| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 4 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201834782 | |
| Published online | 07 February 2019 | |
H2/HD molecular data for analysis of quasar spectra in search of varying constants⋆
1
Department of Physics and Astronomy, Vrije Universiteit, De Boelelaan 1081, 1081 HV Amsterdam, The Netherlands
e-mail: w.m.g.ubachs@vu.nl
2
Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Melbourne, 3122 Victoria, Australia
3
Sorbonne Université, Observatoire de Paris, Université PSL, CNRS, LERMA, 92190
Meudon, France
Received:
5
December
2018
Accepted:
24
December
2018
Context. Absorption lines of H2 and HD molecules observed at high redshift in the line of sight towards quasars are a test ground to search for variation of the proton-to-electron mass ratio μ. For this purpose, results from astronomical observations are compared with a compilation of molecular data of the highest accuracy, obtained in laboratory studies as well as in first-principles calculations.
Aims. A comprehensive line list is compiled for H2 and HD absorption lines in the Lyman (B1Σu+ − X1Σg+) and Werner (C1Πu − X1Σg+) band systems up to the Lyman cutoff at 912 Å. Molecular parameters listed for each line i are the transition wavelength λi, the line oscillator strength fi, the radiative damping parameter of the excited state Γi, and the sensitivity coefficient Ki for a variation of the proton-to-electron mass ratio.
Methods. The transition wavelengths λi for the H2 and HD molecules are determined by a variety of advanced high-precision spectroscopic experiments involving narrowband vacuum ultraviolet lasers, Fourier-transform spectrometers, and synchrotron radiation sources. Results for the line oscillator strengths fi, damping parameters Γi, and sensitivity coefficients Ki are obtained in theoretical quantum chemical calculations.
Results. A new list of molecular data is compiled for future analyses of cold clouds of hydrogen absorbers, specifically for studies of μ-variation from quasar data. The list is applied in a refit of quasar absorption spectra of B0642–5038 and J1237+0647 yielding constraints on a variation of the proton-to-electron mass ratio Δμ/μ consistent with previous analyses.
Key words: molecular data
Tables 1–3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/622/A127
© ESO 2019
1. Introduction
After Thompson (1975) had pointed out that possible variations of the proton-to-electron mass ratio μ = mp/me could be deduced from the spectrum of molecular hydrogen, Varshalovich & Levshakov (1993) performed an early analysis setting a constraint on Δμ/μ over cosmological time scales using a quasar absorption spectrum. The rationale of such an analysis is based on the fact that multiple H2 absorption lines exhibit a different dependence on a possible variation of the fundamental constant μ. While initial work was based on classical spectroscopic studies of the hydrogen molecule (Abgrall et al. 1993a,b), the laser-based studies of H2 (Philip et al. 2003; Ubachs & Reinhold 2004; Reinhold et al. 2006) thereafter increased the precision of such constraints, as did the improved quality of astronomical observations. Several groups have been involved in analyzing H2 in the line of sight of quasars searching for a possible μ-variation (Ivanchik et al. 2005; King et al. 2008, 2011; Thompson et al. 2009; Malec et al. 2010; Wendt & Molaro 2011; Rahmani et al. 2013; Bagdonaite et al. 2014; Albornoz Vásquez et al. 2014; Dapra et al. 2015). The status of searches on a drifting fundamental constant μ has been reviewed (Ubachs et al. 2016; Ubachs 2018), combining analyses of ten quasar absorption systems leading to an overall constraint: the proton electron mass ratio has changed by less than 5 ppm (at 3σ) for redshifts in the range z = 2.0−4.2, corresponding to look-back times of 10–12.4 billion years.
The analyses of astronomical H2 spectra observed in the line-of-sight toward quasars and the extraction of a possible μ-variation depend on the availability of molecular data. Such data have been published on various occasions, such as in the supplementary material to the paper by Malec et al. (2010). However, we have found some inconsistencies and small errors in the data set, in particular for values of line oscillator strengths, and not all data were specified to the best accuracies now available. The purpose of this paper is to provide a comprehensive and accurate data set of H2 and HD line parameters, to be used reliably in future analyses of μ-variation from hydrogen absorption in the early universe.
2. Molecular data for H2
In the analysis of astronomical spectra in a search for a varying μ, the H2 and HD absorption lines are represented by four characteristic values, λi, fi, Γi and Ki. Availability of accurate values for the wavelengths λi of the absorption lines is most crucial. Laboratory wavelengths were determined with the use of a narrow-band tunable laser in the vacuum ultraviolet range in molecular beam spectroscopic studies (Philip et al. 2003; Ubachs & Reinhold 2004; Reinhold et al. 2006). Thereafter, accurate level energies of the 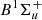 and C1Πu excited states in the H2 molecule were measured via a stepwise method using Doppler-free laser techniques and Fourier-transform emission (Salumbides et al. 2008). From these determinations of level energies, listed by Bailly et al. (2010), the transition wavelengths of individual H2 absorption lines in the Lyman and Werner bands were derived with high accuracy by combining with ground-state level energies (Jennings & Brault 1993). An improvement on the accuracy of ground-state level energies has been produced via ab initio calculations including relativistic and quantum-electrodynamic effects (Komasa et al. 2011). The latter calculations were experimentally tested in precision laser studies (Salumbides et al. 2011; Dickenson et al. 2013) and found to be accurate to 10−4 cm−1. Here we present a new determination of combination differences between excited state level energies (Bailly et al. 2010) and the ground-state level energies (Komasa et al. 2011), resulting in improved values for transition wavelengths of Lyman and Werner lines at accuracies of Δλ/λ < 3 × 10−8. These accurate data for the wavelengths are labeled with “1” in Tables 1 and 2. In view of the fitting and calibration accuracies obtained with the spectrographs mounted on the largest telescopes, these values for the laboratory wavelengths may be considered exact for the purpose of comparison with astronomical data; see also Ubachs et al. (2016).
and C1Πu excited states in the H2 molecule were measured via a stepwise method using Doppler-free laser techniques and Fourier-transform emission (Salumbides et al. 2008). From these determinations of level energies, listed by Bailly et al. (2010), the transition wavelengths of individual H2 absorption lines in the Lyman and Werner bands were derived with high accuracy by combining with ground-state level energies (Jennings & Brault 1993). An improvement on the accuracy of ground-state level energies has been produced via ab initio calculations including relativistic and quantum-electrodynamic effects (Komasa et al. 2011). The latter calculations were experimentally tested in precision laser studies (Salumbides et al. 2011; Dickenson et al. 2013) and found to be accurate to 10−4 cm−1. Here we present a new determination of combination differences between excited state level energies (Bailly et al. 2010) and the ground-state level energies (Komasa et al. 2011), resulting in improved values for transition wavelengths of Lyman and Werner lines at accuracies of Δλ/λ < 3 × 10−8. These accurate data for the wavelengths are labeled with “1” in Tables 1 and 2. In view of the fitting and calibration accuracies obtained with the spectrographs mounted on the largest telescopes, these values for the laboratory wavelengths may be considered exact for the purpose of comparison with astronomical data; see also Ubachs et al. (2016).
The excited-state level energies of Bailly et al. (2010) have some limitations, in that not all high-J levels were probed up to J = 7, and that the C1Πu (v = 4, 5) levels are missing; here J refers to the rotational angular momentum of the ground state. In such cases, data are adopted from the XUV-laser experiments (Philip et al. 2003), while information for P-lines was also extended to wavelengths for R-lines calculated via combination differences based on known ground-state levels (Ubachs et al. 2007). Based on the improved ground-state energies of Komasa et al. (2011), the latter determinations have been verified and improved for accuracy, estimated at Δλ/λ ∼ 10−7. These entries for the wavelengths in Tables 1 and 2 are labeled with “2”. Also uncertainties of the wavelengths are listed for all entries.
In some remaining cases, the wavelengths were taken from classical spectroscopic studies by Abgrall et al. (1993c). In these cases the accuracy is lower and estimated at Δλ/λ ∼ 10−6 − 10−5. The latter entries are labeled with “3” in Tables 1 and 2.
Line oscillator strengths fv″J″, v′J′ involve the square of the transition dipole moment Mα matrix elements connecting the ground 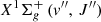 and the (v′,J′) electronic excited states as well as the transition energy:
and the (v′,J′) electronic excited states as well as the transition energy:
All terms are expressed in atomic units, f is dimensionless, and α corresponds to P, Q, and R transitions where ΔJ = J′−J″ = −1, 0, +1, respectively. The matrix elements of the transition moments are computed with the wave functions numerically calculated from the integration of the coupled Schrödinger equations linking the 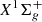 and
and 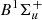 , C1Πu,
, C1Πu, 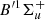 , and D1Πu excited electronic states as described in Abgrall et al. (1993c). The computations include nonadiabatic rotational and radial couplings taking place between the four excited electronic states. Einstein A emission probabilities may be derived from the following expression (in CGS units):
, and D1Πu excited electronic states as described in Abgrall et al. (1993c). The computations include nonadiabatic rotational and radial couplings taking place between the four excited electronic states. Einstein A emission probabilities may be derived from the following expression (in CGS units):
where the value of A is per second (Abgrall et al. 2000).
For the analysis of quasar data, damping coefficients Γi are important, corresponding to the total radiative decay rates of the excited states which are computed from the sum of the Einstein coefficients emitted from a specific excited level (v′,J′). This total radiative decay rate:
includes both bound-bound transitions as well as bound-free transitions, where the integration over the kinetic energy E spanning the continuum of the 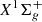 ground electronic state is performed from E = 0, corresponding to the dissociation limit of H2. These different parameters have been checked against experimental studies of H2 UV emission following electronic excitation (Liu et al. 2000; Jonin et al. 2000).
ground electronic state is performed from E = 0, corresponding to the dissociation limit of H2. These different parameters have been checked against experimental studies of H2 UV emission following electronic excitation (Liu et al. 2000; Jonin et al. 2000).
A fourth ingredient for analyzing H2 spectra for a possible variation of the proton-to-electron mass ratio μ is the sensitivity coefficient, which for each line is defined as:
After a first calculation of Ki coefficients based on rotational constants (Varshalovich & Levshakov 1993), a more sophisticated model was developed based on Dunham parameters representing the accurately measured energy level structure (Ubachs et al. 2007). The latter model took into account nonadiabatic couplings in a semi-empirical way. Comparison with values based on a two-state-coupling ab initio calculation (Meshkov et al. 2006) produced agreement between methods within 3 × 10−4, providing confidence in the reliability of the Ki values determined. Thereafter Ki coefficients were calculated in a four-state-coupling calculation (Abgrall et al. 1993c, 2000), comprehensive results of which are considered the most accurate and estimated to be accurate to within ΔKi ∼ 3 × 10−4 (Salumbides et al. 2015). These values are included in the present listing.
The molecular data for H2, for the four relevant parameters λi, fi, Γi and Ki, are collected in the tables provided here. Data are given for all transitions in the Lyman bands (Table 1) and Werner bands (Table 2) originating in the eight lowest rotational quantum states J = 0 − 7, for v = 0. In quasar spectra, typically, lines are observed for quantum states up to J = 5. The first column in the tables refers to the identification of the line in four units: (i) L or W for Lyman or Werner; (ii) the vibrational quantum number v′ of the excited state; (iii) P, Q, or R for the rotational transition; (iv) the J quantum number of the ground level. The molecular data are represented for λi in units of Å, the uncertainty Δλ also in units of Å, fi as a dimensionless line strength, Γi in units of s−1, and Ki as dimensionless numbers. The spectral information is limited to absorption lines that fall redward of the Lyman cutoff, at λ > 912 Å. The Lyman bands are known to exhibit only R- and P-branch lines, while the Werner bands exhibit also Q-lines, besides the R- and P-branch lines.
3. Molecular data for HD
Besides H2 lines HD transitions are also observed in the line-of-sight of quasars. However, HD is present at low abundance in high-redshift galaxies, well below earth abundances and mostly below galactic abundances (Tumlinson et al. 2010). In addition, in view of the small dipole moment of HD the state populations equilibrate to the local temperatures, to the effect that in virtually all observations only R(0) lines are observed, probing the J = 0 population. Only in a single case has the R(1) line of HD been observed (Balashev et al. 2010). Therefore, only information on R(0), R(1) and P(1) lines and, for the Werner bands also the Q(1) line, is compiled for HD in Table 3.
Values for the transition wavelengths λi are obtained from vacuum ultraviolet laser spectroscopy (Ivanov et al. 2008). That study encompasses lines in the Lyman bands for vibrations v′ = 0 − 9 and for v′ = 16 and, for the Werner band, only v′ = 0, all claimed to be accurate to Δλ/λ < 5 × 10−8. It is noted that the assignments of P and R lines in the B−X (16, 0) band were erroneously interchanged. These most accurate entries for HD wavelengths are labeled with “1” in Table 3.
For the remaining lines not covered in the laser-based study (Ivanov et al. 2008), there are two sets with data of equal accuracy, claimed at Δλ/λ < 4 × 10−7. The laser-based study by Hinnen et al. (1995) reports lines for the Lyman bands up to v′ = 19 and Werner bands for v′ = 2 and v′ = 4. These entries are labeled with “2” in Table 3. The remaining lines redward of the Lyman cutoff (up to v′ = 21 for the Lyman bands and up to v′ = 5 for the Werner bands) were taken from a study employing a vacuum ultraviolet Fourier-transform spectrometer fed by synchrotron radiation (Ivanov et al. 2010). Some values of lower accuracy in the laser study (Hinnen et al. 1995) were replaced by those from the synchrotron study, where the latter were found to be more accurate (Ivanov et al. 2010). The entries from the synchrotron study are labeled with “3” in Table 3. It is noted further that the absorption spectrum of HD exhibits some extra lines due to symmetry breaking in the hetero-nuclear hydrogen species, in excitation to the 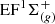 state. Such weak lines were reported in Dabrowksi & Herzberg (1976) and Hinnen et al. (1995), but have not been observed in quasar absorption spectra.
state. Such weak lines were reported in Dabrowksi & Herzberg (1976) and Hinnen et al. (1995), but have not been observed in quasar absorption spectra.
Two independent four-state nonadiabatic perturbation calculations were performed. The first focused on calculations of fi and Einstein coefficients Av′,v″, also yielding values for the damping parameters Γi (Abgrall & Roueff 2006). The second focused on determining values of Ki coefficients (Ivanov et al. 2010). Values from both studies are adopted in Table 3.
4. Tables
The molecular data are presented in three tables:
-
Table 1: Line list and molecular data for the
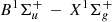 Lyman bands of H2.
Lyman bands of H2. -
Table 2: Line list and molecular data for the
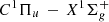 Werner bands of H2.
Werner bands of H2. -
Table 3: Line list and molecular data for the HD molecule. The molecular data in these tables supersede previous compilations with updated values, such as the often-used listing by Malec et al. (2010). Some previous data were not the most accurate, like for transitions with high-J in H2, or were erroneous, like the fi values for the P- and R branches of the H2 Werner bands. Most of the latter lines had fi values off by some 10% or less, except for the R(0) lines, which were off by up to a factor of two. The information on HD is largely updated, since information on many lines not observed yet in quasar absorption studies had not been presented.
5. Implementation in analysis of quasar absorption spectra
A search for a possible variation of the proton-to-electron mass ratio can be made operational by comparing fitted values of the line centers  in absorption spectra of molecular hydrogen in galaxies in the line-of-sight toward quasars with laboratory values
in absorption spectra of molecular hydrogen in galaxies in the line-of-sight toward quasars with laboratory values  via:
via:
where zabs is the redshift of the absorbing cloud. In fitting routines, for each specific absorption line the value of Ki is included to derive a constraint on Δμ/μ.
A fitting procedure may build a synthetic spectrum from the molecular data, including wavelengths λi, line strengths fi, and sensitivity coefficients Ki. In the model spectrum, a value for a Doppler broadening parameter b is built in, convolved with the instrument width and the Lorentzian component Γi, giving each line a composite Voigt profile. This parameter Γi impacts in cases of strong saturated absorption where the absorption line exhibits the typical damping profile. For each ground-state level a population parameter N(J) is attached, which connects the information of multiple lines probing the same level in a physical way. Such a synthetic spectrum is assigned a redshift parameter zabs. This method, referred to as “comprehensive fitting method”, is coded and implemented in a dedicated open-source fitting suite VPFIT developed by Carswell & Webb (2014). It allows for inclusion of more than one velocity component, each component assigned with physical parameters, such as b′ and N′(J), as well as a redshift parameter zabs′. Asymmetric line shapes due to overlapping velocity components can therefore be treated. In addition, the spectral contribution of neutral H I lines, as well as metal lines associated with Fe, Cr, and so on can be included in the fitting routine.
In order to verify the effect of the updates and corrections presented in the molecular data files of Tables 1–3, a re-analysis of two quasar absorption spectra was performed. The quasar absorption spectrum toward J1237+0647 was chosen because it contains two R(0) and two R(1) Werner lines of H2, as well as two R(0) Werner lines of HD; the intensities of these lines are most strongly affected by the molecular data update. J1237+0647 was recently analyzed by Dapra et al. (2015) to yield a constraint of Δμ/μ = ( − 5.54 ± 6.30stat)×10−6 using the older molecular data set (Malec et al. 2010). We note that the uncertainties are expressed in terms of 1σ standard deviations. Again, VPFIT was used with exactly the same settings, and the same treatment of the spectrum, with the same H I assignments, metal absorbers, and velocity components. The re-fit yields a value of Δμ/μ = ( − 4.37 ± 6.30stat)×10−6, hence a difference of the value of Δμ/μ by less than 20% of the standard deviation, while the reduced 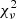 was decreased from 1.327 to 1.318. The latter indicates a slight improvement of the fit as a result of the renewed molecular data set.
was decreased from 1.327 to 1.318. The latter indicates a slight improvement of the fit as a result of the renewed molecular data set.
In addition, the quasar absorption spectrum towards B0642–5038, previously analyzed by Bagdonaite et al. (2014), was refitted. This spectrum contains only a single R(0) Werner line affected by an intensity change. A specific analysis was performed isolating low- and high-J transitions for a one-velocity-component model. For the original molecular data set (Malec et al. 2010), a value of Δμ/μ = ( + 9.88 ± 6.14stat)×10−6 was obtained, and for the new molecular data set this value was found to be Δμ/μ = ( + 9.44 ± 6.09stat)×10−6. The difference between the results amounts to 7% of a standard deviation with the reduced 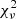 marginally decreasing from 1.189 to 1.188. The fact that the re-analysis of B0642–5038 produces a smaller change than that of J1237+0647 may be attributed to the lesser amount of affected R(0)–R(1) Werner lines in the spectrum.
marginally decreasing from 1.189 to 1.188. The fact that the re-analysis of B0642–5038 produces a smaller change than that of J1237+0647 may be attributed to the lesser amount of affected R(0)–R(1) Werner lines in the spectrum.
Overall, these results demonstrate that the correction to the molecular data set has no significant impact on the previous constraints on a varying proton-to-electron mass ratio and the conclusions drawn from previous analyses as discussed in Ubachs et al. (2016). Apart from the specific application to quasar absorption spectra, the updated and accurate molecular data for H2 and HD may also be applied to investigations of gamma-ray burst afterglows (Bolmer et al. 2019).
6. Conclusion
A molecular data set is compiled for the analysis of H2 and HD absorption spectra in the Lyman and Werner bands redward of the Lyman cutoff. The most accurate values to date are compiled, for transition wavelengths λi, line oscillator strengths fi, and radiative damping coefficients Γi for all spectral lines, as well as sensitivity coefficients Ki to a variation of the proton-to-electron mass ratio μ. The tables provide the required zero-redshift information for the analysis of quasar absorption spectra to retrieve a constraint on Δμ/μ on a cosmological timescale.
Acknowledgments
The authors wish to thank S. A. Balashev for bringing errors and inconsistencies in the previous molecular data list to our attention. J. Bagdonaite and M. Daprà are thanked for discussions and clarifications. W.U. received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant No. 670168).
References
- Abgrall, H., & Roueff, E. 2006, A&A, 445, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abgrall, H., Roueff, E., Launay, F., Roncin, J. Y., & Subtil, J. L. 1993a, A&AS, 101, 273 [NASA ADS] [Google Scholar]
- Abgrall, H., Roueff, E., Launay, F., Roncin, J. Y., & Subtil, J. L. 1993b, A&AS, 101, 323 [NASA ADS] [Google Scholar]
- Abgrall, H., Roueff, E., Launay, F., Roncin, J. Y., & Subtil, J. L. 1993c, J. Mol. Spectr., 157, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Abgrall, H., Roueff, E., & Drira, I. 2000, A&AS, 141, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albornoz Vásquez, D., Rahmani, H., Noterdaeme, P., et al. 2014, A&A, 562, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagdonaite, J., Ubachs, W., Murphy, M. T., & Whitmore, J. B. 2014, ApJ, 782, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Bailly, D., Salumbides, E. J., Vervloet, M., & Ubachs, W. 2010, Mol. Phys., 108, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Balashev, S. A., Ivanchik, A. V., & Varshalovich, D. A. 2010, Astron. Lett., 36, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Bolmer, J., Ledoux, C., Wiseman, P., et al. 2019, A&A, in press DOI: 10.1051/0004-6361/201834422 [EDP Sciences] [Google Scholar]
- Carswell, R. F., & Webb, J. K. 2014, Astrophysics Source Code Library [record ascl:1408.015] [Google Scholar]
- Dabrowksi, I., & Herzberg, G. 1976, Can. J. Phys., 54, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Dapra, M., Bagdonaite, J., Murphy, M. T., & Ubachs, W. 2015, MNRAS, 454, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Dickenson, G. D., Niu, M. L., Salumbides, E. J., et al. 2013, Phys. Rev. Lett., 110, 193601 [PubMed] [Google Scholar]
- Hinnen, P. C., Werners, S. E., Stolte, S., Hogervorst, W., & Ubachs, W. 1995, Phys. Rev. A, 52, 4425 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanchik, A., Petitjean, P., Varshalovich, D., et al. 2005, A&A, 440, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanov, T. I., Roudjane, M., Vieitez, M. O., et al. 2008, Phys. Rev. Lett., 100, 093007 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, T. I., Dickenson, G. D., Roudjane, M., et al. 2010, Mol. Phys., 108, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Jennings, D. E., & Brault, J. W. 1993, J. Mol. Spectr., 102, 265 [Google Scholar]
- Jonin, C., Liu, X., Ajello, J. M., James, G. K., & Abgrall, H. 2000, ApJS, 129, 247 [NASA ADS] [CrossRef] [Google Scholar]
- King, J. A., Webb, J. K., Murphy, M. T., & Carswell, R. F. 2008, Phys. Rev. Lett, 101, 251304 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- King, J. A., Murphy, M. T., Ubachs, W., & Webb, J. K. 2011, MNRAS, 417, 3010 [NASA ADS] [CrossRef] [Google Scholar]
- Komasa, J., Piszczatowski, K., Łach, G., et al. 2011, J. Chem. Theory Comput., 7, 3105 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X., Shemansky, D. E., Ajello, J. M., et al. 2000, A&AS, 129, 267 [Google Scholar]
- Malec, A. L., Buning, R., Murphy, M. T., et al. 2010, MNRAS, 403, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Meshkov, V. V., Stolyarov, A. V., Ivanchik, A. V., & Varshalovich, D. A. 2006, Sov. J. Exp. Theor. Phys., 83, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Philip, J., Sprengers, J. P., Pielage, T., et al. 2003, Can. J. Chem., 82, 713 [CrossRef] [Google Scholar]
- Rahmani, H., Wendt, M., Srianand, R., et al. 2013, MNRAS, 435, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhold, E., Buning, R., Hollenstein, U., et al. 2006, Phys. Rev. Lett., 96, 151101 [NASA ADS] [CrossRef] [Google Scholar]
- Salumbides, E. J., Bailly, D., Khramov, A., et al. 2008, Phys. Rev. Lett., 101, 223001 [NASA ADS] [CrossRef] [Google Scholar]
- Salumbides, E. J., Dickenson, G. D., Ivanov, T. I., & Ubachs, W. 2011, Phys. Rev. Lett., 107, 043005 [NASA ADS] [CrossRef] [Google Scholar]
- Salumbides, E. J., Bagdonaite, J., Abgrall, H., Roueff, E., & Ubachs, W. 2015, MNRAS, 450, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, R. I. 1975, Astroph. Lett., 16, 3 [NASA ADS] [Google Scholar]
- Thompson, R. I., Bechtold, J., Black, J. H., et al. 2009, ApJ, 703, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., Malec, A. L., Carswell, R. F., et al. 2010, ApJ, 718, L156 [NASA ADS] [CrossRef] [Google Scholar]
- Ubachs, W. 2018, Space Sci. Rev., 214, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Ubachs, W., & Reinhold, E. 2004, Phys. Rev. Lett., 92, 101302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ubachs, W., Buning, R., Eikema, K. S. E., & Reinhold, E. 2007, J. Mol. Spectr., 241, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Ubachs, W., Bagdonaite, J., Salumbides, E. J., Murphy, M. T., & Kaper, L. 2016, Rev. Mod. Phys., 88, 021003 [NASA ADS] [CrossRef] [Google Scholar]
- Varshalovich, D. A., & Levshakov, S. A. 1993, JETP Lett., 58, 237 [NASA ADS] [Google Scholar]
- Wendt, M., & Molaro, P. 2011, A&A, 526, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.