| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201834606 | |
| Published online | 12 February 2019 | |
Origin of the multiwavelength emission of PKS 0502+049
1
ICRANet-Armenia, Marshall Baghramian Avenue 24a, Yerevan 0019, Armenia
2
ICRANet, P.zza della Repubblica 10, 65122 Pescara, Italy
e-mail: narek@icra.it
Received:
8
November
2018
Accepted:
15
December
2018
The origin of the multiwavelength emission from PKS 0502+049 neighboring the first cosmic neutrino source TXS 0506+056 is studied using the data observed by Fermi-Large Area Telescope and Swift UltraViolet/Optical Telescope and X-Ray Telescope. This source was in a flaring state in the considered bands before and after the neutrino observations in 2014–2015, characterized by hard emission spectra in the X-ray and γ-ray bands, ≃1.5 − 1.8 and ≤2.0, respectively. During the neutrino observations, the γ-ray spectrum shows a deviation from a simple power-law shape, indicating a spectral cutoff at Ec = 8.50 ± 2.06 GeV. The spectral energy distributions of PKS 0502+049 are modeled within a one-zone leptonic scenario assuming that high energy γ-ray emission is produced either by inverse Compton scattering of synchrotron or dusty torus photons by the electron population that produce the radio-to-optical emission. Alternatively, the observed γ-rays are modeled considering inelastic interaction of protons, when the jet interacts with a dense gaseous target. During the neutrino observations, the γ-ray data are best described when the proton energy distribution is ∼E−2.61p and if the protons are effectively accelerated up to 10 PeV, the expected neutrino rate is ∼1.1 events within 110 days. In principle, if the γ-ray emission with a hard photon index observed during the flaring periods extends up to teraelectronvolt energies, the expected rate can be somewhat higher, but such conditions are hardly possible. Within the hadronic interpretation, the γ-ray data can be reproduced only when the accretion rate of PKS 0502+049 is in the super-Eddington regime, as opposed to the leptonic scenario. From the point of view of the necessary energetics, as well as considering that the required parameters are physically reasonable, when the neutrinos were observed the broadband emission from PKS 0502+049 was most likely of a leptonic origin.
Key words: gamma rays: galaxies / galaxies: active / galaxies: jets / quasars: individual: PKS 0502+049 / radiation mechanisms: non-thermal
© ESO 2019
1. Introduction
The recent observations of very high energy (>100 GeV; VHE) astrophysical neutrinos by IceCube (IceCube Collaboration 2013; Aartsen et al. 2013) have opened a new window on studying the non-thermal hadronic processes in the Universe. The neutrino events are distributed isotropically on the sky, suggesting they are of an extragalactic origin. Different source candidates and scenarios have been proposed to explain the origin of the observed neutrinos (e.g., see Khiali & de Gouveia Dal Pino 2016; Murase et al. 2016; Wang & Liu 2016 and Ahlers & Halzen 2015 for a review) but none of them has so far been statistically supported by the observational data.
The blazar sub-class of active galactic nuclei is often considered as the most likely sources of VHE neutrinos. Such a consideration is natural considering that blazars are among the most luminous and energetic sources in the Universe. Blazars have two jets ejected in opposite directions, one of which is pointing towards the Earth, and they are usually sub-grouped into flat spectrum radio quasars (FSRQs) and BL Lac objects, depending on the emission line properties (Urry & Padovani 1995). The small inclination angle and the relativistic motion in the blazar jets substantially increase their apparent luminosity, so that their emission can be detected across the entire electromagnetic spectrum, from radio to high energy (>100 MeV; HE) or VHE γ-ray bands. The non-thermal spectral energy distribution (SED) of blazars has two broad non-thermal peaks – one at the IR/optical/UV or X-ray and the other at HE γ-ray bands. The first peak is due to synchrotron emission of energetic electrons, while the second one can be explained by several different mechanisms. For example, in the so-called Leptonic scenarios, the HE emission can be explained by inverse Compton scattering of synchrotrons or external photons (Ghisellini et al. 1985; Ghisellini & Tavecchio 2009; Sikora et al. 1994). Generally, these leptonic scenarios are successfully applied to explain the observed properties in different bands, but sometimes fail to reproduce some observed features such as very fast variability almost in all observed bands (e.g., Mrk 501 Albert et al. 2007 or PKS 2155-304 Aharonian et al. 2007).
As an alternative, the HE emission can be explained by the interaction of energetic protons when they are effectively accelerated in the blazar jets. The HE component can be due to proton interaction either with a gaseous target (via proton–proton (pp) collisions; Dar & Laor 1997; Beall & Bednarek 1999; Bednarek & Protheroe 1997) or with a photon field (proton-γ (pγ) when their energy exceeds the threshold of Δ resonance (Mannheim 1995, 1993; Mannheim & Biermann 1989; Mücke & Protheroe 2001; Mücke et al. 2003), or due to proton synchrotron emission (Mücke & Protheroe 2001; Mücke et al. 2003). The photomeson reaction (pγ) is more extensively used to explain the emission from blazars (Böttcher et al. 2013), as it is more likely to have a dense radiation target within the jet than a nuclear one (unless it is of an external origin).
Both types of blazars, FSRQs and BL Lacs, are usually considered as effective neutrino emitters. For example, Kadler et al. (2016) showed that one of the highest neutrino events detected so far (∼2 PeV) possibly correlates with the bright flare of FSRQ PKS B1414-418. On the other hand, different models (e.g., Tavecchio et al. 2014; Tavecchio & Ghisellini 2015) also predict neutrino emission from BL Lac objects: Padovani et al. (2016) showed spatial correlation between the extreme BL Lacs (emitting HE γ-rays above 50 GeV) and the arrival direction of the observed neutrino events, once more confirming the blazar-neutrino association.
Though blazars have been so far considered as the main sources of VHE neutrinos, no significant association between them and neutrino events has yet been found. The most promising candidate so far is the blazar TXS 0506+056 (with the coordinates of RA = 77.36 and Dec = +5.69), which can be associated with the neutrino event IceCube-170922A, detected on 22 September 2017 (IceCube Collaboration et al. 2018). TXS 0506+056 is a bright blazar in the megaelectronvolt (MeV)/gigaelectronvolt (GeV) band at the redshift of z = 0.3365 ± 0.001 (Paiano et al. 2018). The multiwavelength observation campaign started after the neutrino alert showed that the source was in an active state almost in all electromagnetic bands, most interestingly flaring in the HE and VHE γ-ray bands (IceCube Collaboration et al. 2018). Moreover, IceCube has reported an independently observed 3.5σ excess of neutrinos from the direction of TXS 0506+056 between September 2014 and March 2015 (IceCube Collaboration 2018), strengthening the association between the neutrino events and TXS 0506+056. Further, dissection in space, time, and energy of the region around the IceCube-170922A showed that in the γ-ray band the emission from the nearby flaring blazar PKS 0502+049 dominates at low energies, but TXS 0506+056 dominates the sky above energies of a few GeV (Padovani et al. 2018). Also, during the period of the neutrino excess in 2014–2015, the γ-ray emission from TXS 0506+056 hardened with an excess of hard γ-ray radiation at the highest energies observable by the Fermi-Large Area Telescope (Fermi-LAT; Padovani et al. 2018). All these make TXS 0506+056 the most probable source of the observed VHE neutrinos and many different scenarios have been already proposed to explain the observed neutrinos (Ansoldi et al. 2018; Gao et al. 2019; Cerruti et al. 2019; Keivani et al. 2018; Murase et al. 2018; Liao et al. 2018; Wang et al. 2018; Sahakyan 2018).
In this paper, considering the interest toward the region of the sky with TXS 0506+056, the origin of the multiwavelength emission from the neighboring bright source PKS 0502+049 (at z = 0.954, Drinkwater et al. 1997) is investigated using the data from Swift UltraViolet/Optical Telescope (UVOT) and X-Ray Telescope (XRT) and Fermi-LAT observations. This study is motivated by the fact that PKS 0502+049 is only ∼1.2° far from TXS 0506+056 and in principle if the neutrinos are produced in the jet of PKS 0502+049, they could make some contribution to the IceCube observed events. The aims are: (i) the investigation of PKS 0502+049 emission properties when VHE neutrinos were observed, using the multiwavelength light curves, (ii) the testing of various emission scenarios modeling SEDs obtained in different periods and (iii) the estimation of the PKS 0502+049 neutrino emission rate assuming that the observed HE emission is due to the interaction of protons. Such a study will be an independent test of whether, in the case when hadronic processes are responsible for the HE emission from PKS 0502+049, the produced neutrinos can have any contribution to the events observed by IceCube.
The paper is structured as follows. The Fermi-LAT and Swift UVOT/XRT data analyses are described in Sect. 2, while the spectral analyses are presented in Sect. 3. In Sect. 4 the modeling of broadband SEDs within leptonic and hadronic scenarios is presented. The results are discussed and summarized in Sect. 5.
2. Observations and data reduction
2.1. Fermi-LAT
For the current study the Fermi-LAT (Atwood et al. 2009) data accumulated during more than approximately nine years, from 4 August 2008 to 1 January 2018, are used. The 100 MeV–300 GeV events from a 16.9 ° ×16.9° square region of interest (ROI) around the γ-ray position of PKS 0502+049 (RA, Dec) = (76.343, 4.998) were downloaded and analyzed using Fermi Science Tools v10r0p5 with P8R2_SOURCE_V6 instrument response function. The events are binned with gtbin tool into 0.1 ° ×0.1° pixels and 34 logarithmically equal energy intervals. The standard cuts (e.g., on the maximum zenith angle (90°) to filter γ-rays from the Earth’s limb) are applied with gtselect and gtmktime tools. The model file describing the ROI was created using Fermi-LAT eight-year point source list1, including the sources within ROI+5° from the target and Galactic gll_iem_v06 and isotropic iso_P8R2_SOURCE_V6_v06 background models with the normalizations being free parameters. The normalization and spectral indices of the sources within ROI are left as free parameters while for the sources outside the ROI they are fixed to their values obtained during eight years of Fermi-LAT observations. Then, a binned maximum likelihood analyses is performed with the gtlike tool. Initially, the spectrum of PKS 0502+049 was modeled using a log-parabolic model (Massaro et al. 2004; as in the Fermi-LAT catalogs) but for the light curve calculations (for shorter periods) a power-law model was used.
The light curve generated by the adaptive binning method was used to investigate the flux variation in time. This novel method allows us to identify not only different active states of the source but also find rapid changes in the γ-ray band. The considered period was divided into short (not equal) intervals assuming constant 15% uncertainty in each bin. The light curve calculated above E0 = 214 MeV optimum energy (for calculation of E0, see Lott et al. 2012) is shown in Fig. 1 (upper panel). The source quiescent state sometimes was followed by rapid and bright flaring periods. The most bright and prolonged γ-ray active period was observed from approximately MJD 56900 to MJD 57150, when the highest flux of F> 214 MeV = (2.31 ± 0.42)×10−6 photon cm−2 s−1 was observed on MJD 56909.5 for 4.81 h. The photon index variation in time is presented in Fig. 1b, which shows that the flux increase was accompanied by photon index hardening, the hardest photon index being 1.82 ± 0.14, significantly different from the photon index averaged over nine years (2.33 ± 0.02). This photon index is unusual for FSRQs, which typically have a soft photon index in the MeV/GeV band but for several FSRQs occasionally such hard photon index was observed during rapid flares (Sahakyan & Gasparyan 2017; Pacciani et al. 2014; Gasparyan et al. 2018).
 |
Fig. 1. Top panel: γ-ray light curve of PKS 0502+049 above 214.0 MeV from August 4, 2008 to January 1st, 2018, with a constant uncertainty of 15%. Bottom panels: γ-ray light curve (a) and photon index (b), X-ray (c) and optical/UV light curves (d). The periods P1, P2 and P3 are market with light gray, light red and light yellow colors, respectively, and the period when a 3.5σ excess of neutrinos between September 2014 and March 2015 was observed (P0) is in light blue. The blue dot-dashed line shows the period of detection of a HE neutrino event on September 22, 2017. |
Then, the light curves during the flares were further analyzed. The flare rise and decay profiles could be constrained only for the bright period around MJD 57100 (see the light curve with one-day bins in Fig. 2). The flare time profiles were analyzed using the double exponential form function given in Abdo et al. (2010) and the fit results are shown in Fig. 2 with a blue line. The rise and decay times of the flare are tr = 2.00 ± 0.35 days and td = 2.62 ± 0.39 days, respectively, with the flare peak at tp = t0 + tr td/(tr + td)ln(td/tr) = MJD 57103.43. The constant level present in the flare is (5.80 ± 0.39)×10−7 photon cm−2 s−1 with the peak flux of (4.20 ± 0.23)×10−6 photon cm−2 s−1.
 |
Fig. 2. Light curve sub-interval with one-day bins for the flaring period. The blue line shows the flare fit with a double exponential function. |
2.2. Swift XRT/UVOT observations
The Neil Gehrels Swift observatory (Swift; Gehrels et al. 2004) observed PKS 0502+049 thirty-five times during the considered period. All the Swift observations were analyzed using the latest version of Swift data reduction software. The data were reprocessed with the standard filtering and screening criteria with the source- and background- extraction regions being defined correspondingly as a 20 pixel (47″) radius circular region and an annulus with inner and outer radii being 51 (120″) and 85 pixels (200″), respectively, both centered at the source position. For all observations, the count rate was below 0.5 count s−1, implying no evidence of pile-up. Because of the small number of counts, the Cash statistic (Cash 1979) on the unbinned data was used. The spectra were fitted with an absorbed power-law model in the 0.3–10 keV energy band, with a neutral hydrogen column density fixed to its Galactic value 8.76 × 1020 cm−2 using XSPEC v12.9.1a (Arnaud 1996).
The Swift XRT light curve is shown in Fig. 1c and the corresponding parameters are given in Table 1. Although the number of available observations is not sufficient for detailed temporal analyses, the X-ray flux increase during the bright γ-ray periods can be noticed. The highest X-ray flux of (8.91 ± 0.42)×10−12 erg cm−2 s−1 was observed on MJD 56912.78. No significant spectral evolution was observed in the X-ray band, the photon index most of the time being very hard ∼(1.2 − 1.6) and the softest photon index being ΓX ≃ 1.87 ± 0.39.
Summary of Swift XRT and UVOT observations of PKS 0502+049.
The Swift UVOT data have also been analyzed. The source counts were extracted from a circular region of a five-arcsec radius centered on the source, while the background counts from a surrounding annulus (source-free region) which had inner and outer radii of 27″ and 35″, respectively. Counts were converted to fluxes using the uvotsource tool and zero-points from Breeveld et al. (2011). The magnitudes were corrected for extinction, using the reddening coefficient E(B − V) from Schlafly & Finkbeiner (2011) and the ratios of the extinction to reddening Aλ/E(B − A) for each filter from Fitzpatrick (1999), then converting to fluxes following Breeveld et al. (2011). The averaged flux in Swift UVOT bands is given in Table 1 and shown in Fig. 1d. During the γ-ray bright periods, the optical/UV flux has also increased.
3. Spectral analyses
The spectra obtained in the following periods are used for investigation of the origin of the multiwavelength emission from PKS 0502+049:
-
From MJD 56949.0 to 57059.0 (P0) corresponding to the neutrino observation window (IceCube Collaboration 2018), Swift observations around this period, Obsid: 33408003, 33408004, 33408005, and 33408006 were analyzed by merging them in order to increase the exposure and statistics as they have similar X-ray fluxes and photon indices;
-
From MJD 56908.60 to MJD 56909.80 (P1) during the largest γ-ray flaring period with available quasi-simultaneous Swift observation (Obsid: 33408001);
-
From MJD 56909.80 to MJD 56922.23 (P2) when the highest X-ray flux was observed (Obsid: 33408002) with a moderate brightening in the γ-ray band;
-
From MJD 57099.53 to MJD 57108.42 (P3), corresponding to another bright γ-ray flaring state coinciding with the Swift observation of Obsid: 33408009.
These periods are marked with light gray, light red, light blue, and light yellow colors in Fig. 1a. The γ-ray spectra were obtained applying an unbinned likelihood analyses method using a power-law model spectrum with the normalization and index considered as free parameters. After obtaining the best-fit values, we fixed them for the SED calculations.
The results are shown in Fig. 3 and the corresponding parameters in Table 2. The γ-ray spectrum contemporaneous with the IceCube observational window (∼110 days; gray) follows the same tendency as that averaged over nine years (light gray) while the γ-ray spectra in the active periods (blue, red, and magenta) are significantly different. There is an evident curvature in the γ-ray spectra obtained during P0 (see also Liang et al. 2018) so an alternative fit with a power law with an exponential cut-off model in the form of 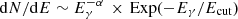 and a log-parabolic function in the form of dN/dE ∼ (Eγ/Ebr)−(α + βlog(Eγ/Ebr)) were applied to check if the curvature in the spectrum is statistically significant. The models are compared using a log likelihood ratio test: the significance is the square root of twice the difference in the log likelihoods. The first model with α = 2.07 ± 0.04 and Ecut = 8.50 ± 2.06 GeV is preferred over the power-law model with a significance of 7.36σ. Also, the second model with α = 2.23 ± 0.02 and β = 0.11 ± 0.01 is preferred with a significance of 6.82σ. The curvature in the blazar emission spectra can be due to different reasons. For example, log-parabolic spectra can be formed when the leptons in the jet undergo stochastic acceleration; a power law with an exponential cut-off spectrum is expected when the energy distribution of the emitting electrons has a sharp energy upper cut-off because of the efficiency of the acceleration mechanisms. These results show that the γ-ray emission from PKS 0502+049 and consequently the spectra of particles responsible for the emission were characterized by a cut-off at tens of GeV when the neutrino events were detected by IceCube. Interestingly, during the flares before (P1 and P2) and after (P3) this period the γ-ray spectra extend up to tens of GeV with a significantly harder photon index, for example Γ = 1.88 ± 0.06 during P1 and Γ ≃ 2.0 during P2 and P3, implying that VHE photons were dominating. This substantial hardening might be caused by an injection of new (fresh) particles and/or a change in the location of the emission region where the acceleration is more efficient or the cooling is rather slow allowing the particles to reach higher energies. To generate X-ray spectra, again the Cash statistic on Swift unbinned data was applied. Then, in order to increase the significance of individual points in the SEDs calculations, a denser rebinning was applied, restricting the energy range to >0.5 keV. The results of the fit are given in Table 1 (similar parameters for the merged observations are: ΓX = 1.56 ± 0.04, FX(0.3 − 10 keV)=(4.85 ± 0.15) × 10−12 erg cm−2 s−1) and the corresponding spectra are shown in Fig. 3. During the bright γ-ray periods both the optical/UV and X-ray fluxes increased: the observed shape of UVOT data suggest that it corresponds to the HE tail of the synchrotron component while the hard X-ray spectra are due to the second emission component (in the case of leptonic interpretation).
and a log-parabolic function in the form of dN/dE ∼ (Eγ/Ebr)−(α + βlog(Eγ/Ebr)) were applied to check if the curvature in the spectrum is statistically significant. The models are compared using a log likelihood ratio test: the significance is the square root of twice the difference in the log likelihoods. The first model with α = 2.07 ± 0.04 and Ecut = 8.50 ± 2.06 GeV is preferred over the power-law model with a significance of 7.36σ. Also, the second model with α = 2.23 ± 0.02 and β = 0.11 ± 0.01 is preferred with a significance of 6.82σ. The curvature in the blazar emission spectra can be due to different reasons. For example, log-parabolic spectra can be formed when the leptons in the jet undergo stochastic acceleration; a power law with an exponential cut-off spectrum is expected when the energy distribution of the emitting electrons has a sharp energy upper cut-off because of the efficiency of the acceleration mechanisms. These results show that the γ-ray emission from PKS 0502+049 and consequently the spectra of particles responsible for the emission were characterized by a cut-off at tens of GeV when the neutrino events were detected by IceCube. Interestingly, during the flares before (P1 and P2) and after (P3) this period the γ-ray spectra extend up to tens of GeV with a significantly harder photon index, for example Γ = 1.88 ± 0.06 during P1 and Γ ≃ 2.0 during P2 and P3, implying that VHE photons were dominating. This substantial hardening might be caused by an injection of new (fresh) particles and/or a change in the location of the emission region where the acceleration is more efficient or the cooling is rather slow allowing the particles to reach higher energies. To generate X-ray spectra, again the Cash statistic on Swift unbinned data was applied. Then, in order to increase the significance of individual points in the SEDs calculations, a denser rebinning was applied, restricting the energy range to >0.5 keV. The results of the fit are given in Table 1 (similar parameters for the merged observations are: ΓX = 1.56 ± 0.04, FX(0.3 − 10 keV)=(4.85 ± 0.15) × 10−12 erg cm−2 s−1) and the corresponding spectra are shown in Fig. 3. During the bright γ-ray periods both the optical/UV and X-ray fluxes increased: the observed shape of UVOT data suggest that it corresponds to the HE tail of the synchrotron component while the hard X-ray spectra are due to the second emission component (in the case of leptonic interpretation).
 |
Fig. 3. SEDs of PKS 0502+049 during the IceCube observational window (P0; gray) and active states P1 (blue), P2 (red), and P3 (magenta). The averaged γ-ray spectrum during the considered nine years and the archival low energy data from ASI science data center are shown in light gray. Gray, blue, and red solid lines show the models when inverse Compton scattering of synchrotron (SSC) and torus (EIC) photons are considered, while the gray dot-dashed line is the fitting only with the SSC component. The model fit parameters are given in Table 3. The inset shows the γ-ray spectra from pp interactions where the solid lines are the modeling when the cut-off energy in the proton spectrum is fixed to 10 PeV and the gray dot-dashed line is the case when the hard spectrum of protons is considered. The axes are the same as in the main plot. All models have been corrected for γγ absorption by the extragalactic background light using the model of Domínguez et al. (2011). |
Parameters of γ-ray spectral analysis.
4. Modeling of broadband spectra
As has been already noted, there are two conceptually different mechanisms that can be responsible for the HE component in blazar emission spectra. The theoretical models are generally divided into leptonic and hadronic ones depending on whether the electrons or protons are responsible for the emission. Here, the multiwavelength emission of PKS 0502+049 is discussed within both leptonic and hadronic emission scenarios.
4.1. Hadronic γ-rays and neutrinos
In the hadronic or lepto-hadronic blazar jet emission scenarios, the relativistic jet material is composed of protons (p) and electrons (e) that start to emit when accelerated to ultra high energies. The low energy component is dominated by direct synchrotron emission of electrons while the HE component is completely or partially formed due to the radiative output of energetic protons. The blazar jets are ideal laboratories where the protons are sometimes accelerated to above 1018 eV (Mannheim & Biermann 1989) and their energy is converted into electromagnetic power either due to interaction with gaseous (Bednarek & Protheroe 1997; Barkov et al. 2010; Araudo et al. 2013; Bednarek & Banasiński 2015; de la Cita et al. 2016) or photon targets (Mannheim 1995, 1993; Mannheim & Biermann 1989; Mücke & Protheroe 2001; Mücke et al. 2003), and/or via synchrotron emission (Mücke & Protheroe 2001; Mücke et al. 2003). These channels might, in fact, operate simultaneously in a competing way and contribute to the total energy loss of protons.
One of the scenarios most widely applied to explain the HE emission component assumes that the protons interact with the photon field of an internal (e.g., synchrotron photons) or external (e.g., disk photon reflected from a broad line region (BLR) or from a dusty torus) origin. Then, γ-rays, neutrinos, and electron-positron pairs (e−, e+) are produced from the decay of neutral and charged pions. The γ-rays and e−, e+ pairs interact and initiate an electromagnetic cascade that reduces the energy of the electromagnetic component down to energies at which the source becomes transparent to the γγ pair production. In this case, the spectra of the produced neutrinos can be well constrained when the data above 100 GeV are present, which are missing for PKS 0502+049. Roughly, assuming that in the pγ interactions comparable energy is released into the electromagnetic component (from X- to γ-rays) and neutrinos, ϕγ ≃ 4 ϕν (e.g., Halzen & Kheirandish 2016; Halzen & Hooper 2005), some constraints on the expected neutrino flux can be imposed. For the X- to γ-ray emission spectrum in the form of dNγ/dEγ = N0, γ(Eγ/100 eV)−Γγ Exp(−Eγ/Ecut) (the power-law spectrum gives poor modeling), the energy flux carried by the electromagnetic component is ϕγ ≃ 9.81 × 10−11 erg cm−2 s−1 estimated by fitting the observed data. In this case, the differential spectrum of the accompanying neutrinos can be estimated from 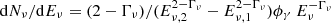 , which predicts a flux of ≃6.55 × 10−16 TeV−1 cm−2 s−1 at 100 TeV assuming a spectral index of 2.1 ± 0.2, adopting Eν, min = 1 TeV and Eν, max = 10 PeV. Even if this is a very strict upper limit (the exact estimations require simulations of the proton acceleration and emission processes as well as detailed tracking of cascade propagation), it is already lower than the IceCube measured flux.
, which predicts a flux of ≃6.55 × 10−16 TeV−1 cm−2 s−1 at 100 TeV assuming a spectral index of 2.1 ± 0.2, adopting Eν, min = 1 TeV and Eν, max = 10 PeV. Even if this is a very strict upper limit (the exact estimations require simulations of the proton acceleration and emission processes as well as detailed tracking of cascade propagation), it is already lower than the IceCube measured flux.
The next scenario for neutrino emission from blazar jets assumes that a dense and compact target (e.g., cloud(s) from BLR, Dar & Laor 1997; Beall & Bednarek 1999; Araudo et al. 2010 or a star/star envelope, Bednarek & Protheroe 1997; Barkov et al. 2010; Araudo et al. 2013; Bednarek & Banasiński 2015; de la Cita et al. 2016) crosses the jet and the accelerated protons penetrating into it interact with the target protons. Depending on the number of jet-crossing targets, the emission can appear as steady (e.g., several clouds can interact with the jet simultaneously) or flare-like. Proton–proton (pp) interactions produce neutral (π0) and charged pions (π±), which then decay into γ-rays (π0 → γγ) and neutrinos (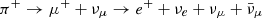 ). Unlike the case of the pγ interaction scenario, a radiation in the MeV/GeV bands is also produced, so the γ-ray data can be used to constrain the proton content in the jet. One of the key points in the jet-target interaction scenario is the acceleration of protons to energies necessary for the production of the observed γ-rays and neutrinos; depending on the distance from the base of the jet, where the penetration occurs, the protons can be either accelerated in the jet or in the target when a strong shock is formed, and their energy can go well beyond 10 PeV (a simple relation between the proton acceleration region size R and cooling timescale yields Emax ≃ 3.0 × 1015 (η/0.1) (B/1G) (R/1013 cm) eV Sahakyan 2018).
). Unlike the case of the pγ interaction scenario, a radiation in the MeV/GeV bands is also produced, so the γ-ray data can be used to constrain the proton content in the jet. One of the key points in the jet-target interaction scenario is the acceleration of protons to energies necessary for the production of the observed γ-rays and neutrinos; depending on the distance from the base of the jet, where the penetration occurs, the protons can be either accelerated in the jet or in the target when a strong shock is formed, and their energy can go well beyond 10 PeV (a simple relation between the proton acceleration region size R and cooling timescale yields Emax ≃ 3.0 × 1015 (η/0.1) (B/1G) (R/1013 cm) eV Sahakyan 2018).
The jet-target interaction scenario requires several parameters for accurate estimation of the duration, rate, and efficiency of interactions. Especially, the parameters describing the target are needed for calculating the related radiative outputs and estimation of the required total energy of protons. In this case, we do not specify the origin of the dense target and only consider its density indirectly constrained by the observations. Namely, the estimated variability of tv ≃ 2 days can be used to define the density of the target (nH), that is, comparing it with the characteristic cooling time of pp interactions, tpp ≃ (KσppnH)−1 ≃ 1015/nH, so nH = 5.78 × 109 cm−3 which is not significantly different from the usually estimated values. As this target density is high, the protons lose a significant fraction of their energy at pp collisions: the interaction is in a radiatively efficient regime, tpp ≤ tv, so most of the γ-rays are emitted around tv rather than when the target is already accelerated to high velocities.
The γ-ray spectra of PKS 0502+049 observed in different periods are modeled by expressing the energy distribution of energetic protons as 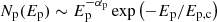 , where the cut-off energy Ep, c is initially considered as a free parameter and then fixed to an arbitrary value of Ec, p = 10 PeV; this is selected to ensure the produced neutrinos will have energy above 100 TeV, but, in principle, a cut-off at much higher energies cannot be excluded. In order to constrain the model parameters more efficiently (the normalization of proton content and their power-law spectral index), that is, to find the parameters that statistically better explain the observed data, the Markov chain Monte Carlo (MCMC) method is employed. This allows us to derive the best-fit and uncertainty distributions of the spectral model parameters through MCMC sampling of their likelihood distributions (Zabalza 2015). The neutrino spectra above 100 GeV are calculated following Kelner et al. (2006) while at lower energies a delta function approximation is used (for exact formula see Sahakyan et al. 2014).
, where the cut-off energy Ep, c is initially considered as a free parameter and then fixed to an arbitrary value of Ec, p = 10 PeV; this is selected to ensure the produced neutrinos will have energy above 100 TeV, but, in principle, a cut-off at much higher energies cannot be excluded. In order to constrain the model parameters more efficiently (the normalization of proton content and their power-law spectral index), that is, to find the parameters that statistically better explain the observed data, the Markov chain Monte Carlo (MCMC) method is employed. This allows us to derive the best-fit and uncertainty distributions of the spectral model parameters through MCMC sampling of their likelihood distributions (Zabalza 2015). The neutrino spectra above 100 GeV are calculated following Kelner et al. (2006) while at lower energies a delta function approximation is used (for exact formula see Sahakyan et al. 2014).
In the inset of Fig. 3, the data observed during P0, P1, and P2 are modeled as γ-rays from the decay of neutral pions (π0). During the neutrino observation in 2014–2015, when the power-law index and cut-off in the proton spectrum are considered as free parameters, the data are best described when αp = 2.60 ± 0.06 and Ep, c = 3.36 ± 2.95 TeV. The power-law index is mostly defined by the observed γ-ray photon index, whereas the cut-off with a large statistical uncertainty is constrained by the last point in the γ-ray spectrum. When the cut-off is fixed to much larger values, Ep, c = 10 PeV (solid gray line), the data can be reproduced when αp = 2.61 ± 0.06, which predicts also an emission beyond the observed γ-ray data. Due to the steep spectrum of emitting protons, the γ-ray emission is dominated by the decay of π0 with a negligible contribution from secondary particles produced by the decay of charged pions. On the other hand, such a steep spectrum also disfavors the possibility of producing a detectable flux of VHE neutrinos. The hardest power-law index when the observed data can still be explained is αp, c = 2.2 (gray dot-dashed line); however, this will heavily overpredict the γ-ray data above ∼2 GeV. Within the applied scenario, the γ-ray spectra observed during the bright P1 and P2 periods can also be modeled (blue and solid lines) when harder indices of αp = 2.14 ± 0.10 and αp = 2.23 ± 0.07 are considered, respectively. Again, the cut-off energy cannot be constrained by the data and, in principle, strong emission of γ-rays and neutrinos up to VHEs can be expected.
In this interpretation the total energy of protons (above 1 GeV) in the jet as well as their luminosity can be estimated. Defining the luminosity as Lpp = Wpp/tpp, where Wpp = ∫ EpNp(Ep)dEp is the total proton energy integrated from Ep, min to Ep, max and tpp = 2 days is the cooling time of protons, the γ-ray data averaged over the IceCube observational window can be modeled when Lpp ≃ 1.60 × 1049 erg s−1. This luminosity can be as large as Lpp ≃ 2.60 × 1050 erg s−1 when the γ-ray active periods are considered. These estimations show that if the γ-rays from PKS 0502+049 are indeed produced in pp interactions, then its jet should be very powerful and efficient in order to transfer a large amount of energy to protons.
Constraining the energy distribution of protons and their luminosity, the differential spectrum of the accompanying neutrinos can be calculated straightforwardly. Then, the number of neutrinos detected in a certain exposure of texp can be estimated from Nν ≃ texp ∫ Aeff(Eν)dNν/dEνdEν, using the effective area Aeff(Eν) from Aartsen et al. (2017). The neutrino rate (> 200 GeV) expected within ∼110 days can be as large as ∼1.1 events when the energy distribution of protons follows 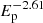 with a cut-off at 10 PeV. In principle, a higher rate (> 20) is possible when αp = 2.2 is considered but in this case the γ-ray data above 1 − 2 GeV cannot be explained. This is similar to the case applied in He et al. (2018) where again the γ-ray emission from PKS 0502+049 was interpreted within a jet-target interaction scenario but using a harder proton index. As in this case, the γ-ray data are not well explained when αp ≤ 2.0, which is natural considering the observed steep spectrum in the γ-ray band; when pp interaction is considered, the produced γ-rays will have nearly the same spectra as those of parent protons, αγ ≃ αp − 0.1. In principle, a hard power-law index of the protons is possible when normalizing it with the sub-GeV γ-ray data, but then a sharp cut-off will be required to describe the observed break at Ec, γ = 8.50 ± 2.06 GeV. Even at the most unrealistic case when Ec, p = 104 × Ec, γ, the neutrino spectrum,
with a cut-off at 10 PeV. In principle, a higher rate (> 20) is possible when αp = 2.2 is considered but in this case the γ-ray data above 1 − 2 GeV cannot be explained. This is similar to the case applied in He et al. (2018) where again the γ-ray emission from PKS 0502+049 was interpreted within a jet-target interaction scenario but using a harder proton index. As in this case, the γ-ray data are not well explained when αp ≤ 2.0, which is natural considering the observed steep spectrum in the γ-ray band; when pp interaction is considered, the produced γ-rays will have nearly the same spectra as those of parent protons, αγ ≃ αp − 0.1. In principle, a hard power-law index of the protons is possible when normalizing it with the sub-GeV γ-ray data, but then a sharp cut-off will be required to describe the observed break at Ec, γ = 8.50 ± 2.06 GeV. Even at the most unrealistic case when Ec, p = 104 × Ec, γ, the neutrino spectrum, 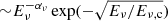 where Eν, c ≃ Ec, p/40 (Kappes et al. 2007), will drop above ∼2.1 TeV predicting almost no VHE neutrinos. Also, the expected number of neutrinos is somewhat uncertain when the γ-ray active periods are considered, as it strongly depends on the energy cut-off, which is unknown. For example, when the cut-off at 10 PeV is considered, the neutrino rate is 14.7 and 22.1 during P1 and P2, respectively, while in the case of ∼10 TeV it is as low as ∼0.75. This makes any possible claim for neutrino detection during the active periods significantly uncertain.
where Eν, c ≃ Ec, p/40 (Kappes et al. 2007), will drop above ∼2.1 TeV predicting almost no VHE neutrinos. Also, the expected number of neutrinos is somewhat uncertain when the γ-ray active periods are considered, as it strongly depends on the energy cut-off, which is unknown. For example, when the cut-off at 10 PeV is considered, the neutrino rate is 14.7 and 22.1 during P1 and P2, respectively, while in the case of ∼10 TeV it is as low as ∼0.75. This makes any possible claim for neutrino detection during the active periods significantly uncertain.
4.2. Leptonic HE γ-rays
In view of the problems in the hadronic scenarios applied (e.g., the required energetics), the observed broadband emission from PKS 0502+049 is discussed also within a leptonic scenario. The multiwavelength spectra for different periods are shown in Fig. 3 where the archival radio-optical data from the space science data center and the γ-ray spectra averaged over nine years are shown in light gray. The spectra in the period when VHE neutrinos were observed (P0) is shown in gray. During the γ-ray active periods, the flux increases in all other bands as well, and both components are shifted to higher energies. Here, in the leptonic interpretations, the broadband emission from PKS 0502+049 is modeled within the one-zone synchrotron/synchrotron self Compton (Maraschi et al. 1992; Bloom & Marscher 1996; Ghisellini et al. 1985) plus external inverse Compton (Sikora et al. 2009; Ghisellini & Tavecchio 2009; Błażejowski et al. 2000) scenarios.
In the framework of one-zone leptonic scenarios, the low energy emission (radio through optical) is described by the synchrotron emission of leptons in the magnetic field (B), while the HE component (from X-ray to HE γ-ray) is due to the inverse Compton scattering of internal photons, for example, synchrotron photons (synchrotron self-Compton (SSC)), or external photons (EIC), such as those emitted from the IR dusty torus. Within this scenario, it is assumed that a spherical region (blob) with a comoving radius Rb is moving with a bulk Lorentz factor Γb toward the observer and is filled with an isotropic population of electrons and a randomly oriented uniform magnetic field B. The energy spectrum of the injected electrons in the jet frame can be expressed as (e.g., Inoue & Takahara 1996)
for 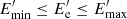 , where
, where 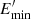 and
and 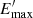 are the minimum and maximum electron energies, respectively. The emitted radiation will be Doppler-boosted by δ, which equals the bulk Lorentz factor for the small jet viewing angles. For the Doppler factor, a typical value of 20 (Ghisellini & Tavecchio 2015) is be adopted, which is usually used for the modeling of emission from FSRQs. The radius of the emission region can be constrained by the variability timescales: the radius cannot be larger than Rb ≤ c × t × δ/(1 + z)≃5.31 × 1016 (δ/20) cm.
are the minimum and maximum electron energies, respectively. The emitted radiation will be Doppler-boosted by δ, which equals the bulk Lorentz factor for the small jet viewing angles. For the Doppler factor, a typical value of 20 (Ghisellini & Tavecchio 2015) is be adopted, which is usually used for the modeling of emission from FSRQs. The radius of the emission region can be constrained by the variability timescales: the radius cannot be larger than Rb ≤ c × t × δ/(1 + z)≃5.31 × 1016 (δ/20) cm.
Usually, the Compton dominance (domination of the second emission peak) observed from FSRQs can be explained by inverse Compton scattering of the external photon fields. If the jet dissipation occurs within the BLR with a radius of 7.6 × 1017 cm for PKS 0502+049 (measured using RBLR ∼ λLλ(5100 Å)0.7 relation Oshlack et al. 2002), the dominant external photon fields are disk photons reflected by the BLR clouds. On the other hand, the recent observations in the VHE γ-ray band indicate that the emission region can also be well beyond the BLR where the dominant photon field is IR radiation of the dust torus (Abeysekara et al. 2015; Ahnen et al. 2015; Aleksić et al. 2011). These regions appear more favorable for the VHE γ-ray emission (e.g., Gasparyan et al. 2018). In the current study, the torus photons are taken into account assuming the emission from the torus has a blackbody spectrum with a temperature of T = 103 K and fills a volume that for simplicity is approximated as a spherical shell with a radius of RIR = 3.54 × 1018(Ldisc/1045)0.5 cm (Nenkova et al. 2008). The corresponding radiation energy density, as measured in the comoving frame, would be 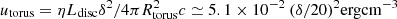 , where η = 0.6 (Ghisellini & Tavecchio 2009). During the fitting, the model free parameters (magnetic field and parameters describing the non-thermal electron distribution) and their uncertainties are estimated applying the MCMC method using the naima package (Zabalza 2015).
, where η = 0.6 (Ghisellini & Tavecchio 2009). During the fitting, the model free parameters (magnetic field and parameters describing the non-thermal electron distribution) and their uncertainties are estimated applying the MCMC method using the naima package (Zabalza 2015).
The modeling of SEDs observed during, P0, P1, and P2 is shown in Fig. 3 and the corresponding parameters are given in Table 3. In all modeling, the radio data are not considered as they are not simultaneous and the emission in this band can be produced from the low energy electrons in more extended regions. Initially, the HE component observed during P0 is modeled considering only SSC mechanisms (gray dot-dashed line) as, due to the compactness of the emitting region, the density of synchrotron photons might be dominating. The observed data are relatively well explained when 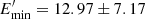 MeV, α = 1.82 ± 0.02, and
MeV, α = 1.82 ± 0.02, and 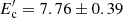 GeV. However, as the HE component exceeds that at lower energies, this modeling requires a strongly particle-dominated jet, Ue/UB ≃ 4.5 × 103 for B = 31.27 ± 0.61 mG. The required extreme parameters can be softened when the contribution from external photons is considered. For example, the solid gray line represents the modeling of the data considering inverse Compton scattering of both synchrotron and torus photons. This requires a softer power-law index for the electrons, α = 2.42 ± 0.28, and as the energy of torus photons exceeds the averaged energy of synchrotron ones, this modeling requires lower minimum and cutoff energies of
GeV. However, as the HE component exceeds that at lower energies, this modeling requires a strongly particle-dominated jet, Ue/UB ≃ 4.5 × 103 for B = 31.27 ± 0.61 mG. The required extreme parameters can be softened when the contribution from external photons is considered. For example, the solid gray line represents the modeling of the data considering inverse Compton scattering of both synchrotron and torus photons. This requires a softer power-law index for the electrons, α = 2.42 ± 0.28, and as the energy of torus photons exceeds the averaged energy of synchrotron ones, this modeling requires lower minimum and cutoff energies of 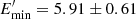 MeV and
MeV and 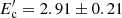 GeV, respectively. In this case, the synchrotron emission of the low energy electrons will exceed the observed radio flux a few times but as the radio data are not contemporaneous, this cannot be a strong argument to disfavor such modeling. Unlike the previous case, the system is close to equipartition, Ue/UB ≃ 19.6. Similarly, the spectra observed in bright P1 and P2 are modeled considering the SSC and EIC mechanisms. For both periods, the optical/UV and X-ray data can be explained by synchrotron/SSC emission, while the γ-ray data are due to the inverse Compton scattering of external photons from the dusty torus. During P1 the power-law index of emitting electrons was α = 1.61 ± 0.05 defined by the hard γ-ray photon index, while it was α = 1.90 ± 0.07 during P2 when a nearly flat spectrum in the γ-ray band was observed. The cut-off energy of
GeV, respectively. In this case, the synchrotron emission of the low energy electrons will exceed the observed radio flux a few times but as the radio data are not contemporaneous, this cannot be a strong argument to disfavor such modeling. Unlike the previous case, the system is close to equipartition, Ue/UB ≃ 19.6. Similarly, the spectra observed in bright P1 and P2 are modeled considering the SSC and EIC mechanisms. For both periods, the optical/UV and X-ray data can be explained by synchrotron/SSC emission, while the γ-ray data are due to the inverse Compton scattering of external photons from the dusty torus. During P1 the power-law index of emitting electrons was α = 1.61 ± 0.05 defined by the hard γ-ray photon index, while it was α = 1.90 ± 0.07 during P2 when a nearly flat spectrum in the γ-ray band was observed. The cut-off energy of 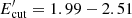 GeV is measured from the optical/UV data, which is not significantly different for the two periods. The magnetic field in P2 (B = 235.93 ± 8.17 mG) is slightly larger than that in P1 (B = 102.92 ± 8.03 mG) in agreement with the observed increase in the optical/UV bands. The total luminosity of the jet defined as Ljet = LB + Le, where
GeV is measured from the optical/UV data, which is not significantly different for the two periods. The magnetic field in P2 (B = 235.93 ± 8.17 mG) is slightly larger than that in P1 (B = 102.92 ± 8.03 mG) in agreement with the observed increase in the optical/UV bands. The total luminosity of the jet defined as Ljet = LB + Le, where  and
and 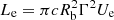 (Celotti & Ghisellini 2008), is in the range of Ljet ≃ (4.50 − 7.56)×1045 erg s−1. During P1 the jet is particle-dominated with Ue/UB = 167.9, while for P2 Ue/UB = 18.1.
(Celotti & Ghisellini 2008), is in the range of Ljet ≃ (4.50 − 7.56)×1045 erg s−1. During P1 the jet is particle-dominated with Ue/UB = 167.9, while for P2 Ue/UB = 18.1.
Parameters of γ-ray spectral analysis.
5. Discussion and conclusions
Blazar jets have always been assumed as the most promising sources of VHE neutrino emission. The recent association between the IceCube-170922A neutrino event with the γ-ray bright BL Lac object TXS 0506+056 has opened new perspectives for investigation of blazar jet physics. For the first time, the emission processes in relativistic jets can be studied using both γ-rays and neutrinos. Though there are various arguments favoring TXS 0506+056 as the main source for the observed VHE neutrinos, additional care must be taken when considering the presence of the nearby powerful γ-ray emitter PKS 0502+049. In this paper the origin of the multiwavelength emission from FSRQ PKS 0502+049 is investigated, aiming to verify whether or not the possible neutrino emission from PKS 0502+049 accompanying the observed γ-ray flux could make any contribution to the IceCube observed events. For this purpose, the γ-ray data from Fermi-LAT and optical/UV/X-ray data from Swift UVOT/XRT observations of PKS 0502+049 in 2008–2018 have been analyzed. In the γ-ray band the source showed several bright periods. The maximum flux of (4.10 ± 0.75)×10−6 photon cm−2 s−1 integrated above 100 MeV was observed on MJD 56909.5 within 4.81 h. During the highest flux, the apparent isotropic γ-ray luminosity is Lγ ≃ 4.72 × 1049 erg s−1 (using a distance of dL ≃ 6269.5 Mpc), which corresponds to Lem, γ = Lγ/2δ2 ≃ 5.90 × 1046 erg s−1 (when δ = 20) total power emitted in the γ-ray band in the proper frame of the jet. The γ-ray photon index varies as well, being very soft during the low states while significantly hardening in the bright periods, the hardest one being Γ = 1.82 ± 0.14. In the X-ray band, the flux is on the order of a few times 10−12 erg cm−2 s−1 but with a hard photon index ≃1.2 − 1.6, unusual for FSRQs. The X-ray flux variation cannot be tested, as there are only a few observations; however, evidence of flux increasing around the γ-ray flares can be seen. A similar tendency is present also in the optical/UV data obtained by Swift UVOT.
The γ-ray spectra when VHE neutrinos were observed as well as during the γ-ray active periods were obtained. The curved γ-ray emission spectrum during MJD 56949-57059 is better explained by a power-law model (∼E−2.07) with a cut-off at Ecut = 8.50 ± 2.06 GeV. This implies the presence of a cut-off in the energy distribution of the parent population of particles responsible for the emission, so the HE processes were not dominant/efficient in the jet of PKS 0502+049 when the neutrinos were observed by IceCube. In this period, the emission from TXS 0506+056 was not dominating in the lower γ-ray band, but there is an indication of a hard emission component in the higher energy γ-rays (Padovani et al. 2018), showing that most likely there was an efficient contribution from the VHE particles. When the active periods before and after the neutrinos observation window are considered, the γ-ray emission from PKS 0502+049 appears with a very hard γ-ray photon index of ≤2.0. This shows that even if there are certain periods when the jet of PKS 0502+049 was in a favorable state for HE and VHE γ-ray emissions, it seems not to be the case when neutrinos were observed.
Nearly symmetric flare time profiles, with the shortest flux e-folding time being tr = 2.00 ± 0.35 days, were obtained for the flare around MJD 57100. The rise and decay of the flare can be explained by the acceleration and cooling of electrons. For example, the cooling of electrons of Ee = 1 GeV within td = 2.62 ± 0.39 day requires a magnetic field of B ≈ 0.30 G (δ/20)−1/2(tdec/2.62 d)−1/2 (Ee/1 GeV)−1/2 (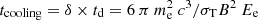 ), which is typical for blazars.
), which is typical for blazars.
The multiwavelength emission from PKS 0502+049 is interpreted within leptonic and hadronic scenarios. In the hadronic interpretations, the absence of VHE γ-ray data prevents exact estimations of expected neutrino rates when the pγ scenario is considered and only quantitative limits can be imposed. In the most optimistic case, the neutrino flux predicted at 100 TeV falls below the IceCube estimated one, implying that the neutrinos accompanying the observed electromagnetic emission (from X- to γ-ray bands) cannot be the source of the observed neutrinos. Next, if the observed γ-rays are due to pp interactions in the dense target crossing the jet, then the energy of protons is mostly released in the GeV band allowing a straightforward measurement of the proton spectra based on the observed γ-ray data. The γ-ray data obtained during the IceCube observational window can be well explained when the energy distribution of protons is 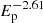 . Then, if the proton cut-off energy is at ∼10 PeV, the maximum possible neutrino detection rate will be ∼1.1 events. A higher neutrino detection rate is possible when a harder power-law index of protons αp = 2.2 is considered; however, it strongly over-predicts the HE γ-ray data above 1 − 2 GeV. Alternatively, a significant neutrino emission is expected during the γ-ray flaring periods when αp = 2.1 − 2.2 and only if Ep, c ≥ 100 TeV; for example, in order to have a detection rate of >4.0 events, it is required that the hard γ-ray spectra extend at least up to ≃Ec, p/40 = 2.5 TeV; these extreme conditions are hardly possible.
. Then, if the proton cut-off energy is at ∼10 PeV, the maximum possible neutrino detection rate will be ∼1.1 events. A higher neutrino detection rate is possible when a harder power-law index of protons αp = 2.2 is considered; however, it strongly over-predicts the HE γ-ray data above 1 − 2 GeV. Alternatively, a significant neutrino emission is expected during the γ-ray flaring periods when αp = 2.1 − 2.2 and only if Ep, c ≥ 100 TeV; for example, in order to have a detection rate of >4.0 events, it is required that the hard γ-ray spectra extend at least up to ≃Ec, p/40 = 2.5 TeV; these extreme conditions are hardly possible.
In the leptonic interpretations, the broadband spectra of PKS 0502+049 are modeled within the one-zone leptonic scenario assuming the emission is produced in the compact region (R ≤ 5.31 × 1016 (δ/20) cm constrained by the observed variability). When the synchrotron/SSC radiation model is considered, the observed data can be explained only when the electron energy density strongly dominates over that of the magnetic field. Instead, the data can be better explained when the inverse Compton scattering of external photons is taken into account; assuming the emitting region is outside the BLR, SSC radiation from the electron population producing the radio-to-optical emission can describe the observed X-ray data, while the emission in the γ-ray band with a large Compton dominance can be explained by the IC scattering of dusty torus photons. This interpretation does not require extreme parameters unlike in the case of the pp interaction scenario; for example, the multiwavelength SED obtained during the IceCube observations can be explained when the electron power-law index is α = 2.42 ± 0.28 above 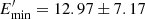 MeV and
MeV and 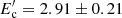 GeV, and the emitting region is not far from equipartition Ue/UB ≃ 19.6. Similar parameters required in the modeling of flaring states are α = 1.6 − 1.9 and Ec ≃ 2.5 GeV and the magnetic field of B = (102.9 − 235.9) mG with an energy density not significantly different from that of the electrons Ue/UB = (18 − 168). The estimated emitting electron parameters are supported by the currently known acceleration theories and the other parameters are physically reasonable.
GeV, and the emitting region is not far from equipartition Ue/UB ≃ 19.6. Similar parameters required in the modeling of flaring states are α = 1.6 − 1.9 and Ec ≃ 2.5 GeV and the magnetic field of B = (102.9 − 235.9) mG with an energy density not significantly different from that of the electrons Ue/UB = (18 − 168). The estimated emitting electron parameters are supported by the currently known acceleration theories and the other parameters are physically reasonable.
In the leptonic and hadronic modeling the required energetics of the system is significantly different. For example, the estimated luminosity in the leptonic scenario varies within Ljet ≃ (4.5 − 18.7)×1045 erg s−1 comfortably below the Eddington luminosity of PKS 0502+049 (LEdd ≃ 9.15 × 1046 erg s−1 for the black hole mass of 7.53 × 108 M⊙; Oshlack et al. 2002), while in the hadronic interpretation, the accretion should be at super-Eddington rates as the required luminosity exceeds the Eddington limit by two to three orders of magnitude. Although a super-Eddington accretion rate is not rare for blazars, it imposes strong difficulties on the hadronic interpretation.
In this paper, we attempt to investigate the origin of multiwavelength emission from PKS 0502+049 during the observation of VHE neutrinos in 2014–2015 and of γ-ray flaring periods, as well as to investigate whether the neutrino emission from PKS 0502+049 can have made contribution to the events observed by IceCube. The spectra observed in all periods can be well reproduced by the leptonic models with physically reasonable parameters unlike the hadronic models, which require a substantially higher jet luminosity. Even in these extreme conditions, based on the γ-ray data the expected neutrino rate can be only ∼1.1 events. In this view, considering the required energetics and predicted spectral shapes, the nearby blazar TXS 0506+056 is a more preferred source of VHE neutrinos. The presented discussion and modeling show that the broadband emission from PKS 0502+049 is most likely of a leptonic origin, leaving TXS 0506+056 as the first extragalactic source of VHE neutrinos.
Acknowledgments
This work was supported by the RA MES State Committee of Science, in the framework of the research project No. 18T-1C335.
References
- Aartsen, M. G., Abbasi, R., Abdou, Y., et al. 2013, Phys. Rev. Lett., 111, 021103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aartsen, M. G., Abraham, K., Ackermann, M., et al. 2017, ApJ, 835, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 722, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Abeysekara, A. U., Archambault, S., Archer, A., et al. 2015, ApJ, 815, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, ApJ, 664, L71 [Google Scholar]
- Ahlers, M., & Halzen, F. 2015, Rep. Prog. Phys., 78, 126901 [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2015, ApJ, 815, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 669, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2011, ApJ, 730, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Ansoldi, S., Antonelli, L. A., Arcaro, C., et al. 2018, ApJ, 863, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2010, A&A, 522, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2013, MNRAS, 436, 3626 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, AIP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Barkov, M. V., Aharonian, F. A., & Bosch-Ramon, V. 2010, ApJ, 724, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Beall, J. H., & Bednarek, W. 1999, ApJ, 510, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W., & Banasiński, P. 2015, ApJ, 807, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W., & Protheroe, R. J. 1997, MNRAS, 287, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Błażejowski, M., Sikora, M., Moderski, R., & Madejski, G. M. 2000, ApJ, 545, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, S. D., & Marscher, A. P. 1996, ApJ, 461, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M., Reimer, A., Sweeney, K., & Prakash, A. 2013, ApJ, 768, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, AIP Conf. Ser., 1358, 373 [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., & Ghisellini, G. 2008, MNRAS, 385, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Cerruti, M., Zech, A., Boisson, C., et al. 2019, MNRAS, 483, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Dar, A., & Laor, A. 1997, ApJ, 478, L5 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cita, V. M., Bosch-Ramon, V., Paredes-Fortuny, X., Khangulyan, D., & Perucho, M. 2016, A&A, 591, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [NASA ADS] [CrossRef] [Google Scholar]
- Drinkwater, M. J., Webster, R. L., Francis, P. J., et al. 1997, MNRAS, 284, 85 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, S., Fedynitch, A., Winter, W., & Pohl, M. 2019, Nat. Astron., 3, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Gasparyan, S., Sahakyan, N., Baghmanyan, V., & Zargaryan, D. 2018, ApJ, 863, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2009, MNRAS, 397, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2015, MNRAS, 448, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Maraschi, L., & Treves, A. 1985, A&A, 146, 204 [NASA ADS] [Google Scholar]
- Halzen, F., & Hooper, D. 2005, Astropart. Phys., 23, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Halzen, F., & Kheirandish, A. 2016, ApJ, 831, 12 [NASA ADS] [CrossRef] [Google Scholar]
- He, H. N., Inoue, Y., Inoue, S., & Liang, Y. F. 2018, ArXiv e-prints [arXiv:1808.04330] [Google Scholar]
- IceCube Collaboration 2013, Science, 342, 1242856 [Google Scholar]
- IceCube Collaboration 2018, Science, 361, 147 [NASA ADS] [Google Scholar]
- IceCube Collaboration, MAGIC, FERMI-LAT, MAGIC, et al. 2018, Science, 361, 6398 [Google Scholar]
- Inoue, S., & Takahara, F. 1996, ApJ, 463, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Kadler, M., Krauß, F., Mannheim, K., et al. 2016, Nat. Phys., 12, 807 [Google Scholar]
- Kappes, A., Hinton, J., Stegmann, C., & Aharonian, F. A. 2007, ApJ, 656, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Keivani, A., Murase, K., Petropoulou, M., et al. 2018, ApJ, 864, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Khiali, B., & de Gouveia Dal Pino, E. M. 2016, MNRAS, 455, 838 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, Y. F., He, H. N., Liao, N. H., et al. 2018, ArXiv e-prints [arXiv:1807.05057] [Google Scholar]
- Liao, N. H., Xin, Y. L., Liang, Y. F., et al. 2018, ArXiv e-prints [arXiv:1807.05210] [Google Scholar]
- Lott, B., Escande, L., Larsson, S., & Ballet, J. 2012, A&A, 544, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannheim, K. 1993, A&A, 269, 67 [NASA ADS] [Google Scholar]
- Mannheim, K. 1995, Astropart. Phys., 3, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K., & Biermann, P. L. 1989, A&A, 221, 211 [NASA ADS] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, E., Perri, M., Giommi, P., Nesci, R., & Verrecchia, F. 2004, A&A, 422, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mücke, A., & Protheroe, R. J. 2001, Astropart. Phys., 15, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Mücke, A., Protheroe, R. J., Engel, R., Rachen, J. P., & Stanev, T. 2003, Astropart. Phys., 18, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Guetta, D., & Ahlers, M. 2016, Phys. Rev. Lett., 116, 071101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Murase, K., Oikonomou, F., & Petropoulou, M. 2018, ApJ, 865, 124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Nikutta, R., Ivezić, Ž., & Elitzur, M. 2008, ApJ, 685, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Oshlack, A. Y. K. N., Webster, R. L., & Whiting, M. T. 2002, ApJ, 576, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Pacciani, L., Tavecchio, F., Donnarumma, I., et al. 2014, ApJ, 790, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Resconi, E., Giommi, P., Arsioli, B., & Chang, Y. L. 2016, MNRAS, 457, 3582 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Giommi, P., Resconi, E., et al. 2018, MNRAS, 480, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Paiano, S., Falomo, R., Treves, A., & Scarpa, R. 2018, ApJ, 854, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Sahakyan, N. 2018, ApJ, 866, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Sahakyan, N., & Gasparyan, S. 2017, MNRAS, 470, 2861 [NASA ADS] [CrossRef] [Google Scholar]
- Sahakyan, N., Piano, G., & Tavani, M. 2014, ApJ, 780, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Stawarz, Ł., Moderski, R., Nalewajko, K., & Madejski, G. M. 2009, ApJ, 704, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2015, MNRAS, 451, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Ghisellini, G., & Guetta, D. 2014, ApJ, 793, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, K., Liu, R. Y., Li, Z., Wang, X. Y., & Dai, Z. G. 2018, ArXiv e-prints [arXiv:1809.00601] [Google Scholar]
- Wang, X.-Y., & Liu, R.-Y. 2016, Phys. Rev. D, 93, 083005 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V. 2015, Proc. of 34th Int. Cosmic Ray Conf., 922 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Top panel: γ-ray light curve of PKS 0502+049 above 214.0 MeV from August 4, 2008 to January 1st, 2018, with a constant uncertainty of 15%. Bottom panels: γ-ray light curve (a) and photon index (b), X-ray (c) and optical/UV light curves (d). The periods P1, P2 and P3 are market with light gray, light red and light yellow colors, respectively, and the period when a 3.5σ excess of neutrinos between September 2014 and March 2015 was observed (P0) is in light blue. The blue dot-dashed line shows the period of detection of a HE neutrino event on September 22, 2017. |
| In the text | |
 |
Fig. 2. Light curve sub-interval with one-day bins for the flaring period. The blue line shows the flare fit with a double exponential function. |
| In the text | |
 |
Fig. 3. SEDs of PKS 0502+049 during the IceCube observational window (P0; gray) and active states P1 (blue), P2 (red), and P3 (magenta). The averaged γ-ray spectrum during the considered nine years and the archival low energy data from ASI science data center are shown in light gray. Gray, blue, and red solid lines show the models when inverse Compton scattering of synchrotron (SSC) and torus (EIC) photons are considered, while the gray dot-dashed line is the fitting only with the SSC component. The model fit parameters are given in Table 3. The inset shows the γ-ray spectra from pp interactions where the solid lines are the modeling when the cut-off energy in the proton spectrum is fixed to 10 PeV and the gray dot-dashed line is the case when the hard spectrum of protons is considered. The axes are the same as in the main plot. All models have been corrected for γγ absorption by the extragalactic background light using the model of Domínguez et al. (2011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} N^{\prime }_{\rm e}(E^{\prime }_{\rm e})= N^{\prime }_{0}\,\left( E^{\prime }_{\rm e}/m_{\rm e}\,c^2\right)^{-\alpha }\,\mathrm{Exp}[-E^{\prime }_{\rm e}/E^{\prime }_{\rm cut}] \end{aligned} $$](/articles/aa/full_html/2019/02/aa34606-18/aa34606-18-eq8.gif)