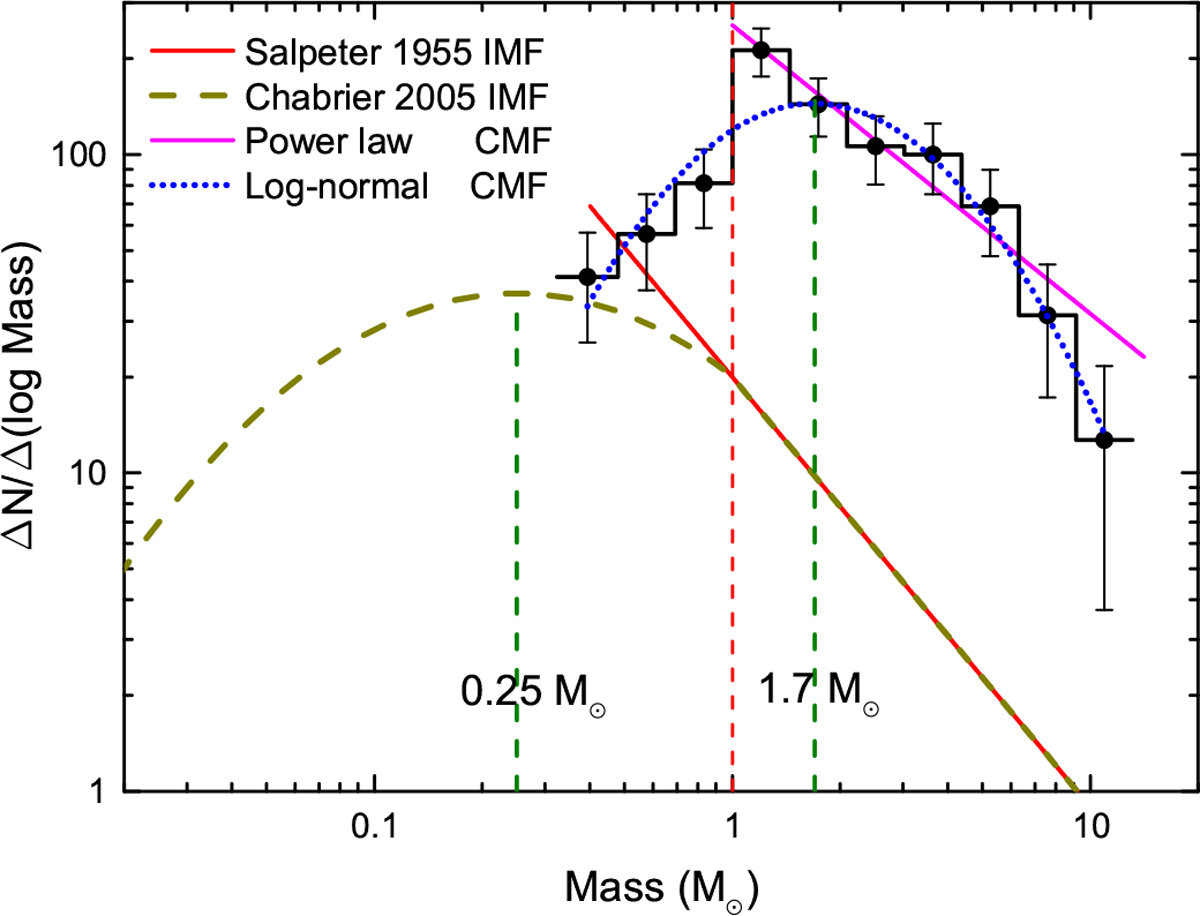
Prestellar CMF fit by power law and log-normal distribution. The error bars correspond to statistical uncertainties. The bin of the prestellar CMF is 0.16 in logarithmic space. The number of the bin is 10. The bins start from 1 M_⊙ to the high- and low-mass end. The prestellar CMF observed above 1 M_⊙ can be fit by a power law with dN∕dlogM ∝ M^−0.9±0.1, which is shallower than the Salpeter (1955) IMF dN∕dlogM ∝ M^−1.35. The prestellar CMF can be well fit by a log-normal with μ = log(1.7 ± 0.1 M_⊙),  σ = 0.37 ± 0.03 in log (M_⊙) unit. 1.7 M_⊙ is the log-normal fit peak value, which also corresponds to the log-normal fit average value, while σ is the standard deviation. The peak value of Chabrier (2005) is 0.25 M_⊙. The prestellar CMF is similar to the IMF. The mass transformation efficiency ϵ from the prestellar core to the star is about 15 ± 1%, as estimatedby comparing the peak value between the CMC log-normal prestellar CMF and the Chabrier (2005) IMF.