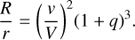| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201834121 | |
| Published online | 12 November 2018 | |
Letter to the Editor
SS 433: Two robust determinations fix the mass ratio
University of Oxford, Department of Physics, Keble Road, Oxford, OX1 3RH UK
e-mail: michael.bowler@physics.ox.ac.uk
Received:
22
August
2018
Accepted:
24
October
2018
Context. The unique Galactic microquasar SS 433 is an X-ray binary with a 13.08 day orbital period. Over some forty years, estimates of the mass of the compact object have spanned the range 1–30 solar masses; from neutron star to massive stellar black hole.
Aims. To fix the mass ratio q and hence the mass of the super-Eddington accretor.
Methods. We present a new and robust estimate of q derived from data on the circumbinary disk and compare it with a recent determination from the observed constancy of the binary period.
Results. These two robust analyses agree to a remarkable extent. They reinforce each other; q is ∼0.7 and the mass of the compact object 15 ± 2 M⊙.
Conclusions. The mass is such as to identify the compact object as a massive stellar black hole.
Key words: stars: individual: SS 433 / binaries: close / circumstellar matter
© ESO 2018
1. Introduction
The Galactic microquasar SS 433 is best known for opposite jets of baryonic material, emitted at speeds ∼0.26c, more or less continuously. The jets precess and make an angle of 20° to the axis, drawing a helix of expanding radius across the sky (Blundell & Bowler 2004). The period of precession is 16 days. The system is an eclipsing binary of orbital period 13.08 days. The compact object is super-Eddington accreting from a comparatively normal star and most of the accreting material is blown from the system in the form of a wind above the accretion disk, ∼10−4 M⊙ yr−1. Review articles are Margon (1984) and Fabrika (2004); recently it has emerged that SS 433 may be the most similar to an Ultra Luminous X-ray source in the Galaxy (Fabrika et al. 2015).
It is therefore of considerable interest to know the mass of the compact object, the only known accretor in the Galaxy involving a mass transfer rate greatly exceeding the Eddington limit; is the compact object a neutron star, a comparatively low mass stellar black hole or a high mass stellar black hole? It would be sufficient to determine the orbital velocity of the companion to the compact object, via periodic variation of spectral lines, but this proved remarkably hard. Emission lines from the companion have never been observed and the best that has been claimed is observation of absorption lines possibly formed in the atmosphere of the companion, yielding companion speeds of ∼132 km s−1 (Cherepashchuk et al. 2005) and ∼60 km s−1 (Hillwig & Gies 2008, see also Kubota et al. 2010). Both sets are consistent with that interpretation but the first implies a fairly high mass black hole; the second a low mass black hole or even a neutron star. Furthermore, similar absorption spectra have been observed that are certainly not consistent with absorption in the atmosphere of the companion (Barnes et al. 2006).
There are very different methods of determining the mass of the compact object. One example is the shape and duration of X-ray eclipses but this paper is concerned with two other totally unrelated methods. The first is from the emission spectra of the circumbinary disk and the second an inference from the stability of the period of the binary orbit. These two methods seem robust and agree remarkably well; this agreement is dramatic in Fig. 3, Sect. 4. The mass of the compact object is thus established as ∼15 M⊙.
2. The mass ratio from the circumbinary disk
The first evidence suggesting that the SS 433 system is surrounded by a circumbinary disk came from observation of the Paschen series stationary lines, displaying the two peak structure characteristic of a disk seen close to edge on, but those data were not sufficient to distinguish between formation in a circumbinary disk or in the accretion disk of SS 433 (Filippenko et al. 1988). The data set from which unambiguous evidence for a circumbinary disk emerged is that of Schmidtobreick & Blundell (2006). The Hα stationary lines have a shape close to that from a uniformly radiating ring or disk; the He I stationary lines have shapes matching a disk radiating proportional to illumination by the intense radiation flux from the photosphere of the accretion disk. These spectra were taken nightly over two and a half orbits; therein lies their particular strength. The most complete analysis of these data (Bowler 2013) explains this difference and accounts in detail for the shape of the He I lines and the periodic variation of these shapes. (A brief summary dealing also with more recent results is Bowler 2017). Thus by 2013 the existence of the circumbinary disk and an orbital speed of ∼240 km s−1 for the glowing material were well established. This speed would be sufficient to determine the mass of the inner system, were the radius of the inner circumbinary orbits known. The innermost radius for a stable orbit about such a binary system is known to be ∼2A, where A is the separation of the two members. On the other hand, any radius approaching that of the L2 point, ∼1.26A, becomes increasingly implausible. For these two examples, system masses of respectively ∼60 M⊙ and ∼26 M⊙ are obtained from Eq. (3) of Bowler (2010). One can (and did) conjecture that the first case, corresponding to q ∼ 1 is something of an upper limit and the second case corresponding to q ∼ 0.5 is ruled out, but a measure of the orbit radius R is necessary to improve the estimate. The breadth of this structure is ∼0.1 R (Bowler 2013).
It is the purpose of this section to demonstrate that such a measurement is implicit in the explanation for the shape of the He I lines as treated in Bowler (2011, 2013) and hitherto unnoticed.
The spectral shape of the He I stationary lines and the variation with orbital phase is very well explained by a model assuming that the emission from any given section of the circumbinary ring is proportional to the radiation incident upon it from the vicinity of the compact object, inverse square. This is dependent on the ratio of the orbital radius R of the glowing ring or inner disk to that of the compact object itself, r. Thus if the ring is far out all parts will be illuminated to much the same extent at all times and there would be little variation in the shape of the line with orbital phase. Contrariwise, if the compact object were orbiting very close to the ring, the line shape would vary much like that produced by a point like object, orbiting with the speed of the ring and a 13 day period. The observed He I shapes are intermediate and well reproduced by a ratio R/r such that illumination at the spot furthest away from the compact object is 0.2 of that closest (Bowler 2011, 2013). The corresponding ratio is 2.62 and hence q is 0.7 (see Eq. (1) below).
Figure 1 shows the configuration of the circumbinary ring and the compact object receding fastest from the observer, orbital phase 0.75 or 270°. The upper panel of Fig. 2 is, for this configuration, the modelled spectral shape; it changes very little over a range of 230–310°. The lower panel is a fit to data, with the contribution of the wind stripped out. (These panels are from Bowler 2011, 2013 respectively). The agreement is very good, but the determination of R/r is not dependent on the bottom panel of Fig. 2 (a little narrower than average) by itself. The original data span JD 2453000+245 to JD +274 and so include two examples of orbital phase 0.75 and three examples of the mirror configuration for phase 0.25. The ratio R/r was selected as the best match overall (Bowler 2013). The whole sequence of He I spectra can be consulted in Fig. 2 of Schmidtobreick & Blundell (2006).
 |
Fig. 1. Configuration of the circumbinary ring (labelled by the orbital radius R) and the compact object (orbital radius r) that stimulates emission. The orbital phase is 0.75, when the compact object is receding fastest. The x and y scales are such that r is unit radius and R = 2.62 units. |
 |
Fig. 2. Upper panel: modelled shape of the He I emission line from the circumbinary ring. For this configuration the receding material is much brighter than that approaching. Lower panel: an observed shape of the disk He I line for this configuration. Flux units arbitrary. |
Since the radius of the compact orbit is known from the period and velocity, knowledge of R/r determines the value of R. In this note I have assumed the following parameters for SS 433: Binary period (P) 13.08 days, orbital speed (v) of compact object 176 ±13 km s−1 (Fabrika 2004), orbital speed (V) of the ring of fire 240 ± ∼10 km s−1 (Bowler 2010, 2011, 2013). The value of R/r is related to the mass ratio q through the following equation:
This relationship is plotted in Fig. 3, where the abscissa is q and the ordinate is R/r. The intersection between the curve and the horizontal crosshair at 2.62 gives the value of q. In the same figure a vertical line corresponds to the value obtained from the constancy of the orbital period.
 |
Fig. 3. Mass ratio q determined from the circumbinary disk agrees with the value inferred from the constancy of the period, see text. The degree of agreement is made manifest by the error box in the bottom right hand quarter. |
The uncertainty on the value of q thus extracted is harder to estimate. The larger the value of R/r the less sensitive to changes is the shape of the He I spectral line. For example, for a value of 4 the model shape is insufficiently skewed to match the data while for a value of 2 the model shape is overskewed to the same extent; the errors are asymmetric. Thus R/r is 2.6 with estimated errors +0.7, −0.2. This corresponds to q of 0.7, +0.14, −0.07. The value of R/r is certainly less than 4 and greater than 2. A reasonable estimate is that q is unlikely to be much greater than 0.8 and probably greater than 0.6.
For a given value of the ratio R/r there are also uncertainties deriving from the uncertainties on v and V. The former case contributes symmetric errors on q of ±0.08 and the latter ±0.05. If all three components of errors are combined in quadrature the result for q is 0.7, +0.17, −0.12.
3. The mass ratio from the constancy of orbital period
The donor companion transfers matter at a surprisingly high rate to the vicinity of the compact object. This rate has been estimated from data on the wind blowing from the accretion disk; ∼10−4 M⊙ yr−1 (Perez & Blundell 2010). A similar estimate of the transfer rate is ∼10−4 M⊙ yr−1, certainly within a factor of 3 (Fuchs et al. 2006). Despite this, no significant change in the period of the binary orbit has been detected since that period was first measured. The absence of any significant change has the immediate implication that the mass ratio q must be high. It is obvious that were the mass transfer conservative, constancy of period would require q ∼ 1. The transfer is not conservative (because most of the transferred matter is blown away in the wind from the disk). Nonetheless, if the period is constant the mass ratio must be high. Fabrika (2004) quotes q = 0.7–0.8 from a calculation made some years earlier. Thereafter this method of estimating q seems to have been forgotten. It has recently been deployed to great effect by Cherepashchuk et al. (2018). Data accumulated over some 28 years (Goranskij 2011) yield for the modulus of Ṗ/P a value < 5.7 × 10−7 yr−1. For a value of precisely zero, the value of q necessary can be calculated using little more than conservation of angular momentum (Postnov & Yungelson 2006). Assuming that (almost) all the material shed by the donor is blown from the accretor in the wind above the disk, with the specific angular momentum of the accretor, Cherepashchuk et al. (2018) find q to be 0.72; this is the origin of the vertical crosshair in Fig. 3.
The limits on the accuracy of this estimate depend on the uncertainty about zero of Ṗ/P and on the rate at which mass is transferred. For 10−4 M⊙ yr−1Cherepashchuk et al. (2018) find that q has an allowed interval between 0.7 and 0.74, also stating that should the rate of mass transfer be a factor of 10 smaller, the limits expand to 0.59–0.94. These authors do not quote formal errors, but it is clear that their accuracy is strongly dependent on the mass transfer rate. This is probably within a factor of a few of 10−4 M⊙ yr−1. For greater values, the already narrow limits constrict further. For a value as low as 3 × 10−5 M⊙ yr−1 I calculate limits 0.67–0.77. In any case, their result for q is of greater precision than my result from the He I spectra. Their calculations establish the compact member of SS 433 as a stellar black hole of high mass (see Cherepashchuk et al. 2018) .
The paper of Cherepashchuk et al. (2018) is of interest in two other respects. First, it casts doubt on the interpretation of Brγ spectra by Robinson et al. (2017) and Cherepashchuk et al. (2018) identify these spectra as belonging to the circumbinary disk (see also Bowler 2017). Secondly, they include a further dicussion of earlier work on X-ray eclipses (Cherepashchuk et al. 2013), now arguing that because the donor can overfill its Roche lobe these data set no upper limit on q, rather than their previous estimate ∼0.6.
4. Discussion
The two methods of determining the mass ratio here discussed are quite independent of each other and indeed independent of other attempts to determine q. Figure 3 illustrates the remarkable degree of agreement between these two robust estimates. The abscissa is q and the ordinate is R/r. Thus the vertical crosshair is the value of q from Cherepashchuk et al. (2018) and the horizontal crosshair is the value of R/r from the He I spectral shapes. The uncertainty on the value (0.72) of q extracted from the constancy of period of the binary system may be as small 0.02, yet even so overlaps the intersection of the curve and the horizontal crosshair in Fig. 3, at q = 0.7. The two methods are entirely consistent; the box in the bottom right hand quarter of Fig. 3 displays the errors as estimated in Sects. 2, 3 and 5.
The absence of any detectable change in the binary period over 28 years establishes that q is greater than or equal to 0.7, provided the rate of mass transfer is ∼10−4 M⊙ yr−1. If most of this mass is ejected from the system with the specific angular momentum of the accretor, then the value of q is within the limits 0.7–0.74 (Cherepashchuk et al. 2018). Thus even this extremely robust method of determining q is not free from assumptions, but note that the circumbinary torus contains only ∼10−8 M⊙ (Bowler 2013).
The present study of the shape of the stationary emission lines and their variation with orbital phase provides totally independent data. First, the value of the ratio R/r is certainly less than 4 and hence q less than 0.9. From Fig. 2 (left panel) of Cherepashchuk et al. (2018) this implies that less than ∼0.1 of the transfer flux joins the circumbinary disk. At the other end, the lowest value that Cherepashchuk et al. (2018) contemplate is 0.6; if this were the case the radius of the ring would be 1.36A and this is very close to radius of the L 2 point, ∼1.26A. Finally, the stationary emission lines give the orbital speed of the radiating circumbinary material, while the He I line shapes determine the ratio R/r. For a fixed value of this ratio, q is a function of that orbital speed. As can be seen from the model calculation in Fig. 2 (upper panel) the line shape determined by the ratio R/r has no scale other than the orbital speed of the ring, determined by matching the scale of the abscissa to the wavelength scale for the measured line shape. For this same shape, had it turned out that the orbital speed were 200 km−1 then q would be 0.51, far below the lowest value permitted by the stability of the orbital period of the binary. These two recent and independent methods of obtaining the mass ratio lock together, bolstering their assumptions either implicit or explicit. I note that the absorption spectra of Cherepashchuk et al. (2018), if attributed to the companion, yield a value for q of 0.75 ± 0.07 and so could be consistent with the two methods discussed here. In contrast, the absorption spectra of Hillwig & Gies (2008) and Kubota et al. (2010) cannot be attributed to the atmosphere of the companion. They do match absorption of light from the companion by the circumbinary ring (Bowler 2010).
5. Conclusions
The principal conclusion is presented graphically in Fig. 3. It is that the two independent methods of determining q fix its value at ∼0.7 and that subject to the validity of the assumptions used in Cherepashchuk et al. (2018) the uncertainty on this value is very small. The previously uncertain parameters for the SS 433 binary can then be established, assuming the other parameters for SS 433 as at the end of Sect. 2. The only problem is the uncertainty in the value of q, dominated by the uncertainty in the rate of mass transfer. This has never been measured precisely but is unlikely to be less than 3 × 10−5 M⊙ yr−1 (see Sect. 3), corresponding to uncertainties ±0.05. I have calculated the numbers in Table 1 for q 0.72 ± 0.05.
Newly established parameters.
It will be noted that R, the effective inner radius of the circumbinary disk, is significantly smaller than that of the innermost stable orbit, ∼2A. Were R to be ∼2A then q would be 0.9, but R/r would have to be ∼4. This is ruled out by the He I spectra. This inner material must be continually refreshed by excretion of matter transferred from the donor, presumably through the L2 point.
At the very least, we can be confident that the mass of the compact object exceeds 10 M ⊙.The compact object in the binary system SS 433 is a stellar black hole of high (but, after 2015, not exceptional) mass.
Acknowledgments
Using R/r determined (five years ago) from the shape of the He I stationary lines to obtain q only occurred to me after I was stimulated by the most interesting paper of Cherepashchuk et al. (2018).
References
- Barnes, A. D., Casares, J., Charles, P. A., et al. 2006, MNRAS, 365, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., & Bowler, M. G. 2004, ApJ, 616, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, M. G. 2010, A&A, 521, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowler, M. G. 2011, A&A, 531, A107 [Google Scholar]
- Bowler, M.G. 2013, A&A, 556, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowler, M. G. 2017, ArXiv e-prints [arXiv:1708.02555] [Google Scholar]
- Cherepashchuk, A. M., Sungaex, R. A., Fabrika, S. N., et al. 2005, A&A, 437, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cherepashchuk, A. M., Sunyaev, R. A., Molkov, S. V., et al. 2013, MNRAS, 436, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Cherepashchuk, A. M., Postnov, K. A., & Belinski, A. A. 2018, MNRAS, 479, 4844 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrika, S. N. 2004, Phys. Rev., 12, 1 [Google Scholar]
- Fabrika, S. N., Abolmasov, P. K., Karpov, S., et al. 2015, Nat. Phys., 11, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Romani, R. W., Sargent, W. L. W., et al. 1988, AJ, 96, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, Y., Koch Miramond, L., & Abraham, P. 2006, A&A, 445, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goranskij, V. 2011, Peremennye Zvezdy, 31 [Google Scholar]
- Hillwig, T. C., & Gies, D. R. 2008, ApJ, 676, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, K., Ueda, Y., Fabrika, S., et al. 2010, ApJ, 709, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Margon, B. 1984, ARA&A, 22, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, S., & Blundell, K.M. 2010, MNRAS, 408, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Postnov, K. A., & Yungelson, L. R. 2006, Liv. Rev. Relativ., 9, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, E. L., Froning, C. S., Jaffe, D. T., et al. 2017, ApJ, 841, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidtobreick, L., & Blundell, K. 2006, VI Microquasar Workshop: Microquasars and Beyond, 94.1 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Configuration of the circumbinary ring (labelled by the orbital radius R) and the compact object (orbital radius r) that stimulates emission. The orbital phase is 0.75, when the compact object is receding fastest. The x and y scales are such that r is unit radius and R = 2.62 units. |
| In the text | |
 |
Fig. 2. Upper panel: modelled shape of the He I emission line from the circumbinary ring. For this configuration the receding material is much brighter than that approaching. Lower panel: an observed shape of the disk He I line for this configuration. Flux units arbitrary. |
| In the text | |
 |
Fig. 3. Mass ratio q determined from the circumbinary disk agrees with the value inferred from the constancy of the period, see text. The degree of agreement is made manifest by the error box in the bottom right hand quarter. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.