| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 6 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201834075 | |
| Published online | 13 November 2018 | |
Unidentified γ-ray emission towards the SNR Kes 41 revisited
1
CONICET – Universidad de Buenos Aires, Instituto de Astronomía y Física del Espacio (IAFE),
Buenos Aires,
Argentina
e-mail: lsupan@iafe.uba.ar
2
Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales,
Buenos Aires,
Argentina
3
School of Physics, University of New South Wales,
Sydney,
NSW
2052,
Australia
4
Armagh Observatory and Planetarium, College Hill,
Armagh
BT61 9DG,
UK
Received:
13
August
2018
Accepted:
13
August
2018
Kes 41 is one of the Galactic supernova remnants (SNRs) that are proposed to be physically linked to γ-ray emission at GeV energies. The nature of the γ-ray photons has been explained, but inconclusively, as hadronic collisions of particles accelerated at the SNR blast wave with target protons in an adjacent molecular clump. We performed an analysis of Fermi-Large Area Telescope (LAT) data of about nine years to assess the origin of the γ-ray emission. To investigate this matter, we also used spectral modelling constraints from the physical properties of the interstellar medium towards the γ-ray emitting region along with a revised radio continuum spectrum of Kes 41 (α = −0.54 ± 0.10, S ∝ να). We demonstrate that the γ-ray fluxes in the GeV range can be explained through bremsstrahlung emission from electrons interacting with the surrounding medium. We also considered a model in which the emission is produced by pion decay after hadronic collisions, and confirm that this mechanism cannot be excluded.
Key words: ISM: supernova remnants / ISM: individual objects: Kes 41 / gamma rays: ISM
© ESO 2018
1 Introduction
Molecular clouds (MCs) house stellar objects at different stages of their evolution, from star-forming regions (SFRs) to the remains of supernovae (SNe). The detection of γ rays at GeV and/or TeV energies from the molecular gas can serve to illuminate the high-energy particle production that occurs in these objects that are located within the cloud and even in its vicinity. At first glance, the spatial correspondence of a cloud with γ-ray emission might explain the latter through collisions of accelerated protons, for instance at supernova remnant (SNR) shock fronts, with target protons (and maybe heavier nuclei; Banik & Bhadra 2017) in the ambient matter. However, this mechanism cannot always be straightforwardly recognised since leptonic processes can also result in γ-ray emission through either bremsstrahlung or inverse-Compton scattering produced by relativistic electrons.
Certainly, the number of γ-ray emitting sources detected at GeV energies by the Fermi Gamma-ray Space Telescope is growing rapidly. More than 3000 sources were reported in the last catalogues presented by Acero et al. (2015) and Ackermann et al. (2016). However, only for ~35 of these sources was a reliable counterpart found that originated in the radio emission from SNRs. Remarkably, approximately only half of these SNRs are clearly found in interaction with surrounding molecular gas1. As a counterpart to the GeV emission, several of the Fermi sources were also detected at TeV energies2 and/or in the radio/X-ray domains (see e.g. Castro et al. 2013; Acero et al. 2016). However, regardless of the existence of a spatially coincident counterpart, in many cases we lack a clear understanding of the relative contribution made by the hadronic and leptonic processes that are responsible for γ-ray production (e.g. Tanaka et al. 2011; Pivato et al. 2013; H.E.S.S. Collaboration 2018a).
Here, we study the nature of the GeV γ-ray emission that has been identified towards (l, b) ≃ (337°.8,0°.0) with the Large Area Telescope (LAT) detector onboard the Fermi satellite. The source known as 3FGL J1838.6−4654 in the Fermi-LAT source catalogue (3FGL; Acero et al. 2015) lies in the GeV-emitting region surveyed in this work3. Given the spatial coincidence on the plane of sky, Liu et al. (2015) considered a link between the GeV emission and the Galactic SNR Kes 41 to be natural. Moreover, using the properties of the molecular gas emission derived by Zhang et al. (2015) in a restricted ~7′ × 4′ area along the western rim of Kes 41, Liu et al. (2015) proposed the hadronic interactions as the most feasible process to explain the production of the γ-ray emission in the GeV domain. The large-scale structure of the ambient matter in which Kes 41 evolves has recently been investigated in the companion paper presented by Supan et al. (2018). As a result, on the basis of molecular and atomic line emission data from the Mopra Southern Galactic Plane CO Survey (Burton et al. 2013) and the Southern Galactic Plane Survey (SGPS; McClure-Griffiths et al. 2005), respectively, along with mid-infrared Spitzer (Churchwell et al. 2009; Carey et al. 2009) information, the authors reported the discovery of the natal cloud (~26′ in size, mass M ~ 10–30 × 105 M⊙) of the SNR and several SFRs around it. Now, in the light of the newly determined physical conditions of the γ-ray emitting cloud, together with an updated set of Fermi-LAT data and radio observations, we re-analysed the suitability of hadronic and leptonic models to fit the broadband spectral energy distribution (SED) for the SNR/γ-ray source system.
2 Observations and data analysis
2.1 γ-ray observations
We analysed the field of Kes 41 at γ-ray energies using GeV data acquired with the Fermi-LAT during about nine years of the mission since its beginning on August 8, 2008, to July 10, 2017 (i.e. the mission elapsed time between 239557417 and 521337605). This time interval greatly increases the observing time by ~71% with respect to the analysis previously presented in Liu et al. (2015), by adding ~3.3 yr of observations with the Fermi-LAT. Our objective is to obtain a current morphological and spectral picture of the GeV sky in the direction of the remnant Kes 41 (i.e. towards the source 3FGL J1838.6−4654), in order to investigate the nature of the observed γ-ray emission.
Events from a region of interest (ROI) with a radius of 10° centred on the source 3FGL J1838.6−4654 (l, b ≃ 337°.798, 0°.054) were selected. The energy range 0.5–400 GeV was chosen for the spatial analysis, as a compromise between limited statistics and angular resolution. For the spatial analysis, the ROI was reconstructed with a pixel size of 0°.025. Scientific products were obtained following a standard reduction chain, employing the Science Tools (ST) package version v10r0p5 and python, with the current version of event reconstruction (Pass 8; Atwood et al. 2013) and the latest instrument response functions (IRFs P8R2_SOURCE_V6)4. In order to consider “good” photons for our analysis, we only kept events that were filtered according to good-time intervals (GTIs) and source class events (evtype = 3), which are indicated for point-source analysis. Additionally, we discarded photons coming from a zenith angle greater than 90° to minimise contamination due to γ rays generated by interactions of cosmic rays with the upper atmosphere.
From the above mentioned filtering process, we obtained a set of high-quality γ-ray data, which we analysed by means of the maximum likelihood technique (Mattox et al. 1996) implemented through the ST routine gtlike. We performed a binned likelihood analysis, dividing the 0.5–400 GeV range into 30 logarithmically spaced energy bins. Background emission was modelled through the user-contributed script make3FGLxml.py including point as well as extended sources in the ROI from the 3FGL catalogue along with the gll_iem_v06 and iso_P8R2_SOURCE_V6_v06 models for the diffuse Galactic and isotropic extragalactic components, respectively. The likelihood optimisation procedure was carried out by fixing spectral parameters (spectral index, normalisation, etc) of the sources beyond 5° from the ROI centre, in order to ensure convergence. A first approximation of the spectral parameters was obtained using the Minuit optimiser, which was then refined with the NewMinuit optimiser until convergence. Normalisation of the Galactic and extragalactic backgrounds was left free.
2.2 Spatial distribution
In order to reveal the appearance of the GeV source in the field, we obtained a test-statistics (TS) map of the region by comparing the emissionfrom the source with that of the constructed background model using the tool gttsmap. The TS parameter is defined as 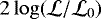 , where
, where 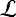 is the likelihood with source included and
is the likelihood with source included and 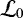 corresponds to the null hypothesis (i.e. the sky subtracting the GeV excess of the source). It is a useful parameter to evaluate the statistical significance of a γ-ray excess, as it is related to the detection significance σ of the sourceaccording to
corresponds to the null hypothesis (i.e. the sky subtracting the GeV excess of the source). It is a useful parameter to evaluate the statistical significance of a γ-ray excess, as it is related to the detection significance σ of the sourceaccording to 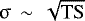 . The new TS map for the region in which we are interested is presented in Fig. 1, where the radio emission at 843 MHz obtained from the Sydney University Molonglo Sky Survey (SUMSS; Bock et al. 1999)is depicted using white contours. For ease of reference, the HII regions in the field are labelled in Fig. 1 with numbers from 1 to 8. The TS angular distribution, with an overall significance of 27σ, is consistent with those presented by Liu et al. (2015).
. The new TS map for the region in which we are interested is presented in Fig. 1, where the radio emission at 843 MHz obtained from the Sydney University Molonglo Sky Survey (SUMSS; Bock et al. 1999)is depicted using white contours. For ease of reference, the HII regions in the field are labelled in Fig. 1 with numbers from 1 to 8. The TS angular distribution, with an overall significance of 27σ, is consistent with those presented by Liu et al. (2015).
 |
Fig. 1 New TS map in the region of SNR Kes 41 generated in the 0.5–400 GeV energy band according to the last update on this source analysed in this work. Contours delineate the radio emission at 843 MHz from SUMSS at levels 0.09, 0.3, 0.5, and 0.7 Jy beam−1. Labels correspond to Kes 41 and the neighbouring HII regions (1:G337.711 −0.056; 2:G337.711+0.089; 3:G337.622−0.067; 4:G337.667−0.167; 5:G337.978−0.144; 6:G338.011+0.022; 7:G337.686+0.137; 8:G338.114 −0.193; Jones & Dickey 2012). The ellipse E1 is the area employed in Supan et al. (2018) to derive the properties of the interstellar medium, used to place constraints on the spectral fitting procedure presented in this work. Further details of the Kes 41 environment are presented in Supan et al. (2018). |
2.3 Spectral analysis
We performed a new binned likelihood analysis of the data in order to study the SED of the source. In this case, we restricted the range to 0.3–143 GeV, which was divided into six spectral bands, and we carried out a separated likelihood analysis for each of them. The extreme energies and the corresponding (logarithmic) central energy Ec as well as the GeV fluxes for each interval are reported in Table 1. The distribution of the spectral points reveals a tendency for the flux of the source to fall below detection limits at an energy ~50 GeV, suggesting a possible low-energy cutoff. This spectral shape may support the idea that events confidently associated with the source for energies above this value are scarce. For energies ≳50 GeV, only upper limits were obtained.
Assuming a power-law spectral shape, the resulting photon index is Γ = 2.45 ± 0.05, which is consistent with the one obtained by Liu et al. (2015). The flux in the 0.3–143 GeV band is determined to be (2.99 ± 0.25) × 10−8 ph cm−2 s−1. The detailed modelling of the broadband SED from radio up to GeV energies is presented in Sect. 4. The uncertainties reported in Table 1 include statistical as well as systematic errors. Systematic errors are mainly associated with the propagation of inaccuracies in the effective area of the instrument, the point spread function (PSF), and with uncertainties related to the normalisation of the Galactic diffuse background. Uncertainties associated with the effective area of the Fermi-LAT vary across the energy range, reaching maximum values of ~10% at the highest energy considered in our study (Ackermann et al. 2012, see also the FSSC web site5). On the other hand, systematics associated with the PSF are on the order of 5% for energies below 100 GeV in our range, linearly increasing up to ~20% at higher energies6. To estimate the systematics associated with the Galactic background, we followed Abdo et al. (2009), that is, after obtaining the best-fit values from the binned likelihood procedure, we varied the normalisation of this background by ±6% in order to determine the departure of the spectral parameters under this artificially fixed model from the previously determined best-fit values.
Fluxes in the GeV range for the γ-ray source detected in correspondence with SNR Kes 41.
3 Supernova remnant Kes 41
Kes 41 (G337.8−0.1) is a Galactic SNR classified, on the basis of the thermal X-ray emission detected towards its interior, as a member of the thermal-composite SNR class (Zhang et al. 2015). Although it was proposed that the remnant might be the result of the collapse of a star no later than a B0-type, with a mass ≳18 M⊙ (Zhang et al. 2015), the lack of a central compact object reported for this remnant casts doubts on the proposed nature of the progenitor star.
Here, we present a thorough study of Kes 41, which, as displayed in Fig. 1, is seen superimposed in projection on the GeV emission detected by Fermi-LAT. A zoomed-in view of the remnant at 843 MHz from SUMSS is shown in Fig. 2a. The remnant exhibits a slightly elongated radio shell of about ~7′.5 × 6′ (equivalent to an average size of 24 pc at the SNR distance of 12 kpc7), brighter towards its Galactic western portion. Supan et al. (2018) demonstrated that this bright emission is morphologically correlated with an enhancement in the molecular gas emission observed between approximately −63 and approximately −48 km s−1 (see Fig. 3 in that paper).
To calculate the global radio spectral index of the remnant, we measured the integrated flux density of the source in images taken from public surveys at 843 and 5000 MHz, and constructed the spectrum shown in Fig. 2b by adding these estimates topreviously published flux density measurements for Kes 41. The list of the integrated flux density estimates is presented inTable 2. The reported values, provided that the information about the primary calibrators is available, were brought onto the flux density scale of Perley & Butler (2017). The spectrum shows that the flux density value at 80 MHz liesbelow the general trend of the data, which in principle may indicate thermal absorption along the line of sight. As only one point is scarce evidence for defining a spectral turnover at low frequencies, we first excluded the flux density value at 80 MHz and calculated the integrated spectral index in the radio band by a single weighted power-law least-squares fit (where Sν ∝ να) to the remaining data points in Fig. 2b. The derived value of the integrated spectral index is α = − 0.54 ± 0.10, which is fairly consistent with the estimate α ≃ − 0.51 presented by Whiteoak & Green (1996) based only on integrated fluxes measured at 408 and 843 MHz. The integrated spectral index is also similar to that measured in other SNRs without a compact remnant in their interior. On the other hand, if the low-frequency turnover is considered valid, a weighted least-squares fit to all the integrated flux densities shown in Fig. 2b using a power law plus an exponential turnover at a fiducial frequency of 408 MHz (![$S_{\nu}= S_{\mathrm{408}} \, (\nu / 408\,{\mathrm{MHz}})^{\upalpha}\, \mathrm{exp}[{-\tau_{408} \, (\nu / 408 \, \mathrm{MHz}})^{-2.1}]$](/articles/aa/full_html/2018/11/aa34075-18/aa34075-18-eq5.png) ) produces a flux S408 = 23.3 ± 2.6 Jy and an optical depth τ408 = 0.037 ± 0.012, which is indicative of an insignificant absorption level at this frequency. The free–free optical depth at 80 MHz is τ80 = 1.13 ± 0.37 (
) produces a flux S408 = 23.3 ± 2.6 Jy and an optical depth τ408 = 0.037 ± 0.012, which is indicative of an insignificant absorption level at this frequency. The free–free optical depth at 80 MHz is τ80 = 1.13 ± 0.37 (![$\tau_{\mathrm{80}}=\tau_{\mathrm{408}}\, [80/408]^{-2.1}$](/articles/aa/full_html/2018/11/aa34075-18/aa34075-18-eq6.png) ). The global spectral index has the same value as is derived when absorption from thermal ionised gas along the line is absent. Certainly, more flux density measurements at frequencies below 100 MHz are needed to clarify the presence of the spectral turnover.
). The global spectral index has the same value as is derived when absorption from thermal ionised gas along the line is absent. Certainly, more flux density measurements at frequencies below 100 MHz are needed to clarify the presence of the spectral turnover.
 |
Fig. 2 Panel a: SUMSS 843 MHz continuum emission from Kes 41, the beam size is ~43′′ × 59′′ and the noise level is ~0.015 Jy beam−1. A linear intensity scale was used for the representation. Panel b: integrated radio spectrum of SNR Kes 41 constructedwith the flux densities measurements reported in Table 2. The solid line corresponds to the weighted linear fit to the points excluding the point at 80 MHz, which yields a global spectral index α = − 0.54 ± 0.10 (Sν ∝ να). The same spectral index with an optical depth at 80 MHz τ80MHz = 1.13 ± 0.37 is obtained by fitting (dotted line) all of the measurements with a low-frequency turnover in the spectrum around 100 MHz. |
Flux densities used to construct the global radio continuum spectrum of Kes 41.
4 Physical scenarios for the GeV γ rays
It is believed that the γ-ray radiation produced in supernova remnants originates in the interaction of accelerated hadrons and/or leptons with surrounding ambient matter and radiation. This high-energy γ-ray flux is enhanced in the presence of dense MCs (see Slane et al. 2015, for a review).
Liu et al. (2015) modelled the γ-ray flux of Kes 41 considering leptonic and hadronic scenarios. Assuming that the γ rays are caused by inverse-Compton scattering of accelerated electrons with the low-energy photons of the cosmic microwave background, they found that the required energy in accelerated electrons to reproduce the observed flux is on the order of 1.3 × 1051 erg. This result is about one order of magnitude larger than the canonical value of 1050 erg, which corresponds to a fraction of 10% of the typical energy released in a supernova explosion. The authors also developed hadronic models that were compatible with the observed flux and also with the canonical values of the energy imparted to the accelerated particles in a supernova explosion.
In the current work, we take the properties derived for the large cloud into account (Supan et al. 2018) and use, for the first time, a broadband spectrum including observations at radio energies to review the plausibility of a hadronic and leptonic origin of the γ-ray flux in the region of the SNR Kes 41.
The energy distribution of the accelerated particles in the hadronic and leptonic scenarios considered here is assumed to be a power law with an exponential cutoff,
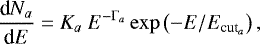 (1)
(1)
where a = {e, p} indicates the particle species (electrons or protons), Ka is a normalisation constant, Γa is the spectral index, and 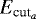 is the cutoff energy.
is the cutoff energy.
We first consider a model in which leptons are the component responsible for the γ-ray flux. In this type of model, the radio flux is due to synchrotron radiation emitted by the propagation of the accelerated electrons in the ambient magnetic field. On the other hand, the γ-ray radiation is generated mainly by the interaction of the accelerated electrons with the ambient matter, through the nonthermal bremsstrahlung process, and with the ambient radiation field, through inverse Compton. We refer to Aharonian et al. (2010) and references therein for calculation details of the synchrotron emissivity. Regarding the inverse-Compton and the nonthermal bremsstrahlung emission, we followed the method given in Jones (1968) for the former, while the method presented in Baring et al. (1999) was used to model the electron–electron bremsstrahlung interaction and in Koch & Motz (1959) and Sturner et al. (1997) for the electron-ion bremsstrahlung process.
In modelling the spectrum from radio to γ-ray energies, we considered the radio observations reported in Table 2 and the updated Fermi-LAT data presented in Sect. 2. The chi-square used to fit the data is given by
![\begin{equation*}\chi^2(\vec{\theta})=\sum_{i=1}^N \frac{(J_i-J(E_i;\vec{\theta}))^2}{\upsigma_i^2} + \frac{(n_{\textrm{p}}-\bar{n}_{\textrm{p}})^2}{\upsigma[n_{\textrm{p}}]^2}, \end{equation*}](/articles/aa/full_html/2018/11/aa34075-18/aa34075-18-eq9.png) (2)
(2)
where Ji corresponds to the observed flux at energy Ei with an uncertainty σi, and J(Ei;θ) is the model under consideration with parameters 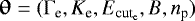 . Here, B is the ambient magnetic field intensity and np is the proton density. We note that the last term in χ2(θ) includes theuncertainty on the determination of the proton density. The values of
. Here, B is the ambient magnetic field intensity and np is the proton density. We note that the last term in χ2(θ) includes theuncertainty on the determination of the proton density. The values of 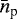 and σ[np] correspond to the E1 region enclosing SNR Kes 41, which is drawn in Fig. 1. A comprehensive analysis of the physical conditions in this region is presented in Supan et al. (2018). The inclusion of the mean proton density as one of the fitting parameters means that the fit takes into account its correlation with the other fitting parameters. Moreover, the covariance matrix of the fit depends on the estimated mean proton density. Therefore, the mean proton density uncertainty is properly propagated (including correlations) in subsequent calculations that are based on the fitting parameters, such as the total energy in accelerated electrons corresponding to the model.
and σ[np] correspond to the E1 region enclosing SNR Kes 41, which is drawn in Fig. 1. A comprehensive analysis of the physical conditions in this region is presented in Supan et al. (2018). The inclusion of the mean proton density as one of the fitting parameters means that the fit takes into account its correlation with the other fitting parameters. Moreover, the covariance matrix of the fit depends on the estimated mean proton density. Therefore, the mean proton density uncertainty is properly propagated (including correlations) in subsequent calculations that are based on the fitting parameters, such as the total energy in accelerated electrons corresponding to the model.
The spectral index of the accelerated electrons energy distribution is fixed during the χ2 minimisation procedure. Figure 3 shows the fit of the experimental data for Γe = 2. This value is motivated by the prediction of the first-order Fermi mechanism and is contained in the 1-σ region of the radio data fit performed in Sect. 3. As Fig. 3 shows, the nonthermal bremsstrahlung process is the dominant contribution to the γ-ray part of the flux. The inverse-Compton component is several orders of magnitude smaller than the corresponding component of the nonthermal bremsstrahlung. The fitted parameters are 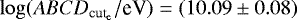 ,
, 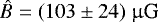 , and
, and 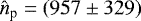 cm−3 (the hat is included to emphasize the maximum likelihood estimate character of the parameters). The obtained cutoff energy of the accelerated electrons is quite small. This is due to the suppression present in the γ-ray data. It is worth mentioning that, the high value of the proton density requires a smaller number of accelerated electrons to reproduce the γ-ray data, and then a high value of the magnetic field is required to reproduce the radio data.
cm−3 (the hat is included to emphasize the maximum likelihood estimate character of the parameters). The obtained cutoff energy of the accelerated electrons is quite small. This is due to the suppression present in the γ-ray data. It is worth mentioning that, the high value of the proton density requires a smaller number of accelerated electrons to reproduce the γ-ray data, and then a high value of the magnetic field is required to reproduce the radio data.
The energy in accelerated electrons is calculated by using Eq. (1). For the spectral index Γe = 2, the following value is obtained:
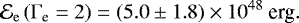 (3)
(3)
The total energy in accelerated electrons is lower than the canonical value of 1050 erg. The maximum energy in accelerated electrons is obtained by fixing the spectral index in Γe = 2.28, which is the upper limit of the 1-σ region obtained from the fit of the radio data (see Sect. 3). In this case, a good fit is still obtained with the following value for the total energy:
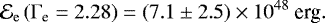 (4)
(4)
This value is still lower than 1050 erg. Therefore, a leptonic origin of the γ-ray flux is compatible with the present data.
We now consider the hadronic model. In this type of models the γ rays originate in the decay of particles, mainly neutral pions, generated in the interactions of accelerated protons with ambient protons. As described before, the energy spectrum of the accelerated protons is assumed to be a power law with an exponential cutoff (see Eq. (1)). The γ-ray flux at Earth can be written as
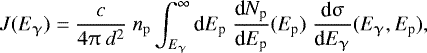 (5)
(5)
where d is the distance to the source, dσ∕dEγ is the differential cross-section in proton–proton collisions, resulting in the γ-ray emission, and c is the speed of light.
The differential cross section of γ rays that originated in proton–proton interactions has been extensively studied in the literature. A comprehensive study has been performed in Kafexhiu et al. (2014), in which a parametrisation of the γ-ray energy spectrum, originated in proton–proton collisions, has been obtained. The projectile proton energy range of the parametrization starts at thekinematic threshold reaching a maximum value of 1 PeV. The differential cross section at low proton energies (≲ 3 GeV) is obtained from a compilation of experimental data, while at high proton energies, it is derived from Monte Carlo simulations. It is very well known that hadronic interactions at the highest energies are unknown. However, there are models that extrapolate low-energy accelerator data to the highest energies. The parametrization in Kafexhiu et al. (2014) includes several options for the high-energy part and has been performed for the hadronic interaction models implemented in Geant 4.10.0 (Agostinelli et al. 2003), PYTHIA 8.18 (Sjöstrand et al. 2008), Sibyll 2.1 (Fletcher et al. 1994), and QGSJET01 (Kalmykov et al. 1997). In this work, we used this parametrisation of the proton–proton collisions resulting in the γ-ray emission with the PYTHIA 8.18 option for the high-energy part. It is worth mentioning that one of the most important aspects of the new parametrisation is the detailed description of the γ-ray spectrum at low proton energies, which represents an important improvement over earlier approaches.
Figure 4 shows the fit of the γ-ray part of the energy spectrum of SNR Kes 41 observed at Earth. In this case, we considered the value of the proton density, np = 950 ± 330 cm−3, in the SNR surroundings, derived inside the E1 region (see also the analysis in Supan et al. 2018). In addition, for this part of our analysis, the spectral index Γp is fixed during the fitting procedure. As in the case of the leptonic model, we consider the canonical value Γp = 2 and the values in the 1-σ region corresponding to the fit of the radio data. The cutoff energy obtained for Γp = 2 is 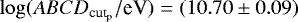 .
.
The energy in accelerated protons calculated for the ambient proton density measured in the E1 region and for Γp = 2 is given by
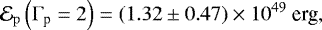 (6)
(6)
which is lower than the canonical value of 1050 erg. Moreover, considering the spectral index Γp = 2.28, the upper limit of the 1-σ region for the fit of the radio data, the maximum value obtained for the energy in accelerated protons is
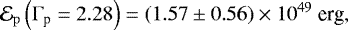 (7)
(7)
which in this case as well is lower than the canonical value.
It is noteworthy that from the leptonic and hadronic models developed in this section in which Γe = Γp = 2, a ratio 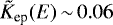 between the differential number of accelerated electrons and the differential number of accelerated protons is obtained for E ≪ 1010 eV. This ratio, defined as (Merten et al. 2017)
between the differential number of accelerated electrons and the differential number of accelerated protons is obtained for E ≪ 1010 eV. This ratio, defined as (Merten et al. 2017)
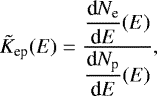 (8)
(8)
is crucial in modelling the nonthermal emission produced in cosmic ray sources. In our leptonic model, it is assumed that the γ-ray part of the flux coming from the hadronic component is much smaller than the one corresponding to bremsstrahlung. Therefore, a value of 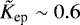 is required in order to obtain a contribution from the proton component that is one order of magnitude smaller than the component corresponding to the bremsstrahlung process. This value is more than one order of magnitude higher than the value inferred from cosmic ray observations (Merten et al. 2017), which is generally assumed to be on the order of 0.01. However, we recall that this number represents an average value and it is not possible to know the differential particle number ratio in each individual source that contributes to the observed average. The canonical value of
is required in order to obtain a contribution from the proton component that is one order of magnitude smaller than the component corresponding to the bremsstrahlung process. This value is more than one order of magnitude higher than the value inferred from cosmic ray observations (Merten et al. 2017), which is generally assumed to be on the order of 0.01. However, we recall that this number represents an average value and it is not possible to know the differential particle number ratio in each individual source that contributes to the observed average. The canonical value of 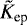 can be obtained theoretically by assuming that the number of protons and electrons that are accelerated is the same and that the spectral indexes of both components after acceleration are also the same, taking a value of ~ 2.2. As discussed in Merten et al. (2017),
can be obtained theoretically by assuming that the number of protons and electrons that are accelerated is the same and that the spectral indexes of both components after acceleration are also the same, taking a value of ~ 2.2. As discussed in Merten et al. (2017), 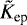 is affected by several factors that can strongly modify its canonical value. In particular, there is evidence both from a theoretical and observational point of view that shows that the spectral indexes of both components can be different. In that work, it is also shown that a large variation of
is affected by several factors that can strongly modify its canonical value. In particular, there is evidence both from a theoretical and observational point of view that shows that the spectral indexes of both components can be different. In that work, it is also shown that a large variation of 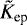 is obtained even for lower values of the difference between the two spectral indexes. For instance, for ΔΓ= ±0.3, the differential particle ratio varies in such a way that
is obtained even for lower values of the difference between the two spectral indexes. For instance, for ΔΓ= ±0.3, the differential particle ratio varies in such a way that 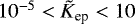 . Therefore, models that requires high values of
. Therefore, models that requires high values of 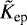 even of order one cannot be discarded (see e.g. H.E.S.S. Collaboration 2018b). We cautiously note that the justification of a negligible contributionof the bremsstrahlung process in the leptonic model of Liu et al. (2015) is based on the assumption of the canonical value of
even of order one cannot be discarded (see e.g. H.E.S.S. Collaboration 2018b). We cautiously note that the justification of a negligible contributionof the bremsstrahlung process in the leptonic model of Liu et al. (2015) is based on the assumption of the canonical value of 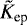 .
.
The analysis using the Fermi-LAT data presented in this paper shows that the γ-ray part of the spectrum of Kes 41 can be dominated by either accelerated leptons producing bremsstrahlung emission or accelerated hadrons that generate γ-ray emission by interacting with the surrounding ambient matter. The γ-ray flux can be properly fitted by these two types of models, and the total energy in accelerated particles is also in all cases lower than the canonical 10% of the typical energy released in a supernova explosion.
 |
Fig. 3 Spectral energy distribution of Kes 41. The curves correspond to the leptonic models fitted to the experimental data. At GeV energies, the statistical uncertainties are indicated by black bars, and the systematic uncertainties are represented in blue. The spectral index of the accelerated electrons used for the fit is Γe = 2. Upper limits for the GeV fluxes correspond to a 95% confidence level, obtained for TS values < 9. |
 |
Fig. 4 Fermi-LAT γ-ray spectrum in the region of SNR Kes 41. The curve corresponds to the hadronic model fitted to the updated experimental data with a fixed spectral index Γp = 2. The statistical and systematic errors are represented by black and blue bars, respectively. Upper limits for the flux correspond to a 95% confidence level, obtained for TS values < 9. |
5 Concluding remarks
This paper is the second in a series focused on the multiwavelength analysis of the counterparts to the unidentified γ-ray emission detected at GeV energies towards SNR Kes 41. Motivated by the new results recently presented in Supan et al. (2018), which revealed the natal molecular cloud of Kes 41, we performed for the first time a global assessment of all available data from radio to γ rays in order to determine the relative contribution of the hadronic and leptonic processes to the overall spectrum. To do this, we re-analysed the Fermi-LAT data to study the γ-ray radiation that is spatially coincident (in projection) with the recently unveiled large-scale molecular material in the region of SNR Kes 41. Using the leptonic models analysed in this work, we demonstrated that if the main contribution to the γ-ray emission comes from the SNR, then both radio and γ-ray data can be successfully modelled by synchrotron radiation and a bremsstrahlung mechanism, respectively. A leptonic contribution from the inverse-Compton emission to explain the production of the emission at GeV energies can be easily excluded. We also modelled the Fermi-LAT spectral data by a hadronic scenario considering the molecular, atomic, and ionised interstellar gases and found that hadronic interactions in a region relatively close to Kes 41 provide a viable mechanism that might explain the observed γ-ray emission, which qualitatively agrees with the results of Liu et al. (2015).
Acknowledgements
The authors wish to thank the anonymous referee since this manuscript was significantly improved by their comments. G.C. and A.D.S. are members of the Carrera del Investigador Científico of CONICET, Argentina. L.S. is a post-doc Fellow of CONICET, Argentina. This research was partially supported by grants awarded by ANPCYT (PICT 1759/15) and the University of Buenos Aires (UBACyT 20020150100098BA), Argentina.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 706, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2016, ApJS, 224, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2016, ApJS, 222, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Agostinelli, S., Allison, J., Amako, K., et al. 2003, Nucl. Instrum. Methods Phys. Res. A, 506, 250 [Google Scholar]
- Aharonian, F. A., Kelner, S. R., & Prosekin, A. Y. 2010, Phys. Rev. D, 82, 043002 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Baldini, L., Bregeon, J., et al. 2013, ApJ, 774, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Banik, P., & Bhadra, A. 2017, Phys. Rev. D, 95, 123014 [NASA ADS] [CrossRef] [Google Scholar]
- Baring, M. G., Ellison, D. C., Reynolds, S. P., Grenier, I. A., & Goret, P. 1999, ApJ, 513, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Bock, D. C.-J., Large, M. I., & Sadler, E. M. 1999, AJ, 117, 1578 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, M. G., Braiding, C., Glueck, C., et al. 2013, PASA, 30, e044 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, D., Slane, P., Carlton, A., & Figueroa-Feliciano, E. 2013, ApJ, 774, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Dulk, P., & Slee, O. 1972, Aust. J. Phys., 25, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, R. S., Gaisser, T. K., Lipari, P., & Stanev, T. 1994, Phys. Rev. D, 50, 5710 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, R. F., Caswell, J. L., & Simons, L. W. J. 1978, Aust. J. Phys. Astrophys. Suppl., 45, 1 [NASA ADS] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., et al.) 2018a, A&A, 612, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., et al.) 2018b, A&A, 612, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, F. C. 1968, Phys. Rev., 167, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C., & Dickey, J. M. 2012, ApJ, 753, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Kafexhiu, E., Aharonian, F., Taylor, A. M., & Vila, G. S. 2014, Phys. Rev. D, 90, 123014 [NASA ADS] [CrossRef] [Google Scholar]
- Kalmykov, N. N., Ostapchenko, S. S., & Pavlov, A. I. 1997, Nucl. Phys. B Proc. Suppl., 52, 17 [Google Scholar]
- Koch, H. W., & Motz, J. W. 1959, Rev. Mod. Phys., 31, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Koralesky, B., Frail, D. A., Goss, W. M., Claussen, M. J., & Green, A. J. 1998, AJ, 116, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B., Chen, Y., Zhang, X., et al. 2015, ApJ, 809, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., et al. 2005, ApJS, 158, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Merten, L., Becker Tjus, J., Eichmann, B., & Dettmar, R.-J. 2017, Astropart. Phys., 90, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2017, ApJS, 230, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Pivato, G., Hewitt, J. W., Tibaldo, L., et al. 2013, ApJ, 779, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Shaver, P. A., & Goss, W. M. 1970, Aust. J. Phys. Astrophys. Suppl., 14, 77 [NASA ADS] [Google Scholar]
- Sjöstrand, T., Mrenna, S., & Skands, P. 2008, Comput. Phys. Commun., 178, 852 [Google Scholar]
- Slane, P., Bykov, A., Ellison, D. C., Dubner, G., & Castro, D. 2015, Space Sci. Rev., 188, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Sturner, S. J., Skibo, J. G., Dermer, C. D., & Mattox, J. R. 1997, ApJ, 490, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Supan, L., Castelletti, G., Supanitsky, A. D., et al. 2018, A&A, 619, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, T., Allafort, A., Ballet, J., et al. 2011, ApJ, 740, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Whiteoak, J. B. Z., & Green, A. J. 1996, A&AS, 118, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, A. E., Griffith, M. R., Burke, B. F., & Ekers, R. D. 1994, ApJS, 91, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, G.-Y., Chen, Y., Su, Y., et al. 2015, ApJ, 799, 103 [NASA ADS] [CrossRef] [Google Scholar]
Details about specifications of the mission, instrumental issues, current event reconstruction framework, background models, etc. can be found at the Fermi-LAT Science Support Center (FSSC) web page: https://fermi.gsfc.nasa.gov/ssc/
The detection of the OH maser spot showed that the remnant encountered dense interstellar gas and served to place the remnant at a distance of ~12 kpc (Koralesky et al. 1998).
All Tables
Fluxes in the GeV range for the γ-ray source detected in correspondence with SNR Kes 41.
All Figures
 |
Fig. 1 New TS map in the region of SNR Kes 41 generated in the 0.5–400 GeV energy band according to the last update on this source analysed in this work. Contours delineate the radio emission at 843 MHz from SUMSS at levels 0.09, 0.3, 0.5, and 0.7 Jy beam−1. Labels correspond to Kes 41 and the neighbouring HII regions (1:G337.711 −0.056; 2:G337.711+0.089; 3:G337.622−0.067; 4:G337.667−0.167; 5:G337.978−0.144; 6:G338.011+0.022; 7:G337.686+0.137; 8:G338.114 −0.193; Jones & Dickey 2012). The ellipse E1 is the area employed in Supan et al. (2018) to derive the properties of the interstellar medium, used to place constraints on the spectral fitting procedure presented in this work. Further details of the Kes 41 environment are presented in Supan et al. (2018). |
| In the text | |
 |
Fig. 2 Panel a: SUMSS 843 MHz continuum emission from Kes 41, the beam size is ~43′′ × 59′′ and the noise level is ~0.015 Jy beam−1. A linear intensity scale was used for the representation. Panel b: integrated radio spectrum of SNR Kes 41 constructedwith the flux densities measurements reported in Table 2. The solid line corresponds to the weighted linear fit to the points excluding the point at 80 MHz, which yields a global spectral index α = − 0.54 ± 0.10 (Sν ∝ να). The same spectral index with an optical depth at 80 MHz τ80MHz = 1.13 ± 0.37 is obtained by fitting (dotted line) all of the measurements with a low-frequency turnover in the spectrum around 100 MHz. |
| In the text | |
 |
Fig. 3 Spectral energy distribution of Kes 41. The curves correspond to the leptonic models fitted to the experimental data. At GeV energies, the statistical uncertainties are indicated by black bars, and the systematic uncertainties are represented in blue. The spectral index of the accelerated electrons used for the fit is Γe = 2. Upper limits for the GeV fluxes correspond to a 95% confidence level, obtained for TS values < 9. |
| In the text | |
 |
Fig. 4 Fermi-LAT γ-ray spectrum in the region of SNR Kes 41. The curve corresponds to the hadronic model fitted to the updated experimental data with a fixed spectral index Γp = 2. The statistical and systematic errors are represented by black and blue bars, respectively. Upper limits for the flux correspond to a 95% confidence level, obtained for TS values < 9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


