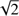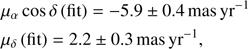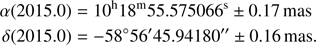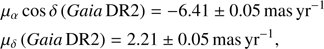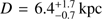EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 619 (November 2018) A&A, 619 (2018) A26 Full HTML
Free Access
Issue
A&A
Volume 619, November 2018
Article Number A26
Number of page(s) 7
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201832572
Published online 05 November 2018

© ESO 2018

1. Introduction

The existence of emission at very high energies (VHE; ≳100 GeV) requires the presence of powerful accelerators that speed particles up to relativistic energies. About two hundred sources have been found to exhibit VHE emission so far1. Most are associated with active galactic nuclei (AGNs), supernova renmants (SNRs), or pulsar wind nebulae (PWNe). However, a handful of these VHE sources are related to Galactic binary systems. With the exception of the colliding-wind binary η-Carinae, recently detected up to 400 GeV (Leser et al. 2017), all of these VHE binaries belong to the subclass of gamma-ray binary systems (see e.g., Dubus 2013, and references therein). These binaries are ideal laboratories to study particle acceleration due to the involved short timescales of the emission, which is modulated by the orbital motion, and their relative proximity to us.

Gamma-ray binaries are composed of a massive star (typically of O or B spectral type) and a compact object, thought to be a young non-accreting neutron star in all cases. Gamma-ray binaries are distinguished from other high-energy binaries by the fact that they exhibit a spectral energy distribution (SED) dominated by the MeV–GeV photons, though emission is observed from radio to TeV γ-rays. In these systems it is thought that a strong shock is produced between the stellar wind and the relativistic wind of the putative young non-accreting neutron star, generating a suitable environment to accelerate particles up to the required energies that subsequently produce the observed radiation (see Dubus 2013, for a detailed review).

Only seven gamma-ray binaries have been discovered to date: PSR B1259−63 (Aharonian et al. 2005b), LS 5039 (Aharonian et al. 2005a), LS I +61 303 (Albert et al. 2006), HESS J0632+057 (Hinton et al. 2009; Skilton et al. 2009), 1FGL J1018.6–5856 (Fermi LAT Collaboration 2012), LMC P3 (Corbet et al. 2016, the first one discovered outside our Galaxy), and PSR J2032+4127 (Lyne et al. 2015; Veritas & MAGIC Collaborations 2017). All of them are nonthermal radio emitters at gigahertz frequencies, with a spectrum dominated by synchrotron emission. All systems but one, LS 5039, show radio light curves modulated with the orbital motion (see Dubus 2013; Marcote et al. 2015, 2016; Marcote 2016), and all gamma-ray binaries explored with very long baseline interferometric (VLBI) observations exhibit a compact, unresolved core plus an extended emission resolved on milliarcsecond scales. This extended emission exhibits morphological changes modulated by the orbital motion and typically represents ∼10% of the total radio emission. It is usually interpreted as radiation emitted from the tail originated from the shocked material, although its origin remains unclear (see e.g., Moldón et al. 2012a,b).

The gamma-ray binary 1FGL J1018.6–58562 was discovered as a periodic GeV source in the Fermi/LAT data (Abdo et al. 2010, 2011; Corbet et al. 2011). Variable nonthermal radio and X-ray counterparts, consistent with the position of a massive star, were later found by Fermi LAT Collaboration (2012). Finally, a TeV source coincident with 1FGL J1018.6–5856 was reported by H. E. S. S. Collaboration (2012) also exhibiting periodic emission (H. E. S. S. Collaboration 2015).

The system is composed of an O6 V((f)) star and a compact object that orbits it every 16.544 ± 0.008 d (Napoli et al. 2011; Fermi LAT Collaboration 2012; An et al. 2015). Assuming a total mass for the system of ≈ 29 M⊙ (Williams et al. 2015) we estimate a semi-major axis of the orbit of ∼0.4 au. The nature of the compact object remains unknown, although a ∼2 M⊙ neutron star is favored (Strader et al. 2015; Williams et al. 2015; Waisberg & Romani 2015; An & Romani 2017; Chen et al. 2017). The distance to 1FGL J1018.6–5856 has been determined to be 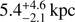5 . 4 − 2.1 + 4.6 kpc $ 5.4_{-2.1}^{+4.6}\,{\mathrm{kpc}} $ through photometric observations (Napoli et al. 2011), while Waisberg & Romani (2015) suggest a distance > 4 kpc due to the observed extinction. We discuss the distance derived by the Gaia Data Release 2 (DR2) Catalog (Gaia Collaboration 2016, 2018) in Sect. 3.3.

The radio emission of 1FGL J1018.6–5856 is orbitally modulated with a quasi-sinusoidal variability that ranges between 1 and 6 mJy, and a flat spectrum of between 5 and 9 GHz (Fermi LAT Collaboration 2012). The maximum emission takes place at orbital phases of ∼0.3, coincident with the maximum emission of the sinusoidal X-ray modulation. These light curves are however anticorrelated with the GeV and TeV ones (see Fig. 3 in H. E. S. S. Collaboration 2015). More recent multifrequency radio observations covering the 2–33 GHz frequency range show that the orbital modulation decreases at higher frequencies, probably due to the presence of free-free absorption (Coley 2015, Coley et al., in prep.).

The gamma-ray binary 1FGL J1018.6–5856 is embedded in the Carina spiral arm, and is spatially coincident with the supernova remnant SNR G284.3−1.8 (also known as MSH 10−53). This SNR was first discovered as a nonthermal radio source by Mills et al. (1961) and Milne & Dickel (1975). Its emission is consistent with a ∼104 yr old type-II SNR originated by a massive progenitor located at a distance of ∼2.9 kpc (Ruiz & May 1986), a value compatible at the ∼1-σ level with the aforementioned distance to 1FGL J1018.6–5856. The expanding shock has interacted with molecular clouds located in the surrounding medium. Milne et al. (1989) reported for the first time the full extent of SNR G284.3−1.8 with observations made with the Molonglo Observatory Synthesis Telescope (MOST) and the Parkes Telescope, and concluded that all the detected radio emission has a nonthermal origin. TeV emission is detected in this region (in excess of 1FGL J1018.6–5856’s contribution), but all of it is probably produced by a PWN powered by the strong pulsar PSR J1016−5857 (with a characteristic age of 21 kyr), located at the western edge of the mentioned SNR (Camilo et al. 2001, 2004). Given the spatial coincidence between SNR G284.3−1.8 and 1FGL J1018.6–5856, that their distances are compatible, and the age of the SNR, the possibility of a physical connection between both sources is not negligible. In that case, the binary system could likely be the progenitor of the SNR (as suggested by e.g. H. E. S. S. Collaboration 2012).

In this paper we present the first VLBI observations of the gamma-ray binary 1FGL J1018.6–5856, which have allowed us to put strong constraints on the compactness of its radio emission. The obtained astrometry, together with archival optical observations and the Gaia DR2 astrometry, provides the first accurate proper motion and distance measurements of the system. Furthermore, these data have allowed us to estimate the peculiar motion of the system within the Galaxy. We present the observations and the data reduction in Sect. 2. We describe the obtained results and present the discussions in Sect. 3: on the observed radio emission of 1FGL J1018.6–5856 (Sect. 3.1), its proper motion (Sect. 3.2) and its distance (Sect. 3.3). Section 3.4 describes the obtained results in the context of the Galaxy: its peculiar motion, its possible relation with SNR G384.3−1.8 and the possible kick received in the system. Finally, we present our conclusions in Sect. 4.

2. Radio observations and data reduction

1FGL J1018.6–5856 was observed with the Australian Long Baseline Array (LBA) at 8.4 GHz on 26 April 2012 from 07:00 to 12:00 UTC (project code V454A; PI: Phil Edwards). The data were recorded with a total bandwidth of 32 MHz divided in four sub-bands of 16 channels each. A two-second integration time was used, recording full circular polarization. Seven stations participated in the observation: the phased Australian Telescope Compact Array (ATCA), Ceduna, Hobart, Mopra, Parkes, Warkworth, and one dish from the Australian Square Kilometre Array Pathfinder (ASKAP). Unfortunately, ASKAP could not produce reliable fringes and its data could not be used. Interferometric ATCA data were also recorded separately with a total bandwidth of 2 GHz (one sub-band of 33 channels) to be sensitive on much larger angular scales.

The source 1057−797 was used as fringe finder and amplitude calibrator. J1019−6047 (located ∼1.9° away from 1FGL J1018.6–5856 with a flux density of ∼0.4 Jy) was observed as phase calibrator in a phase-referencing cycle of 3 min on the calibrator and 3 min on the target source. 1FGL J1018.6–5856 was thus observed during a total on-source time of 107 min. Figure 1 shows the obtained uv-coverage for 1FGL J1018.6–5856 in this observation.

thumbnail Fig. 1.

Resulting uv-coverage for 1FGL J1018.6–5856 in the analyzed LBA observation. The central frequency is 8.4 GHz with a bandwidth of 32 MHz.

The LBA data have been reduced in AIPS3 (Greisen et al. 2003) and Difmap (Shepherd et al. 1994) following standard procedures. A-priori amplitude calibration was performed for each station using the system temperatures recorded during the observation, except for Warkworth where we used nominal system equivalent flux density (SEFD) values. We flagged the bad visibilities manually and then fringe-fitted and bandpass calibrated the data using 1057−797 and J1019−6047. We imaged and self-calibrated the phase calibrator, J1019−6047, to improve the solutions for each station. These solutions were then transferred to the target source, which was finally imaged. Due to the faintness of the emission we used a natural weighting during the imaging, which provides a higher sensitivity at the cost of a lower resolution.

The ATCA data were reduced in Miriad (Sault et al. 1995) and CASA4 following standard procedures. We performed an amplitude calibration using 1057−797, which was observed by the ATCA Calibrator Database5 on 2012 April 22 and May 11 (four days before and 15 days after the LBA observation). After that we phase calibrated the data using J1019−6047. The obtained solutions were then transferred to 1FGL J1018.6–5856, which was finally imaged using a natural weighting. We note that the lack of a calibrator with a well-known and constant flux density introduces an uncertainty in the absolute amplitude scale of the final images.

3. Results and discussion

3.1. Radio emission of 1FGL J1018.6–5856

1FGL J1018.6–5856 is detected as a compact radio source on both arcsec and milliarcsecond scales from the ATCA and LBA data, respectively. The ATCA data, with a synthesized beam of 44 × 13 arcsec2, PA = −6°, and a rms noise level of 90 μJy beam−1, show a compact source with a flux density of 1.22 ± 0.16 mJy. The LBA data (see Fig. 2) show a compact emission of 2.01 ± 0.15 mJy, where the rms noise level of the image is 80 μJy beam−1 and the synthesized beam is 4.8 × 5.6 mas2, PA = −78°.

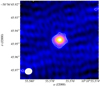thumbnail Fig. 2.

Image of 1FGL J1018.6–5856 obtained by the LBA at 8.5 GHz on 26 April 2012. Contours start at three times the rms noise level of 80 μJy beam−1 and increase by factors of 2 $ \sqrt{2} $. The synthesized beam, shown by the gray ellipse at the bottom-left corner, is 4.8 × 5.6 mas2, PA = −78°.

The obtained flux density values are slightly below but comparable to the values of ∼2–5 mJy expected at that corresponding orbital phase (ϕ = 0.41) from previous observations (Fermi LAT Collaboration 2012; Coley 2015). The fact that the ATCA data did not contain a calibrator with a well-known amplitude does not allow us to establish an accurate absolute amplitude calibration. We can thus only conclude that 1FGL J1018.6–5856 exhibits a flux density of ∼1–2 mJy. The presence of a large longer-term variability, such as in LS I +61 303, is in any case unlikely in 1FGL J1018.6–5856.

By fitting a 2D Gaussian in the uv-plane we obtain an estimation of the source diameter of ∼3 mas (∼20 au given the distance to the source, or around 50 times the semimajor axis of its orbit). Whereas the measured size is only slightly smaller than the synthesized beam and is therefore significant (see Martí-Vidal et al. 2012), we cannot claim that the source is indeed resolved, due to the relatively weak phase calibrator (∼0.4 Jy), its distance to 1FGL J1018.6–5856 (almost 2° away), and the reduced number of stations producing a sparse uv-coverage (see Fig. 1). All these conditions can likely produce errors in the phase solutions transferred from the calibrator to the target source that affect the final calibration and produce an artificially larger source size.

Comparing to the other explored gamma-ray binaries at VLBI scales (see e.g. Moldón 2012), we would expect extended emission on scales of ∼5 mas with flux densities of ∼200 μJy beam−1 (i.e., ∼10% of the total flux density). This emission would not be significant above the rms noise level of our image. The obtained picture therefore shows that 1FGL J1018.6–5856 exhibits an emission which is consistent with respect to the other explored gamma-ray binaries.

The measured source size and flux density from the LBA image can additionally be used to set a lower limit on the brightness temperature of the source. In our case this size implies that Tb ≳ 5.6 × 106 K, thus confirming the nonthermal origin for the radio emission.

The LBA data allowed us to measure the position of 1FGL J1018.6–5856 on milliarcsecond scales. We quote this position in Table 1 compared to the reported ones in the fourth US Naval Observatory CCD Astrograph Catalog (UCAC4, Zacharias et al. 2013) and the Gaia DR2 Catalog (Gaia Collaboration 2016, 2018). The uncertainties in the quoted LBA position take into account the statistical uncertainties in the image (0.2 mas in both α and δ), the systematic uncertainties associated with the uncertainty in the position of the phase calibrator (Beasley et al. 2002; Gordon et al. 2016), and the estimated errors due to the phase-referencing technique (Pradel et al. 2006).

Table 1.

Position of 1FGL J1018.6–5856 as reported in the UCAC4 and Gaia DR2 catalogs, and the position measured from the LBA data.

3.2. Proper motion of 1FGL J1018.6–5856

The position obtained for 1FGL J1018.6–5856 from the LBA observation, together with the positions reported by UCAC4 and Gaia DR2 (see Table 1), allow us to measure the proper motion of the source. A weighted least-squares fit to the data provides a value of

μ α cos δ ( fit ) = − 5.9 ± 0.4 mas yr − 1 μ δ ( fit ) = 2.2 ± 0.3 mas yr − 1 , $$ \begin{aligned}&\mu _{\alpha }\cos \delta \,{\mathrm{(fit)} }={-}5.9 \pm 0.4\,{\mathrm{mas} }\,\mathrm{yr}^{-1}\nonumber \\&\mu _{\delta }\,{\mathrm{(fit)} }=2.2 \pm 0.3\,{\mathrm{mas} }\,\mathrm{yr}^{-1}, \end{aligned} $$(1)

for a reference position at the epoch 2015.0 of

α ( 2015.0 ) = 10 h 18 m 55 . 575066 s ± 0.17 mas δ ( 2015.0 ) = − 58 ∘ 56 ′ 45 . 94180 ″ ± 0.16 mas . $$ \begin{aligned} \alpha ({\mathrm{2015.0} })&=10^\mathrm{h}18^\mathrm{m}55.575066^\mathrm{s} \pm 0.17\,{\mathrm{mas} }\nonumber \\ \delta ({\mathrm{2015.0} })&={-}58^\circ 56^{\prime }45.94180^{\prime \prime }\pm 0.16\,{\mathrm{mas} }. \end{aligned} $$(2)

The obtained proper motion can be compared to the one reported by UCAC4 (−4.7 ± 3.3,   − 0.1 ± 3.3 mas yr−1), which is one order of magnitude less precise, and to the one derived by Gaia DR2:

μ α cos δ ( Gaia DR 2 ) = − 6.41 ± 0.05 mas yr − 1 μ δ ( Gaia DR 2 ) = 2.21 ± 0.05 mas yr − 1 , $$ \begin{aligned}&\mu _{\alpha }\cos \delta \,{({Gaia}\,{\mathrm{DR2} })} = -6.41 \pm 0.05\,\mathrm{mas\,yr^{-1} }\nonumber \\&\mu _{\delta }\,{{({Gaia}\,{\mathrm{DR2} })}} =2.21 \pm 0.05\,{{\mathrm{mas} }\,{\mathrm{yr} }^{-1}}, \end{aligned} $$(3)

for the reference position at the epoch 2015.5 quoted in Table 1.

Figure 3 shows the reported positions and proper motions during the covered period of time (almost 20 yr). We note that both proper motions, and the Gaia DR2 prediction at the LBA epoch, agree within a 1.2-σ confidence level. From now on, we use the proper motion derived by Gaia DR2 due to its smaller uncertainty.

thumbnail Fig. 3.

Astrometry of 1FGL J1018.6–5856 from optical and radio data. The black line represents the proper motion fit to the data and the gray region its 1-σ confidence interval. The dotted orange line represents the proper motion reported by Gaia DR2 and the orange region its 1-σ confidence interval. R represents the residuals from each fit. Error bars show the 1-σ uncertainty on the individual positions. In the case of the Gaia DR2 data the error bars are smaller than the markers. Positions are referred to the Gaia DR2 position at J2015.5.

We note that, as shown in the following section, both the UCAC4 and LBA positions are not affected by the parallax and the orbital motion of 1FGL J1018.6–5856, as the uncertainties in these positions are larger than these motions. We can therefore conclude that the inferred values from our fit are truly dominated by the proper motion of the system. Additionally, we note that the goodness of fit from the Gaia DR2 astrometry is ∼0.1, confirming the reliability of the results.

3.3. Distance to 1FGL J1018.6–5856

1FGL J1018.6–5856 appears in the Gaia DR2 Catalog with a parallax of ϖ = 0.153 ± 0.025 mas. The estimation of the distance to the source from a parallax measurement is not trivial (Bailer-Jones 2015; Luri et al. 2018), and we have considered it as an inference problem where the parallax measurement is described by a Gaussian probability distribution function. We assume a prior 𝒫prior(D) = D2exp(−D/L), where D is the distance and L is the length scale. This prior corresponds to an exponentially decreasing volume density, and is optimal in our case due to its simplistic but physical meaning (see the aforementioned references for a detailed discussion). We have set L to be the previous estimation on the distance to 1FGL J1018.6–5856 (∼5.4 kpc; Napoli et al. 2011), as it represents the a-priori most probable distance from our prior.

Using the Gaia DR2 parallax we derive a mean distance to 1FGL J1018.6–5856 of 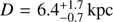D = 6 . 4 − 0.7 + 1.7 kpc $ D = 6.4_{-0.7}^{+ 1.7}\,{\mathrm{kpc}} $, where the median distance is 6.8 kpc (see Fig. 4). From now on we use the derived mean value as the distance to 1FGL J1018.6–5856. We note that the use of different priors (varying L and/or using constant probability functions) produce consistent results (within the reported uncertainties for all reasonable cases).

thumbnail Fig. 4.

Probability distribution function, 𝒫, of the distance D to 1FGL J1018.6–5856 derived from the Gaia DR2 parallax by assuming a prior 𝒫prior(D) = D2exp(−D/L) (see text for more details). The blue vertical line represents the mean distance to the source and the light blue shadowed region represents its ±1σ confidence interval ( D = 6 . 4 − 0.7 + 1.7 kpc $ D = 6.4_{-0.7}^{+ 1.7}\,{\mathrm{kpc}} $). The red vertical line represents the median distance (6.8 kpc).

For consistency we have determined that, at the derived distance, the orbit of 1FGL J1018.6–5856 exhibits an angular size of ≈0.12 mas (for a semi-major axis of ≈0.4 au). This value is lower than our precision in the LBA results. In the case of the Gaia results, we note that the optical emission only arises from the companion star, and therefore these results are exclusively sensitive to the motion of this component, which only represents ≈9 μas (for the masses reported in the introduction). This value is a factor of two lower than the uncertainties in the Gaia results. We can therefore confirm that the orbital motion of the system does not significantly affect the derived proper motion or parallax.

3.4. 1FGL J1018.6–5856 within the Galaxy

In the following we discuss the implications of all the obtained results on the motion of the source within the Galaxy (Sect. 3.4.1) and with respect to SNR G284.3−1.8 (Sect. 3.4.2). We also estimate the mass loss required to produce the observed peculiar motion in Sect. 3.4.3.

3.4.1. Peculiar motion

Transforming the Gaia DR2 proper motion to Galactic coordinates we obtain a Galactic proper motion of μl = −6.57 ± 0.05 mas yr−1 and μb = −1.68 ± 0.05 mas yr−1. Given that 1FGL J1018.6–5856 is located at a negative Galactic latitude (−1.69°), this proper motion implies that the source is going away from the Galactic plane. Given the estimated distance to the source of 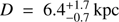D = 6 . 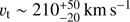4 − 0.7 + 1.7 kpc $ D = 6.4_{-0.7}^{+1.7}\,{\mathrm{kpc}} $ the measured proper motion implies a tangential velocity of υ t ∼ 210 − 20 + 50 km s − 1 $ \upsilon_{\mathrm{t}} \sim 210_{-20}^{+50}\,{{\mathrm{km}}\,\mathrm{s}^{-1}} $.

We can combine these measurements together with the average radial velocity of the source of υr ≈ 30–36 km s−1 (Strader et al. 2015) to determine the peculiar motion of 1FGL J1018.6–5856 within the Galaxy, on its regional standard of rest (RSR; Reid et al. 2014). We have assumed a distance to the Galactic center of 8.34 ± 0.16 kpc, the local standard of rest (LSR) defined by 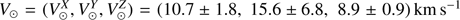V ⊙ = ( V ⊙ X , V ⊙ Y , V ⊙ Z ) = ( 10.7 ± 1.8 , 15.6 ± 6.8 , 8.9 ± 0.9 ) km s − 1 $ V_{\odot} = (V_{\odot}^{X}, V_{\odot}^{Y}, V_{\odot}^{Z}) = (10.7 \pm 1.8,\ 15.6 \pm 6.8,\ 8.9 \pm 0.9)\,{{\mathrm{km}}\,\mathrm{s}^{-1}} $, and a Galactic rotation of Θ0 = 240 ± 8 km s−1 (see model A5 in Reid et al. 2014), where X, Y, Z are defined as X towards the Galactic center, Y towards l = 90° (following the Galactic rotation), and Z towards the north Galactic pole. Using this frame we obtain a peculiar motion in the RSR of 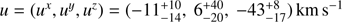u = ( u x , u y , u z ) = ( − 11 − 14 + 10 , 6 − 20 + 40 , 43 − 17 + 8 ) km s − 1 $ u = (u^x, u^y, u^z) = (-11_{-14}^{+10},\ 6_{-20}^{+40},43_{-17}^{+8})\,{{\mathrm{km}}\,\mathrm{s}^{-1}} $, where x, y, z are defined as the RSR frame from 1FGL J1018.6–5856 to the Galactic center, to the Galactic rotating direction, and towards the Galactic north pole, respectively. Figure 5 shows these results as a function of the distance D to 1FGL J1018.6–5856, and Fig. 6 shows the obtained peculiar motion of the source with respect to the Sun and the Galaxy.

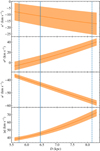thumbnail Fig. 5.

Peculiar motion of 1FGL J1018.6–5856 on its regional standard of rest (RSR) as a function of the distance between the Sun and the source. The orange lines show the average velocity whereas the colored region represents the 1-σ confidence interval. We show the components in the direction to the Galactic center (ux), to the Galactic rotation (uy), and towards the Galactic north pole (uz). The bottom panel shows the module of the peculiar motion (|u|). The vertical blue lines represent the average distance to 1FGL J1018.6–5856 (solid line) and its ±1-σ confidence interval (dashed lines).

thumbnail Fig. 6.

Absolute position and peculiar motion of 1FGL J1018.6–5856 within the Galaxy in a view perpendicular to the Galactic plane (top panel) and parallel to it in the projected direction between the Galactic center and 1FGL J1018.6–5856 (bottom panel). The black dot represents the Galactic center, the orange star represents the Sun, the open red symbol represents SNR G384.3−1.8, and the blue star represents 1FGL J1018.6–5856 at the distance of 6.4 kpc. The blue arrow represents the peculiar motion of the source (in the RSR, after Galactic rotation subtraction) after 70 Myr for reference6. The blue ellipse represents the uncertainty on this motion. The gray ellipses provide a schematic picture of the Galactic plane. Image Credit: NASA/JPL-Caltech/R. Hurt/SSC/Caltech, The Mozilla Foundation.

In summary, we obtain an absolute peculiar motion of 36 <  |u| < 75 km s−1 with an average value of ≈45 km s−1. We note that the final uncertainties quoted on the peculiar motion are dominated by the uncertainty on the distance of the source. OB stars exhibit typical peculiar motions of ≲10 km s−1 (see e.g., Mel’nik & Dambis 2017), although these values can increase up to 10–30 km s−1 in some regions (see e.g., Gómez et al. 2008, for the OrionBN/KL region). Therefore it is unclear if the derived peculiar motion originates from a kick during the stellar core collapse or if it was intrinsic to the system beforehand. We note that the derived motion is similar to the motion of 26 ± 8 km s−1 observed in the gamma-ray binary PSR B1259−63 (Miller-Jones et al. 2018), but lower than the motion of ∼140 km s−1 observed in LS 5039 (Moldón et al. 2012b), and higher than the motion of ∼16 km s−1 observed in LS I +61 303 (Wu et al. 2018). In any case, these motions are well below the velocities observed in isolated pulsars (see e.g., Chatterjee et al. 2005), as expected for binary systems.

3.4.2. Relation with SNR G384.3−1.8

1FGL J1018.6–5856 is located near the center of the 104 yr old SNR G284.3−1.8. Figure 7 shows the field around 1FGL J1018.6–5856 as seen by the Sydney University Molonglo Sky Survey (SUMSS; Mauch et al. 2003) at 843 MHz. We also show the position of 1FGL J1018.6–5856 at the time when the SNR was produced (∼1 arcmin to the SE from its current position) and its direction of motion. Figure 6 shows the 3D position of both the SNR and 1FGL J1018.6–5856 with respect to the Sun.

thumbnail Fig. 7.

Field of 1FGL J1018.6–5856 as seen by the Sydney University Molonglo Sky Survey (SUMSS) at 843 MHz. Contours start at two times the rms noise level of 2 mJy with increments of 2 $ \sqrt{2} $. The emission in the region is dominated by the SNR G284.3−1.8 (delimited by the east and west arcs) and its interaction with molecular clouds (e.g. the north-east strong filament). The filled red dot represents the current position of 1FGL J1018.6–5856, while the empty red dot represents the position of the source 10 kyr ago (when the supernova that created SNR G284.3−1.8 took place). The red arrow represents the proper motion of the binary system and the predicted position in 100 kyr. The orange star in the west denotes the position of the pulsar PSR J1016−5857 and its associated PWN.

Although the distance to SNR G384.3−1.8 (∼2.9 kpc) was initially compatible at ∼1-σ confidence level with the distance to 1FGL J1018.6–5856 reported in the literature (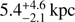 5 . 4 − 2.1 + 4.6 kpc $ 5.4_{-2.1}^{+4.6}\,{\mathrm{kpc}} $), the distance derived in this paper ( 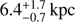6 . 4 − 0.7 + 1.7 kpc $ 6.4_{-0.7}^{+1.7}\,{\mathrm{kpc}} $) rejects the possible association of SNR G384.3−1.8 with the core collapse that led to the compact object in 1FGL J1018.6–5856 at a 5-σ confidence level. We note that Ruiz & May (1986) constrained the distance to SNR G384.3−1.8 to be ≲3.5 kpc (with the aforementioned mean value of 2.9 kpc) due to the strong absorption expected in that line of sight.

Additionally, the obtained proper motion for 1FGL J1018.6–5856 is not compatible with a source moving away from SNR G284.3−1.8 (see Fig. 6), and in any case the binary system could not have traveled the distance of ≳1 kpc in only 104 yr (this would imply velocities of ≳105 km s−1, which would be astonishing for such a system).

We therefore conclude that 1FGL J1018.6–5856 and SNR G284.3−1.8 are completely unrelated systems and do not share any common origin or physical connection. We note that in the vicinity of 1FGL J1018.6–5856 we see no other sources that could be linked to the binary system.

3.4.3. Kick after the stellar core collapse

As mentioned, 1FGL J1018.6–5856 exhibits a peculiar motion slightly (but not significantly) larger than typical OB stars . It is unclear, but likely, that the stellar core collapse that formed the compact object produced a kick in the system and changed its peculiar motion to some extent. We can only provide rough estimations of how much mass was lost from the system during the collapse under the assumptions of a completely symmetric stellar core collapse and that the observed peculiar motion is dominated by the received kick. Under these assumptions the velocity of the center of mass of the binary system would have changed after the collapse by a value of (Nelemans et al. 1999)

Δ M M ⊙ = 1 213 ( υ s km s − 1 ) ( M ∗ M ⊙ ) − 1 ( P re-circ d ) 1 / 3 ( M X + M ∗ M ⊙ ) 5 / 3 , $$ \begin{aligned} \frac{\Delta M}{M_{\odot }} = \frac{1}{213}\left(\frac{{\upsilon}_s}{{\text{ km}}\,{\text{ s}}^{-1}}\right)\left(\frac{M_{*}}{M_{\odot }}\right)^{-1}\left(\frac{P_{\text{ re-circ}}}{ \text{ d}}\right)^{1/3}\left(\frac{M_{\text{ X}}+{\text{ M}_{*}}}{M_{\odot }}\right)^{5/3}, \end{aligned} $$(4)

where ΔM is the lost mass in the collapse (and therefore ejected from the binary system), υs is the velocity of the binary system due to the kick, M* is the initial mass of the companion star, Pre − circ is the orbital period after re-circularization after the collapse, and MX is the remaining mass of the compact object. MX is estimated to be ∼2 M⊙ (as discussed in the introduction). Given that the total mass of the system is ≈29 M⊙, the mass of the companion star must be M* ∼ 27 M⊙. Pre − circ = Porb(1 − e2)3/2 (Nelemans et al. 1999), where Porb is the final orbital period of the system (after the core collapse), and e the final eccentricity of its orbit. Given that e ∼ 0.31 ± 0.16 (Monageng et al. 2017) we obtain Pre − circ ≈ 14.2 d, and therefore 4 ≲ ΔM ≲ 9 M⊙ for the derived peculiar motion of the source.

These values imply that a non-negligible mass was ejected from the system during the core collapse. Considering this lost mass, the progenitor would have a mass of ∼6–11 M⊙, which is smaller than the ∼27 M⊙ companion star. These results suggest that the progenitor lost additional mass before the core collapse, either by mass transfer to the companion star or pulling away from the system via the stellar wind. We note that the lost mass could easily be higher (likely ∼2 times larger given the typical peculiar motions of such systems) if the system has changed the direction of motion during the core collapse.

4. Conclusions

We report the first VLBI observations of 1FGL J1018.6–5856, showing that the source exhibits compact emission on milliarcsecond scales. Its compactness implies a brightness temperature of ≳5.6 × 106 K, confirming the nonthermal origin of the emission. Extended emission on these angular scales is not detected but the current constraints are consistent with a faint emission similar to the one reported in other gamma-ray binaries. An ongoing monitoring of 1FGL J1018.6–5856 with more sensitive and with LBA observations of a slightly higher resolution would allow us to detect the presence of extended emission originating from the putative cometary tail as observed in other gamma-ray binaries, and study its morphological evolution along the orbit.

The presented LBA observation has allowed us to obtain a precise position of the source that, together with archival optical UCAC4 observations and the Gaia DR2 astrometry, provides the most accurate measurements of the proper and peculiar motions and distance to 1FGL J1018.6–5856 so far. The derived results agree with the proper motions reported by Gaia DR2, providing an independent verification for this system. Given the distance and the characteristics of 1FGL J1018.6–5856, we confirm that the orbital motion does not significantly affect the astrometry results. We also conclude that 1FGL J1018.6–5856 cannot physically be related to SNR G284.3−1.8.

The obtained peculiar motion of 1FGL J1018.6–5856 is slightly, but not significantly, faster than the typical motions observed for early-type stars. The system thus did not receive a significant kick after the core collapse that led to the formation of compact object, although a significant amount of mass of 4–9 M⊙ was lost during this collapse

1

See the online TeV Catalog (TeVCat; Wakely & Horan 2008): http://tevcat.uchicago.edu

2

Also known as 3FGL J1018.9–5856.

3

The Astronomical Image Processing System (AIPS) is a software package produced and maintained by the National Radio Astronomy Observatory (NRAO).

4

The Common Astronomy Software Applications, CASA, is also produced and maintained by the NRAO.

6

We note that the expected lifetime of an O6 V star is ≲5 Myr (Massey et al. 2001) and therefore at the quoted time such a star will no longer exist.

Acknowledgments

The Australia Telescope Compact Array and the Australian Long Baseline Array are part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO. This paper includes archived data obtained through the Australia Telescope Online Archive (http://atoa.atnf.csiro.au). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. BM, MR, and JMP acknowledge support from the Spanish Ministerio de Economía y Competitividad (MINECO) under grants AYA2016-76012-C3-1-P, FPA2017-82729-C6-2-R, and MDM-2014-0369 of ICCUB (Unidad de Excelencia “María de Maeztu”). This research made use of APLpy, an open-source plotting package for Python hosted at http://aplpy.github.com, Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013), and Matplotlib (Hunter 2007).

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 723, 649 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 736, L11 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005a, Science, 309, 746 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  4. Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005b, A&A, 442, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Albert, J., Aliu, E., Anderhub, H., et al. 2006, Science, 312, 1771 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  6. An, H., & Romani, R. W. 2017, ApJ, 838, 145 [NASA ADS] [CrossRef] [Google Scholar]
  7. An, H., Bellm, E., Bhalerao, V., et al. 2015, ApJ, 806, 166 [NASA ADS] [CrossRef] [Google Scholar]
  8. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [NASA ADS] [CrossRef] [Google Scholar]
  10. Beasley, A. J., Gordon, D., Peck, A. B., et al. 2002, ApJS, 141, 13 [NASA ADS] [CrossRef] [Google Scholar]
  11. Camilo, F., Bell, J. F., Manchester, R. N., et al. 2001, ApJ, 557, L51 [NASA ADS] [CrossRef] [Google Scholar]
  12. Camilo, F., Gaensler, B. M., Gotthelf, E. V., Halpern, J. P., & Manchester, R. N. 2004, ApJ, 616, 1118 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chatterjee, S., Vlemmings, W. H. T., Brisken, W. F., et al. 2005, ApJ, 630, L61 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chen, A. M., Ng, C. W., Takata, J., Yu, Y. W., & Cheng, K. S. 2017, ArXiv e-prints [arXiv:1703.08080] [Google Scholar]
  15. Coley, J. B. 2015, PhD Thesis, University of Maryland, Baltimore County, USA [Google Scholar]
  16. Corbet, R. H. D., Cheung, C. C., Kerr, M., et al. 2011, ATel, 3221, 1 [NASA ADS] [Google Scholar]
  17. Corbet, R. H. D., Chomiuk, L., Coe, M. J., et al. 2016, ApJ, 829, 105 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dubus, G. 2013, A&ARv, 21, 64 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fermi LAT Collaboration (Ackermann, M., et al.) 2012, Science, 335, 189 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gómez, L., Rodríguez, L. F., Loinard, L., et al. 2008, ApJ, 685, 333 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gordon, D., Jacobs, C., Beasley, A., et al. 2016, AJ, 151, 154 [NASA ADS] [CrossRef] [Google Scholar]
  24. Greisen, E. W. 2003, Astrophys. Space Sci. Lib., 285, 109 [Google Scholar]
  25. H. E. S. S. Collaboration (Abramowski, A., et al.) 2012, A&A, 541, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. H. E. S. S. Collaboration (Abramowski, A., et al.) 2015, A&A, 577, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Hinton, J. A., Skilton, J. L., Funk, S., et al. 2009, ApJ, 690, L101 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  29. Leser, E., Ohm, S., Füßling, M., et al. 2017, Int. Cosmic Ray Conf., 35, 717 [Google Scholar]
  30. Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Lyne, A. G., Stappers, B. W., Keith, M. J., et al. 2015, MNRAS, 451, 581 [NASA ADS] [CrossRef] [Google Scholar]
  32. Marcote, B. 2016, PhD Thesis, University of Barcelona, Spain [Google Scholar]
  33. Marcote, B., Ribó, M., Paredes, J. M., & Ishwara-Chandra, C. H. 2015, MNRAS, 451, 4578 [Google Scholar]
  34. Marcote, B., Ribó, M., Paredes, J. M., et al. 2016, MNRAS, 456, 1791 [NASA ADS] [CrossRef] [Google Scholar]
  35. Martí-Vidal, I., Pérez-Torres, M. A., & Lobanov, A. P. 2012, A&A, 541, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Massey, P., & Meyer, M. 2001, Encyclopedia of Astronomy and Astrophysics, ed. P. Murdin (Bristol: Institute of Physics Publishing), 1882 [Google Scholar]
  37. Mauch, T., Murphy, T., Buttery, H. J., et al. 2003, MNRAS, 342, 1117 [NASA ADS] [CrossRef] [Google Scholar]
  38. Mel’nik, A. M., & Dambis, A. K. 2017, MNRAS, 472, 3887 [NASA ADS] [CrossRef] [Google Scholar]
  39. Miller-Jones, J. C. A., Deller, A. T., Shannon, R. M., et al. 2018, MNRAS, 479, 4849 [NASA ADS] [CrossRef] [Google Scholar]
  40. Mills, B. Y., Slee, O. B., & Hill, E. R. 1961, Aust. J. Phys., 14, 497 [NASA ADS] [CrossRef] [Google Scholar]
  41. Milne, D. K., & Dickel, J. R. 1975, Aust. J. Phys., 28, 209 [Google Scholar]
  42. Milne, D. K., Caswell, J. L., Kesteven, M. J., Haynes, R. F., & Roger, R. S. 1989, PASA, 8, 187 [NASA ADS] [CrossRef] [Google Scholar]
  43. Moldón, J. 2012, PhD Thesis, Universitat de Barcelona, Spain [Google Scholar]
  44. Moldón, J., Ribó, M., & Paredes, J. M. 2012a, A&A, 548, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Moldón, J., Ribó, M., Paredes, J. M., et al. 2012b, A&A, 543, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Monageng, I. M., McBride, V. A., Townsend, L. J., et al. 2017, ApJ, 847, 68 [NASA ADS] [CrossRef] [Google Scholar]
  47. Napoli, V. J., McSwain, M. V., Boyer, A. N. M., & Roettenbacher, R. M. 2011, PASP, 123, 1262 [NASA ADS] [CrossRef] [Google Scholar]
  48. Nelemans, G., Tauris, T. M., & van den Heuvel, E. P. J. 1999, A&A, 352, L87 [NASA ADS] [Google Scholar]
  49. Pradel, N., Charlot, P., & Lestrade, J.-F. 2006, A&A, 452, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
  51. Ruiz, M. T., & May, J. 1986, ApJ, 309, 667 [NASA ADS] [CrossRef] [Google Scholar]
  52. Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, ASP Conf. Ser., 77, 433 [NASA ADS] [Google Scholar]
  53. Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, BAAS, 26, 987 [NASA ADS] [Google Scholar]
  54. Skilton, J. L., Pandey-Pommier, M., Hinton, J. A., et al. 2009, MNRAS, 399, 317 [NASA ADS] [CrossRef] [Google Scholar]
  55. Strader, J., Chomiuk, L., Cheung, C. C., Salinas, R., & Peacock, M. 2015, ApJ, 813, L26 [NASA ADS] [CrossRef] [Google Scholar]
  56. Veritas, & MAGIC Collaborations 2017, ATel, 10810, 1 [Google Scholar]
  57. Waisberg, I. R., & Romani, R. W. 2015, ApJ, 805, 18 [NASA ADS] [CrossRef] [Google Scholar]
  58. Wakely, S. P., & Horan, D. 2008, Int. Cosmic Ray Conf., 3, 1341 [NASA ADS] [Google Scholar]
  59. Williams, B. J., Rangelov, B., Kargaltsev, O., & Pavlov, G. G. 2015, ApJ, 808, L19 [NASA ADS] [CrossRef] [Google Scholar]
  60. Wu, Y. W., Torricelli-Ciamponi, G., Massi, M., et al. 2018, MNRAS, 474, 4245 [NASA ADS] [CrossRef] [Google Scholar]
  61. Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Position of 1FGL J1018.6–5856 as reported in the UCAC4 and Gaia DR2 catalogs, and the position measured from the LBA data.

In the text

All Figures

thumbnail Fig. 1.

Resulting uv-coverage for 1FGL J1018.6–5856 in the analyzed LBA observation. The central frequency is 8.4 GHz with a bandwidth of 32 MHz.
In the text
thumbnail Fig. 2.

Image of 1FGL J1018.6–5856 obtained by the LBA at 8.5 GHz on 26 April 2012. Contours start at three times the rms noise level of 80 μJy beam−1 and increase by factors of 2 $ \sqrt{2} $. The synthesized beam, shown by the gray ellipse at the bottom-left corner, is 4.8 × 5.6 mas2, PA = −78°.
In the text
thumbnail Fig. 3.

Astrometry of 1FGL J1018.6–5856 from optical and radio data. The black line represents the proper motion fit to the data and the gray region its 1-σ confidence interval. The dotted orange line represents the proper motion reported by Gaia DR2 and the orange region its 1-σ confidence interval. R represents the residuals from each fit. Error bars show the 1-σ uncertainty on the individual positions. In the case of the Gaia DR2 data the error bars are smaller than the markers. Positions are referred to the Gaia DR2 position at J2015.5.
In the text
thumbnail Fig. 4.

Probability distribution function, 𝒫, of the distance D to 1FGL J1018.6–5856 derived from the Gaia DR2 parallax by assuming a prior 𝒫prior(D) = D2exp(−D/L) (see text for more details). The blue vertical line represents the mean distance to the source and the light blue shadowed region represents its ±1σ confidence interval ( D = 6 . 4 − 0.7 + 1.7 kpc $ D = 6.4_{-0.7}^{+ 1.7}\,{\mathrm{kpc}} $). The red vertical line represents the median distance (6.8 kpc).
In the text
thumbnail Fig. 5.

Peculiar motion of 1FGL J1018.6–5856 on its regional standard of rest (RSR) as a function of the distance between the Sun and the source. The orange lines show the average velocity whereas the colored region represents the 1-σ confidence interval. We show the components in the direction to the Galactic center (ux), to the Galactic rotation (uy), and towards the Galactic north pole (uz). The bottom panel shows the module of the peculiar motion (|u|). The vertical blue lines represent the average distance to 1FGL J1018.6–5856 (solid line) and its ±1-σ confidence interval (dashed lines).
In the text
thumbnail Fig. 6.

Absolute position and peculiar motion of 1FGL J1018.6–5856 within the Galaxy in a view perpendicular to the Galactic plane (top panel) and parallel to it in the projected direction between the Galactic center and 1FGL J1018.6–5856 (bottom panel). The black dot represents the Galactic center, the orange star represents the Sun, the open red symbol represents SNR G384.3−1.8, and the blue star represents 1FGL J1018.6–5856 at the distance of 6.4 kpc. The blue arrow represents the peculiar motion of the source (in the RSR, after Galactic rotation subtraction) after 70 Myr for reference6. The blue ellipse represents the uncertainty on this motion. The gray ellipses provide a schematic picture of the Galactic plane. Image Credit: NASA/JPL-Caltech/R. Hurt/SSC/Caltech, The Mozilla Foundation.
In the text
thumbnail Fig. 7.

Field of 1FGL J1018.6–5856 as seen by the Sydney University Molonglo Sky Survey (SUMSS) at 843 MHz. Contours start at two times the rms noise level of 2 mJy with increments of 2 $ \sqrt{2} $. The emission in the region is dominated by the SNR G284.3−1.8 (delimited by the east and west arcs) and its interaction with molecular clouds (e.g. the north-east strong filament). The filled red dot represents the current position of 1FGL J1018.6–5856, while the empty red dot represents the position of the source 10 kyr ago (when the supernova that created SNR G284.3−1.8 took place). The red arrow represents the proper motion of the binary system and the predicted position in 100 kyr. The orange star in the west denotes the position of the pulsar PSR J1016−5857 and its associated PWN.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.