A&A 619, C1 (2018)
Master equation theory applied to the redistribution of polarized radiation in the weak radiation field limit
V. The two-term atom (Corrigendum)
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot, Sorbonne Paris Cité 5, Place Jules Janssen, 92190 Meudon, France
e-mail: V.Bommier@obspm.fr
Key words: atomic processes / line: formation / line: profiles / magnetic fields / polarization / errata, addenda
Erratum for: A&A, 607, A50 (2017), https://doi.org/10.1051/0004-6361/201630169
A sign factor was lacking in the expressions of the redistribution matrix in the case of incomplete Paschen-Back effect, Eqs. (A.1) and (A.6) of Bommier (2017). This sign factor is unity in the absence of incomplete Paschen-Back effect. A (2I + 1) denominator was also missing in Eqs. (A.6) and (40), and some typos occurred in Eq. (A.6). The correct formulæ are provided below.
The corrected Eq. (A.1) is:
![$$ \begin{aligned} \begin{array}{ll} \mathcal{R} _{ij}\left( \nu ,\nu _{1},\boldsymbol{\Omega },\boldsymbol{\Omega }_{1}; \boldsymbol{B}\right)&=\mathop {\sum }\limits_{J_{u}\bar{J}_{u}J_{u}^{*}M_{u}J_{u}^{\prime }\bar{J}_{u}^{\prime }J_{u}^{\prime *}M_{u}^{\prime }J_{\ell }\bar{J}_{\ell }J_{\ell }^{*}M_{\ell }J_{\ell }^{\prime }\bar{J} _{\ell }^{\prime }J_{\ell }^{\prime *}M_{\ell }^{\prime }KK^{\prime }Q}\int f(\boldsymbol{\upsilon}){\mathrm{d} }^{3}\boldsymbol{\upsilon}\ (-1)^{Q}\mathcal{T} _{-Q}^{K^{\prime }}(j,\boldsymbol{\Omega }_{1})\mathcal{T} _{Q}^{K}(i,\boldsymbol{\Omega }) \\&\quad \times 3\dfrac{2L_{u}+1}{2S+1}\sqrt{(2K+1)(2K^{\prime }+1)}\ (-1)^{M_{\ell }-M_{\ell }^{\prime }} \left( -1\right) ^{J_{u}+\bar{J}_{u}+J_{u}^{\prime }+\bar{J}_{u}^{\prime }} \left( -1\right) ^{J_{\ell }+\bar{J}_{\ell }+J_{\ell }^{\prime }+\bar{J}_{\ell }^{\prime }} \\&\quad \times \sqrt{(2J_{u}+1)(2\bar{J}_{u}+1)(2J_{u}^{\prime }+1)(2\bar{J} _{u}^{\prime }+1)(2J_{\ell }+1)(2\bar{J}_{\ell }+1)(2J_{\ell }^{\prime }+1)(2 \bar{J}_{\ell }^{\prime }+1)} \\&\quad \times C_{J_{u}^{*}M_{u}}^{J_{u}}\left( B\right) C_{J_{u}^{*}M_{u}}^{\bar{J}_{u}}\left( B\right) C_{J_{u}^{\prime *}M_{u}^{\prime }}^{J_{u}^{\prime }}\left( B\right) C_{J_{u}^{\prime *}M_{u}^{\prime }}^{ \bar{J}_{u}^{\prime }}\left( B\right) C_{J_{\ell }^{*}M_{\ell }}^{J_{\ell }}\left( B\right) C_{J_{\ell }^{*}M_{\ell }}^{\bar{J}_{\ell }}\left( B\right) C_{J_{\ell }^{\prime *}M_{\ell }^{\prime }}^{J_{\ell }^{\prime }}\left( B\right) C_{J_{\ell }^{\prime *}M_{\ell }^{\prime }}^{ \bar{J}_{\ell }^{\prime }}\left( B\right) \\&\quad \times \left\{ \begin{array}{ccc} J_{u}&1&J_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}^{\prime }&1&\bar{J}_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{J}_{u}&1&J_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{J}_{u}^{\prime }&1&\bar{J}_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \\&\quad \times \left( \begin{array}{ccc} J_{u}&1&J_{\ell } \\ -M_{u}&p&M_{\ell } \end{array} \right) \left( \begin{array}{ccc} J_{u}^{\prime }&1&\bar{J}_{\ell } \\ -M_{u}^{\prime }&p^{\prime }&M_{\ell } \end{array} \right) \left( \begin{array}{ccc} \bar{J}_{u}&1&J_{\ell }^{\prime } \\ -M_{u}&p^{\prime \prime \prime }&M_{\ell }^{\prime } \end{array} \right) \left( \begin{array}{ccc} \bar{J}_{u}^{\prime }&1&\bar{J}_{\ell }^{\prime } \\ -M_{u}^{\prime }&p^{\prime \prime }&M_{\ell }^{\prime } \end{array} \right) \\&\quad \times \left( \begin{array}{ccc} 1&1&K^{\prime } \\ -p&p^{\prime }&Q \end{array} \right) \left( \begin{array}{ccc} 1&1&K \\ -p^{\prime \prime \prime }&p^{\prime \prime }&Q \end{array} \right) \\&\quad \times \left\{ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{M_{u}M_{u}^{\prime }}}{\hbar }}\ \delta \left( \tilde{\nu }-\tilde{\nu }_{1}-\nu _{M_{\ell }M_{\ell }^{\prime }}\right) \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }}-\tilde{\nu }_{1}\right) \right] \right. \\&\quad +\left[ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\dfrac{{\mathrm{i } }\Delta E_{M_{u}M_{u}^{\prime }}}{\hbar }}-\dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{M_{u}M_{u}^{\prime }} }{\hbar }}\right] \\&\quad \times \left. \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }}-\tilde{\nu }_{1}\right) \right] \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }^{\prime }}-\tilde{\nu }\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }^{\prime }}-\tilde{\nu }\right) \right] \right\} \end{array} \ . \end{aligned} $$](/articles/aa/full_html/2018/11/aa30169e-16/aa30169e-16-eq1.gif) (A.1)
(A.1)
The corrected Eq. (A.6) is:
![$$ \begin{aligned} \begin{array}{ll} \mathcal{R} _{ij}\left( \nu ,\nu _{1},\boldsymbol{\Omega },\boldsymbol{\Omega }_{1}; \boldsymbol{B}\right)&= \mathop {\displaystyle \sum }\limits_{J_{u}\bar{J}_{u}J_{u}^{*}F_{u}\bar{F} _{u}F_{u}^{*}M_{u}J_{u}^{\prime }\bar{J}_{u}^{\prime }J_{u}^{\prime *}F_{u}^{\prime }\bar{F}_{u}^{\prime }F_{u}^{\prime *}M_{u}^{\prime }J_{\ell }\bar{J}_{\ell }J_{\ell }^{*}F_{\ell }\bar{F}_{\ell }F_{\ell }^{*}M_{\ell }J_{\ell }^{\prime }\bar{J}_{\ell }^{\prime }J_{\ell }^{\prime *}F_{\ell }^{\prime }\bar{F}_{\ell }^{\prime }F_{\ell }^{\prime *}M_{\ell }^{\prime }KK^{\prime }Q} \\&\quad \times \int f(\boldsymbol{\upsilon}){\mathrm{d} }^{3}\boldsymbol{\upsilon}\ (-1)^{Q}\mathcal{T} _{-Q}^{K^{\prime }}(j,\boldsymbol{\Omega }_{1})\mathcal{T} _{Q}^{K}(i,\boldsymbol{\Omega }) \\&\quad \times 3\dfrac{2L_{u}+1}{(2I+1)(2S+1)}\sqrt{(2K+1)(2K^{\prime }+1)}\ (-1)^{M_{\ell }-M_{\ell }^{\prime }} \\&\quad \times \left( -1\right) ^{J_{u}+\bar{J}_{u}+J_{u}^{\prime }+\bar{J}_{u}^{\prime }} \left( -1\right) ^{J_{\ell }+\bar{J}_{\ell }+J_{\ell }^{\prime }+\bar{J}_{\ell }^{\prime }} \left( -1\right) ^{F_{u}+\bar{F}_{u}+F_{u}^{\prime }+\bar{F}_{u}^{\prime }} \left( -1\right) ^{F_{\ell }+\bar{F}_{\ell }+F_{\ell }^{\prime }+\bar{F}_{\ell }^{\prime }} \\&\quad \times \sqrt{(2J_{u}+1)(2\bar{J}_{u}+1)(2J_{u}^{\prime }+1)(2\bar{J} _{u}^{\prime }+1)(2J_{\ell }+1)(2\bar{J}_{\ell }+1)(2J_{\ell }^{\prime }+1)(2 \bar{J}_{\ell }^{\prime }+1)} \\&\quad \times \sqrt{(2F_{u}+1)(2\bar{F}_{u}+1)(2F_{u}^{\prime }+1)(2\bar{F} _{u}^{\prime }+1)(2F_{\ell }+1)(2\bar{F}_{\ell }+1)(2F_{\ell }^{\prime }+1)(2 \bar{F}_{\ell }^{\prime }+1)} \\&\quad \times C_{J_{u}^{*}M_{J_{u}}\left( F_{u}^{*}M_{u}\right) }^{J_{u}}\left( B\right) C_{J_{u}^{*}M_{J_{u}}\left( F_{u}^{*}M_{u}\right) }^{\bar{J}_{u}}\left( B\right) C_{J_{u}^{\prime *}M_{J_{u}}^{\prime }\left( F_{u}^{\prime *}M_{u}^{\prime }\right) }^{J_{u}^{\prime }}\left( B\right) C_{J_{u}^{\prime *}M_{J_{u}}^{\prime }\left( F_{u}^{\prime *}M_{u}^{\prime }\right) }^{\bar{J}_{u}^{\prime }}\left( B\right) \\&\quad \times C_{J_{\ell }^{*}M_{J_{\ell }}\left( F_{\ell }^{*}M_{\ell }\right) }^{J_{\ell }}\left( B\right) C_{J_{\ell }^{*}M_{J_{\ell }}\left( F_{\ell }^{*}M_{\ell }\right) }^{\bar{J}_{\ell }}\left( B\right) C_{J_{\ell }^{\prime *}M_{J_{\ell }}^{\prime }\left( F_{\ell }^{\prime *}M_{\ell }^{\prime }\right) }^{J_{\ell }^{\prime }}\left( B\right) C_{J_{\ell }^{\prime *}M_{J_{\ell }}^{\prime }\left( F_{\ell }^{\prime *}M_{\ell }^{\prime }\right) }^{\bar{J}_{\ell }^{\prime }}\left( B\right) \\&\quad \times C_{F_{u}^{**}\left( J_{u}M_{J_{u}}\right) M_{u}}^{F_{u}}\left( B\right) C_{\bar{F}_{u}^{**}\left( \bar{J} _{u}M_{J_{u}}\right) M_{u}}^{\bar{F}_{u}}\left( B\right) C_{F_{u}^{\prime **}\left( J_{u}^{\prime }M_{J_{u}}^{\prime }\right) M_{u}^{\prime }}^{F_{u}^{\prime }}\left( B\right) C_{\bar{F}_{u}^{\prime **}\left( \bar{J}_{u}^{\prime }M_{J_{u}}^{\prime }\right) M_{u}^{\prime }}^{\bar{F} _{u}^{\prime }}\left( B\right) \\&\quad \times C_{F_{\ell }^{**}\left( J_{\ell }M_{J_{\ell }}\right) M_{\ell }}^{F_{\ell }}\left( B\right) C_{\bar{F}_{\ell }^{**}\left( \bar{J}_{\ell }M_{J_{\ell }}\right) M_{\ell }}^{\bar{F}_{\ell }}\left( B\right) C_{F_{\ell }^{\prime **}\left( J_{\ell }^{\prime }M_{J_{\ell }}^{\prime }\right) M_{\ell }^{\prime }}^{F_{\ell }^{\prime }}\left( B\right) C_{\bar{F}_{\ell }^{\prime **}\left( \bar{J}_{\ell }^{\prime }M_{J_{\ell }}^{\prime }\right) M_{\ell }^{\prime }}^{\bar{F} _{\ell }^{\prime }}\left( B\right) \\&\quad \times \left\{ \begin{array}{ccc} J_{u}&1&J_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}^{\prime }&1&\bar{J}_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{J}_{u}&1&J_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{J}_{u}^{\prime }&1&\bar{J}_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \\&\quad \times \left\{ \begin{array}{ccc} F_{u}&1&F_{\ell } \\ J_{\ell }&I&J_{u} \end{array} \right\} \left\{ \begin{array}{ccc} F_{u}^{\prime }&1&\bar{F}_{\ell } \\ \bar{J}_{\ell }&I&J_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{F}_{u}&1&F_{\ell }^{\prime } \\ J_{\ell }&I&\bar{J}_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{F}_{u}^{\prime }&1&\bar{F}_{\ell }^{\prime } \\ \bar{J}_{\ell }&I&\bar{J}_{u} \end{array} \right\} \\&\quad \times \left( \begin{array}{ccc} F_{u}&1&F_{\ell } \\ -M_{u}&p&M_{\ell } \end{array} \right) \left( \begin{array}{ccc} F_{u}^{\prime }&1&\bar{F}_{\ell } \\ -M_{u}^{\prime }&p^{\prime }&M_{\ell } \end{array} \right) \left( \begin{array}{ccc} \bar{F}_{u}&1&F_{\ell }^{\prime } \\ -M_{u}&p^{\prime \prime \prime }&M_{\ell }^{\prime } \end{array} \right) \left( \begin{array}{ccc} \bar{F}_{u}^{\prime }&1&\bar{F}_{\ell }^{\prime } \\ -M_{u}^{\prime }&p^{\prime \prime }&M_{\ell }^{\prime } \end{array} \right) \\&\quad \times \left( \begin{array}{ccc} 1&1&K^{\prime } \\ -p&p^{\prime }&Q \end{array} \right) \left( \begin{array}{ccc} 1&1&K \\ -p^{\prime \prime \prime }&p^{\prime \prime }&Q \end{array} \right) \\&\quad \times \left\{ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{M_{u}M_{u}^{\prime }}}{\hbar }}\ \delta \left( \tilde{\nu }-\tilde{\nu }_{1}-\nu _{M_{\ell }M_{\ell }^{\prime }}\right) \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }}-\tilde{\nu }_{1}\right) \right] \right. \\&+\left[ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\dfrac{{\mathrm{i } }\Delta E_{M_{u}M_{u}^{\prime }}}{\hbar }}-\dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{M_{u}M_{u}^{\prime }} }{\hbar }}\right] \\&\times \left. \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }}-\tilde{\nu }_{1}\right) \right] \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }^{\prime }}-\tilde{\nu }\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }^{\prime }}-\tilde{\nu }\right) \right] \right\} \end{array} \ . \end{aligned} $$](/articles/aa/full_html/2018/11/aa30169e-16/aa30169e-16-eq2.gif) (A.6)
(A.6)
This equation is in excellent agreement as for the Racah algebra with Eq. (30) of Casini et al. (2014). The product of two coefficients 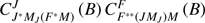 is equal to the coefficient
is equal to the coefficient 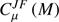 of Casini et al. (2014), because these coefficients all result from matrix diagonalization, performed in one step (FS + HFS) in Casini et al. (2014) and in two steps (FS and HFS) in our case. A similar coefficient is visible in Eq. (3.58) of Landi Degl’Innocenti & Landolfi (2004).
of Casini et al. (2014), because these coefficients all result from matrix diagonalization, performed in one step (FS + HFS) in Casini et al. (2014) and in two steps (FS and HFS) in our case. A similar coefficient is visible in Eq. (3.58) of Landi Degl’Innocenti & Landolfi (2004).
The following equation replaces Eq. (40) of Bommier (2017), by introducing the (2I + 1) denominator
![$$ \begin{aligned} \begin{array}{ll} \mathcal{R} _{ij}( \nu ,\nu _{1},\boldsymbol{\Omega },\boldsymbol{\Omega }_{1}; \boldsymbol{B} = \boldsymbol{0})&=\mathop {\displaystyle \sum }\limits_{J_{u}F_{u}J_{u}^{\prime }F_{u}^{\prime }J_{\ell }F_{\ell }J_{\ell }^{\prime }F_{\ell }^{\prime }KQ}\int f(\boldsymbol{\upsilon}) {\mathrm{d} }^{3}\boldsymbol{\upsilon}\ (-1)^{Q}\mathcal{T} _{-Q}^{K}(j,\boldsymbol{\Omega }_{1}) \mathcal{T} _{Q}^{K}(i,\boldsymbol{\Omega }) \\&\quad \times 3\dfrac{2L_{u}+1}{(2I+1)(2S+1)}(2J_{u}+1)(2J_{u}^{\prime }+1)(2J_{\ell }+1)(2J_{\ell }^{\prime }+1)(2F_{u}+1)(2F_{u}^{\prime }+1)(2F_{\ell }+1)(2F_{\ell }^{\prime }+1)\ (-1)^{F_{\ell }-F_{\ell }^{\prime }} \\&\quad \times \left\{ \begin{array}{ccc} J_{u}&1&J_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}^{\prime }&1&J_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}&1&J_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}^{\prime }&1&J_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \\&\quad \times \left\{ \begin{array}{ccc} F_{u}&1&F_{\ell } \\ J_{\ell }&I&J_{u} \end{array} \right\} \left\{ \begin{array}{ccc} F_{u}^{\prime }&1&F_{\ell } \\ J_{\ell }&I&J_{u}^{\prime } \end{array} \right\} \left\{ \begin{array}{ccc} F_{u}&1&F_{\ell }^{\prime } \\ J_{\ell }&I&J_{u} \end{array} \right\} \left\{ \begin{array}{ccc} F_{u}^{\prime }&1&F_{\ell }^{\prime } \\ J_{\ell }&I&J_{u}^{\prime } \end{array} \right\} \\&\quad \times \left\{ \begin{array}{ccc} K&F_{u}&F_{u}^{\prime } \\ F_{\ell }&1&1 \end{array} \right\} \left\{ \begin{array}{ccc} K&F_{u}&F_{u}^{\prime } \\ F_{\ell }^{\prime }&1&1 \end{array} \right\} \\&\quad \times \left\{ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{F_{u}F_{u}^{\prime }}}{\hbar }}\ \delta \left( \tilde{\nu }-\tilde{\nu }_{1}-\nu _{F_{\ell }F_{\ell }^{\prime }}\right) \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{F_{u}^{\prime }F_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{F_{u}F_{\ell }}-\tilde{\nu }_{1}\right) \right] \right. \\&\quad +\left[ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\dfrac{1}{2} \left[ D^{(K)}(\alpha _{u}F_{u})+D^{(K)}(\alpha _{u}F_{u}^{\prime })\right] + \dfrac{{\mathrm{i} }\Delta E_{F_{u}F_{u}^{\prime }}}{\hbar }}-\dfrac{\Gamma _{R} }{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{F_{u}F_{u}^{\prime }}}{\hbar }}\right] \\&\quad \times \left. \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{F_{u}^{\prime }F_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{F_{u}F_{\ell }}-\tilde{\nu }_{1}\right) \right] \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{F_{u}^{\prime }F_{\ell }^{\prime }}-\tilde{\nu }\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{F_{u}F_{\ell }^{\prime }}-\tilde{\nu }\right) \right] \right\} \end{array}\ , \end{aligned} $$](/articles/aa/full_html/2018/11/aa30169e-16/aa30169e-16-eq5.gif) (40)
(40)
Acknowledgments
The author is very grateful to Ernest Alsina Ballester for having pointed out the errors. Ernest Alsina Ballester redid the calculations in the metalevels formalism (Landi Degl’Innocenti et al. 1997).
References
-
Bommier, V. 2017, A&A, 607, A50
[NASA ADS]
[CrossRef]
[EDP Sciences]
[Google Scholar]
-
Casini, R., Landi Degl’Innocenti, M., Manso Sainz, R., Landi Degl’Innocenti, E. & Landolfi, M. 2014, ApJ, 791, 94
[NASA ADS]
[CrossRef]
[Google Scholar]
-
Landi Degl’Innocenti, E., Landi Degl’Innocenti, M., & Landolfi, M. 1997, Proc. Forum THÉMIS, Science with THÉMIS, eds. N. Mein & S. Sahal-Bréchot (Paris: Obs. Paris-Meudon), 59
[Google Scholar]
-
Landi Degl’Innocenti, E., & Landolfi, M. 2004, Astrophys. Space Sci. Lib., 307
[Google Scholar]
© ESO 2018
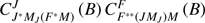 is equal to the coefficient
is equal to the coefficient 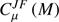 of Casini et al. (2014), because these coefficients all result from matrix diagonalization, performed in one step (FS + HFS) in Casini et al. (2014) and in two steps (FS and HFS) in our case. A similar coefficient is visible in Eq. (3.58) of Landi Degl’Innocenti & Landolfi (2004).
of Casini et al. (2014), because these coefficients all result from matrix diagonalization, performed in one step (FS + HFS) in Casini et al. (2014) and in two steps (FS and HFS) in our case. A similar coefficient is visible in Eq. (3.58) of Landi Degl’Innocenti & Landolfi (2004). Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


![$$ \begin{aligned} \begin{array}{ll} \mathcal{R} _{ij}\left( \nu ,\nu _{1},\boldsymbol{\Omega },\boldsymbol{\Omega }_{1}; \boldsymbol{B}\right)&=\mathop {\sum }\limits_{J_{u}\bar{J}_{u}J_{u}^{*}M_{u}J_{u}^{\prime }\bar{J}_{u}^{\prime }J_{u}^{\prime *}M_{u}^{\prime }J_{\ell }\bar{J}_{\ell }J_{\ell }^{*}M_{\ell }J_{\ell }^{\prime }\bar{J} _{\ell }^{\prime }J_{\ell }^{\prime *}M_{\ell }^{\prime }KK^{\prime }Q}\int f(\boldsymbol{\upsilon}){\mathrm{d} }^{3}\boldsymbol{\upsilon}\ (-1)^{Q}\mathcal{T} _{-Q}^{K^{\prime }}(j,\boldsymbol{\Omega }_{1})\mathcal{T} _{Q}^{K}(i,\boldsymbol{\Omega }) \\&\quad \times 3\dfrac{2L_{u}+1}{2S+1}\sqrt{(2K+1)(2K^{\prime }+1)}\ (-1)^{M_{\ell }-M_{\ell }^{\prime }} \left( -1\right) ^{J_{u}+\bar{J}_{u}+J_{u}^{\prime }+\bar{J}_{u}^{\prime }} \left( -1\right) ^{J_{\ell }+\bar{J}_{\ell }+J_{\ell }^{\prime }+\bar{J}_{\ell }^{\prime }} \\&\quad \times \sqrt{(2J_{u}+1)(2\bar{J}_{u}+1)(2J_{u}^{\prime }+1)(2\bar{J} _{u}^{\prime }+1)(2J_{\ell }+1)(2\bar{J}_{\ell }+1)(2J_{\ell }^{\prime }+1)(2 \bar{J}_{\ell }^{\prime }+1)} \\&\quad \times C_{J_{u}^{*}M_{u}}^{J_{u}}\left( B\right) C_{J_{u}^{*}M_{u}}^{\bar{J}_{u}}\left( B\right) C_{J_{u}^{\prime *}M_{u}^{\prime }}^{J_{u}^{\prime }}\left( B\right) C_{J_{u}^{\prime *}M_{u}^{\prime }}^{ \bar{J}_{u}^{\prime }}\left( B\right) C_{J_{\ell }^{*}M_{\ell }}^{J_{\ell }}\left( B\right) C_{J_{\ell }^{*}M_{\ell }}^{\bar{J}_{\ell }}\left( B\right) C_{J_{\ell }^{\prime *}M_{\ell }^{\prime }}^{J_{\ell }^{\prime }}\left( B\right) C_{J_{\ell }^{\prime *}M_{\ell }^{\prime }}^{ \bar{J}_{\ell }^{\prime }}\left( B\right) \\&\quad \times \left\{ \begin{array}{ccc} J_{u}&1&J_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}^{\prime }&1&\bar{J}_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{J}_{u}&1&J_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{J}_{u}^{\prime }&1&\bar{J}_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \\&\quad \times \left( \begin{array}{ccc} J_{u}&1&J_{\ell } \\ -M_{u}&p&M_{\ell } \end{array} \right) \left( \begin{array}{ccc} J_{u}^{\prime }&1&\bar{J}_{\ell } \\ -M_{u}^{\prime }&p^{\prime }&M_{\ell } \end{array} \right) \left( \begin{array}{ccc} \bar{J}_{u}&1&J_{\ell }^{\prime } \\ -M_{u}&p^{\prime \prime \prime }&M_{\ell }^{\prime } \end{array} \right) \left( \begin{array}{ccc} \bar{J}_{u}^{\prime }&1&\bar{J}_{\ell }^{\prime } \\ -M_{u}^{\prime }&p^{\prime \prime }&M_{\ell }^{\prime } \end{array} \right) \\&\quad \times \left( \begin{array}{ccc} 1&1&K^{\prime } \\ -p&p^{\prime }&Q \end{array} \right) \left( \begin{array}{ccc} 1&1&K \\ -p^{\prime \prime \prime }&p^{\prime \prime }&Q \end{array} \right) \\&\quad \times \left\{ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{M_{u}M_{u}^{\prime }}}{\hbar }}\ \delta \left( \tilde{\nu }-\tilde{\nu }_{1}-\nu _{M_{\ell }M_{\ell }^{\prime }}\right) \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }}-\tilde{\nu }_{1}\right) \right] \right. \\&\quad +\left[ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\dfrac{{\mathrm{i } }\Delta E_{M_{u}M_{u}^{\prime }}}{\hbar }}-\dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{M_{u}M_{u}^{\prime }} }{\hbar }}\right] \\&\quad \times \left. \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }}-\tilde{\nu }_{1}\right) \right] \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }^{\prime }}-\tilde{\nu }\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }^{\prime }}-\tilde{\nu }\right) \right] \right\} \end{array} \ . \end{aligned} $$](/articles/aa/full_html/2018/11/aa30169e-16/aa30169e-16-eq1.gif)
![$$ \begin{aligned} \begin{array}{ll} \mathcal{R} _{ij}\left( \nu ,\nu _{1},\boldsymbol{\Omega },\boldsymbol{\Omega }_{1}; \boldsymbol{B}\right)&= \mathop {\displaystyle \sum }\limits_{J_{u}\bar{J}_{u}J_{u}^{*}F_{u}\bar{F} _{u}F_{u}^{*}M_{u}J_{u}^{\prime }\bar{J}_{u}^{\prime }J_{u}^{\prime *}F_{u}^{\prime }\bar{F}_{u}^{\prime }F_{u}^{\prime *}M_{u}^{\prime }J_{\ell }\bar{J}_{\ell }J_{\ell }^{*}F_{\ell }\bar{F}_{\ell }F_{\ell }^{*}M_{\ell }J_{\ell }^{\prime }\bar{J}_{\ell }^{\prime }J_{\ell }^{\prime *}F_{\ell }^{\prime }\bar{F}_{\ell }^{\prime }F_{\ell }^{\prime *}M_{\ell }^{\prime }KK^{\prime }Q} \\&\quad \times \int f(\boldsymbol{\upsilon}){\mathrm{d} }^{3}\boldsymbol{\upsilon}\ (-1)^{Q}\mathcal{T} _{-Q}^{K^{\prime }}(j,\boldsymbol{\Omega }_{1})\mathcal{T} _{Q}^{K}(i,\boldsymbol{\Omega }) \\&\quad \times 3\dfrac{2L_{u}+1}{(2I+1)(2S+1)}\sqrt{(2K+1)(2K^{\prime }+1)}\ (-1)^{M_{\ell }-M_{\ell }^{\prime }} \\&\quad \times \left( -1\right) ^{J_{u}+\bar{J}_{u}+J_{u}^{\prime }+\bar{J}_{u}^{\prime }} \left( -1\right) ^{J_{\ell }+\bar{J}_{\ell }+J_{\ell }^{\prime }+\bar{J}_{\ell }^{\prime }} \left( -1\right) ^{F_{u}+\bar{F}_{u}+F_{u}^{\prime }+\bar{F}_{u}^{\prime }} \left( -1\right) ^{F_{\ell }+\bar{F}_{\ell }+F_{\ell }^{\prime }+\bar{F}_{\ell }^{\prime }} \\&\quad \times \sqrt{(2J_{u}+1)(2\bar{J}_{u}+1)(2J_{u}^{\prime }+1)(2\bar{J} _{u}^{\prime }+1)(2J_{\ell }+1)(2\bar{J}_{\ell }+1)(2J_{\ell }^{\prime }+1)(2 \bar{J}_{\ell }^{\prime }+1)} \\&\quad \times \sqrt{(2F_{u}+1)(2\bar{F}_{u}+1)(2F_{u}^{\prime }+1)(2\bar{F} _{u}^{\prime }+1)(2F_{\ell }+1)(2\bar{F}_{\ell }+1)(2F_{\ell }^{\prime }+1)(2 \bar{F}_{\ell }^{\prime }+1)} \\&\quad \times C_{J_{u}^{*}M_{J_{u}}\left( F_{u}^{*}M_{u}\right) }^{J_{u}}\left( B\right) C_{J_{u}^{*}M_{J_{u}}\left( F_{u}^{*}M_{u}\right) }^{\bar{J}_{u}}\left( B\right) C_{J_{u}^{\prime *}M_{J_{u}}^{\prime }\left( F_{u}^{\prime *}M_{u}^{\prime }\right) }^{J_{u}^{\prime }}\left( B\right) C_{J_{u}^{\prime *}M_{J_{u}}^{\prime }\left( F_{u}^{\prime *}M_{u}^{\prime }\right) }^{\bar{J}_{u}^{\prime }}\left( B\right) \\&\quad \times C_{J_{\ell }^{*}M_{J_{\ell }}\left( F_{\ell }^{*}M_{\ell }\right) }^{J_{\ell }}\left( B\right) C_{J_{\ell }^{*}M_{J_{\ell }}\left( F_{\ell }^{*}M_{\ell }\right) }^{\bar{J}_{\ell }}\left( B\right) C_{J_{\ell }^{\prime *}M_{J_{\ell }}^{\prime }\left( F_{\ell }^{\prime *}M_{\ell }^{\prime }\right) }^{J_{\ell }^{\prime }}\left( B\right) C_{J_{\ell }^{\prime *}M_{J_{\ell }}^{\prime }\left( F_{\ell }^{\prime *}M_{\ell }^{\prime }\right) }^{\bar{J}_{\ell }^{\prime }}\left( B\right) \\&\quad \times C_{F_{u}^{**}\left( J_{u}M_{J_{u}}\right) M_{u}}^{F_{u}}\left( B\right) C_{\bar{F}_{u}^{**}\left( \bar{J} _{u}M_{J_{u}}\right) M_{u}}^{\bar{F}_{u}}\left( B\right) C_{F_{u}^{\prime **}\left( J_{u}^{\prime }M_{J_{u}}^{\prime }\right) M_{u}^{\prime }}^{F_{u}^{\prime }}\left( B\right) C_{\bar{F}_{u}^{\prime **}\left( \bar{J}_{u}^{\prime }M_{J_{u}}^{\prime }\right) M_{u}^{\prime }}^{\bar{F} _{u}^{\prime }}\left( B\right) \\&\quad \times C_{F_{\ell }^{**}\left( J_{\ell }M_{J_{\ell }}\right) M_{\ell }}^{F_{\ell }}\left( B\right) C_{\bar{F}_{\ell }^{**}\left( \bar{J}_{\ell }M_{J_{\ell }}\right) M_{\ell }}^{\bar{F}_{\ell }}\left( B\right) C_{F_{\ell }^{\prime **}\left( J_{\ell }^{\prime }M_{J_{\ell }}^{\prime }\right) M_{\ell }^{\prime }}^{F_{\ell }^{\prime }}\left( B\right) C_{\bar{F}_{\ell }^{\prime **}\left( \bar{J}_{\ell }^{\prime }M_{J_{\ell }}^{\prime }\right) M_{\ell }^{\prime }}^{\bar{F} _{\ell }^{\prime }}\left( B\right) \\&\quad \times \left\{ \begin{array}{ccc} J_{u}&1&J_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}^{\prime }&1&\bar{J}_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{J}_{u}&1&J_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{J}_{u}^{\prime }&1&\bar{J}_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \\&\quad \times \left\{ \begin{array}{ccc} F_{u}&1&F_{\ell } \\ J_{\ell }&I&J_{u} \end{array} \right\} \left\{ \begin{array}{ccc} F_{u}^{\prime }&1&\bar{F}_{\ell } \\ \bar{J}_{\ell }&I&J_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{F}_{u}&1&F_{\ell }^{\prime } \\ J_{\ell }&I&\bar{J}_{u} \end{array} \right\} \left\{ \begin{array}{ccc} \bar{F}_{u}^{\prime }&1&\bar{F}_{\ell }^{\prime } \\ \bar{J}_{\ell }&I&\bar{J}_{u} \end{array} \right\} \\&\quad \times \left( \begin{array}{ccc} F_{u}&1&F_{\ell } \\ -M_{u}&p&M_{\ell } \end{array} \right) \left( \begin{array}{ccc} F_{u}^{\prime }&1&\bar{F}_{\ell } \\ -M_{u}^{\prime }&p^{\prime }&M_{\ell } \end{array} \right) \left( \begin{array}{ccc} \bar{F}_{u}&1&F_{\ell }^{\prime } \\ -M_{u}&p^{\prime \prime \prime }&M_{\ell }^{\prime } \end{array} \right) \left( \begin{array}{ccc} \bar{F}_{u}^{\prime }&1&\bar{F}_{\ell }^{\prime } \\ -M_{u}^{\prime }&p^{\prime \prime }&M_{\ell }^{\prime } \end{array} \right) \\&\quad \times \left( \begin{array}{ccc} 1&1&K^{\prime } \\ -p&p^{\prime }&Q \end{array} \right) \left( \begin{array}{ccc} 1&1&K \\ -p^{\prime \prime \prime }&p^{\prime \prime }&Q \end{array} \right) \\&\quad \times \left\{ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{M_{u}M_{u}^{\prime }}}{\hbar }}\ \delta \left( \tilde{\nu }-\tilde{\nu }_{1}-\nu _{M_{\ell }M_{\ell }^{\prime }}\right) \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }}-\tilde{\nu }_{1}\right) \right] \right. \\&+\left[ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\dfrac{{\mathrm{i } }\Delta E_{M_{u}M_{u}^{\prime }}}{\hbar }}-\dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{M_{u}M_{u}^{\prime }} }{\hbar }}\right] \\&\times \left. \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }}-\tilde{\nu }_{1}\right) \right] \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{M_{u}^{\prime }M_{\ell }^{\prime }}-\tilde{\nu }\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{M_{u}M_{\ell }^{\prime }}-\tilde{\nu }\right) \right] \right\} \end{array} \ . \end{aligned} $$](/articles/aa/full_html/2018/11/aa30169e-16/aa30169e-16-eq2.gif)
![$$ \begin{aligned} \begin{array}{ll} \mathcal{R} _{ij}( \nu ,\nu _{1},\boldsymbol{\Omega },\boldsymbol{\Omega }_{1}; \boldsymbol{B} = \boldsymbol{0})&=\mathop {\displaystyle \sum }\limits_{J_{u}F_{u}J_{u}^{\prime }F_{u}^{\prime }J_{\ell }F_{\ell }J_{\ell }^{\prime }F_{\ell }^{\prime }KQ}\int f(\boldsymbol{\upsilon}) {\mathrm{d} }^{3}\boldsymbol{\upsilon}\ (-1)^{Q}\mathcal{T} _{-Q}^{K}(j,\boldsymbol{\Omega }_{1}) \mathcal{T} _{Q}^{K}(i,\boldsymbol{\Omega }) \\&\quad \times 3\dfrac{2L_{u}+1}{(2I+1)(2S+1)}(2J_{u}+1)(2J_{u}^{\prime }+1)(2J_{\ell }+1)(2J_{\ell }^{\prime }+1)(2F_{u}+1)(2F_{u}^{\prime }+1)(2F_{\ell }+1)(2F_{\ell }^{\prime }+1)\ (-1)^{F_{\ell }-F_{\ell }^{\prime }} \\&\quad \times \left\{ \begin{array}{ccc} J_{u}&1&J_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}^{\prime }&1&J_{\ell } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}&1&J_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \left\{ \begin{array}{ccc} J_{u}^{\prime }&1&J_{\ell }^{\prime } \\ L_{\ell }&S&L_{u} \end{array} \right\} \\&\quad \times \left\{ \begin{array}{ccc} F_{u}&1&F_{\ell } \\ J_{\ell }&I&J_{u} \end{array} \right\} \left\{ \begin{array}{ccc} F_{u}^{\prime }&1&F_{\ell } \\ J_{\ell }&I&J_{u}^{\prime } \end{array} \right\} \left\{ \begin{array}{ccc} F_{u}&1&F_{\ell }^{\prime } \\ J_{\ell }&I&J_{u} \end{array} \right\} \left\{ \begin{array}{ccc} F_{u}^{\prime }&1&F_{\ell }^{\prime } \\ J_{\ell }&I&J_{u}^{\prime } \end{array} \right\} \\&\quad \times \left\{ \begin{array}{ccc} K&F_{u}&F_{u}^{\prime } \\ F_{\ell }&1&1 \end{array} \right\} \left\{ \begin{array}{ccc} K&F_{u}&F_{u}^{\prime } \\ F_{\ell }^{\prime }&1&1 \end{array} \right\} \\&\quad \times \left\{ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{F_{u}F_{u}^{\prime }}}{\hbar }}\ \delta \left( \tilde{\nu }-\tilde{\nu }_{1}-\nu _{F_{\ell }F_{\ell }^{\prime }}\right) \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{F_{u}^{\prime }F_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{F_{u}F_{\ell }}-\tilde{\nu }_{1}\right) \right] \right. \\&\quad +\left[ \dfrac{\Gamma _{R}}{\Gamma _{R}+\Gamma _{I}+\dfrac{1}{2} \left[ D^{(K)}(\alpha _{u}F_{u})+D^{(K)}(\alpha _{u}F_{u}^{\prime })\right] + \dfrac{{\mathrm{i} }\Delta E_{F_{u}F_{u}^{\prime }}}{\hbar }}-\dfrac{\Gamma _{R} }{\Gamma _{R}+\Gamma _{I}+\Gamma _{E}+\dfrac{{\mathrm{i} }\Delta E_{F_{u}F_{u}^{\prime }}}{\hbar }}\right] \\&\quad \times \left. \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{F_{u}^{\prime }F_{\ell }}-\tilde{\nu }_{1}\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{F_{u}F_{\ell }}-\tilde{\nu }_{1}\right) \right] \left[ \dfrac{1}{2}\Phi _{ba}\left( \nu _{F_{u}^{\prime }F_{\ell }^{\prime }}-\tilde{\nu }\right) +\dfrac{1}{2}\Phi _{ba}^{*}\left( \nu _{F_{u}F_{\ell }^{\prime }}-\tilde{\nu }\right) \right] \right\} \end{array}\ , \end{aligned} $$](/articles/aa/full_html/2018/11/aa30169e-16/aa30169e-16-eq5.gif)