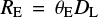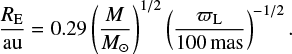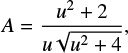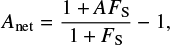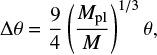| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 9 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201833527 | |
| Published online | 02 October 2018 | |
Twenty years of photometric microlensing events predicted by Gaia DR2
Potential planet-hosting lenses within 100 pc⋆
Lund Observatory, Department of Astronomy & Theoretical Physics, Lund University, Box 43, 221 00 Lund, Sweden
e-mail: alex@astro.lu.se
Received:
29
May
2018
Accepted:
7
July
2018
Context. Gaia Data Release 2 (DR2) offers unparalleled precision on stars’ parallaxes and proper motions. This allows the prediction of microlensing events for which the lens stars (and any planets they possess) are nearby and may be well studied and characterised.
Aims. We identify a number of potential microlensing events that will occur before the year 2035.5, 20 years from the Gaia DR2 reference epoch.
Methods. We query Gaia DR2 for potential lenses within 100 pc, extract parallaxes and proper motions of the lenses and background sources, and identify potential lensing events. We estimate the lens masses from Priam effective temperatures and use these to calculate peak magnifications and the size of the Einstein radii relative to the lens stars’ habitable zones.
Results. We identify seven future events with a probability >10% of an alignment within one Einstein radius. Of particular interest is DR2 5918299904067162240 (WISE J175839.20–583931.6), magnitude G = 14.9, which will lens a G = 13.9 background star in early 2030, with a median 23% net magnification. Other pairs are typically fainter, hampering characterisation of the lens (if the lens is faint) or the ability to accurately measure the magnification (if the source is much fainter than the lens). Of timely interest is DR2 4116504399886241792 (2MASS J17392440–2327071), which will lens a background star in July 2020, albeit with weak net magnification (0.03%). Median magnifications for the other five high-probability events range from 0.3% to 5.3%. The Einstein radii for these lenses are one to ten times the radius of the habitable zone, allowing these lensing events to pick out cold planets around the ice line, and filling a gap between transit and current microlensing detections of planets around very low-mass stars.
Conclusions. We provide a catalogue of the predicted events to aid future characterisation efforts. Current limitations include a lack of many high-proper-motion objects in Gaia DR2 and often large uncertainties on the proper motions of the background sources (or only two-parameter solutions). Both of these deficiencies will be rectified with Gaia DR3 in 2020. Further characterisation of the lenses is also warranted to better constrain their masses and predict the photometric magnifications.
Key words: gravitational lensing: micro / astrometry / planets and satellites: detection
The result table is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/viz-bin/qcat?J/A+A/617/A135
© ESO 2018
1. Introduction
Gravitational microlensing (Einstein 1936; Paczynski 1986, 1996) allows the detection of low-mass planets on orbits in or beyond a star’s habitable zone (Bond et al. 2004; Gaudi 2012; Shvartzvald et al. 2016; Suzuki et al. 2016). However, current microlensing searches are hampered by the small probability of alignments and the need to survey many stars, which are typically distant and therefore faint. Indeed the lens star may not be known at all if it is an M dwarf at a few kiloparsecs. Characterisation of the host and the planetary system is thus often probabilistic, conditioned over a model of Galactic stellar populations (see e.g. Hwang et al. 2018; Jung et al. 2018a, for recent examples).
While detections of microlensing by planet-hosting stars have so far been conducted by wide-field surveys searching for chance alignments (such as the Optical Gravitational Lensing Experiment [OGLE], Udalski 2003; Microlensing Observations in Astrophysics [MOA], Bond et al. 2001; and the Korea Microlensing Telescope Network [KMTNet], Kim et al. 2016), the alignments are themselves determined by the proper motion and parallax of both the source and the lens. With sufficiently accurate astrometry, future lensing events can therefore be predicted in advance, allowing both observations of the lensing event to be optimised, and efforts made to characterise the lensing star and any planetary system (Paczynski 1995; Di Stefano 2008; Di Stefano et al. 2013). The necessary astrometry for predicting future lensing events is provided by the European Space Agency’s ongoing Gaia mission (Gaia Collaboration 2016), which provides proper motions and parallaxes to excellent precision for stars covering the entire sky. In this paper, we show that the second data release (“DR2”, Gaia Collaboration 2018) does indeed allow the prediction of future microlensing events, and we provide a list of candidates and predicted magnifications. Previous work has used pre-Gaia or Data Release 1 (DR1) astrometry to predict lensing events by the nearby α Cen system (Kervella et al. 2016) or by known stellar remnants (Paczynski 2001; Harding et al. 2018; McGill et al. 2018), often focusing on the astrometric signature. However, before Gaia DR2 the proper motion of the background sources in particular was unknown, hampering accurate predictions of the microlensing signal. Recently, Klüter et al. (2018) identified two ongoing astrometric events from Gaia DR2. In this paper, we focus on photometric signatures from lensing events up to 2035 that can be predicted (with associated uncertainties) from Gaia DR21.
Nearby lens stars are of particular interest, but are not well represented in wide-field surveys. Because of their higher proper motions, they cover a larger fraction of sky and have the opportunity to lens more background sources. Because of their proximity, they are bright and therefore easier to characterise or to probe for planets by complementary methods. Ideally the background source star is not too faint however, as a large magnitude difference between source and lens will dilute the photometric microlensing signal and make characterisation of the lens system (including any planets) through the microlensing light curve more challenging.
In this paper we search for alignments between sources and lenses in Gaia DR2 (Gaia Collaboration 2018) and calculate the magnitude of the photometric signal for each pair. We focus on lenses within 100 pc. We describe our sample selection and analysis method in Sect. 3, present results in Sect. 4, and discuss and conclude in Sect. 5. First we briefly review the theoretical background of gravitational microlensing.
A brief note on terminology: the Gaia data releases refer to “sources”. However, in microlensing it is convenient to refer to a foreground “lens” and a background “source”. Here we use the microlensing terminology, and refer to “sources” in Gaia DR2 as “objects”.
2. Microlensing theory
If a foreground lens star lies exactly on a line linking an observer and a background source, the light of the source is distorted into a ring of angular radius
the angular Einstein radius (Einstein 1936; Paczynski 1986, 1996). Here,  is the gravitational constant, M the lens mass, c the speed of light, and
is the gravitational constant, M the lens mass, c the speed of light, and 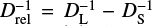 , where DL and DS are the distances to the source and the lens, and ϖL and ϖS their parallaxes. This angular radius corresponds to a physical Einstein radius
, where DL and DS are the distances to the source and the lens, and ϖL and ϖS their parallaxes. This angular radius corresponds to a physical Einstein radius
or, when the lens is nearby (source parallax negligible)
For a lens offset from the source–observer axis by θS, the light from the source is magnified by a factor
where u = θS/θE. A separation of one Einstein radius thus results in a magnification of  .
.
For many microlensing applications the source is a background giant and much brighter than the lens, which is typically an M dwarf at a few kiloparsecs. Dilution of the source light by the lens is therefore usually small. As we shall see, however, the source–lens pairs studied here have lenses comparable to or brighter than the background sources, and when discussing the practical observability of the events we study, we need to calculate the net magnification including dilution by the lens itself. We define
where
GL and GS being the unmagnified G-band magnitudes of the lens and the source.
The timescale of a microlensing event is usually parametrised by the Einstein ring crossing time
 (9)
(9)
(Gaudi 2012), where μrel is the relative proper motion of the source and the lens. Because all of our events are significantly diluted by the lens light, however, in this paper we instead parametrise the duration by the length of time the net magnification exceeds 10−4, a reasonable estimate for the precision attainable by future high-precision photometry such as that from the forthcoming PLATO (Planetary Transits and Oscillations of Stars) observatory (see Sect. 5).
3. Method
3.1. Sample selection
We initially searched for objects within 100 pc of the Sun (nominal parallax ϖ ≥ 10 mas) from the Gaia DR2 archive. This returned 700 055 objects. We then applied the criteria on photometric and astrometric quality described in Lindegren et al. (2018, Appendix C). This reduced the list to 69 979 objects. For each of these objects, we then queried for all sources within a radius of 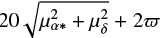 , where μα* and μδ are the object's annual proper motion components in RA and Dec, and ϖ is the parallax. That is, we searched for objects within a radius given by 20 years’ proper motion plus twice the parallax. We found that 2631 objects have at least one other object in this search radius.
, where μα* and μδ are the object's annual proper motion components in RA and Dec, and ϖ is the parallax. That is, we searched for objects within a radius given by 20 years’ proper motion plus twice the parallax. We found that 2631 objects have at least one other object in this search radius.
 |
Fig. 1. Sky locations (Galactic co-ordinates, Aitoff projection) of the 262 objects within 100 pc passing within 1 arcsec of a background source. A concentration towards the Galactic plane is noted. The 30 objects passing within 0.1 arcsec of a background source are highlighted in red. |
From these, we selected objects whose nominal proper motion and parallax takes them within 1 arcsec of another object for further analysis2. This gave 262 objects, which were then propagated with the nominal parallax and proper motion of themselves and the background objects. Objects passing within 0.1 arcsec of another object were then selected for further manual study. There were 30 such objects, listed in Table A.1. The sky locations of these objects are shown in Fig. 1.
3.2. Analysis
For the 30 objects passing within 0.1 arcsec of a background source, we performed a Monte-Carlo simulation of 10 000 samples to estimate the distribution of closest approaches. We used the formal errors on parallax, proper motion, RA, and Dec given in the DR2 catalogue, and accounted for the correlations between these parameters (Luri et al. 2018). Background sources for which only two astrometric parameters are available (RA and Dec) have these parameters randomised but are assigned zero parallax. Proper motions were then assigned by searching for stars within one magnitude of the background source in a 1 arcmin radius, and drawing from Gaussians with the mean and standard deviation of this sample (typically ∼200 objects). If a negative parallax is drawn for the five-parameter objects, it is set to zero. For our purposes here, possible global or local systematics are unimportant, as they take effect on much larger scales than those of a few arcsec considered in this paper; in fact, relative proper motions (considered here) may be slightly more accurate for very close pairs than the formal errors suggest.
Our Monte-Carlo analysis allows us to derive probability distributions for the trajectories on the sky of the source and the lens; the distributions of Einstein radii, of closest approaches, and of the photometric magnifications by lensing; and the probability that a closest approach is within 1RE. To compute the Einstein radius, we used the Teff provided by the Priam algorithm (part of DR2; Andrae et al. 2018) where available, which together with the extinction and bolometric correction (Table 4 of Andrae et al. 2018) we turned into a bolometric luminosity L, and thence into a mass by the mass–luminosity relations of Salaris & Cassisi (2005). Where Teff is unavailable, we assume a lens mass of 0.1 M⊙. Our lens masses calculated in this manner lie in the range 0.09−0.30 M⊙. However, the lens masses calculated in this manner are not monotonic if Teff, and we emphasise the need for follow-up photometry or spectroscopy to better determine these stars’ masses and refine the predictions for Einstein radii and lensing magnifications. The lens co-ordinates were then checked in SIMBAD (Set of Identifications, Measurements and Bibliography for Astronomical Data) and VizieR to find other identifiers (if any) for these objects.
4. Results
We identified 30 sources in Gaia DR2 that will pass within 0.1 arcsec of a background object before AD2035.5. These alignments are concentrated towards the Galactic plane where the density of background sources is higher (Fig. 1), but a few alignments occur at high Galactic latitudes.
 |
Fig. 2. Magnitudes of sources and lenses of the 30 pairs passing within 0.1 arcsec by AD2035.5. The colour scale shows the probability of an alignment within one Einstein radius, taking the lens mass from Priam (Andrae et al. 2018). The dashed line shows the locus of equal source and lens magnitudes. |
 |
Fig. 3. Sky motion of two candidate events. Lens motion is marked in black (moving southwards and westwards in each case) and source motion from 2015.5 to 2035.5 in red (moving away from the red circle, showing the source position at 2015.5), for 100 draws from the Monte-Carlo samples. RA and Dec are given relative to the lens location at 2015.5. Left panel: DR2 5918299904067162240 (lens) and DR2 5918299908365843840 (source). Both source and lens motion are well-constrained, and there is a 46% probability of passing within 1RE, around 2030 April 1. Right panel: DR2 4116504399886241792 (lens) and DR2 4116504399831319424 (source). The background source has only a two-parameter astrometric solution; by assigning it a proper motion drawn from stars in the same field of similar magnitude, we can predict a 20% probability of passing within 1RE, around July 2020. In each panel, the Einstein radius is indicated by a blue circle. |
Lenses are typically brighter than the background sources, as is expected from their closer proximity to Earth. All but two background sources are fainter than G = 17, while all but three lenses are brighter than G = 17. For two alignments the background source is brighter than the lens; one of these (DR2 5918299908365843840) we discuss in more detail below. The magnitudes of the source–lens pairs are plotted in Fig. 2, along with the probability of an alignment within 1RE.
We found 18 such alignments with a non-zero probability of passing within 1RE, including seven with a probability >10%. Details for these seven are given in Table 1 and for all 30 pairs in the appendix. Here we describe the seven likely lensing events, in chronological order.
Seven most probable alignments before 2035.5, ordered chronologically.
4.1. 2020 Jul 3–22: DR2 4116504399886241792
The first potential lensing event will occur two years from now. Gaia DR2 4116504399886241792 will pass close to the background object Gaia DR2 4116504399831319424 in mid 2020 (Fig. 3, right). Unfortunately the background object has only a two-parameter astrometric solution in DR2; by assigning it a proper motion based on stars of similar magnitude in the field, we predict a 20% probability of an alignment within one Einstein radius, with a peak net magnification of 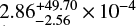 occurring around 2020 Jul 3–22. At this time, the solar elongation will be
occurring around 2020 Jul 3–22. At this time, the solar elongation will be 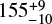 deg, very favourable for observations. As this is before the release of Gaia DR3, further monitoring of the source to better constrain its proper motion is desirable. The lens itself is one of the brighter amongst our full set (G = 13.86) and the brightest of the seven highest-probability lenses, aiding characterisation efforts. Based on position and proper motion, we identify the lens with 2MASS J17392440–2327071 in the high-proper motion catalogue of Lépine (2008), who classed it as a dwarf star. Priam gives Teff = 3554 K, from which we derive a mass of 0.16 M⊙.
deg, very favourable for observations. As this is before the release of Gaia DR3, further monitoring of the source to better constrain its proper motion is desirable. The lens itself is one of the brighter amongst our full set (G = 13.86) and the brightest of the seven highest-probability lenses, aiding characterisation efforts. Based on position and proper motion, we identify the lens with 2MASS J17392440–2327071 in the high-proper motion catalogue of Lépine (2008), who classed it as a dwarf star. Priam gives Teff = 3554 K, from which we derive a mass of 0.16 M⊙.
4.2. 2025 Jul 20–27: DR2 2042703905028908928
Gaia DR2 2042703905028908928 (G = 14.7) will pass close to Gaia DR2 2042703900727995008 (G = 18.6) in late July 2025, and it has the highest probability of an approach within one Einstein radius (77%). Despite the lens being four magnitudes brighter than the source, we predict a large peak net magnification of 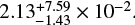 . The solar elongation at peak magnification will be 126 deg. The lens can be identified with G 207–14 based on its position and proper motion (Lépine & Shara 2005). The Priam Teff = 3655 K, and we estimate a lens mass of 0.17 M⊙.
. The solar elongation at peak magnification will be 126 deg. The lens can be identified with G 207–14 based on its position and proper motion (Lépine & Shara 2005). The Priam Teff = 3655 K, and we estimate a lens mass of 0.17 M⊙.
4.3. 2025 Sep 1–16: DR2 2030898139472914688
Gaia DR2 2030898139472914688 (G = 15.6) has a 49% probability of passing within an Einstein radius of Gaia DR2 2030898105088410112 (G = 19.9), with a peak magnification of 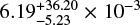 occurring in early September 2025, with a solar elongation of
occurring in early September 2025, with a solar elongation of  deg. Priam gives Teff = 4002 K and we derive a lens mass of 0.14 M⊙.
deg. Priam gives Teff = 4002 K and we derive a lens mass of 0.14 M⊙.
4.4. 2026 May 25–Jun 7: DR2 5903487940560263936
Gaia DR2 5903487940560263936 (G = 14.6) will pass close to Gaia DR2 5903487940560263808 (G = 17.9) in late May or early June 2026, with a 45% probability of passing within one Einstein radius. We predict a peak net magnification of  , and a favourable solar elongation of
, and a favourable solar elongation of 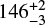 deg. Priam gives Teff = 4065 K for the lens, and we derive a mass of 0.14 M⊙. Based on position, proper motion, and magnitude, the lens is likely USNO-B1.0 0421-0506943.
deg. Priam gives Teff = 4065 K for the lens, and we derive a mass of 0.14 M⊙. Based on position, proper motion, and magnitude, the lens is likely USNO-B1.0 0421-0506943.
4.5. 2028 Jul 10–27: DR2 318399257231042304
Gaia DR2 318399257231042304 (G = 17.3) will pass close to Gaia DR2 318399257231042048 (G = 17.9) in mid–late July 2028, with a 36% probability of passing within one Einstein radius. This pair has a favourable contrast ratio, and our second-highest peak net magnification of 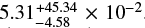 . However, the lens itself is faint, which will hamper characterisation of any planetary system, and the solar elongation at peak magnification is only
. However, the lens itself is faint, which will hamper characterisation of any planetary system, and the solar elongation at peak magnification is only  deg. The lens has no Priam solution for Teff, but has a red colour (GBP − GRP = 3.7). Based on position and proper motion, the lens can be identified with LSPM J0146+3545 (Lépine & Shara 2005).
deg. The lens has no Priam solution for Teff, but has a red colour (GBP − GRP = 3.7). Based on position and proper motion, the lens can be identified with LSPM J0146+3545 (Lépine & Shara 2005).
4.6. 2030 Mar 31–Apr 1: DR2 5918299904067162240
Gaia DR2 5918299904067162240 is a G = 14.9 star that will make its closest approach to the G = 13.9 background source DR2 5918299908365843840 on or close to 2030 April 1. We find a 46% probability of passing within one Einstein radius, and thanks to the background source being one magnitude brighter than the lens we find a large peak net magnification of 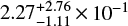 . Solar elongation at peak magnification will be 99 deg. Priam gives Teff = 3613 K for the lens, and we derive a mass of 0.1 M⊙. The lens can be identified with WISE J175839.20–583931.6, classed as a mid-M dwarf by Luhman & Sheppard (2014), so the mass (and therefore the peak magnification) might be higher. The source has Teff = 4964 K and a small parallax of 0.22 ± 0.03 mas.
. Solar elongation at peak magnification will be 99 deg. Priam gives Teff = 3613 K for the lens, and we derive a mass of 0.1 M⊙. The lens can be identified with WISE J175839.20–583931.6, classed as a mid-M dwarf by Luhman & Sheppard (2014), so the mass (and therefore the peak magnification) might be higher. The source has Teff = 4964 K and a small parallax of 0.22 ± 0.03 mas.
4.7. 2034 Sep 7–19: DR2 3425318817510655360
The last of our high-probability alignments, Gaia DR2 3425318817510655360 (G = 16.1) will pass close to Gaia DR2 3425318813215052288 (G = 19.4) in mid September 2034, with a 28% probability of coming within one Einstein radius. The lens is fairly faint and the net magnification also fairly low at 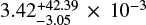 , while the solar elongation will be only
, while the solar elongation will be only 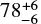 deg. The lens may be identified with LSPM J0609+2319 based on position and proper motion, an M5.0 subdwarf (Lépine et al. 2003). From the Priam Teff = 3546 K we derived a lens mass of 0.15 M⊙.
deg. The lens may be identified with LSPM J0609+2319 based on position and proper motion, an M5.0 subdwarf (Lépine et al. 2003). From the Priam Teff = 3546 K we derived a lens mass of 0.15 M⊙.
5. Discussion
From Gaia DR2 we have identified 30 approaches of lenses within 0.1 arcsec of background sources before 2035.5. Seven lenses have a >10% probability of approaching within 1RE of the background source. The lens G-band magnitudes vary from 10.1 to 19.1, with the seven most probable in the range 13.9 to 17.3. Typically the source is considerably fainter than the lens (Fig. 2), but nevertheless significant net magnifications of up to 20% are possible for the high-probability pairs. The lens G magnitude and the peak net magnification are plotted in Fig. 5, where we also show the nominal photometric precision attainable by PLATO (Catala 2009; Rauer et al. 2014) as an example of future high-precision photometric performance.
Microlensing is most sensitive to planets located at ∼1RE (Gaudi 2012). Because the lens stars are small and nearby, their Einstein radii are less than 1 au in size. The estimated masses of the lens stars are in the range 0.09−0.3 M⊙, giving Einstein radii in the range 0.11−0.36 au. This is a factor of one to ten larger than the stars’ habitable zones RHZ (defined such that the insolation at that orbital radius is equal to that received by Earth). This distance is shown in Fig. 6, together with the peak net magnification. However, we note that further characterisation of the lens stars is necessary to refine their habitable zones, Einstein radii, and indeed the peak magnifications, since the errors on Teff and extinction from Priam are somewhat large.
In Fig. 7 we show potential new planetary discoveries from monitoring these lenses, in the parameter space of the orbital semi-major axis and mass of known planets orbiting very low-mass stars. We took all planets and brown dwarfs orbiting primaries with nominal masses 0.07−0.3 M⊙ from the Extrasolar Planets Encyclopaedia3 on 2018 Jun 20. To give a sense of the region around the Einstein radius where planets may be detectable by microlensing, we overlay wedges showing the region where planets induce “resonant” microlensing perturbations, which has a width around the Einstein radius of
where Mpl is the planet mass and M the lens mass (Dominik 1999). This region of detectability lies interior to the population of planets currently detected by microlensing around these low-mass stars, whose hosts are often very poorly characterised or only estimated based on Galactic models (e.g. Jung et al. 2018b). The region also lies outside the region where transiting planets have been detected so far, which extends to 0.1 au. It is unlikely that significant numbers of planets will be discovered by transit beyond 0.1 au around such low-mass stars: the Transiting Exoplanet Survey Satellite (TESS), for example, covers spectral types down to M5, missing late M dwarfs (Ricker et al. 2015). The region of microlensing detectability overlaps with the most distant planets detected by radial velocity, but microlensing will provide true masses for these objects, with no sin I degeneracy. A more comprehensive study of each source–lens pair would be needed to calculate the microlensing signatures of planets of different masses, at different orbital separations and phases, and to evaluate their detectability.
Gaia DR3 is scheduled to be released in late 2020, and will extend the time baseline of the astrometric measurements analysed by ∼50%. We can expect improvements to the formal errors on parallax and proper motion for our sources and lenses, together with the promotion of many objects from two-parameter to five-parameter astrometric solutions. This will improve our estimates for the alignments of lenses DR2 4063191108246057472 in May 2021 and DR2 4111740078488465408 in the second half of 2033; unfortunately, DR2 4116504399886241792 will lens its two-parameter background star before DR3, as we discussed above. A comparison of the two panels of Fig. 3 shows the improvement in source star motion going from a two-parameter astrometric solution (for source DR2 4116504399831319424) to a high-quality five-parameter solution (for source DR2 5918299908365843840). The quality of the solution for DR2 5918299908365843840 is very good compared to most of the source stars, which tend to show a noticeable fanning-out of trajectories over the 20-yr timescale we have considered, as the signal-to-noise on the sources’ proper motions is often poor. Furthermore, Bramich & Nielsen (2018) note that our lenses tend to have high reduced chi-squared for the Gaia astrometric fits. This, however, is simply the result of the stars being very red (GBP – GRP ∼ 2.9−4.3): compared with stars in general of the same magnitude and colour, they are quite normal. Additionally, many of the lenses can be matched to known high-proper-motion stars, so these solutions are likely not spurious, although they will be improved with DR3. DR3 will permit both a refinement on the lensing probabilities and magnifications, and allow us to predict future events on still longer timescales.
DR3 will also give a more complete and reliable catalogue of nearby lens stars. Around one in six high-proper-motion stars are missing from Gaia DR2 (Gaia Collaboration 2018), so we can expect approximately another five alignments within 0.1 arcsec when DR3 is released from the more complete catalogue. It will also contain a treatment of astrometric binaries, improving the reliability of the proper motions of these objects that are currently modelled as single stars.
Finally, DR3 will offer improved photometry, in particular full spectrophotometry from the red and blue photometers and not only GRP and GBP fluxes (Andrae et al. 2018). Given the cool temperatures of the lenses we have identified, of particular interest for lensing studies will be the treatment of cool dwarfs (e.g. Sarro et al. 2013). While the lenses we have identified from DR2 can be followed up and characterised from the ground prior to DR3, DR3 will permit better estimates to be made of the lens mass when searching for the new alignments that DR3 will reveal.
 |
Fig. 4. Net magnification of the background source DR2 5918299908365843840 by the lens DR2 5918299904067162240 in early 2030. Magnification (including dilution by the lens) is shown for 100 Monte-Carlo samples, for 1 yr around the peak. |
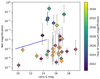 |
Fig. 5. Magnitude of lens in the Gaia G band and net magnification, accounting for dilution by the lens. Fill colour of markers shows the epoch of maximum magnification. Markers outlined in black mark the high-probability events listed in Table 1; the remainder are outlined in red. The blue line shows approximate PLATO precision in 1 h of observations (Catala 2009). |
 |
Fig. 6. Net magnification of each event, plotted against the Einstein radius scaled by the habitable zone width. Fill colour shows the G magnitude of the lens. Marker outlines are as in Fig. 5. |
 |
Fig. 7. Currently known planetary and brown dwarf companions to low-mass (0.07−0.3 M⊙) stars; data from http://exoplanet.eu/ on 2018 Jun 20. Symbol colour shows the discovery method: black for imaging, red for transit, blue for radial velocity, and green for microlensing. The symbol size increases for lower V-band magnitudes; open symbols lack a V-band magnitude. The grey wedges show the region planets close to the Einstein radius causing resonant microlensing distortions (see Eq. (10)). The transparency of the wedges increases as the closest approach increases. |
6. Conclusions
We have searched Gaia DR2 for future photometric microlensing events before 2035.5 where the lens is within 100 pc. We have identified 30 source–lens pairs where the nominal proper motion and parallax create an alignment within 0.1 arcsec.
Of these 30, seven pairs have a >10 probability of passing within one Einstein radius, a regime ideal for detecting low-mass planets orbiting the lens star.
Our candidate lens with highest net magnification is DR2 5918299904067162240 (WISE J175839.20–583931.6), which will have its closest approach to DR2 5918299908365843840 around 2030 Apr 1, with a peak magnification of 23%.
The first of our seven high-probability lenses is DR2 4116504399886241792 (2MASS J17392440–2327071), which will have its closest approach to the background source in early–mid July 2020. As this predates the improved astrometry expected from Gaia DR3 in late 2020, further monitoring of this object is warranted to refine the lensing prediction.
The Einstein radii of these lenses range from 0.1 to 0.4 au, meaning that any planets found by lensing would fill a region of parameter space around low-mass stars that lies between current transit detections at <0.1 au and current microlensing detections at ∼1 au.
Jupyter notebooks to reproduce our analysis, and a machine-readable table of results, are online4
On the day of submission of this paper we became aware of a complementary study by Bramich (2018), which covers events up to the middle of 2026.
Earth ephemeris data for the parallax are taken from the JPL Horizons system https://ssd.jpl.nasa.gov/?horizons (Giorgini et al. 1996).
Acknowledgments
The authors are supported by the IMPACT grant from the Knut & Alice Wallenberg Foundation, and by the Swedish National Space Board. AJM thanks Alcione Mora of the Gaia helpdesk for clarifications, Paul McMillan for useful discussions, the anonymous referee for suggesting a closer look at the properties of detectable planets, and Frédéric Thévenin for drawing our attention to previous work on α Cen. This work has made use of data from the European Space Agency (ESA) mission Gaia https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the SIMBAD database and the VizieR catalogue tool, operated at CDS, Strasbourg, France (Ochsenbein et al. 2000; Wenger et al. 2000). This research made use of Astropy, a communitydeveloped core Python package for Astronomy (Astropy Collaboration 2018). This research has made use of the Extrasolar Planets Encyclopaedia (http://exoplanet.eu/).
References
- Andrae, R., Fouesneau, M., & Creevey, O. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bond, I. A., Abe, F., Dodd, R. J., et al. 2001, MNRAS, 327, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, I. A., Udalski, A., Jaroszy´nski, M., et al. 2004, ApJ, 606, L155 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bramich, D. M. 2018, A&A, in press, DOI: 10.1051/0004-6361/201833505 [Google Scholar]
- Bramich, D. M., & Nielsen, M. B. 2018, [arXiv:1806.10003] [Google Scholar]
- Catala, C. 2009, Exp. Astron., 23, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R. 2008, ApJ, 684, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R., Matthews, J., & Lépine, S. 2013, ApJ, 771, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M. 1999, A&A, 349, 108 [NASA ADS] [Google Scholar]
- Einstein, A. 1936, Science, 84, 506 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaudi, B. S. 2012, ARA&A, 50, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Giorgini, J. D., Yeomans, D. K. , & Chamberlin, A. B. 1996, in AAS, DPS meeting 28, 25.04 [Google Scholar]
- Harding, A. J., Stefano, R. D., Lépine, S., et al. 2018, MNRAS, 475, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, K. H., Ryu, Y. H., & Kim, H. W. 2018, AAS, submitted [arXiv:1805.08888] [Google Scholar]
- Jung, Y. K., Hwang, K. H., & Ryu, Y. H. 2018a, AAS, submitted [arXiv:1805.09983] [Google Scholar]
- Jung, Y. K., Udalski, A., Gould, A., et al. 2018b, AJ, 155, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Mignard, F., Mérand, A., & Thévenin, F. 2016, A&A, 594, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, S.-L., Lee, C.-U., Park, B.-G., et al. 2016, J. Korean Astron. Soc., 49, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Klüter, J., Bastian, U., Demleitner, M., & Wambsganss, J. 2018, A&A, 615, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lépine, S. 2008, AJ, 135, 2177 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., & Shara, M. M. 2005, AJ, 129, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., Rich, R. M., & Shara, M. M. 2003, AJ, 125, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernandez, J., & Bombrun, A. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L., & Sheppard, S. S. 2014, ApJ, 787, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Luri, X., Brown, A. G. A., & Sarro, L. M. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGill, P., Smith, L. C., Wyn Evans, N. , & Belokurov, V. 2018, MNRAS, L72 [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczynski, B. 1986, ApJ, 301, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1995, Acta Astron., 45, 345 [NASA ADS] [Google Scholar]
- Paczynski, B. 1996, ARA&A, 34, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 2001, ArXiv e-prints, [arXiv:astro-ph/0107443] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R.,Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Cassisi, S. 2005, Evolution of Stars and Stellar Populations (Wiley-VCH) [CrossRef] [Google Scholar]
- Sarro, L. M., Berihuete, A., Carrión, C., et al. 2013, A&A, 550, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shvartzvald, Y., Maoz, D., Udalski, A., et al. 2016, MNRAS, 457, 4089 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, D., Bennett, D. P., Sumi, T., et al. 2016, ApJ, 833, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A. 2003, Acta Astron., 53, 291 [NASA ADS] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Details for all alignments
Details of all 30 source–lens pairs approaching within 0.1 arcsec, ordered chronologically by the median epoch of peak magnification.
All Tables
Details of all 30 source–lens pairs approaching within 0.1 arcsec, ordered chronologically by the median epoch of peak magnification.
All Figures
 |
Fig. 1. Sky locations (Galactic co-ordinates, Aitoff projection) of the 262 objects within 100 pc passing within 1 arcsec of a background source. A concentration towards the Galactic plane is noted. The 30 objects passing within 0.1 arcsec of a background source are highlighted in red. |
| In the text | |
 |
Fig. 2. Magnitudes of sources and lenses of the 30 pairs passing within 0.1 arcsec by AD2035.5. The colour scale shows the probability of an alignment within one Einstein radius, taking the lens mass from Priam (Andrae et al. 2018). The dashed line shows the locus of equal source and lens magnitudes. |
| In the text | |
 |
Fig. 3. Sky motion of two candidate events. Lens motion is marked in black (moving southwards and westwards in each case) and source motion from 2015.5 to 2035.5 in red (moving away from the red circle, showing the source position at 2015.5), for 100 draws from the Monte-Carlo samples. RA and Dec are given relative to the lens location at 2015.5. Left panel: DR2 5918299904067162240 (lens) and DR2 5918299908365843840 (source). Both source and lens motion are well-constrained, and there is a 46% probability of passing within 1RE, around 2030 April 1. Right panel: DR2 4116504399886241792 (lens) and DR2 4116504399831319424 (source). The background source has only a two-parameter astrometric solution; by assigning it a proper motion drawn from stars in the same field of similar magnitude, we can predict a 20% probability of passing within 1RE, around July 2020. In each panel, the Einstein radius is indicated by a blue circle. |
| In the text | |
 |
Fig. 4. Net magnification of the background source DR2 5918299908365843840 by the lens DR2 5918299904067162240 in early 2030. Magnification (including dilution by the lens) is shown for 100 Monte-Carlo samples, for 1 yr around the peak. |
| In the text | |
 |
Fig. 5. Magnitude of lens in the Gaia G band and net magnification, accounting for dilution by the lens. Fill colour of markers shows the epoch of maximum magnification. Markers outlined in black mark the high-probability events listed in Table 1; the remainder are outlined in red. The blue line shows approximate PLATO precision in 1 h of observations (Catala 2009). |
| In the text | |
 |
Fig. 6. Net magnification of each event, plotted against the Einstein radius scaled by the habitable zone width. Fill colour shows the G magnitude of the lens. Marker outlines are as in Fig. 5. |
| In the text | |
 |
Fig. 7. Currently known planetary and brown dwarf companions to low-mass (0.07−0.3 M⊙) stars; data from http://exoplanet.eu/ on 2018 Jun 20. Symbol colour shows the discovery method: black for imaging, red for transit, blue for radial velocity, and green for microlensing. The symbol size increases for lower V-band magnitudes; open symbols lack a V-band magnitude. The grey wedges show the region planets close to the Einstein radius causing resonant microlensing distortions (see Eq. (10)). The transparency of the wedges increases as the closest approach increases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.