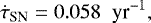| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201832666 | |
| Published online | 15 August 2018 | |
Particle acceleration in the superwinds of starburst galaxies
1
Instituto Argentino de Radioastronomía (IAR, CCT La Plata, CONICET/CIC),
C.C.5, (1984) Villa Elisa,
Buenos Aires, Argentina
e-mail: romero@iar-conicet.gov.ar
2
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata,
Paseo del Bosque s/n,
1900
La Plata, Argentina
3
Institute for Nuclear Physics (IKP), Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany
4
Instituto de Tecnologías en Detección y Astropartículas (CNEA, CONICET, UNSAM),
Buenos Aires, Argentina
Received:
18
January
2018
Accepted:
2
April
2018
Context. Starbursts are galaxies undergoing massive episodes of star formation. The combined effect of stellar winds from hot stars and supernova explosions creates a high-temperature cavity in the nuclear region of these objects. The very hot gas expands adiabatically and escapes from the galaxy creating a superwind which sweeps matter from the galactic disk. The superwind region in the halo is filled with a multi-phase gas with hot, warm, cool, and relativistic components.
Aims. The shocks associated with the superwind of starbursts and the turbulent gas region of the bubble inflated by them might accelerate cosmic rays up to high energies. In this work we calculate the cosmic ray production associated with the superwind using parameters that correspond to the nearby southern starburst galaxy NGC 253, which has been suggested as a potential accelerator of ultra-high-energy cosmic rays.
Methods. We evaluate the efficiency of both diffusive shock acceleration (DSA) and stochastic diffusive acceleration (SDA) in the superwind of NGC 253. We estimate the distribution of both hadrons and leptons and calculate the corresponding spectral energy distributions of photons. The electromagnetic radiation can help to discriminate between the different scenarios analyzed.
Results. We find that the strong mass load of the superwind, recently determined through ALMA observations, strongly attenuates the efficiency of DSA in NGC 253, whereas SDA is constrained by the age of the starburst.
Conclusions. We conclude that NGC 253 and similar starbursts can only accelerate iron nuclei beyond ~1018 eV under very special conditions. If the central region of the galaxy harbors a starved supermassive black hole of ~106 M⊙, as suggested by some recent observations, a contribution in the range 1018−1019 eV can be present for accretion rates ṁ ~ 10−3 in Eddington units. Shock energies of the order of 100 EeV might only be possible if very strong magnetic field amplification occurs close to the superwind.
Key words: acceleration of particles / radiation mechanisms: non-thermal / galaxies: starburst / galaxies: individual
© ESO 2018
1 Introduction
Intense star formation in galaxies results in the ejection of gas into the surrounding medium. This outflow, driven by the collective effect of the stellar winds of hot stars and supernova explosions, plays an important role in galaxy formation and evolution. In particular, it can quench star formation by depleting the gas from the central regions of the galaxy. The outflow thrusted by the starburst constitutes a self-regulatory mechanism that prevents the stellar mass of the galaxy from growing too much. When the gas escapes, star formation ceases, and the outflow stops. Star formation can then be reignited by fresh gas inflow. This might occur as a consequence of gravitational interactions with nearby galaxies or when part of the expelled gas that is still gravitationally bound precipitates back as high-velocity clouds. On the other hand, the outflow transports metals to the intergalactic space and gas to the halo. As a consequence, the intergalactic medium is chemically enriched to the point that a significant fraction of all metals ever created in the Universe lie outside galaxies (e.g., Pagel 2002).
The existence of galactic superwinds remained speculative for a long time. In the last 20 yr a battery of multi-wavelength observations of nearby galaxies such as M82 and NGC 253 has revealed many aspects of the nature, frequency, structure, and role of these winds. All local starburst galaxies appear to have superwinds (e.g., Veilleux et al. 2005) and since star formation increases towards high redshifts, superwinds seem to be ubiquitous in the Universe.
The basic mechanism that creates a superwind in a starburst was established by Chevalier & Clegg (1985) long ago, and since then the basic model has been supported by observations (e.g., Heckman et al. 1990) and complemented with detailed simulations (e.g., Strickland & Stevens 2000; Cooper et al. 2008). The large number of core-collapse supernovae in starbursts results in the merge of supernova remnants before they have had time to lose their energy. Shocks formed in these collisions thermalize the energy released by the explosions creating a cavity filled with hot (T ~ 108 K) gas that is unbound by the gravitational potential because its temperature is greater than the local escape temperature. The hot gas expands adiabatically, becomes supersonic at the edge of the starburst region, and finally escapes the system sweeping up cooler and denser gas from the disk. The outflow is then multi-phased with components of different temperatures. If the velocity of the expanding gas exceeds the escape velocity of the galaxy, part of the swept medium is transferred to the intergalactic space.
The hot gas expanding into the halo creates an X-ray-emitting region surrounded by swept warm (T ~ 104 K) gas that radiates Hα lines. The superwind activity can be traced up to distances of ~10 kpc from the disk of edge-on galaxies (e.g., Strickland et al. 2002). Radio observations of nearby starbursts show up an extended halo of synchrotron radiation (e.g., Heesen et al. 2009a). Such observations support the idea that particle acceleration and transport can be associated with the superwind.
Cosmic ray acceleration in galactic superwinds has already been discussed by Jokipii & Morfill (1985) and Bustard et al. (2017) for the case of our Galaxy, and by Anchordoqui et al. (1999) for the nearby starburst NGC 253. In addition, it has been suggested that the extended gamma-ray bubbles observed by the Fermi satellite (Su et al. 2010) might be the radiative signature of particles accelerated in the termination shock of the large-scale wind produced by a star-formingepisode in the central region of the Galaxy (Lacki 2014). All these models invoke diffusive shock acceleration (DSA) at the termination shock of the outflows. Anchordoqui et al. (1999), in particular, suggested that nearby starburst galaxies might be responsible for the acceleration of heavy nuclei up to ultra-high energies (~ 1020 eV). They based their proposal on three facts: 1) the large extent of the superwind region of nearby starbursts can accommodate high-energy cosmic rays with equipartition magnetic fields; 2) the photon density in the halo, contrary to the central region of these galaxies, is sufficiently low as to prevent photo-disintegration of the nuclei during the acceleration by diffusive processes; and 3) the high metallicity of the wind provides a pool of nuclei from which a Fermi type I mechanism can operate (e.g., Drury 1983; Protheroe 1999) to yield high-energy cosmic rays of heavy composition. At the time of publication by Anchordoqui et al. (1999), little was known about the actual superwind of NGC 253 so their discussion was not informed with realistic estimates of the physical conditions in the outflow region of this galaxy.
In the last 20 yr, many observations across the entire electromagnetic spectrum of NGC 253 and other nearby galaxies have allowed for better characterization of starburst-driven superwinds and their interaction with the intergalacticmedium. Also, the Pierre Auger Observatory (PAO) has detected a change in the composition of cosmic rays towards heavy nuclei at high energies. In particular, the most recent measurements in combination with post-Large Hadron Collider (LHC) hadronic models show the absence or a small fraction of both protons and iron at E > 10 EeV (Aab et al. 2014, 2017c). All this points in the direction of cosmic accelerators with high metallicity. The Telescope Array (TA) data are consistent with protons for pre-LHC models, but do not have sensitivity to distinguish protons from intermediate nuclei at the same energy. A joint analysis of both experiments has shown a consistency of the experimental data on composition between TA and PAO within estimated errors (Abbasi et al. 2016). According to Semikoz et al. (2016) a possible solution consistent with the existing data could be that “cosmic rays at E > 40 EeV are largely composed of intermediate-mass nuclei, and their deflections prevent us from finding sources by correlating arrival directions with the source positions”. Also, differences in the cut-off at the highest energies measured by both experiments might be caused by different nearby sources dominating the Northern and Southern skies. In fact, TA has recently claimed to have detected a “hotspot” in the Northern hemisphere using the 5-yr data recorded up to May 4, 2013 (Abbasi et al. 2014). The hotspot was a cluster of 19 events with energies > 57 EeV occupying a circle of ~20deg in radius close to the Ursa Major cluster of galaxies. The pre-trial statistical significance of the hotspot is 5.1σ, with the post-trial probability of being by chance in an isotropic cosmic ray sky of 3.4σ. Finally, the PAO has found evidence with a significance of 5.2σ of anisotropy in cosmic ray arrival directions at energies >8 × 1018 eV that is indicative of an extragalactic origin (Aab et al. 2017a). A recent analysis of correlations with potential sources yields significances of the excesses around Centaurus A and the most luminous active galactic nuclei (AGNs) detected by Swift-BAT of ~ 3σ, whereas for the star-forming galaxies there is a 4σ deviation from isotropy for energies greater than 39 EeV at an intermediate angular scale of 13deg (Aab et al. 2017b, 2018). Besides these findings with cosmic ray observatories, the nearby starburst galaxies M82 and NGC 253 have been detected in gamma rays by the Fermi satellite and Cherenkov telescopes (Acciari et al. 2009; Acero et al. 2009; Abdo et al. 2010). The observations indicate that the cosmic ray density in the central regions of these galaxies, which is responsible for the γ-radiation, is hundreds of times that of our Galaxy. This overabundance of cosmic rays is expected because of the very high supernova rate in starbursts. The hadronic component of these rays should produce most of the gamma rays through pp collisions with the ambient gas (e.g., Paglione et al. 1996; Domingo-Santamaría & Torres 2005; Ohm 2016). The possible association of these gamma rays with the neutrino candidate events reported by IceCube in the energy range from 30 to 2000 TeV (Aartsen et al. 2014) is discussed by Chang & Wang (2014); Chang et al. (2015); and Anchordoqui et al. (2014). Whether starbursts are actually responsible for the cosmic neutrinos detected by IceCube is still far from clear (Bechtol et al. 2017).
Our goal in this paper is to make a new assessment, informed by the current astronomical data, of the potential of star-forminggalaxies as cosmic-ray accelerators. The recent discoveries mentioned above make such a study timely. We shall focus on the extended superwind region; this region has been mostly neglected in previous discussions of cosmic and gamma ray production in starbursts. We shall adopt the southern starburst NGC 253 as a case study. Since the source is almost a twin galaxy of M82, our conclusions can be easily extrapolated to that source as well.
The structure of the paper is as follows: in the next section we present the general picture of starburst-driven galactic superwinds as it emerges from the most recent observations. Then we characterize the superwind region of NGC 253 in Sect. 3. Particle acceleration in the halo of this source is discussed in Sect. 4. We analyze there both stochastic and diffusive shock accelerations. In Sect. 5 we evaluate the different losses and the maximum energies attainable. The temporal evolution of the particle distributions is presented in Sect. 6, whereas the corresponding spectral energy distributions (SEDs) of the photons produced by these particles areshown in Sect. 7. In Sect. 8 we give a general discussion, including the potential contribution of a hidden supermassive black hole at the Galactic center. Finally, Sect. 9 contains our conclusions. The Appendix is devoted to a discussion of the adiabaticity of the shocks in superwinds.
2 Superwinds from starburst galaxies
The basics of the superwind physics were laid out by Chevalier & Clegg (1985) and developed by Heckman et al. (1990) and Strickland et al. (2002), among others. The superwind occurs when the ejecta from supernovae and stellar winds in the nuclear region of the starburst is efficiently thermalized. The result is a very hot (T ~ 108 K) bubble with high pressure that expands and sweeps the ambient gas. When the bubble disrupts the disk it expands adiabatically into the halo, creating a multi-phased region. The outflow quickly reaches the terminal velocity given by
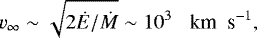 (1)
(1)
where Ė and Ṁ are the total energy release and the mass input. Simulations (e.g., Strickland & Stevens 2000) show that the wind is bipolar and drags gas from the walls of the cavity. This shocked gas forms warm arcs (T ~ 104 K). The swept material accumulated in front of the shocks forms a cold, dense shell around the bubble. The velocity of the shock in the dense medium is much slower than in the hot gas, reaching several hundreds of km s−1. Figure 1 shows a sketch of the situation, adapted from Strickland et al. (2002).
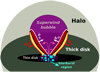 |
Fig. 1 Scheme of the physical scenario considered in this work (not to scale), adapted from Strickland et al. (2002). |
2.1 Scaling relations
Both Ė and Ṁ are proportional to the total contribution of supernovae and stellar winds in the central starbursts. If we denote by * those quantities that correspond to these contributions, the total energy injected will be (e.g., Veilleux et al. 2005; Tanner et al. 2017):
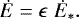 (2)
(2)
Here, ϵ is the thermalization efficiency (the fraction of energy of the central SNe and stellar winds that goes into the outflow). This coefficient is highly dependent on the local conditions. Similarly, the total mass that goes into the outflow is formed by that supplied by the starbursts (Ṁ*) plus gas loaded by the wind from the ambient medium:
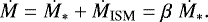 (3)
(3)
The activity in the starburst is determined by the star formation rate (SFR). Both Ė* and Ṁ* scale with the SFR as (Veilleux et al. 2005):
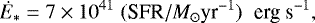 (4)
(4)
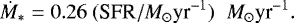 (5)
(5)
The supernova rate in the starbursts also scales with the SFR:
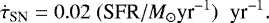 (6)
(6)
Further, since the stars heat the dust that radiates in the infrared (IR), the SFR scales with the IR luminosity, which is a direct observable:
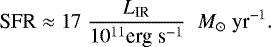 (7)
(7)
It is worth noting that the terminal superwind velocity does not depend on the SFR:
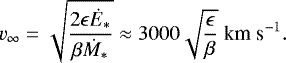 (8)
(8)
The temperature in the central cavity of the starburst is:
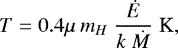 (9)
(9)
where k is Boltzmann constant, mH is the Hydrogen mass, and μ = 1.4. Therefore,
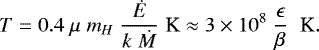 (10)
(10)
The speed of the outer shell is smaller than the terminal velocity. In convenient units (e.g., Veilleux et al. 2005):
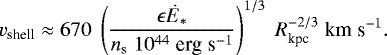 (11)
(11)
In this expression, Rkpc is the radius of the superwind region in kpc and ns the ambient particle density ahead of the shock in cm−3.
2.2 Shocks and thermal cooling
The bubble inflated by the superwind has a dynamical age of 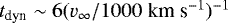 Myr. For a typical value v∞ ~ 103 km s−1, we get tdyn ~ 6 Myr. The cooling time for thermal X-ray radiation of the plasma in the bubble is much longer (
Myr. For a typical value v∞ ~ 103 km s−1, we get tdyn ~ 6 Myr. The cooling time for thermal X-ray radiation of the plasma in the bubble is much longer (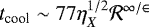 Myr, where the filling factor ηX and the metallicity
Myr, where the filling factor ηX and the metallicity 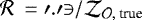 are parameters not very different from one1). The bubble then expands freely and cools adiabatically, but it remains hot. For instance, in order to cool from 3 × 106 to 104 K a time t ~ 3 × 105 (n∕cm−3)−1 yr is necessary. Typically n ~ 10−3 cm−3 (Strickland et al. 2002), meaning that more than 108 yr are required.
are parameters not very different from one1). The bubble then expands freely and cools adiabatically, but it remains hot. For instance, in order to cool from 3 × 106 to 104 K a time t ~ 3 × 105 (n∕cm−3)−1 yr is necessary. Typically n ~ 10−3 cm−3 (Strickland et al. 2002), meaning that more than 108 yr are required.
The expanding wind is surrounded by a boundary discontinuity that separates the hot gas from the swept-up shocked medium. A reverse shock moves through the free wind region. This shock is adiabatic and capable of efficient particle acceleration. The outer blast wave instead is radiative (see the Appendix). There, the dense gas cools down to warm temperatures of ~ 104 K. This shell produces the Hα emission associated with the superwind boundaries. The radiative shock is not suitable for efficient particle acceleration and is not considered below.
Regarding the physical conditions in the hot wind region, the sound speed is
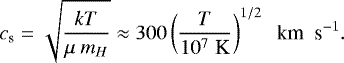 (12)
(12)
For typical values of T inferred from X-ray observations, cs ~ 100 km s−1, and then the Mach number of the reverse shock is 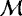 ~ 10. Magnetic field values in this region, inferred from polarization radio observations, are of a few μG (e.g., Beck et al. 1994). A better characterization of the superwind region can be done for specific sources on the basis of multifrequency observations. In what follows we shall study the case of NGC 253, the most prominent starburst galaxy in the southern sky.
~ 10. Magnetic field values in this region, inferred from polarization radio observations, are of a few μG (e.g., Beck et al. 1994). A better characterization of the superwind region can be done for specific sources on the basis of multifrequency observations. In what follows we shall study the case of NGC 253, the most prominent starburst galaxy in the southern sky.
3 The galactic-scale outflow of NGC 253
NGC 253 is an edge-on starburst galaxy at a distance estimated in the range 2.6− 3.9 Mpc (Turner & Ho 1985; Puche & Carignan 1988; Karachentsev et al. 2003). We shall adopt here a value of 2.6 Mpc as Strickland et al. (2002). NGC 253 is, along with M82, the best studied starburst galaxy. It has been observed and detected at all wavelengths, from radio to high-energy gamma rays. The existence of a superwind in this galaxy is well established. Diffuse X-ray emission with a temperature of 3 × 106 K from the halo has been detected by the Chandra satellite (Strickland et al. 2002). In the northern halo, this emission seems to lie in the interior of a region delimited by a shell defined by the Hα emission. Wind activity extends up to distances of ~10 kpc from the nuclear starburst. The IR luminosity of the starburst is LI R = 1.7 × 1010 L⊙ (Radovich et al. 2001). Using Eq. (7), the corresponding SFR is SFRNGC 253 ~ 3 M⊙ yr−1. Using this value, Eqs. (4)–(6) yield:
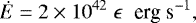 (13)
(13)
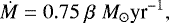 (14)
(14)
that is, one supernova every 17 yr.
The mass load of the superwind of NGC 253 was recently determined through observations of 12CO j = 1−0 transition lines obtained with the Atacama Large Millimeter Array (ALMA) performed by Bolatto et al. (2013). The wind is so heavy that it suppresses the star formation. A conservative estimate of the total molecular mass outflow rate is Ṁ ≈ 9 M⊙ yr−1. From this and Eq. (14) we get a mass loading factor β ≈ 12. The thermalization efficiency is constrained to the range 30%–100% in the case of M82 (Strickland & Heckman 2009). Adopting a value of ϵ = 0.75, we obtain from Eqs. (13)–(14):
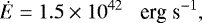 (16)
(16)
 (17)
(17)
and, from Eq. (10), a temperature for the starburst region of T ~ 2 × 107 K.
The X-ray observations of the superwind region by Strickland et al. (2002) allow us to determine the physicalproperties of the plasma in the inflated bubble. Modelling the region as a sphere of radius Rkpc = 5 with an X-ray luminosity of ~5 × 1038 erg s−1 and a temperature 3 × 106 K, the sound speed is cs ≈ 164 km s−1, the particle density is ns ~ 6.8 × 10−3 cm−3 (Strickland et al. 2002), the reverse shock velocity vrev ≈ 750 km s−1, and the velocity of the expanding shell vshell ≈ 298 km s−1. These latter values are only mildly changed if thermalization is highly efficient (ϵ ≈ 1): vrev ≈ 866 km s−1 and vshell ≈ 328 km s−1.
Multifrequency polarimetric radio observations of the halo of NGC 253 by Heesen et al. (2009c) show polarized non-thermal emission that is identified with synchrotron radiation by cosmic ray electrons spiralling in the ambient magnetic field. Heesen et al. (2009c) estimate the magnetic field in the halo in B ~ 5 μG. This implies a magnetic energy density of ~ 1 eV cm−3, and with a volume of ~1.4 × 1067 cm3, a total magnetic energy of ~ 1.4 × 1055 erg. The corresponding Alfvén velocity is
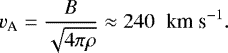 (18)
(18)
The radio observations by Heesen et al. (2009b) indicate that the cosmic ray transport from the disk to the northern halo is mainly convective, with a bulk velocity of ~ 300 km s−1. The averaged diffusion coefficient, measured for the southern wind where the transport seems to be instead diffusive is D ~ 2 × 1029 cm2 s−1.
NGC 253 has been detected at gamma-rays by the Fermi satellite in the GeV energy range (Abdo et al. 2010) and by the HESS telescope array at TeV energies (Acero et al. 2009). The total emission at energies above 200 MeV corresponds to a luminosity of ~ 4.3 × 1039 erg s−1, when a distance of 2.6 Mpc is adopted (see Abramowski et al. 2012). This radiation is thought to be produced mostly in the nuclear region (Domingo-Santamaría & Torres 2005; Rephaeli et al. 2010; Abramowski et al. 2012), although contributions from the superwind region cannot be ruled out.
In Table 1 we summarize the main parameters of NGC 253 and its superwind (SW) region. Table 2 shows the values that depend on the thermalization parameter ϵ for two different values (the mass load β is fixed from observations to β = 12).
Physical properties of NGC 253 and its superwind.
Physical properties of the outflow depending on the thermalization parameter.
4 Particle acceleration
As mentioned in the Introduction, the superwind regions of nearby starbursts are attractive potential sites for particle acceleration. We shall focus our discussion on the northern bubble of NGC 253, but our conclusions can be extended with some caution to M82.
4.1 General requirements
The minimum requirement for a particle acceleration to an energy Emax is that the magnetic field and the physical extent of the acceleration region are such that they can accommodate the particles. This is essentially the Hillas criterion (Hillas 1984). The Larmor radius (in cgs units) of a particle with energy E is:
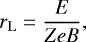 (19)
(19)
where Z is the atomic charge number, e the elementary charge, and B the magnetic field. If we assume that rL = Rkpc, with Rkpc the size scale of the halo created by the superwind in kpc, we can express the maximum theoretical energy as:
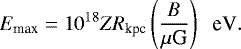 (20)
(20)
From Table 1, Rkpc ~ 5 and B ~ 5 μG. Then, we get:
 (21) (22)
(21) (22)
This of course does not imply that the system will produce particles with such energies. It is only an absolute upper bound. Actual acceleration will depend on the efficiency of the acceleration process, the age of the accelerator, and the losses suffered by the particles. The result might be a much lower maximum energy, that might depend on several local factors.
Any real acceleration process will have an efficiency η < 1. The timescale of the energy gain of the particles is given by (e.g., Aharonian et al. 2002):
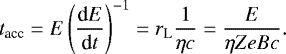 (23)
(23)
The energy gain can be written as :
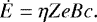 (24)
(24)
The value of η depends on the specific acceleration mechanism that operates in the source. In the case of the shocked plasma bubble created by the superwind in the halo of NGC 253 there are two possible acceleration mechanism that can result in the production of high-energy cosmic rays: stochastic diffusive acceleration (SDA) and DSA in the reverse adiabatic shock. We discuss them separately below.
4.2 Stochastic diffusive acceleration
Since the plasma in the bubble created by the superwind is expected to be turbulent2, stochastic acceleration seems to be a viable mechanism for cosmic ray generation there. Observations of radio polarization suggest that the ratio of ordered to turbulent field is δB∕B0 ~ 1 (Heesen et al. 2009c). Particle interactions with hydromagnetic waves result in a net average energy gain that is of second order in the Alfvén velocity normalized to the speed of light (e.g., Stawarz & Petrosian 2008; O’Sullivan et al. 2009; Petrosian 2012). If the Alfvénic turbulence can be represented by a power spectrum of the form W(k) ∝ k−q, where k is related to the wavelength λ of the Alfvén waves by k = 2π∕λ, the turbulence can be written as (O’Sullivan et al. 2009):
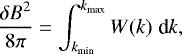 (25)
(25)
where kmax and kmin correspond to the shortest and longest wavelengths. Adopting a spectrum with q = 1, the acceleration timescale is (Stawarz & Petrosian 2008; Hardcastle et al. 2009):
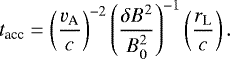 (26)
(26)
In the case of the northern bubble of NGC 253, βA = vA∕c = 8 × 10−4, 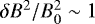 , and taking rL = 5 kpc, we get tacc ~ 2.5 × 1010 yr. Since this is of the order of the Hubble time, it is clear that the maximum theoretical energies cannot be reached.
, and taking rL = 5 kpc, we get tacc ~ 2.5 × 1010 yr. Since this is of the order of the Hubble time, it is clear that the maximum theoretical energies cannot be reached.
In absence of other losses, the maximum energy will be determined by the age of the source. The lifetime of the starbursts, and hence of the superwind activity, is much shorter than the age of the galaxy. An estimate of this age is given by the dynamical timescale, if the star-forming activity was approximately constant during the burst: τ ≈ 2Rbubble∕vsw, where 2Rbubble ~ 10 kpc is the linear extent of the superwind region filled with the hot plasma and vsw is the expansion velocity of the gas in the IGM. For a thermal efficiency ϵ = 0.75, we get τ ≈ 107 yr. Then, setting tacc= τ we get the Larmor radius of the particles with the highest energies: rL ~ 1019 cm. This corresponds to the following maximum energies:
 (27) (28)
(27) (28)
These values are much smaller than those given by the Hillas’s criterion. In the case of electrons, radiative losses make the maximum energies significantly lower than for protons (see Sect. 5 below).
The total luminosity in cosmic rays is:
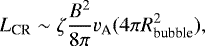 (29)
(29)
where ζ is the fraction of magnetic energy that is converted into cosmic rays. For ζ ~ 10% we get:
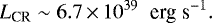 (30)
(30)
4.3 Diffusive shock acceleration
The reverse shock created by the interaction of the superwind with the external medium is adiabatic and hence suitable in principle to accelerate particles by a faster Fermi type I mechanism. If the shock is strong and super-Alfvénic, in the test particle approximation, the energy gain (in cgs units) is (e.g., Drury 1983; Protheroe 1999):
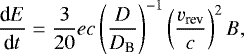 (31)
(31)
where D is the diffusion coefficient at the shock in Bohm units: DB = crL∕3. The acceleration timescale is:
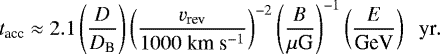 (32)
(32)
Then, equating this to the lifetime of the source, tacc = τ, we get in the Bohm limit D = DB and for a thermalization ϵ = 1, the following maximum particle energies for the parameters of NGC 253:
 (33) (34)
(33) (34)
These values are quite similar to those obtained for the case of SDA. For ϵ = 0.75 (vrev = 750 km s−1), the values reduce to 1.2 × 1016 and 3.1 × 1017 eV, respectively.
The cosmic ray luminosity produced by DSA at the terminal shock is:
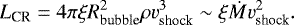 (35)
(35)
Here, ξ is the efficiency of converting shock kinetic energy into cosmic rays. For vshock ~ vrev ~ 750 km s−1 and ξ ~ 0.1, we get: LCR ~ 3.2 × 1041 erg s−1, which is more than an order of magnitude above the cosmic ray power generated in our Galaxy. The actual value of ξ can be constrained by astronomical observations of the non-thermal radiation produced by particles. We discuss these constraints in Sect. 7.
5 Losses and highest energies
In order to obtain final estimates for the highest energies of cosmic rays accelerated in the superwind region of NGC 253 we need to ponder the losses that different species of particles can undergo along the accelerations processes. These losses depend on the conditions in the source and can be divided into radiative and non-radiative losses. For electrons they are caused by synchrotron radiation, inverse Compton (IC) up-scattering of low-energy photons, and relativistic Bremsstrahlung (BS). The non-radiative losses are due to ionization and adiabatic cooling. Below we provide suitable expressions for the timescales of all these losses (see e.g., Bosch-Ramon et al. 2010 and references therein):
 (36)–(39)
(36)–(39)
Specifically, we use the expression provided by Khangulyan et al. (2014) for the calculation of the IC cooling time. Adopting the values of NGC 253, we find that the main losses are caused by synchrotron radiation and IC scattering. The photon fields in the superwind region are the cosmic microwave background with Uph ~ 0.25 eV cm−3 and the IR field, which is the dominant one, with Uph ~ 1 eV cm−3. Using the latter value and B ~ 5μG, we see that tsyn ~ tIC (see Fig. 2). Subsequently, equating 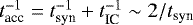 , we find for DSA that
, we find for DSA that 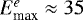 TeV (ϵ = 1) and 30 TeV (ϵ = 0.75).
TeV (ϵ = 1) and 30 TeV (ϵ = 0.75).
Stochastic acceleration is a slower process. For the Alfvén velocity estimated for NGC 253, Eq. (26) can be rewritten as:
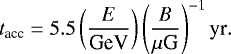 (40)
(40)
The maximum energies achieved by electrons are lower than in the case of DSA: 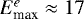 TeV.
TeV.
Protons are affected by pp interactions, photo-pion production, adiabatic losses, and escape by diffusion. Under the physical conditions in the superwind region, all timescales associated with these processes are longer than the dynamical age of the region, so our previous estimates of maximum energies are not affected. The results are shown in Fig. 3, for a thermalization parameter ϵ = 1. In the calculations illustrated by this plot we used the formulae and approximations given by Kelner et al. (2006). Diffusive escape is calculated in the Bohm limit.
 |
Fig. 2 Acceleration and cooling times for the electrons in a 5 μG magnetic field with a thermalization ϵ = 1. |
 |
Fig. 3 Acceleration and cooling times for the protons in a 5 μG magnetic field with a thermalization ϵ = 1. |
6 Particle distributions
A determination of the spectrum Ni(E, t) of the particles accelerated in the superwind region of the starbursts requires solving the transport equation:
![\begin{eqnarray*} \frac{\partial N_{e,p}(E, t)}{\partial t}&=& \frac{\partial}{\partial E} \left[ D(E) \frac{\partial N_{e,p}(E, t)}{\partial E}\right] \nonumber \\ && - \frac{\partial}{\partial E} \left[ \left(\frac{2D(E)}{E} - b_{e,p}(E)\right) N_{e,p}(E, t) \right] \nonumber \\ && + \dot{N}_{e,p;\;\textrm{inj}}.\end{eqnarray*}](/articles/aa/full_html/2018/08/aa32666-18/aa32666-18-eq43.png) (41)
(41)
Here, the index e, p indicates electrons and protons, respectively. The term b(E) = Ė represents the different losses. For protons in the present situation this term can be set to zero, and for electrons it should contain both synchrotron and IC losses. D(E) is the energy diffusion coefficient in the region with magnetic turbulence.
The mechanism that excites the turbulence is not known. A general energy diffusion coefficient can be defined as (e.g., Asano & Mészáros 2016):
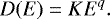 (42)
(42)
For simplicity we shall adopt the most optimistic case D(E) ∝ E that is the counterpart of the Bohm limit in DSA. An index q = 1 is observed, for instance, when Alfvén waves are the scatterers in magnetohydrodynamic simulations by Kowal & Lazarian (2010). The parameter K in Eq. (42) can by approximated as 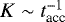 . Subsequently,
. Subsequently,
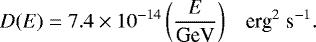 (43)
(43)
For pure SDA of protons (no losses), Eq. (41) reduces to (e.g., O’Sullivan et al. 2009; Chang & Cooper 1970):
![\begin{equation*} \frac{\partial N_{p}(E, t)}{\partial t} {=} \frac{\partial}{\partial E} \left[ D(E) \frac{\partial N_{p}(E, t)}{\partial E}\right] {-}\frac{\partial}{\partial E} \left[\frac{2D(E)}{E} N_{e,p}(E, t)\right].\end{equation*}](/articles/aa/full_html/2018/08/aa32666-18/aa32666-18-eq47.png) (44)
(44)
This equation can be solved for the diffusion coefficient given in Eq. (43) using numerical methods (e.g., Park & Petrosian 1996). In Fig. 4 we show the proton distribution for different times. Because of the importance of the IC and synchrotron radiative losses and the slow acceleration rate in SDA, the electrons reach the steady state after 104 yr. Figure 5 shows the solution of Eq. (41) for electrons at different times until they became steady. We adopt in our calculations the Maxwell–Boltzmann energy distribution as initial particle distribution with T = 3 × 106 K and impose the constraint that the available energy is limited by Eq. (30).
Finally, Figs. 6 and 7 present solutions for the transport equation corresponding to the case of DSA with a constant power-law injection of index − 2.2. This equation can be written as (e.g., Ginzburg & Syrovatskii 1964):
![\begin{equation*} \frac{\partial N_{e,p}(E, t)}{\partial t}+\frac{\partial[b(E) N_{e,p}(E,t)]}{\partial E}+ \frac{N_{p}(E, t)}{t_{\textrm{esc}}}=Q(E).\end{equation*}](/articles/aa/full_html/2018/08/aa32666-18/aa32666-18-eq48.png) (45)
(45)
Here Q(E) is the injection term and tesc is the escape time, which is dominated by the spatial diffusion time tdiff = R2∕D(E). Only particles with tdiff shorter thanthe dominant cooling timescale can escape from the accelerator into the IGM. We consider Bohm diffusion at the shock. For a magnetic field of 5 μG this means DB (E) = 6.6 × 1021(E∕GeV)Z−1 cm2 s−1.
We consider two cases: one where the power in protons and electrons is the same and another where protons dominate by two orders of magnitude, as in the cosmic rays of our Galaxy. If we define a = Lp∕Le, with Li the power in relativistic particles of species i, these cases correspond to a = 1 and a = 100, respectively.
 |
Fig. 4 Proton distributions for a = 1 with a = Lp∕Le in the case of SDA for different times. |
 |
Fig. 5 Electron distributions for a = 1 with a = Lp∕Le in the case of SDA for different times and the final steady state solution. |
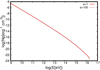 |
Fig. 6 Proton distributions for a = 1 and a = 100 with a = Lp∕Le in the case ofDSA in the reverse shock, assuming thermalization ϵ = 1. |
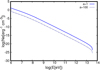 |
Fig. 7 Electron distributions for a = 1 and a = 100 with a = Lp∕Le in the case ofDSA in the reverse shock, assuming thermalization ϵ = 1. |
7 Spectral energy distributions
In this section we present the SEDs of the radiation produced by the cosmic rays in the halo of NGC 253. Different acceleration mechanisms predict different maximum energies for electrons. Hence the radiation they produce, and in particular the location of the cut off of their emission, can be used to discriminate between DSA and SDA in the superwind region. Figure 8 shows the SED obtained in the case of DSA and ratio a = 1, whereas Fig. 9 shows the case of a = 100. We have used the expressions provided by Vila & Aharonian (2009) to calculate the emissions. The efficiency of the shock to convert kinetic energy into cosmic rays ξ, has been adjusted for the SEDs in gamma-rays not to exceed the limits imposed for Fermi and HESS (e.g., Lacki et al. 2011). We see that only ~1% of the shockpower should go to cosmic rays. Figures 10 and 11 represent the SEDs corresponding to SDA, for the same ratios. In principle, X-ray observations can be used to differentiate the models, since in the case of DSA non-thermal X-rays are present (see Fig. 8).
In addition to NGC 253, the nearby starburst galaxies M 82, NGC 4945, and NGC 1068 have been detected by the Fermi satellite and Imaging Atmospheric Cherenkov Telescopes (e.g., Ackermann et al. 2012; Acero et al. 2015). The main characteristics of the gamma-ray emission of these sources are given in Table 3. Given the general similarities between NGC 253 and M 82, it is not surprising that these two sources are also quite alike at high energies. They both present spectra with indices of around − 2.2, which are suggestive of DSA (SDA tends to produce harder spectra, see Figs. 4–7). However, it is important to emphasize that none of these sources is resolved in gamma-rays, so the observed emission might be dominated by contributions from the disk (e.g., Bykov 2014).
The gamma radiation of the galaxy NGC 4945 is also very similar. Its central region, however, harbors a supermassive black hole of ~ 106 M⊙ in addition to the star-forming region. Recent investigations of the correlation between the gamma-ray and the X-ray emission strongly support the theory that the origin of the high-energy radiation is related to the AGN activity, instead of the starburst (Wojaczyński & Niedźwiecki 2017).
Finally, NGC 1068 is the nearest Seyfert 2 galaxy. The gamma-ray luminosity is more than one order of magnitude higher than in the case of NGC 253. Most of this power seems to be associated with an AGN-driven galactic outflow (Lamastra et al. 2016).
We conclude that the best way to assess the nature of the acceleration mechanism in the superwind of starbursts is through high-resolution observations of the non-thermal radiation in the very nearby galaxies NGC 253 and M82 (e.g., with the forthcoming Cherenkov Telescope Array). If the extended gamma-ray emission can be clearly disentangled from the disk contributionand the corresponding spectra well determined, one might favor one of the proposed scenarios over the other.
 |
Fig. 9 Spectral energy distribution in the case of DSA with ratio a = 100, magnetic field B = 5 μG, thermalization ϵ = 1, and shock efficiency ξ = 6 × 10−3. |
 |
Fig. 10 Spectral energy distribution in the case of SDA with ratio a = 1, magnetic field B = 5 μG. |
 |
Fig. 11 Spectral energy distribution in the case of SDA with ratio a = 100, magnetic field B = 5 μG. |
 |
Fig. 8 Spectral energy distribution in the case of DSA with ratio a = 1, magnetic field B = 5 μG, thermalization ϵ = 1, and shock efficiency ξ = 0.012. |
Parameters of gamma-ray emitting starbursts.
8 Discussion
8.1 Stretching the limits
Is there any assumption in the calculations presented so far that might be relaxed to allow for higher energies? The maximum energies obtained for hadrons are limited essentially by the age of the starbursts. We have assumed an age of τ = 10 Myr in accordance with the dynamical age of the source. Given the high mass load of the wind, longer durations for the starburst activity seem extremely unlikely (Bolatto et al. 2013). At most a factor of a few, which would increase the maximum energies by the same amount in the absence of losses (relevant for SDA), might be added. In such a case, the maximum energies would be limited by diffusive escape, unless special conditions at the shock are assumed.
Anotherpossibility is magnetic field amplification in the presence of a strong shock. Enhancement of the magnetic field is well established in supernova remnants. Observations of non-thermal X-ray strips and filaments in some remnants allow us to infer values of the magnetic field far above from what is expected in the shocked interstellar medium (e.g., Bamba et al. 2003; Berezhko et al. 2003; Vink & Laming 2003). The mechanism for field amplification is not known, but there are several proposals in the literature. Bell instability (Bell 2004) is perhaps the most popular mechanism, where the amplification is excited by positive currents of cosmic rays propagating upstream from the shock. The instability, however, seems to be mainly efficient in the fast shocks of young supernova remnants. The saturated magnetic field strength is (e.g., Bustard et al. 2017):
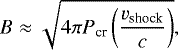 (46)
(46)
where Pcr is the cosmic ray pressure. The field will be high only in sources with fast shocks and high densities of cosmic rays.
Turbulent amplification via small-scale dynamo effects is perhaps another possibility. It can operate either in the precursor of the shock (del Valle et al. 2016) or in the post-shock region (Xu & Lazarian 2017). Amplifications from one to more than three orders of magnitude have been achieved with this mechanism for different setups of initial conditions.
In the case of NGC 253, in the absence of losses we can express the maximum energy as a function of the magnetic field as:
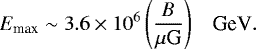 (47)
(47)
Then, for an amplified field of B = 1 mG (amplification factor A = 200), we get:
 (48) (49)
(48) (49)
These estimates are much closer to those of Anchordoqui et al. (1999). However, an amplification factor of 200 seems to be energetically impossible for slow shocks. With shock velocities below 1000 km s−1 the energy density associated to the ram pressure in a medium of number density 0.01 cm−3 is ~ 10−10 erg cm−3. This is about two orders of magnitude smaller than the necessary magnetic energy density B2 ∕8π ~ 4 × 10−8 erg cm−3. So either the shock is faster (of the order of 104 km s−1) or the medium is two orders of magnitude denser. The former case seems impossible on the basis of the well-established properties of the wind and its energy budget (see Sects. 2 and 3). The latter would require acceleration in local regions of very special conditions, like clumps or other dense inhomogeneities in the superwind. Such a possibility will be investigated elsewhere. Nevertheless, it is worth mentioning here that if such extreme amplification of the field occurs somehow, electrons will cool by synchrotron radiation. The regions of high magnetic field will appear as localized non-thermal spots. This will result in X-ray compact sources and X-ray strips, such as those observed in Tycho and other supernova remnants. Deep Chandra observations might reveal such features in the future, clarifying the picture.
8.2 A starving black hole?
The nature of the nucleus of NGC 253 is uncertain. The central region of the galaxy is obscured by gas and dust. Also, the effects of stellar winds affect the determination of rotation curves. Historically, the nucleus has been associated with a strong compact radio source dubbed TH2 (after Turner & Ho 1985). Weaver et al. (2002) detected hard X-ray emission from this source and suggested that it might be a low-luminosity active galactic nucleus (LLAGN). The source does not have, however, any infrared, optical, or soft X-ray counterpart. A young supernova remnant similar to the Crab located at the distance of the center of NGC 253 should be detectable at IR/optical wavelengths, so it seems to be ruled out as an alternative possibility. The absence of counterparts led Fernández-Ontiveros et al. (2009) to propose that TH2 is a starved black hole similar to the Galactic center SgrA*. A reanalysis of Chandra observations by Müller-Sánchez et al. (2010) showed the hard X-ray source is actually located at ~ 0.′′7 southwest from TH2 and is not related to the radio source. This source, called X–1, was suggested to be a hidden LLAGN similarto but weaker than the one detected in the starburst galaxy NGC 4945 (see Müller-Sánchez et al. 2010 for complete discussion). Recent near IR observations performed with the Gemini South telescope led Günthardt et al. (2015) to suggest a new candidate for the nucleus: the IR peak known as IRC, that is coincident with the radio source TH7 and with a massive star cluster of 1.4 × 107 M⊙. Such a cluster can hide a ~106 M⊙ starved black hole.
If a black hole rotates in an external poloidal magnetic field, the field lines are dragged by the ergosphere and a potential drop is created in the magnetosphere. If B is the ordered poloidal field near the hole, h the height of the gap, and a the black hole spin, the induced electromotive force is (e.g., Znajek 1978; Levinson 2000):
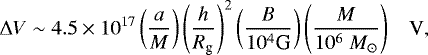 (50)
(50)
where Rg is the gravitational radius of the black hole. The energy density of the magnetic field near the horizon is expected to be in equipartition with the energy density of the accreting matter (Boldt & Ghosh 1999; Levinson & Boldt 2002). This assumption leads to:
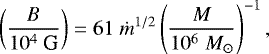 (51)
(51)
where ṁ is the accretion rate in Eddington units (ṀEdd = LEddc2 with LEdd ≈ 1.3 × 1044(M∕106 M⊙) erg s−1).
If there is a black hole of 106 M⊙ in NGC 253, its accretionluminosity cannot be larger than the X-ray luminosity inferred from the observations for the central source (Müller-Sánchez et al. 2010): LX ~ 1040 erg s−1. Adopting an efficiency of 10% (e.g., Romero & Vila 2014), an upper limit ṁ ~ 10−3 is obtained.Then, according to Eq. (51), the magnetic field is B ~ 2 × 104 G. Taking a ~ M and h ~ Rg, Eq. (50) gives:
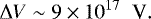 (52)
(52)
This voltage can accelerate charged particles to maximum energies of
 (53) (54)
(53) (54)
The actual energies that can be achieved are limited by radiation losses during the acceleration in the gap. Curvature losses, in particular, can be important (Levinson 2000), resulting in γ-ray production. Photopair and photomeson losses might also play some role, especially for more massive black holes (e.g., Moncada et al. 2017). In the case of a black hole of 106 M⊙ these cooling channels are negligible (Levinson & Boldt 2002).
For lower accretion rates, the maximum energies fall even below what we have obtained in the different cases of diffusive acceleration. For instance, if ṁ ~ 10−6, B ~ 610 G and then,
 (55) (56)
(55) (56)
The total power extracted from the black hole is:
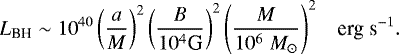 (57)
(57)
Only a fraction αCR of this power goes into cosmic rays:
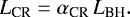 (58)
(58)
In terms of the Eddington luminosity, this can be rewritten as:
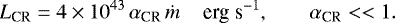 (59)
(59)
If the losses result in a γ-ray luminosity of Lγ = κLCR, we can use γ-ray observations to impose an additional constraint. The integrated flux above 200 MeV of NGC 253 is (Abramowski et al. 2012) Lγ ~ 4.3 × 1039 erg s−1 (assuming a distance of 2.6 Mpc). Then, Eq. (59) with ṁ ~ 10−3 implies αCRκ ~ 0.1. For a radiative efficiency κ ~ 1, we get αCR ~ 10−1 and LCR ~ 4 × 1039 erg s−1. This is similar to the luminosity obtained with SDA and two orders of magnitude less than with DSA (see Sect. 4.3).
8.3 Other potential sources of CR in the disk
In the starburst region of the galaxy, the enhanced star-forming rate can lead to a number of potential sources of ultra-high energy CRs, such as magnetars and mildly relativistic SNe as SNe Ibc, which are more abundant than the classical long GRBs (e.g., Chakraborti et al. 2011; Fang et al. 2012). The detection of such sources in the electromagnetic sector, however, is difficult because of the high absorption in the inner galaxy.
The existence of collective wind effects, otherwise, is indubitable. The interaction of wind-inflated superbubbles with SNe can result is CR acceleration beyond 100 PeV (Bykov 2001, 2014; Bykov et al. 2018). These CRs might be convected by the superwind into the halo region of the galaxy, where some reacceleration might occur at the terminal shock. Adiabatic losses, however, should be important for these particles and it is far from clear whether a significant flux with energies above 1018 eV can be produced and then arrive at the earth (see following section).
8.4 Propagation and effects upon arrival
Recent models of the Galactic magnetic field have been developed which are based on a vast number of measurements of Faraday rotation (Pshirkov et al. 2011). Jansson & Farrar (2012a,b) used polarized synchrotron radiation in addition. Nevertheless, the amount of deflection of extragalactic cosmic rays in the Galactic magnetic field is rather uncertain (Unger & Farrar 2017).
Even in case of assuming nuclei remaining intact without photo-disintegrating due to the relative proximity of NGC 253 (Kampert et al. 2013; Batista et al. 2016), deflections caused by the Galactic magnetic field do not permit the attribution of cosmic rays to a region of a single source at energies derived for the realistic SDA and DSA scenarios; see Eqs. (27) and (28) and Eqs. (33) and (34), respectively. Energies at which particles remain restricted to ballistic trajectories are only possible when stretching the limits using amplified magnetic fields at the source are.
The Galactic magnetic field models mentioned above are used by Erdmann et al. (2016) to determine the minimal rigidity for ballistic deflections to be of the order of E∕Z = 6 EV; a factor of two larger than given in Eq. (48). In particular, the region at latitudes below − 19.5° gives rise to large bulk deflections of up to 50° for a rigidity of E∕Z = 6 EV. The identification of NGC 253 as a starburst galaxy emitting cosmic rays at these rigidities seems therefore difficult to achieve, even if such acceleration actually occurs3.
Given the increasingly heavier average mass of ultra-high-energy cosmic rays from proton-dominated near the ankle region at 1018.33 eV to intermediate masses at 1019.65 eV (Aab et al. 2017b, 2014) the search for multiplets of individual mass groups in the same E∕Z range might be promising (Abreu et al. 2012), but a more detailed assessment of the feasibility needs to be performed and will be given in a forthcoming paper.
9 Conclusions
In this paper we have assessed the potential of starburst galaxies as cosmic ray accelerators. We adopted as a case of study the southern galaxy NGC 253. This class of objects are interesting as cosmic ray sources for several reasons: 1) they are non-thermal radio and gamma-ray emitters, so cosmic rays up to TeV energies are accelerated in them. 2) The star-forming activity releases large amounts of thermal energy that can power very strong winds on galactic scale. 3) These winds create huge bubbles of hot gas above the galactic disks, The size of these regions is large enough as to contain cosmic rays of the highest energies. 4) Strong shocks are produced in the interaction of the superwind with the external medium. Such shocks, as well as the turbulent plasma in the bubbles, can be part of potential mechanisms that accelerate charged particles up to energies far larger than those inferred from the gamma rays. 5) Starburst galaxies are objects of high metallicity, so acceleration of heavy nuclei is favored in them.
Motivated by these considerations, and after using current multi-wavelength observations to characterize the potential acceleration of particles, we conclude that starburst galaxies in general and NGC 253 in particular might produce cosmic rays with energies up to 1018 eV in the superwind region, either by DSA in the reverse terminal shock of the superwind or by SDA in the turbulent gas of the bubbles. We conclude that under normal circumstances acceleration up to 100 EeV is unlikely. The high-mass load of the wind results in moderate shock velocities of less than 1000 km s−1 that avoid efficient acceleration on timescales compatible with the age of the starburst episode. The low Alfvén velocities in the turbulent plasma of the bubbles, on the other hand, limits the effectiveness of stochastic acceleration.
Amplified magnetic fields close to the shock, as observed in supernova remnants, might offer a way to reach energies comparable to those of the more energetic cosmic rays. The shocks and the conditions around them, however, are very different in starbursts galaxies from those found in young supernova remnants, so a separate study should be devoted to this issue. In particular, much higher ram pressures (and hence densities) should occur than what we can presently infer from the observations. We notice here that if fields of the order of 1 mG exist in some parts of the gas shocked by the superwind, features in X-rays and radio should exist, and they may be detectable. This offers a way of testing such a hypothesis, which is otherwise based on a poorly established physical basis.
We conclude that starbursts galaxies are fascinating astrophysical systems, capable of accelerating cosmic rays and producing non-thermal radiation beyond what is seen in our Galaxy. Whether they are actually related to the highest cosmic rays observed on Earth, remains unclear.
Acknowledgments
We thank M. Unger for discussions and an anonymous reviewer for valuable suggestions. G.E.R. is very grateful to the IKP at KIT where this research was done. This work was supported by the Helmholtz Association through a Helmholtz International Fellow Award to GER. Additional support was provided by the Argentine agency CONICET (PIP 2014-00338) and the Spanish Ministerio de Economía y Competitividad (MINECO/FEDER, UE) under grant AYA2016-76012-C3-1-P.
Appendix A Appendix: Adiabaticity and other requirements for efficient particle acceleration at the shocks
As mentioned in Sect. 1, the interaction of the superwind with the halo and swept-up disk material produces two shock waves. One of them propagates through the halo/thick disk with velocity vshell whereas thereverse shock moves through the superwind material with a velocity vrev. In our model, for thermalization ϵ = 0.75, these velocities are 298 and 750 km s−1, respectively, and 328 and 866 km s−1 for ϵ ≈ 1. Using thesevalues and the number density of each pre-shocked medium, nsw= 2 × 10−3 cm−3 for the superwind bubble and nhalo/disk = 6.8 × 10−3 cm−3 for the halo/swept-up material (Strickland et al. 2002), we study the nature of these shocks. For this purpose, we calculate the cooling length RΛ using the following expression (McCray & Snow 1979):
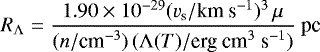 (A.1)
(A.1)
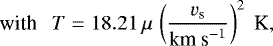 (A.2)
(A.2)
where μ is 0.6 if the material is ionized or 1.3 if neutral, vs is the shock velocity, n is the number density of the non-pertubated medium, and Λ(T) [erg cm3 s−1] is the cooling function (Raymond et al. 1976; Myasnikov et al. 1998):
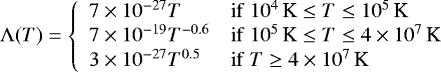 (A.3)
(A.3)
The adiabaticity of the shock can be determined comparing this cooling length with the length traversed by the shock. If the cooling length is longer, the shock is adiabatic, otherwise it is radiative. An equivalent analysis is possible using the timescale of the thermal cooling instead of the cooling length:
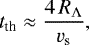 (A.4)
(A.4)
and comparing it with the lifetime of the source. Table A.1 shows the results for the values of the parameter in our model.
Parameters for the forward and reverse shocks.
Since the lifetime of the source is ~107 yr in our model, the forward shocks turn out to be radiative and the reverse shocks adiabatic for both thermalization efficiencies, as we mentioned in the main body of this work.
Anothercondition that must be satisfied by a shock in order to accelerate particles is that the overall shock Mach number exceeds the critical value 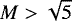 (Vink & Yamazaki 2014). As we can see from Table 1, the Mach numbers are M ≈ 5.3 and M ≈ 4.6, for the thermalization parameters ϵ = 1 and ϵ = 0.75, respectively.The condition, therefore, is largely fulfilled.
(Vink & Yamazaki 2014). As we can see from Table 1, the Mach numbers are M ≈ 5.3 and M ≈ 4.6, for the thermalization parameters ϵ = 1 and ϵ = 0.75, respectively.The condition, therefore, is largely fulfilled.
References
- Aab, A., Abreu, P., Aglietta, M., et al. 2014, Phys. Rev. D, 90, 122006 [NASA ADS] [CrossRef] [Google Scholar]
- Aab, A., Abreu, P., Aglietta, M., et al. 2017a, Science, 357, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Aab, A., Abreu, P., Aglietta, M., et al. 2017b, ArXiv e-prints [arXiv:1708.06592] [Google Scholar]
- Aab, A., Abreu, P., Aglietta, M., et al. 2017c, JCAP, 4, 038 [NASA ADS] [CrossRef] [Google Scholar]
- Aab, A., Abreu, P., Aglietta, M., et al. 2018, ApJ, 853, L29 [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2014, Phys. Rev. Lett., 113, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbasi, R. U., Abe, M., Abu-Zayyad, T., et al. 2014, ApJ, 790, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Bellido, J., Belz, J., et al. 2016, Report of the Working Group on the Composition of Ultra High Energy Cosmic Rays, 010016 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 709, L152 [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, ApJ, 757, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Abreu, P. et al. (Pierre Auger Collaboration) 2012, Astropart. Phys., 35, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, Nature, 462, 770 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Acero, F., Aharonian, F., Akhperjanian, A. G., et al. 2009, Science, 326, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2012, ApJ, 755, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Belyanin, A. A., Derishev, E. V., Kocharovsky, V. V., & Kocharovsky, V. V. 2002, Phys. Rev. D, 66, 023005 [NASA ADS] [CrossRef] [Google Scholar]
- Anchordoqui, L. A. 2018, Phys. Rev. D, 97, 063010 [NASA ADS] [CrossRef] [Google Scholar]
- Anchordoqui, L. A., Romero, G. E., & Combi, J. A. 1999, Phys. Rev. D, 60, 103001 [NASA ADS] [CrossRef] [Google Scholar]
- Anchordoqui, L. A., Paul, T. C., da Silva, L. H. M., Torres, D. F., & Vlcek, B. J. 2014, Phys. Rev. D, 89, 127304 [NASA ADS] [CrossRef] [Google Scholar]
- Asano, K., & Mészáros, P. 2016, Phys. Rev. D, 94, 023005 [NASA ADS] [CrossRef] [Google Scholar]
- Bamba, A., Yamazaki, R., Ueno, M., & Koyama, K. 2003, ApJ, 589, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Batista, R. A., Dundovic, A., Erdmann, M., et al. 2016, CAP, 2016, 038 [Google Scholar]
- Bechtol, K., Ahlers, M., Di Mauro, M., Ajello, M., & Vandenbroucke, J. 2017, ApJ, 836, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Carilli, C. L., Holdaway, M. A., & Klein, U. 1994, A&A, 292, 409 [NASA ADS] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2003, A&A, 412, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Warren, S. R., Leroy, A. K., et al. 2013, Nature, 499, 450 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boldt, E., & Ghosh, P. 1999, MNRAS, 307, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon,V., Romero, G. E., Araudo, A. T., & Paredes, J. M. 2010, A&A, 511, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bustard, C., Zweibel, E. G., & Cotter, C. 2017, ApJ, 835, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M. 2001, Space Sci. Rev., 99, 317 [Google Scholar]
- Bykov, A. M. 2014, A&ARv, 22, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., Ellison, D. C., Marcowith, A., & Osipov, S. M. 2018, Space Sci. Rev., 214, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Chakraborti, S., Ray, A., Soderberg, A. M., Loeb, A., & Chandra, P. 2011, Nat. Comm., 2, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, J. S., & Cooper, G. 1970, J. Comp. Phys., 6, 1 [Google Scholar]
- Chang, X.-C., & Wang, X.-Y. 2014, ApJ, 793, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, X.-C., Liu, R.-Y., & Wang, X.-Y. 2015, ApJ, 805, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Clegg, A. W. 1985, Nature, 317, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, J. L., Bicknell, G. V., Sutherland, R. S., & Bland-Hawthorn, J. 2008, ApJ, 674, 157 [NASA ADS] [CrossRef] [Google Scholar]
- del Valle, M. V., Lazarian, A., & Santos-Lima, R. 2016, MNRAS, 458, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Domingo-Santamaría, E., & Torres, D. F. 2005, A&A, 444, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Erdmann, M., Müller, G., Urban, M., & Wirtz, M. 2016, Astropart. Phys., 85, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, K., Kotera, K., & Olinto, A. V. 2012, ApJ, 750, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Ontiveros, J. A., Prieto, M. A., & Acosta-Pulido, J. A. 2009, MNRAS, 392, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1964, The Origin of Cosmic Rays (New York: Macmillan) [Google Scholar]
- Günthardt, G. I., Agüero, M. P., Camperi, J. A., et al. 2015, AJ, 150, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Cheung, C. C., Feain, I. J., & Stawarz, Ł. 2009, MNRAS, 393, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Armus, L., & Miley, G. K. 1990, ApJS, 74, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Beck, R., Krause, M., & Dettmar, R.-J. 2009a, A&A, 494, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heesen, V., Beck, R., Krause, M., & Dettmar, R.-J. 2009b, Astron. Nachr., 330, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Krause, M., Beck, R., & Dettmar, R.-J. 2009c, A&A, 506, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillas, A. M. 1984, ARA&A, 22, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012a, ApJ, 757, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012b, ApJ, 761, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Jokipii, J. R., & Morfill, G. E. 1985, ApJ, 290, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Kampert, K.-H., Kulbartz, J., Maccione, L., et al. 2013, Astropart. Phys., 42, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Grebel, E. K., Sharina, M. E., et al. 2003, A&A, 404, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Aharonian, F. A., & Kelner, S. R. 2014, ApJ, 783, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Kowal, G., & Lazarian, A. 2010, ApJ, 720, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Lacki, B. C. 2014, MNRAS, 444, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Lacki, B. C., Thompson, T. A., Quataert, E., Loeb, A., & Waxman, E. 2011, ApJ, 734, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Lamastra, A., Fiore, F., Guetta, D., et al. 2016, A&A, 596, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levinson, A. 2000, Phys. Rev. Lett., 85, 912 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Levinson, A., & Boldt, E. 2002, Astropart. Phys., 16, 265 [NASA ADS] [CrossRef] [Google Scholar]
- McCray, R., & Snow, Jr. T. P. 1979, ARA&A, 17, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Moncada, R. J., Colon, R. A., Guerra, J. J., O’Dowd, M. J., & Anchordoqui, L. A. 2017, J. High Energy Astrophys., 13, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., González-Martín, O., Fernández-Ontiveros, J. A., Acosta-Pulido, J. A., & Prieto, M. A. 2010, ApJ, 716, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Myasnikov, A. V., Zhekov, S. A., & Belov, N. A. 1998, MNRAS, 298, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Ohm, S. 2016, Comptes Rendus Physique, 17, 585 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S., Reville, B., & Taylor, A. M. 2009, MNRAS, 400, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J. 2002, ASP Conf. Ser., 253, 489 [NASA ADS] [Google Scholar]
- Paglione, T. A. D., Marscher, A. P., Jackson, J. M., & Bertsch, D. L. 1996, ApJ, 460, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Park, B. T., & Petrosian, V. 1996, ApJS, 103, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V. 2012, Space Sci. Rev., 173, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Protheroe, R. J. 1999, in Topics in Cosmic-Ray Astrophysics, ed. M. A. Duvernois, (New York: Nova Science Pub Inc.) 230, 247 [NASA ADS] [Google Scholar]
- Pshirkov, M. S., Tinyakov, P. G., Kronberg, P. P., & Newton-McGee, K. J. 2011, ApJ, 738, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Puche, D., & Carignan, C. 1988, AJ, 95, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Radovich, M., Kahanpää, J., & Lemke, D. 2001, A&A, 377, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raymond, J. C., Cox, D. P., & Smith, B. W. 1976, ApJ, 204, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., Arieli, Y., & Persic, M. 2010, MNRAS, 401, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., & Vila, G. S., 2014, Lect. Notes Phys., 876 [Google Scholar]
- Semikoz, D., Tinyakov, P., & Zotov, M. 2016, Phys. Rev. D, 93, 103005 [NASA ADS] [CrossRef] [Google Scholar]
- Stawarz, Ł., & Petrosian, V. 2008, ApJ, 681, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., & Heckman, T. M. 2009, ApJ, 697, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., Heckman, T. M., Weaver, K. A., Hoopes, C. G., & Dahlem, M. 2002, ApJ, 568, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Su, M., Slatyer, T. R., & Finkbeiner, D. P. 2010, ApJ, 724, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, R., Cecil, G., & Heitsch, F. 2017, ApJ, 843, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, J. L., & Ho, P. T. P. 1985, ApJ, 299, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Unger, M., & Farrar, G. R. 2017, ArXiv e-prints [arXiv:1707.02339] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Vila, G. S., & Aharonian, F. A. 2009, in Compact Objects and their Emission, eds. G. E. Romero, & P. Benaglia, Asociación Argentina de Astronomía, Book Series (La Plata, Argentina: Editorial Paideia), 1 [Google Scholar]
- Vink, J., & Laming, J. M. 2003, ApJ, 584, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J., & Yamazaki, R. 2014, ApJ, 780, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, K. A., Heckman, T. M., Strickland, D. K., & Dahlem, M. 2002, ApJ, 576, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Wojaczyński,R., & Niedźwiecki, A. 2017, ApJ, 849, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, S., & Lazarian, A. 2017, ApJ, 850, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Znajek, R. L. 1978, MNRAS, 185, 833 [NASA ADS] [CrossRef] [Google Scholar]
Strickland et al. (2002) estimate, for the case of NGC 253, ZO, true ~ 0.5, yielding tcool ~ 19 Myr for a filling factor ηX = 1.
The Reynolds number of the cosmic rays can be roughly calculated as (Bustard et al. 2017):
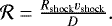 Adopting D ~ 1029 cm2 s−1 (Heesen et al. 2009a), we get
Adopting D ~ 1029 cm2 s−1 (Heesen et al. 2009a), we get 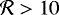 .
.
A different view based upon Anchordoqui et al. (1999) is expressed by Anchordoqui (2018).
All Tables
All Figures
 |
Fig. 1 Scheme of the physical scenario considered in this work (not to scale), adapted from Strickland et al. (2002). |
| In the text | |
 |
Fig. 2 Acceleration and cooling times for the electrons in a 5 μG magnetic field with a thermalization ϵ = 1. |
| In the text | |
 |
Fig. 3 Acceleration and cooling times for the protons in a 5 μG magnetic field with a thermalization ϵ = 1. |
| In the text | |
 |
Fig. 4 Proton distributions for a = 1 with a = Lp∕Le in the case of SDA for different times. |
| In the text | |
 |
Fig. 5 Electron distributions for a = 1 with a = Lp∕Le in the case of SDA for different times and the final steady state solution. |
| In the text | |
 |
Fig. 6 Proton distributions for a = 1 and a = 100 with a = Lp∕Le in the case ofDSA in the reverse shock, assuming thermalization ϵ = 1. |
| In the text | |
 |
Fig. 7 Electron distributions for a = 1 and a = 100 with a = Lp∕Le in the case ofDSA in the reverse shock, assuming thermalization ϵ = 1. |
| In the text | |
 |
Fig. 9 Spectral energy distribution in the case of DSA with ratio a = 100, magnetic field B = 5 μG, thermalization ϵ = 1, and shock efficiency ξ = 6 × 10−3. |
| In the text | |
 |
Fig. 10 Spectral energy distribution in the case of SDA with ratio a = 1, magnetic field B = 5 μG. |
| In the text | |
 |
Fig. 11 Spectral energy distribution in the case of SDA with ratio a = 100, magnetic field B = 5 μG. |
| In the text | |
 |
Fig. 8 Spectral energy distribution in the case of DSA with ratio a = 1, magnetic field B = 5 μG, thermalization ϵ = 1, and shock efficiency ξ = 0.012. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.