| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201732324 | |
| Published online | 05 July 2018 | |
Aluminium abundances in five discrete stellar populations of the globular cluster NGC 2808⋆,⋆⋆
1
INAF-Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
e-mail: eugenio.carretta@oabo.inaf.it
2
INAF-Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
Received:
20
November
2017
Accepted:
25
January
2018
We observed a sample of 90 red giant branch (RGB) stars in NGC 2808 using FLAMES/GIRAFFE and the high resolution grating with the set-up HR21. These stars have previous accurate atmospheric parameters and abundances of light elements. We derived aluminium abundances for them from the strong doublet Al i 8772–8773 Å as in previous works of our group. In addition, we were able to estimate the relative CN abundances for 89 of the stars from the strength of a large number of CN features. When adding self-consistent abundances from previous UVES spectra analysed by our team, we gathered [Al/Fe] ratios for a total of 108 RGB stars in NGC 2808. The full dataset of proton-capture elements is used to explore in detail the five spectroscopically detected discrete components in this globular cluster. We found that various classes of polluters are required to reproduce (anti)-correlations among all proton-capture elements in the populations P2, I1, and I2 with intermediate composition. This is in agreement with the detection of lithium in lower RGB second generation stars, requiring at least two kind of polluters. For chemically homogeneous populations, the best subdivision of our sample is into six components as derived from statistical cluster analysis. By comparing different diagrams [element/Fe] versus [element/Fe], we show for the first time that a simple dilution model is not able to reproduce all the subpopulations in this cluster. Polluters of different masses are required. NGC 2808 is confirmed to be a tough challenge to any scenario for globular cluster formation.
Key words: stars: abundances / stars: atmospheres / stars: population II / globular clusters: general / globular clusters: individual: NGC 2808
Full Tables 1 and 3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/615/A17
© ESO 2018
1. Introduction
Proton-capture reactions involving the complete CNO and the Ne–Na, Mg–Al cycles can simultaneously be at work in H-rich stellar interiors when temperature is high enough (Denisenkov & Denisenkova 1989; Langer et al. 1993) in globular clusters (GCs), which are the first aggregates to appear in the forming galaxy. These reactions produce Na from Ne and N from C and O when the temperature exceeds about 30 MK. Conversion of Mg into Al occurs when H-burning occurs at temperature exceeding 65 MK. If material processed through these reactions is somehow given back to the interstellar medium, we may observe significant deviations from the typical low-Na, high-O plateau established in metal-poor halo stars (e.g. Wheeler et al. 1989). These deviations are those discovered by the Lick-Texas group (see Kraft 1994 for a summary) in a good fraction of GC stars (as reviewed by Gratton et al. 2004). These deviations are only found among GC stars and in virtually all GCs (e.g. Gratton et al. 2000; Carretta et al. 2009a, b; see references in Gratton et al. 2012; Bragaglia et al. 2017; Bastian & Lardo 2017), indicating that this nucleosynthetic signature is related to high density environments, and is not present, for example, among stars in dwarf spheroidal galaxies (see e.g. Carretta 2013; Lardo et al. 2016).
While these alterations are detected in currently evolving GC stars, in situ production is ruled out because temperature in their interior is not high enough. In addition, the distribution of light element abundances is similar for giants with deep convective envelopes and main-sequence stars with negligible convective envelopes (e.g. Cannon et al. 1998; Gratton et al. 2001; Briley et al. 2002, 2004a, b; Harbeck et al. 2003; Cohen et al. 2002, 2005; D’Orazi et al. 2010; Dobrovolskas et al. 2014). The nucleosynthetic site must then be searched in stars of a previous stellar generation (Gratton et al. 2001) more massive than those currently evolving through the red giant branch (RGB) of GCs.
Finally, these star-to-star abundance variations in light elements are typically not accompanied by intrinsic variations in the iron content (constant in most GCs; e.g. (Carretta et al. 2009c), but see e.g. (Johnson et al. 2005) and (Marino et al. 2015) for the growing class of iron complex GCs). The release of protoncapture elements likely did not occurr during the epoch when supernova exploded in the clusters.
More than three decades of spectroscopic observations set the general background of the current paradigm for GCs. These old objects are not as simple as once thought. They formed in at least two close (time delay from a few to a few tens of Myr) bursts of star formation with second generation (SG) stars incorporating the proton-capture yields released at low velocity by some of the massive stars of the first generation (FG). Constraints from the chemical feedback available in FG stars, abundances of the fragile Li detected in SG stars together with matter processed at high temperature, and considerations from stellar nucleosynthesis call for a significant fraction of unprocessed, pristine gas mixed with ashes of H-burning to form all other stellar generations but the FG (Prantzos & Charbonnel 2006; D’Ercole et al. 2011).
While this general framework is broadly, although not universally (see e.g. Bastian & Lardo 2015; Bastian et al. 2015) accepted, many important features are still hotly debated. For instance, it is not entirely clear which class of FG stars was the main player to pollute the intra-cluster medium (e.g. massive binaries, de Mink et al. (2009), massive, fast rotating single stars, FRMS, Decressin et al. (2007); intermediate mass AGB and super AGB stars, Ventura et al. (2001), D’Ercole et al. (2010, 2012)) or whether more than one class was contributing to the SG. The ensemble of nucleosynthesis constraints is not completely satisfied by any of the proposed candidate polluters (Prantzos et al. 2017).
The ubiquitous Na–O anti-correlation alone, which is widespread enough in GCs to be suggested as the main chemical feature characterizing the essence of a genuine Galactic GC (Carretta et al. 2010; see Villanova et al. 2013 for the notable exception of Rup 106), is not sufficient to provide strong constraints: several classes of candidate polluters were able to develop temperatures high enough to manage the proton-capture reactions depleting O and enhancing Na.
More insight is obtained by also considering cycles requiring much higher temperatures, such as the Mg–Al chain. In general, these reactions require higher masses for the polluters. While indications of the activation of this cycle in the GC polluters date back to Kraft et al. (1997), most early studies only considered a small number of clusters (e.g. Johnson et al. 2005) because of limitations in single slit spectrographs. Once efficient multi-object spectrographs became available, much more extensive surveys became possible. Carretta et al. (2009b) performed a homogeneous scrutiny of high resolution UVES-FLAMES spectra of a limited number of RGB stars (max 14) in 17 GCs. These authors showed that an efficient production of Al only occurred in massive and/or metal-poor GCs. This finding was later confirmed by the near-infrared APOGEE survey in ten northern GCs (Mészáros et al. 2015). This indicates that the involved high temperatures were not reached in the H-burning regions of the polluters for the smallest/metal-rich GCs, as instead it happened for the CNO and Ne–Na cycles. This indicated that the typical mass of the polluters correlates with the mass of the cluster. In addition, since the Al content is one order of magnitude less than Mg in the Sun and in metal-poor stars, this means that when a sizeable fraction of the original Mg is transformed into Al, its abundance may change by a huge factor. This offers an extraordinary resolution to probe processes occurring during the formation of GCs allowing for example much better separation of stars into different chemical homogeneous groups.
We begun to systematically exploit this approach by observing large samples of RGB stars (about 100) in NGC 6752 (Carretta et al. 2012a), NGC 1851 (Carretta et al. 2012b), 47 Tuc, and M4 (NGC 6121: Carretta et al. 2012c) with FLAMES/GIRAFFE (Pasquini 2002) and the efficient setup HR21, whose spectral range includes the strong Al i 8772–8773 Å doublet. Briefly, leaving aside the iron complex cluster NGC 1851, we studied the complete and large dataset of homogeneous O, Na, Mg, and Al abundances with a k-means algorithm (Steinhaus 1956; MacQueen 1967) of cluster analysis, finding three discrete populations in both NGC 6752 and 47 Tuc. These two GCs however differ because in the latter it is possible to reproduce the group with intermediate (I) abundances by mixing the compositions of the primordial (P) and extreme (E) populations, whereas for NGC 6752 a simple dilution model cannot account simultaneously for all the P, I, E components. This implies the action of at least two different classes of polluters. The existence of discrete stellar components in NGC 6752 and 47 Tuc is also supported by photometric studies based on larger samples of stars (Carretta et al. 2011; Milone et al. 2013; and Milone et al. 2012, respectively).
The discovery and chemical characterization of possible distinct groups in the multiple stellar populations of a GC is crucial to reconstruct the possible sequence of early star formation in these objects. The question is whether polluters of the same class but different mass ranges contributed, as suggested by the three groups following the dilution track in 47 Tuc, or rather two different kind of contributors, acting at different times, as is likely in NGC 6752.
In the present paper we extend our Al studies to the peculiar GC NGC 2808, where five discrete components with distinct chemical compositions were discovered in Carretta (2015), supporting the analogous finding from photometry (Milone et al. 2015, who discussed the existence of up to seven populations). By more than tripling the sample of giants with Al determinations in this cluster (Carretta 2014) we gather a set of proton-capture elements (O, Na, Mg, Al, Si, and also estimates of N content) and apply the cluster analysis again to search for chemically homogeneous subpopulations and provide more stringent constraints on the formation scenario for this cluster (see D’Antona et al. 2016).
The paper is organized as follows. Section 2 presents the observational data, the data are analysed and abundances are derived in Sect. 3, and these results are discussed in Sect. 4. In Sect. 5 we show results of the statistical cluster analysis, and in Sect. 6 we present final discussion and conclusions.
2. Observations and ancillary data
Our sample of first ascent red giant stars in NGC 2808 was observed in service mode with VLT-UT2/FLAMES on 2015 January 21, with an exposure time of 1 hr at airmass 1.314 with the high resolution GIRAFFE set-up HR21 (R = 17 300 and spectral interval from about 8484 Å to about 9001 Å). As in previous works on Al in NGC 6752 (Carretta et al. 2012a), M4, and 47 Tuc (Carretta et al. 2012c), we adopted the same configurations for fibre positioning that were used to observe stars in NGC 2808 (Carretta et al. 2006) with HR11. This choice permits us to maximize the number of giants with measured abundances of Na because the five distinct populations found by Carretta (2015) were best detected using a combination of Na and Mg.
We obtained spectra for 90 members. Data reduced by ESO personnel with the dedicated pipeline (spectra de-biased, flat-fielded, extracted, and wavelength calibrated) were retrieved, sky subtracted, and shifted to zero radial velocity using IRAF1.
Our target stars are red giants in the magnitude range V = 13.8–15.5. Star identification, coordinates, and Johnson V magnitudes (Carretta et al. 2006) are reported in Table 1, together with the heliocentric radial velocity (RV) we derived. Also listed in this table is the signal-to-noise ratio (S/N) provided by the ESO pipeline as the mean value across the spectrum. The S/N basically scales as a function of the magnitude, apart from a couple of outliers (Fig. 1). The median S/N is 172 for our sample.
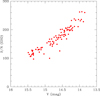 |
Fig. 1. S/Ns from the ESO FLAMES-GIRAFFE pipeline as a function of the V magnitudes for our sample in NGC 2808 |
Atmospheric parameters (effective temperature, surface gravity, model metallicity, and microturbulent velocity) for all stars were adopted from Carretta (2015), since in that work they were updated, with respect to the values in Carretta et al. (2006), to the homogeneous system used in all the other GCs in our FLAMES survey for the Na–O anti-correlation. The abundance ratios [O/Fe], [Na/Fe], [Mg/Fe], and [Si/Fe]2 that, together with Al, complete the dataset of proton-capture elements for NGC 2808, were also taken from Carretta (2015).
Information on stars observed in NGC 2808.
3. Analysis and derived abundances in NGC 2808
Our methods to derive abundances of Al closely followed the procedure described in Carretta et al. (2012a, b, c).
3.1. Estimates of nitrogen abundances
The ubiquitous CN lines present in the spectral range of HR21 may give a certain degree of contamination, spuriously affecting abundances derived from the Al features of interest. At the same time, they offer the opportunity to provide rough estimates of the abundances of N, another light element involved in the proton-capture reactions in H-burning.
We summed the spectra of the 18 coolest stars in our sample (T eff < 4300 K) to obtain a master spectrum of very high S/N. On this co-added spectrum we determined 8 regions to be used as local reference continuum and 20 other regions dominated by CN features. The spectral ranges for the continuum regions coincide with those used in Carretta et al. (2012c), whereas the selected features for CN slightly differ from those adopted for 47 Tuc owing to the different metallicity and quality of spectra. All the regions used for NGC 2808 are listed in Table 2.
For each star, three synthetic spectra were computed with the package ROSA (Gratton 1988) using [N/Fe] = –0.5, +0.25 and +1.0 dex, the Kurucz (1993) grid of model atmospheres (with the overshooting option on), atmospheric parameters from Carretta (2015), the same line list as in Carretta et al. (2012b), and assuming [C/Fe] = 0. This is an arbitrary assumption based on our ignorance of the actual C pattern in giants of NGC 2808. As a consequence, we are actually measuring the abundance of the C × N product. If the actual C content was different from the assumed value, the N abundance would be different so as to keep constant the sum [C/Fe] + [N/Fe].
A weighted reference continuum was derived from all the 8 regions using weights equal to the width of each region. For each CN feature the average flux within the in-line region was measured, and the associated CN abundance was obtained by comparing the normalized flux with the fluxes measured in the same way on the three synthetic spectra. Finally, we applied a 2.5˙ clipping to the average abundance from individual features in each star, after discarding features that visual inspection revealed affected by spikes.
We obtained abundances for 89 stars using on average 18 features, finding on average [CN/Fe] = −0.191 ± 0.014 dex (rms = 0.129 dex) in NGC 2808. Individual values of CN abundances are listed in Table 3.
In Fig. 2 we compare our estimates of the [CN/Fe] ratios to the cyanogen excesses derived by Norris & Smith (1983) for 6 giants of NGC 2808 in common between their study and the present work. The good correlation supports the conclusion that our procedure provides a good estimate of the CN content, despite the arbitrary assumption about the unknown abundance of C. As a final caveat, we recall that the total CN range may be underestimated since it is well documented that C abundances are higher (by about 0.3 dex) in CN-weak, SG stars. However, in M4, which is a GC with similar metallicity, the C abundances for SG, Na-rich stars, and FG, Na-poor stars only differ by 0.06 dex on average (see discussion and references in Carretta et al. 2012c). In the following, to avoid any misunderstanding, we indicate with [CN/Fe] our derived abundance ratios.
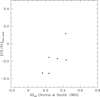 |
Fig. 2. Comparison of our estimates of [CN/Fe] in NGC 2808 with the cyanogen excesses derived in Norris & Smith (1983) for 6 stars in common. |
List of regions used to estimate local continuum and fluxes of CN bands.
Group classification and derived abundances for RGB stars in NGC 2808.
3.2. Aluminium abundances
After estimating the amount of the contaminant CN, we computed for each star three synthetic spectra with [Al/Fe] = −0.5, 0.5, and 1.5 dex to derive Al abundances measuring fluxes in the in-line region from 8772.25 to 8774.57 Å and using the regions 8769.09–8770.00 Å and 8776.40–8777.70 Å for the local reference continuum, again individuated on the co-added, high S/N master spectrum. The contribution from these two regions was averaged with weights given by the number of pixels (i.e. the widths of these intervals).
We first inspected the Al lines and the selected continuum regions on plots of the spectra to be sure that none were affected by a defect, otherwise the region was disregarded. We deemed not possible to derive Al abundances for four stars. Then we interpolated the observed normalized fluxes among those from the above synthetic spectra, obtaining the Al abundance for each star.
Our aim is to gather the largest possible sample of RGB stars in NGC 2808 with homogeneous abundances of light elements. To safely add the sample with high resolution UVES spectra reanalysed in Carretta (2014, 2015), who used the Al doublet at 6696–98 Å, we checked possible offsets in Al using 9 stars with both doublets available. From these stars we found that on average the difference is [Al/Fe](669–977 nm) = +0.068 ± 0.076 dex with rms = 0.229, which is compatible with no significant offset.
As in our previous papers the Al abundances are in local thermodynamic equilibium (LTE) and our adopted solar abundance for Al is 6.23. In the following we then adopt whenever possible [Al/Fe] abundances derived from UVES spectra by Carretta (2014, 2015). Final Al abundances for giants in NGC 2808 are listed in Table 3. We were able to derive an Al value for 86 stars observed with FLAMES/GIRAFFE and HR21. Adding the 31 stars with determinations from UVES (Carretta 2014) and taking into account 9 stars in common we ended up with 108 RGB stars with homogeneous Al abundances.
Recently, D’Orazi et al. (2015) derived Al abundances for a sample of 65 stars in NGC 2808 using the near-infrared doublet at 6696–98 Å. A direct, star-to-star comparison is not possible, since that work was mainly aimed to derive Li abundances, so their sample is made of lower RGB stars that are fainter than any in the present sample. The average value they found ([Al/Fe] = +0.32σ = 0.39 dex) compares well with the mean [Al/Fe] = +0.46σ = 0.47 dex for the sample of 31 giants with UVES spectra (Carretta 2014) and the average value [Al/Fe] = +0.41σ = 0.63 dex from 86 stars with FLAMES HR21 spectra. Differences may be explained by small differences in the derivation of atmospheric parameters; for example the final temperatures are derived here and in Carretta (2014) as a function of the 2MASS K magnitude, whereas D’Orazi et al. used the Johnson V magnitude. The latter authors found that stars in NGC 2808 are split into three main components, according to the Al abundances.
UVES spectra of seven asymptotic giant branch (AGB) stars in NGC 2808 were analysed by Marino et al. (2017). Once Al and Fe are corrected to our scale for offsets due to the adopted solar abundances, these authors derived an average ratio [Al/Fe] = +0.63σ = 0.40 dex. This last sample does not include the most Al-rich population, since apparently these stars – which are probably also He-enriched – miss the AGB phase.
Part of the difference may be due to (neglecting) corrections from departures from the LTE assumption. Nordlander et al. (2017) have claimed that on the lower RGB in metal-poor GCs abundance corrections for Al from optical and near-IR lines depend on the Al abundance, leading to a possible compression of the abundance scale. When the analysis is restricted to a more limited evolutionary phase, as the upper RGB in the present work, this effect should not be of concern. We interpolated the corrections for 1D models of their benchmark stars in their Table 1 and estimated that the NLTE Al abundance for a star with the average parameters in our sample (4442/1.42/–1.13/1.57) is only 0.06 dex larger than the LTE value. The NLTE corrections would be −0.09 and +0.06 dex for our coolest and warmest stars. These corrections are derived from a large number of Al lines from UV to IR. However, from Figs. 13 and 14 in Nordlander et al. (2017) it is possible to conclude that NLTE corrections for the abundances obtained only from the two lines used here are always less than about 0.1 dex. The same approximatively holds for the analysis by D’Orazi et al. and Marino et al. We preferred not to apply any correction for NLTE to be fully consistent with Al analysis in the other paper of this series. The impact on star-to-star comparison in NGC 2808 is negligible.
3.3. Errors
We again closely followed the approach used in Carretta et al. (2012c) to estimate star-to-star errors due to uncertainties in the adopted atmospheric parameters. We need to estimate the internal errors in atmospheric parameters and evaluate the sensitivity of abundances to the adopted parameters. Internal errors associated with the atmospheric parameters are simply taken from Carretta (2015). These errors were estimated as 5 K, 0.041 dex, 0.026 dex, and 0.08 kms−1 for T eff, log g, [A/H], and Vt , respectively (second line in Table 4). To evaluate the sensitivity of Al to changes in atmospheric parameters we considered star 7315, whose effective temperature (4459 K) is very close to the mean T eff = 4456 K of the sample. The analysis was then repeated by changing a single parameter by amounts given in the first line of Table 4 each time, whereas the others were fixed.
A second source of internal errors comes from errors in flux measurements. To evaluate this component we estimated photometric errors from the S/N of the spectra and from the width within each of the reference continuum and the in-line regions (and then the number of pixels used, see Carretta et al. 2012c). We then computed Al abundances with the adopted procedure, but using the new value of the Al line strength index that is the sum of the original value and its error. The comparison with original values provides the errors in [Al/Fe] due to flux measurement errors, listed in Table 3 for individual stars. On average, the impact of this source of error is +0.019 ± 0.001 dex (rms = 0.005 dex, from 86 stars).
The same approach was applied to one of the CN features used to estimate the CN abundance. The average error is +0.018 dex, which is a conservative estimate since final CN abundances were obtained using up to 18 features on average. The corresponding impact on Al abundances is 0.006 dex.
The star-to-star (internal) errors in the Al abundances are obtained by summing in quadrature all the contributions due to atmospheric parameters and flux measurements (both in Al and CN features): the typical internal error is 0.036 dex.
Sensitivities of Al to variations in the atmospheric parameters and to errors in fluxes and errors in abundances [A/Fe] for stars in NGC 2808.
4. Proton-capture elements in NGC 2808
The pattern of abundances of proton-capture elements among red giants in NGC 2808 is summarized in Figs. 3 and 4, where we plotted the abundance ratios derived here ([Al/Fe] and [CN/Fe]) as a function of proton-capture elements. The colour-coding follows the five groups defined by Carretta (2015) using Mg and Na abundances. These groups are the populations with primordial composition (P1, blue; P2, green), two groups with intermediate composition (I1, red; I2, orange), and finally a component with extremely modified composition (E, black).
 |
Fig. 3. Abundance ratios [Al/Fe] as a function of the proton-capture elements O, Na, Mg, Si in RGB stars of NGC 2808. Different colours indicate the five populations as defined in Carretta (2015) using the Mg-Na plane (population P1: blue, P2: green, I1: red, I2: orange, E: black). In each panel the star-to-star error bars are indicated. |
From these figures we see that the newly derived abundances nicely follow the overall pattern of the (anti-)correlations generated by the network of proton-capture reactions. Al is anti-correlated with species depleted in H-burning, such as O and Mg, and is correlated with Na, Si, and CN, whose abundances are enhanced in this nuclear processing. The same holds also for CN.
Four stars classified in the I1 group according to their Mg, Na abundances have [Al/Fe] values that are too low, which clearly shifts these stars to the P2 component. After discarding one of the continuum region in one star and the Al line at 8772 Å in another (due to spikes on the feature), there is no evident reason to doubt of the derived Al abundances. The position of these four stars in the Na–Mg plane (see Carretta 2015) is somewhat intermediate between the P2 and I1 group and it is possible that they should be associated with the former, although their Na values are on average as large as those of the other stars in the I1 component.
Even taking into account these possible outliers, there is a clear progression in the content of light elements among the subpopulations of stars detected in NGC 2808, as shown in Fig. 5, where we plotted the average values for the elements analysed in the present work, CN and Al. The mean values of species enhanced in proton-capture reactions increase when moving from the P1, P2 groups up to the highest values in the component E. The peak-to-valley difference in CN between P1 and E is not dramatically large; this difference is about 0.27 dex, although this range may be somewhat underestimated (see Sect. 3.1). But the average level of Al increases by a full 1.4 dex between the two populations. Allowing for the possibility that the four stars above are spuriously attributed to the I1 group, the trend is still present, and simply the rms scatter is reduced. The trends for CN and Al complete those observed in Carretta (2015) for O, Na, Mg, and Si. In Fig. 6 we plot the average values in the five populations of NGC 2808.
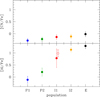 |
Fig. 5. Average values of the [CN/Fe] and [Al/Fe] abundance ratios in the five discrete groups in NGC 2808. The error bar is the rms scatter of the mean. The empty red circle represents the mean value for [Al/Fe] obtained by excluding the four stars with too low Al values (see text). |
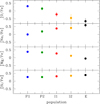 |
Fig. 6. As in Fig. 5 for O, Na, Mg, Si from Carretta (2015). In many cases the rms scatter is within the point symbol. |
As in Carretta (2015) we used the Student and Welch tests to check if the average values for the five groups are significantly different from each other. The average values for CN and Al are listed in Table 5 where we also report the mean values of O, Na, Mg, and Si from Carretta (2015). For each group combination, the two-tail probability value for the mean [Al/Fe] ratio never exceed 1.1 × 10−3 as they are usually much smaller or even zero. For CN, the probability values are generally low, indicating that mean values are actually different and not by mere random chance. The only exception is represented by the I1–I2 combination, in which a two-tail p = 0.63. This is graphically supported by Fig. 5, where the trend of the average CN seems to show a flattening, and by Fig. 4, where the two populations seem to be intermingled (orange and red points).
Anyway, it is clear that in NGC 2808 we see five discrete populations of RGB stars showing different levels of Al, increasing when other elements enhanced in proton-capture reactions simultaneously increase (and the corresponding depleted species decrease). To test whether this is a consequence of nucleosynthesis we simply checked whether the sum of Al+Mg remains constant, as it should if all the Al were produced by conversion of Mg in the Mg–Al cycle during H-burning at high temperature. The result is illustrated in Fig. 7, where the sum [(Al+Mg)/Fe] is plotted as a function of the metallicity, adopting the above colour coding for stars in each subpopulation. We found that the sum is constant: on average, +0.342 ± 0.004 dex, with σ = 0.047 dex (108 stars), to be compared with a total internal error of 0.068 dex in this sum. The production of Al is matched to a corresponding consumption of Mg and this result is only negligibly affected by the three outliers visible at low values in Fig. 7. These three objects cannot be explained by leakage from the Mg–Al cycle on 28Si (Karakas & Lattanzio 2003), since their Si abundance is high, but not the highest in our sample. The same holds for their [K/Fe] values (Mucciarelli et al. 2015), excluding that their position in Fig. 7 is due to neglecting effects of H-processing at very high temperatures.
 |
Fig. 7. Sum Al+Mg as a function of metallicity in the RGB stars in NGC 2808. The colour coding is as in previous figures for stars of different populations. Average internal errors are shown. |
Next, we examined the case in which a single class of polluters converting Mg into Al may be able to reproduce the abundance pattern of the five groups through a simple dilution model (see e.g. Carretta et al. 2009a, b). In this case, the abundances of individual stars are obtained by diluting the pure nuclearly processed matter of putative polluters with variable (increasing) fractions of unpolluted gas having primordial composition.
Results are shown in Fig. 8 for the elements whose abundances were derived in the present study: Al (upper panel) and CN (lower panel). Apparently, in both cases a simple dilution model seems to be a satisfactory match for all the five groups within the observed scatter. We note that the lower panel is actually a link between the O–N and the Mg–Al cycles, occurring a different temperatures, yet the CN–Mg anti-correlation is rather well reproduced.
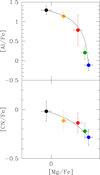 |
Fig. 8. Upper panel: average abundances of Al (this work) and Mg (from Carretta 2015) for the five subpopulations in NGC 2808. A simple dilution model is superimposed on the data. Error bars are rms scatter. Lower panel: the same for CN (from the present work) is shown. |
However, we caution that if the average abundances of the five populations lie along a dilution model, this is a necessary, but not sufficient condition. These plots are made with logarithmic quantities, whereas the linear quantities (the number of atoms of each species) actually vary, and this may give the impression of a good fit along a dilution curve. To verify this issue, we adopted the approach used in Carretta et al. (2012a). If a population/group with intermediate composition is obtained by diluting the material with extreme E composition with pristine gas (of P composition), then we should have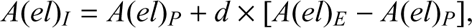 (1)
(1)
where d is the fraction of the material with E-like composition in the I component and A(el) is the number of atoms. In the scenario in which only one class of polluters is at work, the value d should be the same (within the errors) for all the involved elements, whatever pair of species we are considering. In particular, this must be true for pairs of elements involved in H-burning at different temperatures, such as Na–O, Mg–Al, and Al–Si.
We checked whether this happened for all the three components with intermediate composition (P2, I1, and I2), deriving the quantity d from all possible combinations. The results are listed in Table 6, where the dilution fraction for various elements are listed.
From this exercise we conclude that the fraction of material with E-like composition decreases along the sequence I2–I1–P2. This decrease is essentially what we are seeing when considering the average abundances in these three components (e.g. in Fig. 8). Moreover, by comparing the values for the individual species, we found that the d values are different beyond the associated errors. As for the much more simple case of NGC 6752, for which at least two classes of polluters were required, our findings show that the composition of the P2, I1, and I2 groups in NGC 2808 must be produced by different polluters. A simple dilution model with only a class of polluters does not seem to be enough to reproduce the observed pattern of the intermediate populations in NGC 2808.
Finally, we tried to link the information coming from our spectroscopic sample to what is derived on photometric grounds. In particular, we used the preliminary release of the HST UV Legacy programme GO-13297 (see Piotto et al. 2015), downloading the data for NGC 2808 from http://groups.dfa.unipd.it/ESPG/treasury.php. In fact, the filter combination (F275W, F336W, and F438W) used in that programme is particularly efficient in detecting variations in C, N, and O (see Piotto et al. 2015). Milone et al. (2015) employed this dataset, in combination with previous HST data, to study NGC 2808 and deduced the presence of five populations. The correlation between the photometrically and spectroscopically defined multiple population was discussed in Milone et al. (2015) and Carretta (2015), but we add more data.
Figure 9 shows the diagram obtained plotting the pseudocolour C 275,336,438 = F275W − 2 × F336W + F438W against F438W; the figure is very similar to what is shown in Marino et al. (2017, their Fig. 7) even if we did not apply any cut on photometric quality. We crossmatched the HST UV catalogue with ours and found 62 stars in common, 50 of which have all the three magnitudes. These are plotted in Fig. 9 using different colours, according to their spectroscopically defined population. Neglecting the brightest portion of the RGB, where this pseudocolour is no more efficient in separating the populations, the stars cluster along separate RGBs in which distinct populations fall on different RGBs.
 |
Fig. 9. Diagram using the pseudo-colour C 275,336,438 against F438W. The stars in our spectroscopic sample are plotted using larger, filled symbols and adopting the same colour scheme of previous figures (P1: blue, P2: green, I1: red, I2: orange, and E: black). |
Average abundances of CN, Al, and other proton-capture elements in the five groups in NGC 2808.
Dilution values for the components P2, I1, and I2.
5. Cluster analysis
More information can be inferred from the cumulative distributions of abundance ratios along the main anti-correlations among proton-capture elements, shown in Fig. 10.
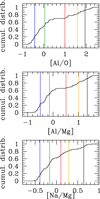 |
Fig. 10. From upper to lower cumulative distribution of the [Al/O], [Al/Mg], and [Na/Mg] abundance ratios in NGC 2808. The vertical lines are traced at the average values for the groups P1, P2, I1, I2, and E using the same colour coding as in previous figures (blue, green, red, orange, and black, respectively). |
Starting with the [Na/Mg] ratio (used by Carretta 2015 to classify the five groups), we plotted vertical lines at the position given by average values for the populations P1, P2, I1, I2, and E, using the same colour coding as before. The five average values bracket four regions for which the cumulative distribution is flat, i.e. the number of stars there does not increase. In other words, the mean values corresponding to the different subpopulations in NGC 2808 bracket gaps in the observed Na–Mg anti-correlation. The same also holds for the ratios [Al/Mg] and [O/Na].
We considered the Sarle bimodality coefficient (BC) for each combined pair of subsamples to quantify the reality of the gaps. These BCs were computed from the skewness and the excess kurtosis, both corrected for sample bias (SAS Institute Inc. 1990). The distributions are shown in the panels of Fig. 11. In each panel we also list the value of the BC.
 |
Fig. 11. Observed distributions along the Na–Mg, Al–Mg, Al–O, and O/Na anti-correlations for the subsamples P1+P2, P2+I1, I1+I2, and I2+E in NGC 2808. In each panel the value of the bimodality coefficient BC is labelled. |
When compared to the critical value 5/9 ∼ 0.555 expected for a uniform distribution, higher values point towards bimodality and lower values towards unimodality. Whereas using this test on the whole sample of stars available in NGC 2808 always indicates that all distributions are not unimodal, the results are more uncertain when splitting the total sample into subgroups that should bracket the gaps defined by [Na/Mg] in Carretta (2015). For example, this coefficient formally does not allow us to recognize the distribution P1–P2 in [Al/Mg], [O/Na], and [Al/O] as bimodal, even if the bimodality is clearly evident by eye for at least the first two (first row in Fig. 11, second and fourth panel). Hence, maybe this is not the best test to quantify the distribution of stars along the anti-correlations.
Next, we resort to cluster analysis using the k–means algorithm (Steinhaus 1956; MacQueen 1967) as implemented in the R statistical package (R Development Core Team 2011; http://www.R-project.org), as carried out in Carretta et al. (2012a, c). We began by selecting the same ratios [Na/Fe] and [Mg/Fe] used by Carretta (2015) to define the five discrete populations on the RGB in NGC 2808.
The algorithm retrieves five groups. Figure 12 is an objective quantification of the populations with distinct chemistry detected by Carretta (2015). The only difference is that four stars of the P2 group are now classified as P1 stars and three stars that were assigned by eye as P1 now move to the P2 group (compare this figure to Fig. 8 in Carretta 2015). The other populations are identical to those defined by eye in Carretta (2015). This is likely because the algorithm favours a subdivision based especially on Na, whose variation is much larger than that of Mg.
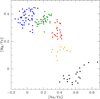 |
Fig. 12. Results of the cluster analysis using the k-means algorithm and the selected ratios [Na/Fe], [Mg/Fe]. |
However, for NGC 2808 we now have six proton-capture elements available, hence we tried a more robust cluster analysis using all stars with CN, O, Na, Mg, Al, and Si abundances. By using all the involved species, we found that only three main groups have robust justifications. These groups correspond essentially to the P, I, and E components as defined in Carretta et al. (2009a). However, the intermediate (I) and extreme (E) groups are not homogeneous, in abundance.
In order to obtain homogeneous populations the best subdivision is into six groups. Results are shown in Fig. 13, showing the relation between the six groups individuated by the k– means algorithm and the five components discussed so far. The colour coding is the same as in previous figures and refers to the five populations determined by Carretta (2015). Different symbols indicate the six components found by the cluster analysis. In general the correspondence is good, but there are exceptions. The homogeneous groups are essentially separated according to the PC1 component, which alone accounts for ∼82% of the variance. One possible way to view these results is that rather than a linear combination of two vectors, this amounts to a non-linear combination of a single vector (a combination of PC1 and PC2), that is the effect of one single physical process. Therefore, while numerically, by definition PC1 and PC2 are orthogonal, that is actually not the case from a physical point of view.
 |
Fig. 13. Results of the cluster analysis using the k-means algorithm only on stars with the full set of CN, O, Na, Mg, Al, and Si abundances. Colour coding is as in previous figures, whereas different symbols indicate the groups found by cluster analysis. |
6. Discussion and conclusions
In the present work we derived homogeneous Al abundances for 108 RGB stars in NGC 2808 along with estimates of the CN content in 89 giants. These elements join the large dataset of proton-capture elements obtained from spectra in this massive globular cluster, and both species nicely fit in the overall pattern of (anti)-correlations produced by the network of proton-capture reactions in H-burning at high temperature (Figs. 3 and 4). We found that Al abundances span an interval of almost 2 dex and are anti-correlated to the Mg abundances that, in turn, are depleted by almost 0.6 dex with respect to the typical overabundances present in metal-poor halo stars in most extreme cases.
The improved statistics allow us to conclude that a unique class of polluters is not enough to reproduce the entire set of anti-correlations among proton-capture elements CN, O, Na, Mg, Al, and Si. When ejecta from the most massive FG stars are mixed up with variable amount of pristine matter in a dilution model our data show that different polluters contribute to the formation of the discrete populations P2, I1, and I2, showing intermediate composition. This is in agreement with the observational constraints derived from Li abundances in lower RGB stars in NGC 2808 by D’Orazi et al. (2015). These authors found that all the Al poor, FG stars in their sample (corresponding to groups P1 and P2 in our nomenclature) are also Li rich. Among the SG Al-rich stars, aside from the extreme population that is devoid of Li, as expected from the high temperatures producing Al enhancement in the FG polluters, they also detected a sample of stars that have Li abundances similar to those of FG stars. About two-thirds of Al-rich stars are also Li rich and about one-third is Li poor. Since the lower and upper RGB stars are drawn from the same population, we should also expect that two-thirds of the combined samples of I1+I2+E stars are Li rich. These observations suggests that at least two different kinds of polluters were active in NGC 2808, one of which is able to produce some amount of fresh lithium.
A one-to-one comparison between the abundances of Li and the elements involved in the p-capture processes is hampered by the lack of stars in common between the present sample and that analysed by D’Orazi et al. However, these samples can be compared in some way using as a common ground the information from HS T photometry by Milone et al. (2015).
Using stars in common between our sample and the preliminary release of HS T photometry available to us (see Sect. 4), we reproduced the CNO two-colours diagram in Fig. 14, where we superimposed our stars, divided into the five chemical groups and the classification from photometry. From this figure and the discussion in Carretta (2015), it is straightforward to identify our P1 group with the group B of Milone et al. (2015). This group should have a normal He content (see also D’Antona et al. 2016). The P2 component coincides with the photometric group C, and the populations I1 and E can be identified with group D and E (Carretta 2015; Milone et al. 2015; D’Antona et al. 2016). The spectroscopic group I2 is not easily associated with a specific photometric group, but the spreads in the photometry exceed the analysis errors, and may even hide more subpopulations.
 |
Fig. 14. CNO-two-colour diagram (D’Antona et al. 2016; Milone et al. 2015: grey points). Larger filled circles are stars with our spectroscopic abundance determination, colour-coded according to the groups in Carretta (2015). Large black letters indicate the five photometric groups. Brown and cyan filled triangles are Li-rich and Li-poor stars from D’Orazi et al. (2015). |
We found that 10 stars from D’Orazi et al. (2015) also have all the required magnitudes to be plotted in Fig. 14. The 8 Lirich stars are distributed in the P1 group (2 stars, group B with Y = 0.278 in Milone et al.), the P2 group (4 stars, group C with Y = 0.280), and in the region populated by I1 and I2 groups (2 stars, group D with Y = 0.318). All estimates of the He mass fraction given in this section are from Milone et al. (2015). Taking into account the very limited sample, the number of Li-rich stars corresponds to a fraction 80 ± 28% and it is consistent with the above estimate of Li-rich stars. Two stars in this sample have moderately low Li abundances. One of these stars lies within the locus of the photometric group A (Y = 0.243), which has no counterpart in the spectroscopic sample, whereas the other star is in the E component (both spectroscopic and photometric groups, with Y = 0.367).
Summarizing, our new data confirm that stars along the RGB in NGC 2808 are segregated into the five distinct groups defined in Carretta (2015) using only the Mg, Na abundances. This is particularly evident in the Mg–Al anti-correlation. The Si–Al correlation (Fig. 3, lower right panel) mirrors the Si– Mg anti-correlation (see Carretta 2015, his Fig. 11) and confirms the existence in this cluster of the leakage from Mg to Si (Karakas & Lattanzio 2003) through a reaction only efficient at temperatures exceeding 65 MK (Arnould et al. 1999).
Together, the high values of Al and the large depletion in Mg reached in the component with the most extreme composition put strong constraints on the nature of possible polluters providing nuclearly processed matter. As discussed in Carretta (2014), in the FRMS scenario there is only a narrow time interval when such high inner temperatures are reached, just at the end of the main-sequence evolution of massive, rotating stars. However, in this phase also Na is destroyed, whereas this species reaches its highest value in the E component. D’Antona et al. (2016) have gone further and have stated that the observed Mg depletion completely rules out any scenario based on massive stars, either single or interacting binaries (de Mink et al. 2009).
On the other hand, even the AGB scenario seems to face several issues when compared to the observational data. Carretta (2014) already pointed out a possible inconsistency. The candidate polluters providing the maximum depletion in Mg are AGB stars with 5–6 M⊙ initial masses (D’Ercole et al. 2012), whose He content is however below the threshold required for the onset of a deep-mixing that is able to push oxygen abundances down to [O/Fe] ≃ −1 dex, as instead observed in very Mg-poor stars in NGC 2808.
How can these new data help to understand the formation scenario in this cluster? Recently, D’Antona et al. (2016) have proposed a temporal sequence to explain the complex pattern of multiple, and discrete, populations in NGC 2808. We sketched their scenario in Fig. 15.
 |
Fig. 15. Sketch of the temporal sequence proposed by D’Antona et al. (2016) to explain the discrete populations in NGC 2808. The dashed line indicates a chemical discontinuity between the photometric groups E and D owing to a sudden dilution with pristine matter. The ordinate is the time (in million years) since the first burst of star formation in the cluster. |
In their scenario the groups B and C share the same normal He content, but only group B is actually composed by first generation stars, which have typical abundances of halo stars. The C component is seen as one of the last formed in the cluster, some 90–110 Myr after the first burst of star formation. As a consequence, the action of the lowest mass AGB stars, i.e. those able to show the effect of third dredge-up episodes, is visible in this group through an enhanced abundance of N, which is higher by 0.4–0.7 dex than the N content of group B. This large difference in N provides the different location of groups B and C in the CNO-two-colours diagram (see D’Antona et al. 2016) that we reproduced in Fig. 14.
However, there seems to be no correspondence for this difference in our spectroscopic data for groups P1 and P2. If we read from the generalised histogram of δS CN in NGC 2808 (Fig. 6 in Norris & Smith 1983) the values corresponding to the most CN-poor populations and we use the calibration in Fig. 2 to convert the values to [CN/Fe] ratios onto our present scale, we find a difference of only 0.13 dex between components P1 and P2, leaving aside an arbitrary zero point due to the unknown C abundances. Moreover, from Table 5, on average the two groups differ by 0.06 dex only in their CN content.
From spectroscopy, apparently we do not find a large difference in CN between the populations with the most primordial composition. This finding is very puzzling since the photometric He-normal, N-rich group is numerically significant with an estimated fraction 26.4 ± 1.2% (Marino et al. 2015).
Turning to the search for a general scenario, the present results imply that in NGC 2808 different classes of polluters were likely at work, producing a syncopated, discrete distribution of different populations (at least five, but probably more) along the main (anti)-correlations among the proton-capture elements.
Our observations, therefore, tend to exclude massive stars as responsible for most of the intermediate populations in NGC 2808, since these stars may only act at the very beginning of the cluster evolution in the first few million years, and moreover they cannot produce the lithium observed in SG stars by D’Orazi et al. (2015). After the massive SN II went off, clearing the gas reservoir, the only way to produce more than two discrete populations in this scenario would be to periodically inject new and variable amounts of pristine, unpolluted gas to be mixed. However, the gas with primordial composition would find no more polluted gas after the SN II epoch. It seems difficult to justify more than two discrete populations within the FRMS framework. However, our data cannot exclude that the FRMS were responsible for the first polluted SG in this cluster.
In the presence of more than two, and discrete, stellar populations in GCs, the AGB scenario has the advantage of providing a range of possibly contributing stellar masses. In turn this offers different processed yields released at (even very) different epochs and with different temperatures involved. Although inconsistencies related to the nucleosynthesis still exist, as outlined above this scenario provides a natural way to explain SG stars in which we see the outcome of the complete Mg–Al–Si, a SG produced by less massive polluters in which the Mg–Al cycle is active, but without touching on Si, down to a SG, in which we only see O depletion and Na enhancement, generated from still less massive stars. Moreover, in this framework it is relatively easy to account for the observational constraints derived from lithium, since not all the AGB stars are good producers of Li.
D’Antona et al. (2016) have exploited these properties by combining a temporal sequence of star formation episodes (sketched in Fig. 15) with dilution events. By tuning star formation bursts and dilution, these authors showed how the chemical composition of the five groups individuated in NGC 2808 may be reproduced. However, the conflicting evidence concerning the N abundances as derived from spectroscopy and photometry possibly uncovered in our present work still remains an open issue.
Recently, Bekki et al. (2017) have claimed that in the scenario by D’Antona et al. no physical mechanism was clearly introduced to stop and restart the star formation and gas accretion several times. Bekki et al. have proposed a model to interrupt the different bursts of star formation and were able to reproduce up to five to six discrete populations using a time-evolving initial mass function. On the other hand, their model does not predict chemical evolution independently, but simply adopts AGB yields from Ventura & D’Antona (2009) and Ventura et al. (2011).
While it is desirable that more and more physically self-consistent chemo-dynamical models are produced, it is also clear that the peculiar globular cluster NGC 2808 is one of the best (and toughest) benchmarks to test any scenario for the origin and evolution of multiple populations in GCs.
Acknowledgments
This research has made use of the SIMBAD database (in particular Vizier), operated at CDS, Strasbourg, France, of the NASA’s Astrophysical Data System, and TOPCAT (http://www.starlink.ac.uk/topcat/). This work made use of R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org.
IRAF is the Image Reduction and Analysis Facility, a general purpose software system for the reduction and analysis of astronomical data. IRAF is written and supported by the IRAF programming group at the National Optical Astronomy Observatories (NOAO) in Tucson, Arizona. NOAO is operated by the Association of Universities for Research in Astronomy (AURA), Inc. under cooperative agreement with the National Science Foundation.
References
- Arnould, M., Goriely, S., & Jorissen, A. 1999, A&A, 347, 572 [NASA ADS] [Google Scholar]
- Bastian, N., & Lardo, C. 2015, MNRAS, 453, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., & Lardo, C. 2017, ArXiv e-prints [arXiv:1712.01286] [Google Scholar]
- Bastian, N., Cabrera-Ziri, I., & Salaris, M. 2015, MNRAS, 449, 3333 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., Jeřábková, T., & Kroupa, P. 2017, MNRAS, 471, 2242 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Carretta, E., D’Orazi, V., et al. 2017, A&A, 607, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briley, M. M., Cohen, J. G., & Stetson, P. B. 2002, AJ, 123, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- Briley, M. M., Cohen, J. G., & Stetson, P. B. 2004a, AJ, 127, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Briley, M. M., Harbeck, D., Smith, G. H., & Grebel, E. K. 2004b, AJ, 127, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, R. D., Croke, B. F. W., Bell, R. A., Hesser, J. E., & Stathakis, R. A. 1998, MNRAS, 298, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2013, A&A, 557, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E. 2014, ApJ, 795, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2015, ApJ, 810, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009b, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., D’Orazi, V., & Lucatello, S. 2009c, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., & Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., D’Orazi, V., & Lucatello, S. 2011, A&A, 535, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., Lucatello, S., & D’Orazi, V. 2012a, ApJ, 750, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., D’Orazi, V., Gratton, R. G., & Lucatello, S. 2012b, A&A, 543, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Gratton, R. G., Bragaglia, A., D’Orazi, V., & Lucatello, S. 2012c, A&A, 550, A34 [Google Scholar]
- Cohen, J. G., Briley, M. M., & Stetson, P. B. 2002, AJ, 123, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Briley, M. M., & Stetson, P. B. 2005, AJ, 130, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., Vesperini, E., D’Ercole, A., et al. 2016, MNRAS, 458, 2122 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel C., Prantzos, N., & Ekstrom, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denisenkov, P. A., & Denisenkova, S. N. 1989, A.Tsir., 1538, 11 [Google Scholar]
- D’Ercole, A., D’Antona, F., Ventura, P., Vesperini, E., & McMillan, S. L. W. 2010, MNRAS, 407, 854 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- D’Ercole, A., D’Antona, F., & Vesperini, E. 2011, MNRAS, 415, 1304 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- D’Ercole, A., D’Antona, F., Carini, R., Vesperini, E., & Ventura, P. 2012, MNRAS, 423, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrovolskas, V., Kučinskas, A., Bonifacio, P. et al. 2014, A&A, 565, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Orazi, V., Lucatello, S., Gratton, R. G., et al. 2010, ApJ, 713, L1 [NASA ADS] [CrossRef] [Google Scholar]
- D’Orazi, V., Gratton, R. G., Angelou, G. C. et al. 2015, MNRAS, 449, 4038 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G. 1988, Rome Obs. Preprint Ser., 29 [Google Scholar]
- Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E. & Bragaglia, A., 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
- Harbeck, D., Smith, G. H., & Grebel, E. K. 2003, AJ, 125, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Kraft, R. P., Pilachowski, C. A., et al. 2005, PASP, 117, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2003, PASA, 20, 279 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kraft, R. P. 1994, PASP, 106, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., Sneden, C., Smith, G. H, et al. 1997, AJ, 113, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, CD-ROM 13 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Langer, G. E., Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Lardo, C., Battaglia, G., Pancino, E., et al. 2016, A&A, 585, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacQueen, J. B. 1967, Mathematical Statistics and Probability (California: University of California Press.), 281 [Google Scholar]
- Marino, A. F., Milone, A. P., Karakas, A. I. et al. 2015, MNRAS, 450, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, A. F., Milone, A. P., Yong, D. et al. 2017, ApJ, 843, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, S., Martell, S .L., Shetrone, M. et al. 2015, AJ, 149, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A., Piotto, G., Bedin, L. et al. 2012, ApJ, 744, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Marino, A. F., Piotto, G. et al. 2013, ApJ, 767, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Marino, A. F., Piotto, G. et al. 2015, ApJ, 808, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Bellazzini, M., Merle, T., et al. 2015, ApJ, 801, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlander, T., Lind, K. 2017, A&A, 607, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, J., & Smith, G. H. 1983, ApJ, 275, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Piotto, G., Milone, A. P., & Bedin, L. R. 2015, AJ, 149, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., & Charbonnel, C. 2006, A&A, 458, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., Charbonnel, C., & Iliadis, C. 2017, A&A, 608, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinhaus, H. 1956, Bull. Acad. Polon. Sci. 4, 801 [Google Scholar]
- Ventura, P., & D’Antona, F. 2009, A&A, 499, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Carini, R., D’Antona, F. 2011, MNRAS, 415, 3865 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Geisler, D., Carraro, G., Moni Bidin, C., & Munoz, C. 2013, ApJ, 778, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, J. C., Sneden, C., & Truran, J. W .Jr 1989, ARA&A, 27, 279 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Sensitivities of Al to variations in the atmospheric parameters and to errors in fluxes and errors in abundances [A/Fe] for stars in NGC 2808.
Average abundances of CN, Al, and other proton-capture elements in the five groups in NGC 2808.
All Figures
 |
Fig. 1. S/Ns from the ESO FLAMES-GIRAFFE pipeline as a function of the V magnitudes for our sample in NGC 2808 |
| In the text | |
 |
Fig. 2. Comparison of our estimates of [CN/Fe] in NGC 2808 with the cyanogen excesses derived in Norris & Smith (1983) for 6 stars in common. |
| In the text | |
 |
Fig. 3. Abundance ratios [Al/Fe] as a function of the proton-capture elements O, Na, Mg, Si in RGB stars of NGC 2808. Different colours indicate the five populations as defined in Carretta (2015) using the Mg-Na plane (population P1: blue, P2: green, I1: red, I2: orange, E: black). In each panel the star-to-star error bars are indicated. |
| In the text | |
 |
Fig. 4. As in Fig. 3 for the derived [CN/Fe] abundance ratios. |
| In the text | |
 |
Fig. 5. Average values of the [CN/Fe] and [Al/Fe] abundance ratios in the five discrete groups in NGC 2808. The error bar is the rms scatter of the mean. The empty red circle represents the mean value for [Al/Fe] obtained by excluding the four stars with too low Al values (see text). |
| In the text | |
 |
Fig. 6. As in Fig. 5 for O, Na, Mg, Si from Carretta (2015). In many cases the rms scatter is within the point symbol. |
| In the text | |
 |
Fig. 7. Sum Al+Mg as a function of metallicity in the RGB stars in NGC 2808. The colour coding is as in previous figures for stars of different populations. Average internal errors are shown. |
| In the text | |
 |
Fig. 8. Upper panel: average abundances of Al (this work) and Mg (from Carretta 2015) for the five subpopulations in NGC 2808. A simple dilution model is superimposed on the data. Error bars are rms scatter. Lower panel: the same for CN (from the present work) is shown. |
| In the text | |
 |
Fig. 9. Diagram using the pseudo-colour C 275,336,438 against F438W. The stars in our spectroscopic sample are plotted using larger, filled symbols and adopting the same colour scheme of previous figures (P1: blue, P2: green, I1: red, I2: orange, and E: black). |
| In the text | |
 |
Fig. 10. From upper to lower cumulative distribution of the [Al/O], [Al/Mg], and [Na/Mg] abundance ratios in NGC 2808. The vertical lines are traced at the average values for the groups P1, P2, I1, I2, and E using the same colour coding as in previous figures (blue, green, red, orange, and black, respectively). |
| In the text | |
 |
Fig. 11. Observed distributions along the Na–Mg, Al–Mg, Al–O, and O/Na anti-correlations for the subsamples P1+P2, P2+I1, I1+I2, and I2+E in NGC 2808. In each panel the value of the bimodality coefficient BC is labelled. |
| In the text | |
 |
Fig. 12. Results of the cluster analysis using the k-means algorithm and the selected ratios [Na/Fe], [Mg/Fe]. |
| In the text | |
 |
Fig. 13. Results of the cluster analysis using the k-means algorithm only on stars with the full set of CN, O, Na, Mg, Al, and Si abundances. Colour coding is as in previous figures, whereas different symbols indicate the groups found by cluster analysis. |
| In the text | |
 |
Fig. 14. CNO-two-colour diagram (D’Antona et al. 2016; Milone et al. 2015: grey points). Larger filled circles are stars with our spectroscopic abundance determination, colour-coded according to the groups in Carretta (2015). Large black letters indicate the five photometric groups. Brown and cyan filled triangles are Li-rich and Li-poor stars from D’Orazi et al. (2015). |
| In the text | |
 |
Fig. 15. Sketch of the temporal sequence proposed by D’Antona et al. (2016) to explain the discrete populations in NGC 2808. The dashed line indicates a chemical discontinuity between the photometric groups E and D owing to a sudden dilution with pristine matter. The ordinate is the time (in million years) since the first burst of star formation in the cluster. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


