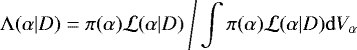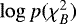| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 4 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201732461 | |
| Published online | 08 June 2018 | |
Bayesian model checking: A comparison of tests
Astrophysics Group, Blackett Laboratory, Imperial College London,
Prince Consort Road,
London SW7 2AZ, UK
e-mail: l.lucy@imperial.ac.uk
Received:
14
December
2017
Accepted:
7
February
2018
Two procedures for checking Bayesian models are compared using a simple test problem based on the local Hubble expansion. Over four orders of magnitude, p-values derived from a global goodness-of-fit criterion for posterior probability density functions agree closely with posterior predictive p-values. The former can therefore serve as an effective proxy for the difficult-to-calculate posterior predictive p-values.
Key words: methods: statistical / binaries: general
© ESO 2018
1 Introduction
In a recent paper (Lucy 2018; L18), straightforward procedures are proposed for Bayesian model checking.
Because all Bayesian inferences derive from the posterior probability density function Λ(α|D), where α is the parameter vector and D is the data, these tests check the global goodness-of-fit (GOF) to D provided by Λ. The proposed checks take the form of p-values closely analogous to those familiar in frequentist analyses. The first test derives from the 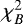 statistic (L18, Appendix C) for uncorrelated measurement errors. The second test derives from the
statistic (L18, Appendix C) for uncorrelated measurement errors. The second test derives from the 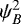 statistic (L18, Appendix C.1) for correlated measurement errors.
statistic (L18, Appendix C.1) for correlated measurement errors.
The need for readily-applied Bayesian model checking procedures has recently been persuasively ponted out by Ford - see Sect. 4.1 in Fischer et al. (2016). Ford attributes the frequent neglect of model checking by Bayesians to the absence of a “neat and tidy” test criterion for Bayesian analyses, in contrast to the χ2 criterion for frequentist analyses. For Bayesian model checking, Ford recommends the book by Gelman et al. (2013), which advocates posterior predictive checks.
In Sect. 6.4 of L18, a numerical experiment is briefly reported in which p-values from posterior predictive checking are compared to those derived from the same data with the 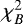 statistic. Given the importance of establishing the merits of the simpler approach provided by the
statistic. Given the importance of establishing the merits of the simpler approach provided by the 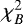 statistic, this short paper presents the numerical experiment in some detail.
statistic, this short paper presents the numerical experiment in some detail.
2 Bayesian p-values
In this section, the basics of the p-values to be compared are stated.
2.1 Posterior predictive p-value
On the assumption that χ2 is an appropriate test quantity - other possibilities are discussed in Gelman et al. (2013), the steps required to obtain the posterior predictive p-value are as follows:
- 1)
Compute the posterior probability density function, given by
where π is the prior, and  , the likelihood, is given by
, the likelihood, is given by
![\begin{equation*} {\cal L} (\alpha|D) = Pr(D|\alpha) \propto \exp[ - \frac{1}{2} \: \chi^{2}(\alpha|D) ]. \end{equation*}](/articles/aa/full_html/2018/06/aa32461-17/aa32461-17-eq7.png) (2)
(2)
- 2)
Randomly select a point α′ from the posterior density Λ(α|D).
- 3)
Compute a simulated data set D′ at α′ by randomly sampling Pr(D|α′).
- 4)
Compute and record the values of χ2(α′|D′) and χ2(α′|D).
- 5)
Repeat steps 2) to 5)
 times.
times.
The resulting Bayesian p-value is then
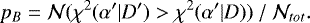 (3)
(3)
2.2 p-value from the 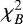 statistic
statistic
Following earlier work (Lucy 2016; L16) on the statistical properties of the posterior mean of χ2 , the general form of the 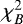 statistic is (Appendix C in L18)
statistic is (Appendix C in L18)
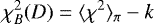 (4)
(4)
where k is the number of parameters and
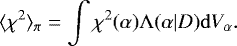 (5)
(5)
The p-value corresponding to the 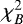 statistic is derived from the χ2 distribution with ν = n − k degrees of freedom, where n is the number of measurements. Specifically,
statistic is derived from the χ2 distribution with ν = n − k degrees of freedom, where n is the number of measurements. Specifically,
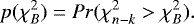 (6)
(6)
The theoretical basis of this p-value is as follows: in the majority of astronomical applications of Bayesian methods, the priors are weak and non-informative. Typically, π(α) defines a box in α-space representing a search volume that the investigator is confident includes all points α with significant likelihood. In consequence, a weak prior has neglible effect on the posterior density Λ and therefore also on any resulting inferences.
In the weak prior limit, Eq. (1) simplifies to
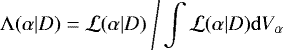 (7)
(7)
and the resulting posterior mean of χ2 is written as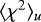 .
.
Now, in Appendix A of L16, it is proved that, for linearity in α and normally-distributed measurement errors,
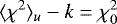 (8)
(8)
where 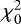 is the minimum value of χ2 (α|D). Since, under the stated assumptions, the minimum-χ2 solution
is the minimum value of χ2 (α|D). Since, under the stated assumptions, the minimum-χ2 solution 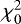 has a
has a 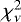 distribution with ν = n − k degrees of freedom, it follows that, with the extra assumption of a weak prior, the statistic
distribution with ν = n − k degrees of freedom, it follows that, with the extra assumption of a weak prior, the statistic 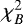 defined in Eq. (4) is distributed as
defined in Eq. (4) is distributed as 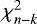 . This is the theoretical basis of the p-value given in Eq. (6).
. This is the theoretical basis of the p-value given in Eq. (6).
2.3 p-value from the 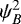 statistic
statistic
The 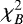 statistic of Sect. 2.2 is appropriate when the measurement errors are uncorrelated. When errors are correlated, χ2 (α|D) is replaced by (see Appendix C.1 in L18)
statistic of Sect. 2.2 is appropriate when the measurement errors are uncorrelated. When errors are correlated, χ2 (α|D) is replaced by (see Appendix C.1 in L18)
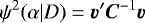 (9)
(9)
where C is the covariance matrix and v is the vector of residuals. The statistic ψ2 reduces to χ2 when the off-diagonal elements of C−1 are zero – i.e., no correlations.
By analogy with the statistic 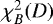 , a statistic
, a statistic 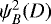 is derived from the posterior mean of ψ2. Specifically,
is derived from the posterior mean of ψ2. Specifically,
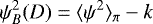 (10)
(10)
with corresponding p-value
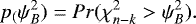 (11)
(11)
The theoretical basis for this p-value is essentially identical to that for the p-value derived from 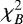 . If we have linearity in α and normally-distributed errors, then in the weak prior limit
. If we have linearity in α and normally-distributed errors, then in the weak prior limit
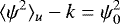 (12)
(12)
and 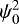 is distributed as
is distributed as 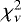 with ν = n − k degrees of freedom.
with ν = n − k degrees of freedom.
Note that posterior predictive p-values (Sect. 2.1) can similarly be generalized to treat correlated measurement errors. The quantity ψ2 replaces χ2 , and the random sampling to create simulated data sets can be accomplished with a Cholesky decompostion of the covariance matrix (e.g., Gentle 2009).
3 Test model
A simple 1-D test model is now defined. This allows numerous simulated data sets to be created so that the p-values computed according to Sects. 2.1 and 2.2 can be compared and any differeces established with high statistical confidence.
3.1 Hubble expansion
The null hypothesis is that the local Universe is undergoing an isotropic, cold Hubble expansion with Hubble parameter h0 = 70 km s−1 Mpc−1. Moreover throughout the local Universe there exists a population of perfect standard candles of absolute bolometric magnitude M = −19.0. Finally, we suppose that the redshifts z of these standard candles are measured exactly, but that their apparent bolometric magnitudes m have normally-distributed measurement errors with σm = 0.3 mag.
3.2 Ideal samples
In order to test p-values when the null hypothesis is correct, we need data sets consistent with the above description of the Hubble flow.
We define the local Universe as extending to zmax = 0.2, so that to a good approximation the geometry is Euclidean. If we suppose the standard candles to be uniformly distributed in space, a sample {zi} is created with the formula
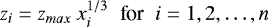 (13)
(13)
where the xi are independent random numbers ∈ (0, 1). The distances of these n standard candles are
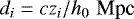 (14)
(14)
and their measured apparent bolometric magnitudes are
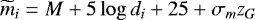 (15)
(15)
where the zG are independent gaussian variates from 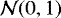 .
.
The n pairs 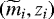 comprise a data set D from which the posterior probability density Λ(h|D) of the Hubble parameter h can be inferred. Moreover, the global GOF between Λ(h|D) and D can be tested with the p-values of Sects. 2.1 and 2.2.
comprise a data set D from which the posterior probability density Λ(h|D) of the Hubble parameter h can be inferred. Moreover, the global GOF between Λ(h|D) and D can be tested with the p-values of Sects. 2.1 and 2.2.
3.3 Imperfect samples
In order to test p-values when the null hypothesis is false, we need to modify either the model or the data. If we continue to make inferences based on the Hubble flow defined in Sect. 3.1, we can introduce a violation of the null hypothesis by contaminating the data sample with an unrecognized second class of standard candles with a different absolute bolometric magnitude. Thus the data set D now comprises n1 pairs 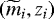 with
with 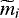 given by Eq. (15) and n2 pairs
given by Eq. (15) and n2 pairs 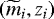 with
with 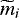 given by
given by
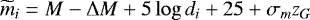 (16)
(16)
and where n = n1 + n2. Thus, the sample is now contaminated with a second population of standard candles that are brighter by Δ M magnitudes. The investigator is unaware of this, and so carries out a Bayesian analysis assuming an ideal sample.
4 Comparison of p-values
The Bayesian p-values defined in Sect. 2 are now computed for simulated data samples derived as described in Sect. 3.
 |
Fig. 1 Comparison of p-values. For J = 200 ideal samples Dj, |
4.1 Null hypothesis correct
In order to compare p-values in this case, J independent ideal samples Dj are created as described in Sect. 3.2, and then p-values for each Dj computed as described in Sects. 2.1 and 2.2.
With a constant prior π(h) in the interval (h1, h2) with h1 = 64 and h2 = 76 km s−1 Mpc−1, the posterior density Λ(h|Dj) is obtained from Eq. (1) with the scalar h replacing the vector α.
The posterior predictive p-value for Dj is computed as described in Sect. 2.1. First, a value h′ is derived byrandomly sampling Λ(h, Dj). This is achieved by solving the equation
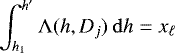 (17)
(17)
where xℓ is a random number ∈ (0, 1). Second, an ideal sample D′ for Hubble parameter h′ is computed according to Sect. 3.2. Third, the GOF values χ2 (h′|D′) and χ2 (h′|Dj) are computed, where
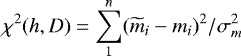 (18)
(18)
where the predicted apparent bolometric magnitude is
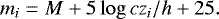 (19)
(19)
These steps are repeated 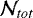 times with independent random numbers xℓ in Eq. (17). The posterior predictive p-value for the ideal sample Dj is then given by Eq. (3).
times with independent random numbers xℓ in Eq. (17). The posterior predictive p-value for the ideal sample Dj is then given by Eq. (3).
The corresponding p-value for Dj from the 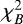 statistic is given by Eq. (4), where
statistic is given by Eq. (4), where
 (20)
(20)
with χ2(h, D) from Eq. (18).
The calculations described in Sects. 4.1 and 4.2 are carried out for J = 200 ideal samples Dj , with Dj comprising n = 200 pairs 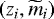 . In calculating posterior predictive p-values, we take
. In calculating posterior predictive p-values, we take  randomly selected Hubble parameters h′ for each Dj in order to achieve high precision for pB.
randomly selected Hubble parameters h′ for each Dj in order to achieve high precision for pB.
The results are plotted in Fig. 1. This reveals superb agreement between the two p-values with no outliers. The mean value of |Δlog p| = 2.3 × 10−3 confirms that there is almost exact agreement. Accordingly, this experiment indicates that the readily-calculated 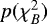 is an almost exact proxy for the posterior predictive p-value pB , the calculation of which is undoubtedly cumbersome.
is an almost exact proxy for the posterior predictive p-value pB , the calculation of which is undoubtedly cumbersome.
 |
Fig. 2 Comparison of p-values for imperfect samples. Each imperfect sample contains 180 standard candles of magnitude M and 20 of magnitude M −ΔM with Δ M = 0.5. |
 |
Fig. 3 p-values for imperfect samples. Each imperfect sample contains 180 standard candles of magnitude M and 20 of magnitude M −ΔM. For each ΔM, the p values are computed for 200 independent samples. |
4.2 Null hypothesis false
In order to compare p-values when p≲0.001, J = 200 independent imperfect samples Dj are created as described in Sect. 3.3. Again  and n = 200, but now n =n1 + n2, with n1 = 180 perfect standard candles and n2 = 20 belonging to a second population brighter by ΔM = 0.5 mag. With these changes, the calculations described above are repeated.
and n = 200, but now n =n1 + n2, with n1 = 180 perfect standard candles and n2 = 20 belonging to a second population brighter by ΔM = 0.5 mag. With these changes, the calculations described above are repeated.
The results are plotted in Fig. 2. Because the null hypothesis is false, p-values < 0.01 occur frequently, so that the comparison provided by Fig. 1 now extends to p≲10−4. However, at these small p-values, the values of pB are subject to noticeable Poisson noise even with  . Because of this, |Δlog p| = 3.2 × 10−2, somewhat larger than in Sect. 4.1 but neverthless again confirming the excellent agreement between the two p-values.
. Because of this, |Δlog p| = 3.2 × 10−2, somewhat larger than in Sect. 4.1 but neverthless again confirming the excellent agreement between the two p-values.
In Fig. 3, the behavior of the p-values derived fromthe 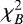 statistic as a function of ΔM is plotted. With increasing ΔM, the points shift to smaller p-values, increasing the likelihood that the investigator will conclude that the Bayesian model is suspect.
statistic as a function of ΔM is plotted. With increasing ΔM, the points shift to smaller p-values, increasing the likelihood that the investigator will conclude that the Bayesian model is suspect.
5 Conclusion
The aim of this paper is to investigate the performance of a recenly proposed global GOF criterion 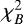 for posterior probability densities functions. To do this, a toy model of the local Hubble expansion is defined (Sect. 3) for which both ideal (Sect. 3.2) and flawed (Sect. 3.3) data samples can be created . The p-values derived for such samples from
for posterior probability densities functions. To do this, a toy model of the local Hubble expansion is defined (Sect. 3) for which both ideal (Sect. 3.2) and flawed (Sect. 3.3) data samples can be created . The p-values derived for such samples from 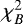 are then compared to the p-values obtained with the well-established procedure of posterior predictive checking. The two p-values are found to be in close agreement (Figs. 1 and 2) throughout the interval (0.0001, 1.0), thus covering the range of p-values expected when a Bayesian model is supported (p≳0.01) to those when the model is suspect (p≲0.01).
are then compared to the p-values obtained with the well-established procedure of posterior predictive checking. The two p-values are found to be in close agreement (Figs. 1 and 2) throughout the interval (0.0001, 1.0), thus covering the range of p-values expected when a Bayesian model is supported (p≳0.01) to those when the model is suspect (p≲0.01).
Because carrying out a posterior predictive check is cumbersome or even infeasible, the p-value derived from 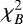 can serve asan effective proxy for posterior predictive checking. Of course, this recommendation derives from just one statistical experiment. Other investigators may wish to devise experiments relevant to different areas of astronomy.
can serve asan effective proxy for posterior predictive checking. Of course, this recommendation derives from just one statistical experiment. Other investigators may wish to devise experiments relevant to different areas of astronomy.
References
- Fischer, D. A., Anglada-Escude, G., Arriagada, P., et al. 2016, PASP, 128, 6001 [Google Scholar]
- Gelman, A., Carlin, J. B., Stern, H. S., et al. 2013, Bayesian Data Analysis (Boca Raton, FL: CRC Press) [Google Scholar]
- Gentle, J. E. 2009, Computational Statistics (New York: Springer) [CrossRef] [Google Scholar]
- Lucy, L. B. 2016, A&A, 588, A19 (L16) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2018, A&A, in press, DOI: 10.1051/0004-6361/201732145 (L18) [Google Scholar]
All Figures
 |
Fig. 1 Comparison of p-values. For J = 200 ideal samples Dj, |
| In the text | |
 |
Fig. 2 Comparison of p-values for imperfect samples. Each imperfect sample contains 180 standard candles of magnitude M and 20 of magnitude M −ΔM with Δ M = 0.5. |
| In the text | |
 |
Fig. 3 p-values for imperfect samples. Each imperfect sample contains 180 standard candles of magnitude M and 20 of magnitude M −ΔM. For each ΔM, the p values are computed for 200 independent samples. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.