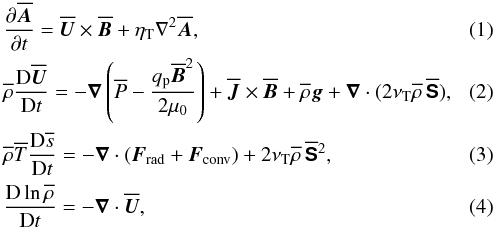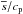| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201730421 | |
| Published online | 23 January 2018 | |
Spontaneous flux concentrations from the negative effective magnetic pressure instability beneath a radiative stellar surface
1 DSM/IRFU/SAp, CEA-Saclay and UMR AIM, CEA-Université Paris 7, 91191 Gif-sur-Yvette, France
e-mail: barbara.perri@cea.fr
2 JILA and Department of Astrophysical and Planetary Sciences, University of Colorado, Boulder, CO 80303, USA
3 Department of Astronomy, AlbaNova University Center, Stockholm University, 10691 Stockholm, Sweden
4 Nordita, KTH Royal Institute of Technology and Stockholm University, 10691 Stockholm, Sweden
5 Laboratory for Atmospheric and Space Physics, University of Colorado, Boulder, CO 80303, USA
Received: 11 January 2017
Accepted: 19 October 2017
Context. The formation of sunspots requires the concentration of magnetic flux near the surface. The negative effective magnetic pressure instability (NEMPI) might be a possible mechanism for accomplishing this, but it has mainly been studied in simple systems using an isothermal equation of state without a natural free surface.
Aims. We study NEMPI in a stratified Cartesian mean-field model where turbulence effects are parameterized. We use an ideal equation of state and include radiation transport, which establishes selfconsistently a free surface.
Methods. We use a Kramers-type opacity with adjustable exponents chosen such that the deeper layers are approximately isentropic. No convection is therefore possible in this model, allowing us to study NEMPI with radiation in isolation. We restrict ourselves to two-dimensional models. We use artificially enhanced mean-field coefficients to allow NEMPI to develop, thereby making it possible to study the reason why it is much harder to excite in the presence of radiation.
Results. NEMPI yields moderately strong magnetic flux concentrations a certain distance beneath the surface where the optical depth is unity. The instability is oscillatory and in the form of upward traveling waves. This seems to be a new effect that has not been found in earlier models without radiative transport. The horizontal wavelength is about ten times smaller than what has previously been found in more idealized isothermal models.
Conclusions. In our models, NEMPI saturates at field strengths too low to explain sunspots. Furthermore, the structures appear too narrow and too far beneath the surface to cause significant brightness variations at the radiative surface. We speculate that the failure to reproduce effects resembling sunspots may be related to the neglect of convection.
Key words: radiative transfer / hydrodynamics / Sun: atmosphere / sunspots
© ESO, 2018
1. Introduction
Sunspots are a highly intermittent manifestation of strong magnetic flux concentrations at the solar surface. The underlying magnetic fields are produced by hydromagnetic turbulence in the convection zone beneath the surface (Brun et al. 2004; Brown et al. 2011; Käpylä et al. 2012a; Augustson et al. 2015). Numerous simulations of turbulence and turbulent convection have displayed such magnetic field production by a dynamo process (Brandenburg & Subramanian 2005). This alone, however, does not explain the occasional concentration into spots. On the other hand, more realistic simulations that include the effects of strong density stratification near the surface, as well as radiation and ionization, have been able to demonstrate the appearance of magnetic spots (Stein & Nordlund 2012). Furthermore, it is known that strong density stratification can lead to a large-scale instability of an initially unstructured random magnetic field (Kleeorin et al. 1989, 1990). This instability leads to magnetic flux concentrations and even magnetic spots (Brandenburg et al. 2013; Warnecke et al. 2013) through the negative effective magnetic pressure instability (NEMPI). NEMPI has been associated with sunspot formation by Kleeorin et al. (1995, 1996), following a series of earlier work on its theoretical foundations (Kleeorin et al. 1993; Kleeorin & Rogachevskii 1994; Rogachevskii & Kleeorin 2007).
Numerical simulations have also displayed types of magnetic flux concentrations that are not straightforwardly associated with NEMPI. This tends to be the case when the magnetic field is produced by a large-scale dynamo some distance beneath the surface (Mitra et al. 2014; Jabbari et al. 2015, 2016). Nevertheless, also in those cases, strong stratification was shown to be essential, as has been demonstrated by comparing with weakly stratified cases.
In the case of NEMPI, the underlying instability can well be modeled using mean-field magnetohydrodynamics, where the negative effective magnetic pressure is parameterized in terms of the mean magnetic field; see Brandenburg et al. (2016) for a review. In some of those cases there is good quantitative agreement between direct numerical simulations (DNS) and mean field simulations (MFS), as has been demonstrated in several papers (Kemel et al. 2013; Losada et al. 2013).
The main difference between MFS and DNS is the inclusion of the parameterization of the small-scale unresolved motions 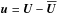 and magnetic fields
and magnetic fields 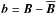 in the MFS. Here, the overbar denotes a suitably defined average, which, in practice, could be a spatial average. The evolution equations for
in the MFS. Here, the overbar denotes a suitably defined average, which, in practice, could be a spatial average. The evolution equations for 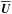 involve correlations of the form
involve correlations of the form 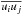 and
and 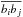 that need to be expressed in terms of
that need to be expressed in terms of 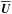 and
and 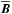 . They are similar to the parameterization in terms of the rate-of-strain tensor of the mean flow involving turbulent viscosity, but there are also contributions that are quadratic in
. They are similar to the parameterization in terms of the rate-of-strain tensor of the mean flow involving turbulent viscosity, but there are also contributions that are quadratic in 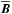 . Similar parameterizations also exist for the Maxwell stresses in the momentum equation and the electromotive force in the induction equation.
. Similar parameterizations also exist for the Maxwell stresses in the momentum equation and the electromotive force in the induction equation.
Before we can think of applying NEMPI to real sunspot formation, we must begin to address the effects of radiation, ionization, and other potentially important surface effects. Here, we focus on radiative transfer. Radiation has two important effects; on the one hand, it leads to the establishment of a natural surface from which most of the observed radiation is emitted and above which the density drops off sharply, and on the other hand, radiation also leads to the equilibration of temperature differences between neighboring fluid elements. Earlier investigations suggested that this may indeed be the case and that NEMPI may be difficult to excite in the presence of radiation (Barekat 2013; Bhat & Brandenburg 2016). This is also the reason why we focus here on mean-field simulations, because they allow us to artificially exaggerate the effects of NEMPI by choosing unrealistically large mean-field parameters, which enables us to study the properties of NEMPI in that case and helps us to determine the conditions under which NEMPI may still operate.
Most of the earlier investigations of NEMPI were carried out in an isothermally stratified layer using an isothermal equation of state. This means that no energy equation was solved. This was also true in simulations with an outer coronal envelope (Warnecke et al. 2013), where the interface was characterized by a layer above which the driving of turbulence was turned off. The aim of the present paper is therefore to study NEMPI in a simple model with radiative heating and cooling included.
2. The model
2.1. Mean-field equations and radiative transfer
We consider the mean-field equations in Cartesian coordinates, but restrict ourselves to including only the effects of turbulent magnetic diffusion, turbulent viscosity, and the negative effective magnetic pressure effect, which means that the ordinary magnetic pressure from the mean field, 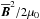 , is modified and becomes
, is modified and becomes 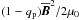 , where
, where 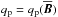 depends on the local magnetic field strength. We write the mean magnetic field as
depends on the local magnetic field strength. We write the mean magnetic field as 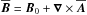 , where B0 = (0,0,B0) is an imposed vertical field, and
, where B0 = (0,0,B0) is an imposed vertical field, and 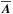 is the mean magnetic vector potential. We thus solve the equations for
is the mean magnetic vector potential. We thus solve the equations for 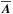 , the mean velocity
, the mean velocity 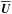 , the mean specific entropy
, the mean specific entropy 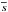 , and the mean density
, and the mean density 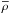 in the form
in the form
where ηT = η + ηt is the total magnetic diffusivity consisting of a microphysical and a turbulent value, νT = ν + νt is the total viscosity consisting again of a microphysical and a turbulent value, 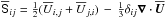 is the traceless rate-of-strain tensor,
is the traceless rate-of-strain tensor, 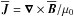 is the Lorentz force from the mean fields (without the effects of turbulence that are being parameterized through qp), g = (0,0,−g) is the gravitational acceleration,
is the Lorentz force from the mean fields (without the effects of turbulence that are being parameterized through qp), g = (0,0,−g) is the gravitational acceleration, 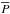 is the mean gas pressure,
is the mean gas pressure, 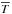 is the mean temperature,
is the mean temperature, 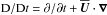 is the advective derivative, Frad is the radiative flux, and Fconv is the convective flux; but this latter will be neglected in our present exploratory work.
is the advective derivative, Frad is the radiative flux, and Fconv is the convective flux; but this latter will be neglected in our present exploratory work.
The radiative flux divergence is obtained by solving the radiative transfer equations for the intensity 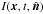 in the gray approximation in the form (Nordlund 1982)
in the gray approximation in the form (Nordlund 1982) 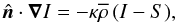 (5)along a set of rays in different directions
(5)along a set of rays in different directions 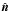 , where κ is the opacity and
, where κ is the opacity and 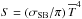 is the source function with σSB being the Stefan–Boltzmann constant. The radiative flux divergence is found by integrating Eq. (5) over all directions, that is,
is the source function with σSB being the Stefan–Boltzmann constant. The radiative flux divergence is found by integrating Eq. (5) over all directions, that is, 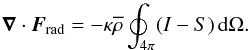 (6)We adopt the equation of state for a perfect gas, that is,
(6)We adopt the equation of state for a perfect gas, that is, 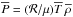 , where ℛ is the universal gas constant and μ the mean specific weight. The mean specific entropy is, up to an irrelevant additive constant, given by
, where ℛ is the universal gas constant and μ the mean specific weight. The mean specific entropy is, up to an irrelevant additive constant, given by 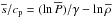 , where γ = cp/cv is the ratio of specific heats at constant pressure and constant density, respectively, and ℛ /μ = cp−cv. In the following, we take γ = 5/3 which is appropriate for a monatomic gas and in the absence of ionization. The pressure scale height,
, where γ = cp/cv is the ratio of specific heats at constant pressure and constant density, respectively, and ℛ /μ = cp−cv. In the following, we take γ = 5/3 which is appropriate for a monatomic gas and in the absence of ionization. The pressure scale height, 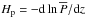 , is then given by
, is then given by 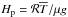 . In the isothermal part near the top, pressure and density scale heights are equal, that is, Hρ = Hp, where
. In the isothermal part near the top, pressure and density scale heights are equal, that is, Hρ = Hp, where 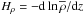 . However, in the deeper isentropic parts, we have Hρ = γHp.
. However, in the deeper isentropic parts, we have Hρ = γHp.
2.2. Parameterizations
Turbulence effects such as NEMPI depend on the relative importance of the magnetic field to the equipartition field strength with respect to the turbulent energy, that is, on 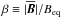 . Here, the equipartition field strength Beq is given by
. Here, the equipartition field strength Beq is given by 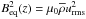 . The effective magnetic pressure is characterized by the functional form of qp = qp(β), for which we assume (Kemel et al. 2012)
. The effective magnetic pressure is characterized by the functional form of qp = qp(β), for which we assume (Kemel et al. 2012) 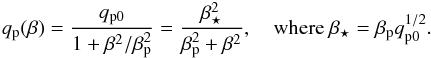 (7)In addition, we have to specify ηT and νT, which we assume to be constant and equal to each other, that is, we assume the turbulent magnetic Prandtl number PrM = νT/ηT to be unity (Yousef et al. 2003). We define a fiducial model where we take qp0 = 300 and βp = 0.05. Earlier work of Kemel et al. (2013) showed that the growth rate is mainly dependent on the parameter β⋆, whose value is then 0.87. For comparison, Kemel et al. (2012) and Käpylä et al. (2012b) used the parameter combination qp0 = 40 and βp = 0.05, which then yields about a third for β⋆ = 0.32. Our value of β⋆ is thus much higher than what has been assumed before, which should help us to study the effects of radiation in the development of NEMPI. Following earlier work of Barekat (2013) and Barekat & Brandenburg (2014), we assume a Kramers-like opacity law for κ of the form
(7)In addition, we have to specify ηT and νT, which we assume to be constant and equal to each other, that is, we assume the turbulent magnetic Prandtl number PrM = νT/ηT to be unity (Yousef et al. 2003). We define a fiducial model where we take qp0 = 300 and βp = 0.05. Earlier work of Kemel et al. (2013) showed that the growth rate is mainly dependent on the parameter β⋆, whose value is then 0.87. For comparison, Kemel et al. (2012) and Käpylä et al. (2012b) used the parameter combination qp0 = 40 and βp = 0.05, which then yields about a third for β⋆ = 0.32. Our value of β⋆ is thus much higher than what has been assumed before, which should help us to study the effects of radiation in the development of NEMPI. Following earlier work of Barekat (2013) and Barekat & Brandenburg (2014), we assume a Kramers-like opacity law for κ of the form 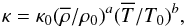 (8)with constant coefficients κ0, ρ0, and T0, and given exponents a and b. The resulting radiative conductivity is then given by (Barekat & Brandenburg 2014)
(8)with constant coefficients κ0, ρ0, and T0, and given exponents a and b. The resulting radiative conductivity is then given by (Barekat & Brandenburg 2014) ![\begin{equation} K=K_0\,{(\meanT/T_0)^{3-b}\over(\meanrho/\rho_0)^{1+a}} =K_0\,\left[{(\meanT/T_0)^n\over\meanrho/\rho_0}\right]^{1+a}, \end{equation}](/articles/aa/full_html/2018/01/aa30421-17/aa30421-17-eq65.png) (9)where
(9)where 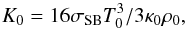 (10)which is a constant and
(10)which is a constant and 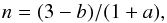 (11)which is, for n> −1, related to the polytropic index of the resulting stratification. The radiative diffusivity is
(11)which is, for n> −1, related to the polytropic index of the resulting stratification. The radiative diffusivity is 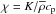 . The optical depth is
. The optical depth is 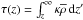 . The region where τ ≪ 1 is optically thin, while the region where τ ≫ 1 is optically thick, which corresponds to the convection zone in the Sun; τ = 1 represents thus the solar surface.
. The region where τ ≪ 1 is optically thin, while the region where τ ≫ 1 is optically thick, which corresponds to the convection zone in the Sun; τ = 1 represents thus the solar surface.
2.3. Boundary conditions and numerical aspects
We adopt impenetrable stress-free boundary conditions in the z direction, so the velocity obeys 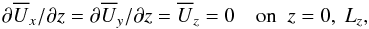 (12)where Lz is the vertical extent of the computational domain and the bottom boundary is at z = 0. For the magnetic field we adopt the vertical field condition,
(12)where Lz is the vertical extent of the computational domain and the bottom boundary is at z = 0. For the magnetic field we adopt the vertical field condition, 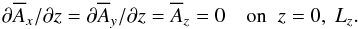 (13)We assume zero incoming intensity at the top, and compute the incoming intensity at the bottom from a quadratic Taylor expansion of the source function, which implies that the diffusion approximation is obeyed; see Appendix A of Heinemann et al. (2006) for details. As in Barekat & Brandenburg (2014), we fix the temperature at the bottom,
(13)We assume zero incoming intensity at the top, and compute the incoming intensity at the bottom from a quadratic Taylor expansion of the source function, which implies that the diffusion approximation is obeyed; see Appendix A of Heinemann et al. (2006) for details. As in Barekat & Brandenburg (2014), we fix the temperature at the bottom, 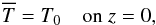 (14)while the temperature at the top is allowed to evolve freely. There is no boundary condition on the density, but since no mass is flowing in or out, the volume-averaged density is automatically constant; see Appendix C of Barekat & Brandenburg (2014).
(14)while the temperature at the top is allowed to evolve freely. There is no boundary condition on the density, but since no mass is flowing in or out, the volume-averaged density is automatically constant; see Appendix C of Barekat & Brandenburg (2014).
To reduce the computational expense, we solve Eqs. (1)–(6) in two spatial dimensions. In an earlier investigation of NEMPI, Losada et al. (2012) found that this simplification can lead to about two times smaller growth rates, but the qualitative dependencies on various input parameters were still reproduced correctly. In the present model, we use either 288 or 576 meshpoints in the z direction. The number of mesh points in the x direction depends on the domain size and is constrained such that the mesh spacings δx and δz are equal in the two directions. We employ the Pencil Code1, where all relevant terms are readily implemented. The code uses a high-order finite-difference scheme. The radiation module was implemented by Heinemann et al. (2006).
2.4. Comparison with the optically thick approximation
It will be instructive to compare with the more familiar case in which Frad is computed in the optically thick approximation as 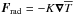 in a domain 0 ≤ z ≤ d, where d is less than the Lz used in the general case with full radiative transfer. At z = d, we apply a radiative boundary condition
in a domain 0 ≤ z ≤ d, where d is less than the Lz used in the general case with full radiative transfer. At z = d, we apply a radiative boundary condition 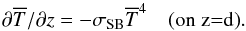 (15)The value of d is computed as (see Sect. 3.12 of Barekat & Brandenburg 2014)
(15)The value of d is computed as (see Sect. 3.12 of Barekat & Brandenburg 2014) 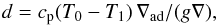 (16)where ∇ad = 1−1 /γ and ∇ = 1/(1 + n) with n given by Eq. (11), and
(16)where ∇ad = 1−1 /γ and ∇ = 1/(1 + n) with n given by Eq. (11), and 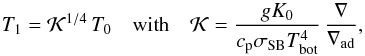 (17)where K0 is given by Eq. (10). The quantities in Eqs. (16), (17) are fully determined by the parameters of the radiative model. We emphasize that the temperature at the top is close to T1, but is allowed to evolve freely subject to Eq. (15). Computationally, the optically thick approximation is cheaper by about a factor of two, but it is more restrictive, because the values of d and T1 are intimately tied to the choice of κ0 and cannot be varied independently.
(17)where K0 is given by Eq. (10). The quantities in Eqs. (16), (17) are fully determined by the parameters of the radiative model. We emphasize that the temperature at the top is close to T1, but is allowed to evolve freely subject to Eq. (15). Computationally, the optically thick approximation is cheaper by about a factor of two, but it is more restrictive, because the values of d and T1 are intimately tied to the choice of κ0 and cannot be varied independently.
2.5. Scale separation ratio
In our mean-field model, turbulence is parameterized in terms of a magnetic turbulent diffusivity, which is estimated to be ηt = urms/ 3kf (Sur et al. 2008), where kf is the wavenumber of the energy-carrying motions. We compare this with the reference wavenumber k1 = 2π/Lz based on our domain of height Lz. We refer to kf/k1 as the scale separation ratio. Thus, we have (Jabbari et al. 2014) 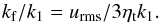 (18)This ratio must be large enough for NEMPI to be excited (Brandenburg et al. 2012). Early DNS of Brandenburg et al. (2011), where NEMPI was excited, used kf/k1 = 15, but with kf/k1 = 30, NEMPI became much more pronounced (Käpylä et al. 2012b).
(18)This ratio must be large enough for NEMPI to be excited (Brandenburg et al. 2012). Early DNS of Brandenburg et al. (2011), where NEMPI was excited, used kf/k1 = 15, but with kf/k1 = 30, NEMPI became much more pronounced (Käpylä et al. 2012b).
Following the work of Barekat & Brandenburg (2014), we measure length in Mm, velocity in km s-1, and density in g cm-3. We choose Lz = 5 Mm. We adopt a squared domain, Lx = Lz, and assume for the turbulent small-scale velocity urms = 1 km s-1. Thus, we have ηt = 5 × 10-3 Mm km s-1, so we have kf/k1 = 53, which should be large enough for NEMPI to be excited (Brandenburg et al. 2012). In some models with larger resolution (5762 meshpoints), we used ηt = 2 × 10-3 Mm km s-1, corresponding to kf/k1 = 133; see Table 1 for the conversion of several quantities from code units to cgs units. Following earlier work (Brandenburg et al. 2011), we also define the general turbulent–diffusive time 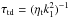 .
.
 |
Fig. 1 Stratification of |
Units used in this paper and conversion into cgs units.
3. Results
We design the model such that it has an isentropic deeper part. The stratification in our model is similar to Run B7 of Barekat & Brandenburg (2014) with a = 1 and b = 0, which, as discussed above, yields n = 1.5. In particular, we use κ0 = 107 Mm-1 cm3 g-1, which results in a surface temperature of around 5000 K. As in Barekat & Brandenburg (2014), we compute a hydrostatic equilibrium solution (u = 0) by solving Eqs. (1)–(6) only in the z direction in one dimension. The result is shown in Fig. 1, where we plot the z dependence of 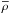 ,
, 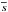 ,
, 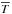 , and χ. In the deeper parts, where τ ≫ 1,
, and χ. In the deeper parts, where τ ≫ 1, 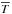 increases linearly with depth and, because
increases linearly with depth and, because 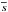 is nearly constant in that part,
is nearly constant in that part, 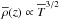 , which is in agreement with the expected polytropic stratification. Above the surface,
, which is in agreement with the expected polytropic stratification. Above the surface, 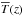 is approximately constant, so
is approximately constant, so 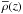 falls off exponentially with height, as expected for an isothermal stratification. We begin by discussing in some detail a run with 200 G, which will later also be referred to as Run B′′; see Table 2. The presence of an imposed field changes the stratification, but this change is small: T decreases by ≈4 K for B0 = 200 G.
falls off exponentially with height, as expected for an isothermal stratification. We begin by discussing in some detail a run with 200 G, which will later also be referred to as Run B′′; see Table 2. The presence of an imposed field changes the stratification, but this change is small: T decreases by ≈4 K for B0 = 200 G.
Summary of Runs A–H.
 |
Fig. 2 Gray scale representation of vertical velocity together with magnetic field lines in white for a run with B0 = 200 G (Run B′′). The yellow and red horizontal lines are the τ = 1 and τ = 100 surfaces, respectively. |
3.1. Early evolution into saturation
In the early phase of the evolution, structures form where 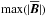 is at z = zB ≈ 2.5 Mm and a horizontal wavenumber k = 4 k1; see Fig. 2. These structures gradually move downward, disappear, and new ones form at z ≈ 3 Mm. Those structures then also move downward, and so on. The structures occur well below the τ = 1 line and are close to the τ = 100 line. Here, the photon mean-free path,
is at z = zB ≈ 2.5 Mm and a horizontal wavenumber k = 4 k1; see Fig. 2. These structures gradually move downward, disappear, and new ones form at z ≈ 3 Mm. Those structures then also move downward, and so on. The structures occur well below the τ = 1 line and are close to the τ = 100 line. Here, the photon mean-free path, 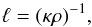 (19)is about 0.05 Mm, while at τ = 1, it is about 0.14 Mm. The downward motions are associated with local field enhancements, as can clearly be seen from field lines becoming more concentrated in some locations. At later times, the field becomes more irregular, but retains a typical horizontal wavenumber of 4 k1. In some cases, however, we found that, in the late nonlinear stage, k can decrease from four to three.
(19)is about 0.05 Mm, while at τ = 1, it is about 0.14 Mm. The downward motions are associated with local field enhancements, as can clearly be seen from field lines becoming more concentrated in some locations. At later times, the field becomes more irregular, but retains a typical horizontal wavenumber of 4 k1. In some cases, however, we found that, in the late nonlinear stage, k can decrease from four to three.
The growth of structures can be characterized both by the typical velocities 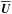 in the domain and the departures from the imposed field
in the domain and the departures from the imposed field  . In Fig. 3, we show for two independent realizations of Run B′′ (with Lx = Lz) the evolution of the rms values,
. In Fig. 3, we show for two independent realizations of Run B′′ (with Lx = Lz) the evolution of the rms values, 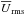 and
and 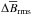 , with different seeds for the random initial velocity perturbations. We clearly see an oscillatory growth of both quantities, as can also be seen by showing a plot compensated by exp(−λt), where λ ≈ 0.048 ks-1 is the growth rate, as determined during the exponential growth phase of the instability. In the following, we measure the period Posc as the volume-integrated rms velocity of the mean field and record the frequency ω = 2π/Posc. The frequency of the actual (signed) magnetic field is half that value.
, with different seeds for the random initial velocity perturbations. We clearly see an oscillatory growth of both quantities, as can also be seen by showing a plot compensated by exp(−λt), where λ ≈ 0.048 ks-1 is the growth rate, as determined during the exponential growth phase of the instability. In the following, we measure the period Posc as the volume-integrated rms velocity of the mean field and record the frequency ω = 2π/Posc. The frequency of the actual (signed) magnetic field is half that value.
The growth rate is independent of the initial seed for the random number generator, but the detailed nonlinear evolution does depend on it (compare the lines in each of the panels of Fig. 3). This suggests that the evolution of NEMPI is chaotic in the nonlinear regime. Animations show that the field lines are constantly swinging back and forth. This type of time dependence of NEMPI is new and has not previously been seen – neither in isothermal nor in polytropic calculations. It may therefore be an effect related to the presence of radiation. The slight apparent difference in oscillation amplitudes of the compensated plots in the insets is caused by the fact that both have been compensated by the same factor, but the amplitudes were slightly different by the time the eigenfunction begins to be established.
 |
Fig. 3 Evolution of |
 |
Fig. 4
|
The spatio-temporal evolution of NEMPI is seen more clearly in Fig. 4, where we show 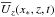 for x∗ = −1.7 Mm. This position x∗ is where
for x∗ = −1.7 Mm. This position x∗ is where 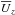 has an anti-node during the linear growth phase. At t = 1740 ks, the slope in the tz diagram corresponds to a pattern speed of about 0.2 km s-1, which is small compared with the sound speed cs ≈ 20 km s-1 at z ≈ 2.5 Mm, and is also small compared with the turbulent rms velocity of 1 km s-1, but agrees with the typical NEMPI-produced downflow speeds found earlier for isothermal NEMPI experiments (Brandenburg et al. 2014).
has an anti-node during the linear growth phase. At t = 1740 ks, the slope in the tz diagram corresponds to a pattern speed of about 0.2 km s-1, which is small compared with the sound speed cs ≈ 20 km s-1 at z ≈ 2.5 Mm, and is also small compared with the turbulent rms velocity of 1 km s-1, but agrees with the typical NEMPI-produced downflow speeds found earlier for isothermal NEMPI experiments (Brandenburg et al. 2014).
3.2. Dependence on control parameters
We now consider the dependence of NEMPI on B0, κ0, and ηt. We revisit some of these dependencies later in more detail. Several input and output parameters of our runs are summarized in Table 2. Although most of the runs discussed in this paper are performed for a domain with Lx = Lz = 5 Mm, several aspects can also be reproduced in narrower domains with Lx/Lz = 0.5 and 0.25. The growth rate λ is rather sensitive to this, while the oscillation frequency ω = 2π/Posc and the position zB of the magnetic field maximum are less sensitive. For Runs A–C with κ0 = 107 Mm-1 cm3 g-1, the growth rates are roughly in the range between λ = 0.01 ks-1 and 0.03 ks-1 and do not seem to be systematically dependent on the value of B0. This is mainly related to the fact that NEMPI can develop deeper down as B0 is increased; see Kemel et al. (2012). This is characterized by the value of zB given in Table 2; compare especially with the value for Run C. Our results thus confirm that the structures develop at larger depths when the field becomes stronger. This is in agreement with earlier work (Kemel et al. 2012; Losada et al. 2014).
3.3. Comparison with earlier work
In units of τtd (defined in Sect. 2.5), the growth rate is 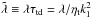 , which is equal to about 6 for Run B′′. However, if we normalize instead by actual horizontal wavenumber k of the structures, which is four times larger than k1 (see Fig. 2), we have λ/ηtk2 ≈ 0.4. This value is rather low and comparable to the value in the first DNS of Brandenburg et al. (2011), where the scale separation ratio was much lower (kf/k1 = 15 compared to 53 in the present case).
, which is equal to about 6 for Run B′′. However, if we normalize instead by actual horizontal wavenumber k of the structures, which is four times larger than k1 (see Fig. 2), we have λ/ηtk2 ≈ 0.4. This value is rather low and comparable to the value in the first DNS of Brandenburg et al. (2011), where the scale separation ratio was much lower (kf/k1 = 15 compared to 53 in the present case).
Earlier work using isothermal layers has shown that the horizontal wavenumber of the instability is comparable to the inverse density scale height; Kemel et al. (2013) found kHρ = 1.1–1.5. Subsequent work showed that during the nonlinear evolution of the instability, kHρ can decrease from about 0.8 to 0.2. This has been associated with an inverse cascade-type behavior (Brandenburg et al. 2014). The polytropic simulations of Losada et al. (2014) gave larger values: kHρ = 1 in the upper layers and kHρ = 2 in deeper ones; see their Fig. 12. In the present case, at the height where the instability based on the absolute field strength is strongest (z = 3 Mm), and for k/k1 = 4, we find kHp = 5; see the dashed line in Fig. 5a. This is a striking difference between the present models and the earlier ones using an isothermal equation of state.
 |
Fig. 5 Vertical dependence of kHp for k/k1 = 1 and 4 (a), and of Beq(b). The vertical lines denote the surface where τ = 1. In panel a, we also show the dependence of kℓ in red. |
Figure 5b shows that, in the region where NEMPI develops, the equipartition field strength Beq(z) is around 3000–4000 G. This is about 20 times larger than the strength of the imposed field, which is typical of NEMPI and in agreement with earlier results (Losada et al. 2014; Brandenburg et al. 2014).
3.4. Magnetic field dependence
As alluded to above, there are several other aspects of NEMPI that can be compared with what has been found earlier. We now compare our results with Fig. 6 of Brandenburg et al. (2014), where the vertical dependence of the maximum field in the structures, Bmax(z), was plotted, normalized either by B0 or by Beq(z). The corresponding result for our present simulations is shown in Fig. 6. The local maxima in Bmax(z) are caused by the spatial wave-like structures seen in Figs. 2 and 4.
 |
Fig. 6 Vertical dependence of the normalized magnetic field for different times in the nonlinear phase for B0 = 200 G (Run B′′). The location of τ = 1 is marked with a red filled symbol, while the diamond indicates τ = 0.1 and the two crosses denote τ = 10 and 100. |
Unlike the earlier work for isothermal layers, where the slope of Beq/B0 was constant, it varies in the present case. More importantly, the magnetic field drops significantly near the surface and does not cross the Beq/B0 line. This means that, unlike the earlier work with imposed vertical fields (Brandenburg et al. 2014), the field in the vertical flux tubes never exceeds Beq.
The magnetic field strengths of the flux concentrations are obviously much weaker than what is expected for the Sun. More surprising is perhaps the fact that they are also much weaker than in the earlier isothermal models. For 200 G, the ratio Bmax/B0 reaches 1.1, while for 500 G, it reaches 0.94. In the isothermal case, this value could easily reach 50. We can also observe that, when we increase the external field, Bmax becomes smaller.
 |
Fig. 7 Effective magnetic pressure and its derivative with respect to the magnetic field strength for B0 = 100 G (black), 200 G (red), and 500 G (blue), corresponding to B0/Beq0 = 0.01, 0.03, and 0.07. The solid lines are based on using just the imposed magnetic field, β0, while the dotted lines are based on the actual field. |
3.5. Effective magnetic pressure
In Fig. 7 we plot the normalized effective magnetic pressure, ![\begin{equation} \Peff(\beta)=\half[1-\qp(\beta)]\beta^2, \end{equation}](/articles/aa/full_html/2018/01/aa30421-17/aa30421-17-eq241.png) (20)against z. We compare this with Fig. 9 of Losada et al. (2014), which was a polytropic run with γ = 5/3. In the present work, the values of
(20)against z. We compare this with Fig. 9 of Losada et al. (2014), which was a polytropic run with γ = 5/3. In the present work, the values of 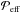 are about ten times larger than in the earlier polytropic models. This is probably related to the rather large values of qp0 and β⋆. However, the shapes of the curves are similar in those two models. Our values of the relative strength of the imposed field are similar: for B0 = 200 G we have B/Beq = 0.05, which is comparable to the value of Losada et al. (2014). Our value of 100 G corresponds to their ratio 0.01, while 500 G corresponds to 0.07. The results change slightly when replacing β0 ≡ B0/Beq by the value for the actual magnetic field β = | B | /Beq. Furthermore, the changes in the effective magnetic pressure caused by the induced magnetic field are rather strong; see the dashed lines in Fig. 7. We also see regular variations in the vertical direction, which are associated with corresponding (time-dependent) extrema in the actual magnetic field.
are about ten times larger than in the earlier polytropic models. This is probably related to the rather large values of qp0 and β⋆. However, the shapes of the curves are similar in those two models. Our values of the relative strength of the imposed field are similar: for B0 = 200 G we have B/Beq = 0.05, which is comparable to the value of Losada et al. (2014). Our value of 100 G corresponds to their ratio 0.01, while 500 G corresponds to 0.07. The results change slightly when replacing β0 ≡ B0/Beq by the value for the actual magnetic field β = | B | /Beq. Furthermore, the changes in the effective magnetic pressure caused by the induced magnetic field are rather strong; see the dashed lines in Fig. 7. We also see regular variations in the vertical direction, which are associated with corresponding (time-dependent) extrema in the actual magnetic field.
 |
Fig. 8 Comparison of the vertical profiles of ⟨ δlnB2 ⟩ 1/2 and ⟨ δlnT ⟩ (scaled by a factor 1000) for runs with different values of κ0 = 2 × 107 Mm-1 cm3 g-1(a), 5 × 107(b), and 108 cm3 s-1 Mm-1(c). The τ = 10, 1, and 0.1 surfaces are indicated in gray (from left to right). |
3.6. Dependence on κ0
Increasing κ0 means decreasing the radiative diffusion in the deeper parts, which tends to let NEMPI appear sooner and grow faster. It also reduces the temperature near the top of the surface and therefore also the density scale height Hρ0.
To see whether radiation has a noticeable effect on NEMPI, we compare in Fig. 8 vertical profiles of the relative magnetic and temperature fluctuations ⟨ δlnB2 ⟩ 1/2 and ⟨ δlnT ⟩ for runs with different values of κ0 = 2 × 107, 5 × 107, and 108 Mm-1 cm3 g-1. The effect is surprisingly small. The magnetic fluctuations are of the order of unity (and somewhat larger for κ0 = 2 × 107 Mm-1 cm3 g-1), while the relative temperature fluctuations are at most 5 × 10-4.
The vigor of the temporal variation of the field increases considerably as we increase κ0, even though the relative strength of the variations and the effect on the temperature remain comparable.
 |
Fig. 9 Gray scale representation of vertical velocity together with magnetic field lines in white for the optically thick model at four times around saturation of NEMPI with otherwise the same parameters as Run B′′ with B0 = 200 G. |
 |
Fig. 10 Similar to Fig. 9, but for the isentropic model. We note that also the color bar is unchanged. |
3.7. Dependence on qpz and β⋆
When the value of qp0 is below 250, keeping βp = 0.05 fixed, so β⋆ = 079, NEMPI is found to be no longer excited and thus no magnetic structures are created. This remains true even when we increase κ0 to 5 × 107 Mm-1 cm3 g-1, which is generally more favorable to the onset of NEMPI. This may indicate that there is a threshold for β⋆ for the excitation of NEMPI in the presence of radiation, which would be somewhere between 0.7 and 0.8.
4. Comparison with simpler models
To trace the origin of the difference to earlier results, we compare with models without radiative transfer. The next closest model to those fully radiative models is that described in Sect. 2.4, in which the dynamics is optically thick, but a radiative boundary condition (15) is adopted at the top. The height where this condition is applied is z = d, which corresponds to the position where τ = 1 in the fully radiative model; see Fig. 1. This is at z = d = 4.3 Mm, where the mean-free path is ℓ = 0.14 Mm, so structures that are smaller than that experience reduced radiative heat exchange with the surroundings in the fully radiative model, but not in the optically thick treatment.
Another type of simplified model is one where 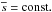 in space and time. This is a strictly isentropic case, where Eq. (3) is ignored. Other than that, it has the same height and density stratification as both the optically thick model and the fully radiative one.
in space and time. This is a strictly isentropic case, where Eq. (3) is ignored. Other than that, it has the same height and density stratification as both the optically thick model and the fully radiative one.
4.1. Optically thick case
To shed some light on the occurrence of small horizontal length scales of NEMPI in our radiative transfer models, we now compare with the optically thick approximation discussed in Sect. 2.4. The result is shown in Fig. 9 for a model that is comparable to Run B with κ0 = 107. In that case, Eqs. (16), (17) yield d = 4.3 Mm, T1 = 4998 K, and 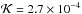 . It turns out that structures now develop at z ≈ 4 Mm, which is close to the top of the domain; see Fig. 9. With radiative transfer, by comparison, structures typically develop deeper down at z ≈ 3 Mm. However, the structures still have very small length scales comparable to those in the models with radiative transfer. By comparing with Fig. 2 it is evident that in the models with optically thin radiative transfer, the formation of structures at z ≈ 4 Mm appears to be suppressed. The mean free path is only about ℓ = 0.14 Mm for our structures with k/k1 = 4; see the red dashed line in Fig. 5a. This is rather small and can therefore not be an explanation for the suppression of structures in the models with optically thin radiative transfer. There is, however, another difference between the models with optically thin radiative transfer and the optically thick approximation that has nothing to do with NEMPI. All models with optically thick radiative transfer have a stably stratified layer at the top, where the entropy increases with height. Therefore, a downdraft pulls with it high-entropy material, contrary to the case with a radiative boundary condition at z = d, where downdrafts always have low entropy. This difference was already noted by Barekat & Brandenburg (2014); it explains why NEMPI does not develop near the τ = 1 surface at z = 4.3 Mm in the optically thin radiative transfer model. However, it does not explain the small size of NEMPI structures. We should also point out here that, in the optically thick model, NEMPI is no longer oscillatory.
. It turns out that structures now develop at z ≈ 4 Mm, which is close to the top of the domain; see Fig. 9. With radiative transfer, by comparison, structures typically develop deeper down at z ≈ 3 Mm. However, the structures still have very small length scales comparable to those in the models with radiative transfer. By comparing with Fig. 2 it is evident that in the models with optically thin radiative transfer, the formation of structures at z ≈ 4 Mm appears to be suppressed. The mean free path is only about ℓ = 0.14 Mm for our structures with k/k1 = 4; see the red dashed line in Fig. 5a. This is rather small and can therefore not be an explanation for the suppression of structures in the models with optically thin radiative transfer. There is, however, another difference between the models with optically thin radiative transfer and the optically thick approximation that has nothing to do with NEMPI. All models with optically thick radiative transfer have a stably stratified layer at the top, where the entropy increases with height. Therefore, a downdraft pulls with it high-entropy material, contrary to the case with a radiative boundary condition at z = d, where downdrafts always have low entropy. This difference was already noted by Barekat & Brandenburg (2014); it explains why NEMPI does not develop near the τ = 1 surface at z = 4.3 Mm in the optically thin radiative transfer model. However, it does not explain the small size of NEMPI structures. We should also point out here that, in the optically thick model, NEMPI is no longer oscillatory.
4.2. Isentropic case
In Fig. 10, we show the same model as in Fig. 9, but now with fixed mean specific entropy, so 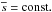 , that is, Eq. (3) is not solved. This means that the negative buoyancy is simply the result of the negative effective magnetic pressure, without any influence from changes in specific entropy or temperature. By contrast, when temperature and entropy are allowed to change, this can either enhance or diminish the effect of NEMPI. The answer discussed below is not completely straightforward.
, that is, Eq. (3) is not solved. This means that the negative buoyancy is simply the result of the negative effective magnetic pressure, without any influence from changes in specific entropy or temperature. By contrast, when temperature and entropy are allowed to change, this can either enhance or diminish the effect of NEMPI. The answer discussed below is not completely straightforward.
In a stratified layer, a downdraft, even if it is initiated by NEMPI (instead of thermal buoyancy, for example), will always be compressed, so its density increases. This leads to adiabatic heating, and the corresponding radiation causes a loss of entropy, so those structures become even more negatively buoyant. This happens most efficiently at the scale of the photon mean free path or at the radiative diffusion scale. Both scales are rather small and this might explain the observed tendency for small structures to develop in our model. At the same time, however, those small length scales also make NEMPI less efficient. In this sense, radiation both promotes NEMPI by enhancing buoyancy effects (both negative and positive ones), and counteracts NEMPI, because it operates on progressively smaller length scales.
5. Conclusions
We have presented here the first calculations of NEMPI with radiation. Within the limitations of our simplified model, NEMPI would not have been excited had we chosen the previously determined control parameters for the negative effective magnetic pressure effect, that is, β⋆ and βp. By using a nearly three times larger value of β⋆, we were able to study the reason behind this. It turns out that in our model with radiation, the horizontal wavelength of the instability is dramatically decreased. As a consequence, turbulent and radiative diffusion have much stronger effects, suppressing, therefore, the instability. Nevertheless, even with a strongly enhanced value of β⋆, the resulting magnetic structures are still far too weak to form sunspots.
We found for the first time that NEMPI can display oscillatory behavior during the linear phase of the instability. These oscillations are associated with traveling waves moving upward with a speed of 0.2 km s-1. The oscillations have a period of about 4–9 ks in the volume-integrated velocity, but since the period of the actual (signed) magnetic field is twice as long, the recurrence time of pronounced downward flows is 8–18 ks.
We do not yet know enough about the nature of the oscillations and whether they could also exist in reality. To address this question further, we have to focus on the limitations associated with the small horizontal length scales of NEMPI in the presence of radiation. Given that the oscillations occur only in the presence of a stably stratified layer above, it is possible that they are related to buoyancy oscillations in a thin upper radiative layer, where the stratification is sufficiently stable, while still being coupled to NEMPI in the deeper layers through suction along magnetic field lines.
The treatment of turbulent magnetic diffusion as a multiplicative factor in front of a Laplacian diffusion operator becomes invalid on small length scales, so the actual diffusion will be smaller; see Brandenburg et al. (2008). It is also possible that the opacity is still not large enough, and therefore the radiative diffusivity is too large. This is another unrealistic limitation of our present model. On the other hand, in the deeper layers, the radiative diffusivity is already now smaller than the turbulent magnetic diffusivity. One would therefore not have expected this to be the limiting factor. Most important is perhaps the limitation associated with the neglect of turbulent convection in the deeper parts. Convection would imply the presence of a strongly negative entropy gradient just below the surface. Therefore, the stabilizing effect from the top layers encountered in the present model would be absent. However, NEMPI would still lead to small length scales, except that now turbulent convection leads to an effective thermal diffusivity that is much larger than the radiative one. Moreover, the transition between a radiative surface above and strong turbulence with small-scale convection beneath the surface would be very abrupt. Given that NEMPI is most effective for large-scale separation (small-scale turbulence) and the stratification is strongest near the surface, it might still be a viable alternative for the formation of sunspots. Extending our model by including convection in parameterized form would therefore be the first task to be addressed in a follow-up investigation.
Ultimately, the aim is to model the formation of sunspots, where convective heat transport is either suppressed by the magnetic field (Biermann 1941) or the cooling is enhanced (Parker 1974a). The former effect may lead to its own instability, which was modeled by Kitchatinov & Mazur (2000) using a mean-field approach. This instability could be strengthened further by the effects of ionization and would therefore be another urgent target for subsequent investigations.
Acknowledgments
We thank the referee for useful comments and Sacha Brun for support and encouragement. Support through the NSF Astrophysics and Astronomy Grant Program (grant 1615100) and the Research Council of Norway (FRINATEK grant 231444) are gratefully acknowledged. We acknowledge the allocation of computing resources provided by the Swedish National Allocations Committee at the Center for Parallel Computers at the Royal Institute of Technology in Stockholm. This work utilized the Janus supercomputer, which is supported by the National Science Foundation (award number CNS-0821794), the University of Colorado Boulder, the University of Colorado Denver, and the National Center for Atmospheric Research. The Janus supercomputer is operated by the University of Colorado Boulder.
References
- Augustson, K., Brun, A. S., Miesch, M., & Toomre, J. 2015, ApJ, 809, 149 [Google Scholar]
- Barekat, A. 2013, Hydrodynamic simulations with a radiative surface, DiVA.org:su-90307 (Stockholm University) [Google Scholar]
- Barekat, A., & Brandenburg, A. 2014, A&A, 571, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhat, P., & Brandenburg, A. 2016, A&A, 587, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biermann, L. 1941, Vierteljahresschr. Astron. Gesellsch., 76, 194 [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Rädler, K.-H., & Schrinner, M. 2008, A&A, 482, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., Kemel, K., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2011, ApJ, 740, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Kemel, K., Kleeorin, N., & Rogachevskii, I. 2012, ApJ, 749, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2013, ApJ, 776, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Gressel, O., Jabbari, S., Kleeorin, N., & Rogachevskii, I. 2014, A&A, 562, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., Rogachevskii, I., & Kleeorin, N. 2016, New J. Phys., 18, 125011 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, B. P., Miesch, M. S., Browning, M. K., Brun, A. S., & Toomre, J. 2011, ApJ, 731, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Miesch, M. S., & Toomre, J. 2004, ApJ, 614, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Heinemann, T., Dobler, W., Nordlund, Å., & Brandenburg, A. 2006, A&A, 448, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jabbari, S., Brandenburg, A., Losada, I. R., Kleeorin, N., & Rogachevskii, I. 2014, A&A, 568, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jabbari, S., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2015, ApJ, 805, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Jabbari, S., Brandenburg, A., Mitra, D., Kleeorin, N., & Rogachevskii, I. 2016, MNRAS, 459, 4046 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., & Brandenburg, A. 2012a, ApJ, 755, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Brandenburg, A., Kleeorin, N., Mantere, M. J., & Rogachevskii, I. 2012b, MNRAS, 422, 2465 [NASA ADS] [CrossRef] [Google Scholar]
- Kemel, K., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2012, Astron. Nachr., 333, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Kemel, K., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2013, Sol. Phys., 287, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Mazur, M. V. 2000, Sol. Phys., 191, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Kleeorin, N., & Rogachevskii, I. 1994, Phys. Rev. E, 50, 2716 [NASA ADS] [CrossRef] [Google Scholar]
- Kleeorin, N. I., Rogachevskii, I. V., & Ruzmaikin, A. A. 1989, Pis. Astron. Zh., 15, 639 [NASA ADS] [Google Scholar]
- Kleeorin, N. I., Rogachevskii, I. V., & Ruzmaikin, A. A. 1990, Sov. Phys. JETP, 70, 878 [Google Scholar]
- Kleeorin, N., Mond, M., & Rogachevskii, I. 1993, Phys. Fluids, 5, 4128 [Google Scholar]
- Kleeorin, N., Mond, M., & Rogachevskii, I. 1996, A&A, 307, 293 [NASA ADS] [Google Scholar]
- Kleeorin, N., Rogachevskii, I., & Ruzmaikin, A. 1995, A&A, 297, 159 [NASA ADS] [Google Scholar]
- Losada, I. R., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2012, A&A, 548, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Losada, I. R., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2013, A&A, 556, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Losada, I. R., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2014, A&A, 564, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitra, D., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2014, 445, 761 [Google Scholar]
- Nordlund, Å. 1982, A&A, 107, 1 [Google Scholar]
- Parker, E. N. 1974a, Sol. Phys., 36, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1974b, Sol. Phys., 37, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Rogachevskii, I., & Kleeorin, N. 2007, Phys. Rev. E, 76, 056307 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2012, ApJ, 753, L13 [Google Scholar]
- Sur, S., Brandenburg, A., & Subramanian, K. 2008, MNRAS, 385, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J., Losada, I. R., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2013, ApJ, 777, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Yousef, T. A., Brandenburg, A., & Rüdiger, G. 2003, A&A, 411, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Stratification of |
| In the text | |
 |
Fig. 2 Gray scale representation of vertical velocity together with magnetic field lines in white for a run with B0 = 200 G (Run B′′). The yellow and red horizontal lines are the τ = 1 and τ = 100 surfaces, respectively. |
| In the text | |
 |
Fig. 3 Evolution of |
| In the text | |
 |
Fig. 4
|
| In the text | |
 |
Fig. 5 Vertical dependence of kHp for k/k1 = 1 and 4 (a), and of Beq(b). The vertical lines denote the surface where τ = 1. In panel a, we also show the dependence of kℓ in red. |
| In the text | |
 |
Fig. 6 Vertical dependence of the normalized magnetic field for different times in the nonlinear phase for B0 = 200 G (Run B′′). The location of τ = 1 is marked with a red filled symbol, while the diamond indicates τ = 0.1 and the two crosses denote τ = 10 and 100. |
| In the text | |
 |
Fig. 7 Effective magnetic pressure and its derivative with respect to the magnetic field strength for B0 = 100 G (black), 200 G (red), and 500 G (blue), corresponding to B0/Beq0 = 0.01, 0.03, and 0.07. The solid lines are based on using just the imposed magnetic field, β0, while the dotted lines are based on the actual field. |
| In the text | |
 |
Fig. 8 Comparison of the vertical profiles of ⟨ δlnB2 ⟩ 1/2 and ⟨ δlnT ⟩ (scaled by a factor 1000) for runs with different values of κ0 = 2 × 107 Mm-1 cm3 g-1(a), 5 × 107(b), and 108 cm3 s-1 Mm-1(c). The τ = 10, 1, and 0.1 surfaces are indicated in gray (from left to right). |
| In the text | |
 |
Fig. 9 Gray scale representation of vertical velocity together with magnetic field lines in white for the optically thick model at four times around saturation of NEMPI with otherwise the same parameters as Run B′′ with B0 = 200 G. |
| In the text | |
 |
Fig. 10 Similar to Fig. 9, but for the isentropic model. We note that also the color bar is unchanged. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.