EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 606 (October 2017) A&A, 606 (2017) A147 Full HTML
Free Access
Issue
A&A
Volume 606, October 2017
Article Number A147
Number of page(s) 9
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201731015
Published online 27 October 2017

© ESO, 2017

1. Introduction

Non-local thermodynamic equilibrium (non-LTE) modeling of stellar spectra is important for many fundamental problems in modern astrophysics (see, e.g., reviews Asplund 2005; Mashonkina 2014; Barklem 2016a, and references therein). One of the important fundamental problems of interest is determining absolute and relative abundances for different chemical elements in different stars.

For a given atomic species, non-LTE modeling requires detailed and complete information about the radiative and the non-radiative inelastic collision processes. The most important collisions are those with electrons, with hydrogen atoms, and with hydrogen negative ions. Information about the inelastic processes in collisions with hydrogen gives the main uncertainty for non-LTE studies (see Asplund 2005; Mashonkina 2014; Barklem 2016a, for reviews).

The most accurate information about inelastic processes in low-energy collisions with hydrogen is that obtained by full quantum calculations. They have been performed for collisions of hydrogen with a few chemical elements only: Na (Belyaev et al. 1999, 2010), Li (Croft et al. 1999a,b; Belyaev & Barklem 2003), Mg (Guitou et al. 2011, 2015; Belyaev et al. 2012), He (Belyaev 2015), and H (Stenrup et al. 2009). Full quantum calculations are seldom done because they are time-consuming. Owing to high demand in atomic data for inelastic processes in collisions with hydrogen, the Drawin formula (Drawin 1968, 1969; Drawin & Emard 1973; Steenbock & Holweger 1984; Lambert 1993) was proposed and widely used for non-LTE modeling. Nevertheless, it was recognized that the Drawin formula is not reliable, and Asplund (2005) stated that “replacing classical recipes like the Drawin formula must be considered a top priority for making progress on abundance determinations”. Later on, Barklem et al. (2011) made the critical analysis of the Drawin formula and concluded that for low-energy atomic collisions with hydrogen the Drawin formula (i) is not based on correct physics; (ii) overestimates inelastic rates up to several orders of magnitude for optically allowed atomic transitions; (iii) underestimates rates for optically forbidden transitions; and (iv) gives zero rates for mutual neutralization and ion-pair formation processes, which have the highest rates according to quantum calculations. Since the Drawin formula is not reliable, Barklem et al. (2011) emphasized the importance of deriving an approximate model approach to inelastic atomic collisions with hydrogen atoms, an approach that would be physically reliable but computationally not as expensive as a complete quantum study. Two such approaches for nonadiabatic nuclear dynamics have been proposed: the quantum branching probability current method (Belyaev 2013a) and the quantum multichannel analytic approach (Belyaev 1993; Belyaev et al. 2014; Yakovleva et al. 2016). Both approaches are based on electronic structure calculations and the Landau-Zener model. For electronic structure calculations, in addition to ab initio methods, the approximate methods have been used: the asymptotic method (Belyaev 2013a) and the linear combinations of atomic orbitals (LCAO) method (Barklem 2016b). The quantum model approaches have been successfully applied to a number of chemical elements relevant to non-LTE modeling (see, e.g., Belyaev 2013b; Belyaev et al. 2014, 2016; Barklem 2016b; Yakovleva et al. 2016, and references therein). The applications of the calculated rate coefficients into non-LTE models have demonstrated that the most important inelastic processes are those that have high and moderate rates (see, e.g., Mashonkina 2014; Barklem 2016a).

Although the approximate calculations are less time-consuming than the full quantum ones, they are still more complicated than the use of the Drawin formula. So, further simplifications for the quantum approximate approaches are highly desirable so that order of magnitude estimates can be obtained more easily, especially for inelastic processes with high and moderate rate coefficients. We propose a simplified model in order to estimate rate coefficients for low-energy inelastic processes with high and moderate values. This simplified model is derived here and is applied to potassium-hydrogen collisions.

2. Simplified model for inelastic collision rate coefficients

2.1. General remarks and basic formulas

The goal of the present paper is to propose a simplified model for approximate estimates of rate coefficients for inelastic processes in collisions of atoms and positive ions of different chemical elements with atoms and negative ions of hydrogen, that is, for the processes of mutual neutralization, ion-pair formation, excitation, and de-excitation. It should be emphasized that derived estimates (though approximate) have higher accuracy for rate coefficients with high and intermediate values and lower accuracy for rates with low values. Previous astrophysical applications, in particular non-LTE stellar atmosphere modelings, have shown that inelastic processes with high and intermediate collision rates are the most important for applications, while inelastic processes with low collision rates are negligible. So, the derived model is addressed to provide approximate estimates for rate coefficients with relatively high values, that is, for the processes from an optimal window (Belyaev 2013a). By “an optimal window” we mean an electronic energy interval for atomic states whose participation in inelastic collision processes leads to relatively high rate coefficients. We also define “the most optimal window” as rate coefficient values exceeding 10-8 cm3/ s and “the least optimal window” as rate coefficient values exceeding 10-10 cm3/ s (see below).

The proposed model is derived within the Born-Oppenheimer approach, which is the most widely used for treating heavy-particle collision processes. The same approach is used in both the full quantum and the approximate quantum calculations. Within the Born-Oppenheimer formalism a collision problem is treated in a molecular-state representation, that is, a collision problem is studied in two steps: (i) a fixed-nuclei electronic structure calculation for a (quasi-)molecule created by collisional partners and (ii) a study of the nonadiabatic nuclear dynamics.

As discussed by Belyaev (2013a), high values of inelastic cross sections and rate coefficients are determined by long-range nonadiabatic regions. Several mechanisms of collision processes have been found and discussed (see, e.g., Belyaev et al. 2012, and references therein), and it has been concluded (Belyaev et al. 2012, 2014; Belyaev 2013a; Yakovleva et al. 2016) that the highest values of rate coefficients are determined by nonadiabatic transitions in long-range regions created by ionic-covalent interactions, including the regions that correspond to optimal windows. Thus, the present model is based on long-range nonadiabatic regions due to interactions of molecular ionic and molecular covalent states.

Within a molecular-state representation, a rate coefficient Kif(T) of a particular inelastic process (for a transition i → f) is calculated as the sum of rate coefficients 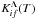KifΛ(T)\hbox{$K_{if}^{\Lambda}(T)$} over all possible molecular state symmetries 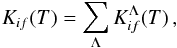Kif(T)=∑ΛKifΛ(T) ,\begin{equation} K_{if}(T) = \sum_{\Lambda} K_{if}^{\Lambda}(T) \, , \label{eq:rate-sum} \end{equation}(1)Λ being an absolute value of an electronic orbital momentum quantum number of molecular states treated (within the LS coupling scheme) and T the temperature. In general, Eq. (1) should be taken not only over Λ, but also over other quantum numbers of molecular states treated, in particular electronic spin, but the following features should be taken into account. The highest rates are based on ionic-covalent interactions, and considering that ionic molecular states of interest are created by interactions of H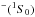(1−S0)\hbox{$^-(^1S_0)$} with positive ions; therefore, the electronic spin of a ground ionic molecular state is equal to a spin of a positive ion. Finally, Eq. (1) should be taken over ionic (molecular) Λ quantum numbers only.

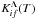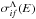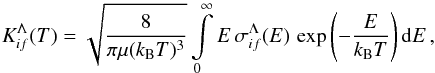Within a molecular symmetry Λ, a rate coefficient KifΛ(T)\hbox{$K_{if}^{\Lambda}(T)$} is calculated from a partial cross section σifΛ(E)\hbox{$\sigma_{if}^{\Lambda}(E)$} as KifΛ(T)=8πμ(kBT)3∫0∞E σifΛ(E) exp(−EkBT)dE ,\begin{equation} K_{if}^{\Lambda}(T) = \sqrt{\frac{8}{\pi \mu (k_{\rm B} T)^3}} \int\limits_0^\infty E\, \sigma_{if}^{\Lambda}(E)\, \exp \left(-\frac{E}{k_{\rm B} T}\right){\rm d}E \, , \label{eq:rate-partial} \end{equation}(2)where E is the collision energy, kB the Boltzmann constant, and μ the reduced nuclear mass. A cross section reads 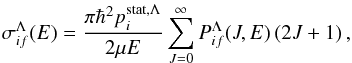σifΛ(E)=πħ2pistat,Λ2μE∑J=0∞PifΛ(J,E) (2J+1) ,\begin{equation} \sigma_{if}^{\Lambda}(E) = \frac{\pi \hbar^2 p_i^{\rm stat,\Lambda}}{2\mu E} \sum_{J=0}^\infty P_{if}^{\Lambda}(J,E) \, (2J+1) \, \label{eq:sigma} , \end{equation}(3)where J is the total angular momentum quantum number, 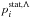pistat,Λ\hbox{$p_i^{\rm stat,\Lambda}$} a statistical probability for population of the initial molecular state i with a given molecular symmetry Λ from a scattering channel, and 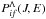PifΛ(J,E)\hbox{$P_{if}^{\Lambda}(J,E)$} a probability of an inelastic transition from an initial molecular state i to a final molecular state f. The main challenge for a collision treatment is a calculation of an inelastic transition probability 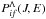PifΛ(J,E)\hbox{$P_{if}^{\Lambda}(J,E)$} for each transition and for each molecular symmetry of interest, for a given quantum number J and for a given collision energy E.

Equations (1)–(3) can be re-written in the form 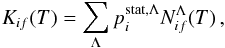Kif(T)=∑Λpistat,ΛNifΛ(T) ,\begin{equation} K_{if}(T) = \sum_{\Lambda} p_i^{\rm stat,\Lambda} N_{if}^{\Lambda}(T) \, , \label{eq:rate-sum-model} \end{equation}(4)where 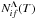NifΛ(T)\hbox{$N_{if}^{\Lambda}(T)$} is a reduced rate coefficient to be calculated (or estimated) for each transition i → f and for each quantum number Λ, which corresponds to a ground-state (diabatic) molecular ionic symmetry. The reduced rate coefficients are different for mutual neutralization and ion-pair formation processes on the one hand, and for excitation and de-excitation processes on the other hand. We keep the notation 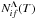NifΛ(T)\hbox{$N_{if}^{\Lambda}(T)$} in Eq. (4) for mutual neutralization and ion-pair formation processes, while for excitation and de-excitation processes we use the notation 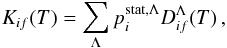Kif(T)=∑Λpistat,ΛDifΛ(T) ,\begin{equation} K_{if}(T) = \sum_{\Lambda} p_i^{\rm stat,\Lambda} D_{if}^{\Lambda}(T) \, , \label{eq:rate-sum-model-exc} \end{equation}(5)where the reduced rate coefficient 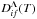DifΛ(T)\hbox{$D_{if}^{\Lambda}(T)$} has a meaning similar to the function 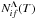NifΛ(T)\hbox{$N_{if}^{\Lambda}(T)$}, but for another class of the processes, namely for de-excitation and excitation.

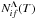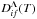Thus, in order to estimate rate coefficients the reduced rate coefficients NifΛ(T)\hbox{$N_{if}^{\Lambda}(T)$} and DifΛ(T)\hbox{$D_{if}^{\Lambda}(T)$} must be known for each molecular symmetry of interest. In many cases of interest a ground ionic state only has the Σ molecular symmetry, Λ = 0, but in some cases a ground ionic state has several molecular symmetries. An example is SiH; the ground ionic state has two molecular symmetries, Σ+ and Π, so it is necessary to treat two sets of molecular states in order to calculate rate coefficients in Si + H and Si+ + H− collisions (Belyaev et al. 2014).

2.2. Dependences on electronic bound energies

As stated above, within each molecular symmetry the state-to-state inelastic transition probabilities 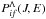PifΛ(J,E)\hbox{$P_{if}^{\Lambda}(J,E)$} with high values are usually determined by nonadiabatic transitions in long-range regions created by a ground ionic molecular diabatic state interacting with covalent molecular diabatic states. A location of each long-range nonadiabatic region can be evaluated by the asymptotic method (Belyaev 2013a) and is uniquely determined by an electronic bound energy Ej1 of an atomic state to which a covalent diabatic molecular state corresponds. Moreover, a nonadiabatic transition probability in each avoided-crossing nonadiabatic region can be evaluated by means of the Landau-Zener model (Landau 1932a,b; Zener 1932). The way to calculate Landau-Zener parameters in a nonadiabatic region formed by one covalent and one ionic molecular state by means of the asymptotic approach is described in detail in Belyaev (2013a). Within this approach, off-diagonal matrix elements are calculated by the semi-empirical formula2 (Olson et al. 1971) and depend on the same electronic bound energies of an atom. Finally, the Landau-Zener parameters are entirely determined by the electronic bound energies Ej.

Within each molecular symmetry, the inelastic transition probabilities 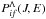PifΛ(J,E)\hbox{$P_{if}^{\Lambda}(J,E)$} with high values are usually determined by several nonadiabatic regions, due to interactions of an ionic molecular state with several covalent molecular states. A number of nonadiabatic regions is an individual characteristic of each chemical element interacting with hydrogen. In the case of several nonadiabatic regions, the state-to-state inelastic transition probabilities 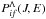PifΛ(J,E)\hbox{$P_{if}^{\Lambda}(J,E)$} with high values can be calculated by means of the multichannel approach (see Belyaev 1993; Yakovleva et al. 2016, for details and references). This approach takes into account the presence of several nonadiabatic regions, as well as other features of the nuclear dynamics. To apply the multichannel approach, a nonadiabatic transition probability in each nonadiabatic region is needed; such probabilities are calculated in the present work by means of the Landau-Zener model. In order to get general estimates, the multichannel approach can be further simplified by considering a minimum number of nonadiabatic regions, which should be taken into account to evaluate state-to-state inelastic transition probabilities, inelastic cross sections, and inelastic rate coefficients. This minimum number is different for mutual-neutralization/ion-pair-formation processes and for excitation/de-excitation processes, one for the former and two for the latter.

In the case of mutual-neutralization and ion-pair-formation processes A+ + H− ⇌ A(f) + H, the basic mechanism mainly corresponds to transitions in a single nonadiabatic region formed by an ionic A+ + H− and a covalent A(f) + H molecular state. Other nonadiabatic regions formed by the same ionic and other covalent states provide corrections to the dominant transition probability. Thus, in this case, the state-to-state inelastic transition probability, the inelastic cross section, and the rate coefficient are mainly determined by the electronic bound energy Ef ≡ EA(f) of the atomic state f. Finally, the reduced rate coefficient 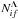NifΛ\hbox{$N_{if}^{\Lambda}$} for the mutual neutralization process i → f (see Eq. 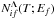(4)) depends on a single bound energy Ef, i.e., NifΛ(T;Ef)\hbox{$N_{if}^{\Lambda}(T; E_f)$}.

In the case of excitation and de-excitation processes A(i) + H → A(f) + H, the basic mechanism is determined by transitions in two nonadiabatic regions formed by an initial covalent state i, a final covalent state f, and an ionic molecular state which interacts with both covalent states. Other nonadiabatic regions give some corrections to the dominant transition probabilities. Thus, in this case, the state-to-state nonadiabatic transition probability, the inelastic cross section, and the inelastic rate coefficient depend on two electronic bound energies, Ei ≡ EA(i) and Ef ≡ EA(f). Finally, the reduced rate coefficient 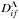DifΛ\hbox{$D_{if}^{\Lambda}$} for a transition i → f (see Eq. 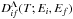(5)) depends on two bound energies, i.e., DifΛ(T;Ei,Ef)\hbox{$D_{if}^{\Lambda}(T; E_i, E_f)$}.

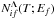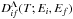Thus, the remaining problem consists in estimating the reduced rate coefficients NifΛ(T;Ef)\hbox{$N_{if}^{\Lambda}(T; E_f)$} and DifΛ(T;Ei,Ef)\hbox{$D_{if}^{\Lambda}(T; E_i, E_f)$} for a given temperature T as functions of the electronic bound energies Ej (one and two energies, respectively). As noted above, these reduced rate coefficients are determined by the different minimum numbers of nonadiabatic regions (one and two, respectively), so these functions are different.

2.3. Reduced rate coefficients for mutual neutralization and ion-pair formation processes

As discussed above, for each molecular symmetry Λ of an ionic molecular state, a reduced rate coefficient for mutual neutralization and ion-pair formation processes 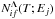NifΛ(T;Ej)\hbox{$N_{if}^{\Lambda}(T; E_j)$} with relatively high values is mainly determined by transitions in a single nonadiabatic region formed by an ionic A+ + H− and a covalent A(j) + H molecular states. A location and a Landau-Zener parameter of this region can be evaluated by the asymptotic approach (Belyaev 2013a) in combination with the semi-empirical formula (Olson et al. 1971). Since the location and the Landau-Zener parameter of this region are uniquely determined by the electronic bound energy of the atomic state A(j), so are the state-to-state inelastic transition probabilities 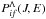PifΛ(J,E)\hbox{$P_{if}^{\Lambda}(J,E)$} and finally the inelastic cross sections and the inelastic rate coefficients (see Eqs. (2)–(4)). Based on the Landau-Zener model, all these values can be calculated numerically (see the formulas in Yakovleva et al. 2016). The rate coefficients for mutual neutralization (exothermic) processes depend weakly on the temperature, while the rates for ion-pair formation processes depend strongly. Taking this into account, it is better first to calculate the rate coefficients Kjk(T) for exothermic processes (j → k transitions, the mutual neutralization processes at present, j = ionic) and then to calculate the rate coefficients Kkj(T) for the inverse endothermic processes (k → j transitions, the ion-pair formation processes at present) by means of the detailed balance relation 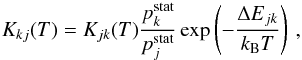Kkj(T)=Kjk(T)pkstatpjstatexp(−ΔEjkkBT) ,\begin{equation} K_{kj} (T ) = K_{jk}(T) \frac{p^{\rm stat}_k}{p^{\rm stat}_j} \exp \left( - \frac{ \Delta E_{jk}}{k_{\rm B} T} \right) \, , \label{eq:balance} \end{equation}(6)ΔEjk = Ej−Ek being the energy defect of the process. We note that for exothermic processes (j → k) ΔEjk is positive.

In the present work, we have calculated the reduced rate coefficient 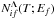NifΛ(T;Ef)\hbox{$N_{if}^{\Lambda}(T; E_f)$} for mutual neutralization process A+ + H− → A(f) + H as a function of the electronic bound energy Ef of the final atomic state A(f) and for different temperatures T. It should be noted that within the approximation used in the present simplified model the reduced rate coefficients do not depend on the quantum number Λ, but this quantum number must be taken into account when applying the simplified model to particular systems where the nonadiabatic transitions between molecular states are determined (see below). The numerical data for the reduced rate coefficient 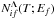NifΛ(T;Ef)\hbox{$N_{if}^{\Lambda}(T; E_f)$} are presented as the supplementary materials to the present paper. As an example, the reduced rate coefficient 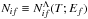Nif≡NifΛ(T;Ef)\hbox{$N_{if} \equiv N_{if}^{\Lambda}(T; E_f)$} for the temperature T = 6000 K is plotted in Fig. 1 as the solid line.

thumbnail Fig. 1

Mutual-neutralization reduced rate coefficients Nif≡NifΛ(T;Ef)\hbox{$N_{if} \equiv N_{if}^{\Lambda}(T; E_f)$} for the temperature T = 6000 K as a function of the electronic bound energy Ef. The bound energy is measured from the atomic ionization limit. The solid line shows the reduced rate coefficient calculated by means of the present simplified model; the symbols show the coefficients calculated by means of both the full quantum approach and the model approach for different collision partners and for different final states (hence with different electronic bound energies): H− + Li+ (Croft et al. 1999a,b), Na+ (Barklem et al. 2010), Mg+ (Guitou et al. 2015), Al+ (Belyaev 2013b), Be+ (Yakovleva et al. 2016), Ca+ (Belyaev et al. 2016).

It can be seen in this figure that the reduced rate coefficient reaches the maximum value 6.8 × 10-8 cm3/ s at the bound energy Ef = −2 eV. Also, within the most optimal window [–2.7, –1.5] eV the reduced rates have the highest values above 10-8 cm3/ s, while within the less optimal window (roughly [–4.0, –1.3] eV) the reduced rates have moderate values above 10-10 cm3/ s (down to nearly three orders of magnitude smaller than the maximum value). Outside of these optimal windows the reduced rates have negligible values. It is important to remember that the rate coefficients Kif(T) must be calculated by multiplying the reduced rates Nif by statistical probabilities and summed up over all possible symmetries of initial ionic molecular states (see Eq. (4)). Though within the simplified model the reduced rates are independent of the quantum number Λ (see above), but not all atomic states create all possible molecular ionic states with different Λ.

The same Fig. 1 shows the comparison of the reduced rate coefficients 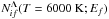NifΛ(T=6000K;Ef)\hbox{$N_{if}^{\Lambda}(T=6000~{\rm K}; E_f)$} for mutual neutralization processes calculated by means of the present simplified model with those calculated by means of the full quantum approaches for the same processes in collisions of H− with Li+ (Croft et al. 1999a,b), Na+ (Belyaev et al. 2010; Barklem et al. 2010), and Mg+ (Belyaev et al. 2012; Guitou et al. 2015), and by means of the quantum model approaches in collisions of H− with Al+ (Belyaev 2013a,b), Be+ (Yakovleva et al. 2016), and Ca+ (Belyaev et al. 2016). The final states of the mutual neutralization processes are determined by electronic bound energies Ef of corresponding atomic states. It can be seen that there is a general good agreement between the results obtained by the simplified model and those obtained by the accurate and approximate quantum approaches. For the most optimal window, the deviation ranges from 0% (exact agreement) to 50%; for the less optimal window from 0 up to a factor of 5, but mainly within a small percentage. There are two differences: the quantum approaches account for more long- and short-range nonadiabatic regions than the simplified model, and they provide more accurate electronic structure calculations especially for low-lying states. Outside of the optimal windows, the accuracy of the simplified model is lower, but rate coefficients are typically negligibly small. The example of this is the mutual neutralization into the Mg(3s3p 3P) state (Ef = −4.93 eV), where the discrepancy is nearly 2 orders of magnitude; as discussed by Belyaev (2013a), taking account of short-range nonadiabatic regions can increase low-valued rate coefficients dramatically, but weakly affects rate coefficients with relatively high values.

Thus, the present simplified model indicates which processes have substantial rate coefficients (i.e., it picks up final states lying in the optimal windows) and provides reliable estimates for rate coefficients with high and moderate values, which is the main goal of approximate models in general, and the present model in particular. Rate coefficients for ion-pair formation processes (the inverse of mutual neutralization processes) are determined by the detailed balance Eq. (6). It is better to calculate ion-pair-formation rates by the detailed balance equation since mutual-neutralization rates are weakly dependent on the temperature T.

2.4. Reduced rate coefficients for de-excitation and excitation processes

The reduced rate coefficients 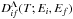DifΛ(T;Ei,Ef)\hbox{$D_{if}^{\Lambda}(T; E_i, E_f)$} (see Eq. (5)) for de-excitation and excitation processes A(i) + H → A(f) + H depend on two bound energies: on the electronic bound energy Ei of the atomic state A(i) and on the electronic bound energy Ef of the atomic state A(f). The mechanism of these processes corresponds to transitions into two nonadiabatic regions, a region created by an initial covalent molecular state and an ionic molecular state, and another region created by a final covalent molecular state and the same ionic molecular state. The reduced rate coefficients for (de-)excitation processes are calculated in the present paper by means of the simplified model; the results are tabulated and presented as the supplementary materials to the paper for different temperatures. Again, within the simplified model, the reduced rates are the same for all molecular symmetries, but the ionic-molecular-state symmetries determine which ones should be taken into account and which atomic states can create these symmetries. The example of the reduced rate coefficient 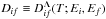Dif≡DifΛ(T;Ei,Ef)\hbox{$D_{if} \equiv D_{if}^{\Lambda}(T; E_i, E_f)$} for the temperature T = 6000 K is plotted in Fig. 2 as a function of Ei and Ef. When Ef<Ei, Dif corresponds to a de-excitation process, otherwise to an excitation process.

thumbnail Fig. 2

Excitation and de-excitation reduced rate coefficient Dif≡DifΛ(T;Ei,Ef)\hbox{$D_{if} \equiv D_{if}^{\Lambda}(T; E_i, E_f)$} as a function of the electronic bound energies Ei and Ef for the temperature T = 6000 K. The bound energies are measured from the atomic ionization limit. These two panels present the same surface for the reduced rate Dif shown from different view points.

It can be seen from Fig. 2 that the reduced rate Dif reaches the maximum of 1.4 × 10-8 cm3/ s at a point Ei ≈ Ef ≈ −2 eV and slightly exceeds the value of 10-8 cm3/ s in a narrow region in the vicinity of this point. It is worth emphasizing that the maximum of the reduced rate coefficient Nif for mutual neutralization is nearly 5 times higher than that for de-excitation Dif. The reduced rate coefficient Dif exceeds the value of 10-10 cm3/ s when roughly both bound energies Ei and Ef belong to the interval [–3.3, –1.4] eV, and exceeds the value of 10-11 cm3/ s when Ei and Ef belong to the interval [–4.0, –1.3] eV. These are the optimal windows for the excitation and de-excitation processes. Outside the optimal windows the reduced rate coefficients are negligibly small. The accuracy of the simplified model for (de-)excitation processes is similar to that for neutralization processes: reduced-rate estimates are more reliable for the processes with high and moderate rate coefficients, and less accurate for whose with low rates.

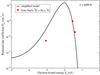thumbnail Fig. 3

Reduced rate coefficients Dif for the excitation and de-excitation processes in Na(4s) + H collisions as a function of the electronic bound energy Ef of the final states for the temperature T = 6000 K. The initial bound energy for Na(4s) is Ei = −1.95 eV. The bound energies are measured from the atomic ionization limit. The solid line shows the calculation using the simplified model; symbols show the full quantum calculation (Belyaev et al. 2010; Barklem et al. 2010).

thumbnail Fig. 4

Reduced rate coefficients Dif for the excitation and de-excitation processes in Al(4p) + H collisions as a function of the electronic bound energy Ef of the final states for the temperature T = 6000 K. The initial bound energy for Al(4p) is Ei = −1.90 eV. The bound energies are measured from the atomic ionization limit. The solid line shows the calculation using the simplified model; symbols show the full quantum calculation (Belyaev 2013a,b).

The comparison of the simplified model estimates of the reduced rate coefficients with those obtained by the full quantum calculation for Na(4s) + H collisions (Belyaev et al. 2010; Barklem et al. 2010) is shown in Fig. 3; the comparison with the quantum model approach for Al(4p) + H collisions (Belyaev 2013a,b) is shown in Fig. 4. The good agreement between the rates obtained by the simplified model and those obtained by more accurate approaches is clearly seen.

The simplified model estimates in Figs. 3 and 4 are obtained as cuts of the general 2D surface plotted in Fig. 2 at the corresponding bound energies of the initial atomic states Na(4s) and Al(4p), respectively. It should be noted that the two sections plotted in Figs. 3 and 4 correspond to the initial bound energies belonging to the most optimal window, so these two curves go through the maximum for Dif. Nevertheless, the final bound energies for Na and Al are discrete and are such that the de-excitation reduced rate in Al + H collisions indeed reaches nearly the maximum value, 10-8 cm3/ s, while the highest (de-)excitation reduced rates in Na + H collisions has a value that is an order of magnitude smaller, 10-9 cm3/ s. If an initial bound energy does not belong to the most optimal window, the corresponding section does not go through the maximum, so the corresponding reduced rate sections have different highest values, which are smaller than the global maximum.

Thus, the present simplified model provides reliable estimates for rate coefficients for excitation and de-excitation processes as well. For processes with high and moderate rates the estimates have higher accuracy; for those with low rates the accuracy is lower, but these processes can be neglected. We note that the rate coefficients Kif must be obtained from the reduced rate coefficients Dif by multiplying the latter by the corresponding statistical probabilities (see Eq. (5)). Since the de-excitation rates weakly depend on the temperature, it is better to estimate de-excitation rates first and then to calculate excitation rates by means of the detailed balance Eq. (6).

In summary, to estimate the rate coefficients of inelastic processes in collisions with hydrogen by means of the simplified method proposed in the present paper, the following simple steps are necessary:

Step 1: determining a molecular symmetry for the ground ionic (diabatic A+ + H−) molecular state within the LS scheme, i.e., determining a total electronic spin S and an electronic orbital projection quantum number Λ. An anion H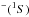(1−S)\hbox{$^-(^1S)$} has both spin and orbital quantum numbers equal to zero; therefore, S and Λ for the ionic molecular state are uniquely determined by the ground state of a cation A+ (S has a single value, Λ might have several values);

Step 2: determining atomic states, which produce covalent molecular (A(j) + H) states of the same symmetry as the ground ionic state determined in Step 1, and which correspond to a single-electron transition for the ionic-covalent interaction A+ + H− → A(j) + H. The bound energies Ej for the selected atomic states A(j) must be determined (e.g., from the NIST data base). It is sufficient to take into account atomic states with bound energies from the interval [–5.0, –1.2] eV; outside of this interval the rate coefficients are negligibly small;

Step 3: this step is slightly different for mutual-neutralization and for de-excitation processes:

Step 3a: for mutual-neutralization processes A+ + H− → A(f) + H. For a particular final state A(f), the corresponding electronic bound energy Ef is taken and then used to determine the corresponding reduced rate coefficient Nif from the tabulated function Nif(Ef) presented in Fig. 1 by the solid line (for T = 6000 K) and provided in the supplementary material (for T = 1000–10 000 K); in other words, Nif = Nif(Ef) is determined from the calculated function Nif(T,Ef) for a given temperature T;

Step 3b: for de-excitation processes A(i) + H → A(f) + H. For a particular initial state A(i) and a particular final state A(f), the corresponding electronic bound energies Ei and Ef are taken and then used to determine the corresponding reduced rate coefficient Dif from the tabulated function Dif(Ei,Ef) presented in Fig. 2 as the 2D surface (for T = 6000 K) and provided in the supplementary material (for T = 1000–10 000 K); in other words, Dif = Dif(Ei,Ef) is determined from the calculated function Dif(T,Ei,Ef) for a given temperature T. This can be done in one step by using the 2D function Dif(Ei,Ef) or in two steps by first taking a cut of the 2D function Dif(Ei,Ef) at a given bound energy Ei for the initial state A(i) and then by treating the 1D function Dif(Ef) at the given bound energy Ef;

Step 4: in order to get the rate coefficient for mutual-neutralization or for de-excitation processes, a statistical probability for the population of the initial molecular state is calculated and the reduced rate is multiplied by this statistical probability according to Eqs. (4) or (5), respectively. If the ground ionic state corresponds to different molecular symmetries (several Λ), then a sum over Λ should be taken. In order to get the rate coefficient for ion-pair formation or for excitation processes, calculate the rate coefficient for an inverse process from the corresponding rate coefficient for the direct process according to the detailed balance relation (6).

3. Application to potassium-hydrogen collisions

In the present section, we show how the simplified model can be applied to estimating rate coefficients of mutual neutralization, ion-pair formation, and excitation and de-excitation processes using the example of potassium-hydrogen collisions. To the best of our knowledge no potassium-hydrogen collision rates have been published.

Step 1: determining a ground ionic (diabatic) molecular state symmetry. For potassium-hydrogen collisions, the ground ionic K+(3p61S) + H−(1s2 1S) molecular state has the only symmetry, KH(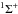Σ+1\hbox{$^1\Sigma^+$}). In this case, each sum in Eqs. (4) and (5) only has the term with Λ = 0 and total spin S = 0;

Step 2: determining the potassium atomic states to be treated and the corresponding electronic bound energies. It is necessary to determine potassium atomic states which (i) create KH(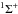Σ+1\hbox{$^1\Sigma^+$}) molecular states and (ii) correspond to single-electron transitions to the ground ionic state. Only the atomic states with the electronic bound energies from the interval [–5.0, –1.2] eV are taken into account; outside of this interval rate coefficients are negligibly small. These potassium atomic states (and the ionic state) with the corresponding scattering channels, bound energies, and statistical probabilities are collected in Table 1;

Table 1

Scattering channels correlated to KH(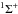Σ+1\hbox{$^1\Sigma^+$}) molecular states, their statistical probabilities 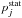pjstat\hbox{$p_j^{\rm stat}$}, and the asymptotic energies equal to the electronic bound energies Ej (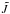˜J\hbox{$\tilde J$}-average experimental values taken from NIST; Kramida et al. 2012) with respect to the ionization limit K+(3p61S) + H(1s 2S).

Step 3: determining reduced rate coefficients:

Step 3a: in order to estimate rate coefficients for mutual neutralization processes, a reduced rate Nif(T,Ef) should be taken at a given temperature as a function of a final-state bound energy Ef. At T = 6000 K this function is plotted in Fig. 1 and shown again in Fig. 5 (solid lines). The reduced rate coefficients for particular mutual neutralization processes in K+ + H− collisions are determined by the values of the function Nif(T,Ef) at the particular final bound energies Ef from Table 1 (see the symbols in Fig. 5). For example, the atomic state K(5s 2S) has the electronic bound energy Ef = −1.734 eV. The corresponding reduced rate coefficient for the mutual neutralization process K+ + H− → K(5s 2S) + H is equal to Nif(T = 6000 K,Ef = −1.734 eV) = 3.55 × 10-8 cm3/ s (see Fig. 5);

thumbnail Fig. 5

General dependence of mutual-neutralization reduced rate coefficient (solid line) on a final bound energy Ef and the particular reduced rate coefficients for K+ + H− → K(f) + H processes (symbols) obtained by means of the present simplified model at T = 6000 K.

Step 3b: in order to estimate rate coefficients for de-excitation and excitation processes, a reduced rate Dif(T,Ei,Ef) should be taken at a given temperature as a 2D function of the initial- and final-state bound energies. At T = 6000 K this function is plotted in Fig. 2. The reduced rate coefficients for particular excitation and de-excitation processes K(i) + H → K(f) + H at a given temperature can first be determined as a cut of the 2D surface Dif(T,Ei,Ef) at an initial bound energy Ei, and then by taking particular values of this cut of Dif at the final bound energies Ef (see Table 1). The examples of the excitation and de-excitation processes in potassium-hydrogen collisions are shown in Figs. 6–8 for the initial states i = 2,3,4; for the initial states i = 1 and 5 the rate coefficients are much smaller;

thumbnail Fig. 6

Cut of de-excitation/excitation reduced rate coefficient Dif(Ei,Ef) for particular de-excitation and excitation processes K(4p) + H → K(f) + H for the initial bound energy Ei = E2 as a function of a final bound energy Ef (solid line) and the particular reduced rate coefficients for the same processes (symbols) obtained by means of the present simplified model at T = 6000 K.

thumbnail Fig. 7

Cut of de-excitation/excitation reduced rate coefficient Dif(Ei,Ef) for particular de-excitation and excitation processes K(5s) + H → K(f) + H for the initial bound energy Ei = E3 as a function of a final bound energy Ef (solid line) and the particular reduced rate coefficients for the same processes (symbols) obtained by means of the present simplified model at T = 6000 K.

thumbnail Fig. 8

Cut of de-excitation/excitation reduced rate coefficient Dif(Ei,Ef) for particular de-excitation and excitation processes K(3d) + H → K(f) + H for the initial bound energy Ei = E4 as a function of a final bound energy Ef (solid line) and the particular reduced rate coefficients for the same processes (symbols) obtained by means of the present simplified model at T = 6000 K.

Step 4: estimating rate coefficients. Since the statistical probability 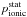pionicstat\hbox{$p_{\rm ionic}^{\rm stat}$} for the ionic channel is presently equal to 1, the rate coefficients of the mutual neutralization processes Kif coincide with the corresponding reduced rate coefficients Nif (see Eq. (4)). Rate coefficients for the ion-pair formation processes are calculated from the mutual neutralization rates by the detailed balance Eq. (6). The rate coefficients Kif for the de-excitation processes are calculated from the reduced rate coefficients Dif by multiplying the latter by the statistical probability 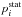pistat\hbox{$p_{i}^{\rm stat}$} (see Eq. (5)). Although rate coefficients Kif for excitation processes can be calculated directly from the reduced rate coefficients Dif, it is more practical first to calculate the rate coefficients for the de-excitation processes and then to compute Kif for excitation processes from the rate coefficients for the de-excitation processes using the detailed balance Eq. (6).

The rate coefficients Kif(T) for all possible processes in potassium-hydrogen collisions are estimated by the present simplified model and presented in Table 2 for the temperature range T = 1000–10 000 K.

Table 2

Rate coefficients, in units of cm3/s, for selected temperatures in the range T = 1000–10 000 K for the excitation, de-excitation, ion-pair formation, and mutual neutralization processes in potassium-hydrogen collisions.

4. Conclusion

In the present paper, the simplified model is derived for estimating rate coefficients of inelastic processes in low-energy collisions of hydrogen atoms and negative ions with atoms and positive ions of other chemical elements. The main goal of the model is to estimate rate coefficients with high and moderate values, that is, the rates which are important for non-LTE modeling. The model is based on the main reaction mechanism of these processes, which is determined by nonadiabatic transitions in long-range regions created by interactions of ionic and covalent molecular states of treated quasi-molecules. Within the derived model, the rate coefficients are expressed via reduced rate coefficients that are different for mutual-neutralization/ion-pair-formation processes and for excitation/de-excitation processes. It turns out that the reduced rate coefficients for mutual-neutralization/ion-pair-formation processes depend on a single bound energy of an atomic state which correlates to a corresponding covalent state, while the reduced rate coefficients for excitation/de-excitation processes depend on two bound energies: electronic bound energies for an initial and a final atomic state. In the present paper, the reduced rate coefficients are calculated and tabulated. Optimal windows for mutual-neutralization/ion-pair-formation and for excitation/de-excitation processes are determined. The reduced rate coefficients are compared with available data obtained by full quantum and by quantum model calculations. The reasonable agreement is found. For the most optimal windows the agreement is within a small percentage and up to 50%. For the less optimal windows the agreement is within a factor of 5.

It is worth pointing out that the simplified method derived in the present paper does not have any adjustable parameters. Without any additional calculation, the method indicates which processes have high and moderate rate coefficients, and hence are expected to be important for non-LTE stellar atmosphere modeling. Moreover, the simplified method helps in understanding a general distribution of inelastic rate coefficients in collisions of different chemical elements with hydrogen. In particular, the method selects atomic states which are efficiently involved in the inelastic H-collision processes. This is done by determining the optimal windows of atomic states, that is, by determining the electronic bound energy intervals for atomic states whose participation leads to high and moderate rate coefficients. It is shown that these intervals are the same for all chemical elements, namely they are located in the vicinity of the electronic bound energy –2 eV.

The simplified method allows rate coefficients to be estimated for mutual neutralization, ion-pair formation, excitation, and de-excitation processes in collisions of hydrogen with many chemical elements. In the present paper, the simplified model is applied to hydrogen-potassium collisions. The rate coefficients for the most important mutual neutralization, ion-pair formation, excitation, and de-excitation processes are estimated. In future work, the model will be applied to other collisions of astrophysical interest.

1

In the present paper, an electronic bound energy is measured from an ionization limit of an atom, hence it is negative. If an electronic energy 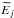􏽥Ej\hbox{$\widetilde{E}_j$} is measured from an atomic ground-state energy as a zero-energy level, then the electronic bound energy should be recalculated as 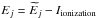Ej=􏽥Ej−Iionization\hbox{$E_j = \widetilde{E}_j - I_{\rm ionization}$}, where Iionization is an ionization potential of an atom.

2

This formula is only applicable to single-electron transitions.

Acknowledgments

The authors gratefully acknowledge partial support from the Ministry for Education and Science (Russian Federation), Project Nos. 3.1738.2017/4.6, 3.5042.2017/6.7.

References

  1. Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
  2. Barklem, P. S. 2016a, A&ARv, 24, 9 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barklem, P. S. 2016b, Phys. Rev. A, 93, 042705 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barklem, P. S., Belyaev, A. K., Dickinson, A. S., & Gadea, F. X. 2010, A&A, 519, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Barklem, P. S., Belyaev, A. K., Guitou, M., et al. 2011, A&A, 530, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Belyaev, A. K. 1993, Phys. Rev. A, 48, 4299 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Belyaev, A. K. 2013a, Phys. Rev. A, 88, 052704 [NASA ADS] [CrossRef] [Google Scholar]
  8. Belyaev, A. K. 2013b, A&A, 560, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Belyaev, A. K. 2015, Phys. Rev. A, 91, 062709 [NASA ADS] [CrossRef] [Google Scholar]
  10. Belyaev, A. K., & Barklem, P. S. 2003, Phys. Rev. A, 68, 062703 [NASA ADS] [CrossRef] [Google Scholar]
  11. Belyaev, A. K., Grosser, J., Hahne, J., & Menzel, T. 1999, Phys. Rev. A, 60, 2151 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  12. Belyaev, A. K., Barklem, P. S., Dickinson, A. S., & Gadéa, F. X. 2010, Phys. Rev. A, 81, 032706 [NASA ADS] [CrossRef] [Google Scholar]
  13. Belyaev, A. K., Barklem, P., Spielfiedel, A., et al. 2012, Phys. Rev. A, 85, 032704 [NASA ADS] [CrossRef] [Google Scholar]
  14. Belyaev, A. K., Yakovleva, S. A., & Barklem, P. S. 2014, A&A, 572, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Belyaev, A. K., Yakovleva, S., Guitou, M., et al. 2016, A&A, 587, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Croft, H., Dickinson, A. S., & Gadéa, F. X. 1999a, J. Phys. B: At. Mol. Opt. Phys., 32, 81 [NASA ADS] [CrossRef] [Google Scholar]
  17. Croft, H., Dickinson, A. S., & Gadéa, F. X. 1999b, MNRAS, 304, 327 [NASA ADS] [CrossRef] [Google Scholar]
  18. Drawin, H.-W. 1968, Z. Phys., 211, 404 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Drawin, H.-W. 1969, Z. Phys., 225, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Drawin, H.-W., & Emard, F. 1973, Phys. Lett. A, 43, 333 [NASA ADS] [CrossRef] [Google Scholar]
  21. Guitou, M., Belyaev, A. K., Barklem, P. S., Spielfiedel, A., & Feautrier, N. 2011, J. Phys. B, 44, 035202 [Google Scholar]
  22. Guitou, M., Spielfiedel, A., Rodionov, D. S., et al. 2015, Chem. Phys., 462, 94 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team 2012, in NIST Atomic Spectroscopy Database, Version 5.0, http://physics.nist.gov/asd (Gaithersburg: National Institute of Standards and Technology) [Google Scholar]
  24. Lambert, D. L. 1993, Phys. Scr. T, 47, 186 [NASA ADS] [CrossRef] [Google Scholar]
  25. Landau, L. D. 1932a, Phys. Z. Sowietunion, 1, 88 [Google Scholar]
  26. Landau, L. D. 1932b, Phys. Z. Sowietunion, 2, 46 [Google Scholar]
  27. Mashonkina, L. 2014, IAU Symp., 298, 355 [NASA ADS] [Google Scholar]
  28. Olson, R. E., Smith, F. T., & Bauer, E. 1971, Appl. Opt., 10, 1848 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  29. Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
  30. Stenrup, M., Larson, A., & Elander, N. 2009, Phys. Rev. A, 79, 012713 [NASA ADS] [CrossRef] [Google Scholar]
  31. Yakovleva, S., Voronov, Y. V., & Belyaev, A. K. 2016, A&A, 593, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Zener, C. 1932, Proc. Roy. Soc. A, 137, 696 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Scattering channels correlated to KH(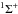Σ+1\hbox{$^1\Sigma^+$}) molecular states, their statistical probabilities 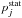pjstat\hbox{$p_j^{\rm stat}$}, and the asymptotic energies equal to the electronic bound energies Ej (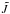˜J\hbox{$\tilde J$}-average experimental values taken from NIST; Kramida et al. 2012) with respect to the ionization limit K+(3p61S) + H(1s 2S).

In the text
Table 2

Rate coefficients, in units of cm3/s, for selected temperatures in the range T = 1000–10 000 K for the excitation, de-excitation, ion-pair formation, and mutual neutralization processes in potassium-hydrogen collisions.

In the text

All Figures

thumbnail Fig. 1

Mutual-neutralization reduced rate coefficients Nif≡NifΛ(T;Ef)\hbox{$N_{if} \equiv N_{if}^{\Lambda}(T; E_f)$} for the temperature T = 6000 K as a function of the electronic bound energy Ef. The bound energy is measured from the atomic ionization limit. The solid line shows the reduced rate coefficient calculated by means of the present simplified model; the symbols show the coefficients calculated by means of both the full quantum approach and the model approach for different collision partners and for different final states (hence with different electronic bound energies): H− + Li+ (Croft et al. 1999a,b), Na+ (Barklem et al. 2010), Mg+ (Guitou et al. 2015), Al+ (Belyaev 2013b), Be+ (Yakovleva et al. 2016), Ca+ (Belyaev et al. 2016).
In the text
thumbnail Fig. 2

Excitation and de-excitation reduced rate coefficient Dif≡DifΛ(T;Ei,Ef)\hbox{$D_{if} \equiv D_{if}^{\Lambda}(T; E_i, E_f)$} as a function of the electronic bound energies Ei and Ef for the temperature T = 6000 K. The bound energies are measured from the atomic ionization limit. These two panels present the same surface for the reduced rate Dif shown from different view points.

In the text
thumbnail Fig. 3

Reduced rate coefficients Dif for the excitation and de-excitation processes in Na(4s) + H collisions as a function of the electronic bound energy Ef of the final states for the temperature T = 6000 K. The initial bound energy for Na(4s) is Ei = −1.95 eV. The bound energies are measured from the atomic ionization limit. The solid line shows the calculation using the simplified model; symbols show the full quantum calculation (Belyaev et al. 2010; Barklem et al. 2010).

In the text
thumbnail Fig. 4

Reduced rate coefficients Dif for the excitation and de-excitation processes in Al(4p) + H collisions as a function of the electronic bound energy Ef of the final states for the temperature T = 6000 K. The initial bound energy for Al(4p) is Ei = −1.90 eV. The bound energies are measured from the atomic ionization limit. The solid line shows the calculation using the simplified model; symbols show the full quantum calculation (Belyaev 2013a,b).

In the text
thumbnail Fig. 5

General dependence of mutual-neutralization reduced rate coefficient (solid line) on a final bound energy Ef and the particular reduced rate coefficients for K+ + H− → K(f) + H processes (symbols) obtained by means of the present simplified model at T = 6000 K.
In the text
thumbnail Fig. 6

Cut of de-excitation/excitation reduced rate coefficient Dif(Ei,Ef) for particular de-excitation and excitation processes K(4p) + H → K(f) + H for the initial bound energy Ei = E2 as a function of a final bound energy Ef (solid line) and the particular reduced rate coefficients for the same processes (symbols) obtained by means of the present simplified model at T = 6000 K.
In the text
thumbnail Fig. 7

Cut of de-excitation/excitation reduced rate coefficient Dif(Ei,Ef) for particular de-excitation and excitation processes K(5s) + H → K(f) + H for the initial bound energy Ei = E3 as a function of a final bound energy Ef (solid line) and the particular reduced rate coefficients for the same processes (symbols) obtained by means of the present simplified model at T = 6000 K.
In the text
thumbnail Fig. 8

Cut of de-excitation/excitation reduced rate coefficient Dif(Ei,Ef) for particular de-excitation and excitation processes K(3d) + H → K(f) + H for the initial bound energy Ei = E4 as a function of a final bound energy Ef (solid line) and the particular reduced rate coefficients for the same processes (symbols) obtained by means of the present simplified model at T = 6000 K.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.