EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 606 (October 2017) A&A, 606 (2017) A11 Full HTML
Free Access
Issue
A&A
Volume 606, October 2017
Article Number A11
Number of page(s) 7
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201730864
Published online 26 September 2017

© ESO, 2017

1. Introduction

Magnesium is an element of significant astrophysical importance. It is an α-element produced by hydrostatic carbon burning in massive stars and ejected in core-collapse supernovae occurring just a few years after carbon burning is complete (C burning itself takes a few hundred years). Its significant abundance combined with its array of spectral features across the UV, visual, and IR spectrum, means that it is observable in stars of all spectral types, and even in the most metal-poor stars. Its production depends sensitively on the progenitor mass of the star (e.g. Woosley & Weaver 1995; Limongi et al. 2000), and is therefore an important diagnostic of this in supernova spectral analysis (e.g. Fransson & Chevalier 1989). From an atomic physics point of view, Mg is also attractive for study, as it is a quasi two-electron system and thus often tractable to full-quantum treatments using recently-developed computational methods.

Modelling of astrophysical gas and plasma out of equilibrium requires that all relevant radiative and collisional processes on the atom of interest be described, and modern high quality observations demand better modelling, which in turn demands better input atomic data. For any astrophysical gas with a significant degree of ionisation, collisions involving electrons are very important, due to predominantly their higher speed than the heavier particles, which in turn leads to relatively large collision rates and usually larger cross sections.

Non-local thermodynamic equilibrium (non-LTE) modelling of Mg is done for a range of purposes. Some recent examples include the measurement of stellar abundances in cool stars (Bergemann et al. 2015; Osorio et al. 2015; Osorio & Barklem 2016) and in hot stars (Przybilla et al. 2001), the use of the Mg i intercombination line at 457 nm as a temperature diagnostic of the solar chromosphere (Langangen & Carlsson 2009), and as a probe of velocity fields in giants stars (Vieytes et al. 2011). In addition, IR lines of Mg at 12 and 18 μm that are seen in emission in some cool stars (Chang & Noyes 1983) may have future diagnostic potential, and they are known to form in far from LTE conditions (Chang et al. 1991; Carlsson et al. 1992; Sundqvist et al. 2008; Osorio et al. 2015). Mg lines are important in the modelling of spectra of supernovae ejecta (Jerkstrand et al. 2012, 2015), where the main line seen in nebular SN spectra is the Mg i 457 nm intercombination line, although Mg i 1.50 μm is also normally seen when NIR observations are taken.

Many of the studies mentioned above use data for inelastic electron collision processes on neutral Mg assembled by Mauas et al. (1988). These data were collected from various sources, and are a mixture of theoretical, semi-empirical, and experimental results. Recently, attempts have been made to improve the situation and provide a coherent and consistent dataset from modern close-coupling calculations, namely the B-spline R-matrix (BSR) method and the R-matrix with pseudostates (RMPS) method. Merle et al. (2015) presented data based on the BSR method (Zatsarinny et al. 2009). However, this dataset did not include triplet-triplet transitions, and thus is of limited usefulness for modelling the Mg atom as a whole. Osorio et al. (2015) presented data obtained with the RMPS method. In this case the data cover only the lowest ten states, and for higher-lying states had to be complemented by the use of the impact parameter method (Seaton 1962) for optically allowed transitions, and in the case of forbidden transitions by assuming similar behaviour as the R-matrix calculations for low-lying states. We note that various lines of interest, for example at 552.8 nm, involve such higher-lying states.

Thus, though the recent work of Merle et al. (2015) and Osorio et al. (2015) are no doubt improvements on the data in Mauas et al. (1988), both works have shortcomings in terms of the completeness one would wish for in non-LTE modelling of the entire Mg atom. The aim of the present work, therefore, is to provide a set of electron collision data for neutral magnesium that is both reliable and approaching the level of completeness required. For this purpose, calculations have been performed using the convergent close-coupling (CCC) method, as well as new calculations with the BSR method. In this paper we will present effective collision strengths calculated from these methods for transitions between the 25 lowest-lying states (i.e. up to 3s6p1P). The results are compared to give an indication of the reliabilities of the datasets.

2. Theory and calculations

Calculations have been done using the CCC (Bray & Stelbovics 1995; Bray et al. 2002) and BSR methods (see Zatsarinny & Bartschat 2013, and references therein). These calculations are now detailed in turn.

The CCC method has already been extensively applied to the electron-magnesium collision system (Fursa & Bray 2001; Bartschat et al. 2004; Brown et al. 2005; Bray et al. 2015). The atomic target is treated as two-electrons above an inert Hartree-Fock core (Fursa & Bray 1997). The target states are acquired by first obtaining one-electron orbitals by diagonalising the Mg+ Hamiltonian in a Laguerre basis, and then constructing two-electron configurations from the orbitals and diagonalising the Mg Hamiltonian. The states are used to define the close-coupling equations in momentum space, which are solved separately for every partial wave and incident energy. The convergence of the results is tested by increasing the size of the Laguerre basis, and utilising the resulting increased number of states in the calculations. The present CCC results were obtained by taking the Laguerre basis size to be Nl = 30−l for lmax = 4, which generated a total of 259 states. These were checked for convergence against calculations with Nl = 25−l, which generated 209 states. Only the results of the largest CCC calculation are being presented.

For the present work a new calculation has been performed with the BSR method, which improves upon the earlier calculation presented in Zatsarinny et al. (2009) and Merle et al. (2015). This model includes 32 bound states of Mg plus 680 continuum pseudostates with energies up to 30 eV. These R-matrix with pseudostates calculations are similar to the recent BSR calculations for e+Be (Zatsarinny et al. 2016) and e+B (Wang et al. 2016), where more computational details are given. The target states in the BSR calculations were generated in the same scheme as in Zatsarinny et al. (2009); however, the R-matrix radius was reduced from 80 to 45 a.u. to cover a larger range in the Mg pseudospectrum.

In both the CCC and BSR calculations, the 25 lowest contiguous physical states of Mg, up to 3s6p1P, fit into the effective boxes defined in the computational models (either by the exponent in the Laguerre basis or by the R-matrix radius), and robust cross sections obtained. Table 1 presents the considered states, along with their experimental excitation energies. In both cases, the collision calculations were performed for electron energies from threshold to about 100 eV. Cross sections for selected cases of electric dipole, non-dipole spin-conserving, and spin-changing transitions are shown in Figs. 1−3, respectively. We note that BSR structure calculations for Mg were presented and discussed in Zatsarinny et al. (2009). Overall, they present an accurate description of the binding energies and oscillator strengths. However, in the scattering calculations the calculated excitation energies are adjusted to the experimental ones in Table 1 to remove possible additional uncertainties related to the error in the excitation thresholds. In the CCC calculations, the energies from the structure calculations are retained and therefore the cross section comparisons in the figures checks both the target structure and collision dynamics of the calculations.

Table 1

Physical states for which data are provided from the CCC and BSR calculations, along with experimental excitation energies (Eexpt) from NIST (Kramida et al. 2016; Martin & Zalubas 1980).

thumbnail Fig. 1

Cross sections for selected electric dipole transitions.

thumbnail Fig. 2

Cross sections for selected spin-conserving non-electric dipole transitions.

thumbnail Fig. 3

Cross sections for selected spin-changing transitions.

The present CCC and BSR calculations are performed in a nonrelativistic formulation of these methods. Mg i is a light atom and it is expected that relativistic effects are small for both collision dynamics and target wave functions. As a consequence, excitation of Mg i triplet states proceeds via exchange scattering. We have verified this by performing fully relativistic CCC calculations (Fursa & Bray 2008) at a number of energies and finding good agreement with nonrelativistic CCC and BSR results. A comparison of relativistic and nonrelativistic cross sections requires a transformation from LS to LSJ coupling for the nonrelativistic theory and introduction of statistical weights (1/3 for the 3s3p3P state) that multiply the nonrelativistic cross sections. A simple way to estimate the importance of relativistic effects is to evaluate how they affect the target wave functions. For example, for the 3s3p3P1 state this can be approximately described by the singlet-triplet mixing of the nonrelativistic wave functions with a mixing coefficient of order 10-3. The effect on the cross sections is proportional to the square of the mixing coefficient and is negligible at all incident electron energies considered in this paper. Note, however, that the radiative intercombination 3s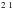S−3s3p 3P1 line is a result of relativistic effects.

In applications, the rate coefficient is required, which is calculated by folding the cross sections σ with the velocity distribution, assumed here to be the Maxwell distribution. That is 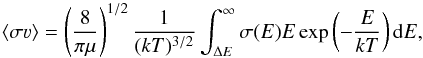(1)where μ is the reduced mass of the colliding system, ΔE is the energy threshold for the given process, E is the collision energy (in the centre-of-mass frame), and other symbols have their usual meanings. Following Seaton (1953), one can define the thermally-averaged or effective collision strength, which is related to the rate coefficients by simple expressions. In cgs units, for Ej>Ei, and thus for excitation we have 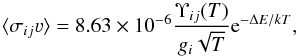(2)where ΔE = Ej−Ei, and for deexcitation (via the detailed balance relation), 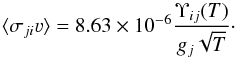(3)The collision strengths have the advantage of being both dimensionless and symmetric. We have therefore chosen to present and discuss effective collision strengths Υij, even though rate coefficients ⟨ σijν ⟩ are required in non-LTE applications. The calculation of the effective collision strengths was done in all cases by first calculating the rate coefficient from the excitation cross sections via Eq. (1), and then transforming to the effective collision strength using Eq. (2), using the data in Table 1.

3. Results and discussion

The results of the calculations for the effective collision strengths Υij from the CCC and BSR calculations are presented for temperatures T ranging from 1000 K to 10 000 K in steps of 1000 K, with additional results for 500 K at the cool end, and 15 000 K and 20 000 K at the hot end. This temperature grid is chosen to focus on the range of temperatures where the abundance of neutral magnesium will be significant. At cooler temperatures, there will be significant molecule formation, and at hotter temperatures Mg will be ionised. The data are presented as matrices, following the ordering of indexes in Table 1 (i.e. the transition 1–2 corresponds to element (1, 2)), one for each temperature. An example matrix each for the CCC and BSR calculations at 5000 K is shown in Tables 2 and 3, respectively. The full tables, and tables for other temperatures, are available electronically at CDS.

Table 2

Sample of electronic table for effective collision strengths Υij at 5000 K from the CCC calculation.

Table 3

Sample of electronic table for effective collision strengths Υij at 5000 K from the BSR calculation.

thumbnail Fig. 4

Comparison of the effective collision strengths Υij at 5000 K from CCC and BSR. The central dashed line shows the one-to-one relation, with the outer dashed lines showing factors of two and ten departures from this relation. Circled points are transitions involving the lowest five states of Mg. Points shown surrounded by a square are the transitions from the ground state to the two lowest-lying excited states, i.e. 3s–3s3p3P and 3s–3s3p1P, the former always having a larger effective collision strength.

The results from the CCC and BSR calculations at 5000 K are compared in Fig. 4. The agreement between the calculations is quantified in Table 4, where statistical measures of the location (offset) and scale (scatter) of the ratios of thermally averaged collision strengths are given. The agreement between the CCC and BSR calculations is very good, with an offset of only 4% (BSR larger than CCC), and a scatter of less than 30%. The agreement between the CCC and BSR results, from independent methods and calculations, suggests that these datasets are reliable to this level of accuracy.

Table 4

The location and scale of the ratio Υij(1)/Υij(2), where Υij(1) corresponds to dataset 1, and Υij(2) corresponds to dataset 2.

As mentioned in Sect. 1, the set of electron collision data assembled by Mauas et al. (1988, M88) is widely used in astrophysical applications. It combines data from theory, usually in the Born approximation, experimental results where available, and results from the semi-empirical Bethe-Born formula of van Regemorter (1962) for optically allowed transitions, and an arbitrary scaling of the van Regemorter formula for forbidden transitions. Figure 5 shows the comparison of the effective collision strengths corresponding to the data from M88 with the CCC results at 5000 K, and the statistical comparisons with other datasets also quantified in Table 4. It is seen that the agreement is usually within a factor of ten, but with some cases disagreeing by significantly more1. The transition between the two lowest states, 3s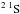–3s3p3P, is of particular relevance, as it corresponds to the intercombination line at 457 nm, and thus controls this transition. We note that the value in M88 is significantly lower, only 40% of the values found in the CCC and BSR calculations, a factor of 2.5 lower.

thumbnail Fig. 5

Comparison of the effective collision strengths Υij from Mauas et al. (1988), with those from the CCC calculations, at 5000 K. The lines and points follow the description in Fig. 4.

The precise origin of this discrepancy is difficult to determine. Mauas et al. state that to obtain the data for this transition they “combined the absolute value of Robb (1974) and the energy dependence measured by Aleksakhin et al. (1973)”. The mentioned paper by Robb presents Born cross sections for the resonance 3s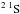–3s3p1P transition at electron energies above 10 eV, but does not cover the 3s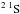–3s3p3P transition. We note that another paper by the same author, Robb (1975), employs the R-matrix method and does indeed include results for the 3s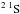–3s3p3P transition; these results are reproduced by Fabrikant et al. (1988, see Fig. 21). This calculation obtains a maximum cross section of about 22 × 10-16 cm2, while the present results have a maximum cross section of about 25 × 10-16 cm2; see Fig. 3. However, we note that the energy dependence measured by Aleksakhin et al. (1973) obtains its maximum value at ~4.5 eV, with significantly lower values near the threshold at 2.7 eV. In contrast, the present results find the maximum value very close to threshold, 2.7–3.0 eV, and the cross section has already decreased to half the maximum value by ~4.5 eV. Thus, it seems likely that the discrepancy primarily originates in the different threshold behaviours of the present calculations compared to those measured and presented by Aleksakhin et al. (1973). It is unclear to what degree the details of these experimental results are reliable. We also note that the threshold behaviour for the 3s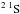–3s3p1P transition obtained by Aleksakhin et al. is also considerably less steep than that measured by Leep & Gallagher (1976; see Fig. 2 of that paper), which may indicate an appreciable uncertainty.

Comparisons with the data of Merle et al. (2015) and Osorio et al. (2015) were also performed, but for the sake of simplicity of presentation, we have chosen not to present or analyse these in detail. It suffices to say that these datasets compare significantly better than M88 with the new data, with agreement to better than a factor of two. However, the agreement is certainly worse than the internal agreement of the present CCC and BSR results.

4. Applications

To make an initial assessment of the impact of the new data, we performed a small number of calculations in example astrophysical applications: in late-type stellar atmosphere models, and in a supernova ejecta model.

4.1. Late-type stellar atmospheres

To test the effects on modelling of Mg lines in late-type stellar atmospheres, we computed synthetic non-LTE spectra following Osorio et al. (2015). As in that paper, we employ four atmospheric models from the MARCS grid (Gustafsson et al. 2008): two giants (Teff(K), log g = 4500, 1.5) and two dwarfs (Teff(K), log g = 6000, 4.5); in each case one with solar metallicity, [Fe/H] = 0.0, and the other metal-poor, [Fe/H] = −2.0. The model atoms used are identical to the final model atom in Osorio et al. (model “F”) differing only in the electron collision data. For collisions between the states shown in Table 1 we used the CCC data in one version of the model atom, and BSR in another. For the remaining transitions, the impact parameter (IP) formula from Seaton (1962) was used. Additionally, we constructed a model atom with the electron collision data from M88 and again used the IP formula for the remaining transitions. Osorio et al. should be consulted for additional details regarding the model atom and the non-LTE radiative transfer calculations.

All the spectral lines considered in Table 1 of Osorio et al. were computed, and the effects examined. The new data have no effect in any of the models on the infrared lines at 7, 12 and 18 μm, as would be reasonably expected from the fact that these lines arise from levels lying higher than those for which new data is available. Regarding the absorption lines at λ< 1 μm, we examined the effects on the final abundance corrections2ΔA(Mg), and for all lines these were found to be <0.01 dex in all four stellar models, except in the case of the 457 nm line. The abundance corrections for this line for the four atmospheric models, using the various electron collision datasets, are shown in Fig. 6. For both dwarf models, this line also shows negligible differences in ΔA(Mg) regardless of the electron collisional data used. It is also worth to note here that the predicted centre-to-limb variation is also practically unchanged in the dwarf models, and thus the same is expected in the Sun.

thumbnail Fig. 6

Abundance corrections for the 457 nm line using four atmospheric models and four model atoms differing only in the electron collisional data used. The parameters of the atmospheric models are shown in the bottom left of each panel in the format Teff/log g/[Fe/H]. The M88 model atom (solid line) includes data from Mauas et al. (1988), the RMPS model is the model “F” used in Osorio et al. (2015; dashed line), the CCC model uses the CCC data presented in this work (dot-dashed line) and the BSR model uses the BSR data presented here (triple-dot-dashed line). The shaded region shows the expected values of A(Mg) for a typical star of the given metallicity. The points show the calculated points.

The giant atmospheric models, however, show significant differences in ΔA(Mg). This result is not surprising, as the 457 nm line in giants was singled out in Table 1 of Osorio et al. as being sensitive to the electron collision data, and we have already noted the significant differences between the M88 and CCC/BSR data for this transition. The low densities in the line forming regions of giant atmospheres means this difference has a large impact on the statistical equilibrium. For the solar metallicity case, abundance corrections are ~0.1 dex larger in the M88 model than in both the CCC and BSR models, while for the metal-poor case, the difference in ΔA(Mg) between M88 and BSR/CCC is ~0.08 dex. This difference stems from the much larger collision rate for this transition in the new datasets, mentioned in the previous section. The abundance corrections obtained in Osorio et al. are also shown in Fig. 6 for comparison (RMPS), and also seen to be larger than those using BSR or CCC. This stems from the fact that the rate for this transition at temperatures of order 5000 K is roughly a factor of two smaller in the RMPS calculations of Osorio et al. than in the CCC and BSR datasets. Thus, the new data provide an important improvement to the results of Osorio et al. (2015) and Osorio & Barklem (2016) for this line in giant stars. We note that the oscillator strength for this line has recently been calculated by Rhodin et al. (2017), with log gf increasing by more than 0.2 dex (60%) compared to the value from NIST (Kramida et al. 2016) used in those works. A broader and more detailed study including both of these improvements, and comparison with standard stars should be performed, and this will be the subject of future work.

4.2. Supernovae ejecta

Accurate thermal collision strengths are critical for modelling of the Mg i 457 nm intercombination line in supernovae ejecta in the emission line phase (t ≳ 100 days post explosion). Although the neutral fraction is quite low in typical models, ~10-3 for Mg, the 457 nm line can still be an important coolant. The electron densities are generally below the critical density, so the line is formed in non-LTE, with a strength directly proportional to the collision strength.

Figure 7 compares model spectra of a stripped-envelope supernova from a MZAMS = 13 M⊙ star (Jerkstrand et al. 2015), computed with the M88 collision strengths and the values calculated here. At the Mg zone temperature in the model (T ~ 3200 K), the CCC/BSR collision strengths calculated here are about a factor two higher than in M88. This translates in this model to a factor 1.5 brighter Mg i 457 nm line, as there is also some contribution due to recombination. Depending on the model and epoch, the line can change by both more or less, sometimes up to the full factor of two difference. This model improvement translates directly to new (lower) estimates of the magnesium mass in the ejecta. It alleviates the discrepancy where the 457 nm line in typical models with Mg/O ratios close to solar tended to be too weak compared to observations (Jerkstrand et al. 2015).

thumbnail Fig. 7

Model spectra for a supernova from a MZAMS = 13 M⊙ star showing the Mg i 457 nm line computed with electron collisions data from M88 (full red line) and with the CCC/BSR data from this work (dashed blue line).

5. Conclusions

The agreement between the CCC and BSR results suggests that the effective collision strengths from these methods, and thus the rate coefficients, are reliable in most cases to better than 30%. Comparison with the data from M88 suggests those data are only reliable within a factor of six or so. Thus, the modern close-coupling results are to be strongly preferred for non-LTE modelling. In particular, it is found that the collision strength for the transition corresponding to the Mg i 457 nm line is significantly underestimated. The improved data provided here leads to important changes in predictions of the Mg i 457 nm line in non-LTE line formation models of late-type stellar atmospheres and for supernovae ejecta.

1

This comparison only covers the data tabulated in Tables 2 and 3 of Mauas et al. (1988). The arbitrary values listed in the note to Table 3 are not included. These would make the comparison significantly worse.

2

Defined as ΔA(Mg) = A(Mg)non−LTE−A(Mg)LTE, with A(Mg) = log (NMg/NH) + 12.

Acknowledgments

P.S.B. gratefully acknowledges the support of the Swedish Research Council. P.S.B. is also supported by the project grant “The New Milky Way” from the Knut and Alice Wallenberg foundation. Y.O. acknowledges funds from the Alexander von Humboldt Foundation in the framework of the Sofja Kovalevskaja Award endowed by the Federal Ministry of Education and Research. D.F. and I.B. acknowledge the support of the Australian Research Council, the National Computer Infrastructure, and the Pawsey Computer Centre of Western Australia. O.Z. and K.B. acknowledge NSF support through grants Nos. PHY-1403245, PHY-1520970, and the XSEDE supercomputer allocation No. PHY-090031. A.J. acknowledges funding by the European Union’s Framework Programme for Research and Innovation Horizon 2020 under Marie Sklodowska-Curie grant agreement No. 702538.

References

  1. Aleksakhin, I. S., Zapesochnyi, I. P., Garga, I. I., & Starodub, V. P. 1973, Opt. Spectr., 34, 1053 [Google Scholar]
  2. Bartschat, K., Zatsarinny, O., Bray, I., Fursa, D. V., & Stelbovics, A. T. 2004, J. Phys. B: At. Mol. Opt. Phys., 37, 2617 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bergemann, M., Kudritzki, R.-P., Gazak, Z., Davies, B., & Plez, B. 2015, ApJ, 804, 113 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bray, I., & Stelbovics, A. T. 1995, Adv. Atom. Mol. Phys., 35, 209 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bray, I., Fursa, D. V., Kheifets, A. S., & Stelbovics, A. T. 2002, J. Phys. B: At. Mol. Opt. Phys., 35, R117 [CrossRef] [MathSciNet] [Google Scholar]
  6. Bray, I., McNamara, K., & Fursa, D. V. 2015, Phys. Rev. A, 92, 022705 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brown, D. O., Crowe, A., Fursa, D. V., Bray, I., & Bartschat, K. 2005, J. Phys. B: At. Mol. Opt. Phys., 38, 4123 [NASA ADS] [CrossRef] [Google Scholar]
  8. Carlsson, M., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 253, 567 [NASA ADS] [Google Scholar]
  9. Chang, E. S., & Noyes, R. W. 1983, ApJ, 275, L11 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chang, E. S., Avrett, E. H., Noyes, R. W., Loeser, R., & Mauas, P. J. 1991, ApJ, 379, L79 [NASA ADS] [CrossRef] [Google Scholar]
  11. Fabrikant, I. I., Shpenik, O. B., Snegursky, A. V., & Zavilopulo, A. N. 1988, Phys. Rep., 159, 1 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fransson, C., & Chevalier, R. A. 1989, ApJ, 343, 323 [NASA ADS] [CrossRef] [Google Scholar]
  13. Fursa, D. V., & Bray, I. 1997, J. Phys. B: At. Mol. Opt. Phys., 30, 5895 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fursa, D. V., & Bray, I. 2001, Phys. Rev. A, 63, 032708 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fursa, D. V., & Bray, I. 2008, Phys. Rev. Lett., 100, 113201 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Jerkstrand, A., Fransson, C., Maguire, K., et al. 2012, A&A, 546, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Jerkstrand, A., Ergon, M., Smartt, S. J., et al. 2015, A&A, 573, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team 2016, NIST Atomic Spectra Database (Version 5.4), http://physics.nist.gov/asd [Google Scholar]
  20. Langangen, Ø., & Carlsson, M. 2009, ApJ, 696, 1892 [NASA ADS] [CrossRef] [Google Scholar]
  21. Leep, D., & Gallagher, A. 1976, Phys. Rev. A, 13, 148 [NASA ADS] [CrossRef] [Google Scholar]
  22. Limongi, M., Straniero, O., & Chieffi, A. 2000, ApJS, 129, 625 [NASA ADS] [CrossRef] [Google Scholar]
  23. Martin, W. C., & Zalubas, R. 1980, J. Phys. Chem. Ref. Data, 9, 1 [NASA ADS] [CrossRef] [Google Scholar]
  24. Mauas, P. J., Avrett, E. H., & Loeser, R. 1988, ApJ, 330, 1008 [NASA ADS] [CrossRef] [Google Scholar]
  25. Merle, T., Thévenin, F., & Zatsarinny, O. 2015, A&A, 577, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Osorio, Y., & Barklem, P. S. 2016, A&A, 586, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Osorio, Y., Barklem, P. S., Lind, K., et al. 2015, A&A, 579, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Przybilla, N., Butler, K., Becker, S. R., & Kudritzki, R. P. 2001, A&A, 369, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Rhodin, A. P., Hartman, H., Nilsson, H., & Jönsson, P. 2017, A&A, 598, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Robb, W. D. 1974, J. Phys. B: At. Mol. Phys., 7, 1006 [NASA ADS] [CrossRef] [Google Scholar]
  31. Robb, W. D. 1975, in Proc. 9th Int. Conf. on Physics of Electronic and Atomic Collisions (Seattle: University of Washington Press), 1113 [Google Scholar]
  32. Seaton, M. J. 1953, Proc. Roy. Soc. London Ser. A., Math. Phys. Sci., 218, 400 [NASA ADS] [CrossRef] [Google Scholar]
  33. Seaton, M. J. 1962, Proc. Phys. Soc., 79, 1105 [NASA ADS] [CrossRef] [Google Scholar]
  34. Sundqvist, J. O., Ryde, N., Harper, G. M., Kruger, A., & Richter, M. J. 2008, A&A, 486, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
  36. Vieytes, M., Mauas, P., Cacciari, C., Origlia, L., & Pancino, E. 2011, A&A, 526, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Wang, K., Zatsarinny, O., & Bartschat, K. 2016, Phys. Rev. A, 93, 052715 [NASA ADS] [CrossRef] [Google Scholar]
  38. Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
  39. Zatsarinny, O., & Bartschat, K. 2013, J. Phys. B: At. Mol. Opt. Phys., 46, 112001 [NASA ADS] [CrossRef] [Google Scholar]
  40. Zatsarinny, O., Bartschat, K., Gedeon, S., et al. 2009, Phys. Rev. A, 79, 052709 [NASA ADS] [CrossRef] [Google Scholar]
  41. Zatsarinny, O., Bartschat, K., Fursa, D. V., & Bray, I. 2016, J. Phys. B: At. Mol. Opt. Phys., 49, 235701 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Physical states for which data are provided from the CCC and BSR calculations, along with experimental excitation energies (Eexpt) from NIST (Kramida et al. 2016; Martin & Zalubas 1980).

In the text
Table 2

Sample of electronic table for effective collision strengths Υij at 5000 K from the CCC calculation.

In the text
Table 3

Sample of electronic table for effective collision strengths Υij at 5000 K from the BSR calculation.

In the text
Table 4

The location and scale of the ratio Υij(1)/Υij(2), where Υij(1) corresponds to dataset 1, and Υij(2) corresponds to dataset 2.

In the text

All Figures

thumbnail Fig. 1

Cross sections for selected electric dipole transitions.
In the text
thumbnail Fig. 2

Cross sections for selected spin-conserving non-electric dipole transitions.

In the text
thumbnail Fig. 3

Cross sections for selected spin-changing transitions.
In the text
thumbnail Fig. 4

Comparison of the effective collision strengths Υij at 5000 K from CCC and BSR. The central dashed line shows the one-to-one relation, with the outer dashed lines showing factors of two and ten departures from this relation. Circled points are transitions involving the lowest five states of Mg. Points shown surrounded by a square are the transitions from the ground state to the two lowest-lying excited states, i.e. 3s–3s3p3P and 3s–3s3p1P, the former always having a larger effective collision strength.

In the text
thumbnail Fig. 5

Comparison of the effective collision strengths Υij from Mauas et al. (1988), with those from the CCC calculations, at 5000 K. The lines and points follow the description in Fig. 4.

In the text
thumbnail Fig. 6

Abundance corrections for the 457 nm line using four atmospheric models and four model atoms differing only in the electron collisional data used. The parameters of the atmospheric models are shown in the bottom left of each panel in the format Teff/log g/[Fe/H]. The M88 model atom (solid line) includes data from Mauas et al. (1988), the RMPS model is the model “F” used in Osorio et al. (2015; dashed line), the CCC model uses the CCC data presented in this work (dot-dashed line) and the BSR model uses the BSR data presented here (triple-dot-dashed line). The shaded region shows the expected values of A(Mg) for a typical star of the given metallicity. The points show the calculated points.
In the text
thumbnail Fig. 7

Model spectra for a supernova from a MZAMS = 13 M⊙ star showing the Mg i 457 nm line computed with electron collisions data from M88 (full red line) and with the CCC/BSR data from this work (dashed blue line).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.