| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 17 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201730818 | |
| Published online | 04 October 2017 | |
Gravity darkening in stars with surface differential rotation
1 Sorbonne Universités, UPMC Université Paris 6 et CNRS, UMR 7095 Institut d’Astrophysique de Paris, 75014 Paris, France
2 CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98bis Bd. Arago, 75014 Paris, France
e-mail: zorec@iap.fr
3 Université de Toulouse, UPS-OMP, IRAP, 31062 Toulouse, France
4 CNRS, IRAP, 14 avenue Edouard Belin, 31400 Toulouse, France
5 University of Alcalá, 28871, Alcalá de Henares, Spain
6 Royal Observatory of Belgium, 3 Av. Circulaire, 1180 Bruxelles, Belgium
7 Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS UMR 7293, Lagrange, 28 avenue Valrose, 06108 Nice Cedex 2, France
8 GEPI, Observatoire de Paris, PSL Research University, CNRS UMR 8111, 5 place Jules Janssen, 92190 Meudon, France
Received: 18 March 2017
Accepted: 10 May 2017
Context. The interpretation of stellar apparent fundamental parameters (viewing-angle dependent) requires that they be treated consistently with the characteristics of their surface rotation law.
Aims. We aim to develop a model to determine the distribution of the effective temperature and gravity, which explicitly depend on the surface differential rotation law and on the concomitant stellar external geometry.
Methods. The basic assumptions in this model are: a) the external stellar layers are in radiative equilibrium; b) the emergent bolometric flux is anti-parallel with the effective gravity; c) the angular velocity in the surface obeys relations like Ω(θ) = Ωo [ 1 + αΥ(θ,k) ] where Υ(θ,k) = coskθ or sinkθ, and where (α,k) are free parameters.
Results. The effective temperature varies with co-latitude θ, with amplitudes that depend on the differential-rotation law through the surface effective gravity and the gravity-darkening function (GDF). Although the derived expressions can be treated numerically, for some low integer values of k, analytical forms of the integral of characteristic curves, on which the determination of the GDF relies, are obtained. The effects of the quantities (η,α,k) (η = ratio between centrifugal and gravitational accelerations at the equator) on the determination of the Vsini parameter and on the gravity-darkening exponent are studied. Depending on the values of (η,α,k) the velocity V in the derived Vsini may strongly deviate from the equatorial rotational velocity. It is shown that the von Zeipel’s-like gravity-darkening exponent β1 depends on all parameters (η,α,k) and that its value also depends on the viewing-angle i. Hence, there no unique interpretation of this exponent determined empirically in terms of (i,α).
Conclusions. We stress that the data on rotating stars should be analyzed by taking into account the rotational effects through the GDF, by assuming k = 2 as a first approximation. Instead of the classic pair (η,β1), it would be more useful to determine the quantities (η,α,i) to characterize stellar rotation.
Key words: stars: rotation
© ESO, 2017
1. Introduction
Rotation induces a geometrical deformation to the stars characterized by a polar flattening and an equatorial stretching. Since the radiation tends to emerge isotropically from the object, the radiation flux becomes a function of the stellar latitude known as the gravitational-darkening effect.
According to Poincaré-Wavre’s theorem, in barotropic systems any of the following statements implies the three others (Tassoul 1978): 1) the angular velocity depends only on the distance ϖ to the rotational axis, Ω = Ω(ϖ); 2) the effective gravity is derived from a total gravitation-rotational potential, Φ; 3) the effective gravity is normal to the isopycnic surfaces; 4) the isobaric and isopycnic surfaces coincide. If the stellar atmospheres of barotropic stars are also in hydrostatic and radiative equilibrium, a relation holds between the bolometric radiation flux F and the effective gravity, geff, known as von Zeipel’s theorem (von Zeipel 1924) 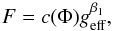 (1)where Φ is the total gravitation-rotational potential describing the stellar surface and c(Φ) is thus a constant. This relation holds when the radiation flux can be written in the diffusion approximation, which is an asymptotic solution for the radiation field valid at great depths in a semi-infinite atmosphere. In this case, the gravity-darkening exponent takes the value β1 = 1.0.
(1)where Φ is the total gravitation-rotational potential describing the stellar surface and c(Φ) is thus a constant. This relation holds when the radiation flux can be written in the diffusion approximation, which is an asymptotic solution for the radiation field valid at great depths in a semi-infinite atmosphere. In this case, the gravity-darkening exponent takes the value β1 = 1.0.
It was recognized very early on that in rotating objects simultaneous hydrostatic and radiative equilibrium contradict each other (Osaki 1966). However, if radiative equilibrium is maintained forcibly in baroclinic stars, meaning that their rotation laws are non-conservative, Ω = Ω(ϖ,z) (z coordinate parallel to the rotation axis), authors have shown that β1 = β1(θ) ≤ 1, where θ is the co-latitude (Smith & Worley 1974; Kippenhahn 1977; Maeder 1999; Lovekin et al. 2006; Claret 2012).
For the particular case of a strict solid-body rotation, Espinosa Lara & Rieutord (2011) have shown that Eq. (1) can take another formal aspect. Using full two-dimensional stellar models (e.g. Rieutord et al. 2016), they noted that, to a high degree of approximation, the emerging radiation flux-vector F emitted by an axially symmetric stellar atmosphere in radiative equilibrium is anti-parallel to the vector of the local effective gravity geff. Thus, assuming this parallelism, they write 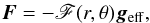 (2)where (r,θ) are the spherical coordinates. The function F(r,θ) is hereinafter called the gravity-darkening function (GDF). We note that before Espinosa Lara & Rieutord (2011), F(r,θ) was simply the constant c(Φ) in Eq. (1). It entered the formulation of the known paradox of von Zeipel, which stipulates the impossibility of having stable barotropic stellar models in radiative equilibrium (e.g. Roxburgh 1966, p. 211).
(2)where (r,θ) are the spherical coordinates. The function F(r,θ) is hereinafter called the gravity-darkening function (GDF). We note that before Espinosa Lara & Rieutord (2011), F(r,θ) was simply the constant c(Φ) in Eq. (1). It entered the formulation of the known paradox of von Zeipel, which stipulates the impossibility of having stable barotropic stellar models in radiative equilibrium (e.g. Roxburgh 1966, p. 211).
To determine F(r,θ) in the case of a rigidly rotating star, Espinosa Lara & Rieutord (2011) maintain the condition of radiative equilibrium written in its general form (Mihalas 1979) and solved the following differential equation 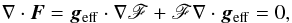 (3)and obtained that β1 depends on the co-latitude angle θ and that it is everywhere a decreasing function of the the stellar flattening, ε = 1 − Rp/Re (Rp and Re are polar and equatorial radii, respectively). We note that current interferometric imaging and modelling of rapidly rotating atmospheres produce inferences of the gravity-darkening exponent in intermediate-mass stars
(3)and obtained that β1 depends on the co-latitude angle θ and that it is everywhere a decreasing function of the the stellar flattening, ε = 1 − Rp/Re (Rp and Re are polar and equatorial radii, respectively). We note that current interferometric imaging and modelling of rapidly rotating atmospheres produce inferences of the gravity-darkening exponent in intermediate-mass stars  (Monnier et al. 2007, 2012; Zhao et al. 2009; Che et al. 2011; Domiciano de Souza et al. 2014), although within the current measurement uncertainties, these values are
(Monnier et al. 2007, 2012; Zhao et al. 2009; Che et al. 2011; Domiciano de Souza et al. 2014), although within the current measurement uncertainties, these values are 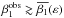 systematically, where
systematically, where 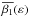 is an average relation between β1 and ε (see Eq. (40) in Sect. 7.1).
is an average relation between β1 and ε (see Eq. (40) in Sect. 7.1).
Apart from the above mentioned radiation transfer reasons, the exponent β1 determined observationally can also be dependent on: 1) the line-of-sight angle i of stars, because β1 is a function of θ; 2) the differential rotation of the stellar surface, which introduces a stronger dependence of effective temperature with co-latitude than in stars with solid-body rotation. In this respect, Delaa et al. (2013) noted that differential rotation introduces additional contrast on the brightness distribution over the stellar disc, which increases the dependence of β1 with the line-of-sight angle.
We can think of the surface differential rotation as the external imprint of the internal rotation law in baroclinic stars (Espinosa Lara & Rieutord 2007, 2013). Statistical inferences concerning intermediate-mass stars suggest that their atmospheres may have differential rotation (Zorec & Royer 2012). The rotational increase of the radiative gradient in the envelope of massive rapid rotators significantly enlarges the external convective zones (Clement 1979; Maeder et al. 2008). Like in the Sun, the interaction of rotation with convection may keep driving differential rotation in these regions that in turn can be responsible for the surface differential rotation (Zorec et al. 2011, 2017).
The aim of the present work is to obtain solutions for the function F(r,θ) by imposing the condition of radiative equilibrium in the stellar atmosphere (cf. Eq. (3)), while the stellar surface rotates differentially. We explore the incidence of this rotation on the observed stellar fundamental parameters, in particular the measured Vsini parameter and the so-called gravity-darkening exponent β1.
 |
Fig. 1 Surface angular velocity Ω as a function of colatitude θ as given by Eqs. (4) and (5). Panel a: Υ(θ) = coskθ for α = + 0.5 and − 0.5, and several values of k from 0.5 to 10. Panel b: Υ(θ) = sinkθ for α′ = − 1 / 3 and α′ = + 1.0[ α′ = − α/ (1 + α ], and the same values of k as in (a). Colours identify the values of k. |
 |
Fig. 2 Geometrical deformation of stellar surfaces produced by differential rotation laws given by Eqs. (4) and (5). Panel a: Stellar geometries calculated using Υ(θ) = coskθ, rotational ratio η = 0.8, differential rotation parameters α = − 0.5, 0.0 (solid body rotation) and 0.5, and powers k = 0.5, 2.0 and 6.0. Panel b: Calculations done with Υ(θ) = sinkθ and the same values of η and powers k, but for α′ = − α/ (1 + α). In all cases the colours identify the values of the power k, while the line-styles characterize the values of the differential-rotation parameter α, and the corresponding α′. |
2. The surface differential rotation law
Having no a priori indications on a general form of the function describing the surface differential rotation law Ω(θ), but inspired by the simplified Maunder’s relation in the solar example (e.g. Maunder & Maunder 1905, p. 819), we propose to use the following relation ![\begin{eqnarray} \Omega(\theta) = \Omega_{\rm o}[1+\alpha\Upsilon(\theta)], \label{maund} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq57.png) (4)where α is a free parameter called the differential rotation parameter. The case α = 0 corresponds to rigid rotation. Accordingly, we adopt two exploratory forms for the function Υ(θ), namely
(4)where α is a free parameter called the differential rotation parameter. The case α = 0 corresponds to rigid rotation. Accordingly, we adopt two exploratory forms for the function Υ(θ), namely 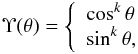 (5)where k is also a free quantity that takes any real positive value. Figure 1 shows the behaviour of the assumed angular velocity laws given by Eqs. (4) and (5) for α = + 0.5 (α′ = − 1 / 3), α = 0.0 and − 0.5 (α′ = 1.0), and several values of k from 0.5 to 10.0. The higher the value of k the larger the domain sketched as nearly a solid body rotation. This domain occurs near the equator for Υ(θ) = coskθ and near the pole for Υ(θ) = sinkθ. When Υ(θ) = coskθ we have Ωo = Ωe, while for Υ(θ) = sinkθ, Ωo = Ωe(1 + α)-1. In both cases Ωe is the angular velocity at the equator.
(5)where k is also a free quantity that takes any real positive value. Figure 1 shows the behaviour of the assumed angular velocity laws given by Eqs. (4) and (5) for α = + 0.5 (α′ = − 1 / 3), α = 0.0 and − 0.5 (α′ = 1.0), and several values of k from 0.5 to 10.0. The higher the value of k the larger the domain sketched as nearly a solid body rotation. This domain occurs near the equator for Υ(θ) = coskθ and near the pole for Υ(θ) = sinkθ. When Υ(θ) = coskθ we have Ωo = Ωe, while for Υ(θ) = sinkθ, Ωo = Ωe(1 + α)-1. In both cases Ωe is the angular velocity at the equator.
In order to grasp the differences inherent to the use of one of the two Υ-functions given in Eq. (5), it is necessary to compare the effects produced by rotation laws implying the same ratio Ωp/ Ωe. Thus, for a given value of α used with Υ(θ) = coskθ, we have to take α′ = − α/ (1 + α) associated with Υ(θ) = sinkθ so that Ω(θ) = Ωo [ 1 + α′sinkθ ]. Obviously, when k = 2 both Υ(θ) represent the same rotation law. Nevertheless, keeping the reciprocity between α and α′, the functions Υ(θ) = coskθ and Υ(θ) = sink′θ can produce resembling behaviours of predicted parameters (although not exactly the same), because 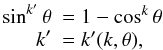 (6)independently of the value of α. Taking the average of the two thirds of powers k′(k,θ) calculated in the middle points of the θ-interval – neglecting the two halves of the remaining third of points situated in the extremes of the interval where in any case the predicted functions fit the right values because of the boundary conditions, it comes, for example that Υ(θ) = coskθ with k = 0.5 will lead to resembling results as Υ(θ) = sink′θ when k′ ≃ 7.0, or coskθ with k = 6.0 similar results as sink′θ where k′ ≃ 0.5 (this effect is illustrated in many figures below, as: Figs. 4a and f, or Figs. 4c and d; Figs. 5a and f, or Figs. 5c and d; Figs. 6a, d and 6b, d, or Figs. 7c, f and 7a, c; Figs. 12a and f, or Figs. 12c and d).
(6)independently of the value of α. Taking the average of the two thirds of powers k′(k,θ) calculated in the middle points of the θ-interval – neglecting the two halves of the remaining third of points situated in the extremes of the interval where in any case the predicted functions fit the right values because of the boundary conditions, it comes, for example that Υ(θ) = coskθ with k = 0.5 will lead to resembling results as Υ(θ) = sink′θ when k′ ≃ 7.0, or coskθ with k = 6.0 similar results as sink′θ where k′ ≃ 0.5 (this effect is illustrated in many figures below, as: Figs. 4a and f, or Figs. 4c and d; Figs. 5a and f, or Figs. 5c and d; Figs. 6a, d and 6b, d, or Figs. 7c, f and 7a, c; Figs. 12a and f, or Figs. 12c and d).
In principle we could let − ∞ <α< + ∞, but we shall limit the values of the differential rotation parameter to − 1 ≤ α< ∞ so as to prevent extreme cases where the pole and the equator rotate in opposite senses. Furthermore, according to statistical suggestions based on a study of Be stars (Zorec et al. 2017), in the present work we limit the values of α to the interval − 0.5 <α ≤ + 0.5. We note that the solar surface differential rotation can be sketched with α ≃ − 0.3 and Υ(θ) = cos2θ. On the other hand, Espinosa Lara & Rieutord (2013) predicted α ≳ − 0.2 for stars with masses 2 ≲ M/M⊙ ≲ 4.
Instead of using Ωe/ Ωc to characterize the rotational velocity at the equator, in this paper we use the ratio η between the centrifugal and gravitational acceleration at the equator defined as follows 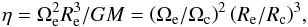 (7)where M is the stellar mass, G the graviational constant; Ωc and Rc are the critical angular velocity and the critical radius at the equator, respectively. To make easier any comparison of the expressions derived in the present paper with those in Espinosa Lara & Rieutord (2011) where the ratio Ve/VK is used as the non-dimensional parameter characterizing the stellar rotation (Ve and VK are the actual and Keplerian linear equatorial velocities, respectively), we note that η = (Ve/VK)2, so that it holds 0 ≤ η ≤ Ve/VK≤ Ωe/ Ωc ≤ 1.
(7)where M is the stellar mass, G the graviational constant; Ωc and Rc are the critical angular velocity and the critical radius at the equator, respectively. To make easier any comparison of the expressions derived in the present paper with those in Espinosa Lara & Rieutord (2011) where the ratio Ve/VK is used as the non-dimensional parameter characterizing the stellar rotation (Ve and VK are the actual and Keplerian linear equatorial velocities, respectively), we note that η = (Ve/VK)2, so that it holds 0 ≤ η ≤ Ve/VK≤ Ωe/ Ωc ≤ 1.
Equatorial to polar radii ratio Re/Rp as a function of η, k and α, for Υ = coskθ and Υ = sinkθ.
3. The stellar geometry and the surface gravity
When the rotation law is conservative, the geometry of the stellar surface can be described with a total gravity-rotation potential. As noted in Sect. 1, the rotation law given in Eq. (4)represents the boundary condition in the surface of an internal non-conservative rotational law Ω = Ω(r,θ). Unlike for barotropic models, in these baroclinic stars it is no longer possible to define a rotational potential. According to Maeder (2009), the surface in such objects should be the region where an arbitrary displacement ds does not imply any work done by the effective gravity geff, i.e. geff ds = 0. In the present paper we adopted this approach as it was previously done also in Zorec et al. (2011). Figure 2 shows the geometries obtained with this method when the rotation law is given by Eqs. (4) and (5), and taking into account several values of α and k. The rotation at the equator is characterized by the rotational ratio η = 0.8. In all cases of Fig. 2 the colours identify the values of the power k, while the line-styles characterize the values of the differential-rotation parameter α (and the corresponding α′). The green curves are for α = 0.
In Table 1 we give the radii ratios Re/Rp for η = 0.2 (Ω / Ωc = 0.69; V/Vc = 0.52) and η = 0.8 (Ω / Ωc = 0.99; V/Vc = 0.92), for several values of k and α. In each series of parameters (η,k,α) the radii ratios were calculated also for Υ = sinkθ and α′ = − α/ (1 + α).
Zahn et al. (2010) have shown that the level surfaces of models with shellular rotation laws have the same shape as those for solid-body rotation, including the stellar surface. Moreover, the effect of the internal mass distribution on the surface layer at equatorial critical rotation deviates from a genuine central gravitational field by no more than some 2%. The same conclusion was also put forward by Zorec et al. (2011) in models calculated using Clement’s like conservative rotation laws for kinetic-energy parameters higher than κ = K/ | W | = 0.10 (K is the kinetic rotational energy stored by the star; W is the gravitational potential energy). Thus, we can safely use the Roche approximation for the surface effective gravity geff and write ![\begin{eqnarray} && \vec{g}_{\rm eff} = g_{r}\,\hat{\vec{e}}_{r} +g_{\theta}\,\hat{\vec{e}}_{\theta} \notag\\[1.5mm] && g_{r} = -\frac{GM}{{r}^2} +\Omega^2{r}\sin^2\theta \notag\\ && g_{\theta} = \Omega^2{r}\sin\theta\cos\theta, \label{geff} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq120.png) (8)where G is the gravitational constant; M is the stellar mass; Ω = Ω(θ) is the angular velocity given by Eqs. (4) and (5); êr and êθ are the unit vectors associated with the spherical coordinates (r,θ). In what follows, we use the dimensionless radial coordinate r = r/Re, where Re is the rotationally modified stellar equatorial radius. To simplify notation we write geff = | − geff | and introduce the dimensionless expression for the effective gravity γ(r,θ) as follows
(8)where G is the gravitational constant; M is the stellar mass; Ω = Ω(θ) is the angular velocity given by Eqs. (4) and (5); êr and êθ are the unit vectors associated with the spherical coordinates (r,θ). In what follows, we use the dimensionless radial coordinate r = r/Re, where Re is the rotationally modified stellar equatorial radius. To simplify notation we write geff = | − geff | and introduce the dimensionless expression for the effective gravity γ(r,θ) as follows ![\begin{eqnarray} && g_{\rm eff} = \left(g^2_{r}+g^2_{\theta}\right)^{1/2} = \langle{g}\rangle\gamma(r,\theta) \notag\\[1.5mm] && \gamma(r,\theta) = \frac{1}{r^2}\left\{1+\left[\left(1-\tilde{\eta}r^3\right)^2-1\right] \sin^2\theta\right\}^{1/2} \notag\\[1.5mm] && \tilde{\eta} = \eta\left[\frac{\Omega(\theta)}{\Omega_{\rm e}}\right]^2 \notag\\[1.5mm] && \langle{g}\rangle = g_{\rm o}\left(\frac{R_{\rm o}}{R_{\rm e}}\right)^2, \label{geff_2} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq128.png) (9)where
(9)where 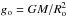 is the surface gravity of the stellar parent non-rotating counterpart having a spherical radius Ro and the same mass M as the rotating object.
is the surface gravity of the stellar parent non-rotating counterpart having a spherical radius Ro and the same mass M as the rotating object.
From Eq. (9) it follows that the extreme values of γ(r,θ) are: γe = γ(r,π/ 2) =1 − η and γp = γ(r,0) =(Re/Rp)2, which are functions of (η,α) and are dependent on the function Υ(θ) adopted (see Table 1).
4. The gravity-darkening function
The gravity darkening function F(r,θ), as defined by Eq. (2), is constrained by the boundary condition obtained when r → 0, namely 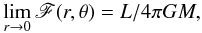 (10)where L is the stellar bolometric luminosity emitted by the stellar core, whose physical properties depend on the total amount and distribution of the angular momentum inside the star (e.g. Sackmann 1970; Bodenheimer 1971; Clement 1979; Eriguchi & Mueller 1991; Uryu & Eriguchi 1994, 1995; Maeder & Meynet 2000; Deupree 2001; Jackson et al. 2005; Espinosa Lara & Rieutord 2007, 2013; Ekström et al. 2008; Maeder 2009; Fujisawa 2015). In what follows, we use the dimensionless form of F
(10)where L is the stellar bolometric luminosity emitted by the stellar core, whose physical properties depend on the total amount and distribution of the angular momentum inside the star (e.g. Sackmann 1970; Bodenheimer 1971; Clement 1979; Eriguchi & Mueller 1991; Uryu & Eriguchi 1994, 1995; Maeder & Meynet 2000; Deupree 2001; Jackson et al. 2005; Espinosa Lara & Rieutord 2007, 2013; Ekström et al. 2008; Maeder 2009; Fujisawa 2015). In what follows, we use the dimensionless form of F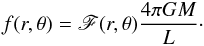 (11)From Eq. (10) we have
(11)From Eq. (10) we have 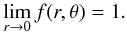 (12)Using spherical coordinates, the relation in Eq. (3) becomes the following linear partial differential equation:
(12)Using spherical coordinates, the relation in Eq. (3) becomes the following linear partial differential equation: 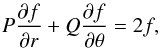 (13)where the notations stand for
(13)where the notations stand for ![\begin{eqnarray} && P = -\frac{g_r}{\Omega\left[\Omega+ (\partial\Omega/\partial\theta) \sin\theta\cos\theta\right]} \notag\\[1.5mm] && Q = -\frac{g_{\theta}}{r\Omega\left[\Omega+ (\partial\Omega/\partial\theta) \sin\theta\cos\theta\right]}\cdot \label{rdfe} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq143.png) (14)The integration of Eq. (13) can be reduced to the integration of Lagrange’s system of ordinary linear differential equations, called also method of characteristics. Let us follow Rieutord (2016). We first eliminate the RHS of Eq. (13) by writing the equation for lnf and setting:
(14)The integration of Eq. (13) can be reduced to the integration of Lagrange’s system of ordinary linear differential equations, called also method of characteristics. Let us follow Rieutord (2016). We first eliminate the RHS of Eq. (13) by writing the equation for lnf and setting: 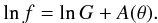 (15)After some calculations we find that
(15)After some calculations we find that ![\begin{eqnarray} A(\theta) = -\ln\left[\Omega^2(\theta)\tan^2\theta\right]. \label{new_eq2} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq146.png) (16)Now, Eq. (13) may be rewritten
(16)Now, Eq. (13) may be rewritten 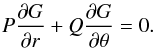 (17)The characteristic lines of G in the (r,θ)-plane, are the lines where G is constant. On these lines ∂rGdr + ∂θGdθ = 0, so that on these lines we have
(17)The characteristic lines of G in the (r,θ)-plane, are the lines where G is constant. On these lines ∂rGdr + ∂θGdθ = 0, so that on these lines we have 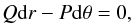 (18)which is the equation of characteristic lines. After some simplifications it reads
(18)which is the equation of characteristic lines. After some simplifications it reads 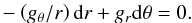 (19)To solve (19), we need to transform it into an exact differential. We can indeed multiply the equation by any function of (r,θ). It turns out that if we multiply (19) by
(19)To solve (19), we need to transform it into an exact differential. We can indeed multiply the equation by any function of (r,θ). It turns out that if we multiply (19) by 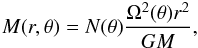 (20)it can be integrated. Indeed, demanding that
(20)it can be integrated. Indeed, demanding that 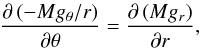 (21)leads to the following expression for N(θ):
(21)leads to the following expression for N(θ): 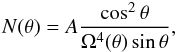 (22)where A is an arbitrary constant.
(22)where A is an arbitrary constant.
Thus G is constant on the lines τ(r,θ) = Cst, if τ verifies: ![\begin{eqnarray} && \frac{\partial\tau}{\partial{r}} = -\frac{Mg_\theta}{r} = \frac{r^2\Omega^2_{\rm o}}{GM}\cos^3\theta \notag\\[1.5mm] &&\frac{\partial\tau}{\partial\theta} = M g_r= \frac{\cos\theta\cot\theta}{\left[1+\alpha\Upsilon(\theta)\right]^2}-\frac{r^3\Omega^2_{\rm o}}{GM}\sin\theta\cos^2\theta, \label{dtautt} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq159.png) (23)where we chose
(23)where we chose 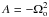 . Since the RHS of the previous equations have been chosen such that dτ is an exact differential, the integration is straightforward and gives
. Since the RHS of the previous equations have been chosen such that dτ is an exact differential, the integration is straightforward and gives 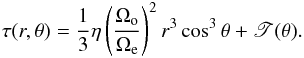 (24)The function T(θ), here referred to as the integral of characteristic curves, is finally given by
(24)The function T(θ), here referred to as the integral of characteristic curves, is finally given by ![\begin{eqnarray} \mathscr{T}(\theta) = \int_{\pi/2}^{\theta} \frac{\cos\phi\cot\phi}{\left[1+\alpha\Upsilon(\phi)\right]^2}{\rm d}\,\phi \label{intau} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq164.png) (25)that can be calculated numerically for any real positive value of k. For some low natural number k, the integral in Eq. (25) admits analytical expressions that are given in Appendix A.
(25)that can be calculated numerically for any real positive value of k. For some low natural number k, the integral in Eq. (25) admits analytical expressions that are given in Appendix A.
 |
Fig. 3 Function lnf(θ) given by Eq. (11) against the colatitude θ, calculated for η = 0.2 and 0.8, with both functions Υ(θ) given in Eq. (5), differential-rotation parameters α = − 0.5, 0.0, and 0.5, and for powers k = 0.5, 2.0 and 6.0. Blocks (a) and (b) are for Υ(θ) = coskθ. Blocks (c) and (d) are for Υ(θ) = sinkθ. Colours indicate the power k and they are the same for all blocks. The line-styles identify the values of α and they are the same for α′ = − α/ (1 + α) where α are the same as in (a) and (b). |
 |
Fig. 4 Panels a–c: Effective temperature Teff(θ,η,α) / ⟨ T ⟩ given by Eq. (34) as a function of the co-latitude θ when Υ(θ) = coskθ, for η = 0.8, k = 0.5, 2.0 and 6.0, and α = − 0.5, 0.0 and +0.5. Panels d–f: Same for Υ(θ) = sinkθ and the same values of k as before, but for α′ = − α/ (1 + α) where α is the same as in (a) to (c). The black-dashed lines correspond to the classic von Zeipel approximation normalized in θ = 0 at the curve corresponding to α = 0.0. |
 |
Fig. 5 Panels a–c: Effective temperature ratios |
In this work we used only numerical estimates of T(θ). The numerical estimates of the integral in Eq. (25) were obtained proceeding to the change of variable u = lntan(φ/ 2) and using the 16-point Gauss-Legendre quadrature rule. The function T(θ) thus obtained was also calculated for all values of k for which we could obtain the analytical expressions given in Appendix A. We thus noted that the errors of the numerical estimates of Eq. (25) are δT ≲ 10-6 at θ ~ 10-5 rad ( ), and they become δT ≲ 10-12 as soon as θ ≳ 0.07 rad (θ ≳ 8°). The precision of the numerical estimates increases even more as θ → π/ 2.
), and they become δT ≲ 10-12 as soon as θ ≳ 0.07 rad (θ ≳ 8°). The precision of the numerical estimates increases even more as θ → π/ 2.
The limit expression of T(θ) for α = 0 comes directly from Eq. (25), which is also obeyed by all analytical expressions given in Appendix A: 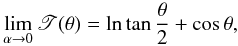 (26)which is the form of T(θ) obtained by Espinosa Lara & Rieutord (2011, see their Eq. (20)).
(26)which is the form of T(θ) obtained by Espinosa Lara & Rieutord (2011, see their Eq. (20)).
Because τ ≡ τ(r,θ), where r and θ are independent variables, we can use instead the pairs (r,τ) or (θ,τ) as independent variables to obtain two simplified forms of Eq. (13) valid over the τ-characteristic curves 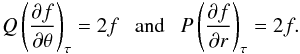 (27)The first differential equation in Eq. (27) can be easily integrated to obtain
(27)The first differential equation in Eq. (27) can be easily integrated to obtain ![\begin{eqnarray} f(r,\theta) = \frac{\Psi(\tau)}{\tan^2\theta[1+\alpha\Upsilon(\theta)]^2}, \label{solf_t} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq183.png) (28)where the factor Ψ(τ) is an integration constant that carries the dependence of f with r through a transcendental function ϑ(r,θ) defined, using Eq. (24), as
(28)where the factor Ψ(τ) is an integration constant that carries the dependence of f with r through a transcendental function ϑ(r,θ) defined, using Eq. (24), as 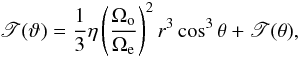 (29)which assumes that there is a unique relation between ϑ and τ. From Eq. (29) it appears that ϑ → θ as r → 0. Therefore, noting that τ(r,θ) is constant over a characteristic curve, the value of Ψ(τ) can be specified at any point (r,θ) on the characteristic, in particular at r = 0. Thus, making use of the boundary condition in Eq. (12) we obtain
(29)which assumes that there is a unique relation between ϑ and τ. From Eq. (29) it appears that ϑ → θ as r → 0. Therefore, noting that τ(r,θ) is constant over a characteristic curve, the value of Ψ(τ) can be specified at any point (r,θ) on the characteristic, in particular at r = 0. Thus, making use of the boundary condition in Eq. (12) we obtain ![\begin{eqnarray} \Psi(\tau) = \tan^2\vartheta\,\left[1+\alpha\Upsilon(\vartheta)\right]^2. \label{psi_t} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq193.png) (30)Introduced into Eq. (28), it leads to
(30)Introduced into Eq. (28), it leads to ![\begin{eqnarray} f(r,\theta) = \left(\frac{\tan\vartheta}{\tan\theta}\right)^2\left[\frac{1+\alpha\Upsilon(\vartheta)}{1+\alpha\Upsilon(\theta)}\right]^2\cdot \label{f_th} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq194.png) (31)Equation (31) is the generalized version of that obtained by Espinosa Lara & Rieutord (2011), which is valid for α = 0 (their Eq. (26)).
(31)Equation (31) is the generalized version of that obtained by Espinosa Lara & Rieutord (2011), which is valid for α = 0 (their Eq. (26)).
Equations (24) and (29), together with Eq. (25), or the forms for T(θ) given in Appendix A, define ϑ(r,θ) for every chosen point (r,θ), in particular for the stellar surface represented by the function r = r(θ). To this end it is worth noting that because ϑ ≠ θ except at the extremes ϑ = θ = 0 and ϑ = θ = π/ 2, it is impossible to derive reliable values of ϑ = ϑ(r,θ) from Eq. (29) if the stellar geometry, i.e. r = r(θ), is not determined consistently with the rotation law on which depends T(θ).
We have calculated GDF numerically using Eq. (31), where r(θ) is the radius-vector that describes the stellar surface. The function ϑ(θ) is determined with Eqs. (24) and (29) by interpolation, where T(ϑ) at a given θ is taken as a linear function of lnθ. For values of ϑ when θ → π/ 2 we consider T(ϑ) as a linear function of its expression for α = 0, so that ϑ is derived by iterating Eq. (26).
The behaviour of the function f(θ) calculated for Υ = coskθη = 0.2, 0.8, and for several values of α and k is shown in Fig. 3. In this figure the function f(θ) calculated with Υ = sinkθ and α′ =− α/ (1 + α) is also shown. It shows that f [ coskθ,α ] ≠f [ sinkθ,α′(α) ], except for k = 2 where f(θ) is the same for both Υ(θ) functions. The function f(θ) obtained for α = 0.0 (green curves in Fig. 3) corresponds to the solution previously obtained by Espinosa Lara & Rieutord (2011).
 |
Fig. 6 Panels a–c: Parameters Vsini determined with the FT method using the He i 4471 line produced in atmospheres having a rotation law given by Eq. (4)with Υ = coskθ and characterized by different values of k and α, against the actual Veqsini in stars having M = 9 M⊙ and t/tMS = 0.6, and rotating with several equatorial ratios η. Panels d–f: Same for the Mg ii 4481 line. |
 |
Fig. 7 Similar as Fig. 6 but for Υ = sinkθ. The cases with k = 2 are omitted as they are identical to those in Fig. 6. |
From Eq. (15) we can derive the limits of f(r,θ) when θ → 0 and θ → π/ 2![\begin{eqnarray} && \lim_{\theta\to0}f = f^{\rm pole} = \exp\left[\frac{2}{3}\eta\left(\frac{R_{\rm p}}{R_{\rm e}}\right)^3\left(\frac{\Omega_{\rm p}}{\Omega_{\rm e}}\right)^2\right] \notag\\[1.5mm] && \lim_{\theta\to\pi/2}f = f^{\rm eq} = (1-\eta)^{-2/3}, \label{limts} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq214.png) (32)where Rp and Re are the polar and equatorial radii, respectively. Ωp is the polar angular velocity, which imply that Ωp/ Ωe = 1 + α when Υ(θ) = coskθ and Ωp/ Ωe = (1 + α′)-1 = (1 + α) for Υ(θ) = sinkθ. The dependence of fpole with α and k is given through the radii ratio Rp/Re, which is a function of them both and on the function Υ(θ) chosen. However, feq depends only on the ratio η. It may be worth noting that for η = 0, it is ϑ ≡ θ so that in Eq. (31) the GDF becomes f(r,θ) = 1. This also makes that from Eq. (31) we have fpole = feq = 1.
(32)where Rp and Re are the polar and equatorial radii, respectively. Ωp is the polar angular velocity, which imply that Ωp/ Ωe = 1 + α when Υ(θ) = coskθ and Ωp/ Ωe = (1 + α′)-1 = (1 + α) for Υ(θ) = sinkθ. The dependence of fpole with α and k is given through the radii ratio Rp/Re, which is a function of them both and on the function Υ(θ) chosen. However, feq depends only on the ratio η. It may be worth noting that for η = 0, it is ϑ ≡ θ so that in Eq. (31) the GDF becomes f(r,θ) = 1. This also makes that from Eq. (31) we have fpole = feq = 1.
For a given ratio η we obtain the same value feq whatever the function Υ(θ). We may wonder then whether the same value for fpole can be derived whatever the chosen function Υ(θ) provided we use the appropriate reciprocal gravity-darkening parameter, i.e. α or α′ = − α/ (1 + α), as it is apparent form the expression of fpole given in Eq. (32). Actually, this reciprocity is valid only for k = 2. In the next section we show that for k ≠ 2 this apparent reciprocity does not produce the same ratio Rp/Re, and the geometry of the stellar surface is not the same either. This is due to the fact that Re/Rp = 1 + ηΓ, with ![\hbox{$\Gamma=\int_0^{\pi/2}[\Omega(\theta)/\Omega_{\rm e}]^2 \ldots {\rm d}\theta$}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq227.png) (see Zorec et al. 2011) where, as seen from Fig. 1, Ω(θ) / Ωe depends on Υ(θ) for k ≠ 2, even if we use α and its reciprocal α′ according to each case. Consequently, the behaviour of the resulting GDF, f(θ), over the interval 0 <θ<π/ 2 will depend in a strict sense on the chosen Υ(θ) function if k ≠ 2.
(see Zorec et al. 2011) where, as seen from Fig. 1, Ω(θ) / Ωe depends on Υ(θ) for k ≠ 2, even if we use α and its reciprocal α′ according to each case. Consequently, the behaviour of the resulting GDF, f(θ), over the interval 0 <θ<π/ 2 will depend in a strict sense on the chosen Υ(θ) function if k ≠ 2.
5. The effective temperature as a function of the colatitude
The magnitude of the flux-vector in Eq. (2) can be rewritten as 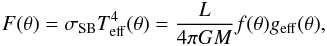 (33)where σSB is the Štefan-Boltzmann constant. Using Eqs. (9) and (11) this relation can be translated into
(33)where σSB is the Štefan-Boltzmann constant. Using Eqs. (9) and (11) this relation can be translated into ![\begin{eqnarray} T_{\rm eff}(\theta) = \langle T\rangle\left[f(\theta)\gamma(\theta)\right]^{1/4}, \label{teff} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq232.png) (34)where the radial variable r = r(θ) was used as the radius-vector representing the stellar surface, so that γ becomes a function of θ only, apart from its dependence on (η,α). It is obvious that for η = 0 (no rotation), f(θ) = γ(θ) = 1 and Teff(θ) = ⟨ T ⟩. The factor ⟨ T ⟩ is the uniform effective temperature over a sphere of radius Re(η) radiating the luminosity L
(34)where the radial variable r = r(θ) was used as the radius-vector representing the stellar surface, so that γ becomes a function of θ only, apart from its dependence on (η,α). It is obvious that for η = 0 (no rotation), f(θ) = γ(θ) = 1 and Teff(θ) = ⟨ T ⟩. The factor ⟨ T ⟩ is the uniform effective temperature over a sphere of radius Re(η) radiating the luminosity L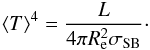 (35)It must be understood that when interpreting observations the quantity ⟨ T ⟩ is a free parameter, because the bolometric luminosity L depends on physical conditions that characterize the core of rotating stars. This luminosity depends, among other factors, on the total angular momentum stored in the star and on its internal distribution, which are unknown. In Figs. 4a to c Teff(θ,η,α) / ⟨ T ⟩ is shown as a function of the co-latitude θ when Υ(θ) = coskθ, η = 0.8, k = 0.5, 2.0 and 6.0, and for several values of α ranging from − 0.5 to + 0.5. Figures 4d to f show Teff(θ,η,α) / ⟨ T ⟩ against θ for Υ(θ) = sinkθ and (k,α′), where α′ = − α/ (1 + α). The green curves correspond to Teff(θ) / ⟨ T ⟩ for α = α′ = 0, previously obtained for rigid rotators by Espinosa Lara & Rieutord (2011). In Fig. 5 we plot the effective temperature ratios
(35)It must be understood that when interpreting observations the quantity ⟨ T ⟩ is a free parameter, because the bolometric luminosity L depends on physical conditions that characterize the core of rotating stars. This luminosity depends, among other factors, on the total angular momentum stored in the star and on its internal distribution, which are unknown. In Figs. 4a to c Teff(θ,η,α) / ⟨ T ⟩ is shown as a function of the co-latitude θ when Υ(θ) = coskθ, η = 0.8, k = 0.5, 2.0 and 6.0, and for several values of α ranging from − 0.5 to + 0.5. Figures 4d to f show Teff(θ,η,α) / ⟨ T ⟩ against θ for Υ(θ) = sinkθ and (k,α′), where α′ = − α/ (1 + α). The green curves correspond to Teff(θ) / ⟨ T ⟩ for α = α′ = 0, previously obtained for rigid rotators by Espinosa Lara & Rieutord (2011). In Fig. 5 we plot the effective temperature ratios 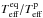 as a function of η and different values k and α, when Υ(θ) = coskθ or Υ(θ) = sinkθ.
as a function of η and different values k and α, when Υ(θ) = coskθ or Υ(θ) = sinkθ.
 |
Fig. 8 Effective temperature given as ln [ Teff(θ) / ⟨ T ⟩ ] 4 against ln [ geff(θ) / ⟨ g ⟩ ] for η = 0.8. Panels a–c: are for Υ(θ) = coskθ with k = 0.5, 2.0 and 6.0, respectively and α ranging from − 0.5 to + 0.5. Panels d–f: are for Υ(θ) = sinkθ with k = 0.5, 2.0 and 6.0, respectively and α′(α) ranging from − 1.0 to + 1.0. In all cases the left-bottom corner corresponds to the equator and the right-upper corner to the pole. |
6. The V sini parameter
Vsini is a parameter that mainly reflects the global broadening of a spectral line. It was shown in Zorec et al. (2017) that this broadening is produced by monochromatic contributions from curved loci of points over the observed stellar hemisphere having the same Doppler displacement. The shape of these curves depend on the differential rotation law and on the inclination angle, while for rigid rotation these curves are straight lines which are independent of the inclination angle. Due to the differentiated sensitivity of spectral lines to the physical formation conditions (Thomas 1983; Zorec et al. 2017), according to the spectral line, the different regions on the observed stellar hemisphere do not contribute with the same efficiency to the rotational broadening because of the non uniform distribution of temperature and gravity. To illustrate this effect, we have calculated He i 4471 and Mg ii 4481 lines broadened by differential rotators with rotation laws given by Eq. (4) and both forms of Υ(θ) given in Eq. (5). For this exercise we used a model star with mass M = 9 M⊙ and fractional age t/tMS = 0.6 (tMS is the time a rotating star spends in the main sequence evolutionary phase). Rotation laws are characterized by several parameters k, α, and different equatorial velocities parametrized according to η. Applying the classic Fourier transform method we determined the Vsini parameters shown in Figs. 6 and 7 where we compare the resulting Veqsini with the actual input Veqsini corresponding to the given values of η and inclination angles. We note that deviations from the identity relation (y = x line) also exist for rigid rotators. They are due to the gravitational darkening effect, which is not taken into account in the classic rigid-rotation broadening function GR(λ) (Gray 1992).
Because it has become of common use today, the classic method based on the FT was employed to determine the Vsini. This method assumes, however, that the observed rotationally broadened line profile F(λ) can be represented as the convolution with an analytical rotation broadening-function GR(λ) of a flux line-profile F(λ) emitted by a non-rotating star having uniform effective temperature and gravity. The specific intensity I(λ,μ) contributing to the observed line flux F(λ) is thus the same over the entire stellar disc, which obviously does not occur in rotating stars. The derivation of an analytical expression for GR(λ) that is independent of the inclination angle requires that the star be spherical and behaves as a rigid rotator (Gray 1975, 1992), i.e. the monochromatic Doppler displacements are produced over straight strips of constant radial velocities. The Vsini is then obtained by comparing the zeros of the flux line-profile FT F(λ) with the corresponding zeros of the FT of the function GR(λ).
In Zorec et al. (2017) it has been shown that depending on the spectral line and on the value of α, the FT of lines may have unusual shapes, making the zeros difficult to identify and to interpret. This difficultly is a direct consequence of the inconsistency raised by the use an analytic expression GR(λ) adapted for uniform rigid rotators, which does not take into account: a) the actual shape of curves of constant radial velocity contributing to the individual rotational Doppler-displacements, and b) the non uniformity of the effective temperature and surface effective gravity determining the local monochromatic specific intensities I(λ,μ).
Figures 6 and 7 reveal that the Vsini obtained using the FT-method can be overestimated when α> 0, and underestimated for α< 0, as compared to its value for rigid rotators. We notice that for Υ(θ) = coskθ and a given | α | the deviations are larger when α< 0 than for α> 0. For Υ(θ) = sinkθ the deviations reverse according to the α-corresponding reciprocal parameter α′. Finally, according to the spectral line used, the obtained Vsini is not exactly the same. To apprehend what can be the possible deviations that the current Vsini determinations may incur, let us recall that in the Sun α ≃ − 0.3 and Υ(θ) = cos2θ, and that predictions made by Espinosa Lara & Rieutord (2013) for rapid rotators of masses 2 ≲ M ≲ 4 M⊙ foresee α ≳ − 0.2. Facing the likely possibility that stars are differential rotators, these results warn us that the current interpretations based on the rigid rotation hypothesis could be misleading. However, detailed modelling of spectral lines can be made today to account for the noted differences in the Vsini obtained from different spectral lines. They could help us to derive indications on the value of the α parameter.
Needless to say that the classic method of determining Vsini based on the FWHM (full-width at half-maximum) produces the same type of deviations, because the comparisons are made also with the rotational broadening of spectral lines produced by classic spherical rigid rotators.
 |
Fig. 9 Panels a–c: Gravity-darkening slope |
7. The gravity-darkening exponent
The gravity-darkening exponent was introduced with the purpose of representing in a simple way the distribution of the local effective temperature Teff(θ) over a rotating stellar surface. As noted in Sect. 1, the known von Zeipel’s relation that holds for barotropic objects 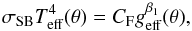 (36)is characterized by the constant gravity-darkening exponent β1, and the constant CF which depends on the gravity-rotation equipotential of the stellar surface. The notation β1 is used here to distinguish it from the exponent β = β1/ 4 that is also frequently employed to characterize the gravity-darkening effect. In the following section, we will comment on some drawbacks of using Eq. (36).
(36)is characterized by the constant gravity-darkening exponent β1, and the constant CF which depends on the gravity-rotation equipotential of the stellar surface. The notation β1 is used here to distinguish it from the exponent β = β1/ 4 that is also frequently employed to characterize the gravity-darkening effect. In the following section, we will comment on some drawbacks of using Eq. (36).
 |
Fig. 10 Average gravitational-darkening slope ⟨ B1 ⟩ given by Eq. (40) as function of η, calculated respectively for: a) Υ(θ) = coskθ; b) sinkθ. The colours identify the differential rotation parameter α, while k is identified using different line-styles. |
7.1. Dependence of the gravity-darkening exponent with colatitude
Up to now, the relation in Eq. (36) has been used to interpret the observations of rapidly rotating stars regardless of whether they are barotropic or baroclinic. However, β1 and CF cannot be assumed independent of the colatitude-angle θ even in barotropic model-stars having atmospheres in radiative equilibrium (Espinosa Lara & Rieutord 2011; Rieutord 2016).
To inquire on the effects that a surface differential rotation can induce on β1 and CF, Fig. 8 shows the relation between lnTeff(θ) calculated with Eq. (34) against lngeff(θ) using both forms of Υ(θ) in Eq. (5). The model-stars are assumed to rotate with η = 0.8 with several values of α and k. Obviously, similar behaviours are noted for other values of η.
Because the curves in Fig. 8 are not straight lines, neither CF nor β1 can be considered as genuine constants, even though a quasi-linear relation between lnTeff(θ) and lngeff(θ) seems to exist over some intervals of θ. To emphasize more clearly the lack of constancy of β1 and CF, we define a pseudo-exponent or gravity-darkening slope b1(θ) as ![\begin{eqnarray} \ln T^4_{\rm eff}(\theta) = b_1(\theta)\ln g_{\rm eff}(\theta)+\ln \left[C_{\rm F}(\theta)/\sigma_{\rm SB}\right], \label{defpsb1} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq276.png) (37)and consider that between two successive, close discrete points θi and θi + 1,
(37)and consider that between two successive, close discrete points θi and θi + 1, 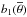 and
and 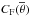 can be assumed constant; i.e.:
can be assumed constant; i.e.: ![\begin{equation} b_1 \left(\overline{\theta_i}\right) = 4\frac{\ln\left[T_{\rm eff}\left(\theta_{i+1}\right)/T_{\rm eff} \left(\theta_i\right)\right]}{\ln \left[g_{\rm eff}\left(\theta_{i+1}\right)/g_{\rm eff}\left(\theta_i\right)\right]}; \ \ \ \overline{\theta_i} = \left(\theta_i+\theta_{i+1}\right)/2. \label{defpsb2} \end{equation}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq279.png) (38)Inserting the values
(38)Inserting the values 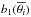 in Eq. (37), the corresponding
in Eq. (37), the corresponding 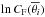 can be estimated. The inferred quantities
can be estimated. The inferred quantities 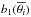 and
and 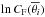 are shown in Fig. 9. They clearly demonstrate that both b1 and CF are dependent on θ and that consequently they cannot be used as constants in Eq. (36).
are shown in Fig. 9. They clearly demonstrate that both b1 and CF are dependent on θ and that consequently they cannot be used as constants in Eq. (36).
7.2. The observed gravity-darkening slope
7.2.1. Neglecting the viewing angle
Replacing in Eq. (37) the expressions for geff and Teff given respectively by Eqs. (9) and (34), and imposing that b1 and CF do not depend on θ, it follows that ![\begin{eqnarray} B_1(\theta) = 1+ \frac{\ln\left[f(\theta)/f^{\rm pole}\right]}{\ln\left[\gamma(\theta)/\gamma^{\rm pole}\right]}, \label{defb1} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq284.png) (39)where fpole and γpole are the values of the functions f(θ) and γ(θ) in θ = 0. The function B1(θ) behaves in a similar way as b1(θ), so that it is needless to reproduce it graphically. Instead, we can replace f(θ) and γ(θ) in Eq. (39) by their values at θ = π/ 2 (see Eq. (32)) to obtain a kind of average ⟨ B1(θ) ⟩ that takes the form
(39)where fpole and γpole are the values of the functions f(θ) and γ(θ) in θ = 0. The function B1(θ) behaves in a similar way as b1(θ), so that it is needless to reproduce it graphically. Instead, we can replace f(θ) and γ(θ) in Eq. (39) by their values at θ = π/ 2 (see Eq. (32)) to obtain a kind of average ⟨ B1(θ) ⟩ that takes the form ![\begin{eqnarray} \langle{B_1}\rangle = 1-\frac{2}{3}\left[\frac{\ln(1-\eta)+\eta\left(R_{\rm p}/R_{\rm e}\right)^3\left(\Omega_{\rm p}/\Omega_{\rm e}\right)^2}{\ln \Big[(1-\eta)+2\ln\left(R_{\rm p}/R_{\rm e}\right)}\right], \label{gd_co4} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq290.png) (40)which is a generalized version of ⟨ B1 ⟩ obtained by Espinosa Lara & Rieutord (2011) for rigid rotators. In Fig. 10, ⟨ B1 ⟩ is shown as a function of η for − 0.5 ≤ α ≤ 0.5, k = 0.5, 2, 6, and for both functions Υ(θ). The expression of ⟨ B1 ⟩ for α = 0 was sometimes used in the literature to compare the exponents b1 derived from interferometric observations.
(40)which is a generalized version of ⟨ B1 ⟩ obtained by Espinosa Lara & Rieutord (2011) for rigid rotators. In Fig. 10, ⟨ B1 ⟩ is shown as a function of η for − 0.5 ≤ α ≤ 0.5, k = 0.5, 2, 6, and for both functions Υ(θ). The expression of ⟨ B1 ⟩ for α = 0 was sometimes used in the literature to compare the exponents b1 derived from interferometric observations.
 |
Fig. 11 Relation between the apparent 4ln [ Teff(i) / ⟨ T ⟩ ] and ln [ geff(i) / ⟩ ⟨ g ⟩ ]; a)–c) for Υ(θ) = coskθ with α from − 0.5 to +0.5; d)–f) for sinkθ and α′ =− α/ (1 = α). All curves are for η = 0.8, with k = 0.5, 2.0, 6.0. The colour-codes according to α and α′ indicated in the respective blocks for k = 2 hold for all curves having the same Υ(θ). The equator-on seeing directions (i → π/ 2) are in the lower left corner of each block, while the polar-on directions (i → 0) are in the upper right corner. |
7.2.2. Considering the viewing angle
Any parameter describing a physical property of a rotating stellar atmosphere that depends on the co-latitude θ, automatically becomes a function of the viewing angle i when it is determined from observational data of angularly unresolved stars. This must also happen to the gravity-darkening slope given by Eq. (39). Such a quantity should thus depend on the apparent average effective temperature and gravity that characterize the observed stellar hemisphere, which are named hereafter as ⟨ Teff(i) ⟩ and ⟨ geff(i) ⟩, respectively.
Let us define ⟨ Teff(i) ⟩ and ⟨ geff(i) ⟩ so as to obtain a slope that might be assimilated with an empirically derived gravity-darkening slope. The apparent effective temperature ⟨ Teff(i) ⟩ can be written as 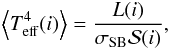 (41)where
(41)where 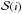 is the effective emitting area of the i-dependent rotationally deformed stellar hemisphere. In this expression, the apparent bolometric luminosity L(i) emitted by the stellar disc projected towards the observer is given by (Collins 1965; Maeder & Peytremann 1970; Collins 1973)
is the effective emitting area of the i-dependent rotationally deformed stellar hemisphere. In this expression, the apparent bolometric luminosity L(i) emitted by the stellar disc projected towards the observer is given by (Collins 1965; Maeder & Peytremann 1970; Collins 1973) 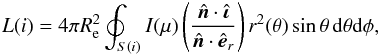 (42)where
(42)where 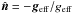 is the unit vector normal to the stellar surface;
is the unit vector normal to the stellar surface;  is the unit vector directed towards the observer; êr is the unit vector associated with the r-spherical coordinate; S(i) indicates the observed region of the stellar hemisphere over which the integration is carried out. μ is the directional cosine
is the unit vector directed towards the observer; êr is the unit vector associated with the r-spherical coordinate; S(i) indicates the observed region of the stellar hemisphere over which the integration is carried out. μ is the directional cosine 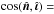
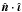 ; I(μ) is the bolometric specific intensity of the radiation for which we use a quadratic form
; I(μ) is the bolometric specific intensity of the radiation for which we use a quadratic form ![\begin{eqnarray} I(\mu) = I_1\left[1-\epsilon_1(1-\mu)-\epsilon_2\left(1-\mu^2\right)\right], \label{i_bol1} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq312.png) (43)whose limb-darkening coefficients ϵ1,2 have been interpolated in the tables given by Claret (2000) for each pair of local fundamental parameters [Teff(θ),geff(θ)]. Knowing that for each point over the stellar surface we have
(43)whose limb-darkening coefficients ϵ1,2 have been interpolated in the tables given by Claret (2000) for each pair of local fundamental parameters [Teff(θ),geff(θ)]. Knowing that for each point over the stellar surface we have 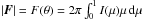 , the intensity I1 = I(μ = 1) can be written as
, the intensity I1 = I(μ = 1) can be written as ![\begin{eqnarray} I_1(\theta)=\frac{6}{\pi}\left[\frac{F(\theta)}{6-2\epsilon_1-3\epsilon_2}\right], \label{i_bol2} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq317.png) (44)which depends on f(θ) and γ(θ) through F(θ) given in Eq. (33).
(44)which depends on f(θ) and γ(θ) through F(θ) given in Eq. (33).
Consistently with the definition of ⟨ Teff(i) ⟩, we can use Eq. (33) to estimate ⟨ geff(i) ⟩ using the expression 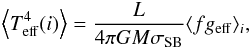 (45)that with Eqs. (41) and (42) leads to
(45)that with Eqs. (41) and (42) leads to 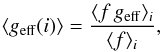 (46)where ⟨ f ⟩ i is given by
(46)where ⟨ f ⟩ i is given by ![\begin{eqnarray} \langle f\rangle_i & =& \left.\oint_{S(i)}f(\theta)\phi(\mu)\left(\frac{\hat{\vec{n}}\cdot\hat{\boldsymbol\iota}}{\hat{\vec{n}}\cdot\hat{\vec{e}}_r}\right)r^2(\theta)\sin\theta\,{\rm d}\theta {\rm d}\phi\middle/\mathcal{S}(i)\right. \notag\\[1.5mm] \phi(\mu) & =& \pi^{-1} \left[1 - \epsilon_1 (1 - \mu) - \epsilon_2 \left(1 - \mu^2\right)\right]/\left(1 - \epsilon_1/3 - \epsilon_2/2\right). \label{geff_iii} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq322.png) (47)For the numerical estimates of the apparent ⟨ Teff(i) ⟩ and ⟨ geff(i) ⟩ the knowledge of absolute values of Teff(θ) and geff(θ) are required. To get a rough insight on their amplitude variation, we have assumed model-stars with mass M = 9 M⊙ and fractional age t/tMS = 0.6 (tMS is the time spent by a rotating star in the main sequence phase). The bolometric luminosity L was calculated with the rotationally induced mass-compensation effect parametrized as in Frémat et al. (2005), where it is assumed that the stellar core rotates rigidly. The equatorial radii ratio Re/Ro (Ro is the equatorial radius of a parent non-rotating object having the same mass) is given by the models of Zorec et al. (2011).
(47)For the numerical estimates of the apparent ⟨ Teff(i) ⟩ and ⟨ geff(i) ⟩ the knowledge of absolute values of Teff(θ) and geff(θ) are required. To get a rough insight on their amplitude variation, we have assumed model-stars with mass M = 9 M⊙ and fractional age t/tMS = 0.6 (tMS is the time spent by a rotating star in the main sequence phase). The bolometric luminosity L was calculated with the rotationally induced mass-compensation effect parametrized as in Frémat et al. (2005), where it is assumed that the stellar core rotates rigidly. The equatorial radii ratio Re/Ro (Ro is the equatorial radius of a parent non-rotating object having the same mass) is given by the models of Zorec et al. (2011).
The relations between ln [ ⟨ Teff(i) ⟩ / ⟨ T ⟩ ] and ln [ ⟨ geff(i) ⟩ / ⟨ g ⟩ ] shown in Fig. 11 are calculated using Υ(θ) = coskθ and sinkθ, for η = 0.8, k = 0.5, 2.0, 6.0, and − 0.5 ≤ α ≤ − 0.5. While Fig. 8 represents the variation of Teff against geff over the stellar surface, Fig. 11 represents these parameters integrated over a stellar surface seen according to different viewing angles. The upper right corner corresponds to pole-on seeing directions and the lower left corners to the equator-on directions. For a given geometrical deformation of stars parameterized here with the ratio η, it turns out that the resolution among these curves according to the differential parameter α is a strong function of the power k used in Υ(θ).
From Fig. 11 it seems legitimate to assume relations of the type 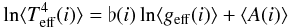 (48)for each [ Υ,k,α ] so as to represent the dependence of the slope ♭(i) with the stellar inclination, as we did for b1(θ) with θ, i.e. by taking here ♭(i) and ⟨ A(i) ⟩ as constants between two successive inclinations ij and ij + 1 in a given discretization of this variable in 0° ≤ i ≤ 90°. The values of ♭(i) obtained for three inclination angles: i = 0°, 45° and 90° against the ratio η are shown in Fig. 12. Figures 12a–c are for Υ = coskθ with k = 0.5, 2 and 6, while Figs. 12d–f are for Υ = sinkθ and the same exponents k. In these figures we note that the ♭(i) curves have a global behaviour that is similar to ⟨ B1 ⟩ in Fig. 10, except for their spread as a function of i.
(48)for each [ Υ,k,α ] so as to represent the dependence of the slope ♭(i) with the stellar inclination, as we did for b1(θ) with θ, i.e. by taking here ♭(i) and ⟨ A(i) ⟩ as constants between two successive inclinations ij and ij + 1 in a given discretization of this variable in 0° ≤ i ≤ 90°. The values of ♭(i) obtained for three inclination angles: i = 0°, 45° and 90° against the ratio η are shown in Fig. 12. Figures 12a–c are for Υ = coskθ with k = 0.5, 2 and 6, while Figs. 12d–f are for Υ = sinkθ and the same exponents k. In these figures we note that the ♭(i) curves have a global behaviour that is similar to ⟨ B1 ⟩ in Fig. 10, except for their spread as a function of i.
In Fig. 13 we show the values of 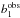 determined with interferometric data (see Domiciano de Souza et al. 2014), where the interpretation of observations was done using Eq. (36). These points have been originally given as a function of the stellar flattening ε = 1 − Rp/Re. We have converted ε into η considering, as the authors themselves did, that stars are rigid rotators, i.e. Re/Rp = 1 + η/ 2, which imply that η = 2ε/ (1 − ε). In this diagram the curves ♭1(i) are reproduced for Υ(θ) = coskθ with k = 2 and different values of α, in particular those suited for rigid rotators, i.e. α = 0 (green curves). In Sect. 8 we discuss the reason of using k = 2. Taking into account the observational uncertainties, we can conclude that half of the observed points are located outside the zone limited by ♭1(i = 0) and ♭1(i = π/ 2) of rigid rotators. Two of them are likely situated in the region of α> 0, while there is one in the zone of α< 0, which indicates that other solutions than rigid rotation might also suit these objects.
determined with interferometric data (see Domiciano de Souza et al. 2014), where the interpretation of observations was done using Eq. (36). These points have been originally given as a function of the stellar flattening ε = 1 − Rp/Re. We have converted ε into η considering, as the authors themselves did, that stars are rigid rotators, i.e. Re/Rp = 1 + η/ 2, which imply that η = 2ε/ (1 − ε). In this diagram the curves ♭1(i) are reproduced for Υ(θ) = coskθ with k = 2 and different values of α, in particular those suited for rigid rotators, i.e. α = 0 (green curves). In Sect. 8 we discuss the reason of using k = 2. Taking into account the observational uncertainties, we can conclude that half of the observed points are located outside the zone limited by ♭1(i = 0) and ♭1(i = π/ 2) of rigid rotators. Two of them are likely situated in the region of α> 0, while there is one in the zone of α< 0, which indicates that other solutions than rigid rotation might also suit these objects.
 |
Fig. 12 Gravitational-darkening slope ♭1(i) against the rotational ratio η. The colours identify the values of the differential parameter α, and the line-styles are for the inclination angles. In a) to c) the slope ♭1(i) was calculated with Υ(θ) = coskθ and from d) to f) b1(i) was obtained with Υ(θ) = sinkθ. As throughout in this work, rigid rotation (α = 0) is identified with green lines. |
 |
Fig. 13 Comparison of the empirical gravitational-darkening slope |
However, according to the diagrams in Fig. 12 it clearly appears that there is not a unique way to characterize the studied stars with β1 as rotators, since many solutions can be envisioned in terms of [ Υ,k,α ]. On the other hand, there is a strong concern with the interpretation of the observed values 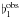 , because β1 and CF were considered as constants in the reduction of data. Due to these ambiguities, it would perhaps be wiser to abandon the parameter β1 to model fluxes and rather concentrate on determining them using the differential rotation parameter α and the inclination angle i (Domiciano de Souza et al. 2004).
, because β1 and CF were considered as constants in the reduction of data. Due to these ambiguities, it would perhaps be wiser to abandon the parameter β1 to model fluxes and rather concentrate on determining them using the differential rotation parameter α and the inclination angle i (Domiciano de Souza et al. 2004).
8. Discussion and conclusion
Continuing the work initiated by Espinosa Lara & Rieutord (2011) to represent the distribution of the effective temperature in rotating stars, where the only requirement is that the outermost layers of the envelope be in radiative equilibrium and the radiation flux vector be dominantly anti-parallel to the effective surface gravity, we have discussed the case where these layers are in differential rotation. We have studied the particular case where the angular velocity is given by Eqs. (4) and (5), and obtained relationships that generalize those previously derived by Espinosa Lara & Rieutord (2011) for rigid rotators. As a further step, we have studied the effects of the surface differential rotation on the determination of the Vsini parameter and concluded that strong deviations can be expected. They seem to be large enough to be exploited empirically. We also find that a constant gravity-darkening exponent is inappropriate for describing stars as rotators. In fact, as this exponent is a function of the stellar co-latitude (Rieutord 2016), it becomes a function of the viewing angle that induces ambiguities in the interpretation of observations. The modelling of observed parameters of rotating stars must then be done directly through the gravity-darkening-function (GDF), f(θ), which describes the distribution of the effective temperature as indicated by Eqs. (34), (31), (29) and (25), for which the stellar geometry must be calculated consistently. According to discussions carried out in this work, the interpretation of observations would then require one to determine the set of quantities (η,α,Υ) instead of the simple pair (η,β1).
In the approach where differential rotation is considered, a significant uncertainty remains in the choice of the function Υ(θ). Indeed, up to now, and except for the Sun, no empirical indication exists on the actual nature of Υ(θ) in stars. The quantity that needs to be inferred first is a parameter related to the average surface gradient ⟨ d Ω / d θ ⟩. To this end, the simplest expression for Υ(θ) could be 2θ/π. This makes α the unique free parameter characterizing the surface differential rotation, but in this case the calculation of the integral T(θ) (Eq. (25)) has some annoying numerical subtleties. However, we have shown in Sect. 2 that for the same ratio Ωp/ Ωe, no significant differences in the prediction or analysis of observed parameters may arise if we use only Υ(θ) = coskθ or sink′θ, because reliable correspondences can be established between (α,k) and (α′,k′). According to this finding, we can adopt Υ(θ) = coskθ and show easily that the weighted average gradient over the stellar surface ![\begin{eqnarray} \left \langle {\rm d}\left(\Omega/\Omega_{\rm o}\right)/{\rm d}\theta\right\rangle = \int_0^{\pi/2} \left[{\rm d}\left(\Omega/\Omega_{\rm o}\right)/{\rm d}\theta\right]\sin\theta {\rm d}\,\theta \label{weig_om} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq355.png) (49)is equal to ⟨ d(Ω / Ωo) / dθ ⟩ = 2α/π if k = 2.55. Although nothing prevents us from making numerical models with k = 2.55, the results for Teff(θ), Vsini and other parameters, show that no significant differences occur on the predicted or analyzed parameters if we simply adopt k = 2. Moreover, the representation Υ(θ) = cos2θ of Maunder & Maunder (1905) accounts for the solar surface differential rotation. Two first order indications could then be reliably drawn from observations: a) whether the surface differential rotation in stars is significant or not; b) what is its character: accelerated towards the pole or accelerated towards the equator. We note that for some forms of Υ(θ,k), in particular for k = 2, analytical expressions of T(θ) exist and can help to proceed in a similar way as for rigid rotators with the formulas developed by Espinosa Lara & Rieutord (2011).
(49)is equal to ⟨ d(Ω / Ωo) / dθ ⟩ = 2α/π if k = 2.55. Although nothing prevents us from making numerical models with k = 2.55, the results for Teff(θ), Vsini and other parameters, show that no significant differences occur on the predicted or analyzed parameters if we simply adopt k = 2. Moreover, the representation Υ(θ) = cos2θ of Maunder & Maunder (1905) accounts for the solar surface differential rotation. Two first order indications could then be reliably drawn from observations: a) whether the surface differential rotation in stars is significant or not; b) what is its character: accelerated towards the pole or accelerated towards the equator. We note that for some forms of Υ(θ,k), in particular for k = 2, analytical expressions of T(θ) exist and can help to proceed in a similar way as for rigid rotators with the formulas developed by Espinosa Lara & Rieutord (2011).
Acknowledgments
We are thankful to the referee for his/her attentive reading of the manuscript and for his/her suggestions to improve the presentation of our results.
References
- Bodenheimer, P. 1971, ApJ, 167, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Che, X., Monnier, J. D., Zhao, M., et al. 2011, ApJ, 732, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A. 2012, A&A, 538, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clement, M. J. 1979, ApJ, 230, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, II, G. W. 1965, ApJ, 142, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, II, G. W. 1973, A&A, 26, 315 [NASA ADS] [Google Scholar]
- Delaa, O., Zorec, J., Domiciano de Souza, A., et al. 2013, A&A, 555, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deupree, R. G. 2001, ApJ, 552, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Domiciano de Souza, A., Zorec, J., Jankov, S., et al. 2004, A&A, 418, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Moser Faes, D., et al. 2014, A&A, 569, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eriguchi, Y., & Mueller, E. 1991, A&A, 248, 435 [NASA ADS] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2007, A&A, 470, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frémat, Y., Zorec, J., Hubert, A.-M., & Floquet, M. 2005, A&A, 440, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujisawa, K. 2015, MNRAS, 454, 3060 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1975, ApJ, 202, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1992, The observation and analysis of stellar photospheres (Camb. Astrophys. Ser.) [Google Scholar]
- Jackson, S., MacGregor, K. B., & Skumanich, A. 2005, ApJS, 156, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R. 1977, A&A, 58, 267 [NASA ADS] [Google Scholar]
- Lovekin, C. C., Deupree, R. G., & Short, C. I. 2006, ApJ, 643, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1999, A&A, 347, 185 [NASA ADS] [Google Scholar]
- Maeder, A., Georgy, C., & Meynet, G. 2008, A&A, 479, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [Google Scholar]
- Maeder, A., & Peytremann, E. 1970, A&A, 7, 120 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars, Astronomy and Astrophysics Library, Volume. ISBN 978-3-540-76948-4 (Berlin, Heidelberg: Springer) [Google Scholar]
- Maunder, E. W., & Maunder, A. S. D. 1905, MNRAS, 65, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1979, MNRAS, 189, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Monnier, J. D., Che, X., Zhao, M., et al. 2012, ApJ, 761, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Osaki, Y. 1966, PASJ, 18, 7 [NASA ADS] [Google Scholar]
- Rieutord, M. 2016, in Cartography of the Sun and the Stars, eds. J.-P. Rozelot & C. Neiner (Berlin: Springer Verlag), 914, Lect. Notes Phys., 101 [Google Scholar]
- Rieutord, M., Espinosa Lara, F., & Putigny, B. 2016, J. Comp. Phys., 318, 277 [Google Scholar]
- Roxburgh, I. W. 1966, MNRAS, 132, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sackmann, I. J. 1970, A&A, 8, 76 [NASA ADS] [Google Scholar]
- Smith, R. C., & Worley, R. 1974, MNRAS, 167, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, J.-L. 1978, Theory of rotating stars (Princeton: University Press) [Google Scholar]
- Thomas, R. N. 1983, NASA-CNRS Monograph Series on Nonthermal Phenomena in Stellar Atmospheres [Google Scholar]
- Uryu, K., & Eriguchi, Y. 1994, MNRAS, 269, 24 [NASA ADS] [Google Scholar]
- Uryu, K., & Eriguchi, Y. 1995, MNRAS, 277, 1411 [NASA ADS] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P., Ranc, C., & Morel, P. 2010, A&A, 517, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, M., Monnier, J. D., Pedretti, E., et al. 2009, ApJ, 701, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Zorec, J., Frémat, Y., Domiciano de Souza, A., et al. 2011, A&A, 526, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J., Frémat, Y., Domiciano de Souza, A., et al. 2017, A&A, 602, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J., & Royer, F. 2012, A&A, 537, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: The functions T(θ)
The analytical expressions obtained of the function T(θ) with Υ(θ) = cosk(θ) by integrating Eq. (23) for the natural numbers k = 1, 2, 3 and 4 are:
k = 1
k = 2
k = 3
k = 4
![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{array}{rcl} \displaystyle \mathscr{T}(\theta) & = & \left\{ \begin{array}{ll} \displaystyle\frac{1}{(1+\alpha)^2}\left\{\ln\tan\frac{\theta}{2}+\frac{\left[3-\alpha+\sqrt{\alpha}(5+\alpha)\right]}{16\sqrt{2}\alpha^{1/4}}\ln\left[\frac{1+\alpha^{1/4}\cos\theta(\sqrt{2}+\alpha^{1/4}\cos\theta)}{1-\alpha^{1/4}\cos\theta(\sqrt{2}-\alpha^{1/4}\cos\theta)}\right] \right. & \\[6mm] \displaystyle +\left.\frac{\left[3-\alpha-\sqrt{\alpha}(5+\alpha)\right]}{8\sqrt{2}\alpha^{1/4}}\arctan\left(\frac{\sqrt{2}\alpha^{1/4}\cos\theta}{1-\alpha^{1/2}\cos^2\theta}\right)+\frac{(1+\alpha)}{4}\cos\theta\left(\frac{1-\alpha\cos^3\theta}{1+\alpha\cos^4\theta}\right)\right\} & {\rm for}\ \alpha \geq 0 \\[6mm] \end{array} \right. \end{array} \label{tau_k4} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq366.png) The corresponding analytical expressions of T(θ) with Υ(θ) = sink(θ) by integrating Eq. (23) for the natural numbers k = 1 and 2, are:
The corresponding analytical expressions of T(θ) with Υ(θ) = sink(θ) by integrating Eq. (23) for the natural numbers k = 1 and 2, are:
k = 1
k = 2
![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{array}{rcl} \displaystyle \mathscr{T}(\theta) & = & \displaystyle \ln\tan\frac{\theta}{2} + \left\{ \begin{array}{ll} \displaystyle \frac{1}{2}\left(\frac{\cos\theta}{1+\alpha\sin^2\theta}\right)-\frac{1}{4}\frac{(1+2\alpha)}{[\alpha(1+\alpha)]^{1/2}}\ln\left(\frac{1-u}{1+u}\right); \ \ \ u = \left(\frac{\alpha}{1+\alpha}\right)^{1/2}\!\!\!\!\cos\theta; \ \ \ {\rm for} \ \alpha \geq 0 & \\[6mm] \displaystyle \frac{1}{2}\left(\frac{\cos\theta}{1-|\alpha|\sin^2\theta}\right)+\frac{1}{2}\frac{(1+2|\alpha|)}{[|\alpha|(1-|\alpha|)]^{1/2}}\arctan\left[\left(\frac{|\alpha|)}{1-|\alpha|}\right)^{1/2}\!\!\!\!\cos\theta\right] \ \ \ {\rm for} \ \ \alpha < 0 . \end{array} \right. \end{array} \label{tau_ks2} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq369.png) (A.6)In spite of the formal difference between Eqs. (A.2) and (A.6), they are equivalent. They can be converted to each other knowing that sin2θ + coskθ = 1, making the transformation α into − α/ (1 + α) and considering the sign of α.
(A.6)In spite of the formal difference between Eqs. (A.2) and (A.6), they are equivalent. They can be converted to each other knowing that sin2θ + coskθ = 1, making the transformation α into − α/ (1 + α) and considering the sign of α.
Appendix B: Limit forms of f (r,θ)
Integrating Eq. (25) by parts, we obtain the following expression equivalent to Eq. (24) ![\appendix \setcounter{section}{2} \begin{eqnarray} \begin{array}{rcl} \displaystyle \ln\left[\frac{\tan(\vartheta/2)}{\tan(\theta/2}\right]+\cos\vartheta-\cos\vartheta\left[\frac{1+\alpha\Upsilon(\vartheta)}{1+\alpha\Upsilon(\theta)}\right]^2- 2\alpha[1+\alpha\Upsilon(\vartheta)]\mathscr{I}(\vartheta,\theta) & = & \frac{1}{3}\frac{\Omega^2_{\rm o}R^3}{GM}\cos^3\theta[1+\alpha\Upsilon(\vartheta)] \\ \displaystyle \mathscr{I}(\vartheta,\theta) & = & \int_{\theta}^{\vartheta}\frac{\sin^{-1}x\cos^2x}{[1+\alpha\Upsilon(x)]^2}\left(\frac{{\rm d}\Upsilon}{{\rm d}x}\right)\,dx. \end{array} \label{solf_ta} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq372.png) (B.1)As θ → 0 and θ → π/ 2, also ϑ → 0 and ϑ → π/ 2, respectively. Moreover, θ → 0 both θ and ϑ are infinitesimals of the same order, so that we can write ϑ = pθ where p is constant. Expanding the function tanx for small values of x and knowing that αΥ < 1, we derive
(B.1)As θ → 0 and θ → π/ 2, also ϑ → 0 and ϑ → π/ 2, respectively. Moreover, θ → 0 both θ and ϑ are infinitesimals of the same order, so that we can write ϑ = pθ where p is constant. Expanding the function tanx for small values of x and knowing that αΥ < 1, we derive -2\alpha[1+\Upsilon(p\theta)]\mathscr{I}(p\theta,\theta) & = & \frac{1}{3}\eta\left(\frac{\Omega_{\rm o}}{\Omega_{\rm e}}\right)^2\!\!\!r^3\!\!\!\cos^3\theta[1+\alpha\Upsilon(p\theta)]^2. \end{array} \label{lim1} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq380.png) (B.2)Taking the limit of this expression for θ → 0, and identifying r(θ = 0 with stellar surface it comes that
(B.2)Taking the limit of this expression for θ → 0, and identifying r(θ = 0 with stellar surface it comes that 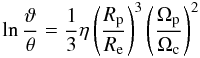 (B.3)which introduced into Eq. (31) leads to
(B.3)which introduced into Eq. (31) leads to ![\appendix \setcounter{section}{2} \begin{eqnarray} \begin{array}{l} \displaystyle \lim\limits_{\substack{\vartheta\to0 \\ \theta\to0}}f(r,\theta) = f^{\rm pole} = \exp\left]\frac{2}{3}\eta\left(\frac{R_{\rm p}}{R_{\rm e}}\right)^3\left(\frac{\Omega_{\rm p}}{\Omega_{\rm c}}\right)^2\right] \end{array} \label{tt1} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq383.png) (B.4)where Ωp is the polar angulat velocity, which carries that Ωp/ Ωe = 1 + α when Υ(θ) = cosk(θ) and Ωp/ Ωe = (1 + α)-1 for Υ(θ) = sink(θ). We note that the dependence of fpole with α and k is given through the radii ratio Rp/Re.
(B.4)where Ωp is the polar angulat velocity, which carries that Ωp/ Ωe = 1 + α when Υ(θ) = cosk(θ) and Ωp/ Ωe = (1 + α)-1 for Υ(θ) = sink(θ). We note that the dependence of fpole with α and k is given through the radii ratio Rp/Re.
To calculate the limit of f(r,θ) as θ → π/ 2 we make the change of variables ϑ → π/ 2 − ϵϑ and θ → π/ 2 − ϵθ, where ϵϑ → 0 and ϵθ → 0 are infinitesimals of the same order. This operation implies the following changes of functions 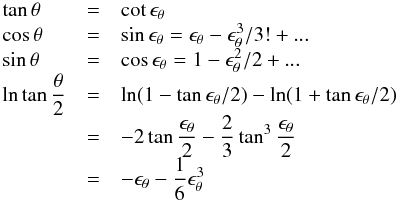 (B.5)and similar expressions for the functions dependent on ϑ. Introducing this terms into Eq. (B.1), it is obtained
(B.5)and similar expressions for the functions dependent on ϑ. Introducing this terms into Eq. (B.1), it is obtained ![\appendix \setcounter{section}{2} \begin{eqnarray} \begin{array}{rcl} \displaystyle \frac{1}{3}(\epsilon^3_{\theta}-\epsilon^3_{\vartheta})-(\epsilon_{\theta}-\frac{1}{6}\epsilon^3_{\theta}+...)[\alpha(\Upsilon_{\theta}-\Upsilon_{\vartheta})+...]-2\alpha(1+\alpha\Upsilon_{\vartheta})^2\int_{\pi/2-\epsilon_{\theta}}^{\pi/2-\epsilon_{\vartheta}}...{\rm d}\,x & = & \displaystyle \frac{1}{3}\eta\left(\frac{\Omega_{\rm o}}{\Omega_{\rm e}}\right)^2[1+\alpha\Upsilon(p\epsilon_{\theta})]^2 \end{array} \label{lim2} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq392.png) (B.6)which for ϵθ → 0 reduces to
(B.6)which for ϵθ → 0 reduces to ![\appendix \setcounter{section}{2} \begin{eqnarray} \begin{array}{rcl} \displaystyle \frac{1}{3}\left(1-\frac{\epsilon^3_{\vartheta}}{\epsilon^3_{\theta}}\right) & = & \displaystyle \frac{1}{3}\eta\left(\frac{\Omega_{\rm o}}{\Omega_{\rm e}}\right)^2[1+\alpha \lim_{\epsilon_{\theta}\to0}\Upsilon(p\epsilon_{\theta})]^2 \end{array} \label{lim3} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq393.png) (B.7)where
(B.7)where 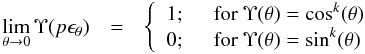 (B.8)and Ωo/ Ωe = 1 when Υ(θ) = cosk(θ), or Ωo/ Ωe = 1 / (1 + α) if Υ(θ) = sink(θ).
(B.8)and Ωo/ Ωe = 1 when Υ(θ) = cosk(θ), or Ωo/ Ωe = 1 / (1 + α) if Υ(θ) = sink(θ).
Finally, with Eqs. (B.7) and (31) we obtain 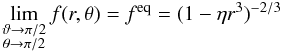 (B.9)which is independent of α and k, and where for the stellar surface it is limθ → π/ 2r = 1.
(B.9)which is independent of α and k, and where for the stellar surface it is limθ → π/ 2r = 1.
The forms Eqs. (B.4) and (B.9) can also be derived using the analytical expressions from Eqs. (A.1) to (A.6) by using series expansions for lntanx, arctanx and ln(1 ± x) valid for x< 1 and relations in Eq. (B.5).
All Tables
Equatorial to polar radii ratio Re/Rp as a function of η, k and α, for Υ = coskθ and Υ = sinkθ.
All Figures
 |
Fig. 1 Surface angular velocity Ω as a function of colatitude θ as given by Eqs. (4) and (5). Panel a: Υ(θ) = coskθ for α = + 0.5 and − 0.5, and several values of k from 0.5 to 10. Panel b: Υ(θ) = sinkθ for α′ = − 1 / 3 and α′ = + 1.0[ α′ = − α/ (1 + α ], and the same values of k as in (a). Colours identify the values of k. |
| In the text | |
 |
Fig. 2 Geometrical deformation of stellar surfaces produced by differential rotation laws given by Eqs. (4) and (5). Panel a: Stellar geometries calculated using Υ(θ) = coskθ, rotational ratio η = 0.8, differential rotation parameters α = − 0.5, 0.0 (solid body rotation) and 0.5, and powers k = 0.5, 2.0 and 6.0. Panel b: Calculations done with Υ(θ) = sinkθ and the same values of η and powers k, but for α′ = − α/ (1 + α). In all cases the colours identify the values of the power k, while the line-styles characterize the values of the differential-rotation parameter α, and the corresponding α′. |
| In the text | |
 |
Fig. 3 Function lnf(θ) given by Eq. (11) against the colatitude θ, calculated for η = 0.2 and 0.8, with both functions Υ(θ) given in Eq. (5), differential-rotation parameters α = − 0.5, 0.0, and 0.5, and for powers k = 0.5, 2.0 and 6.0. Blocks (a) and (b) are for Υ(θ) = coskθ. Blocks (c) and (d) are for Υ(θ) = sinkθ. Colours indicate the power k and they are the same for all blocks. The line-styles identify the values of α and they are the same for α′ = − α/ (1 + α) where α are the same as in (a) and (b). |
| In the text | |
 |
Fig. 4 Panels a–c: Effective temperature Teff(θ,η,α) / ⟨ T ⟩ given by Eq. (34) as a function of the co-latitude θ when Υ(θ) = coskθ, for η = 0.8, k = 0.5, 2.0 and 6.0, and α = − 0.5, 0.0 and +0.5. Panels d–f: Same for Υ(θ) = sinkθ and the same values of k as before, but for α′ = − α/ (1 + α) where α is the same as in (a) to (c). The black-dashed lines correspond to the classic von Zeipel approximation normalized in θ = 0 at the curve corresponding to α = 0.0. |
| In the text | |
 |
Fig. 5 Panels a–c: Effective temperature ratios |
| In the text | |
 |
Fig. 6 Panels a–c: Parameters Vsini determined with the FT method using the He i 4471 line produced in atmospheres having a rotation law given by Eq. (4)with Υ = coskθ and characterized by different values of k and α, against the actual Veqsini in stars having M = 9 M⊙ and t/tMS = 0.6, and rotating with several equatorial ratios η. Panels d–f: Same for the Mg ii 4481 line. |
| In the text | |
 |
Fig. 7 Similar as Fig. 6 but for Υ = sinkθ. The cases with k = 2 are omitted as they are identical to those in Fig. 6. |
| In the text | |
 |
Fig. 8 Effective temperature given as ln [ Teff(θ) / ⟨ T ⟩ ] 4 against ln [ geff(θ) / ⟨ g ⟩ ] for η = 0.8. Panels a–c: are for Υ(θ) = coskθ with k = 0.5, 2.0 and 6.0, respectively and α ranging from − 0.5 to + 0.5. Panels d–f: are for Υ(θ) = sinkθ with k = 0.5, 2.0 and 6.0, respectively and α′(α) ranging from − 1.0 to + 1.0. In all cases the left-bottom corner corresponds to the equator and the right-upper corner to the pole. |
| In the text | |
 |
Fig. 9 Panels a–c: Gravity-darkening slope |
| In the text | |
 |
Fig. 10 Average gravitational-darkening slope ⟨ B1 ⟩ given by Eq. (40) as function of η, calculated respectively for: a) Υ(θ) = coskθ; b) sinkθ. The colours identify the differential rotation parameter α, while k is identified using different line-styles. |
| In the text | |
 |
Fig. 11 Relation between the apparent 4ln [ Teff(i) / ⟨ T ⟩ ] and ln [ geff(i) / ⟩ ⟨ g ⟩ ]; a)–c) for Υ(θ) = coskθ with α from − 0.5 to +0.5; d)–f) for sinkθ and α′ =− α/ (1 = α). All curves are for η = 0.8, with k = 0.5, 2.0, 6.0. The colour-codes according to α and α′ indicated in the respective blocks for k = 2 hold for all curves having the same Υ(θ). The equator-on seeing directions (i → π/ 2) are in the lower left corner of each block, while the polar-on directions (i → 0) are in the upper right corner. |
| In the text | |
 |
Fig. 12 Gravitational-darkening slope ♭1(i) against the rotational ratio η. The colours identify the values of the differential parameter α, and the line-styles are for the inclination angles. In a) to c) the slope ♭1(i) was calculated with Υ(θ) = coskθ and from d) to f) b1(i) was obtained with Υ(θ) = sinkθ. As throughout in this work, rigid rotation (α = 0) is identified with green lines. |
| In the text | |
 |
Fig. 13 Comparison of the empirical gravitational-darkening slope |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



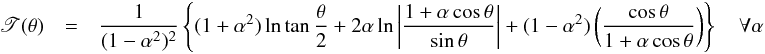
![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{array}{rcl} \displaystyle \mathscr{T}(\theta) & = & \left\{ \begin{array}{ll} \displaystyle\frac{1}{(1+\alpha)^2}\left[\ln\tan\frac{\theta}{2}+(1-\alpha)\frac{\arctan(\sqrt{\alpha}\cos\theta)}{2\sqrt{\alpha}} \right. + \left.\frac{(1+\alpha)}{2}\left(\frac{\cos\theta}{1+\alpha\cos^2\theta}\right)\right] & {\rm for}\ \alpha \geq 0 \\ \\ \displaystyle \frac{1}{(1-|\alpha|)^2}\left[\ln\tan\frac{\theta}{2}+ \left(\frac{1+|\alpha|}{4\sqrt{|\alpha|}}\right)\ln\left(\frac{1+\sqrt{|\alpha|}\cos\theta}{1-\sqrt{|\alpha|}\cos\theta}\right)\right. + \left.\left(\frac{1-|\alpha|}{2}\right)\left(\frac{\cos\theta}{1-|\alpha|\cos^2\theta} \right)\right] & {\rm for}\ \alpha<0 \end{array} \right. \end{array} \label{tau_k2} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq362.png)
![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{array}{rcl} \displaystyle \mathscr{T}(\theta) & = & \left\{ \begin{array}{ll} \displaystyle \frac{1}{(1-\alpha^2)^2}\left\{(1+\alpha^2)\ln\tan\frac{\theta}{2}-2\alpha\ln\sin\theta+\frac{2}{3}\alpha\ln(1\pm u^3)+ \frac{2}{3}[1+2\alpha^2+|\alpha|^{2/3}(2+\alpha^2)]\left(\frac{A}{|\alpha|^{1/3}}\right)\right. & \\ \displaystyle +\left.\frac{2}{3}[1+2\alpha^2-|\alpha|^{2/3}(2+\alpha^2)]\left(\frac{B}{|\alpha|^{1/3}}\right)+\frac{1}{3}\frac{\cos\theta}{(1\pm u^3)}[1-\alpha\cos\theta(1-\alpha\cos\theta)]\right\} & \\ \displaystyle u = |\alpha|^{1/3}\cos\theta; \ \ \ A = \frac{1}{6}\ln\left[\frac{(1\pm u)^2}{1-(\pm)u+u^2}\right]; \ \ \ B = \frac{1}{\sqrt{3}}\left[\arctan\left(\frac{2u-(\pm)1}{\sqrt{3}}\right)\pm\frac{\pi}{6}\right]; & \\ ``+"\ \ {\rm for}\ \alpha \geq 0 \ \ \ {\rm and} \ \ \ ``-" \ \ {\rm for}\ \alpha < 0 \\ \end{array} \right. \end{array} \label{tau_k3} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq364.png)
![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{array}{rcl} \displaystyle \mathscr{T}(\theta) & = & \displaystyle \ln\tan\frac{\theta}{2}+ \frac{\cos\theta}{1+\alpha\sin\theta}-\frac{2\alpha}{(1-\alpha^2)^{1/2}}\left\{\arctan\left[\frac{\tan\frac{\theta}{2}+\alpha}{1-\alpha^2)^{1/2}}\right]-\arctan\left(\frac{1+\alpha}{1-\alpha}\right)^{1/2}\right\}; \ \ \ {\rm for} \ \ \alpha^2<1 \end{array} \label{tau_ks1} \end{eqnarray}](/articles/aa/full_html/2017/10/aa30818-17/aa30818-17-eq368.png)