| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201730646 | |
| Published online | 05 September 2017 | |
Regular and transitory showers of comet C/1979 Y1 (Bradfield)
1 Astronomical Institute, Slovak Academy of Science, Dúbravská cesta 9, 84504 Bratislava, Slovakia
e-mail: astromia@savba.sk
2 Astronomical Institute, Slovak Academy of Science, 05960 Tatranská Lomnica, Slovakia
e-mail: ne@ta3.sk
Received: 17 February 2017
Accepted: 17 May 2017
Aims. We intend to map the whole meteor complex of the long-period comet C/1979 Y1 (Bradfield), which is a proposed parent body of the July Pegasids, No. 175 in the list of meteor showers established by the Meteor Data Center (MDC) of the International Astronomical Union (IAU).
Methods. For five perihelion passages of the parent comet in the past, we model associated theoretical stream, its parts, each consisting of 10 000 test particles, and follow the dynamical evolution of these parts up to the present. Subsequently, we analyze the mean orbital characteristics of those particles of the parts that approach the Earth’s orbit and, thus, create a shower or showers. The showers are compared with their observed counterparts separated from photographic, radio, and several video databases.
Results. The modeled stream of C/1979 Y1 approaches the Earth’s orbit in two filaments that correspond to two regular (annual) showers. We confirm the generic relationship between the studied parent comet and 175 July Pegasids. The other predicted shower is a daytime shower with the mean radiant situated symmetrically to the July Pegasids with respect to the apex of the Earth’s motion. This shower is not in the IAU MDC list, but we separated it from the Cameras-for-Allsky-Meteor-Surveillance (CAMS) and SonotaCo video data as a new shower. We suggest naming it α-Microscopiids. The stronger influence of the Poynting-Robertson drag deflects the stream away from the Earth’s orbit in those sections that correspond to the July Pegasids and the predicted daytime shower, but it makes the stream cross the Earth’s orbit in other sections. Corresponding showers are, however, only expected to survive during a limited period and to consist of particles of sizes in a narrow interval. We identified one of these “transitory” filaments to the 104 γ-Bootids in the IAU MDC list of meteor showers.
Key words: comets: individual: C/1979 Y1 (Bradfield) / meteorites, meteors, meteoroids
© ESO, 2017
1. Introduction
The orbit of the parent body of the meteoroid stream is commonly situated within the orbital corridor of the respective stream. However, the perturbations of major planets can change the initial orbits of a part of the stream and alternative corridors of orbits can be formed. If more than a single corridor of a given stream passes through the Earth’s orbit, we observe several meteor showers associated with the same parent body.
The alteration of the initial orbital corridor can be revealed by modeling the stream and studying its dynamical evolution for a suitably long period. Meteoroid streams of several parent bodies were studied with the help of various stream models (e.g., Asher & Emel’yanenko 2002; Lyytinen & Jenniskens 2003; Wiegert et al. 2005; Vaubaillon et al. 2005a,b; Vaubaillon & Jenniskens 2007; Kaňuchová & Neslušan 2007, Asher 2008, Jenniskens & Vaubaillon (2010); Vereš et al. 2011; Jopek & Williams 2013; Sekhar & Asher 2013; 2014a,b; Neslušan et al. 2013a,b; Neslušan & Hajduková 2014; Babadzhanov et al. 2008, 2013, 2015a,b; Jakubík & Neslušan 2015; Kasuga & Jewitt 2015; Kokhirova & Babadzhanov 2015; Kornoš et al. 2015; Rudawska & Vaubaillon 2015; Ryabova 2007, 2016; Tomko & Neslušan 2012, 2016; Micheli et al. 2016; Abedin et al. 2015, 2017).
In our work modeling streams, we attempt not only to find new parent bodies of known meteor showers, but also to predict new meteor showers associated with as many as possible known periodic comets. Most of our previous studies deal with parent bodies on short-period orbits. In this contribution, we focus our attention on the long-period comet C/1979 Y1 (Bradfield). We model and study the dynamical evolution of the stream related to this comet, which allows us to map its whole meteor shower complex.
The association of comet C/1979 Y1 to the July Pegasids has been suggested by several authors (e.g., Rendtel et al. 1995; Jenniskens 2006, Table 7, #175 on page 715). The July Pegasid shower (No. 175 in the IAU MDC list of established showers) is a weak meteor shower with a short activity period. The shower was observed by the IMO Video Meteor Network (Rendtel et al. 1995; Molau & Rendtel 2009), the SonotaCo Network (Ueda 2012), the Croatian Meteor Network (Andreić et al. 2013), and by the Cameras for Allsky Meteor Surveillance (Gural 2011; Jenniskens et al. 2011; Holman & Jenniskens 2012). The latter authors also proposed the C/1771 A1 as a possible parent comet, suggesting that both C/1979 Y1 and C/1771 A1 may be the same comet or they may have originated from a common progenitor at the time of the formation of the July Pegasid shower.
As in several previous papers (e.g., Neslušan et al. 2013b), we use the words “complex” and “stream” as synonyms referring to the whole structure of meteoroids released from the parent body. The complex consists of several “filaments”. If the particles of a filament hit the Earth, they can cause the meteor “shower” corresponding to the filament.
2. The orbit of the parent comet
In our study, we consider the orbit of comet C/1979 Y1 with the orbital elements published in the JPL small-body browser (Giorgini et al. (1996)1. Specifically, the orbit referred to epoch 1980 January 25.0 (JDT = 2 444 263.5) has elements: q = 0.5452748296 ± 0.000030079 au, e = 0.987952184 ± 0.000098692, a = 45.25923 ± 0.37324 au ω = 257.60493676° ± 0.0054013°, Ω=103.21615886° ± 0.00092632°, i=148.60242336° ± 0.00030014°, and = 2 444 229.10764317 (1979 December 21.60764317). Hereinafter, this orbit is referred to as the nominal orbit. The orbital period of the comet in the nominal orbit is 304.5 yrs.
To follow the past evolution of this orbit, including the uncertainty of its determination, we create 100 clones, using the method by Chernitsov et al. (1998). If the orbital elements of the nominal orbit are written in the form of covariant 6 × 1 matrix yo, the corresponding covariant matrix with the elements of the orbit of the jth clone, yj, can be calculated as 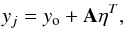 (1)where A is such a triangle matrix that the product AAT equals the covariance matrix related to the process of nominal-orbit determination (the covariance matrix can again be found on the website of the JPL browser). Since we have six elements, A is a 6 × 6 matrix. η is a 1 × 6 matrix with each element; ηi being a random number from the interval (0, 1), that is 0 ≤ ηi ≤ 1. ηT is its covariant form.
(1)where A is such a triangle matrix that the product AAT equals the covariance matrix related to the process of nominal-orbit determination (the covariance matrix can again be found on the website of the JPL browser). Since we have six elements, A is a 6 × 6 matrix. η is a 1 × 6 matrix with each element; ηi being a random number from the interval (0, 1), that is 0 ≤ ηi ≤ 1. ηT is its covariant form.
We integrated the nominal orbit and all the orbits of the clones backward in time, down to 80 000 yr. The past evolution of the orbits of the clones and the nominal orbit is shown in Fig. 1.
The minimum distance of both pre-perihelion and post-perihelion arcs of C/1979 Y1’s orbit from the Earth’s orbit is shown in Fig. 2. Both orbital arcs approach the orbit of our planet at present relatively closely, within 0.15 au, and, thus, both could induce a meteor shower. The positions of the nodes of the nominal orbit during the last 40 millennia can be seen in Fig. 3.
3. Modeling the stream
To study the theoretical stream of comet C/1979 Y1, we use the procedure suggested by Neslušan (1999), which was slightly modified and described in more detail by Tomko & Neslušan (2012). The orbit of the parent body is integrated backward in time, to the moment of the body’s perihelion passage, which happened closest to an arbitrarily chosen time tev. In the perihelion, a cloud of 10 000 test particles around the parent body is modeled and all this assembly is integrated forward in time, up to the present. At the end of the integration, the particles moving in the orbits that approach the Earth’s orbit within 0.05 au are selected and used to predict the mean characteristics of the expected shower. A search for a corresponding shower is then made in the meteor database(s) available. A brief summary of the method can also be found in papers by Neslušan et al. (2013b), Jakubík & Neslušan (2015), and others. Since the method has been described several times, we do not repeat its more detailed description in the present paper.
 |
Fig. 1 Behavior of perihelion distance (plot a), semi-major axis (b), eccentricity (c), argument of perihelion (d), longitude of ascending node (e), and inclination to the ecliptic (f) of the nominal orbit of comet C/1979 Y1 (red curve) and the orbits of its clones (green curves) mapping the uncertainty of the determination of nominal orbit. The evolution is reconstructed backward for 80 000 yr. |
To integrate the orbits, we use integrator RA15 (Everhart 1985) within the software package MERCURY (Chambers 1999). The gravitational perturbations of eight planets, Mercury to Neptune, are taken into account.
In the simulations performed, the acceleration due to the Poynting-Robertson (P-R) effect is considered. When speaking about the P-R effect acting on meteoroid particles, we mean an action of radial electromagnetic radiation pressure as well as the velocity-dependent effects. In contrast to all the papers we have co-authored in the past, in this work we include the effects of solar wind (in addition to radiation) in our calculation of the acceleration. Specifically, here we use the improved formulas derived by Klačka (2014). Assuming constant solar wind, the radial and transversal components of the acceleration due to these effects are ![\begin{eqnarray} && a_{r} = \beta \frac{GM_{\odot}}{r^{2}}\left[ 1 - \left( 2 + \frac{\eta_{1} + \eta_{2}}{Q_{\rm pr}'}\right) \frac{v_{r}}{c}\right], \label{arPR} \\ && a_{t} = -\beta \frac{GM_{\odot}}{r^{2}}\left( 1 + \frac{\eta_{2}} {Q_{\rm pr}'}\right) \frac{v_{t}}{c}, \label{atPR} \end{eqnarray}](/articles/aa/full_html/2017/09/aa30646-17/aa30646-17-eq29.png) and the perpendicular component is zero. In Eqs. (2) and (3), β is the ratio of the acceleration due to both effects to gravitational acceleration by the Sun, G is the gravitational constant, M⊙ is the mass of the Sun, r is the heliocentric distance of the meteoroid particle, vr and vt are the radial and transversal components of its heliocentric velocity, and c is the speed of light in a vacuum. Component vt is assumed to lay in the particle’s orbital plane (therefore, the perpendicular component of the velocity vector must be zero). Further,
and the perpendicular component is zero. In Eqs. (2) and (3), β is the ratio of the acceleration due to both effects to gravitational acceleration by the Sun, G is the gravitational constant, M⊙ is the mass of the Sun, r is the heliocentric distance of the meteoroid particle, vr and vt are the radial and transversal components of its heliocentric velocity, and c is the speed of light in a vacuum. Component vt is assumed to lay in the particle’s orbital plane (therefore, the perpendicular component of the velocity vector must be zero). Further, 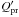 is the dimensionless efficiency factor of the radiation pressure averaged over the solar spectrum, and η1 and η2 are the parameters characterizing the solar wind.
is the dimensionless efficiency factor of the radiation pressure averaged over the solar spectrum, and η1 and η2 are the parameters characterizing the solar wind.
In the solar system, the recommended values for η1 and η2 are η1 = 1.1 and η2 = 1.4. We assume the efficiency factor 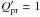 . The relation between the parameter β and the efficiency factor
. The relation between the parameter β and the efficiency factor 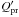 is
is 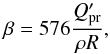 (4)where ρ is the mean mass density of a meteoroid particle in kilograms per cubic meter and R is its average radius in microns.
(4)where ρ is the mean mass density of a meteoroid particle in kilograms per cubic meter and R is its average radius in microns.
 |
Fig. 2 Evolution of the minimum distance between the orbital arcs of comet C/1979 Y1 and Earth from a time 40 000 yr before the present to the present. The minimum distance of post-perihelion (pre-perihelion) arc is shown by the red solid (blue dashed) curve. |
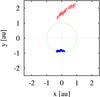 |
Fig. 3 Positions of the orbital nodes of comet C/1979 Y1 during the last 40 000 yr. The green circle indicates the orbit of the Earth. The red dots outside the Earth’s orbit (blue dots inside the Earth’s orbit) show the positions of ascending (descending) node. |
In the formula for the calculation of β, its dependence on the size (geometrical cross-section), density, light-scattering effectivity (then on albedo and light-absorption ability), and mass of the particles is seen. In our case, these properties are rather uncertain, therefore we could calculate the value of β with a large uncertainty. Instead of such a calculation, we regard β as a free parameter and search, as far as possible, for its value to achieve the best agreement between the predicted and observed characteristics of found filaments of C/1979 Y1’s complex.
Mean geophysical characteristics of the predicted annual meteor showers.
Mean orbital characteristics with the dispersion (characterized by standard deviation) of the predicted annual meteor showers associated with the parent body considered.
We create a series of models for various combinations of specific values of evolutionary time tev and parameter β. Hence, a given model does not represent a whole stream, since the real stream consists of the particles of various sizes and densities and, therefore, parameter β ranges in a wider interval of values. Also, the particles are released at various times in reality, therefore their evolutionary time is different and can acquire a value from a wider interval. The sufficient combinations of tev and β are found by comparing predicted and observed showers. The agreement implies that the particles with the properties in the given model, with the given tev and β, are likely also present in the real stream. A more complex description of the latter is achieved as a composition of successful models.
We compare our theoretical results for the predicted showers with the corresponding observed showers selected from two International Astronomical Union (IAU) Meteor Data Center (MDC) databases: photographic, version-2013 (Porubčan et al. 2011; Neslušan et al. 2014) and Cameras for Allsky Meteor Surveillance (CAMS) video (Gural 2011; Jenniskens et al. 2011, 2016a–c; Jenniskens & Nénon 2016). In addition, we use the 2007−2015 SonotaCo video (SonotaCo 2009, 2016), EDMOND video (Kornoš et al. 2014a,b), and radio-meteor (Hawkins 1963; Sekanina & Southworth 1975; Lindblad, priv. comm.) databases. These databases contain 4873, 110 521, 208 826, 145 830, and 62 907 records on meteor orbits and geophysical data, respectively.
To identify a predicted shower and match it to its potential counterpart in a given database, we use the “break-point method” (Neslušan et al. 1995, 2013c). The method is based on an analysis of the dependence of the number of the selected meteors of a shower on the limiting value of the SH D discriminant, Dlim, used for the selection. If a shower is present in a database, then the dependence N = N(Dlim) has a convex behavior with a constant or almost constant part – a plateau. The break-point is a critical point in the dependence, giving the most suitable limiting value for the D discriminant for the selection of the densest part of a particular shower from the near orbital phase space. Recently, Moorhead (2016) suggested a similar method for isolating meteor showers from the sporadic background, emphasizing that a cut-off value chosen has to reflect the strength of the shower compared to the local sporadic background. This demand is satisfied by the break-point method.
Within the break-point method, one considers all meteors from an used database and calculates their D discriminant with respect to assumed mean orbit. All meteors with D ≤ Dlim are selected and a new mean orbit is determined. This is done as an iteration process, which is finished when the given mean orbit negligibly differs from the previous mean orbit. In the beginning, one needs an initial mean orbit. In our approach, we consider all predicted mean orbits of all filaments as the initial orbits entering the iteration.
4. The predicted showers
In the first stage, we model a theoretical stream of C/1979 Y1 for all combinations of time tev equal to 5, 10, 20, 40, and 80 kyr and P-R-effect parameter β = 0.00001, 0.0001, and 0.001. It appears that the modeled stream crosses the Earth’s orbit in two filaments, labeled as F1 and F2, which correspond to two potential showers of the comet, one before (F1) and one after (F2) perihelion (see Sect. 4.2 later). In a further process, we model the streams also for various higher values of parameter β. The mean geophysical parameters of all the filaments in the models with low β-values are given in Table 1 and their mean orbital elements can be seen in Table 2.
 |
Fig. 4 Positions of radiants of theoretical particles in filaments F1, F2 (red full squares), and transitory filaments crossing the Earth’s orbit. For a better transparency, the radiants of filaments F1 and F2 are shown only in the model for tev = 10 kyr and β = 0.00001, and radiants of transitory filaments for all considered tev, but only for β = 0.0045 (crosses) and 0.006 (empty triangles; the symbols can be distinguished when the image is magnified on a computer screen). In the case of transitory filaments, the individual colors – blue, violet, cyan, black, and gray – distinguish between the radiants in the models for tev = 80, 40, 20, 10, and 5 kyr, respectively. The mean radiants of filaments F1 and F2 are shown by the green empty squares and are connected with the green dashed abscissa passing through the coordinate origin. The radiants are shown in the modified ecliptical coordinate frame with the center in the apex of the Earth’s motion. |
 |
Fig. 5 Positions of radiants of theoretical particles representing the quasi-stable part (filaments F1 and F2) of the modeled stream of comet C/1979 Y1, which currently move in orbits, along which they can approach the Earth’s orbit within 0.05 au (plot a). The radiant positions of the meteors of corresponding showers separated from the CAMS (red crosses for F1 and Dlim = 0.07 and blue asterisks for larger Dlim and both F1 and F2) and SonotaCo (green empty squares) video databases are shown in plot b. The shown theoretical radiants of filaments F1 and F2 were obtained in the models for tev = 20 kyr and β = 0.00001. The positions are shown in the equatorial coordinate frame. The sinusoid-like curve illustrates the ecliptic. |
After selecting the particles approaching the Earth’s orbit within the chosen limit, 0.05 au, we get a set of particles that are mixed from all the filaments. The separation of particles from the individual filaments is done on the basis of the different positions of their radiant areas. The areas of filaments F1 and F2 are defined to lay in the part of the sky delimited by 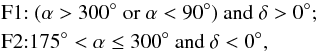 where α and δ are equatorial coordinates of the geocentric radiant. F1 (F2) is situated northward (southward) from the ecliptic. The areas are in the vicinity of the ecliptic; therefore, the corresponding showers can be classified as ecliptical.
where α and δ are equatorial coordinates of the geocentric radiant. F1 (F2) is situated northward (southward) from the ecliptic. The areas are in the vicinity of the ecliptic; therefore, the corresponding showers can be classified as ecliptical.
The areas of the filaments F1 and F2, which consist of particles that were not significantly influenced by the non-gravitational P-R effect, are symmetric in respect to the apex of the Earth’s motion around the Sun. This fact can be seen in Fig. 4, where the radiants of the theoretical particles of these two filaments, as well as other filaments discussed below, are plotted in the Hammer projection of the celestial sphere. In the figure, the modified ecliptical coordinate system is used. In contrast to the common ecliptical coordinates, the ecliptical longitude, λ, is replaced with the coordinate λ2 related to the latter and the solar longitude λ⊙ as 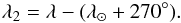 (5)Concerning the radiant areas of so-called transitory filaments (Sect. 4.3), it appears that, in a specific model, only a single filament occurs in the first and/or second parts of the sky delimited by
(5)Concerning the radiant areas of so-called transitory filaments (Sect. 4.3), it appears that, in a specific model, only a single filament occurs in the first and/or second parts of the sky delimited by 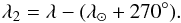 A more detailed description of the individual filaments is given in the following subsections.
A more detailed description of the individual filaments is given in the following subsections.
 |
Fig. 6 Dependence of the number of selected meteors on the threshold Southworth-Hawkins (1963) D-discriminant, Dlim, for the shower corresponding to filament F1 separated from the F – IAU MDC photographic (plot a), C – IAU MDC CAMS video (b), S – SonotaCo video (c), E – EDMOND video (d), and R – radio-meteor (e) database. The “break point” in plot b) is indicated with an arrow. The arrow with the question mark in this plot indicates an alternative break point. |
4.1. Filament F1 – 175 July Pegasids
Meteors in filament F1 are predicted to be relatively numerous (see the penultimate column in Table 1) and the filament has a prolonged radiant area, which can be seen in Fig. 5a. It is in the vicinity of the ecliptic. The angular distance of its mean radiant from the Sun is significantly larger than 90° (see values of γ in Table 1). Therefore, the meteors of the corresponding shower are detectable on the night sky.
In more detail, the larger particles, which are not significantly influenced by the P-R effect, tend to be in the orbits on a collisional course with the Earth. These particles are characterized by 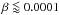 . In the models for β = 0.00001 and β = 0.0001, there are only minute differences in the predicted mean characteristics. The P-R effect starts to be significant for
. In the models for β = 0.00001 and β = 0.0001, there are only minute differences in the predicted mean characteristics. The P-R effect starts to be significant for 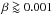 .
.
Using the break-point method (Neslušan et al. 1995, 2013c), we attempted to separate the shower corresponding to filament F1 from all the databases considered. Unfortunately, the dependence of the number of selected meteors, N, on the threshold Southworth-Hawkins (1963) D-discriminant, Dlim, does not exhibit a clear break point. For all five databases, the dependence N = N(Dlim) is shown in Fig. 6 for F1. In the photographic data (Fig. 6a), the first meteor with an orbit similar to the mean orbit of filament F1 is separated no earlier than for Dlim = 0.19. Then the number increases up to 7 for Dlim = 0.27, but this increase is steep, without any plateau. The subsequent decrease means a departure to a different phase space. Therefore, there is no pattern of a shower corresponding to F1 in these data. Such a shower is also absent in the radio data (Fig. 6e) where no meteor is separated up to the relatively high value of Dlim = 0.25, eight meteors are separated for Dlim = 0.26, but only six meteors for the subsequent value Dlim = 0.27. The decrease again means a loss of the relationship of the separated group of meteors with F1.
In the SonotaCo (Fig. 6c) and EDMOND (Fig. 6d) video data, the N = N(Dlim) curve does not have a parabola-like shape, which is typical for a sporadic background. Therefore, there are probably some meteors in orbits similar to the mean orbit of F1. However, there is no apparent plateau and so it is difficult to determine the appropriate Dlim to separate the shower. In addition, the absence of a plateau implies a strong contamination of the phase space of the showers examined with meteors that are not its members. We would rather not separate any showers from these databases.
A certain plateau seems to only be in the N = N(Dlim) dependence in the CAMS video data (Fig. 6b). It is situated beyond the value Dlim = 0.17, which is regarded as the value corresponding to the break point and used to separate the shower. In Fig. 6b, the point concerned is indicated with an arrow. The shower consists of 81 meteors. Nonetheless, we cannot regard this separation as reliable. To check if the separation procedure provides the meteors in the same phase space for Dlim ranging from 0.04 (no meteors are separated for a lower Dlim) to 0.17, we also consider the sub-group of 21 meteors separated for Dlim = 0.07. In Fig. 6b, the corresponding point is indicated with an arrow beside the question mark. The point is at the beginning of a short, alternative plateau.
The mean characteristics of the separated shower are very similar to the July Pegasids, No. 175 in the IAU MDC list of established showers (Jopek & Kaňuchová 2014)2. Therefore, we identify filament F1 to the July Pegasids. The level of the agreement between the mean parameters predicted in this work and determined by several independent authors can be seen in Tables 1–3.
In the phase space of orbital elements, the shower occurs in the close vicinity of another established shower, 522 Southern α-Pegasids. Andreić et al. (2013) deemed it identical to 175 July Pegasids and recommended that it be removed from the list. Similarly, shower No. 462 July γ-Pegasids was identified as part of the 175 July Pegasids (Rudawska & Jenniskens 2014; Kornoš et al. 2014b) and was subsequently removed from the IAU MDC list. This might be an example of a meteor shower being alternatively named multiple times.
The radiants of the particles approaching the Earth’s orbit within 0.05 au in the models for β = 0.00001 and all considered evolutionary times tev are shown in Fig. 7a. The size of radiant area increases with increasing evolutionary time. This fact is evidence that the spatial corridor of the July Pegasids is not delimited by the resonance action of a planet. The dispersion of the shower members increases with time. Here, we observe a normal aging of the shower. Comparing the theoretical radiant areas in Fig. 7a to their real counterparts in Fig. 7b, we can state that the separated July Pegasids are likely younger than 10 kyr.
4.2. Shower corresponding to filament F2
The mean orbit of filament F2 is almost identical to the mean orbit of filament F1 (see Table 2), suggesting that there is only a single filament, in fact. Two potential showers are predicted because the filament of large meteoroids, not significantly influenced by the P-R effect, crosses the orbit of our planet in two positions. In this case, the denotation F1 and F2 refers to two crossing positions of one filament with the Earth’s orbit rather than to two individual filaments. This is analogous to the stream of comet 1P/Halley, which also crosses the Earth’s orbit twice, as η-Aquariids and Orionids. In contrast to the night showers of the 1P stream, the shower corresponding to F2 is predicted to be a daytime shower since the angular distance of its radiant from the Sun is only γ ~ 63° (see Table 1). It should be active in the middle of January.
We also attempted to separate a shower corresponding to filament F2 from all of the data sets considered. Because there are still some minute differences between the mean orbits of both F1 and F2 filaments, we did the separation for F2 again, with the initial orbits of F2 entering the iteration procedure. The behaviors of the N = N(Dlim) dependence are shown in Fig. 8 in this case. No corresponding shower can be found in the photographic database (Fig. 8a). For values Dlim< 0.27, there is no apparent plateau and a decrease occurs beyond this value. The curve in Fig. 8a can be seen to be very similar to that in Fig. 6a. This is a consequence of the fact that the mean orbit of both filaments is almost the same and the orbital phase space in the vicinity of F2 orbit is poorly filled with meteors. Therefore, the separation procedure proceeds in the same way, starting with almost the same initial orbit.
In the EDMOND video (Fig. 8d) and radio data (Fig. 8e), a plateau starts at Dlim = 0.14 and 0.20, respectively. However, only three meteors would be separated for these values of Dlim. Another one or two meteors would be added for some larger values, corresponding to the middle of the plateau. Nevertheless, it would still be a relatively low number in the case of the relatively abundant EDMOND and radio data. We do not consider these sparse showers in our discussion.
A break point can be found in the N = N(Dlim) dependence for IAU MDC CAMS (Fig. 8b) and SonotaCo (Fig. 8c) video databases. In the plots, the break points are shown with arrows. The critical value of Dlim to separate the shower corresponding to F2 from CAMS (SonotaCo) data is 0.19 (0.15) and the separated shower consists of ten (five) meteors. (Whether or not we should consider the sparse (five-member) shower from the large SonotaCo database was debatable. We decided to consider it because the break point is well-defined and the shower is consistent with that obtained from the CAMS data.)
 |
Fig. 7 Positions of radiants of theoretical particles (plot a)) of filament F1 and those of real meteors of the corresponding shower b). The meteors were separated from the CAMS (blue asterisks for Dlim = 0.17 and red crosses for Dlim = 0.07) video database. The shown theoretical radiants were obtained in the models for β = 0.00001 and tev = 5, 10, 20, 40, and 80 kyr. The positions for the different tev are distinguished using the different marks and colors. The coordinate frame is equatorial. |
Mean radiants and the numbers of particles in the individual filaments when the P-R effect is calculated according to two different formulas.
 |
Fig. 8 Dependence of the number of selected meteors on the threshold Southworth-Hawkins (1963) D-discriminant, Dlim, for the shower corresponding to filament F2 separated from the F – IAU MDC photographic (plot a), C – IAU MDC CAMS video (b), S – SonotaCo video (c), E – EDMOND video (d), and R – radio-meteor (e) database. The points on the curves in plots b and c regarded as the “break points” are indicated by arrows. |
One could, perhaps, regard the points corresponding to Dlim = 0.31 for CAMS and Dlim = 0.20 for SonotaCo data as the alternative break points. We also separated the showers for these values of Dlim. Their mean characteristics were, however, significantly different from those for the values of Dlim = 0.19 and 0.15, respectively, as well as from the predicted mean parameters. The iteration within the separation procedure obviously proceeded into other orbital phase space.
Matching a predicted shower to a shower in the IAU MDC list of all showers was unsuccessful. In addition, no success was achieved in matching the separated shower to the showers in the list; no shower with mean parameters similar to those for F2 can be found there. The average increase in the number of separated meteors in the part of the curve for Dlim lower than the threshold value is only moderate, as with the CAMS database (Fig. 8b) and also with the SonotaCo data set (Fig. 8c). This is likely the reason why the shower was not separated within our automatized separation of all showers described in our earlier paper (Neslušan & Hajduková 2017).
The mean radiant of the newly separated shower is situated near star α in constellation Microscopium. We suggest to name the shower α-Microscopiids.
The positions of the radiants of the particles that constitute filament F2 in the models for β = 0.00001 and all considered evolutionary times, tev, are shown in Fig. 9a. The dispersion again increases with increasing time due to aging of the stream. Comparison of predicted (Fig. 9a) and observed (Fig. 9b) radiant areas confirms the age of the shower, corresponding to F2 and the whole F1–F2 filament; shorter than 10 kyr.
 |
Fig. 9 Positions of radiants of theoretical particles (plot a) of filament F2 and those of real meteors in orbits resembling those of theoretical particles (b). The meteors were separated from the CAMS (blue asterisks) and SonotaCo (green empty squares) video databases. The shown theoretical radiants were obtained in the models for β = 0.00001 and tev = 5, 10, 20, 40, and 80 kyr. The positions for the different tev are distinguished using the different marks and colors. The coordinate frame is equatorial. |
4.3. The transitory filaments
Besides the models for the low-value β-parameter, we also modeled the stream considering a set of larger β values. Specifically, we mainly considered the values β = 0.0045, 0.005, 0.006, 0.007, 0.008, and 0.01. For the highest value and tev ≤ 40 kyr, no shower was predicted. As expected, a stronger P-R effect deflects the particles in both F1 and F2 filaments away from the Earth’s orbit and, thus, from a collisional course with our planet.
However, a complete deflection does not always occur. Sometimes, the stream is deflected away from the Earth’s orbit in its section corresponding to filament F1 or F2, but it starts to cross this orbit at other sections. In contrast to filaments F1 and F2, a new filament occurs only in a model, or a few models with neighboring β values, for a specific combination of tev and β. Therefore, it is expected to survive only during a limited period and, likely, to consist of particles that have a narrow interval of sizes. We refer to such a filament as a “transitory filament” in contrast to F1 and F2, which are predicted in almost all created models and which are regarded as annual showers.
We modeled the theoretical streams for all combinations of tev = 5, 10, 20, 40, and 80 kyr and β = 0.0045, 0.005, 0.006, 0.007, and 0.008 (in addition to values 0.00001, 0.0001, and 0.001). The transitory filaments occurred only for several combinations of tev and β. The mean geophysical data characterizing the occurred transitory filaments as well as filaments F1 and F2 for the large β-values are given in Table 3. The positions of the radiants of the particles in all filaments, F1 and F2 included, are shown in Fig. 10. In more detail, a given plot illustrates the radiants for a single tev and all values of β, which are distinguished by the use of different colors.
The number of particles approaching the Earth’s orbit within filament F1 decreases with increasing β-values. In the models for tev = 5, 10, 20, and 40 kyr, this filament disappears when β reaches 0.005. For the longest investigated evolutionary period of tev = 80 kyr, it persists up to β ~ 0.007.
Two largely different transitory filaments occur in the radiant area TF1 for 0.005 ≤ β ≤ 0.008 and 0.005 ≤ β ≤ 0.010, but only after a relatively long time of the dynamical evolution of the stream, tev ≥ 40 kyr. These filaments differ from each other, especially in their geocentric velocity; 50.0 versus 37.7 km s-1.
Filament F2 is also less and less populated with increasing β-values, like F1, and practically disappears at β ~ 0.003. The particles with a higher β are obviously removed from the orbits in which they cross the Earth’s orbit at its arc, which corresponds to the solar longitude λ⊙ ~ 295°. At the same time, it seems that the small particles, characterized by β ~ 0.005−0.008, are moved to orbits which closely encounter the Earth’s orbit at its arcs with different λ⊙-values (Table 3). A few transitory filaments occur in the parts of the sky defined in the beginning of Sect. 4 as TF1 and TF2. The particles characterized by 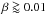 are completely moved into orbits in which they cannot collide with the Earth.
are completely moved into orbits in which they cannot collide with the Earth.
The chance of detecting and recording a significant number of meteors of a transitory filament is not very high. Nevertheless, we tried to separate the real showers that correspond to all found transitory filaments, represented by the number of selected particles Ns ≥ 5. Overall, our attempt was unsuccessful. In the case of F1, the separation resulted in the real showers already found in the separation for the theoretical orbits predicted for low β-values, which are given in Tables 1 and 2. Starting from the different initial orbits, the separation procedure resulted, sometimes, in a slightly different set of shower meteors, with slightly different mean parameters.
In the case of transitory filaments, the single success we achieved was an occurrence of similarity between the transitory filament with the radiant in radiant area TF1, models for tev = 80 kyr, and shower 104 γ-Bootids in the IAU MDC list of all showers (Table 3). In the list, this shower is not classified as an established shower, and it is currently represented by only two meteors (see Table 7, #104, page 695 in Jenniskens 2006). Moreover, its existence was not confirmed in a recent study by Jenniskens et al. (2016b). Nevertheless, the predicted parameters agree well with their observed counterparts, except for relatively large differences in the declination of radiant, solar longitude, and, hence, longitude of ascending node. The predicted longitudes are larger (about 24°) and predicted declination is about 6° lower than observed. It is possible that a better match would occur for other evolutionary times, tev.
The transitory filaments do not exhibit symmetry in respect to the apex of the Earth motion (Fig. 4), in contrast to filaments F1 and F2.
To see a difference in the dynamics of a stream that is influenced by the P-R effect calculated by the new, improved formulas by Klačka and by the old formulas (the new formulas (2) and (3) are reduced to old ones putting η1 = η2 = 0), we calculated the evolution of the modeled streams listed in Table 4 by using both sets of formulas. The result, according to the old, classical (new, Klačka’s) formulas is given in Cols. 3−6 (7−10) of the table. We observe only small differences. This is not surprising since the dominant term of the P-R effect is the first term, βGM⊙/r2, of the radial component of the acceleration due to this effect and this term is the same in both old and new formulas. Nonetheless, the result is not identical. Therefore, the use of the new formulas is advantageous.
 |
Fig. 10 Positions of theoretical radiants predicted with the models of C/1979 Y1-stream for tev = 5 (plot a), 10 (b), 20 (c), 40 (d), and 80 kyr (e). Filaments F1 and F2 corresponding to the annual showers, as well as the transitory filaments TF, are plotted. The positions are shown in the Hammer projection of celestial sphere in the equatorial coordinates. The sinusoid-like curve is the ecliptic. |
5. Conclusions
We modeled a theoretical stream of comet C/1979 Y1 (Bradfield). The models are characterized by a variety of values of free parameters, evolutionary time, and strength of the Poynting-Robertson drag β, and were used to predict a part or parts of the stream that can collide with the Earth. We aimed to predict the meteor shower(s) of the comet. Our modeling was successful, and we were therefore able, subsequently, to separate some corresponding showers from the considered databases of real meteors and compare the prediction with the observation. Also, we searched for the corresponding showers in the IAU MDC list of showers. A comparison between the predicted showers and their real existing counterparts enabled us to identify the values of the free parameters that are relevant to the real showers.
Specifically, we found, in an agreement with other researchers, that the comet is the parent body of the established shower 175 July Pegasids. Further, we found that it is the parent body of a new daytime shower, which we named α-Microscopiids. In addition, the comet is likely the parent body of 104 γ-Bootids given in the IAU MDC list of all showers. The characteristics of this shower were, however, derived from only two observed meteors (Jenniskens 2006, Table 7, #104 on page 695), therefore its existence is still questionable.
The July Pegasids are predicted by the models with the particles characterized by a wide range of values of the P-R-effect parameter β, from practically zero to about 0.007. On the contrary, the transitory γ-Bootids have to consist of particles in a narrow size interval, corresponding to the values of β ranging from ~0.006 to ~0.010. Assuming a mean density of the particles equal to 1000 kg m-3, their mean radii should span from ~60 to ~100 μm. Furthermore, the γ-Bootids had to be released from the parent body a long time ago; ~80 kyr. This is an acceptably long time, and corresponds to only about 260 orbital revolutions of the parent comet around the Sun. We remind readers that the active phase, as the parent body of a meteoroid stream, of the other long-period comet, 1P/Halley, is estimated to have already made approximately 2300 orbital revolutions (~175 kyr) (Hajduk 1987).
While the relatively large meteoroids, which are not significantly influenced by the P-R effect, collide with the Earth in filaments F1 and F2, with the radiant areas that are situated symmetrically with respect to the Earth’s apex, smaller meteoroids are predicted to collide with our planet in the filaments with radiants that do not possess any such symmetry. The filaments with asymmetric radiant areas are, obviously, those that occur exclusively due to the action of the P-R effect.
Our study of the stream of C/1979 Y1 confirms the important role of the P-R effect in the dynamical evolution of meteoroid streams. We learnt that, due to this effect, the stream can be so variable that some showers associated with a considered parent body might not be revealed in a study which included only the gravitational perturbations.
Acknowledgments
This article was supported by the realization of the Project ITMS No. 26220120029, based on the supporting operational Research and development program financed from the European Regional Development Fund. The work was also supported, in part, by the VEGA – the Slovak Grant Agency for Science, grants No. 2/0031/14 and 1/0225/14, and by the Slovak Research and Development Agency under the contract No. APVV-0517-12.
References
- Abedin, A., Spurný, P., Wiegert, P., et al. 2015, Icarus, 261, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Abedin, A., Wiegert, P., Pokorný, P., & Brown, P. 2017, Icarus, 281, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Andreić, Ž., Šegon, D., Korlević, K., et al. 2013, WGN, J. International Meteor Organization, 41, 103 [Google Scholar]
- Asher, D. J. 2008, Earth Moon and Planets, 102, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Asher, D. J., & Emel’yanenko, V. V. 2002, MNRAS, 331, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Babadzhanov, P. B., Williams, I. P., & Kokhirova, G. I. 2008, MNRAS, 386, 2271 [NASA ADS] [CrossRef] [Google Scholar]
- Babadzhanov, P. B., Williams, I. P., & Kokhirova, G. I. 2013, A&A, 556, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babadzhanov, P. B., Kokhirova, G. I., & Khamroev, U. K. 2015a, Adv. Space Res., 55, 1784 [NASA ADS] [CrossRef] [Google Scholar]
- Babadzhanov, P. B., Kokhirova, G. I., & Obrubov, Y. V. 2015b, A&A, 579, A119 [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chernitsov, A. M., Baturin, A. P., & Tamarov, V. A. 1998, Sol. Syst. Res., 32, 405 [EDP Sciences] [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proceedings of IAU Colloq., 83, held in Rome, Italy, June 11–15, 1984, eds. A. Carusi, & G. B. Valsecchi (Dordrecht: Reidel), Astrophys. Space Sci. Lib., 115, 185 [Google Scholar]
- Giorgini, J. D., Yeomans, D. K., Chamberlin, A. B., et al. 1996, in AAS/Division for Planetary Sciences Meeting Abstracts #28, BAAS, 28, 1158 [Google Scholar]
- Gural, P. S. 2011, in Proc. International Meteor Conference, 29th IMC, Armagh, Northern Ireland, 2010, 28 [Google Scholar]
- Hajduk, A. 1987, A&A, 187, 925 [Google Scholar]
- Hawkins, G. S. 1963, Smithsonian Contributions to Astrophysics, 7, 53 [Google Scholar]
- Holman, D., & Jenniskens, P. 2012, WGN, J. International Meteor Organization, 40, 166 [Google Scholar]
- Jakubík, M., & Neslušan, L. 2015, MNRAS, 453, 1186 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P. 2006, Meteor Showers and their Parent Comets (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Jenniskens, P., & Nénon, Q. 2016, Icarus, 266, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., & Vaubaillon, J. 2010, AJ, 139, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Gural, P. S., Dynneson, L., et al. 2011, Icarus, 216, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Nénon, Q., Albers, J., et al. 2016a, Icarus, 266, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Nénon, Q., Gural, P. S., et al. 2016b, Icarus, 266, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Nénon, Q., Gural, P. S., et al. 2016c, Icarus, 266, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., & Kaňuchová, Z. 2014, Meteoroids 2013, 353 [Google Scholar]
- Jopek, T. J., & Williams, I. P. 2013, MNRAS, 430, 2377 [NASA ADS] [CrossRef] [Google Scholar]
- Kasuga, T., & Jewitt, D. 2015, AJ, 150, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Kaňuchová, Z., & Neslušan, L. 2007, A&A, 470, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klačka, J. 2014, MNRAS, 443, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Kokhirova, G. I., & Babadzhanov, P. B. 2015, Meteoritics and Planetary Science, 50, 461 [CrossRef] [Google Scholar]
- Kornoš, L., Koukal, J., Piffl, R., & Tóth, J. 2014a, in Proc. International Meteor Conference, Poznan, Poland, 22–25 August 2013, eds. M. Gyssens, P. Roggemans, & P. Zoladek, 23 [Google Scholar]
- Kornoš, L., Matlovič, P., Rudawska, R., et al. 2014b, Meteoroids 2013, 225 [Google Scholar]
- Kornoš, L., Tóth, J., Porubčan, V., et al. 2015, Planet. Space Sci., 118, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Lyytinen, E., & Jenniskens, P. 2003, Icarus, 162, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Micheli, M., Tholen, D. J., & Jenniskens, P. 2016, Icarus, 267, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Molau, S., & Rendtel, J. 2009, WGN, J. International Meteor Organization, 37, 98 [Google Scholar]
- Moorhead, A. V. 2016, MNRAS, 455, 4329 [NASA ADS] [CrossRef] [Google Scholar]
- Neslušan, L. 1999, A&A, 351, 752 [Google Scholar]
- Neslušan, L., & Hajduková, M. 2014, A&A, 566, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neslušan, L., & Hajduková, M. 2017, A&A, 598, A40 [CrossRef] [EDP Sciences] [Google Scholar]
- Neslušan, L., Svoreň, J., & Porubčan, V. 1995, Earth Moon and Planets, 68, 427 [Google Scholar]
- Neslušan, L., Hajduková, M., & Jakubík, M. 2013a, A&A, 560, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neslušan, L., Kaňuchová, Z., & Tomko, D. 2013b, A&A, 551, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neslušan, L., Svoreň, J., & Porubčan, V. 2013c, Earth Moon and Planets, 110, 41 [Google Scholar]
- Neslušan, L., Porubčan, V., & Svoreň, J. 2014, Earth Moon and Planets, 111, 105 [Google Scholar]
- Porubčan, V., Svoreň, J., Neslušan, L., & Schunova, E. 2011, in Meteoroids: The Smallest Solar System Bodies, eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, 338 [Google Scholar]
- Rendtel, J., Arlt, R., Koschak, R., et al. 1995, in Handbook for visual meteor observers, eds. J. Rendtel, R. Arlt, & A. McBeath (Potsdam, Germany: International Meteor Organization), 169 [Google Scholar]
- Rudawska, R., & Jenniskens, P. 2014, Meteoroids 2013, 217 [Google Scholar]
- Rudawska, R., & Vaubaillon, J. 2015, Planet. Space Sci., 118, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2007, MNRAS, 375, 1371 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2016, MNRAS, 456, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z., & Southworth, R. B. 1975, Physical and dynamical studies of meteors. Meteor-fragmentation and stream-distribution studies, Tech. rep. [Google Scholar]
- Sekhar, A., & Asher, D. J. 2013, MNRAS, 433, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Sekhar, A., & Asher, D. J. 2014a, MNRAS, 437, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Sekhar, A., & Asher, D. J. 2014b, Meteoritics and Planetary Science, 49, 52 [Google Scholar]
- SonotaCo 2009, WGN, J. International Meteor Organization, 37, 55 [Google Scholar]
- SonotaCo 2016, WGN, J. International Meteor Organization, 44, 42 [Google Scholar]
- Tomko, D., & Neslušan, L. 2012, Earth Moon and Planets, 108, 123 [Google Scholar]
- Tomko, D., & Neslušan, L. 2016, A&A, 592, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ueda, M. 2012, WGN, J. International Meteor Organization, 40, 59 [Google Scholar]
- Vaubaillon, J., & Jenniskens, P. 2007, in BAAS, AAS/Division for Planetary Sciences Meeting Abstracts #39, 535 [Google Scholar]
- Vaubaillon, J., Arlt, R., Shanov, S., Dubrovski, S., & Sato, M. 2005a, MNRAS, 362, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- Vaubaillon, J., Colas, F., & Jorda, L. 2005b, A&A, 439, 761 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vereš, P., Kornoš, L., & Tóth, J. 2011, MNRAS, 412, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegert, P. A., Brown, P. G., Vaubaillon, J., & Schijns, H. 2005, MNRAS, 361, 638 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mean orbital characteristics with the dispersion (characterized by standard deviation) of the predicted annual meteor showers associated with the parent body considered.
Mean radiants and the numbers of particles in the individual filaments when the P-R effect is calculated according to two different formulas.
All Figures
 |
Fig. 1 Behavior of perihelion distance (plot a), semi-major axis (b), eccentricity (c), argument of perihelion (d), longitude of ascending node (e), and inclination to the ecliptic (f) of the nominal orbit of comet C/1979 Y1 (red curve) and the orbits of its clones (green curves) mapping the uncertainty of the determination of nominal orbit. The evolution is reconstructed backward for 80 000 yr. |
| In the text | |
 |
Fig. 2 Evolution of the minimum distance between the orbital arcs of comet C/1979 Y1 and Earth from a time 40 000 yr before the present to the present. The minimum distance of post-perihelion (pre-perihelion) arc is shown by the red solid (blue dashed) curve. |
| In the text | |
 |
Fig. 3 Positions of the orbital nodes of comet C/1979 Y1 during the last 40 000 yr. The green circle indicates the orbit of the Earth. The red dots outside the Earth’s orbit (blue dots inside the Earth’s orbit) show the positions of ascending (descending) node. |
| In the text | |
 |
Fig. 4 Positions of radiants of theoretical particles in filaments F1, F2 (red full squares), and transitory filaments crossing the Earth’s orbit. For a better transparency, the radiants of filaments F1 and F2 are shown only in the model for tev = 10 kyr and β = 0.00001, and radiants of transitory filaments for all considered tev, but only for β = 0.0045 (crosses) and 0.006 (empty triangles; the symbols can be distinguished when the image is magnified on a computer screen). In the case of transitory filaments, the individual colors – blue, violet, cyan, black, and gray – distinguish between the radiants in the models for tev = 80, 40, 20, 10, and 5 kyr, respectively. The mean radiants of filaments F1 and F2 are shown by the green empty squares and are connected with the green dashed abscissa passing through the coordinate origin. The radiants are shown in the modified ecliptical coordinate frame with the center in the apex of the Earth’s motion. |
| In the text | |
 |
Fig. 5 Positions of radiants of theoretical particles representing the quasi-stable part (filaments F1 and F2) of the modeled stream of comet C/1979 Y1, which currently move in orbits, along which they can approach the Earth’s orbit within 0.05 au (plot a). The radiant positions of the meteors of corresponding showers separated from the CAMS (red crosses for F1 and Dlim = 0.07 and blue asterisks for larger Dlim and both F1 and F2) and SonotaCo (green empty squares) video databases are shown in plot b. The shown theoretical radiants of filaments F1 and F2 were obtained in the models for tev = 20 kyr and β = 0.00001. The positions are shown in the equatorial coordinate frame. The sinusoid-like curve illustrates the ecliptic. |
| In the text | |
 |
Fig. 6 Dependence of the number of selected meteors on the threshold Southworth-Hawkins (1963) D-discriminant, Dlim, for the shower corresponding to filament F1 separated from the F – IAU MDC photographic (plot a), C – IAU MDC CAMS video (b), S – SonotaCo video (c), E – EDMOND video (d), and R – radio-meteor (e) database. The “break point” in plot b) is indicated with an arrow. The arrow with the question mark in this plot indicates an alternative break point. |
| In the text | |
 |
Fig. 7 Positions of radiants of theoretical particles (plot a)) of filament F1 and those of real meteors of the corresponding shower b). The meteors were separated from the CAMS (blue asterisks for Dlim = 0.17 and red crosses for Dlim = 0.07) video database. The shown theoretical radiants were obtained in the models for β = 0.00001 and tev = 5, 10, 20, 40, and 80 kyr. The positions for the different tev are distinguished using the different marks and colors. The coordinate frame is equatorial. |
| In the text | |
 |
Fig. 8 Dependence of the number of selected meteors on the threshold Southworth-Hawkins (1963) D-discriminant, Dlim, for the shower corresponding to filament F2 separated from the F – IAU MDC photographic (plot a), C – IAU MDC CAMS video (b), S – SonotaCo video (c), E – EDMOND video (d), and R – radio-meteor (e) database. The points on the curves in plots b and c regarded as the “break points” are indicated by arrows. |
| In the text | |
 |
Fig. 9 Positions of radiants of theoretical particles (plot a) of filament F2 and those of real meteors in orbits resembling those of theoretical particles (b). The meteors were separated from the CAMS (blue asterisks) and SonotaCo (green empty squares) video databases. The shown theoretical radiants were obtained in the models for β = 0.00001 and tev = 5, 10, 20, 40, and 80 kyr. The positions for the different tev are distinguished using the different marks and colors. The coordinate frame is equatorial. |
| In the text | |
 |
Fig. 10 Positions of theoretical radiants predicted with the models of C/1979 Y1-stream for tev = 5 (plot a), 10 (b), 20 (c), 40 (d), and 80 kyr (e). Filaments F1 and F2 corresponding to the annual showers, as well as the transitory filaments TF, are plotted. The positions are shown in the Hammer projection of celestial sphere in the equatorial coordinates. The sinusoid-like curve is the ecliptic. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


