| Issue |
A&A
Volume 604, August 2017
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201730739 | |
| Published online | 27 July 2017 | |
Can BL Lacertae emission explain the neutrinos above 0.2 PeV?
1 Gran Sasso Science Institute, 67100 L’Aquila, Italy
e-mail: andrea.palladino@gssi.infn.it
2 Laboratori Nazionali del Gran Sasso, 67100 Assergi (L’Aquila), Italy
Received: 6 March 2017
Accepted: 26 May 2017
Context. Multi-messenger astronomy can help to investigate the sources of the high-energy neutrinos observed by the high-energy neutrino telescope IceCube.
Aims. We consider the hypothesis that the highest energy neutrinos are produced by BL Lacs, arguing that this is not contradicted severely by any known fact.
Methods. We check the BL Lac hypothesis by searching for correlations between the through-going muon events of IceCube and the BL Lacs of the second catalog of Fermi-LAT (2FHL).
Results. We expect 10.2 ± 2.4 correlated events but we find that just 1 event has a BL Lac as counterpart. We also assess the probability of observing one multiplet from the same source, finding that the present null result is not yet of critical significance.
Conclusions. We conclude that the hypothesis that the BL Lacs are the main emitters of the highest-energy neutrinos observed by IceCube is disfavored at 3.7σ. We discuss implications and possible ways out; for example, this could work if the angular resolution was 4°, which is much more than expected.
Key words: neutrinos / astroparticle physics
© ESO, 2017
1. Introduction
The observations of the high-energy neutrino telescope IceCube (we refer to Aartsen et al. 2017, 2016, for recent results and references therein) are at least as exciting as those concerning solar and supernova neutrinos that begun neutrino astronomy and were recognized by the Nobel prize in physics in 2002. The high-energy neutrinos might well eventually constitute a new and rich chapter of neutrino astronomy. This precise field of research is still gathering speed, but some relevant elements have already been obtained. The highest-energy events that have been observed cannot be entirely attributed to the secondary particles produced by cosmic-ray interactions with the atmosphere. These observations can instead be explained invoking the existence of a population of neutrinos of cosmic origin. Interestingly, the arrival directions of the events of highest energy are compatible with an isotropic origin, which suggests that most of them are extragalactic. It is now time to form hypotheses on what the sources of these particles could be.
To date, we do not have a clear idea and/or astrophysical picture of what the sources of these, presumably extragalactic, neutrinos are. Even if one might imagine exotic processes or mechanisms of production, it seems plausible a priori that the IceCube neutrinos originate in some astrophysical environment, rich with cosmic rays and target particles, that allows collisions and therefore the production of secondary particles. In our view, this hypothesis should be investigated thoroughly and the present study can be regarded as a contribution to this discussion.
In order to proceed, it is natural to rely on synergies with other astronomies, that is, to exploit the potential of a “multi-messenger” investigation. In fact, the neutrinos from cosmic ray collisions are accompanied by γ-rays; therefore, the hypothetical sources of neutrinos must also be sources of γ-rays. The possibility of observing the γ-rays is by no means guaranteed. For example, the γ-rays could have a different distribution from those of the neutrinos (e.g., if the neutrinos are emitted isotropically near the nuclear region of an active galactic nucleus (AGN), whereas the γ rays emerge as a collimated beam of one jet instead) or could, possibly, be absorbed and/or strongly reprocessed at the source. However the intergalactic medium does not absorb γ-rays with energies below 100 GeV or so. Thus, through the use of results from astrophysical modeling, there is hope for revealing a correlation between these γ-rays and the observed neutrinos.
In this connection, Fermi-LAT, that has obtained a relatively complete survey of the γ-ray sky below a few 100 GeV, has produced results that are of special interest. In the region Eγ> 10 GeV, the brightest objects are the blazars (we refer to e.g., Padovani 2007, for a review), radio-loud AGN whose relativistic jet is closely aligned with the line of sight. They are broadly classified as BL Lacs (namely BL Lacertae) and as flat spectrum radio quasars (FSRQ). BL Lacs are characterized by featureless optical spectra (i.e., lacking strong emission/absorption lines). A finer classification of BL Lacs is considered below.
Blazars are widely considered to be promising candidates for high-energy neutrino emission (Protheroe 1997; Atoyan & Dermer 2001; Essey et al. 2010; Murase et al. 2014; Halzen & Kheirandish 2016; Murase & Waxman 2016; Resconi et al. 2017; Padovani et al. 2016; Miranda et al. 2016; Aartsen et al. 2017; Glüsenkamp 2016; Gao et al.2017). Moreover, certain analyses of IceCube data (we refer to Padovani et al. 2016, for a very recent and comprehensive work) suggest that a fraction of the events seen by IceCube could be attributed to blazars.
In recent works (Tavecchio et al. 2014; Padovani & Resconi 2014; Tavecchio & Ghisellini 2015; Righi et al. 2017) focus was put on the subclass of blazars called BL Lacs; the present study also concentrates on this hypothesis. In the models of Tavecchio et al. (we refer to in particular Tavecchio et al. 2014; Tavecchio & Ghisellini 2015; Righi et al. 2017), the secondary high-energy particles (neutrinos and γ-rays) are to a good extent produced in alignment with the direction of the jet (spine-layer model) and therefore one expects a tight correlation of the signals. This highly definite astrophysical setup adds motivations to the present investigation.
At this point we can formulate the question that we examine and discuss: are the highest energy extragalactic neutrinos seen by IceCube fully attributable to BL Lacs? This hypothesis, presented in a slightly more general form in Fig. 1, is investigated in this work. We note that neutrinos and the γ-rays are observed at rather different energies in IceCube and Fermi-LAT, respectively, and that the details of the connections greatly depend upon on uncertain theoretical modeling. Thus, the investigation is bound to proceed on phenomenological grounds. We refer to Aartsen et al. (2017) for a similar and complementary study of blazars and neutrinos.
The outline of this work is as follows. In Sect. 2 we define the context of the discussion; we discuss under which conditions the above hypothesis is viable. Then we perform the crucial test, by searching for correlations between extragalactic neutrinos and the subclass of high-energy emitting BL Lacs that are identified astronomically. We argue in Sect. 3 that the number of observed correlations is too small and that the hypothesis is not supported. We also derive the expectation on multiplets of neutrino events and compare this with the observations (Sect. 4). We discuss, in Sect. 5, the results and the possible ways out from the conclusion that the observed neutrinos with energy above 200 TeV receive only a minor contribution from BL Lacs.
 |
Fig. 1 Scheme of the present investigation: we assume that a part of the high energy neutrino signal seen by IceCube includes extragalactic neutrinos. We investigate whether the extragalactic emission can be attributed largely or fully to BL Lac emission, relying on the fact that a large fraction of BL Lacs, as discussed in Sect. 2, is observed by Fermi-LAT. |
2. Extragalactic neutrinos and BL Lacs
Before examining the connection, we need to discuss a few important questions: 1) which set of neutrino data gives us the best chance of extracting and identifying the extragalactic part of the signal; 2) what is the fraction of the extragalactic neutrinos of IceCube that should correlate with BL Lacs; 3) how do we compare with the limit on neutrino emission from blazars obtained by IceCube in Aartsen et al. (2017)?
2.1. Importance of the high-energy through-going events
The largest high-energy neutrino telescope today in operation is IceCube. This observatory consists in a volume of about 1 km3 of Antarctic ice, monitored by strings of phototubes. When the neutrinos interact inside or nearby the detector, they produce charged particles that allow for the detection of the presence of high-energy neutrinos and the measurement, to a certain extent, of their energy, direction, and flavor (i.e., electron, muon or tau). There are two main classes of signals detected in IceCube: 1) The through-going events, that are muons (or antimuons) due to neutrinos interacting outside the detector; and 2) the high-energy starting events (HESE), whose vertex is instead contained inside the instrumented volume. Among HESE, one distinguishes those events where there is a track, associated to charged-current muon neutrino interactions, and those where the track is absent and the energy is deposited in a small region, that are associated to the other types of flavor and interactions.
Recently IceCube has published a relatively large set of 29 through-going events, collected over six years (Aartsen et al. 2016) and with very high energy; all of them have energy ≥0.2 PeV and the highest energy event seen to date corresponds to a neutrino with more than 4.5 PeV and belongs to only this dataset. These through-going events provide strong support for the observation of a signal of cosmic neutrinos previously claimed by IceCube with the HESE dataset. When comparison is possible, the two datasets are consistent with a common, simple interpretation. In this paragraph we discuss the three main reasons why we consider that this specific dataset is particularly important for the investigation of the BL Lac hypothesis.
Energy distributionThe neutrino signal corresponding to the through-going event dataset is compatible with a single power-law distribution with a spectral index γ = 2.13 ± 0.13 (Aartsen et al. 2016). It is remarkable that this distribution agrees well with the high-energy part of the HESE dataset, as argued in Palladino et al. (2016) and eventually proved in Aartsen et al. (2016)1. The bulk of the HESE data, that includes the events collected at lower energies, indicates a different spectral index instead, closer to γ = 2.5. This feature of the HESE data can be attributed to the onset of another component of the signal with lower energy that is plausibly not entirely of extragalactic origin, as discussed in Spurio (2014), Palladino & Vissani (2016), Palladino et al. (2016). We note that a relatively hard distribution of extragalactic neutrinos can be extrapolated at lower energies without particular difficulty, whereas, if the extragalactic neutrinos were distributed as  at low energies, this would imply an excessive amount of γ-rays (Esmaili et al. 2016), or too many low-energy track events, similar to those expected from prompt atmospheric neutrinos and for which we have no evidence (Palladino et al. 2016). Thus, in order to remain cautious for what concerns the interpretation of the extragalactic neutrino distribution (i.e., the population of neutrinos that is relevant to assess the BL Lacs contribution) we deem that it is preferable to focus the discussion on the high-energy part of the spectrum.
at low energies, this would imply an excessive amount of γ-rays (Esmaili et al. 2016), or too many low-energy track events, similar to those expected from prompt atmospheric neutrinos and for which we have no evidence (Palladino et al. 2016). Thus, in order to remain cautious for what concerns the interpretation of the extragalactic neutrino distribution (i.e., the population of neutrinos that is relevant to assess the BL Lacs contribution) we deem that it is preferable to focus the discussion on the high-energy part of the spectrum.
Northern hemisphere.The through-going events originate from muon neutrinos/antineutrinos that are converted into muons/antimuons near the detector. For this class of signal events, the Earth works, at once, as a neutrino converter and as a screen for the atmospheric muons. Thus, most of the events come from below the horizon; in the case of IceCube this means the Northern hemisphere. In this hemisphere, it is expected that the contribution of the signal due to galactic sources is small or absent. This statement is even more true for the specific dataset used in Aartsen et al. (2016), which satisfies also the high-energy criterion discussed immediately above. We refer to Spurio (2014), Palladino & Vissani (2016), Palladino et al. (2016) for further discussion.
Pointing of through-going events.The last and most important characteristic of through-going events is that their arrival directions are known relatively well. This is a general feature of events of the track type, although in some cases the precision is bad, similar to the one of the HESE, shower events. In Table 4 of Aartsen et al. (2016), the declinations δ and the right ascension α are given along with their asymmetric errors δ± and α±, at the 50% CL and at 90% CL. We have checked that the errors in the two cases scale roughly according to a Gaussian distribution but we use, as a rule, the more conservative case (90% CL) in our analysis. The angular span of these two angular coordinates is given by the sum of the upper and lower ranges, that are, in general, different: Δδ(i) = Δδ+(i) + Δδ−(i) and likewise Δα(i) = Δα+(i) + Δα−(i) where i = 1,2,3...29. Each event subtends a solid angle of Ω(i) = Δδ(i) × Δα(i), that, according to the quoted confidence levels, is expected to include the true direction with a confidence level of 0.92 = 81%. We note that the total angular size spanned by the neutrino events is small  (1)where we compare with the solid angle subtended by Northern sky. It is also convenient to define a single (linear) angle that quantifies the region around the individual event as follows,
(1)where we compare with the solid angle subtended by Northern sky. It is also convenient to define a single (linear) angle that quantifies the region around the individual event as follows,  (2)We refer to this angle as the “average angular resolution”. A histogram of values based on the 29 events is shown in Fig. 2. We note the presence of two outlying events, whose direction is identified only poorly. These are event number 6 and event number 14 in Table 4 of Aartsen et al. (2016). In order to be more quantitative, we note that 1) the event number 6 alone covers 61% of the solid angle spanned by neutrinos given in Eq. (1); and that 2) if we exclude the two outliers, and consider the angle spanned by the remaining 27 events, 3.5% → 0.9%. Considering the angular resolutions shown in Fig. 2 and excluding the two outliers, we have the average angular resolution
(2)We refer to this angle as the “average angular resolution”. A histogram of values based on the 29 events is shown in Fig. 2. We note the presence of two outlying events, whose direction is identified only poorly. These are event number 6 and event number 14 in Table 4 of Aartsen et al. (2016). In order to be more quantitative, we note that 1) the event number 6 alone covers 61% of the solid angle spanned by neutrinos given in Eq. (1); and that 2) if we exclude the two outliers, and consider the angle spanned by the remaining 27 events, 3.5% → 0.9%. Considering the angular resolutions shown in Fig. 2 and excluding the two outliers, we have the average angular resolution  .
.
 |
Fig. 2 Values for the 29 through-going events of the average angular resolution, defined as described in Eq. (2). We note the two outliers, discussed in the text. |
Investigation of the origin of the extragalactic component.The first reason why the 29 through-going events, the largest sample of high-energy events collected by IceCube, are so important to us is that they are compatible with an extragalactic origin. The fact that these events come from the Northern hemisphere gives us further confidence supporting the hypothesis that the cosmic neutrino signal that contributes to this dataset has an extragalactic origin. The latter feature (i.e., pointing) offers us the chance to use these data to identify the sources of the events; we use it in Sect. 3 to test our assumption on the high-energy neutrino emission from BL Lac.
2.2. Fraction of correlated neutrino events
Modeling of BL Lac.The γ-rays telescopes and in particular Fermi-LAT can see individually only a fraction of the BL Lacs. The rest corresponds to objects that are too dim (i.e., too far and/or too under-luminous) to be observed; we refers to these as un-resolved BL Lacs. This fraction is of the order of one and it is widely believed that the class of BL Lacs that are un-resolved gives an important contribution to the “diffuse” γ ray emission at the highest energies.
It is possible to be more precise thanks to the model of Ajello et al. (2014). In this paper, a detailed parameterization of the luminosity function of the BL Lacs distribution, differential in 0.1−100 GeV luminosity (Lγ), redshift (z) and photon index (Γ),  (3)is studied. The parameters are obtained, within errors, thanks to the observational data. The result depends on modeling and in the following we adopt the result from the two best models of Ajello et al. (2014), there referred to as LDDE (luminosity-dependent density evolution) and PLE (pure luminosity evolution).
(3)is studied. The parameters are obtained, within errors, thanks to the observational data. The result depends on modeling and in the following we adopt the result from the two best models of Ajello et al. (2014), there referred to as LDDE (luminosity-dependent density evolution) and PLE (pure luminosity evolution).
Exploiting the results of this analysis it is not difficult to calculate the total flux of γ-rays due to BL Lacs,  (4)where dF/ dE is the differential flux of the single power-law source, that integrated over the energies gives,
(4)where dF/ dE is the differential flux of the single power-law source, that integrated over the energies gives,  (5)where Dc(z) is the comoving distance and the factor (1 + z)− Γ accounts for the redshift. For a sample plot of the total flux in the case of LDDE model, obtained using Eq. (4), see Fig. 3 of Esmaili et al. (2016).
(5)where Dc(z) is the comoving distance and the factor (1 + z)− Γ accounts for the redshift. For a sample plot of the total flux in the case of LDDE model, obtained using Eq. (4), see Fig. 3 of Esmaili et al. (2016).
The result of the calculations of the quantities relevant for the present papers, namely the γ-ray fluxes from resolved and un-resolved BL Lacs, are given in Esmaili et al. (2016), which is fully based on the work of Ajello et al. (2014). The flux of γ-rays due to the resolved BL Lacs is, 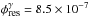 ph/(cm2 s sr), with a small uncertainty. The flux of the un-resolved BL Lacs is given by
ph/(cm2 s sr), with a small uncertainty. The flux of the un-resolved BL Lacs is given by  , thus, its value depends on theoretical modeling. Table 2 of Esmaili et al. (2016) gives the result for the two models mentioned above:
, thus, its value depends on theoretical modeling. Table 2 of Esmaili et al. (2016) gives the result for the two models mentioned above:  ph/(cm2 s sr) and
ph/(cm2 s sr) and  ph/(cm2 s sr). We use conservatively the upper range of the largest prediction (PLE),
ph/(cm2 s sr). We use conservatively the upper range of the largest prediction (PLE),  ph/(cm2 s sr) and the lower range of the smallest prediction (LDDE),
ph/(cm2 s sr) and the lower range of the smallest prediction (LDDE),  ph/(cm2 s sr), thereby finding the fraction of the γ ray flux due to resolved BL Lacs,
ph/(cm2 s sr), thereby finding the fraction of the γ ray flux due to resolved BL Lacs,  (6)Therefore, this fraction is relatively well-known, the uncertainty being about 20% (we note incidentally that the un-resolved flux can account for a large part of the diffuse flux observed above 10 GeV as argued in Ajello et al. 2014).
(6)Therefore, this fraction is relatively well-known, the uncertainty being about 20% (we note incidentally that the un-resolved flux can account for a large part of the diffuse flux observed above 10 GeV as argued in Ajello et al. 2014).
An important remark is as follows. On the one hand, we would like to have information on γ ray emission at the highest energy, but on the other hand, the Universe becomes opaque to γ rays above 100 GeV, and this limits the useful observational window. From this point of view, the subset of BL Lacs characterized by an intense emission above 50 GeV, collected in the catalog 2FHL, Ackermann et al. (2016), is particularly interesting for us and we use it in the following. A complete model of the cosmological evolution of these objects is not yet available; however, the BL Lacs of the 2FHL catalog belong mostly to the subclass of the high-frequency synchrotron peak (HSP) that were studied in Ajello et al. (2014). We note that the HSP have a fast cosmological evolution, that is, they are more abundant at low redshift values (we refer in particular to Fig. 11 of Ajello et al. 2014). From this consideration, it is expected that the visible fraction of the BL Lacs included in Ackermann et al. (2016) is possibly even higher than 0.5. This conclusion is very important in view of the subsequent analysis.
Hypothesis on neutrino emission.In most theoretical models, the neutrino luminosity is proportional to the γ ray luminosity; we refer to Stecker (1979); Protheroe (1997), Atoyan & Dermer (2001), Essey et al. (2010), Halzen & Kheirandish (2016), Murase et al. (2014), Murase & Waxman (2016), Turley et al. (2016), Righi et al. (2017). Therefore, we assume that the fraction of the extragalactic neutrino flux fν that corresponds to resolved BL Lacs (i.e., the tagged fraction) equates the fraction determined immediately above2,  (7)and we assume that this is true in particular for what concerns the BL Lacs that emit the very-high-energy events observed by means of through-going muons.
(7)and we assume that this is true in particular for what concerns the BL Lacs that emit the very-high-energy events observed by means of through-going muons.
Since we use the integrated quantities, this inference should be relatively stable and not crucially dependent upon the detailed connection between neutrinos and rays. We argued that the fraction of neutrinos due to the BL Lacs that emits γ-rays at the highest observed energies (in particular those included in 2FHL catalog) is not underestimated by fγ. In other words, when we use Eq. (6) along with the high-energy neutrino signal, we obtain the minimum number of expected correlations with the BL Lacs in the 2FHL catalog.
2.3. Comparison with the bound on neutrinos obtained by IceCube
Recently IceCube has published a study (Aartsen et al. 2017) concerning neutrinos from blazars where a limit on the fraction of the signal neutrino events observed and attributable to these astrophysical objects was obtained. This study is relatively similar in spirit to the present work, namely, it is a search for correlations between certain classes of astronomical objects and the observed neutrinos, hypothesized to originate from these objects. Thus, it is especially important to highlight the differences between our approaches and theirs:
-
1.
IceCube collaboration focusses on the study of blazars whereaswe prefer to be more specific and emphasize the comparison withthe BL Lacs instead.
-
2.
The result of IceCube is based on data of energy above 10 TeV, that is, well below the lowest energy of the through-going muon dataset that we use, 200 TeV.
-
3.
Finally and most importantly, we consider the total set of BL Lacs, not only those that are resolved, since it is presumable that also the ones that are not resolved emit high energy neutrinos.
Therefore, we examine here the bound of IceCube from a different perspective.
We consider the simplest description of the neutrino signal that explains the through-going muons flux. This is a power law with α = 2, a value admitted within 1σ, as illustrated in Fig. 6 of Aartsen et al. (2016). From the same figure we find that the normalization of flux of νμ and 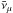 is equal to
is equal to  (8)with an uncertainty of about 30% on the normalization. This describes the extragalactic neutrino flux that we assume to be fully explained by BL Lac emission. In order to calculate the fraction of the neutrino flux due to resolved BL Lacs, we simply have to multiply it by the fraction given in Eq. (6), obtaining
(8)with an uncertainty of about 30% on the normalization. This describes the extragalactic neutrino flux that we assume to be fully explained by BL Lac emission. In order to calculate the fraction of the neutrino flux due to resolved BL Lacs, we simply have to multiply it by the fraction given in Eq. (6), obtaining  (9)where we summed the uncertainties in quadrature. The bound obtained by IceCube is reported in Table 3 of Aartsen et al. (2017) for the case where α = 2, “All 2LAC Blazars” and “equal weighting”. The bound is
(9)where we summed the uncertainties in quadrature. The bound obtained by IceCube is reported in Table 3 of Aartsen et al. (2017) for the case where α = 2, “All 2LAC Blazars” and “equal weighting”. The bound is  (10)where we use the 1σ uncertainty instead of the 90% confidence level (C.L) quoted in the table. This bound is not incompatible with the hypothesis that BL Lacs produce all the extragalactic neutrino flux. We note that the second reason why we have chosen to discuss the spectral index α = 2 for the through-going muons flux is that this value permits a direct comparison between the measured fluxes and the bound. The bound of IceCube becomes tighter by increasing α and for α = 2.2 excludes that the blazars of Ackermann et al. (2016) emit more that 50% of the neutrinos (Aartsen et al. 2017). However, in view of Eq. (6), this is not incompatible with the hypothesis that the BL Lacs (those resolved and unresolved) account for the full extragalactic neutrino emission. Similar analyses, using a wider set of catalogs for the γ-ray sources, are presented in Padovani et al. (2016); the results are slightly tighter but comparable with those of IceCube.
(10)where we use the 1σ uncertainty instead of the 90% confidence level (C.L) quoted in the table. This bound is not incompatible with the hypothesis that BL Lacs produce all the extragalactic neutrino flux. We note that the second reason why we have chosen to discuss the spectral index α = 2 for the through-going muons flux is that this value permits a direct comparison between the measured fluxes and the bound. The bound of IceCube becomes tighter by increasing α and for α = 2.2 excludes that the blazars of Ackermann et al. (2016) emit more that 50% of the neutrinos (Aartsen et al. 2017). However, in view of Eq. (6), this is not incompatible with the hypothesis that the BL Lacs (those resolved and unresolved) account for the full extragalactic neutrino emission. Similar analyses, using a wider set of catalogs for the γ-ray sources, are presented in Padovani et al. (2016); the results are slightly tighter but comparable with those of IceCube.
 |
Fig. 3 Map, in Galactic coordinates, of the γ-ray sky observed by Fermi-LAT, from Ackermann et al. (2016). The red points indicate the 29 through-going muons, with a deposited energy above 200 TeV, observed by IceCube over 6 yr; their angular uncertainties are not represented in this figure, but are taken into account in the calculations. The brown lines represent intervals of declination of 30°. |
3. Spatial connection between BL Lacs and high-energy neutrinos
Here we investigate whether the counterparts of high-energy neutrino events contained in Aartsen et al. (2016) are the BL Lacs.
3.1. The number of expected correlations
Cosmic rays that hit the terrestrial atmosphere yield secondary particles that act as background events, that is, they contaminate the observational sample: these are (1) muons that come mostly from the sky above the detector and affect the interpretation of the HESE dataset but not much the through-going muons and (2) neutrinos and antineutrinos that have a different (softer) energy spectrum than the signal and are mostly muon neutrinos and antineutrinos at relatively low energies. The role of neutrinos in the decay of charmed mesons is not known precisely and this creates uncertanty in the inferences at a few 100 TeV; however it is possible to use the data themselves to obtain a bound on this component that is not far from the current theoretical predictions as shown in Aartsen et al. (2016).
In order to calculate the number of expected correlations, the first step is the evaluation of the number of tracks that can be attributed to the signal, that is, to astrophysical neutrinos. This can be done using Table 4 of Aartsen et al. (2016), where the “signalness” si for each event i = 1,2...29 is given. This quantity is defined as the ratio of the astrophysical expectation over the sum of the atmospheric and astrophysical expectations for a given energy proxy and the best-fit spectrum. We use these values of si to build a likelihood function that estimates the total number of events that can be attributed to the signal, or equivalently, the number of events that have to be attributed to the background. This is obtained expanding the polynomial  ,
,![\begin{equation} \mathcal{P}(x)= \prod_{i=1}^{29} [s_i x+(1-s_i)] = \sum_{n=0}^{29} p_n x^n , \end{equation}](/articles/aa/full_html/2017/08/aa30739-17/aa30739-17-eq57.png) (11)where the coefficient pn ≤ 1 represents the probability that there are exactly Nsignal = n signal events; the consistency condition
(11)where the coefficient pn ≤ 1 represents the probability that there are exactly Nsignal = n signal events; the consistency condition  holds true. In this manner, we found that the through-going event dataset contains a number of signal events equal to
holds true. In this manner, we found that the through-going event dataset contains a number of signal events equal to  (12)where we quote the uncertainty at 1σ. When we combine this information with that provided by Eq. (6), we find that the number of neutrino events, which should show a spatial correlation with BL Lacs, is simply
(12)where we quote the uncertainty at 1σ. When we combine this information with that provided by Eq. (6), we find that the number of neutrino events, which should show a spatial correlation with BL Lacs, is simply  (13)The contribution to its uncertainty is given both by the uncertainty on the experimental data Ns and by the uncertainty on f, as follows:
(13)The contribution to its uncertainty is given both by the uncertainty on the experimental data Ns and by the uncertainty on f, as follows:  (14)This results in
(14)This results in 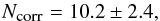 (15)that has an uncertainty of 25%. Therefore, we assume that the likelihood ℒth(n) that gives the expected number of correlations is a Gaussian function, with mean value μ = 10.2 and standard deviation σ = 2.4.
(15)that has an uncertainty of 25%. Therefore, we assume that the likelihood ℒth(n) that gives the expected number of correlations is a Gaussian function, with mean value μ = 10.2 and standard deviation σ = 2.4.
3.2. Number of observed correlations estimated adopting IceCube uncertainties
In order to search for the counterparts of the high-energy neutrinos, we use the coordinates of the through-going muons and also the uncertainties3 listed in Table 4 of Aartsen et al. (2016) along with the 2FHL catalog of the γ-ray sources of the Fermi-LAT collaboration (Ackermann et al. 2016). These data are shown in Fig. 3. We note that most of the neutrino events come from the region between 0° ≤ δ ≤ 30°; this is consistent with the fact that other neutrinos in this sample are largely absorbed in the Earth, since they have high declinations and high energies (namely, a reconstructed energy of muons above 200 TeV): Aartsen et al. (2016).
When we compare them with the positions of the BL Lacs in Ackermann et al. (2016), we find that there is only one correlation within the 81% C.L. More precisely, the neutrino event number 6 of Table 4 of Aartsen et al. (2016) can be associated with the BL Lac J1725.1+1154 or the BL Lac J1555.7+1111. (As already discussed, we used the confidence level interval reported in Table 4 of Aartsen et al. 2016. This corresponds to 90% C.L. for declination and right ascension, and therefore the two dimensional confidence level is slightly less, i.e. 0.9 × 0.9 = 81%.)
It is important to underline that the direction of the neutrino event number 6 is not well reconstructed. In fact this event is one of the two outliers illustrated in Fig. 2 and its angular uncertainty is of the order of 10°, much larger than the typical value of about ~1°. Therefore this correlation could be attributed to the poor angular uncertainty of the events. However, in order to be conservative, we do not rule out this correlation in the rest of this analysis.
Number of correlations as a function of k and the corresponding confidence level (C.L.).
In order to generalize the procedure, we scale the uncertainties given in Table 4 of Aartsen et al. (2016) by a coefficient k, in the following manner:  (16)where Δ90% are the uncertainties on the declination and on the right ascension quoted in the table at 90% C.L., Δ(k) are the new uncertainties of α and δ, and k denotes the number of (one dimensional) σ of our interval. The value of the two-dimensional confidence level is given simply by the square of the integral of the standard normal distribution between − k and k,
(16)where Δ90% are the uncertainties on the declination and on the right ascension quoted in the table at 90% C.L., Δ(k) are the new uncertainties of α and δ, and k denotes the number of (one dimensional) σ of our interval. The value of the two-dimensional confidence level is given simply by the square of the integral of the standard normal distribution between − k and k, ![\begin{equation} \mbox{C.L.}(\mbox{2 d.o.f},k) = \left[ \int_{-k}^{k} \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} \ {\rm d}x \right]^2 . \end{equation}](/articles/aa/full_html/2017/08/aa30739-17/aa30739-17-eq83.png) (17)Some values of k, the corresponding confidence levels and the number of correlations observed within a certain C.L. are reported in Table 1. The number of correlations within a certain C.L. (see Table 1) is reasonably well fitted by a probability density function with an exponential shape. Therefore the Probability Distribution Function (PDF) of the observed number of correlations is given by the derivative of
(17)Some values of k, the corresponding confidence levels and the number of correlations observed within a certain C.L. are reported in Table 1. The number of correlations within a certain C.L. (see Table 1) is reasonably well fitted by a probability density function with an exponential shape. Therefore the Probability Distribution Function (PDF) of the observed number of correlations is given by the derivative of  (18)In Fig. 4 we show how many correlations are present within a certain confidence level. The PDF is shown in Fig. 4 by an orange line. The average number of correlations is 0.9 whereas the median value is 0.6. In the same figure the distribution of the expected number of correlations from theoretical considerations is also illustrated (blue line).
(18)In Fig. 4 we show how many correlations are present within a certain confidence level. The PDF is shown in Fig. 4 by an orange line. The average number of correlations is 0.9 whereas the median value is 0.6. In the same figure the distribution of the expected number of correlations from theoretical considerations is also illustrated (blue line).
 |
Fig. 4 The orange line is the PDF of the observed number of correlations. In blue line we show the expected number of correlations, assuming that the BL Lacs are the main emitters of high-energy neutrinos, discussed after Eq. (15). |
In order to compare two different distributions, that is, the expected theoretical correlations ℒth(n) and the observed correlations ℒexp(n), we use the same procedure described in Palladino & Vissani (2016), adopting the following formula to evaluate the “distance” between the distributions:  (19)We found that ℒ(δ) is in good approximation and normally distributed, with a mean value of μ = 9.4 and a standard deviation of σ = 2.5. The null value is excluded at 3.7σ and this represents the difference between these two distributions. Taking into account the uncertainty in the fit of ℒth(n) we found a similar result, since the two distributions are different with a significance of 3.7 ± 0.1σ. Excluding the outliers, that is, the neutrino event numbers 6 and 14, the difference between the two distributions has a significance of 4.1σ. These considerations are true under the hypothesis that neutrinos are produced in the BL Lacs, associated to the γ-rays that we observe from those sources. We refer to Kalashev et al. (2013) for an alternative scenario in which high-energy neutrinos are not produced directly in the source but are given by the interaction of cosmic rays produced in a generic AGN and the EBL.
(19)We found that ℒ(δ) is in good approximation and normally distributed, with a mean value of μ = 9.4 and a standard deviation of σ = 2.5. The null value is excluded at 3.7σ and this represents the difference between these two distributions. Taking into account the uncertainty in the fit of ℒth(n) we found a similar result, since the two distributions are different with a significance of 3.7 ± 0.1σ. Excluding the outliers, that is, the neutrino event numbers 6 and 14, the difference between the two distributions has a significance of 4.1σ. These considerations are true under the hypothesis that neutrinos are produced in the BL Lacs, associated to the γ-rays that we observe from those sources. We refer to Kalashev et al. (2013) for an alternative scenario in which high-energy neutrinos are not produced directly in the source but are given by the interaction of cosmic rays produced in a generic AGN and the EBL.
Combining the information provided by the theoretical likelihood and the experimental likelihood, it is also possible to find the contribution of the BL Lacs to the IceCube neutrinos above 0.2 PeV. We can estimate the fraction ξ of the events, that can be attributed to the BL Lacs, by means of the following likelihood function:  (20)In this way, we find that the fraction is ξ = 0.11 at 67% C.L. and ξ = 0.23 at 90% C.L. Considering the present data, the probability that the BL Lacs contribute more than 50% to the through-going muons above 0.2 PeV is less than 1%.
(20)In this way, we find that the fraction is ξ = 0.11 at 67% C.L. and ξ = 0.23 at 90% C.L. Considering the present data, the probability that the BL Lacs contribute more than 50% to the through-going muons above 0.2 PeV is less than 1%.
3.3. Number of observed correlations estimated varying the angular intervals
An alternative procedure is the following one. If we disregard the angular resolution quoted by the IceCube collaboration, and we vary it instead, it is interesting to ask how many events have a counterpart within a certain angular distance. Considering a neutrino event with coordinates (α1,δ1) and a BL Lac with coordinates (α2,δ2), the angular distance d is given by the spherical distance, defined as follows:  (21)This expression can be obtained by expanding for δ1 ≈ δ2 and α1 ≈ α2, the scalar product of the two unit vectors in the given directions, cos(d) ≡ (n1,n2). Therefore, d subtends the region of solid angle
(21)This expression can be obtained by expanding for δ1 ≈ δ2 and α1 ≈ α2, the scalar product of the two unit vectors in the given directions, cos(d) ≡ (n1,n2). Therefore, d subtends the region of solid angle  (22)and it is directly comparable with the average angular resolution θ defined in Eq. (2).
(22)and it is directly comparable with the average angular resolution θ defined in Eq. (2).
Using this procedure we find that only one event has a counterpart at distance d ≤ 1°; it is the through-going event number 23 of Table 4 of Aartsen et al. (2016) that can be correlated with the BL Lac J0211.2+1050. We have tested that within d ≤ 2° there are two possible counterparts. Finally, for completeness, we report in Tables 2 the 4 events4 that show at least one correlation with a BL Lac within ~3°.
In Fig. 5 we present a generalization of this analysis. Assuming that the BL Lacs are the counterpart of the IceCube neutrino events, we wonder how much the angular resolution of the tracks should be worsened, in order to observe a certain number of correlations.
If we want to recover the agreement with the expectation at 90% C.L., we need an average angular distance of d ≃ 4°, namely, Ω = 50 square degrees (Eq. (22)). This value is very different from the angular resolution declared for the tracks, typically close to 1° and more precisely equal to  for the present through-going muons dataset, as discussed after Eq. (2). Therefore the required angular resolution of 4° is in tension with the declared angular resolution with a significance of 3σ and could only be justified invoking a very large value of the systematic uncertainty.
for the present through-going muons dataset, as discussed after Eq. (2). Therefore the required angular resolution of 4° is in tension with the declared angular resolution with a significance of 3σ and could only be justified invoking a very large value of the systematic uncertainty.
 |
Fig. 5 Number of correlations found as a function of the angular distance between the position of the neutrino events and the position of the BL Lac. Within 1 degree, only 1 correlation has been observed. The horizontal band shows the expectations given in Eq. (15). |
Four events are reported here that show correlation with BL Lacs within 3°.
4. Multiplets
Here, we discuss a more refined test of the hypothesis that BL Lacs are the main emitters of high-energy neutrinos: we evaluate the probability of observing at least one multiplet, that is, two or more events from the same source. In this analysis we refer to identified BL Lacs contained in the second Fermi-Lat catalog (Ackermann et al. 2016).
As is clear from Fig. 3, most through-going muons come from the region 0° ≤ δ ≤ 30°. This is expected for the high-energy neutrino signal, due to the absorption in the Earth; this conclusion is consistent with the discussion given in Aartsen et al. (2016). Therefore we limit our analysis to the cleaner subset of BL Lacs that are contained in this part of the Northern sky. Repeating the same calculation of Sec. 3.1, for the subset of 23 events included in the interval of declination 0° ≤ δ ≤ 30°, we find that the number of events that can be attributed to cosmic neutrinos is equal to, Nsignal(0° ≤ δ ≤ 30°) = 16.9 ± 2.1 at 1σ. Using Eq. (13) we find that the number of signal events, expected to show a correlation due to their common origin, is equal to  (23)at a C.L. of 1σ , which becomes 8.5 ± 3.2 at 90% C.L.
(23)at a C.L. of 1σ , which becomes 8.5 ± 3.2 at 90% C.L.
In this angular region, 43 BL Lacs are present in the Fermi-LAT catalog (Ackermann et al. 2016). Assuming that the probability of emitting a neutrino is proportional to the luminosity of the sources, as argued in Righi et al. (2017), we define a weight wi as follows:  (24)where Li and Ltot, taken from Ackermann et al. (2016), are the luminosity of a single source and the sum of luminosity of the 43 sources, respectively. In order to evaluate the expected number of multiplets, as a function of the number of individual correlations, we perform several cycles of random extractions of 43 numbers, each one with a probability of extraction equal to wi. Each one of these extractions can be thought of as a simulated experiment. Then, we count the frequency of occurrence of a multiplet with at least two or three events from the same source5.
(24)where Li and Ltot, taken from Ackermann et al. (2016), are the luminosity of a single source and the sum of luminosity of the 43 sources, respectively. In order to evaluate the expected number of multiplets, as a function of the number of individual correlations, we perform several cycles of random extractions of 43 numbers, each one with a probability of extraction equal to wi. Each one of these extractions can be thought of as a simulated experiment. Then, we count the frequency of occurrence of a multiplet with at least two or three events from the same source5.
The outcome is illustrated in Fig. 6. With the expected number of individual correlations, shown as a vertical band in the figure, the probability of non observation of a multiplet from a single source is between 25−75%. Thus, the fact that we do not observe any multiplet is not yet an issue. The lack of such an observation would become significant if the expected number of events was instead of the order of about 15−20. Therefore, this test will become important when the current 6-yr statistics are doubled, or when we have 2−3 yr of data from IceCube-Gen2, due to the bigger effective area of the incoming detector described in Aartsen et al. (2014).
This analysis strongly depends on the class of objects considered and the absence of multiplets is not (yet) a problem assuming that high-energy cosmic neutrinos, above 0.2 PeV, are fully produced by BL Lacs. We refer to Murase & Waxman (2016) for a scenario in which, on the contrary, the absence of multiplets represents an issue even with the present IceCube data.
 |
Fig. 6 Probability of observing one multiplet as a function of the number of correlations. We consider the 43 BL Lacs contained in the 2FHL Fermi-LAT catalog in the region 0° ≤ δ ≤ 30°. The luminosities of BL Lacs are taken into account in the calculation of the expectations. The expected number of correlations, assuming that the BL Lacs are the main emitters of high-energy neutrinos (Eq. (23)), is indicated by the vertical band. |
5. Summary and discussion
The BL Lacs are potentially good candidates for emitters of high-energy neutrinos. The existing upper bound on neutrino flux emitted from the resolved blazars, obtained by the IceCube collaboration (Aartsen et al. 2017), is not incompatible with the assumption that the BL Lacs account for the full high-energy part of the spectrum, measured by means of the through-going muons above 0.2 PeV, described in Aartsen et al. (2016).
We have performed a refined test of this hypothesis. Among the through-going muon dataset, approximately two thirds of the events should be attributed to the astrophysical neutrinos. Assuming that these are produced in BL Lacs, we find that half of them, that is, approximately one third of the complete dataset, should be correlated with a BL Lac of the second Fermi-LAT catalog (2FHL). This leads us to expect some ten correlations with an uncertainty of about 25%. However we found that only the event number 6 has a BL Lac counterpart at 81% C.L. Even enlarging the search window, in order to reach 99% C.L., we find only three possible correlations. Generalizing, the average number of tracks that can be correlated with known BL Lacs is well below expectations.
This represents a serious issue for the hypothesis that the BL Lacs are the main sources of neutrinos above 0.2 PeV. Assuming that the systematic uncertainty (quoted in Aartsen et al. 2016 only for the most energetic event) is smaller than the statistical uncertainty, this hypothesis turns out to be disfavored at about 3.7σ. Moreover, the direction of event number 6, that shows a correlation within 81% C.L., is not well reconstructed, since the uncertainty on its direction is of the order of 10°. Therefore the correlation with the BL Lac could simply be a coincidence due to poor angular resolution. If the result discussed above is not due to a statistical fluctuation and there are no unaccounted systematic effects, the most plausible inference is that the BL Lacs are not the main emitters of the high-energy neutrinos above 0.2 PeV.
In view of the significance of this conclusion, it is important to discuss possible ways-out from the strong bound on the possible high-energy neutrino emission that we have obtained, that implies the conclusion that the observed neutrinos with energy above 200 TeV receive only a minor contribution from BL Lacs. We have shown that this hypothesis could be reconciled with the observations if the angular resolution of the tracks in IceCube was not as good as is quoted. The angular resolution of track-like events should be of ~4° to reconcile the expectations with the observations. The required departure is quite large and this makes this interpretation less plausible. For this reason, we are inclined to believe that this result argues in favor of the hypothesis that the high-energy neutrinos come from a population of faint neutrino emitters, meaning that most of the neutrino-emitting sources are not resolved with the present instrument; from a truly diffuse source (e.g., the halo of our Galaxy as argued in Taylor et al. 2014); or from a type of source where γ-rays are heavily reprocessed and the radiation shifted at much lower energies. We note that it is also not possible to exclude the theory that BL Lacs themselves, as identified by γ-ray astronomy, are the sources of the highest-energy neutrinos seen by IceCube, if the neutrinos are emitted in a significantly wider angular range; this would imply a drastic departure from the spine-layer model of Tavecchio et al. (2014), Tavecchio & Ghisellini (2015), Righi et al. (2017). Finally, we remark that we cannot even exclude the possibility that BL Lacs are good emitters of neutrinos below 0.2 PeV, since this energy region has not been investigated in the present work.
In this paper, we have also tested the probability of observing at least two events from the same source, assuming that BL Lacs are the high-energy neutrino emitters. Our result is that the non observation of multiplets does not represent an issue for the BL Lac hypothesis nowadays, but will become crucial in the future, especially after IceCube-Gen2 begins collecting data.
To conclude, some important remarks are in order: First, we highlight that our result complements and strengthens the recent upper bound on the blazar emission derived by IceCube in Aartsen et al. (2017). Second, we have argued that a correct understanding of the true spectrum of the extragalactic neutrinos is of utmost importance for multi-messenger astronomy. Third, we note that multi-messenger adopted in this work has great scientific potential and will allow us to proceed in the study of the origin of astrophysical neutrinos observed by IceCube, also for other types of astrophysical sources.
A featureless and hard power-law spectrum would suggest a pp production mechanism for neutrino production, rather than the usually expected pγ mechanism. However, it is not possible to say that the pγ mechanism is unavoidable for BL Lacs. Moreover, the spectrum is measured only in a small range of energy between 200 TeV and some PeV. The high energy part of the spectrum is not yet sensitive to mechanism of production, and this is not a critical aspect of the BL Lac hypothesis. We refer to Winter (2013), Hummer et al. (2010) for a detailed discussion of the photohadronic interaction.
We note that we do not need to introduce a proportionality coefficient between the flux of γ-rays and the flux of neutrinos, since we are only interested in the fraction of visible flux with respect to the theoretical (expected) total flux. E.g., in Righi et al. (2017) the almost constant coefficient φν = 0.46φγ is obtained in a BL Lac scenario, but it disappears from the ratio of Eq. (6).
We note that the two correlations between the through-going muon number 6 and the BL Lacs are not present in this table, since the angular distance between them is larger than 3°, using the best fit coordinates of the neutrino directions. However, the very large uncertainties would not permit us to rule out the correlations between them.
Acknowledgments
We thank E. Resconi, S. Celli, M. Spurio, V. Kudryavtsev, A. Esmaili, M. Tavani, F. Tavecchio, and C. Righi for precious discussions.
References
- Aartsen, M. G., et al. (IceCube) 2014 [arXiv:1412.5106] [Google Scholar]
- Aartsen, M. G., Abraham, K., Ackermann, M., et al. (IceCube) 2016, ApJ, 833, 3 [Google Scholar]
- Aartsen, M. G., Abraham, K., Ackermann, M., et al. (IceCube) 2017, ApJ, 835, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2016, ApJS, 222, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Romani, R. W., Gasparrini, D., et al. 2014, Astrppys. J., 780, 73 [Google Scholar]
- Atoyan, A., & Dermer, C. D. 2001, Phys. Rev. Lett., 87, 221102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Esmaili, A., Palladino, A., & Vissani, F. 2016, EPJ Web Conf., 116, 11002 [CrossRef] [EDP Sciences] [Google Scholar]
- Essey, W., Kalashev, O. E., Kusenko, A., & Beacom, J. F. 2010, Phys. Rev. Lett., 104, 141102 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, S., Pohl, M., & Winter, W. 2017, ApJ, 843, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Glüsenkamp, T. 2016, EPJ Web Conf., 121, 05006 [CrossRef] [EDP Sciences] [Google Scholar]
- Halzen, F., & Kheirandish, A. 2016, ApJ, 831, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Hummer, S., Ruger, M., Spanier, F., & Winter, W. 2010, ApJ, 721, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Kalashev, O. E., Kusenko, A., & Essey, W. 2013, Phys. Rev. Lett., 111, 041103 [NASA ADS] [CrossRef] [Google Scholar]
- Miranda, L. S., de León, A. R., & Sahu, S. 2016, Eur. Phys. J., C76, 402 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murase, K., & Waxman, E. 2016, Phys. Rev. D, 94, 103006 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Inoue, Y., & Dermer, C. D. 2014, Phys. Rev. D, 90, 023007 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P. 2007, Astrophys. Space Sci., 309, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., & Resconi, E. 2014, MNRAS, 443, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Resconi, E., Giommi, P., Arsioli, B., & Chang, Y. L. 2016, MNRAS, 457, 3582 [NASA ADS] [CrossRef] [Google Scholar]
- Palladino, A., & Vissani, F. 2016, ApJ, 826, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Palladino, A., Spurio, M., & Vissani, F. 2016, JCAP, 1612, 045 [NASA ADS] [CrossRef] [Google Scholar]
- Protheroe, R. J. 1997, ASP Conf. Ser., 121, 585 [NASA ADS] [Google Scholar]
- Resconi, E., Coenders, S., Padovani, P., Giommi, P., & Caccianiga, L. 2017, MNRAS, 468, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Righi, C., Tavecchio, F., & Guetta, D. 2017, A&A, 598, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spurio, M. 2014, Phys. Rev. D, 90, 103004 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W. 1979, ApJ, 228, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2015, MNRAS, 451, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Ghisellini, G., & Guetta, D. 2014, ApJ, 793, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. M., Gabici, S., & Aharonian, F. 2014, Phys. Rev. D, 89, 103003 [NASA ADS] [CrossRef] [Google Scholar]
- Turley, C. F., Fox, D. B., Murase, K., et al. 2016, ApJ, 833, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, W. 2013, Phys. Rev. D, 88, 083007 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Number of correlations as a function of k and the corresponding confidence level (C.L.).
All Figures
 |
Fig. 1 Scheme of the present investigation: we assume that a part of the high energy neutrino signal seen by IceCube includes extragalactic neutrinos. We investigate whether the extragalactic emission can be attributed largely or fully to BL Lac emission, relying on the fact that a large fraction of BL Lacs, as discussed in Sect. 2, is observed by Fermi-LAT. |
| In the text | |
 |
Fig. 2 Values for the 29 through-going events of the average angular resolution, defined as described in Eq. (2). We note the two outliers, discussed in the text. |
| In the text | |
 |
Fig. 3 Map, in Galactic coordinates, of the γ-ray sky observed by Fermi-LAT, from Ackermann et al. (2016). The red points indicate the 29 through-going muons, with a deposited energy above 200 TeV, observed by IceCube over 6 yr; their angular uncertainties are not represented in this figure, but are taken into account in the calculations. The brown lines represent intervals of declination of 30°. |
| In the text | |
 |
Fig. 4 The orange line is the PDF of the observed number of correlations. In blue line we show the expected number of correlations, assuming that the BL Lacs are the main emitters of high-energy neutrinos, discussed after Eq. (15). |
| In the text | |
 |
Fig. 5 Number of correlations found as a function of the angular distance between the position of the neutrino events and the position of the BL Lac. Within 1 degree, only 1 correlation has been observed. The horizontal band shows the expectations given in Eq. (15). |
| In the text | |
 |
Fig. 6 Probability of observing one multiplet as a function of the number of correlations. We consider the 43 BL Lacs contained in the 2FHL Fermi-LAT catalog in the region 0° ≤ δ ≤ 30°. The luminosities of BL Lacs are taken into account in the calculation of the expectations. The expected number of correlations, assuming that the BL Lacs are the main emitters of high-energy neutrinos (Eq. (23)), is indicated by the vertical band. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


