| Issue |
A&A
Volume 604, August 2017
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629934 | |
| Published online | 03 August 2017 | |
Flattening and surface-brightness of the fast-rotating star δ Persei with the visible VEGA/CHARA interferometer
1 Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, UMR 7293, 06304 Nice Cedex 4, France
e-mail: mounir.challouf@oca.eu
2 Laboratoire Dynamique Moléculaire et Matériaux Photoniques, UR11ES03, Université de Tunis/ENSIT, Tunis, Tunisie
3 Université Lyon1, ENS Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR 5574, 69230 Saint-Genis-Laval, France
4 CHARA Array, Mount Wilson Observatory, 91023, Mount Wilson, Pasadena, CA 91109, USA
5 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille), UMR 7326, 13388 Marseille, France
Received: 20 October 2016
Accepted: 26 April 2017
Context. Rapid rotation is a common feature for massive stars, with important consequences on their physical structure, flux distribution and evolution. Fast-rotating stars are flattened and show gravity darkening (non-uniform surface intensity distribution). Another important and less studied impact of fast-rotation in early-type stars is its influence on the surface brightness colour relation (hereafter SBCR), which could be used to derive the distance of eclipsing binaries.
Aims. The purpose of this paper is to determine the flattening of the fast-rotating B-type star δ Per using visible long-baseline interferometry. A second goal is to evaluate the impact of rotation and gravity darkening on the V − K colour and surface brightness of the star.
Methods. The B-type star δ Per was observed with the VEGA/CHARA interferometer, which can measure spatial resolutions down to 0.3 mas and spectral resolving power of 5000 in the visible. We first used a toy model to derive the position angle of the rotation axis of the star in the plane of the sky. Then we used a code of stellar rotation, CHARRON, in order to derive the physical parameters of the star. Finally, by considering two cases, a static reference star and our best model of δ Per, we can quantify the impact of fast rotation on the surface brightness colour relation (SBCR).
Results. We find a position angle of 23 ± 6 degrees. The polar axis angular diameter of δ Per is θp = 0.544 ± 0.007 mas, and the derived flatness is r = 1.121 ± 0.013. We derive an inclination angle for the star of i = 85+ 5-20 degrees and a projected rotation velocity Vsini = 175+ 8-11 km s-1 (or 57% of the critical velocity). We find also that the rotation and inclination angle of δ Per keeps the V − K colour unchanged while it decreasing its surface-brightness by about 0.05 mag.
Conclusions. Correcting the impact of rotation on the SBCR of early-type stars appears feasible using visible interferometry and dedicated models.
Key words: stars: early-type / stars: rotation / methods: data analysis / instrumentation: interferometers / techniques: interferometric
© ESO, 2017
1. Introduction
The equilibrium structure of a rotating star is achieved by the interplay of three forces: the usual gravity and force of pressure, and an additional one, the centrifugal force. Because this centrifugal force depends on latitude (zero at the poles and maximum at the equator) the stellar photosphere is not spherical but becomes flattened, resembling a two-axis ellipsoid (see for example Kopal 1987). Rapid rotation also induces a gravity darkening, that is a flux (effective temperature) gradient from the poles to the equator of the star (von Zeipel 1924). Both deformation and gravity darkening affect the distribution of the surface brightness at the star photosphere (Challouf et al. 2015a,b). Another consequence linked to the existence of gravity darkening and rotation is the creation inside the star of a slow flow of matter (e.g. Rieutord 2006). This flow has a multitude effect on the star properties, such as: i) suppling the core with hydrogen and thus increase the lifetime of the star; ii) enriching the outer layers with metals; iii) transporting the angular moment of the core to the surface and thus increase the rotational velocity of the photosphere (Meynet & Maeder 2000; Ekström et al. 2008).
Fast rotating stars and their environments are known to have an impact on the calibration of SBCR of early-type stars, limiting the precision on the relation to around 0.16 mag (Challouf et al. 2014b). The SBCR is necessary to derive the distance of early-type eclipsing binaries (O, B, A), which are much brighter and thus easier to detect than late-type eclipsing binaries (Pietrzyński et al. 2009; Mochejska et al. 2001; Vilardell et al. 2006; Pawlak et al. 2013). However, to achieve 1% precision in term of distances or 0.02 mag of precision on the SBCR, one has to consider massive star properties, such as rotation. In this context δ Per is a good target to study the effects of the rapid rotation.
In Sect. 2, we present our VEGA/CHARA observations and data processing and show that the fast rotating star δ Per is currently in its B-type phase. In Sect. 3, we analyze our data with different models and in Sect. 4, we compare the V − K colour and surface brightness of a static reference star (without flattening) with our best model of δ Per.
2. VEGA/CHARA observations of δ Per
The Center for High Angular Resolution Astronomy (CHARA) array operates in the visible and the near-infrared (ten Brummelaar et al. 2005). Located at the Mount Wilson Observatory, north of Los Angeles (California, USA), the CHARA Array consists of six 1-m telescopes in a non-redundant Y-shaped configuration that offers 15 different baselines between 34 and 331 m. The Visible spEctroGraph and polArimeter (VEGA; Mourard et al. 2009) is one of the beam combiners installed on the CHARA Array. It works in the visible and can combine up to four different telescopes (Mourard et al. 2011). With the longest baseline, in the visible domain, one can reach a spatial resolution of 0.3 mas (and 1.6 mas in the near-infrared).
Journal of observations.
Reference stars and their parameters, including the mV and mk magnitudes, and the predicted uniform disc angular diameter (in mas) in the R band.
δ Per was observed with VEGA/CHARA over a three year period from August 2012 to December 2014 (Table 1). An interferometric observation requires the acquisition of a number of calibrators before and after the target (Challouf et al. 2012, 2014a). To provide a better estimation of the transfer function during the observations of the target, each measurement was calibrated using stars listed in Table 2 with a sequence C-T-C (C referring to the calibrator and T to the science target), several times in a row when possible. These calibrators were selected using the SearchCal1 software developed by the Jean-Marie Mariotti Center (JMMC; Bonneau et al. 2006). Six different telescopes configurations taken at different hour angles allowed us to obtain measurements well distributed over the (u, v) plane (see Table 1 and Fig. 1).
 |
Fig. 1 (u − v) plane coverage of VEGA observations. |
We also used two spectral bands of Δλ = 20 nm centered on λ = 715 nm and λ = 735 nm, in the medium spectral resolving power mode of VEGA (R = 5000). In Fig 2, we show also one of our Hα line profile of δ Per. This profile is in absorption, without any signature of a circumstellar disc, which means that δ Per was not active at the time of observations (i.e. between 2012 and 2014), which is consistent with the ELODIE2 spectra obtained in 1997. Thus our observations show that δ Per is a B-type star, which allows an accurate determination of its rotation (i.e. without contamination by a circumstellar disc).
Our VEGA measurements corresponds to 30 blocks of observations, each block containing 2500 images of ten milliseconds. For each block, the raw squared visibility is estimated using the auto-correlation mode (Mourard et al. 2009, 2011). The sequence of calibrators permits the estimate of the transfer function and then allows derivation the calibrated visibility of the target (Vtarget). The visibility systematic uncertainties that stem from the uncertainty on the reference stars are calculated according to the method described in Mourard et al. (2012) and presented in details in Appendix A. In our case, in the worse situation, we found a systematic error of 0.008 compared to a statistical error of 0.062. Therefore we consider these systematic errors as negligible in our study. Fabricius & Makarov (2000) shows that δ Per is a binary star. It has an optical companion with an apparent magnitude of +6.17 at an angular separation of 0.330 arcsec and a position angle of 221°. Given the large difference of magnitude and the separation between the two components, the binarity of δ Per does not impact our data.
3. Modelling of δ Per
3.1. A toy model
The calibrated visibilities obtained for each observation are used to constrain a model of uniform elongated disc, with only three geometrical parameters: the minor axis diameter or polar diameter 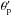 (apparent diameter), the elongation ratio r′ defined along the major axis as the ratio between the major apparent diameter and the minor one, and the position angle φ of the rotation axis of the star (i.e. the minor axis), equal to the angle between the positive vertical semi-axis (i.e. north direction) and the major axis towards to the positive horizontal semi-axis (i.e. east direction). This is performed using the LITpro3 software developed by the JMMC (Tallon-Bosc et al. 2008). We find
(apparent diameter), the elongation ratio r′ defined along the major axis as the ratio between the major apparent diameter and the minor one, and the position angle φ of the rotation axis of the star (i.e. the minor axis), equal to the angle between the positive vertical semi-axis (i.e. north direction) and the major axis towards to the positive horizontal semi-axis (i.e. east direction). This is performed using the LITpro3 software developed by the JMMC (Tallon-Bosc et al. 2008). We find 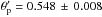 mas, φ = 23 ± 6 degrees and r′ = 1.115 ± 0.024 (with a reduced χ2 of 2.7, while we obtain 3.8 if we fit a uniform disc to the data). The elongation of δ Per is thus detected (at 5σ) and refined in next section using a dedicated model.
mas, φ = 23 ± 6 degrees and r′ = 1.115 ± 0.024 (with a reduced χ2 of 2.7, while we obtain 3.8 if we fit a uniform disc to the data). The elongation of δ Per is thus detected (at 5σ) and refined in next section using a dedicated model. 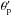 is consistently lower than the mean spectrophotometric diameter of 0.583 ± 0.013 mas found by Zorec et al. (2009), while the equatorial diameter (0.611 ± 0.022 mas) is indeed larger. The position angle φ, which is uncorrelated with the two other parameters, is used in the next subsection in order to constrain the dedicated model of δ Per.
is consistently lower than the mean spectrophotometric diameter of 0.583 ± 0.013 mas found by Zorec et al. (2009), while the equatorial diameter (0.611 ± 0.022 mas) is indeed larger. The position angle φ, which is uncorrelated with the two other parameters, is used in the next subsection in order to constrain the dedicated model of δ Per.
3.2. A fast rotating star model: CHARRON
The second step of the modelling was done with the code for high angular resolution of rotating objects in nature (CHARRON) described by Domiciano de Souza et al. (2012a,b, 2002). The stellar photospheric shape is given by the commonly adopted Roche approximation, which is well adapted to non-degenerate, fast-rotating stars. The effective temperature (Teff) at the surface of fast rotators is not uniform (depending on the colatitude θ) owing to the decreasing effective gravity (geff – gravitation plus centrifugal acceleration) from the poles to the equator (gravity darkening effect). We modelled the gravity darkening as a generalized form of the von Zeipel law (von Zeipel 1924): 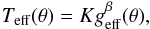 (1)where β is the gravity darkening coefficient. von Zeipel (1924) derived a theoretical value of 0.25 for early-type stars with radiative external layers and pressure, only depending on the density (barotropic approximation). However, recent interferometric observations have measured somewhat lower values for β (e.g. Che et al. 2011; Domiciano de Souza et al. 2014). The value of 0.20 seems a good compromise between the theoretical value of von Zeipel and the values measured from interferometric observations of fast-rotating stars and also with theoretical models of gravity darkening (e.g. Espinosa Lara & Rieutord 2011; Claret 2012). We thus considered β = 0.20 for our model of δ Per.
(1)where β is the gravity darkening coefficient. von Zeipel (1924) derived a theoretical value of 0.25 for early-type stars with radiative external layers and pressure, only depending on the density (barotropic approximation). However, recent interferometric observations have measured somewhat lower values for β (e.g. Che et al. 2011; Domiciano de Souza et al. 2014). The value of 0.20 seems a good compromise between the theoretical value of von Zeipel and the values measured from interferometric observations of fast-rotating stars and also with theoretical models of gravity darkening (e.g. Espinosa Lara & Rieutord 2011; Claret 2012). We thus considered β = 0.20 for our model of δ Per.
 |
Fig. 2 VEGA/CHARA normalized spectrum of δ Per (R ≃ 5000) around the Hα spectral line. |
 |
Fig. 3 Calibrated VEGA/CHARA squared visibilities are plotted as a function of the spatial frequency (red points). The open black circles are the synthetic visibilities obtained from the FFT of the image of δ Per obtained with the CHARRON code. The bottom panel shows the residuals of the visibilities. |
The K quantity is the proportionality constant between Teff(θ) and geff(θ). It depends on the stellar physical input parameters of the model, which are: the mean effective temperature (Teff), the mass (M), and the equatorial radius (Req). Table 3 lists the fundamental parameters considered as an input to the model, together with their corresponding references. In addition to these parameters, the orientation in the plane of the sky (φ) was fixed to 23 degrees as found in Sect. 3.1 using the toy model. We basically fitted two parameters: the inclination (i) and the rotation velocity Vrot. This was done by considering different values of i∈ [0°, 90°] and Vrot∈ [0Vc, 0.95Vc] with steps of 5° and 3 km s-1, respectively. For each model, we computed an intensity distribution of the star using the ATLAS9 stellar atmosphere models (Kurucz 1979) and the spectral synthesis code SYNSPEC (Hubeny & Lanz 2011). To compare the theoretical and observed calibrated squared visibilities, we calculate the fast Fourier transform (FFT hereafter) of this intensity distribution following the theorem of Zernike-Van Cittert (van Cittert 1934; Zernike 1938). We calculate for each model a reduced χ2 and find that the best parameters (with a reduced χ2 of 2.8) are: 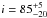 degrees and
degrees and 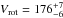 km s-1 (or 57% of the critical velocity). The derived projected rotational velocity is consistent with previous studied: Vrotsini = 200 ± 40 km s-1 (Slettebak et al. 1975; Wolff et al. 1982) and 190 ± 24 km s-1 (Abt et al. 2002). The CHARRON model provides the true parameters (i.e. not apparent), taking into account the gravity darkening. We find: θp = 0.544 ± 0.007 mas and r = 1.121 ± 0.013. The synthetic intensity distribution of the star with the observed and computed calibrated squared visibilities are plotted in Fig. 3. The final parameter values for the best-fit model are presented in Table 3. From the θp and θe (in mas) and the parallax π (in second of arc), we estimated the linear radius and its error by using a simple Monte Carlo simulation:
km s-1 (or 57% of the critical velocity). The derived projected rotational velocity is consistent with previous studied: Vrotsini = 200 ± 40 km s-1 (Slettebak et al. 1975; Wolff et al. 1982) and 190 ± 24 km s-1 (Abt et al. 2002). The CHARRON model provides the true parameters (i.e. not apparent), taking into account the gravity darkening. We find: θp = 0.544 ± 0.007 mas and r = 1.121 ± 0.013. The synthetic intensity distribution of the star with the observed and computed calibrated squared visibilities are plotted in Fig. 3. The final parameter values for the best-fit model are presented in Table 3. From the θp and θe (in mas) and the parallax π (in second of arc), we estimated the linear radius and its error by using a simple Monte Carlo simulation: 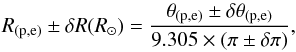 (2)we obtain finally a polar radius of Rp = 9.25 ± 1.60R⊙ and an equatorial radius of Re = 10.39 ± 1.60R⊙. We note that the uncertainty on the radius is dominated by the parallax uncertainty.
(2)we obtain finally a polar radius of Rp = 9.25 ± 1.60R⊙ and an equatorial radius of Re = 10.39 ± 1.60R⊙. We note that the uncertainty on the radius is dominated by the parallax uncertainty.
 |
Fig. 4 Intensity map of the best CHARRON model of δ Per. The flatness of the star is of r = 1.121 with an inclination angle of i = 85° and an rotation velocity of 57% of Vc. The image is given in units of the equatorial radius, 0.611X0.611 mas. |
Physical parameters of δ Per.
4. Impact of the rotation on the V – K colour and surface brightness of δ Per
We derived the V − K and Sv following the methodology described below and detailed in Challouf et al. (2014c), Challouf et al. (2015b). The surface brightness is defined as Sλ = mλ + 5log θLD, with mλ the absolute visual magnitude and θLD the limb-darkened angular diameter of the star. The photometric magnitudes in the V and K bands are derived from the CHARRON model, following the method described in Domiciano de Souza et al. (2014). The squared visibilities (V2) obtained from the intensity distribution (previous section) are then interpreted using a simple uniform disc model. The equivalent uniform disc angular diameter θUD was then converted into a limb-darkened disc using the relation of Hanbury Brown et al. (1974).
The value of the surface-brightness is, by construction, biased by the rotation of the star. The V − K colour is an output of the model, and is also impacted by the rotation. This procedure is done for our best model of δ Per indicated in Fig. 5. Also indicated in Fig. 5 is the corresponding static model (i.e. without rotation) considering the physical input parameters (Table 3). We can make the following specific remarks:
-
1.
The static and the best model of δ Per have the same V − K colour.
-
2.
The rotation and inclination of δ Per decrease its surface-brightness (compared to a static model) by about 0.05 mag.
-
3.
This bias of 0.05 mag found for δ Per is much lower than the 1σ intrinsic dispersion (or 0.16 mag) found on the SBCR by Challouf et al. (2014b), and is consistent with the bias on the SBCR (offset and dispersion) due to rotation estimated in Challouf et al. (2015b).
 |
Fig. 5 The surface brightness for the CHARRON model is plotted versus the V − K colour in order to illustrate the impact of the rotation and inclination (see the text). |
5. Conclusions
We derive here, for the first time, the flatness of δ Per (r = 1.121 ± 0.013) using the visible VEGA/CHARA interferometer and the CHARRON model. The derived rotation velocity is 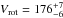 km s-1 (or 57% of the critical velocity). We find that the rotation of δ Per (combined with its inclination angle of
km s-1 (or 57% of the critical velocity). We find that the rotation of δ Per (combined with its inclination angle of 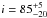 degrees) has no impact on the derived V − K colour while it reduces its surface brightness of 0.05 mag. We conclude that δ Per, as many fast rotators should not be used in order to calibrate the SBCR at the 0.05 mag level (or 2.5%) for early-type stars (Challouf et al. 2015b), unless a correction in the V − K colour and the surface brightness is done based on a dedicated modelling.
degrees) has no impact on the derived V − K colour while it reduces its surface brightness of 0.05 mag. We conclude that δ Per, as many fast rotators should not be used in order to calibrate the SBCR at the 0.05 mag level (or 2.5%) for early-type stars (Challouf et al. 2015b), unless a correction in the V − K colour and the surface brightness is done based on a dedicated modelling.
Available at http://www.jmmc.fr/searchcal
Available at http://atlas.obs-hp.fr/elodie/
Available at http://www.jmmc.fr/litpro
Available at http://www.jmmc.fr/aspro
Available at http://www.jmmc.fr/searchcal
Available at http://cdsweb.u-strasbg.fr/
LITpro software available at http://www.jmmc.fr/litpro
Available at http://oidb.jmmc.fr
Acknowledgments
The authors acknowledge financial support from “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France. This work is based upon observations obtained with the Georgia State University Center for High Angular Resolution Astronomy Array at Mount Wilson Observatory. The CHARA Array is supported by the National Science Foundation under Grant No. AST-1211929. Institutional support has been provided from the GSU College of Arts and Sciences and the GSU Office of the Vice President for Research and Economic Development. This research has made use of the Jean-Marie Mariotti Center Aspro service1, and the electronic bibliography maintained by the NASA/ADS system. This research has made use of the Jean-Marie Mariotti Center SearchCal service2 co-developed by FIZEAU and LAOG/IPAG, and CDS Astronomical Databases SIMBAD and VIZIER3. This research has made use of the Jean-Marie Mariotti Center LITpro service co-developed by CRAL, IPAG, and LAGRANGE4. This research has made use of the Jean-Marie Mariotti Center OiDB service5.
References
- Abt, H. A., Levato, H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Bonneau, D., Clausse, J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Challouf, M., Nardetto, N., Mourard, D., Aroui, H., & Chesneau, O. 2012, in SF2A-2012: Proc. Annual meeting French Society of Astronomy and Astrophysics, eds. S. Boissier, P. de Laverny, N. Nardetto, et al., 299 [Google Scholar]
- Challouf, M., Nardetto, N., Mourard, D., Aroui, H., & Delaa, O. 2014a, in SF2A-2014: Proc. Annual meeting French Soc. Astron. Astrophys., eds. J. Ballet, F. Martins, F. Bournaud, R. Monier, & C. Reylé, 471 [Google Scholar]
- Challouf, M., Nardetto, N., Mourard, D., et al. 2014b, A&A, 570, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Challouf, M., Nardetto, N., De Souza, A., et al. 2014c, Proc. Int. Astron. Union, 9, 288 [CrossRef] [Google Scholar]
- Challouf, M., Nardetto, N., Domiciano de Souza, A., et al. 2015a, IAU Symp., 307, 288 [NASA ADS] [Google Scholar]
- Challouf, M., Nardetto, N., Domiciano de Souza, A., et al. 2015b, A&A, 579, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Che, X., Monnier, J. D., Zhao, M., et al. 2011, ApJ, 732, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2012, A&A, 538, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Code, A. D., Bless, R. C., Davis, J., & Brown, R. H. 1976, ApJ, 203, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Domiciano de Souza, A., Vakili, F., Jankov, S., Janot-Pacheco, E., & Abe, L. 2002, A&A, 393, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Hadjara, M., Vakili, F., et al. 2012a, A&A, 545, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Zorec, J., & Vakili, F. 2012b, in SF2A-2012: Proc. Annual meeting French Soc. Astron. Astrophys., eds. S. Boissier, P. de Laverny, N. Nardetto, R. Samadi, D. Valls-Gabaud, & H. Wozniak, 321 [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Moser Faes, D., et al. 2014, A&A, 569, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Meynet, G., Chiappini, C., Hirschi, R., & Maeder, A. 2008, A&A, 489, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabricius, C., & Makarov, V. V. 2000, A&A, 356, 141 [NASA ADS] [Google Scholar]
- Hanbury Brown, R., Davis, J., Lake, R. J. W., & Thompson, R. J. 1974, MNRAS, 167, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 2011, Astrophysics Source Code Library [record ascl: 1109.022] [Google Scholar]
- Kopal, Z. 1987, Ap&SS, 133, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Mochejska, B. J., Kaluzny, J., Stanek, K. Z., & Sasselov, D. D. 2001, AJ, 122, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Mourard, D., Clausse, J. M., Marcotto, A., et al. 2009, A&A, 508, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mourard, D., Bério, P., Perraut, K., et al. 2011, A&A, 531, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mourard, D., Challouff, M., Ligi, R., et al. 2012, in Performance, results, and prospects of the visible spectograph VEGA on CHARA, SPIE Conf. Ser., 8445, 84450K [Google Scholar]
- Pawlak, M., Graczyk, D., Soszyński, I., et al. 2013, Acta Astron., 63, 323 [NASA ADS] [Google Scholar]
- Pietrzyński, G., Thompson, I. B., Graczyk, D., et al. 2009, ApJ, 697, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M. 2006, A&A, 451, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slettebak, A., Collins, II, G. W., Parkinson, T. D., Boyce, P. B., & White, N. M. 1975, ApJS, 29, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Tallon-Bosc, I., Tallon, M., Thiébaut, E., et al. 2008, in LITpro: a model Fitting software for optical interferometry, SPIE Conf., 7013, 7013J [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Underhill, A. B., Divan, L., Prevot-Burnichon, M.-L., & Doazan, V. 1979, MNRAS, 189, 601 [NASA ADS] [CrossRef] [Google Scholar]
- van Cittert, P. H. 1934, Physica, 1, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Vilardell, F., Ribas, I., & Jordi, C. 2006, A&A, 459, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Winzer, P. J. 2000, Rev. Sci. Instr., 71, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, S. C., Edwards, S., & Preston, G. W. 1982, ApJ, 252, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Zernike, F. 1938, Physica, 5, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Zorec, J., Cidale, L., Arias, M. L., et al. 2009, A&A, 501, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Estimation of the error on the calibrated squared visibilities
The squared visibility of the target may be written as follows: 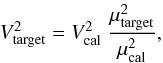 (A.1)where
(A.1)where 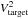 and
and 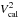 are the true squared visibility of the target and the calibrator respectively, and
are the true squared visibility of the target and the calibrator respectively, and 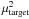 and
and 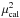 their measured squared visibility. This equation assumes the constancy of the transfer function between the observations of the target and the calibrator.
their measured squared visibility. This equation assumes the constancy of the transfer function between the observations of the target and the calibrator.
The three terms of the right side of the equality are independent random variables. Whereas the product of two random variables, as 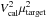 , is calculable, the quotient of two random variables, here
, is calculable, the quotient of two random variables, here 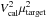 by
by 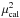 , follows a law which does not have moments: neither the mean nor the variance is calculable and both must be estimated approximately. The approximation can be of a different order, depending on the value of the signal-to-noise ratio (S/N) of the denominator, meaninf here on
, follows a law which does not have moments: neither the mean nor the variance is calculable and both must be estimated approximately. The approximation can be of a different order, depending on the value of the signal-to-noise ratio (S/N) of the denominator, meaninf here on 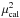 . The S/N of a random variable is equal to the ratio of its mean on its standard deviation (or square root of its variance). To simplify the writing, we call α,β,γ the S/N of
. The S/N of a random variable is equal to the ratio of its mean on its standard deviation (or square root of its variance). To simplify the writing, we call α,β,γ the S/N of 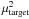 ,
, 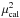 and
and 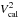 :
: 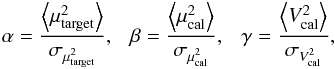 <> denoting the mean and σ the standard deviation. Using the study of Winzer (2000) and the independence of the variables (cancelling covariance-terms), we found, if β is larger than four, the following second order approximation with about 1% accuracy of both first moments of the quotient of Eq. (A.1):
<> denoting the mean and σ the standard deviation. Using the study of Winzer (2000) and the independence of the variables (cancelling covariance-terms), we found, if β is larger than four, the following second order approximation with about 1% accuracy of both first moments of the quotient of Eq. (A.1): ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:V2target_mean} &&\left\langle V^2_{\rm target} \right\rangle ~\simeq ~\left\langle V^2_{\rm cal} \right\rangle^2 ~\frac{\left\langle \mu^2_{\rm target} \right\rangle^2}{\left\langle \mu^2_{\rm cal} \right\rangle^2}\left[1 +\frac{1}{\beta^2}\right] , \\ \label{eq:V2target_var} &&{\sigma^2_{V^2_{\rm target}}}~ \simeq~~ \left\langle V^2_{\rm target} \right\rangle^2 \left[\frac{1}{\alpha^2}+\frac{1}{\beta^2}+\frac{1}{\gamma^2} +\frac{1}{\beta^2\gamma^2} -\frac{1}{\beta^4}\right] , \end{eqnarray}](/articles/aa/full_html/2017/08/aa29934-16/aa29934-16-eq104.png) Eq. (A.3) shows that the quadratic error on
Eq. (A.3) shows that the quadratic error on 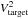 may be written as the sum of two terms, one of those being independent of γ, which we call statistic quadratic error. The second term is named systematic quadratic error:
may be written as the sum of two terms, one of those being independent of γ, which we call statistic quadratic error. The second term is named systematic quadratic error: ![\appendix \setcounter{section}{1} \begin{eqnarray} &&{\sigma^2_{V^2_{\rm target}}}_{\rm stat} ~ \simeq~ \left\langle V^2_{\rm cal} \right\rangle^2 ~\frac{\left\langle \mu^2_{\rm target} \right\rangle^2}{\left\langle \mu^2_{\rm cal} \right\rangle^2}~\left[\frac{1}{\alpha^2}+\frac{1}{\beta^2}-\frac{1}{\beta^4}\right],\\ &&{\sigma^2_{V^2_{\rm target}}}_{\rm syst} ~ \simeq~ \left\langle V^2_{\rm cal} \right\rangle^2 ~\frac{\left\langle \mu^2_{\rm target} \right\rangle^2}{\left\langle \mu^2_{\rm cal} \right\rangle^2}~\frac{1}{\gamma^2} \left[1 +\frac{1}{\beta^2}\right] . \end{eqnarray}](/articles/aa/full_html/2017/08/aa29934-16/aa29934-16-eq106.png)
Appendix A.1: Influence of the true visibility of the calibrator
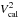 is a statistical variable whose mean is the squared visibility related to the supposed geometrical shape of the calibrator. If this is a uniform disc of diameter θUD, the relation is:
is a statistical variable whose mean is the squared visibility related to the supposed geometrical shape of the calibrator. If this is a uniform disc of diameter θUD, the relation is: 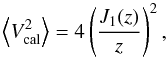 (A.6)with z = π⟨θUD⟩B/λ where B is the baseline and λ the wavelength. ⟨θUD⟩ is given for example by SearchCal (Bonneau et al. 2006) after a polynomial fit in the (angular diameter, colour indices) space with a standard deviation at one σ. We have numerically shown that, if γ is larger than four, γ is proportional to the SNR of θUD as follows:
(A.6)with z = π⟨θUD⟩B/λ where B is the baseline and λ the wavelength. ⟨θUD⟩ is given for example by SearchCal (Bonneau et al. 2006) after a polynomial fit in the (angular diameter, colour indices) space with a standard deviation at one σ. We have numerically shown that, if γ is larger than four, γ is proportional to the SNR of θUD as follows: 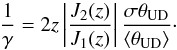 (A.7)Equations (A.6) and (A.7) are then inserted into the final equations. We may verify that if the calibrator is well known, i.e. with a small uncertainty, 1 /γ2 strongly decreases and the systematic quadratic error becomes negligible.
(A.7)Equations (A.6) and (A.7) are then inserted into the final equations. We may verify that if the calibrator is well known, i.e. with a small uncertainty, 1 /γ2 strongly decreases and the systematic quadratic error becomes negligible.
Appendix A.2: Extension of the formalism to the case of several calibrators
An interferometric observation of a target classically needs the acquisition of a number n of calibrators sequences. They can be from the same calibrator but observed before and after the target, or from several different objects of reference. For estimating the calibrated 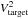 , we choose to consider the weighted mean of the estimators given by each calibrator individually, the weight beeing dependent on the statistic quadratic errors only:
, we choose to consider the weighted mean of the estimators given by each calibrator individually, the weight beeing dependent on the statistic quadratic errors only: 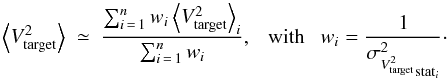 (A.8)For the square standard deviation, taking care of always distinguish the systematic errors from the statistic ones yields a total quadratic error equal to the sum of both following terms:
(A.8)For the square standard deviation, taking care of always distinguish the systematic errors from the statistic ones yields a total quadratic error equal to the sum of both following terms: 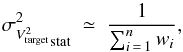 (A.9)
(A.9)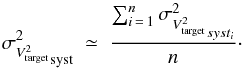 (A.10)Equations (A.8)−(A.10) are inserted into the VEGA post-reduction tools. The latter warn the user of their limit of application: if β or γ is smaller than four, the user is informed that the uncertainty on respectively, the measurements or the diameter of the calibrator, is not sufficient to be confident about the value of the calibrated squared visibility.
(A.10)Equations (A.8)−(A.10) are inserted into the VEGA post-reduction tools. The latter warn the user of their limit of application: if β or γ is smaller than four, the user is informed that the uncertainty on respectively, the measurements or the diameter of the calibrator, is not sufficient to be confident about the value of the calibrated squared visibility.
All Tables
Reference stars and their parameters, including the mV and mk magnitudes, and the predicted uniform disc angular diameter (in mas) in the R band.
All Figures
 |
Fig. 1 (u − v) plane coverage of VEGA observations. |
| In the text | |
 |
Fig. 2 VEGA/CHARA normalized spectrum of δ Per (R ≃ 5000) around the Hα spectral line. |
| In the text | |
 |
Fig. 3 Calibrated VEGA/CHARA squared visibilities are plotted as a function of the spatial frequency (red points). The open black circles are the synthetic visibilities obtained from the FFT of the image of δ Per obtained with the CHARRON code. The bottom panel shows the residuals of the visibilities. |
| In the text | |
 |
Fig. 4 Intensity map of the best CHARRON model of δ Per. The flatness of the star is of r = 1.121 with an inclination angle of i = 85° and an rotation velocity of 57% of Vc. The image is given in units of the equatorial radius, 0.611X0.611 mas. |
| In the text | |
 |
Fig. 5 The surface brightness for the CHARRON model is plotted versus the V − K colour in order to illustrate the impact of the rotation and inclination (see the text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


