EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 603 (July 2017) A&A, 603 (2017) A9 Full HTML
Free Access
Issue
A&A
Volume 603, July 2017
Article Number A9
Number of page(s) 7
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201629610
Published online 30 June 2017

© ESO, 2017

1. Introduction

The r-mode instability is of great astrophysical importance, since it occurs in all rotating perfect fluid neutron stars (Andersson 1998; Friedman & Morsink 1998). This instability is driven by gravitational radiation via the Chandrasekhar-Friedman-Schutz mechanism (Chandrasekhar 1970; Friedman & Schutz 1978), which leads to rapid growth of the r-mode amplitude, while viscosity acts to suppress the instability. Given the dependence of gravitational wave emission on the neutron star spin and the dependence of viscosity on the neutron star temperature, the critical angular velocity-temperature curve dividing the r-mode stability from instability (hereafter r-mode instability window) was obtained by Lindblom et al. (1998), who also found that gravitational radiation of the l = 2 current multipole is stronger than the other multipoles. Owen et al. (1998) carried out a detailed study of the r-mode instability in rapidly rotating neutron stars and calculated the gravitational wave forms. Such gravitational wave signals might be detected at a distance of 20 Mpc by the advanced Laser Interferometer Gravitational-wave Observatory (aLIGO). Further studies were carried out to obtain the properties of the r-mode instability especially for gravitational waves from rotating neutron stars (Andersson et al. 1999a, 2000, 2001; Kokkotas & Stergioulas 1999; Lindblom et al. 1999, 2000, 2001; Bildsten & Ushomirsky 2000; Lindblom & Mendell 2000; Arras et al. 2003; Bondarescu et al. 2007, 2009; Yang et al. 2010; Haskell et al. 2012; Alford & Schwenzer 2014a,b, 2015; Chugunov 2015; Haskell 2015; Mytidis et al. 2015) and rotating strange stars (Madsen 1998, 2000; Andersson et al. 2002; Zheng et al. 2006; Yu et al. 2009; Alford & Schwenzer 2014b; Dai et al. 2016).

Neutron stars form during supernova (SN) explosions. Fall-back accretion could happen after the core collapse of massive stars (Michel 1988; Chevalier 1989). Owing to rotating progenitors, a disk is likely to form before fall-back materials are accreted onto the neutron star surface (e.g., we refer to Piro & Ott 2011). Such a fall-back disk is responsible for the jets of pulsars (Blackman & Perna 2004), and early afterglows of gamma-ray bursts (GRBs; Dai & Liu 2012). The r-mode instability of neutron stars (with sub-Eddington accretion) in low-mass X-ray binary (LMXB) systems was investigated (Levin 1999; Andersson et al. 1999b; Brown & Ushomirsky 2000; Haskell et al. 2012; Mahmoodifar & Strohmayer 2013). The accreted materials in LMXBs spin up old neutron stars significantly and cause these stars to enter the r-mode instability window again. Following this, the heating due to shear viscosity affects the stellar thermal evolution while gravitational radiation spins down the star. The effects of hypercritical advection-dominated accretion flows without magnetic fields in close binary systems were investigated by Yoshida & Eriguchi (2000), who found that hyperaccreting disks considerably increase the stellar angular momentum, which can balance the spin-down due to gravitational radiation.

Newborn neutron stars are generally strongly magnetized. The average magnetic field of isolated radio pulsars is ~2 × 1012 G (Arzoumanian et al. 2002). However, some astrophysical phenomena were driven by magnetars with field strengths up to 1016 G, for example GRBs (Usov 1992; Dai & Lu 1998a,b; Zhang & Mészáros 2001; Thompson et al. 2004; Metzger et al. 2007; Dall’Osso et al. 2011), soft gamma-ray repeaters (SGRs, Thompson & Duncan 1995, 1996; Vasisht & Gotthelf 1997; Kouveliotou et al. 1998) and some superluminous supernovae (Kasen & Bildsten 2010; Woosley 2010; Wang et al. 2015). Based on the Australia Telescope National Facility (ATNF) catalog1 (Manchester et al. 2005), the highest magnetic field discovered so far is ~2 × 1015 G in SGR 1806-20. Such an ultrastrong magnetic field plays an important role in r-mode evolution (Ho & Lai 2000; Rezzolla et al. 2000, 2001a,b; Lee 2005; Cuofano & Drago 2010; Cuofano et al. 2012; Abbassi et al. 2012; Asai et al. 2015; Chugunov 2015).

Fall-back accretion of rapidly rotating magnetars could drive a subset of transients. For example, the propeller effect during fall-back accretion of newborn millisecond magnetars could directly power some broad-lined type Ib/c or IIP SNe (Piro & Ott 2011); the early bumps of some GRB afterglows also hint that their central engines are hyper-accreting millisecond magnetars (Dai & Liu 2012). On one hand, the r-mode could be unstable in these magnetars and affect the spin evolution via gravitational radiation. On the other hand, both magnetic dipole radiation and fall-back accretion can affect evolution of the stellar spin and r-mode amplitude. In this paper, we explore the effects of the r-mode instability on evolution of newborn hyper-accreting magnetars, and test whether or not gravitational waves due to the r-mode are detectable. If detected, such gravitational waves could provide an important probe for central engines of some SNe and GRBs. It was found that magnetars could be gravitational wave sources due to toroidal magnetic field-induced distortion of the neutron star (Cutler 2002; Dall’Osso et al. 2009) and the bar-mode instability (Corsi & Mészáros 2009). Piro & Thrane (2012) studied gravitational radiation due to bar-mode-like oscillations in accreting magnetars. They found that for a magnetar with radius ~20 km gravitational radiation lasts between hundreds of and a few thousand seconds at typical frequencies of 1000−2000 Hz (Piro & Thrane 2012). However, the r-mode instability could dominate gravitational radiation if the saturation amplitude is large enough. In this case, the frequencies of gravitational waves due to r-mode instability are ~100–1000 Hz as is shown below, which are the most sensitive frequencies of aLIGO (Harry & LIGO Scientific Collaboration 2010) and the Einstein Telescope (ET; Hild et al. 2011). Thus future detections of gravitational waves could distinguish between these two kinds of oscillations.

In this paper, we investigate the effects of the r-mode instability on a newborn rapidly-rotating magnetar with fall-back accretion. In Sect. 2, we present some basic equations of the r-mode instability and hyper-accreting disks in magnetars and then we obtain evolution equations of the stellar spin and r-mode amplitude. The numerical and semi-analytical results are presented in Sect. 3. In Sect. 4, we estimate the detectability of gravitational waves due to the r-mode instability. Our conclusions and brief discussions are given in Sect. 5.

2. Basic equations of R-mode instability

2.1. Gravitational radiation and viscosities

The r-mode instability is generically driven by gravitational radiation and dissipated by viscosities. The typical timescales of gravitational radiation (tgw), shear viscosity (tsv), and bulk viscosity (tbv) depend on the stellar equation of state (EOS). A polytropic EOS of N = 0 or 1 is usually used, while the resulting timescales for these two polytropic EOSs differ only by roughly a factor of two (we refer to a review by Andersson et al. 2001 and references therein). The effects of more realistic EOSs have been tested by Papazoglou & Moustakidis (2016), whose results show only small differences from those of the N = 1 polytropic EOS. Following Alford et al. (2012a,b), we consider the Akmal-Pandharipande-Ravenhall (APR) EOS (Akmal et al. 1998), since this EOS gives a better approximation of the equilibrium configuration than the polytropic EOSs for r-mode oscillations.

The gravitational radiation timescale is given by (Lindblom et al. 1998) and Owen et al. (1998), 1tgw=−32πGΩ2l+2c2l+3(l−1)2l[(2l+1)!!]2 ×(l+2l+1)2l+2∫0Rρ(r)r2l+2dr,\begin{eqnarray} \frac{1}{t_{\rm gw}} & =& -\frac{32\pi G \Omega^{2l+2}}{c^{2l+3}}\frac{(l-1)^{2l}}{[(2l+1)!!]^2}\nonumber \\ && \quad \times \left(\frac{l+2}{l+1}\right)^{2l+2} \int_0^{R}\rho(r) r^{2l+2} {\rm d}r, \end{eqnarray}(1)where G is the gravitational constant. The strongest gravitational radiation reaction comes from the l = m = 2 mode (Lindblom et al. 1998; Owen et al. 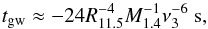1998), so we obtain tgw≈−24R11.5-4M1.4-1ν3-6s,\begin{equation} t_{\rm{gw}}\approx-24 R_{11.5}^{-4}M_{1.4}^{-1}\nu_{3}^{-6}~{\rm s},\label{tgw} \end{equation}(2)where the radius of the magnetar is R = 11.5R11.5 km, the mass is M = 1.4 M⊙ × M1.4, and ν = Ω/2π = 103ν3 Hz is the rotational frequency of the magnetar.

Usually very simple models of shear and bulk viscosities are adopted. However, these models are inconsistent with observations of LMXBs even if taking into account the effect of an Ekman layer (Alford & Schwenzer 2014a), and thus reevaluations of the relevant physics are needed (Ho et al. 2011; Haskell et al. 2012; Gusakov et al. 2014; Haskell 2015). Here we consider more recent and complex models to calculate the dissipation timescales of viscosities. The shear viscosity is found to be contributed by electron scattering (Shternin & Yakovlev 2008; Shternin et al. 2013). Following Alford et al. (2012a,b), we adopt this electron scattering model to calculate the dissipation timescale of shear viscosity in this paper, which is 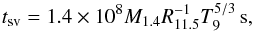tsv=1.4×108M1.4R11.5-1T95/3 s,\begin{eqnarray} t_{\rm sv}=1.4\times10^8M_{1.4}R_{11.5}^{-1}T_9^{5/3}\,{\rm s}, \end{eqnarray}(3)where T = T9109 K is the core temperature of the neutron star.

The bulk viscosity is more important, since it is the dominant dissipation mechanism for newly-born neutron stars. Most previous studies have focused on the effects of the bulk viscosity from the linear perturbation theory. However, as the r-mode amplitude (α) grows large enough α ≳ O(1), the bulk viscosity is significantly enhanced due to the suprathermal effect (Alford et al. 2012b). This effect provides an alternative mechanism to saturate the r-mode amplitude with the order O(1) to O(10) (Alford et al. 2012b). In this case, the dissipation timescale of the bulk viscosity (tbv) also depends on the r-mode amplitude α. For a neutron star dominated by the modified-URCA processes, this time-scale is expressed as (for more details, we refer to Alford et al. 2012b), 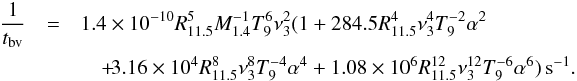1tbv=1.4×10-10R11.55M1.4-1T96ν32(1+284.5R11.54ν34T9-2α2\begin{eqnarray} \frac{1}{t_{\rm bv}} &=& 1.4\times10^{-10}R_{11.5}^5M_{1.4}^{-1}T_9^6 \nu_3^2(1+284.5R_{11.5}^4\nu_3^4T_9^{-2}\alpha^2 \nonumber\\ &&\quad +\! 3.16\times10^4R_{11.5}^8\nu_3^8T_9^{-4}\alpha^4+ 1.08 \times 10^6R_{11.5}^{12}\nu_3^{12}T_9^{-6}\alpha^6)\,{\rm s}^{-1}.\label{tbv} \end{eqnarray}(4)The first term on the right-hand side, namely 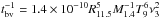tbv-1=1.4×10-10R11.55M1.4-1T96ν32\hbox{$t_{\rm bv}^{-1}=1.4\times10^{-10}R_{11.5}^5M_{1.4}^{-1}T_9^6 \nu_3^2$}, is consistent with the results from the linear perturbation theory in previous studies (Lindblom et al. 1998; Owen et al. 1998).

2.2. Effect of magnetic field

In rotating stars, the Coriolis force (Fc) provides the restoring force. However, in strongly-magnetized neutron stars, the magnetic force (FB) also acts on the fluid motion. The effects of a magnetic field have been studied widely (Ho & Lai 2000; Rezzolla et al. 2000, 2001a,b; Lee 2005; Cuofano & Drago 2010; Cuofano et al. 2012; Abbassi et al. 2012; Asai et al. 2015; Chugunov 2015). Differential rotation might be induced, and thus transfer energy to produce a toroidal magnetic field (Rezzolla et al. 2000, 2001a,b). We consider the damping timescale due to the generation of a toroidal magnetic field following Cuofano & Drago (2010) and Cuofano et al. (2012), that is, 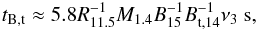tB,t≈5.8R11.5-1M1.4B15-1Bt,14-1ν3s,\begin{eqnarray} t_{\rm B,t}\approx 5.8 R_{11.5}^{-1}M_{1.4}B_{15}^{-1}B_{\rm t,14}^{-1}\nu_{3} ~{\rm s},\label{tbt} \end{eqnarray}(5)where B = B151015 G is the surface magnetic field of the magnetar and Bt = Bt,141014 G is the volume-averaged toroidal magnetic field, which follows from 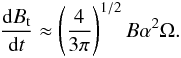dBtdt≈(43π)1/2Bα2Ω.\begin{eqnarray} \dfrac{{\rm d} B_{\rm t}}{{\rm d} t}\approx \left(\dfrac{4}{3\pi}\right)^{1/2}B\alpha^2\Omega.\label{tbevo} \end{eqnarray}(6)A toroidal magnetic field in the interior can deform the neutron star to an ellipsoid, which leads to gravitational radiation and meanwhile spins down the star by a torque of NB,gw = −IΩ /tB,gw, where tB,gw is the timescale of gravitational radiation related to this torque, 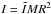I=˜IMR2\hbox{$I=\tilde{I} M R^2$} is the moment of inertia, and 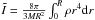˜I=8π3MR2∫0Rρr4dr\hbox{$\tilde{I}={8\pi\over3MR^2}\int_0^R\rho r^4{\rm d}r$}. It is a non-trivial problem that the gravitational radiation from such a magnetically-distorted neutron star depends on details of the magnetic field distribution in the stellar interior, as discussed by many authors (Cutler 2002; Dall’Osso et al. 2009, 2015; Corsi & Mészáros 2009; Cuofano et al. 2012). If the inclination angle between the magnetic dipole moment and the rotation axis is χ = π/ 2, the time-varying mass quadrupole of the neutron star and consequently the gravitational radiation efficiency are maximized; otherwise, the gravitational radiation efficiency should be smaller. If a neutron star has an initial temperature T0 = 1010 K and cools down via the modified URCA process, as found by Dall’Osso et al. (2009), then the inclination angle evolves following 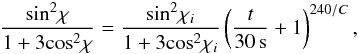sin2χ1+3cos2χ=sin2χi1+3cos2χi(t30 s+1)240/C,\begin{eqnarray} \frac{\mbox{sin}^2 \chi}{1+3\mbox{cos}^2 \chi} = \frac{\mbox{sin}^2 \chi_i}{1+3\mbox{cos}^2 \chi_i} \left(\frac{t}{30\,{\rm s}} +1 \right)^{240/C}, \end{eqnarray}(7)where χi is the initial inclination angle, which is usually small, and 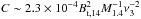C~2.3×10-4Bt,142M1.4-1ν3-2\hbox{$C\sim2.3\times10^{-4}B_{\rm t,14}^2M_{1.4}^{-1}\nu_{3}^{-2}$}. Thus the magnetic dipole moment will be orthogonal to the rotation axis in less than ~1 ms when χi = 1deg. For the APR equation of state, we obtain 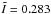˜I=0.283\hbox{$\tilde{I}=0.283$} for a neutron star with mass 1.4 M⊙ and radius R = 11.5 km (Owen et al. 1998). The timescale tB,gw with χ = π/ 2 reads (Cuofano et al. 2012) 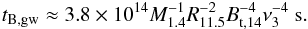tB,gw≈3.8×1014M1.4-1R11.5-2Bt,14-4ν3-4s.\begin{eqnarray} t_{\rm B,gw}\approx 3.8\times10^{14} M_{1.4}^{-1}R_{11.5}^{-2}B_{\rm t,14}^{-4}\nu_{3}^{-4} ~{\rm s}.\label{tbgw} \end{eqnarray}(8)The surface magnetic field also slows down the magnetar. For simplicity, the magnetic dipole radiation model is adopted. The torque due to magnetic dipole radiation and corresponding timescale are then given by 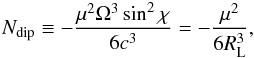Ndip≡−μ2Ω3sin2χ6c3=−μ26RL3,\begin{eqnarray} N_{\rm dip}\equiv -\frac{\mu^2\Omega^3\sin^2\chi}{6c^3}=-{\mu^2\over6R_{\rm L}^3}, \end{eqnarray}(9)and 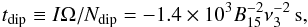tdip≡IΩ/Ndip=−1.4×103B15-2ν3-2 s,\begin{eqnarray} t_{\rm dip}\equiv I\Omega/N_{\rm dip}=-1.4\times10^3 B_{15}^{-2} \nu_{3}^{-2}\,{\rm s}, \end{eqnarray}(10)where tdip is the typical timescale due to magnetic dipole radiation and we set 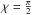χ=π2\hbox{$\chi={\pi \over 2}$}. RL is the radius of the light cylinder 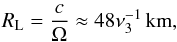RL=cΩ≈48ν3-1 km,\begin{eqnarray} R_{\rm L}=\frac{c}{\Omega}\approx48\nu_{3}^{-1}\,{\rm km},\label{rl} \end{eqnarray}(11)where c is the speed of light. The matter outside RL no longer interacts with the magnetar.

2.3. Hypercritical accretion of a magnetar

Previous studies of the r-mode instability in accretion neutron stars have focussed on LMXB systems (Andersson et al. 1999b; Brown & Ushomirsky 2000; Yoshida & Eriguchi 2000; Bondarescu et al. 2007). Here we consider hypercritical fall-back accretion of newborn rapidly rotating magnetars, where the accretion torque can be either positive or negative. Following MacFadyen et al. (2001), Zhang et al. (2008) and Piro & Thrane (2012), we parameterize the fall-back accretion rate as 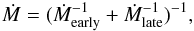Ṁ=(Ṁ-1early+Ṁ-1late)-1,\begin{eqnarray} \dot{M}=(\dot{M}_{\rm early}^{-1}+\dot{M}_{\rm late}^{-1})^{-1}, \end{eqnarray}(12)where 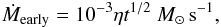Ṁearly=10-3ηt1/2M⊙ s-1,\begin{eqnarray} \dot{M}_{\rm early}=10^{-3}\eta t^{1/2}~M_\odot\,{\rm s}^{-1},\label{accearly} \end{eqnarray}(13)and 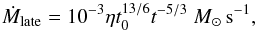Ṁlate=10-3ηt013/6t−5/3M⊙ s-1,\begin{eqnarray} \dot{M}_{\rm late}=10^{-3}\eta t_0^{13/6}t^{-5/3}~M_\odot\,{\rm s}^{-1},\label{acclate} \end{eqnarray}(14)where η ≈ 0.01−10 is a factor which accounts for explosion energies, t is in units of seconds and t0 ~ 102−103 s is the typical time at which the accretion rate starts to decrease (MacFadyen et al. 2001). At late times, the accretion rate decreases as Ṁ ∝ t− 5/3 (Chevalier 1989). We thus obtain the total baryonic mass of the neutron star at an arbitrary time t, 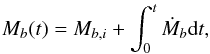Mb(t)=Mb,i+∫0tṀbdt,\begin{eqnarray} M_b(t)=M_{b,i}+\int_0^t\dot M_b {\rm d}t, \end{eqnarray}(15)where Mb,i is the initial baryonic mass of the magnetar. A fraction of the accreted mass will turn into the binding energy that will be radiated away in the form of neutrinos. Hence, the gravitational mass (M) is more applicable (Lattimer & Prakash 2001), M=Mb(t)[1+35GMb(t)Rc2]-1·\begin{eqnarray} M=M_b\left(t\right)\left[1+\frac{3}{5}\frac{GM_b\left(t\right)}{R c^2}\right]^{-1}\cdot \end{eqnarray}(16)We take R to be a constant in this paper. In reality, the radius R changes especially when the mass grows very large (Lattimer & Prakash 2001). However, a small change of R cannot affect our results significantly, since the timescales acting on the r-mode mainly depend on the core temperature and the spin.

In order to parameterize the torques due to accretion and magnetic dipole radiation, we introduce two useful radii. The first one is the co-rotation radius where the Keplerian angular velocity of the disk equals the angular velocity of the neutron star Ω, 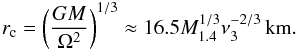rc=(GMΩ2)1/3≈16.5M1.41/3ν3−2/3 km.\begin{eqnarray} r_{\rm c}=\left(\frac{GM}{\Omega^2}\right)^{1/3}\approx16.5M_{1.4}^{1/3}\nu_3^{-2/3}\,{\rm km}.\label{rc} \end{eqnarray}(17)The second one is the magnetospheric (Alfvén) radius where the ram pressure of the fall-back materials balances the magnetic pressure, rm=(μ4GMṀ2b)1/7≈31.2B154/7R11.512/7M1.4−1/7Ṁ−2/7-3 km,\begin{eqnarray} r_{\rm m}=\left(\frac{\mu^4}{GM\dot M_b^2}\right)^{1/7} \approx31.2B_{15}^{4/7}R_{11.5}^{12/7}M_{1.4}^{-1/7}\dot M_{-3}^{-2/7}\,{\rm km},\label{rm} \end{eqnarray}(18)where μ = BR3 is the magnetic dipole moment and Ṁ-3 = Ṁb/ (10-3M⊙/s).

Usually the fastness parameter ω is defined as the ratio of the stellar angular velocity and the Keplerian angular velocity at the magnetospheric radius rm (we refer to e.g., Elsner & Lamb 1977; Ghosh & Lamb 1979), 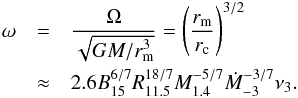ω=ΩGM/rm3=(rmrc)3/2≈\begin{eqnarray} \omega & =& \frac{\Omega}{\sqrt{GM/r_{\rm m}^3}}=\left(\frac{r_{\rm m}}{r_{\rm c}}\right)^{3/2}\nonumber \\ & \approx& 2.6B_{15}^{6/7}R_{11.5}^{18/7}M_{1.4}^{-5/7}\dot M_{-3}^{-3/7}\nu_{3}.\label{omega} \end{eqnarray}(19)Using these parameters, we can parameterize the accretion torque and corresponding timescale through 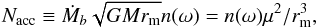Nacc≡ṀbGMrmn(ω)=n(ω)μ2/rm3,\begin{equation} N_{\rm acc} \equiv\dot M_b \sqrt{GM r_{\rm m}}n(\omega)=n(\omega)\mu^2/ r_{\rm m}^3,\label{tacc} \end{equation}(20)and 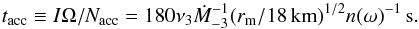tacc≡IΩ/Nacc=180ν3Ṁ-1-3(rm/18 km)1/2n(ω)-1 s.\begin{equation} t_{\rm acc}\equiv I\Omega/N_{\rm acc}=180\nu_{3}\dot M_{-3}^{-1}({r_{\rm m}/18\,{\rm km}})^{1/2}n(\omega)^{-1}\,{\rm s}. \end{equation}(21)If rm<rc, the accreted matter transfers its angular momentum to the magnetar, and thus provides a positive torque. Otherwise, the fall-back matter acts as a propeller and offers a negative torque. A detailed picture of accretion onto magnetic stars has been elucidated by many authors, for example Pringle & Rees (1972), Illarionov & Sunyaev (1975), Ghosh & Lamb (1979), Aly (1980), Ekşi et al. (2005), and Dai & Liu (2012). The expression of n(ω) differs slightly in different models. For simplification, we here adopt n(ω) = 1−ω, as in Piro & Ott (2011). This form of n(ω) includes the main properties of an interaction between the accretion disk and the magnetar. Furthermore, it has two advantages; n(ω) is continuous for all ω and becomes zero when rm = rc.

2.4. Evolution of the r-mode

We quantify the r-mode model based on Owen et al. (1998). The total angular momentum J is given by 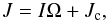J=IΩ+Jc,\begin{eqnarray} J=I \Omega +J_{\rm c},\label{J} \end{eqnarray}(22)where Jc is the canonical angular momentum of the r-mode (Owen et al. 1998), 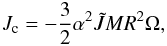Jc=−32α2˜JMR2Ω,\begin{eqnarray} J_{\rm c}=-\frac{3}{2} \alpha ^2 \tilde{J} M R^2 \Omega,\label{Jc} \end{eqnarray}(23)where 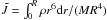˜J=∫0Rρr6dr/(MR4)\hbox{$\tilde{J}=\int_0^R\rho r^6{\rm d}r/(MR^4)$} and for a neutron star with the APR EOS, whose mass is 1.4 M⊙ and radius is R = 11.5 km, we have 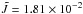˜J=1.81×10-2\hbox{$\tilde{J}=1.81\times 10^{-2}$} (Owen et al. 1998). The canonical energy of the r-mode is given by (Owen et al. 1998), 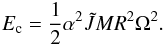Ec=12α2˜JMR2Ω2.\begin{eqnarray} E_{\rm c}=\frac{1}{2} \alpha ^2 \tilde{J} M R^2 \Omega ^2.\label{Ec} \end{eqnarray}(24)We obtain evolution of the r-mode using the time derivative of J and Ec (Owen et al. 1998; Andersson et al. 2001; Cuofano et al. 2012), 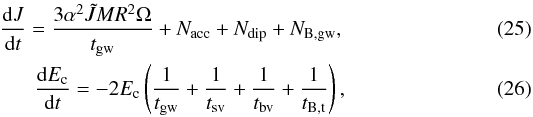dJdt=3α2˜JMR2Ωtgw+Nacc+Ndip+NB,gw,dEcdt=−2Ec(1tgw+1tsv+1tbv+1tB,t),\begin{eqnarray} \frac{{\rm d} J}{{\rm d}t}=\frac{3 \alpha ^2 \tilde{J} M R^2 \Omega }{t_{\rm gw}}+N_{\rm acc}+ N_{\rm dip}+N_{\rm B,gw},\label{dJ}\\ \frac{{\rm d} E_{\rm c}}{{\rm d}t}=-2 E_{\rm c} \left(\frac{1}{t_{\rm gw}}+ \frac{1}{t_{\rm sv}}+\frac{1}{t_{\rm bv}}+\frac{1}{t_{\rm B,t}}\right),\label{dE} \end{eqnarray}where the torques due to accretion (Nacc) and magnetic dipole radiation (Ndip) affect the total stellar angular momentum together.

Substituting Eqs. (22)–(24) into Eqs. (25) and (26), we obtain the evolution equations of Ω and α, 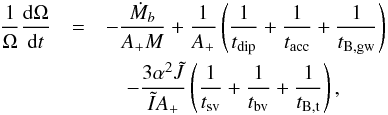1ΩdΩdt=−ṀbA+M+1A+(1tdip+1tacc+1tB,gw)\begin{eqnarray} {1\over\Omega}\frac{{\rm d}\Omega }{{\rm d}t} &=& -\frac{\dot M_b }{ A_{+}M} +\frac{1}{A_{+}}\left(\frac{1}{t_{\rm dip}}+\frac{1}{t_{\rm acc}}+\frac{1}{t_{\rm B,gw}} \right) \nonumber\\ &&\quad-\frac{3 \alpha ^2 \tilde{J}}{\tilde{I}A_{+}} \left(\frac{1}{t_{\rm sv}}+\frac{1}{t_{\rm bv}}+\frac{1}{t_{\rm B,t}}\right),\label{oevo} \end{eqnarray}(27)and 1αdαdt=ṀbA−2MA+−A−A+(1tsv+1tbv+1tB,t)\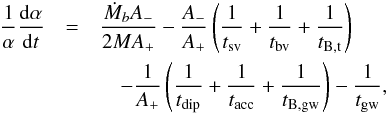begin{eqnarray} {1\over\alpha}\frac{{\rm d}\alpha }{{\rm d}t} & =& \frac{\dot M_b A_{-}}{2 M A_{+}} -\frac{A_{-}}{ A_{+}}\left(\frac{1}{t_{\rm sv}}+\frac{1}{t_{\rm bv}}+\frac{1}{t_{\rm B,t}}\right) \nonumber\\ &&\quad-\frac{1}{ A_{+}}\left(\frac{1}{t_{\rm dip}}+\frac{1}{t_{\rm acc}}+\frac{1}{t_{\rm B,gw}} \right)-\frac{1 }{t_{\rm gw}}\label{aevo}, \end{eqnarray}(28)where A±=1±3α2˜J/2˜I\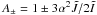hbox{$A_{\pm}=1\pm 3 \alpha ^2 \tilde{J}/2\tilde{I}$}. We see that accretion and magnetic dipole radiation affect the amplitude and spin evolution simultaneously. The magnetic braking increases the r-mode amplitude while it spins down the magnetar. The effect of accretion is slightly complicated, since accretion can either spin up or down the magnetar while it can also either decrease or increase the r-mode amplitude.

In order to solve the above evolution equations, we must also know how the interior temperature of the magnetar evolves. The fall-back accretion will start ~100 s later after the stellar birth (MacFadyen et al. 2001; Dai & Liu 2012). Meanwhile, the proto-neutron star will become a neutron star ~50 s later after its birth, and at this time the neutron star is transparent to neutrinos (Ferrari et al. 2003). Thus we consider a hot young isothermal neutron star with an initial temperature of T0 = 1010 K. The newborn neutron star is then cooled down by the modified-URCA processes, whose luminosity is 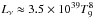Lν≈3.5×1039T98\hbox{$L_{\nu}\approx3.5\times10^{39}T_9^8$} erg/s (Shapiro & Teukolsky 1986; Alford & Schwenzer 2014b). The direct URCA processes might set in when the star grows heavy enough. But since we only consider the time (the first ~104 s) when gravitational radiation is significant, the direct URCA processes do not significantly affect our results. We also take into account the heating effect due to shear viscosity in this paper, namely, Hv = 2Ec/tsv. We do not consider the heating effect of accreted materials, since these materials have been cooled down by neutrinos in the accretion disk (Kohri & Mineshige 2002; Zhang & Dai 2010) and the accretion column (Piro & Ott 2011). The temperature evolution is then given by 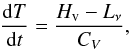dTdt=Hv−LνCV,\begin{eqnarray} \frac{{\rm d}T}{{\rm d}t}=\frac{H_{\rm v}-L_{\nu}}{C_V},\label{Tevo} \end{eqnarray}(29)where CV ≈ 7.0 × 1038T9 erg K-1 (Shapiro & Teukolsky 1986) is the heat capacity of the neutron star.

3. Results

Integrating Eq. (6), (27)–(29), we can obtain evolution of the r-mode amplitude, spin, and temperature. The initial spin is of the order of one millisecond, but since accretion spins up the star near the mass-shedding limit, the effect of the initial spin is less important than that of accretion. Therefore, we mainly focus on effects of accretion and initialize the spin at P0 = 1 /ν0 = 3 ms. The initial baryonic mass and radius of the magnetar in our model are taken to be Mb,i = 1.4 M⊙ and R = 11.5 km, and thus the gravitational mass is Mi ≃ 1.26 M⊙. The initial amplitude of the r-mode is fixed at 10-8.

Figure 1 gives four examples of evolution of the r-mode amplitude (α), spin (ν) and toroidal magnetic field (Bt). We study two specific accretion rates; η = 0.01 with t0 = 3000 s (red lines) and η = 0.1 with t0 = 300 s (blue lines). The magnetic field is typically chosen to be B = 2 × 1014 G (solid lines) and B = 5 × 1014 G (dashed lines). For comparison, we also study the case without accretion for B = 2 × 1014 G (black solid line). It is shown that the combination of accretion and magnetic fields can significantly affect the r-mode amplitude evolution. If the accretion can spin up the neutron star significantly, the amplitude grows quickly to the maximum value of ~ 0.001. Otherwise, the growth speed might be considerably suppressed. In the following, we use a semi-analytical method to analyze the amplitude and spin evolution.

To find which mechanism dominates the evolution, we compare the terms in the right hand side of Eqs. (27) or (28). We take the pre-factor A± ≈ 1, since the amplitude is very small in an early stage. Since the viscosity terms and the gravitational wave terms due to magnetic deformation are very small, we mainly consider the other terms. Firstly, we compare the accretion torque with the first term in Eq. (27), that is, 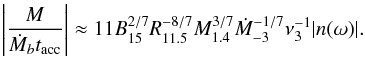|MṀbtacc|≈11B152/7R11.5−8/7M1.43/7Ṁ−1/7-3ν3-1|n(ω)|.\begin{eqnarray} \left|{M\over\dot M_b t_{\rm acc}}\right| \approx 11B_{15}^{2/7}R_{11.5}^{-8/7}M_{1.4}^{3/7}\dot M_{-3}^{-1/7} \nu_{3}^{-1}|n(\omega)|. \end{eqnarray}(30)Generally, ν< 103 Hz holds in most of the evolution time (Fig. 1) and n(ω) is in the range of − 0.5 to 0.5, so we treat with the accretion torque as the dominant term over the first term.

thumbnail Fig. 1

r-mode amplitude (α), spin (ν) and toroidal magnetic field (Bt) as functions of time. The black solid line is plotted for B = 2 × 1014 G and η = 0 . The red solid or dashed lines are obtained in the case of η = 0.01 and t0 = 3000 s for B = 2 × 1014 G or B = 5 × 1014 G. The blue solid or dashed lines are obtained in the case of η = 0.1 and t0 = 300 s for B = 2 × 1014 G or B = 5 × 1014 G.

The torque due to magnetic dipole radiation is smaller than the accretion torque, since the magnetospheric radius is generally much smaller than the light cylinder radius and n(ω) ∈ [−0.5,0.5] in the amplitude growing stage so that 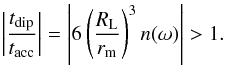|tdiptacc|=|6(RLrm)3n(ω)|>1.\begin{eqnarray} \left|{t_{\rm dip}\over t_{\rm acc}}\right|= \left|6\left({ R_{\rm L}\over r_{\rm m}}\right)^3 n(\omega)\right|>1. \end{eqnarray}(31)The toroidal magnetic field damping term is comparable to the accretion term, if the toroidal magnetic field grows strong enough, since we have 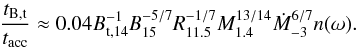tB,ttacc≈0.04Bt,14-1B15−5/7R11.5−1/7M1.413/14Ṁ6/7-3n(ω).\begin{eqnarray} {t_{\rm B,t}\over t_{\rm acc}}\approx 0.04 B_{\rm t,14}^{-1} B_{15}^{-5/7}R_{11.5}^{-1/7}M_{1.4}^{13/14}\dot M_{-3}^{6/7} n(\omega). \label{accovergw} \end{eqnarray}(32)However, for the spin evolution (Eq. (27)), there is a pre-factor 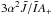3α2˜J/˜IA+\hbox{${3 \alpha ^2 \tilde{J}}/{\tilde{I}A_{+}}$}. Considering in this paper (Fig. 1) that the amplitude is generally much smaller than 0.2, we can assume that the accretion term dominates the spin evolution.

Adopting Eqs. (13) and (14) and considering only the accretion term in the right-hand side of Eq. (27), we obtain an approximate spin evolution, ν≈{\begin{eqnarray} \nu\approx \left\{ \begin{array}{ll} \nu_0+3.7n(\omega)\eta t^{3/2},~~~~{\rm if}~~t\lesssim t_0,\\ \nu_{\rm c}+8.3n(\omega)t_0^{3/2}\eta[1-(t_0/t)^{2/3}],~~{\rm if}~~t\gtrsim t_0, \label{oad} \end{array} \right. 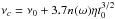\end{eqnarray}(33)where νc=ν0+3.7n(ω)ηt03/2\hbox{$\nu_{c}=\nu_0+3.7n(\omega)\eta t_0^{3/2}$}. Substituting Eq. (33) into Eq. 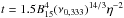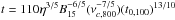(19), we find that n(ω) = 0 happens at t=1.5B154(ν0,333)14/3η-2\hbox{$t=1.5B_{15}^4 (\nu_{0,333})^{14/3}\eta^{-2}$} s or t=110η3/5B15−6/5(νc,800−7/5)(t0,100)13/10\hbox{$t=110\eta^{3/5}B_{15}^{-6/5}(\nu_{c,800}^{-7/5})(t_{0,100})^{13/10}$} s, where ν0,333 = ν0/ 333 Hz, νc,800 = νc/ 800 Hz and t0,100 = t0/ 100 s. The second solution (t ~ 110η3/5(t0,100)13/10 s) corresponds to the time when the maximum spin is reached, which hints that before ~t0 the spin is increasing. This analytical expression for ν is consistent with the result shown in Fig. 1.

The amplitude evolution begins to be affected by the gravitational wave emission when 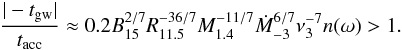|−tgw|tacc≈0.2B152/7R11.5−36/7M1.4−11/7Ṁ6/7-3ν3-7n(ω)>1.\begin{eqnarray} {|-t_{\rm gw}|\over t_{\rm acc}}\approx0.2 B_{15}^{2/7}R_{11.5}^{-36/7}M_{1.4}^{-11/7}\dot M_{-3}^{6/7} \nu_{3}^{-7}n(\omega)>1. \label{accovergw} \end{eqnarray}(34)This means that gravitational radiation dominates when 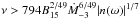ν>794B152/49Ṁ6/49-3|n(ω)|1/7\hbox{$\nu>794B^{2/49}_{15}\dot M^{6/49}_{-3}|n(\omega)|^{1/7}$} Hz. 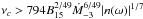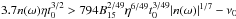Approximately, it is required that νc>794B152/49Ṁ6/49-3|n(ω)|1/7\hbox{$\nu_{c}>794B^{2/49}_{15}\dot M^{6/49}_{-3}|n(\omega)|^{1/7}$}, which is roughly 3.7n(ω)ηt03/2>794B152/49η6/49t03/49|n(ω)|1/7−ν0\hbox{$3.7n(\omega)\eta t_0^{3/2}>794B^{2/49}_{15} \eta^{6/49}t_0^{3/49}|n(\omega)|^{1/7}-\nu_0$}.

We also numerically show that the timescales − tgw (purple lines), tB,t (brown lines) and tacc (orange lines) evolve with time in Fig. 2. The accretion rate is fixed to be η = 0.01 at t0 = 3000 s. The solid lines correspond to the case of B = 2 × 1014 G and dashed lines to B = 5 × 1014 G. The sharp transitions happen when ω → 1, which leads to tacc → ∞.

thumbnail Fig. 2

Evolution of timescales − tgw (purple lines), tB,t (brown lines) and tacc (orange lines) in the cases with η = 0.01 and t0 = 3000 s. The solid lines correspond to the case of B = 2 × 1014 G and dashed lines to B = 5 × 1014 G.

The amplitude is suppressed by the positive accretion torque before ~t0. After that, if the spin of the neutron star increases significantly enough, which leads to gravitational radiation dominating the r-mode amplitude (| tgw | < | tacc |), rapid growth of the amplitude occurs (Fig. 1). To calculate this rapid growth, we only consider the contribution of gravitational radiation in Eq. (28), and obtain 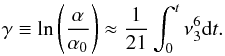γ≡ln(αα0)≈121∫0tν36dt.\begin{eqnarray} \gamma\equiv\ln\left(\frac{\alpha}{\alpha_0}\right)\approx {1\over21}\int_0^t\nu_3^6 {\rm d}t.\label{gamma} \end{eqnarray}(35)Substituting Eq. (33) into this equation, we find 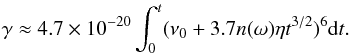γ≈4.7×10-20∫0t(ν0+3.7n(ω)ηt3/2)6dt.\begin{eqnarray} \gamma\approx 4.7\times10^{-20}\int_0^t(\nu_0+3.7n(\omega)\eta t^{3/2})^6 {\rm d}t\label{gammagw}. \end{eqnarray}(36)The rapid growth happens only when ν0< 3.7 | n(ω) | ηt3/2, in which case we can ignore the ν0 term in Eq. (36). Therefore, we get 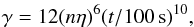γ=12(nη)6(t/100 s)10,\begin{eqnarray} \gamma=12(n\eta)^6 ({t/100\,{\rm s}})^{10}\label{gammafinal}, \end{eqnarray}(37)which is strongly dependent on n, η and t, meaning the amplitude can grow quickly with time. To reach saturation, the amplitude should grow up to αs/α0 = 103−108, which means γ = ln(αs/α0) ≈ 7−18. This implies that gravitational radiation can drive r-mode to saturation in a few hundred seconds if the star accretes a significant amount of matter. 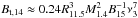In this case, the maximum amplitude is reached when tgw + tB,t ≈ 0, which is Bt,14≈0.24R11.53M1.42B15-1ν37\hbox{$B_{\rm t,14}\approx0.24R_{11.5}^{3}M_{1.4}^2B_{15}^{-1}\nu_{3}^7$}.

However, if the spin grows very slowly, the accretion torque will dominate the amplitude growth (| tgw/tacc | > 1). Considering only the accretion torque term in Eq. (28) and using Eq. 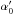(33), we approximately obtain the growth rate of the r-mode amplitude due to accretion, γ=8.3n(ω)t03/2η[1−(t0/t)2/3]νc+8.3n(ω)t03/2η[1−(t0/t)2/3],\begin{eqnarray} \gamma ={8.3n(\omega)t_0^{3/2}\eta[1-(t_0/t)^{2/3}] \over \nu_{\rm c}+8.3n(\omega)t_0^{3/2}\eta[1-(t_0/t)^{2/3}]},\label{aacc} \end{eqnarray}(38)where n(ω) is negative and α0′\hbox{$\alpha'_0$} is the amplitude when the accretion torque becomes dominant. In this case, the amplitude grows very slowly with time. Then, the maximum amplitude is reached when tB,t + tacc ≈ 0, which is 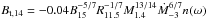Bt,14=−0.04B15−5/7R11.5−1/7M1.413/14Ṁ6/7-3n(ω)\hbox{$B_{\rm t,14}=-0.04 B_{15}^{-5/7}R_{11.5}^{-1/7}M_{1.4}^{13/14}\dot M_{-3}^{6/7} n(\omega)$}, where n(ω) < 0.

4. Detectability of gravitational waves

When the r-mode is unstable in a magnetar, gravitational waves are emitted. The r-mode became very interesting after gravitational waves from the merger of double black holes were detected by aLIGO (Abbott et al. 2016). We now test whether or not such a gravitational wave signal from a single source can be detectable by gravitational observatories such as ET. The gravitational wave strain amplitude for the r-mode, which is averaged over polarizations and orientations, is given by Owen et al. (1998) as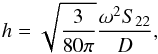h=380πω2S22D,\begin{eqnarray} h=\sqrt{3\over80\pi}{\omega^2S_{22}\over D}, \end{eqnarray}(39)where D is the distance of the source and 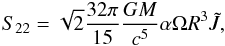S22=232π15GMc5αΩR3˜J,\begin{eqnarray} S_{22}=\sqrt{2}{32\pi\over15}{GM\over c^5}\alpha\Omega R^3\tilde{J}, \end{eqnarray}(40)where c is the speed of light. We mainly focus on the frequency spectrum of the gravitational wave by using the Fourier-transform, 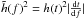˜h(f)2=h(t)2|dtdf|\hbox{$\tilde{h}(f)^2=h(t)^2|{{\rm d}t\over {\rm d}f}|$} (Owen et al. 1998), where f ≈ 2Ω/3π is the frequency of the gravitational wave for the l = m = 2 current multipoles. A characteristic amplitude 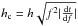hc=hf2|dtdf|\hbox{$h_{\rm c}=h\sqrt{f^2|{{\rm d}t\over {\rm d}f}|}$} is usually defined and we show it in Fig. 3 for different cases versus the rms strain noise 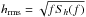hrms=fSh(f)\hbox{$h_{\rm rms}=\sqrt{fS_h(f)}$} of ET, where Sh(f) is the noise strain amplitude.

The red, blue, magenta, and orange solid curves in Fig. 3 are the characteristic amplitude hc in the cases with different accretion rates and magnetic fields, when the sources locate at a distance of D = 1 Mpc. The green line is the ET noise rms strain amplitude (Hild et al. 2011) and the characteristic amplitudes are higher than the noise curves. Thus it is possible to detect such sources once ET works.

thumbnail Fig. 3

Characteristic strain amplitude of the r-mode instability for accreting magnetars locating at a distance D = 1 Mpc. The green curve corresponds to ET noise rms strain amplitude. The red, blue, magenta, and orange curves correspond to the cases: B = 2 × 1014 G, η = 0.01, and t0 = 3000 s; B = 2 × 1014 G, η = 0.1, and t0 = 300 s; B = 5 × 1014 G, η = 1, and t0 = 100 s; and B = 5 × 1014 G, η = 10, and t0 = 15 s, respectively.

5. Discussion and conclusion

In this paper, we have explored the r-mode instability in newborn rapidly-rotating hyper-accreting magnetars. Their spin evolution is influenced by the accretion torque. There are two possibilities. Case I: if the neutron star is spun up significantly by accretion, namely, the parameters must satisfy the condition of 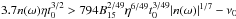3.7n(ω)ηt03/2>794B152/49η6/49t03/49|n(ω)|1/7−ν0\hbox{$3.7n(\omega)\eta t_0^{3/2}>794B^{2/49}_{15} \eta^{6/49}t_0^{3/49}|n(\omega)|^{1/7}-\nu_0$}, the r-mode amplitude will grow quickly due to the gravitational radiation ln [α(t) /α0] = 12(nη)6(t/ 100 s)10. The saturation happens when the damping due to the generation of a toroidal magnetic field balances the gravitational radiation for 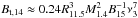Bt,14≈0.24R11.53M1.42B15-1ν37\hbox{$B_{\rm t,14}\approx0.24R_{11.5}^{3}M_{1.4}^2B_{15}^{-1}\nu_{3}^7$}. The generated magnetic field reaches a value that is slightly weaker than the poloidal field. The saturation amplitude is ~0.001.

However, if the spin-up is not significant (Case II), the accretion torque will dominate the amplitude growth, which leads to a much slower growth (Eq. (38)). The saturation is then met when 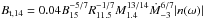Bt,14=0.04B15−5/7R11.5−1/7M1.413/14Ṁ6/7-3|n(ω)|\hbox{$B_{\rm t,14}=0.04 B_{15}^{-5/7}R_{11.5}^{-1/7}M_{1.4}^{13/14}\dot M_{-3}^{6/7} |n(\omega)|$}. The maximum saturation amplitude is of the order of ~10-6 to 10-5. The generated toroidal field is much weaker than that in the case of a significant spin-up.

If the magnetar is sufficiently spun-up (i.e., Case I discussed here), the gravitational radiation from such a magnetar would be possibly detectable with the future mission ET, if the source were located at a distance <1 Mpc. Core-collapse SNe and gamma-ray bursts are electromagnetic counterparts of such gravitational wave sources. However, based on the recent estimates (Li et al. 2011; Strolger et al. 2015), the local core-collapse supernova rate is ~a few × 10-2 Mpc-3 per century. Thus, the detectable gravitational wave event rate with ET is as low as roughly one per millennium.

Acknowledgments

We thank the referee for valuable comments and constructive suggestions that have allowed us to improve our manuscript significantly. We also thank Yi-Ming Hu, Yan Yan and Yun-Wei Yu for their helpful discussions. This work is supported by the National Basic Research Program (“973” Program) of China (grant No. 2014CB845800) and the National Natural Science Foundation of China (grant No. 11573014).

References

  1. Abbassi, S., Rieutord, M., & Rezania, V. 2012, MNRAS, 419, 2893 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. Lett., 116, 061102 [Google Scholar]
  3. Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C (Nucl. Phys.), 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
  4. Alford, M. G., Mahmoodifar, S., & Schwenzer, K. 2012a, Phys. Rev. D, 85, 024007 [NASA ADS] [CrossRef] [Google Scholar]
  5. Alford, M. G., Mahmoodifar, S., & Schwenzer, K. 2012b, Phys. Rev. D, 85, 044051 [NASA ADS] [CrossRef] [Google Scholar]
  6. Alford, M. G., & Schwenzer, K. 2014a, Phys. Rev. Lett., 113, 251102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Alford, M. G., & Schwenzer, K. 2014b, ApJ, 781, 26 [NASA ADS] [CrossRef] [Google Scholar]
  8. Alford, M. G., & Schwenzer, K. 2015, MNRAS, 446, 3631 [NASA ADS] [CrossRef] [Google Scholar]
  9. Aly, J. J. 1980, A&A, 86, 192 [Google Scholar]
  10. Andersson, N. 1998, ApJ, 502, 708 [NASA ADS] [CrossRef] [Google Scholar]
  11. Andersson, N., Kokkotas, K., & Schutz, B. F. 1999a, ApJ, 510, 846 [NASA ADS] [CrossRef] [Google Scholar]
  12. Andersson, N., Kokkotas, K. D., & Stergioulas, N. 1999b, ApJ, 516, 307 [NASA ADS] [CrossRef] [Google Scholar]
  13. Andersson, N., Jones, D. I., Kokkotas, K. D., & Stergioulas, N. 2000, ApJ, 534, L75 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Andersson, N., & Kokkotas, K. D. 2001, Int. J. Mod. Phys. D, 10, 381 [NASA ADS] [CrossRef] [Google Scholar]
  15. Andersson, N., Jones, D. I., & Kokkotas, K. D. 2002, MNRAS, 337, 1224 [NASA ADS] [CrossRef] [Google Scholar]
  16. Arras, P., Flanagan, E. E., Morsink, S. M., et al. 2003, ApJ, 591, 1129 [NASA ADS] [CrossRef] [Google Scholar]
  17. Arzoumanian, Z., Chernoff, D. F., & Cordes, J. M. 2002, ApJ, 568, 289 [NASA ADS] [CrossRef] [Google Scholar]
  18. Asai, H., Lee, U., & Yoshida, S. 2015, MNRAS, 449, 3620 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bildsten, L., & Ushomirsky, G. 2000, ApJ, 529, L33 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  20. Blackman, E. G., & Perna, R. 2004, ApJ, 601, L71 [NASA ADS] [CrossRef] [Google Scholar]
  21. Bondarescu, R., Teukolsky, S. A., & Wasserman, I. 2007, Phys. Rev. D, 76, 064019 [NASA ADS] [CrossRef] [Google Scholar]
  22. Bondarescu, R., Teukolsky, S. A., & Wasserman, I. 2009, Phys. Rev. D, 79, 104003 [NASA ADS] [CrossRef] [Google Scholar]
  23. Brown, E. F., & Ushomirsky, G. 2000, ApJ, 536, 915 [NASA ADS] [CrossRef] [Google Scholar]
  24. Chandrasekhar, S. 1970, Phys. Rev. Lett., 24, 611 [NASA ADS] [CrossRef] [Google Scholar]
  25. Chevalier, R. A. 1989, ApJ, 346, 847 [NASA ADS] [CrossRef] [Google Scholar]
  26. Chugunov, A. I. 2015, MNRAS, 451, 2772 [NASA ADS] [CrossRef] [Google Scholar]
  27. Corsi, A., & Mészáros, P. 2009, ApJ, 702, 1171 [NASA ADS] [CrossRef] [Google Scholar]
  28. Cutler, C. 2002, Phys. Rev. D, 66, 084025 [NASA ADS] [CrossRef] [Google Scholar]
  29. Cuofano, C., & Drago, A. 2010, Phys. Rev. D, 82, 084027 [NASA ADS] [CrossRef] [Google Scholar]
  30. Cuofano, C., Dall’Osso, S., Drago, A., & Stella, L. 2012, Phys. Rev. D, 86, 044004 [NASA ADS] [CrossRef] [Google Scholar]
  31. Dai, Z. G., & Liu, R.-Y. 2012, ApJ, 759, 58 [NASA ADS] [CrossRef] [Google Scholar]
  32. Dai, Z. G., & Lu, T. 1998a, Phys. Rev. Lett., 81, 4301 [NASA ADS] [CrossRef] [Google Scholar]
  33. Dai, Z. G., & Lu, T. 1998b, A&A, 333, L87 [NASA ADS] [Google Scholar]
  34. Dai, Z. G., Wang, S. Q., Wang, J. S., Wang, L. J., & Yu, Y. W. 2016, ApJ, 817, 132 [NASA ADS] [CrossRef] [Google Scholar]
  35. Dall’Osso, S., Shore, S. N., & Stella, L. 2009, MNRAS, 398, 1869 [NASA ADS] [CrossRef] [Google Scholar]
  36. Dall’Osso, S., Stratta, G., Guetta, D., et al. 2011, A&A, 526, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Dall’Osso, S., Giacomazzo, B., Perna, R., & Stella, L. 2015, ApJ, 798, 25 [NASA ADS] [CrossRef] [Google Scholar]
  38. Ekşi, K. Y., Hernquist, L., & Narayan, R. 2005, ApJ, 623, L41 [NASA ADS] [CrossRef] [Google Scholar]
  39. Elsner, R. F., & Lamb, F. K. 1977, ApJ, 215, 897 [NASA ADS] [CrossRef] [Google Scholar]
  40. Ferrari, V., Miniutti, G., & Pons, J. A. 2003, MNRAS, 342, 629 [NASA ADS] [CrossRef] [Google Scholar]
  41. Friedman, J. L., & Schutz, B. F. 1978, ApJ, 222, 281 [NASA ADS] [CrossRef] [Google Scholar]
  42. Friedman, J. L., & Morsink, S. M. 1998, ApJ, 502, 714 [NASA ADS] [CrossRef] [Google Scholar]
  43. Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
  44. Gusakov, M. E., Chugunov, A. I., & Kantor, E. M. 2014, Phys. Rev. D, 90, 063001 [NASA ADS] [CrossRef] [Google Scholar]
  45. Harry, G. M., & LIGO Scientific Collaboration 2010, Class. Quant. Grav., 27, 084006 [NASA ADS] [CrossRef] [Google Scholar]
  46. Haskell, B. 2015, Int. J. Mod. Phys. E, 24, 1541007 [NASA ADS] [CrossRef] [Google Scholar]
  47. Haskell, B., Degenaar, N., & Ho, W. C. G. 2012, MNRAS, 424, 93 [Google Scholar]
  48. Hild, S., Abernathy, M., Acernese, F., et al. 2011, Class. Quant. Grav., 28, 094013 [NASA ADS] [CrossRef] [Google Scholar]
  49. Ho, W. C. G., & Lai, D. 2000, ApJ, 543, 386 [NASA ADS] [CrossRef] [Google Scholar]
  50. Ho, W. C. G., Andersson, N., & Haskell, B. 2011, Phys. Rev. Lett., 107, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  51. Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
  52. Kasen, D., & Bildsten, L. 2010, ApJ, 717, 245 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kohri, K., & Mineshige, S. 2002, ApJ, 577, 311 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kokkotas, K. D., & Stergioulas, N. 1999, A&A, 341, 110 [NASA ADS] [Google Scholar]
  55. Kouveliotou, C., Dieters, S., Strohmayer, T., et al. 1998, Nature, 393, 235 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426 [NASA ADS] [CrossRef] [Google Scholar]
  57. Lee, U. 2005, MNRAS, 357, 97 [NASA ADS] [CrossRef] [Google Scholar]
  58. Levin, Y. 1999, ApJ, 517, 328 [NASA ADS] [CrossRef] [Google Scholar]
  59. Li, W., Chornock, R., Leaman, J., et al. 2011, MNRAS, 412, 1473 [NASA ADS] [CrossRef] [Google Scholar]
  60. Lindblom, L., & Mendell, G. 2000, Phys. Rev. D, 61, 104003 [NASA ADS] [CrossRef] [Google Scholar]
  61. Lindblom, L., Owen, B. J., & Morsink, S. M. 1998, Phys. Rev. Lett., 80, 4843 [NASA ADS] [CrossRef] [Google Scholar]
  62. Lindblom, L., Mendell, G., & Owen, B. J. 1999, Phys. Rev. D, 60, 064006 [NASA ADS] [CrossRef] [Google Scholar]
  63. Lindblom, L., Owen, B. J., & Ushomirsky, G. 2000, Phys. Rev. D, 62, 084030 [NASA ADS] [CrossRef] [Google Scholar]
  64. Lindblom, L., Tohline, J. E., & Vallisneri, M. 2001, Phys. Rev. Lett., 86, 1152 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  65. MacFadyen, A. I., Woosley, S. E., & Heger, A. 2001, ApJ, 550, 410 [NASA ADS] [CrossRef] [Google Scholar]
  66. Madsen, J. 1998, Phys. Rev. Lett., 81, 3311 [NASA ADS] [CrossRef] [Google Scholar]
  67. Madsen, J. 2000, Phys. Rev. Lett., 85, 10 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  68. Mahmoodifar, S., & Strohmayer, T. 2013, ApJ, 773, 140 [NASA ADS] [CrossRef] [Google Scholar]
  69. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
  70. Metzger, B. D., Thompson, T. A., & Quataert, E. 2007, ApJ, 659, 561 [NASA ADS] [CrossRef] [Google Scholar]
  71. Michel, F. C., 1988, Nature, 333, 644 [NASA ADS] [CrossRef] [Google Scholar]
  72. Mytidis, A., Coughlin, M., & Whiting, B. 2015, ApJ, 810, 27 [NASA ADS] [CrossRef] [Google Scholar]
  73. Owen, B. J., Lindblom, L., Cutler, C., Schutz, B. F., Vecchio, A., & Andersson, N. 1998, Phys. Rev. D, 58, 084020 [NASA ADS] [CrossRef] [Google Scholar]
  74. Papazoglou, M. C., & Moustakidis, C. C. 2016, Ap&SS, 361, 98 [NASA ADS] [CrossRef] [Google Scholar]
  75. Piro, A. L., & Ott, C. D. 2011, ApJ, 736, 108 [NASA ADS] [CrossRef] [Google Scholar]
  76. Piro, A. L., & Thrane, E. 2012, ApJ, 761, 63 [NASA ADS] [CrossRef] [Google Scholar]
  77. Pringle, J. E., & Rees, M. J. 1972, A&A, 21, 1 [NASA ADS] [Google Scholar]
  78. Rezzolla, L., Lamb, F. K., & Shapiro, S. L. 2000, ApJ, 531, L139 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  79. Rezzolla, L., Lamb, F. K., Marković, D., & Shapiro, S. L. 2001a, Phys. Rev. D, 64, 104013 [NASA ADS] [CrossRef] [Google Scholar]
  80. Rezzolla, L., Lamb, F. K., Marković, D., & Shapiro, S. L. 2001b, Phys. Rev. D, 64, 104014 [NASA ADS] [CrossRef] [Google Scholar]
  81. Shapiro, S. L., & Teuklosky, S. A. 1986, Black Holes, White Dwarfs, and Neutron Stars (New York: Wiley) [Google Scholar]
  82. Shternin, P. S., & Yakovlev, D. G. 2008, Phys. Rev. D, 78, 063006 [NASA ADS] [CrossRef] [Google Scholar]
  83. Shternin, P. S., Baldo, M., & Haensel, P. 2013, Phys. Rev. C (Nucl. Phys.), 88, 065803 [NASA ADS] [CrossRef] [Google Scholar]
  84. Strolger, L. G., Dahlen, T., Rodney, S. A., et al. 2015, ApJ, 813, 93 [NASA ADS] [CrossRef] [Google Scholar]
  85. Thompson, C., & Duncan, R. C. 1995, MNRAS, 275, 255 [NASA ADS] [CrossRef] [Google Scholar]
  86. Thompson, C., & Duncan, R. C. 1996, ApJ, 473, 322 [NASA ADS] [CrossRef] [Google Scholar]
  87. Thompson, T. A., Chang, P., & Quataert, E. 2004, ApJ, 611, 380 [NASA ADS] [CrossRef] [Google Scholar]
  88. Usov, V. V. 1992, Nature, 357, 472 [NASA ADS] [CrossRef] [Google Scholar]
  89. Vasisht, G., & Gotthelf, E. V. 1997, ApJ, 486, L129 [NASA ADS] [CrossRef] [Google Scholar]
  90. Wang, S. Q., Wang, L. J., Dai, Z. G., & Wu, X. F. 2015, ApJ, 799, 107 [NASA ADS] [CrossRef] [Google Scholar]
  91. Woosley, S. E., 2010, ApJ, 719, L204 [NASA ADS] [CrossRef] [Google Scholar]
  92. Yang, S.-H., Zheng, X.-P., Pi, C.-M., & Yu, Y.-W. 2010, MNRAS, 403, 2007 [NASA ADS] [CrossRef] [Google Scholar]
  93. Yoshida, S., & Eriguchi, Y. 2000, MNRAS, 316, 917 [NASA ADS] [CrossRef] [Google Scholar]
  94. Yu, Y.-W., Cao, X.-F., & Zheng, X.-P. 2009, ApJ, 706, L221 [NASA ADS] [CrossRef] [Google Scholar]
  95. Zhang, D., & Dai, Z. G. 2010, ApJ, 718, 841 [NASA ADS] [CrossRef] [Google Scholar]
  96. Zhang, B., & Mészáros, P. 2001, ApJ, 552, L35 [NASA ADS] [CrossRef] [Google Scholar]
  97. Zhang, W., Woosley, S. E., & Heger, A. 2008, ApJ, 679, 639 [NASA ADS] [CrossRef] [Google Scholar]
  98. Zheng, X.-P., Yu, Y.-W., & Li, J.-R. 2006, MNRAS, 369, 376 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

r-mode amplitude (α), spin (ν) and toroidal magnetic field (Bt) as functions of time. The black solid line is plotted for B = 2 × 1014 G and η = 0 . The red solid or dashed lines are obtained in the case of η = 0.01 and t0 = 3000 s for B = 2 × 1014 G or B = 5 × 1014 G. The blue solid or dashed lines are obtained in the case of η = 0.1 and t0 = 300 s for B = 2 × 1014 G or B = 5 × 1014 G.

In the text
thumbnail Fig. 2

Evolution of timescales − tgw (purple lines), tB,t (brown lines) and tacc (orange lines) in the cases with η = 0.01 and t0 = 3000 s. The solid lines correspond to the case of B = 2 × 1014 G and dashed lines to B = 5 × 1014 G.

In the text
thumbnail Fig. 3

Characteristic strain amplitude of the r-mode instability for accreting magnetars locating at a distance D = 1 Mpc. The green curve corresponds to ET noise rms strain amplitude. The red, blue, magenta, and orange curves correspond to the cases: B = 2 × 1014 G, η = 0.01, and t0 = 3000 s; B = 2 × 1014 G, η = 0.1, and t0 = 300 s; B = 5 × 1014 G, η = 1, and t0 = 100 s; and B = 5 × 1014 G, η = 10, and t0 = 15 s, respectively.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.