| Issue |
A&A
Volume 602, June 2017
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201731044 | |
| Published online | 13 June 2017 | |
Three planets around HD 27894
A close-in pair with a 2:1 period ratio and an eccentric Jovian planet at 5.4 AU⋆
1 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117, Heidelberg, Germany
e-mail: trifonov@mpia.de
2 Institut für Astrophysik, Georg-August-Universität, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
3 Main Astronomical Observatory, National Academy of Sciences of the Ukraine, Ukraine
4 Landessternwarte, Zentrum für Astronomie der Universität Heidelberg, Königstuhl 12, 69117 Heidelberg, Germany
5 Department of Earth Sciences, The University of Hong Kong, Pokfulam Road, Hong Kong
6 Department of Physics, The University of Hong Kong, Pokfulman Road, Hong Kong
7 European Southern Observatory (ESO), Alonso de Cordova 3107, Vitacura, Santiago de Chile, Chile
8 UCO/Lick Observatory, University of California, Santa Cruz, CA, 95064, USA
Received: 25 April 2017
Accepted: 30 May 2017
Aims. Our new program with HARPS aims to detect mean motion resonant planetary systems around stars which were previously reported to have a single bona fide planet, often based only on sparse radial velocity data.
Methods. Archival and new HARPS radial velocities for the K2V star HD 27894 were combined and fitted with a three-planet self-consistent dynamical model. The best-fit orbit was tested for long-term stability.
Results. We find clear evidence that HD 27894 is hosting at least three massive planets. In addition to the already known Jovian planet with a period Pb≈ 18 days we discover a Saturn-mass planet with Pc≈ 36 days, likely in a 2:1 mean motion resonance with the first planet, and a cold massive planet (≈5.3 MJup) with a period Pd ≈ 5170 days on a moderately eccentric orbit (ed = 0.39).
Conclusions. HD 27894 is hosting a massive, eccentric giant planet orbiting around a tightly packed inner pair of massive planets likely involved in an asymmetric 2:1 mean motion resonance. HD 27894 may be an important milestone for probing planetary formation and evolution scenarios.
Key words: techniques: radial velocities / planetary systems / planets and satellites: dynamical evolution and stability
© ESO, 2017
1. Introduction
The radial velocity (RV) technique is very successful in determining the orbital architectures of multiple extrasolar planetary systems. In some exceptional cases N-body modeling of precise Doppler data in resonant systems can even reveal the system’s short-term dynamics and constrain the planetary true masses and mutual inclinations (Bean & Seifahrt 2009; Rivera et al. 2010; Trifonov et al. 2014). Therefore, RV multiple planetary system discoveries are fundamentally important in order to understand planet formation and evolution in general. Many RV planet discoveries, however, have been announced based on sparse data samples, and sometimes incomplete phase coverage leading to ill-determined system architectures. For example, the combined RV signal of a pair of planets in low eccentricity orbits near a 2:1 mean motion resonance (MMR) can be misinterpreted as a single planet with moderate eccentricity if the data are sparse (Anglada-Escudé et al. 2010; Wittenmyer et al. 2013; Kürster et al. 2015). In addition, the detection of long-period massive planets needs continuous precise RV measurements taken over a sufficient temporal baseline.
An example is the moderately hot (a = 0.125 AU, P ≈ 18 days) Jovian planet HD 27894 b (Moutou et al. 2005), which was discovered based on only twenty RV measurements taken with the ESO HARPS spectrograph (La Silla Observatory, Chile, Mayor et al. 2003). Recently, Kürster et al. (2015) illustrated how the sparse RV data for HD 27894 can actually be modeled well with an additional Neptune-mass planet in an inner orbit near the 2:1 resonance with the known Jovian planet. Later we found that an outer Saturn-mass planet with a period of ≈36 days provides an even better fit to the data.
We included HD 27894 in our HARPS RV monitoring program following up 35 stars that were previously reported to harbor a single planet in order to look for additional planets. The additional HARPS observations of HD 27894 confirm the existence of planet c with a 36-day period, and reveal an additional long-period RV signal consistent with a massive Jovian planet (m sini = 5.4 MJup, planet d) with a period of ≈5200 days. In this paper we present an updated orbital configuration for the HD 27894 system; according to our self-consistent N-body analysis of the RV data, the system is composed of three planets, the inner two likely in a 2:1 MMR.
The paper is organized as follows. In Sect. 2 we start with an overview of the HARPS measurements and in Sect. 3 we present results from our dynamical modeling, which reveals the three-planet system. In Sect. 4 we present a long-term dynamical analysis of HD 27894 and we discuss the possible 2:1 MMR between planets b and c. In Sect. 5 we discuss the unusual orbital architecture of the HD 27894 system.
2. HARPS data for HD 27894
HD 27894 is a non-active solar-type star of spectral type K2V with an estimated mass of 0.8 M⊙ and metallicity of [ Fe / H ] = 0.30 ± 0.07 dex (Moutou et al. 2005). The star is an ideal HARPS target, due to its low declination (δ = − 59°24′41.40″), visual brightness of V = 9.36 mag, and slow rotation period of Prot ~ 44 days (Moutou et al. 2005).
Based on the first twenty HARPS RV measurements taken from 2003 to 2005 Moutou et al. (2005) announced HD 27984 b, a Jovian planet with a minimum mass of 0.62 MJup, orbiting at a semi-major axis of 0.125 AU in a nearly circular orbit (eccentricity 0.049 ± 0.008). Subsequently, an additional 21 HARPS RVs were obtained in 2006, and one more in 2013. Thus, we found a total of 42 HARPS spectra in the ESO archive. The archival RVs already clearly showed that HD 27984 b is not alone, and so we included the star in our ongoing HARPS program aimed at finding hidden multiple planetary systems, and obtained 16 more RV measurements in 2016.
All RVs were recomputed with the SERVAL pipeline (Zechmeister et al., in prep.), which was originally developed for the CARMENES project (Quirrenbach et al. 2016). It includes a “shifting and co-adding” χ2 fitting algorithm, where one of the fitting parameters is the RV (Anglada-Escudé & Butler 2012).
The latest HARPS measurements were taken after the upgrade of the HARPS fibers in May 2015, which introduces a notable RV offset between data taken before and after the upgrade. Lo Curto et al. (2015) investigated the typical offsets introduced for various spectral types, ranging from − 2 m s-1 for M stars up to 20 m s-1 for F stars. For K stars such as HD 27894, the mean offset value is 13.4 m s-1, with a rather small dispersion of only 2.5 m s-1 among the five K stars. We thus subtracted this offset value from the post-2015 HARPS radial velocities in order to put them on the same scale as the older velocities. We also tried to fit for this RV offset, but it turns out that it is not well constrained by our HARPS data set of HD 27894 alone.
 |
Fig. 1 GLS periodograms of the RV data of HD 27894 with FAP levels of 10%, 1%, and 0.1% calculated from a bootstrap analysis. Panel a): the HARPS RVs resulted in many significant peaks especially at long periods. Panel b): after removal of the RV signal from planet d (Pb = 5174 days), the dominant peaks left are at 18.0 and 36.7 days (due to planets b and c), and at 12.0 and 57.1 days (aliases). Panel c): no significant peaks are left after fitting a 3PDM (see Table 1). |
3. RV analysis
In Fig. 1 we show the generalized Lomb-Scargle periodogram (GLS; Zechmeister & Kürster 2009) of the available HARPS data with false alarm probability (FAP) levels of 10%, 1%, and 0.1% calculated by randomly reordering 1000 bootstrap copies of the RV data (Kuerster et al. 1997). We find many significant peaks, the most significant ones around 18 and 36 days (due to planets b and c) and several longer periods at ~431, 1402, 2367, and 3990 days, one of them possibly due to planet d; the rest are likely aliases. When it is assumed that the HD 27894 system is composed only of planets b and d, our best two-planet Keplerian model (2PKM) yields reduced χ2 (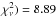 and rms = 3.05 m s-1; periods Pb,d = 18.02, 5067 days; eccentricities eb,d = 0.04, 0.34; and minimum masses mb,dsini = 0.64 and 6.20 MJup, respectively, and represents a very strong minimum in the least-constrained Pd − ed parameter space. Indeed, an outer massive companion with a ~5000 day orbit and moderate eccentricity explains the data well since subtracting its RV signal from the data also removes the power at smaller periods, except the peaks near 18 and 36 days and a few others near 12 and 57 days. The 12-day peak is a clear alias of two periods at 18 and 36 days (planets b and c), while the 57-day peak is likely an alias of the sampling frequency (likely related to the lunar cycle of ~28 days) and planet b. All significant peaks disappear when we remove planets b, c, and d (see Fig. 1).
and rms = 3.05 m s-1; periods Pb,d = 18.02, 5067 days; eccentricities eb,d = 0.04, 0.34; and minimum masses mb,dsini = 0.64 and 6.20 MJup, respectively, and represents a very strong minimum in the least-constrained Pd − ed parameter space. Indeed, an outer massive companion with a ~5000 day orbit and moderate eccentricity explains the data well since subtracting its RV signal from the data also removes the power at smaller periods, except the peaks near 18 and 36 days and a few others near 12 and 57 days. The 12-day peak is a clear alias of two periods at 18 and 36 days (planets b and c), while the 57-day peak is likely an alias of the sampling frequency (likely related to the lunar cycle of ~28 days) and planet b. All significant peaks disappear when we remove planets b, c, and d (see Fig. 1).
We thus fitted a three-planet Keplerian model (3PKM) to the RV data and obtained periods Pb,c,d = 18.02, 36.44, 5051 days; eccentricities of eb,c,d = 0.03, 0.06, 0.39; and RV semi-amplitudes of Kb,c,d = 60.8, 11.1, 89.4 m s-1, consistent with mb,c,dsini = 0.67, 0.16, and 6.02 MJup and orbital semi-major axes of ab,c,d = 0.125, 0.199, and 5.363 AU. The 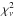 of the fit corresponds to 6.18, and the rms value to 2.55 m s-1, which represents a significant improvement over the 2PKM. The 3PKM Doppler signals are illustrated in Fig. 2.
of the fit corresponds to 6.18, and the rms value to 2.55 m s-1, which represents a significant improvement over the 2PKM. The 3PKM Doppler signals are illustrated in Fig. 2.
 |
Fig. 2 Panels a) and b): 3PKM signals of planets b and c, phase folded to their periods of about 18 and 36 days, respectively. Panel c): Doppler signal induced by planet d; panel d): residuals of the 3PKM. |
As a next step we adopted the 3PKM best-fit parameters as an initial guess for a self-consistent three-planet dynamical model (3PDM), which optimizes the planetary parameters by integrating the equations of motion in Jacobi orbital coordinates (e.g., Lee & Peale 2003; Tan et al. 2013). This model provides more realistic orbital parameter estimates than the unperturbed Keplerian model because it takes into account the gravitational interactions between the bodies while fitting the Doppler data. As we will show, this is necessary for our proposed three-planet system around HD 27894, given the large minimum masses and small period differences of planets b and c. For our dynamical fitting we assumed only coplanar and edge-on fits (i = 90°); the investigation of other orbital architectures is beyond the scope of the current paper.
The 3PDM resulted in an even smaller 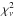 of 3.621, and rms value of 2.04 m s-1. For the outermost companion we derive a period of Pd = 5174 d (ad = 5.45 AU), dynamical mass of md = 5.4 MJup, and moderate eccentricity of ed = 0.389. The inner planets have Pb = 18.02 days and Pc = 36.07 days, low eccentricities of eb = 0.05 and ec = 0.015, and minimum dynamical masses of mb = 0.664 MJup and mc = 0.162 MJup, suggesting a Jupiter- and a Saturn-mass planet interacting gravitationally, possibly in a 2:1 MMR. The 3PDM best-fit parameters and their uncertainties valid for JD = 2 452 941.826 are listed in Table 1. The asymmetric uncertainties of the orbital parameters were estimated by drawing 5000 model independent bootstrap synthetic samples (e.g., Press et al. 1992), fitted with a 3PDM.
of 3.621, and rms value of 2.04 m s-1. For the outermost companion we derive a period of Pd = 5174 d (ad = 5.45 AU), dynamical mass of md = 5.4 MJup, and moderate eccentricity of ed = 0.389. The inner planets have Pb = 18.02 days and Pc = 36.07 days, low eccentricities of eb = 0.05 and ec = 0.015, and minimum dynamical masses of mb = 0.664 MJup and mc = 0.162 MJup, suggesting a Jupiter- and a Saturn-mass planet interacting gravitationally, possibly in a 2:1 MMR. The 3PDM best-fit parameters and their uncertainties valid for JD = 2 452 941.826 are listed in Table 1. The asymmetric uncertainties of the orbital parameters were estimated by drawing 5000 model independent bootstrap synthetic samples (e.g., Press et al. 1992), fitted with a 3PDM.
3.1. Significance of the three-planet dynamical model
The RV signals from planets b and d are large and can be well explained with periodic Keplerian motion. Planet c, however, has Pc ≈ 2Pb and 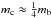 , thus yielding a smaller RV semi-amplitude (11.57 m s-1) than its more massive neighbors. Since we still have relatively sparse RV data to strongly constrain a three-planet system, we need to exclude the possibility that the supposed planet c is not real.
, thus yielding a smaller RV semi-amplitude (11.57 m s-1) than its more massive neighbors. Since we still have relatively sparse RV data to strongly constrain a three-planet system, we need to exclude the possibility that the supposed planet c is not real.
In order to convince ourselves of the existence of planet c, we qualitatively compared a two-planet dynamical model (2PDM) consisting only of planets b and d with our 3PDM. While the best 2PDM (without planet c) yields 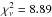 and rms = 3.05 m s-1, a 3PDM (including planet c) yields
and rms = 3.05 m s-1, a 3PDM (including planet c) yields  and rms = 2.04 m s-1, which – according to the F-Test – is a significantly better fit (FAP = 9.1 × 10-8). Similarly, the best 3PKM with the same number of fitting parameters as the 3PDM has
and rms = 2.04 m s-1, which – according to the F-Test – is a significantly better fit (FAP = 9.1 × 10-8). Similarly, the best 3PKM with the same number of fitting parameters as the 3PDM has 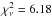 and rms = 2.55 m s-1, showing that including the dynamical interactions between planets b and c indeed leads to a better fit.
and rms = 2.55 m s-1, showing that including the dynamical interactions between planets b and c indeed leads to a better fit.
Best edge-on coplanar 3PDM for HD 27894.
4. System long-term dynamics
The long-term dynamical analysis of our three-planet model was carried out using the SyMBA symplectic integrator (Duncan et al. 1998), modified to work directly with the best-fit Jacobi orbits. We integrated the system for 10 Myr with a step of 0.1 days to ensure accurate simulation and high orbital phase resolution. We monitored the evolution of the planetary semi-major axes ab, ac, ad and eccentricities eb, ec, ed as a function of time to assure that the system remains regular and well separated at any given time of the simulation. Any deviation of the planetary semi-major axes by more than 20% from their starting values, or eccentricities leading to crossing orbits, were considered unstable.
4.1. Stability of the three-planet system
We find that the HD 27894 system is generally stable for 10 Myr. The orbital evolution is regular with no significant configuration anomalies. The massive outer planet HD 27984 d experiences almost no change in its orbital separation and eccentricity, staying at ad = 5.4 AU, ed = 0.39 through the course of the integration. Owing to the large separation, the secular perturbation of the inner pair of planets due to planet d is negligible.
Planets b and c, however, are dynamically very active, which is expected given their large masses and small orbital separation. They have a period ratio close to 2:1, and mean eccentricities of eb = 0.036 and ec = 0.047. As a large-scale stability test we integrated our 5000 3PDM bootstrap fits for 10 kyr and and we find overall similar orbital behavior. Thus, we conclude that the HD 27984 system is long-term stable.
4.2. A closer look at the inner pair
The period ratio close to 2:1 suggests that the inner planets b and c are in resonance. A 2:1 MMR is the lowest order resonance characterized by the two resonance angles θ1 = λb − 2λc + ϖb,θ2 = λb − 2λc + ϖc (where λb,c = Mb,c + ϖb,c is the mean longitude of planet b and c, respectively; see Lee 2004). At least one of these variables must librate to find the system in a 2:1 MMR. In addition, the secular resonant angle Δω = ϖb - ϖc = θ1 − θ2 is an important indicator for a libration in a secular resonance.
 |
Fig. 3 One-hundred year time interval of the orbital evolution of HD 27894 b and c, with initial eccentricities eb = 0.052 and ec = 0.035 (within the formal uncertainties of the 3PDM). In this configuration the planetary eccentricity eb oscillates between 0.02 and 0.07, and ec between 0.02 and 0.06, with mean values of 0.050 and 0.037, respectively. The resonance angles θ1 ≈ − 50°, θ2 ≈ − 100°, and Δω ≈ 50° are oscillating with large amplitudes in a clear asymmetric 2:1 MMR. |
We examined the orbital evolution of θ1,θ2, and Δω of the 3PDM and we find that all three angles circulate from 0° to 360°, indicating a regular secular motion with a 2:1 period ratio, but no explicitly resonant motion. According to Lee (2004) a stable 2:1 MMR configuration with both θ1 and θ2 librating can be achieved by smooth migration capture. For cases where a pair of planets with mass ratio of 2.75 ≲ mb/mc ≲ 5 migrates with sufficiently small eccentricities, Lee (2004) suggests that θ1 and θ2 could in principle be trapped in an anti-aligned libration leading to Δω = 180°, or in the case of larger eccentricities at any angle exhibiting an asymmetric 2:1 MMR (see also Beaugé et al. 2003; Ferraz-Mello et al. 2003).
Therefore, with the aim of understanding how the dynamical properties of planets b and c depend on their eccentricities and orbital alignment, we studied a large number of three-planet configurations similar to the 3PDM. We systematically varied eb, ec, ωb, ωc, Mb, and Mc within their 1σ bootstrap confidence levels, while keeping the remaining parameters fixed at the 3PDM best-fit values. We integrated these configurations for 10 kyr, and we evaluated whether the resonance angles θ1,θ2, and Δω were librating. We found that when eb and ec are very small, the two planets exhibit an anti-aligned resonance with θ1 ≈ 0°, θ2 ≈ 180°, and Δω ≈ 180°, which is expected if planets b and c have been trapped in a 2:1 MMR during migration with near zero eccentricities. However, when eb and ec are close to their 1σ upper limits, we found configurations with θ1≈ − 50°, θ2 ≈ − 100°, and Δω ≈ 50°, which is an asymmetric 2:1 MMR, as predicted by Beaugé et al. (2003), Ferraz-Mello et al. (2003), and Lee (2004). Perhaps this is the more likely scenario, since the two giant planets can have somewhat larger eccentricities during migration. A 100 yr time interval illustrating the evolution of such an asymmetric 2:1 MMR is shown in Fig. 3. This configuration has eb = 0.052 and ec = 0.035 initially, which is within the formal uncertainties of the 3PDM and thus represents a possible configuration of HD 27894’s inner planet pair.
5. Discussion
The co-existence of a massive, distant, and moderately eccentric Jovian planet and a possibly resonant inner pair of massive planets makes the HD 27984 system truly unique. The orbital configuration may suggest that planet formation and evolution depends strongly on the disk properties and migration rate of the planets during the protoplanetary disk stage. The inner pair of planets has probably been trapped in a 2:1 MMR by smooth migration capture, while the outer massive Jovian planet migrated to 5.4 AU before the circumstellar disk evaporated, thus halting the migration.
There are some strong indications that the inner two planets are in a 2:1 MMR, although so far we have been unable to definitely confirm the resonance based on the best-fit dynamics. For the formal best fit, the mean period ratio of the inner planets is very close to 2:1, but the resonance angles θ1 and θ2 circulate from 0° to 360°. Our first attempt to find a stable librating solution within the 1σ confidence region of our 3PDM, however, was successful. We identified resonant configurations where we either see anti-aligned resonances with Δω ≈ 180°, or an asymmetric configuration where Δω≈ 50° and θ1 ≈ − 50°, θ2 ≈ − 100°. To our knowledge, HD 27894 is the first system to show signs of an asymmetric 2:1 MMR in agreement with the migration theory for a mass ratio of 4 ≲ mb/mc.
Nevertheless, more work and more data are needed to understand and resolve the possible resonance between planets b and c, as well as its origin. The current data allowed us to conclusively confirm the presence of three planets, but more data are needed to confirm the resonant nature of the inner planets and to further constrain the orbital parameters, especially of HD 27894 d. The outermost planet is currently sparsely covered by the RV data and thus we cannot exclude the possibility that its true Pd, ed, and mdsini are not within our 3PDM best-fit uncertainties. We plan to continue our HARPS monitoring of HD 27894, which will allow us to extend our orbital RV analysis using a multidimensional parameter grid-search or Bayesian framework for parameter estimation, and to carry out a more conclusive long-term dynamical analysis.
The planetary system around HD 27894 is important for probing planetary formation and evolution scenarios and illustrates the importance of further follow-up of RV planet hosts.
Acknowledgments
We thank Megan Bedell and Oscar Barragan for observations of this target in the framework of observing time exchange. We also thank Gaspare Lo Curto for very useful discussions during the course of our survey. M.Z. has received financial support from the DFG under RE 1664/12-1. Z.O.V. acknowledges a German Academic Exchange Service (DAAD) stipend (91613113). M.H.L. was supported in part by the Hong Kong RGC grant HKU 7024/13P. This work used the python package astroML (VanderPlas et al. 2012) for the calculation of the GLS periodogram. We thank the anonymous referee for the constructive comments that helped to improve this paper.
References
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., López-Morales, M., & Chambers, J. E. 2010, ApJ, 709, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., & Seifahrt, A. 2009, A&A, 496, 249 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Beaugé, C., Ferraz-Mello, S., & Michtchenko, T. A. 2003, ApJ, 593, 1124 [Google Scholar]
- Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferraz-Mello, S., Beaugé, C., & Michtchenko, T. A. 2003, Cel. Mech. Dyn. Astron., 87, 99 [Google Scholar]
- Kuerster, M., Schmitt, J. H. M. M., Cutispoto, G., & Dennerl, K. 1997, A&A, 320, 831 [NASA ADS] [Google Scholar]
- Kürster, M., Trifonov, T., Reffert, S., Kostogryz, N. M., & Rodler, F. 2015, A&A, 577, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. H. 2004, ApJ, 611, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. H., & Peale, S. J. 2003, ApJ, 592, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- LoCurto, G., Pepe, F., Avila, G., et al. 2015, The Messenger, 162, 9 [NASA ADS] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Moutou, C., Mayor, M., Bouchy, F., et al. 2005, A&A, 439, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing (CUP) [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 990812 [Google Scholar]
- Rivera, E. J., Laughlin, G., Butler, R. P., et al. 2010, ApJ, 719, 890 [Google Scholar]
- Tan, X., Payne, M. J., Lee, M. H., et al. 2013, ApJ, 777, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Trifonov, T., Reffert, S., Tan, X., Lee, M. H., & Quirrenbach, A. 2014, A&A, 568, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VanderPlas, J., Connolly, A. J., Ivezic, Z., & Gray, A. 2012, in Proc. Conf. Intelligent Data Understanding (CIDU), 47 [Google Scholar]
- Wittenmyer, R. A., Wang, S., Horner, J., et al. 2013, ApJS, 208, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Additional table
HARPS radial velocity measurements for HD 27894.
All Tables
All Figures
 |
Fig. 1 GLS periodograms of the RV data of HD 27894 with FAP levels of 10%, 1%, and 0.1% calculated from a bootstrap analysis. Panel a): the HARPS RVs resulted in many significant peaks especially at long periods. Panel b): after removal of the RV signal from planet d (Pb = 5174 days), the dominant peaks left are at 18.0 and 36.7 days (due to planets b and c), and at 12.0 and 57.1 days (aliases). Panel c): no significant peaks are left after fitting a 3PDM (see Table 1). |
| In the text | |
 |
Fig. 2 Panels a) and b): 3PKM signals of planets b and c, phase folded to their periods of about 18 and 36 days, respectively. Panel c): Doppler signal induced by planet d; panel d): residuals of the 3PKM. |
| In the text | |
 |
Fig. 3 One-hundred year time interval of the orbital evolution of HD 27894 b and c, with initial eccentricities eb = 0.052 and ec = 0.035 (within the formal uncertainties of the 3PDM). In this configuration the planetary eccentricity eb oscillates between 0.02 and 0.07, and ec between 0.02 and 0.06, with mean values of 0.050 and 0.037, respectively. The resonance angles θ1 ≈ − 50°, θ2 ≈ − 100°, and Δω ≈ 50° are oscillating with large amplitudes in a clear asymmetric 2:1 MMR. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


