| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 5 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201630246 | |
| Published online | 04 April 2017 | |
September epsilon Perseid cluster as a result of orbital fragmentation
1 Astronomical Institute, CAS, Fričova 298, 25165 Ondřejov, Czech Republic
e-mail: pavel.koten@asu.cas.cz
2 Institut de Mécanique Céleste et de Calcul des Éphémérides, 77 avenue Denfert-Rochereau, 75014 Paris, France
3 Institute of Atmospheric Physics, CAS, 14131 Prague, (station Nýdek), Czech Republic
Received: 14 December 2016
Accepted: 13 February 2017
Context. A bright fireball was observed above the Czech Republic on September 9, 2016, at 23:06:59 UT. Moreover, the video cameras at two different stations recorded eight fainter meteors flying on parallel atmospheric trajectories within less than 2 s. All the meteors belong to the September epsilon Perseid meteor shower. The measured proximity of all meteors during a very low activity meteor shower suggests that a cluster of meteors was observed.
Aims. The goal of the paper is first to determine whether this event was a random occurrence or a real meteor cluster and second, if it was a cluster, to determine the epoch and at what distance from the Earth the separation of the particles occurred.
Methods. The atmospheric trajectories of the observed meteors, masses, and relative distances of individual particles were determined using a double-station observation. According to the distances and masses of the particles, the most probable distance and time of fragmentation is determined.
Results. The observed group of meteors is interpreted as the result of the orbital fragmentation of a bigger meteoroid. The fragmentation happened no earlier than 2 or 3 days before the encounter with the Earth at a distance smaller than ~0.08 AU from the Earth.
Key words: meteorites, meteors, meteoroids
© ESO, 2017
1. Introduction
Visual and telescopic observers have repeatedly reported that some meteors appear in pairs or even groups. As these observational methods are rather subjective, more reliable results can be provided by instrumental observations. Earlier studies of the major meteor showers and sporadic meteors usually lead to contradictory results. A comprehensive overview of this matter is provided by Porubčan et al. (2002), which analysed recent Leonid storms observed in 1966, 1969, and 1999, as well as April Lyrid activity observed by radar in 1982. The authors used statistical methods to distinguish non-random grouping of meteors and found positive results for the youngest streams. In the case of older showers no grouping of meteoroids over the random level was found.
Hapgood & Rothwell (1981) reported a double-station television observation of three Perseid meteors arriving within a time interval of 1.3 s on parallel trajectories on August 12, 1977. They showed that the probability of a random clustering in this case is very small (~3 × 10-11). The event is interpreted as a result of a fragmentation which happened at least 1700 km above the Earth’s surface. The upper limit of the breakup distance was constrained between 0.004 and 0.04 AU.
Another unusual cluster of five nearly simultaneous meteors was observed by Piers & Hawkes (1993) on October 18, 1985. All the meteors appeared within a limited area of the sky: the largest angular separation was 1.2°, while the temporal spread for similar positions was only 0.1 s. It corresponds to a spatial separation of about 4 km. However, because this observation was performed with a single-station observation the shower membership was uncertain.
Leonid meteor storms at the turn of the century provided a unique opportunity to test the hypothesis of the meteor clustering. Kinoshita et al. (1999) observed between 100 and 150 meteors which appeared within 2 s during the 1997 Leonids. Watanabe et al. (2002) observed at least 15 meteors within four seconds during the Leonids 2002. Both observations were only single station. Double-station data of another event were provided by Watanabe et al. (2003) who also observed 38 meteors within 2 s during the 2002 Leonid campaign; the paper summarized all three events as the cases of meteor clusters and discussed their origin.
In this paper we report the double-station observation of a September epsilon Perseid cluster consisting of one fireball and eight fainter meteors.
 |
Fig. 1 Detailed view of the EN090916 SPE fireball recorded by the Digital Autonomous Fireball Observatory (DAFO) at the Czech station Kocelovice. The image of the fireball is interrupted by electronic shutter at a frequency of 16 Hz. |
2. Observations and results
2.1. Data acquisition and processing
The fireball belonging to the September epsilon Perseid meteor shower (208 SPE according to the IAU Meteor Data Center list) was observed by the cameras of the Czech fireball network (Spurný 2016) on September 9, 2016, at 23:06:59 UT (Fig. 1). Based on photographic records taken from five stations closest to the fireball, its atmospheric trajectory and heliocentric orbit were calculated (Table 1) with very high precision1.
Radiant and heliocentric orbit (J2000.0) of the fireball EN090916.
 |
Fig. 2 Composite image of the fireball and eight faint meteors trails. The trail without a number is a fireball reflection. |
The same event was also recorded by the digital video camera system MAIA (Koten et al. 2011; Vítek et al. 2016) deployed at the Kunžak station (λ = 15°12′ E; ϕ = 49°6′ N, altitude = 652 m). This camera records digital video at 61.15 frames per second in 10 bits of the signal depth, and provides a circular field of view (FOV) with a diameter of about 50°. The automatic detection software dMAIA (Koten et al. 2014) revealed eight fainter meteors accompanying the fireball on parallel paths recorded within less than two seconds (Fig. 2). Another video record was obtained by a Watec 910HX camera dedicated to transient luminous events observation at Nýdek station (λ = 18°46′ E; ϕ = 49°40′ N, altitude = 475 m). The FOV of this camera is about 49° × 39°. The UFOCapture software is used for the detection of meteors and other events (SonotaCo 2009). The second record shows the fireball and five faint meteors. The distance between the two stations is 266 km, and the intersection angle of the planes was about 20°.
Beginning HB and end HE height, zenith distance of the radiant ZD, maximum brightness Mmax and photometric mass mphot of the video meteors.
The video records from the stations were both processed using MAIAMetPho software (Koten et al. 2016). This is a semi-automatic software which enables the positional and the photometric measurements of the meteors. The atmospheric trajectories and heliocentric orbits were computed using a least-squares method (Borovicka 1990). More details about the method are provided in Koten et al. (2004). The photometric mass of the meteor was derived from the measured magnitudes using the Ceplecha formula (Ceplecha 1988), 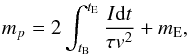 (1)where I is the luminosity of the meteor computed from absolute meteor brightness MV using I = 10− 0.4 ∗ MV, v is the meteor velocity, mE is the terminal mass (zero in this case), τ is the luminous efficiency, and tB/tE is the beginning/end time of the meteor.
(1)where I is the luminosity of the meteor computed from absolute meteor brightness MV using I = 10− 0.4 ∗ MV, v is the meteor velocity, mE is the terminal mass (zero in this case), τ is the luminous efficiency, and tB/tE is the beginning/end time of the meteor.
The precision of the video data is lower than with the fireball network data, but the video camera recorded the initial part of the luminous trajectory when the meteor did not reach the sensitivity limit of the fireball cameras. The beginning height from the photographic cameras was 118 km, whereas the first video appearance of the meteor was at almost 145 km. On the other hand a terminal point at 74 km was the same for both video and photographic data.
 |
Fig. 3 Three-dimensional plot of the meteor trajectories in the atmosphere. The time from the beginning of the fireball is colour-coded (scale in seconds). All the trails are projected onto the area of about 11 500 km2. The single-station meteors are marked with an asterisk. |
2.2. Atmospheric trajectories of meteors
In addition to the fireball, the meteors’ positions and brightness were measured using the video records from both stations. According to the timing and relative position of the fireball, the pairs were identified and their trajectories and orbits computed. The remaining three meteors were treated as single-station ones by assuming the same apparent radiant and velocity as the fireball. Using this assumption their trajectories and orbits were estimated. Since the Watec camera is less sensitive than the image intensifier video, and the distance of the second station from the meteors was quite high (between 350 and 400 km), the Nýdek records consist of only 3 to 5 frames. The results for all of the meteors are summarized in Table 2. We use the frame number of the Kunžak camera as the time reference. With a frame rate of 61.15 frames per second we conclude that all the meteors appeared within 1.5 s.
Given the atmospheric trajectories, we can analyse the relative positions of the individual meteors. Figure 3 shows a 3D plot of the meteor trajectories in the atmosphere. All the trails are projected into an area of 1.2° × 1.2° on the Earth’s surface. At the latitude of 50° it translates to approximately 86 × 133 km.
As the meteors appeared at slightly different times it is more useful to calculate the absolute distance of the individual fragments than to measure the distances between their trails. Table 3 shows that the closest pair consists of meteors Nos. 1 and 5, whose trails were only separated by 14 kilometres. On the other hand, trail No. 3 was separated from the main fireball by 105 km. The fireball also has the highest mean distance to all the other meteors followed by No. 3. It is interesting that all the faint meteors appeared to the right of the fireball path (i.e. opposite the Sun). Although the fireball did not appear in the middle of the FOV, there is still enough space on the left side to reveal one or two meteors in the cases when the cluster was centred on it, but no meteor was recorded in that area. This may support the idea that smaller meteoroids were pushed from the main body in a preferred anti-Sun direction.
Relative distances of individual meteors in the atmosphere (in km).
3. Discussion
3.1. Statistics
The activity of the September epsilon Perseid meteor shower was very low during the night of the observation. The MAIA camera recorded about five additional meteors with similar flight direction and angular velocity to the fireball within 8.5 h. When clusters of meteors were observed in the past, it usually happened during high meteor shower activity or even a meteor storm.
If the occurrence of the meteor is random, then the number of expected clusters N is given by the Poisson distribution (Porubčan et al. 2002; Sampson 2007) 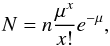 (2)where n is the number of intervals, μ is the mean rate of meteors per interval, and x is the number of meteors in the cluster. If we take 2 s as an interval (all the meteors appeared within 2 s), then n = 1800. Observing one meteor per hour gives us μ = 0.00056. The number of meteors within the cluster is x = 9. Then the expected number of clusters is 3 × 10-32. Therefore, the probability that such a cluster of nine meteors appears coincidentally is practically zero.
(2)where n is the number of intervals, μ is the mean rate of meteors per interval, and x is the number of meteors in the cluster. If we take 2 s as an interval (all the meteors appeared within 2 s), then n = 1800. Observing one meteor per hour gives us μ = 0.00056. The number of meteors within the cluster is x = 9. Then the expected number of clusters is 3 × 10-32. Therefore, the probability that such a cluster of nine meteors appears coincidentally is practically zero.
Japanese radio astronomers reported some activity during the night of September 9–10 with a narrow peak reaching a zenith hourly rate of ~25 (Sugimoto 2016). Taking into account such activity we obtain N = 9 × 10-20. The probability of observing a random cluster is extremely small. We conclude that a real cluster of meteors was observed.
3.2. Meteoroid velocity dispersion
The fireball meteoroid has a mass more than 100 times higher than the other meteoroids in the cluster. We suppose that smaller meteoroids separated from this body, and then use the distances of all the fragments as a clue to the origin of the cluster.
First we look at the possibility that the fragments were released directly from the parent comet. The SPE parent body is unknown. The heliocentric trajectories suggest that this body could be a long-period comet. We can use an analogy with the Leonid meteor shower. Vaubaillon et al. (2005) considered ejection velocities between 10 and 40 m s-1 for comet Temple-Tuttle. The dispersion of velocities is of the order of 10 m s-1. With such a velocity the separation distance with the parent body can reach a distance of 100 km within only 3 h. This makes ejection from the comet as the source of this cluster unrealistic.
Relative distances up to 100 km strongly suggest that the separation happened before the meteoroid entered the atmosphere. It cannot occur in the atmosphere. Travelling at a velocity of 66 km s-1 with respect to the Earth implies that a gap between 10 and 100 km should be reached within a few seconds. The separation velocities should be of the order of 10–100 km s-1.
We assume a mean relative velocity of the fragments to be 1 m s-1. In such a case the mean distance of the fragments from the fireball (69 km) would be reached within 19.2 h and the separation would happen at a distance of about 4.5 million kilometres from the Earth. Assuming 19.2 h for the closest (32 km for No. 2) and the most distant (105 km for No. 3) fragments we get a range of relative velocities between 0.5 and 1.5 m s-1. For comparison, Hapgood & Rothwell (1981) suppose a range of relative velocities from 0.6 to 6.6 m s-1 for the fragmentation caused by a collision with a small dust particles.
3.3. Cluster as a result of fragmentation
We can estimate the upper limit for the time of parent meteoroid breakup. Recent results of the Rosetta mission have shown that extremely fluffy and fragile particles are released from comet nuclei (Langevin et al. 2016). As a consequence of such loose cohesion forces, it is possible that the fragmentation happens at zero ejection velocity. We assume the same density ρ = 800 kg m-3 for the parent meteoroid and fragments. Such density is consistent with properties of “regular cometary material” (Ceplecha 1988). The size of the parent meteoroid and fragments is therefore ~2.6 cm and ~1.3–3.7 mm, respectively. We assume that small fragments move only due to the action of solar radiation pressure. The relative position of meteors and the fireball with respect to the direction to the Sun is in agreement with this assumption. We do not consider the tangential component of the acceleration, which is important for the long-term evolution of the orbit (Poynting-Robertson effect) but is negligible in our case. The corresponding accelerations in the opposite direction to the Sun depend on the fragments’ diameter d and can be estimated as (Finson & Probstein 1968) 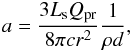 where Ls is the solar luminosity, Qpr = 1 is the radiation pressure efficiency factor, c is the speed of light, and r is the heliocentric distance.
where Ls is the solar luminosity, Qpr = 1 is the radiation pressure efficiency factor, c is the speed of light, and r is the heliocentric distance.
From the values of acceleration and displacements of the fragments from the most massive meteoroid (see Table 3), the upper limit for the time of the fragmentation event can be determined. For particular fragments we obtain values between 1.4 days to 3 days. From the median value, we can roughly estimate that the fragmentation of the parent meteoroid happened no earlier than 2.1 days before encounter with the Earth at less than 0.08 AU from the Earth. We can obtain very similar results if another value of density ρ, appropriate for regular cometary material, is used.
In order to constrain the maximum age of the fragmentation we have also simulated the ejection of fragments at zero ejection velocity, following the method by Vaubaillon et al. (2005). The distance between the parent fragment and other subfragments was computed. The simulations were run for sub-mm and mm-sized particles. Figure 4 shows the minimum, maximum, and median distance of the fragments from the main parent as a function of time after the release. Given our measurements of the distance between the observed fragments, we conclude again that, even for zero ejection velocity, the fragmentation cannot have occurred earlier than a few days prior to the observations. This shows that, regardless of the ejection process, the fragmentation was very young at the time of the observations.
 |
Fig. 4 Minimum, maximum (dashed lines), and median (solid lines) distance of milimetre (blue) and submilimetre-sized (red) particles from the parent fragment. |
Our findings are in agreement with a generally accepted explanation that meteor clusters are produced by breakups of parent meteoroids before their collision with the Earth (Hapgood & Rothwell 1981; Watanabe et al. 2003). Watanabe et al. (2003) prefers thermal effects at perihelion in the case of the Leonid meteoroid cluster, while Hapgood & Rothwell (1981) assumed collision with a dust particle in the case of a group of three Perseid meteors. Another possible mechanism can be rotational bursting.
We now briefly discuss possible scenarios of fragmentation. The collisions can be either catastrophic, causing the destruction of both the projectile and the target particles, or erosive, resulting in the erosion of smaller particles from the target and the volatilization of the projectile (Grün et al. 1985). Since we observed one bright fireball and eight faint meteors it seems that – if the cluster is a result of the collision with a dust particle – it was an erosive collision. In this case the target body survived the collision and a group of smaller particles separated from it. Their relative velocities with respect to the main body depend on the specific condition of the collision, i.e. the velocity of the projectile, the angle of the collision, the strength of both projectile and target, etc.
Another possibility is the rotational bursting mechanism. Meteoroids rotate at their release from the parent cometary nucleus (Čapek 2014). The rotation speed continues to increase, due to the action of reflected sunlight on their irregular surface, and it can finally reach the bursting limit (Paddack 1969). We can consider that the small fragments are released from the surface of the main meteoroid. It can be simply estimated that the observed dispersion of small fragments can be reached within 2.1 days (i.e. peripheral speed of the main meteoroid ~0.13 m s-1) if the mechanical strength of the meteoroid is of the order of 100 Pa. More detailed analysis is, however, beyond the scope of this paper and we postpone it to future papers.
It seems that both scenarios are possible and our observational data does not allow us to pinpoint the exact mechanism of the fragmentation.
4. Conclusions
A cluster of a fireball and eight fainter meteors occurring within 1.5 s was observed using photographic and video cameras. All the meteors belong to the September epsilon Perseid meteor shower (208 SPE). It was shown that statistically such clustering cannot be a random event. The probability of a random appearance of such a compact group of meteors is lower than 10-19. It means that a real meteor cluster was observed. Previously reported clusters were usually observed during high activity of strong meteor showers. This is not the case of this event. All the meteors belong to a very low-activity meteor shower, which makes this observation even more important.
It is evident that the cluster is a result of fragmentation in interplanetary space. Taking into account the size of the meteoroids, we can say that the fragmentation occurred no earlier than 2 or 3 days before entering the Earth’s atmosphere assuming zero relative velocity. This was also confirmed by the numerical simulation of the fragment movements done for sub-mm and mm-sized particles, which showed that the observed separation of the particles can be reached within several days of the fragmentation point. As the zero initial velocity of the fragments is unrealistic, it is actually probable that the fragmentation occurred even closer to the Earth.
We cannot determine what fragmentation mechanism was responsible for this event. We see that erosion collision and rotational bursting are both possible scenarios. Identification of the mechanisms which lead to the creation of such clusters is one of the tasks for future works.
Acknowledgments
This work was supported by the Grant Agency of the Czech Republic grants 14-25251S and 16-00761S, Praemium Academiae from the Czech Academy of Sciences, the Czech-France bilateral project 7AMB16FR025 from Ministry of Education, Youth and Sport, and the institutional project RVO:67985815. M. Popek acknowledges support from the Grant Agency of the Czech Republic grant 14-31899S. Simulations were performed at the CINES super-computer facility. Finally we thank the anonymous referee, who helped us to improve the paper.
References
- Borovicka, J. 1990, Bulletin of the Astronomical Institutes of Czechoslovakia, 41, 391 [Google Scholar]
- Ceplecha, Z. 1988, Bulletin of the Astronomical Institutes of Czechoslovakia, 39, 221 [Google Scholar]
- Čapek, D. 2014, A&A, 568, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finson, M. J., & Probstein, R. F. 1968, ApJ, 154, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Grün, E., Zook, H. A., Fechtig, H., & Giese, R. H. 1985, Icarus, 62, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Hapgood, M. A., & Rothwell, P. 1981, Nature, 290, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Kinoshita, M., Maruyama, T., & Sagayama, T. 1999, Geophys. Res. Lett., 26, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Koten, P., Borovička, J., Spurný, P., Betlem, H., & Evans, S. 2004, A&A, 428, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koten, P., Fliegel, K., Vítek, S., & Páta, P. 2011, Earth Moon and Planets, 108, 69 [Google Scholar]
- Koten, P., Páta, P., Fliegel, K., & Vítek, S. 2014, in Proc. International Meteor Conference, Poznan, Poland, 22–25 August 2013, eds. M. Gyssens, P. Roggemans, & P. Zoladek, 53 [Google Scholar]
- Koten, P., Štork, R., Páta, P., Fliegel, K., & Vítek, S. 2016, in International Meteor Conference Egmond, the Netherlands, 2–5 June 2016, eds. A. Roggemans, & P. Roggemans, 133 [Google Scholar]
- Langevin, Y., Hilchenbach, M., Ligier, N., et al. 2016, Icarus, 271, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Paddack, S. J. 1969, J. Geophys. Res., 74, 4379 [NASA ADS] [CrossRef] [Google Scholar]
- Piers, P. A., & Hawkes, R. L. 1993, WGN, J. International Meteor Organization, 21, 168 [NASA ADS] [Google Scholar]
- Porubčan, V., Tóth, J., & Yano, H. 2002, Contributions of the Astronomical Observatory Skalnate Pleso, 32, 132 [NASA ADS] [Google Scholar]
- Sampson, R. D. 2007, J. Roy. Astron. Soc. Canada, 101, 57 [NASA ADS] [Google Scholar]
- SonotaCo. 2009, WGN, J. International Meteor Organization, 37, 55 [Google Scholar]
- Spurný, P. 2016, in Asteroids: New Observations, New Models, eds. S. R. Chesley, A. Morbidelli, R. Jedicke, & D. Farnocchia, IAU Symp., 318, 69 [Google Scholar]
- Sugimoto, H. 2016, 2016 Sept. epsilon Perseids and epsilon Eridanids Radio results, http://www5f.biglobe.ne.jp/hro/Flash/2016/SPE/index.html [Google Scholar]
- Vaubaillon, J., Colas, F., & Jorda, L. 2005, A&A, 439, 761 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vítek, S., Páta, P., Koten, P., & Fliegel, K. 2016, Sensors, 16, 1493 [CrossRef] [Google Scholar]
- Watanabe, J.-I., Sekiguchi, T., Shikura, M., Naito, S., & Abe, S. 2002, PASJ, 54, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, J.-I., Tabe, I., Hasegawa, H., et al. 2003, PASJ, 55, L23 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Beginning HB and end HE height, zenith distance of the radiant ZD, maximum brightness Mmax and photometric mass mphot of the video meteors.
All Figures
 |
Fig. 1 Detailed view of the EN090916 SPE fireball recorded by the Digital Autonomous Fireball Observatory (DAFO) at the Czech station Kocelovice. The image of the fireball is interrupted by electronic shutter at a frequency of 16 Hz. |
| In the text | |
 |
Fig. 2 Composite image of the fireball and eight faint meteors trails. The trail without a number is a fireball reflection. |
| In the text | |
 |
Fig. 3 Three-dimensional plot of the meteor trajectories in the atmosphere. The time from the beginning of the fireball is colour-coded (scale in seconds). All the trails are projected onto the area of about 11 500 km2. The single-station meteors are marked with an asterisk. |
| In the text | |
 |
Fig. 4 Minimum, maximum (dashed lines), and median (solid lines) distance of milimetre (blue) and submilimetre-sized (red) particles from the parent fragment. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


