| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201629533 | |
| Published online | 14 March 2017 | |
Wings of the butterfly: Sunspot groups for 1826–2015⋆
1 Space Climate Research Unit, University of Oulu, 90014 Oulu, Finland
e-mail: Ilya.Usoskin@oulu.fi
2 Sodankylä Geophysical Observatory, University of Oulu, 90014 Oulu, Finland
3 Leibniz Institute for Astrophysics Potsdam (AIP), 14482 Potsdam, Germany
4 Institut für Physik und Astronomie, Universität Potsdam, 14476 Potsdam, Germany
Received: 16 August 2016
Accepted: 9 December 2016
The spatio-temporal evolution of sunspot activity, the so-called Maunder butterfly diagram, has been continously available since 1874 using data from the Royal Greenwich Observatory, extended by SOON network data after 1976. Here we present a new extended butterfly diagram of sunspot group occurrence since 1826, using the recently digitized data from Schwabe (1826–1867) and Spörer (1866–1880). The wings of the diagram are separated using a recently developed method based on an analysis of long gaps in sunspot group occurrence in different latitude bands. We define characteristic latitudes, corresponding to the start, end, and the largest extent of the wings (the F, L, and H latitudes). The H latitudes (30°–45°) are highly significantly correlated with the strength of the wings (quantified by the total sum of the monthly numbers of sunspot groups). The F latitudes (20°–30°) depict a weak tendency, especially in the southern hemisphere, to follow the wing strength. The L latitudes (2°–10°) show no clear relation to the wing strength. Overall, stronger cycle wings tend to start at higher latitudes and have a greater wing extent. A strong (5–6)-cycle periodic oscillation is found in the start and end times of the wings and in the overlap and gaps between successive wings of one hemisphere. While the average wing overlap is zero in the southern hemisphere, it is two to three months in the north. A marginally significant oscillation of about ten solar cycles is found in the asymmetry of the L latitudes. The new long database of butterfly wings provides new observational constraints to solar dynamo models that discuss the spatio-temporal distribution of sunspot occurrence over the solar cycle and longer.
Key words: Sun: activity / sunspots / history and philosophy of astronomy
Digital data for Fig. 1 are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/599/A131
© ESO, 2017
1. Introduction
The time-latitude evolution of sunspot occurrence, known as the Maunder butterfly diagram, is one of the most spectacular manifestations of the cyclic variability of solar activity, resulting from the action of the solar dynamo in the Sun’s convection zone (Charbonneau 2010; Hathaway 2015). With the butterfly diagram, we can study the detailed evolution of the latitude distribution of sunspots and, thus, the dynamo wave propagation (e.g., Newton & Milsom 1955; Carbonell et al. 1993; Pulkkinen et al. 1999; Li et al. 2002; Ballester et al. 2005; Berdyugina et al. 2006).
Historically, the butterfly diagram has been studied using the data from the Royal Greenwich Observatory (RGO), which started producing daily photographs of the Sun in 1874. Recently, the butterfly diagram has been studied for earlier times using digitized sunspot drawings of Staudacher (Arlt 2009), Schwabe (Arlt et al. 2013), and Spörer (Diercke et al. 2015). The latter two datasets now enable us to compose a continuous butterfly diagram since 1826, extending the RGO-based diagram by almost 50 years. Here we present the first systematic analysis of the butterfly diagram of sunspot group occurrence in 1826–2015, using the combined dataset. We separate the butterfly wings using a recently developed method (Leussu et al. 2016) and analyze the separate wings for systematic relationships and patterns.
The paper is organized as follows. In Sect. 2 we introduce the dataset we used. Section 3 describes the wing separation process. The latitudinal evolution of the wings is analyzed in Sect. 4, their relation with the wing strength is studied in Sect. 5, and the synchronization of the wings is studied in Sect. 6. Conclusions are given in Sect. 7.
2. Data
The dataset of sunspot group positions and sizes consists of three subsets: the revised version 1.3 of Schwabe data (Arlt 2011; Arlt et al. 2013) for the period 1826–1867, the newly digitized Spörer data (Diercke et al. 2015) for 1868–1874 (although these data are available from 1861–1894, we use them here only to fill the gap between Schwabe and RGO data), and the RGO/USAF/NOAA/SOON compilation1 referred to collectively as the RGO data since 1875.
Since the original RGO series was terminated in 1976, its extension with SOON (Solar Observing Optical Network) data (Neidig et al. 1998) may have a transition inhomogeneity related to the reported group areas (Lockwood et al. 2014; Hathaway 2015). However, this transition does not affect the present analysis, where we only consider the number and position of spot groups, not their sizes. However, the RGO data quality is known to be rather low before 1880 (Sarychev & Roshchina 2009; Aparicio et al. 2014) during the incomplete cycle 11. The uneven quality of RGO data may extend, although less dramatically, even until 1900 (Clette et al. 2014), possibly affecting cycles 12 and 13. This uncertainty does not affect definitions of the latitudes, but it may alter the strengths of the cycles. Accordingly, we also considered the “corrected” strengths of cycles 12 (increased by 25%) and 13 (increased by 10%), following the curve in Fig. 24 of Clette et al. (2014). The total group area might have been a more robust index than just the number of spots or groups, but it adds a different information about the strength of solar activity: it scales well with the total emerging magnetic flux, but is mostly blind to how this field is fragmented into distinct local magnetic elements (elementary emerging dipoles).
The RGO dataset only includes data of sunspot groups, not of individual sunspots. Although the Schwabe and Spörer data include information on individual spots, we aggregated this information by considering only sunspot groups, in order to be consistent with the RGO data. For each sunspot group we calculated the mean latitude, weighted by the sunspot sizes (umbral area). We used the revised version of the Schwabe data with sunspot groups defined according to modern understanding (for details see Senthamizh Pavai et al. 2015). This sunspot grouping is somewhat different from that made originally by Schwabe and later used by Wolf, but it ensures consistency with the RGO dataset.
Schwabe and Spörer were good observers, with observational acuity thresholds, as estimated by Usoskin et al. (2016), of 13 ± 5 and 3 ± 2 msd (millionths of the solar disk), respectively. This is comparable to that of the RGO, indicating that only very small short-lived groups could have been missed by Schwabe and Spörer with respect to the reference dataset. Accordingly, we did not apply any correction to this possible minor inconsistency. We only consider the high-quality Schwabe data with the quality tag 1, which means the highest possible accuracy for sunspot positions within the data (Arlt et al. 2013). However, in some cases, particularly those related to the high-latitude spots, the accuracy of latitude determination may not be very high for Schwabe data, even for the best values were obtained from data with the formal quality tag.
Spörer provided drawings of the Sun in which each observed group was plotted when it was near the central meridian. The spots were identified and measured in an automated search delivering whole-spot areas and locations for individual sunspots (Diercke et al. 2015). Very few sunspots were reported in the Spörer data at the beginning of his observing period, as compared to data by Richard Carrington during a small overlapping period in 1861 (Zolotova et al. 2010), but later they reached a higher more normal level. This early inconsistency of the Spörer data has no effect here, since we use these data only beginning in 1868.
To avoid the effect of weighting the results with the lifetime of sunspot groups and group migration, we only took each sunspot group at its first appearance in the record. Subsequent appearances of the same group were ignored. This also emphasizes positions of the groups close to their formation (emergence of the magnetic flux tube), which minimizes their further migration. We note that for the Spörer data, the first crossing of the central meridian was considered since he mentioned spots only at these moments.
3. Separation of the butterfly wings
Using the combined RGO, Schwabe, and Spörer datasets described in Sect. 2, we constructed the butterfly diagram shown in Fig. 2. The wings of the diagram were separated using the method described by Leussu et al. (2016) for each hemisphere and solar cycle. The method is based on finding long gaps in the appearance of sunspot groups in narrow latitude bands, and ascribes each sunspot group to a certain wing, separating the old and the new cycles during their overlap. Since we consider only the first appearance of each group, in contrast to our previous work (Leussu et al. 2016), where all daily group appearances were used, we renewed the separation of the wings, using the same method, but with the dataset of the first appearance. However, the qualitative difference to the diagram of Leussu et al. (2016) is minor. Since the Spörer data overlap with both the Schwabe and RGO datasets, we separated the wings for that dataset separately. The resulting wings for the Spörer dataset are superimposed (in red and blue) on the Schwabe and RGO data wings (shown in green and black) in Fig. 2. The Spörer data are clearly well consistent with both Schwabe and RGO-based wings, as shown in Fig. 1: the mean latitude difference between the Spörer and Schwabe (RGO) sunspot positions was 0.25 ± 3° (−0.2 ± 2.2°) for the periods with overlapping data. The data for the butterfly diagram are available at the CDS.
 |
Fig. 1 Histograms of the occurrence of the difference Δlat between mean latitudes, as defined from Spörer and other observer’s data for Carrington rotations during the period of the data overlap. Panel a): Spörer vs. RGO (the mean of the distribution is −0.2°, the standard deviation σ = 2.2°). Panel b): Spörer vs. Schwabe (0.25°, σ = 3°). |
 |
Fig. 2 Butterfly diagram with individual wings indicated by color, constructed for sunspot groups on their first appearance. The green and black wings are for the Schwabe and RGO datasets, and the red and blue wings represent the Spörer data. |
Latitude parameters (F, H, and L latitudes) as well as wing strength I, listed separately for the two hemispheres (denoted N and S) and the whole Sun.
4. Evolution of characteristic wing latitudes
Visual inspection of the butterfly wings shown in Fig. 2 reveals some typical features of the cycle wings, like Spörer’s law of the decreasing mean latitude of sunspot occurrence during the solar cycle (e.g., Hathaway 2015). All wings start at mid-latitudes, then quickly spread out, occupying a fairly wide range of latitudes, and finally converge at low latitudes around the equator. Thus, the latitude evolution of each wing can be roughly characterized by three latitudes:
-
The latitude at which the first sunspot groups appear, calledhenceforth the F latitude, defines the latitude where the new wingstarts.
-
The maximum latitude of sunspot group occurrence in each wing, called the H latitude, defines the greatest latitudinal extent of the wing.
-
The latitude at which the last sunspot groups appear, called the L latitude, characterizes the end of the wing. The last groups of the old cycle wing may appear later than the first groups of the new cycle wing.
Using the individual very first, the highest latitude, or the very last sunspot groups causes the corresponding F, H, and L latitudes (and related times) to be rather arbitrary and prone to large uncertainties. On the other hand, increasing the statistics by considering, for example, the mean latitude of groups during the first year of each wing may dilute some important features. As a compromise between sufficient statistics and exactness of results, we consider the first 1%, the highest latitude 1%, and the last 1% fractions of sunspot groups in each wing to define the F, H, and L latitudes, respectively. The 1% percentile typically includes 9–25 sunspot groups per wing, which gives a fairly reliable estimate of the characteristic latitudes. Thus, the F and L latitudes were computed as the mean latitudes and the standard error of the mean (SEM) for the first and last 1% of groups in each wing, and the H latitudes as the mean latitudes of 1% of groups with the highest latitudes (positive for north and negative for south), regardless of the time of their occurrence in the wing. The H-latitude groups typically appear within several years after the start of the wing. We checked that varying the percentage of the F, H, and L latitude definition using 1.5% or 2% percentiles does not alter the main results.
Figure 3 depicts the latitudes and times of the sunspot groups on the first 1% (red), highest latitude 1% (black), and last 1% (blue) along with their mean latitudes (filled circles connected by lines).
 |
Fig. 3 Time-latitude diagram of the first 1% (red crosses) and the last 1% groups (blue dots), as well as the highest latitude 1% of groups (black dots) for each wing shown separately. The mean F, H, and L latitudes are shown by filled circles connected by lines of the corresponding color. |
The so-defined F, H, and L latitudes for each wing are shown in Fig. 4 along with their SEM errors. The F, H, and L latitudes are also collected in Table 1 along with their SEM values, separately for each hemisphere and for the whole Sun (the two hemispheres combined). Some parameters for some wings cannot be defined because the dataset is incomplete:
-
The very beginning of cycle 7 was not observed by Schwabe,making it impossible to define the F latitudes of this cycle, whilewe can still define the H and L latitudes.
-
Since cycle 24 is not yet completed at the time of writing this paper, the L latitudes of this cycle cannot be defined.
Figure 4 shows that the F latitudes appear in a latitudinal band of about 20–30° without a significant variation or trend during the centennial evolution. F latitudes during the first half of the period are slightly lower, on average, than those for the latter half, but this difference is not statistically significant. The F latitudes of the two hemispheres are significantly (p-value 0.03) correlated (the Pearson correlation coefficient is 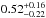 ), including the dips for cycles 9 and 12. The L latitudes are limited to the band of 2°–10°. They do not depict a clear pattern either, while the variability is fairly well synchronized between the two hemispheres (
), including the dips for cycles 9 and 12. The L latitudes are limited to the band of 2°–10°. They do not depict a clear pattern either, while the variability is fairly well synchronized between the two hemispheres (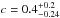 , p = 0.1).
, p = 0.1).
 |
Fig. 4 Panel a): mean latitude and its standard error of the first 1% spots of each wing (F latitudes). Panel b): mean latitude and its standard error of the highest 1% spots of each wing (H latitudes). Panel c): mean latitude and its standard error of the last 1% spots of each wing (L latitudes). Data for the north and south hemispheres are shown in blue and red (slightly offset horizontally for better visibility), respectively. |
However, the evolution of the H latitudes depicts a clear centennial oscillation: a fairly systematic decrease of H latitudes in both hemispheres from cycle 7 to the all-time minimum in cycle 12, followed by a rise with the maximum during cycles 19–22, turning to a new decrease thereafter. This evolution closely follows the overall trend of solar activity. The two hemispheres depict synchronous variations, with a highly significant (p< 3 × 10-4) correlation (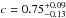 ) between the hemispheres. We note that the values of the H latitudes for the early Schwabe data (cycles 7–8) are probably slightly too high due to the enhanced uncertainty in the high-latitude determination at that time (Arlt et al. 2013). The centennial variability of H latitudes during the most credible period (cycles 9–24) is about 15° (30°–45°). The early Schwabe data remain within this range except for one wing.
) between the hemispheres. We note that the values of the H latitudes for the early Schwabe data (cycles 7–8) are probably slightly too high due to the enhanced uncertainty in the high-latitude determination at that time (Arlt et al. 2013). The centennial variability of H latitudes during the most credible period (cycles 9–24) is about 15° (30°–45°). The early Schwabe data remain within this range except for one wing.
The fact that the two hemispheres depict synchronous variations for all the three characteristic latitudes suggests that these parameters are representative of the latitudinal evolution of the wings, reflect real physical processes of sunspot formation, and are not dominated by noise.
5. Relation to wing strength
We have compared the cycle-to-cycle variation of the characteristic wing latitudes with the wing strengths. As the wing strength we considered, similarly to Leussu et al. (2016), the total sum I of the monthly mean numbers of all the sunspot groups (not only the first occurrence) over that wing, using Schwabe and RGO data. The strengths are listed in Table 1 and are plotted in Fig. 5. The strength series may be not fully homogeneous since there might be an inhomogeneity in the earlier part of the RGO and Schwabe series in the sense of group numbers, and the intensity cannot be directly computed for the Spörer data. For the former, we also present corrected strengths for solar cycles 12 and 13 (see Sect. 2 for details).
Figure 6 depicts scatter plots for the H, F, and L latitudes as a function of the wing strength in panels a to c, respectively.
 |
Fig. 5 Strength of cycle wings separately for N and S hemispheres, as indicated in the legend. The mean of the two hemispheres is shown as the dashed G curve. The asterisks depict the strengths of cycles 12 and 13 corrected for a possible inhomogeneity of the RGO data (see Sect. 2). |
 |
Fig. 6 Relation between the wing strength (the cumulative sum of the monthly numbers of sunspot groups) and the H, F, and L latitudes in panels a) to c), respectively, separately for the two datasets (RGO and Schwabe) and the two hemispheres, as denoted in the legend of panel a). The blue and red dotted lines depict the best-fit linear trends for the N and S hemispheres, respectively, using the RGO data. |
Linear correlation coefficients between F, H, and L latitudes and the wing strength for cycles 12–23, separately for each hemisphere (N and S), and for the combined hemispheres. p-values for the correlation coefficients are given in parentheses (“ins” means insignificant).
Linear correlation coefficients between the characteristic latitudes and wing strengths are listed in Table 2. Only cycles 12 through 23 based on the RGO series were used because of a possible inhomogeneity between Schwabe and RGO data. Including the Schwabe data does not qualitatively alter the results for F and L latitudes, but weakens the correlation for the H latitudes because of the relatively higher values of the latitudes (see the discussion above).
Figure 6 shows a clear tendency that the H latitudes are related to the wing strength with high statistical confidence, better than 0.02. We have checked that this tendency remains robust independently of the exact percentile of the definition of characteristic latitudes: for example, the correlation between the wing strengths and the H latitudes, defined using the 2% percentile of sunspot groups, is 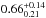 (p = 0.02) for N and S hemispheres both (cf. Table 2). This implies that the latitudinal extent of the wings is quite robustly related to the strength of the corresponding hemispheric wing, as shown earlier by Jiang et al. (2011) for full cycles. On the other hand, because of the great scatter of points in Fig. 6b, this relation has little predictive power but only indicates a statistical tendency. The L latitudes depict no dependency on the wing strength. The situation is uncertain with the F latitudes. The correlation with the wing strength is statistically significant for the southern hemisphere, but insignificant for the northern hemisphere.
(p = 0.02) for N and S hemispheres both (cf. Table 2). This implies that the latitudinal extent of the wings is quite robustly related to the strength of the corresponding hemispheric wing, as shown earlier by Jiang et al. (2011) for full cycles. On the other hand, because of the great scatter of points in Fig. 6b, this relation has little predictive power but only indicates a statistical tendency. The L latitudes depict no dependency on the wing strength. The situation is uncertain with the F latitudes. The correlation with the wing strength is statistically significant for the southern hemisphere, but insignificant for the northern hemisphere.
We also calculated the characteristic latitudes for combined N and S wings with unsigned latitudes. While the strength of these combined wings of the cycles is simply the sum of the hemispheric wing strengths, the characteristic latitudes need to be recalculated. We therefore computed the combined F, H, and L latitudes in the same way as for the individual wings, but using unsigned latitudes without separating the hemispheres. Figure 7 depicts the time evolution of the combined F, H, and L latitudes for the combined wings. The corresponding latitudes are denoted in Table 1 as “combined” and the correlations are shown in the last column of Table 2. While the combined correlations for the H and L latitudes are entirely consistent with those for separated wings (highly significant and insignificant, respectively), the correlation is marginally significant for the F latitudes.
We also repeated the analysis using the corrected strengths for solar cycles 12 and 13. The tendency remains solid with slightly smaller correlation coefficients. The only change is that the correlation for the F latitudes and combined hemispheres becomes insignificant (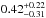 , p = 0.17), all other relations remain qualitatively the same.
, p = 0.17), all other relations remain qualitatively the same.
 |
Fig. 7 F, H, and L latitudes for the combined hemispheres, with 1σ standard errors. |
6. Wing lengths, overlaps, and asymmetries
We define the start and end times of the wings as the mean time of the first and last 1% percentile sunspot group occurrence, respectively. These times are listed in Table 3.
Dates of the start and end of each wing defined as the mean time of the first (last) 1% percentile of sunspot groups in the N and S hemispheres, respectively.
From the start and end dates we calculated the time spans of the wings, as shown in Fig. 8. We note that our definition is different from the traditional cycle length determination between consecutive cycle minima of (total) sunspot activity. There is a quasi-periodicity with a timescale of about 5–6 cycles, which is more pronounced in the northern hemisphere than in the southern hemisphere.
 |
Fig. 8 Total lengths of hemispheric wings separately for northern (blue) and southern (red) hemispheres. The uncertainties are typically within a few months. |
 |
Fig. 9 Time difference between the end of the wing of one cycle and the start of the next cycle wing. Positive values correspond to overlaps between the wings, negative values correspond to gaps. |
Figure 9 shows the overlaps and gaps between the wings, defined as the difference between the end time of one wing and the start time of the next wing in the same hemisphere. Accordingly, positive difference implies an overlap (sunspot groups of the new cycle appear before the old cycle ends), and negative difference indicates a gap. Figure 9 depicts both (negative) time gaps and (positive) overlaps between the wings of typically within about one year, occasionally slightly longer. These time differences in the S hemisphere remain somewhat smaller than in the north, and their overall mean is close to zero. However, in the north, they vary considerably, and on average there is a (2–3)-month overlap. Moreover, the time differences in the N-hemisphere depict a clear (5–6)-cycle quasi-periodicity, obviously roughly in phase with the wing length. Thus, longer wings are typically overlapping with each other, while shorter wings are more separated from each other. No distinguishable periodicity is found for the S hemisphere.
Figure 10 shows the time difference in the start and end times between the two hemispheres (north minus south). Overall, there is more variability in the hemispheric differences for the end times than for the start times. Both differences are within about 1.5 yr. There is an anticorrelation in the start and end times. This implies that a wing that starts earlier tends to end slightly later and has a longer overall length.
Finally, we studied the hemispheric asymmetry of the start and end latitudes. The asymmetry is defined as the difference in the mean F and L latitudes between the N and S wings of the same cycles (see Table 1). These asymmetries are shown in Fig. 11. Overall, they are clearly quite symmetric (the mean value is about zero), but there is an oscillation with the duration of about ten cycles in the end latitudes (panel b). However, this is only marginally significant (p-value 0.09).
 |
Fig. 11 Difference between the mean latitudes of the start (F latitudes, blue) and end (L latitudes, red) of each wing (see Table 1). |
7. Summary
We presented a butterfly diagram of sunspot group occurrences for the first time continuously since 1826, using three subsets of sunspot group occurrence: an updated analysis of solar drawings from Schwabe (1826–1867), newly digitized data of solar drawings by Spörer (1866–1880), and data from photographic images of the RGO since 1875, extended by SOON-network data after 1976. Only the first appearance of each sunspot group was considered.
We performed a full separation of the butterfly wings, using the method developed by Leussu et al. (2016), so that each sunspot group was uniquely ascribed to a wing (solar cycle and hemisphere) of the butterfly diagram. A digital database is available at the CDS.
Using the new database, we analyzed the characteristic latitudes, corresponding to the start, end, and the latitudinal extent of the wings and their times. We found that the two hemispheres depict synchronous variations in all the three latitudes, implying that they are representative of the latitudinal evolution of the wings, reflect real physical processes of sunspot formation, and are not dominated by noise. This also implies a fairly strong interconnection between the two solar hemispheres.
We found that the first (1%) sunspot groups occur in each wing (F latitudes) at moderate latitudes of 20°–30°. The F latitudes depict a marginal tendency, especially in the S hemisphere, to follow the wing strength (quantified by the total sum of the monthly numbers of sunspot groups). The H latitudes (1% of the groups occurring at the highest latitudes) are significantly (about 10°) higher than the F latitudes and vary greatly over 30–45°. They are significantly correlated with the wing strength during the period covered by the RGO data (cycles 12–23). Including data from Schwabe weakens the relation because of the possibly less reliable identification of high-latitude spots (see Sect. 2). The mean latitudes of the last 1% of sunspot groups (L latitudes) vary within 2°–10° and show no clear relation to the wing strength. Stronger cycle wings tend to start at higher latitudes and to have a greater latitudinal extent. This confirms earlier results from Jiang et al. (2011), for example, that stronger cycles tend to have a greater latitudinal extent, which has been found previously for solar cycles and is now generalized for the hemispheric wings.
We discussed uncertainties and robustness of the conclusions, in particular with respect to the possible inhomogeneity of the RGO dataset before 1900.
We also performed a first analysis of the timing of the butterfly wings. We found that the longer hemispheric wings always end later and also mostly start earlier than the shorter wings. Although on average there is no gap between two successive wings of the southern hemisphere (the new wing starts at the time that the old wing ends), there is an overall average overlap of 2–3 months between the successive wings in the northern hemisphere. Moreover, we found a (5–6)-cycle oscillation in the overlap or gap of wings in the north. The northern hemisphere also exhibits a (5–6)-cycle oscillation in the wing length. We also noted a marginally significant oscillation with a period of about ten cycles in the hemispheric asymmetry of the L latitudes.
Although we only presented here a basic analysis, the new long database of butterfly wings provides new observational constraints to solar dynamo models that discuss the spatio-temporal distribution of sunspot occurrence over the solar cycle and longer. It opens a possibility for detailed focused studies such as “active latitudes” and their drifts over solar cycles (Kilcik et al. 2016).
Acknowledgments
We are grateful to the anonymous referee, whose valuable and thorough comments led to a significant improvement of the quality of this work. Support by the Academy of Finland to the ReSoLVE Center of Excellence (project No. 272157) and the Deutsche Forschungsgemeinschaft (No. AR 355/10-1) is acknowledged.
References
- Aparicio, A. J. P., Vaquero, J. M., Carrasco, V. M. S., & Gallego, M. C. 2014, Sol. Phys., 289, 4335 [NASA ADS] [CrossRef] [Google Scholar]
- Arlt, R. 2009, Sol. Phys., 255, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Arlt, R. 2011, Astron. Nachr., 332, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Arlt, R., Leussu, R., Giese, N., Mursula, K., & Usoskin, I. G. 2013, MNRAS, 433, 3165 [NASA ADS] [CrossRef] [Google Scholar]
- Ballester, J. L., Oliver, R., & Carbonell, M. 2005, A&A, 431, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Moss, D., Sokoloff, D., & Usoskin, I. G. 2006, A&A, 445, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carbonell, M., Oliver, R., & Ballester, J. 1993, A&A, 274, 497 [NASA ADS] [Google Scholar]
- Charbonneau, P. 2010, Liv. Rev. Sol. Phys., 7, 3 [Google Scholar]
- Clette, F., Svalgaard, L., Vaquero, J., & Cliver, E. 2014, Space Sci. Rev., 186, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Diercke, A., Arlt, R., & Denker, C. 2015, Astron. Nachr., 336, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H. 2015, Liv. Rev. Sol. Phys., 12, 4 [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011, A&A, 528, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kilcik, A., Yurchyshyn, V., Clette, F., Ozguc, A., & Rozelot, J.-P. 2016, Sol. Phys., 291, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Leussu, R., Usoskin, I. G., Arlt, R., & Mursula, K. 2016, A&A, 592, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, K. J., Wang, J. X., Xiong, S. Y., et al. 2002, A&A, 383, 648 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lockwood, M., Owens, M. J., & Barnard, L. 2014, J. Geophys. Res., Space Phys., 119, 5172 [Google Scholar]
- Neidig, D., Wiborg, P., Confer, M., et al. 1998, in Synoptic Solar Physics, eds. K. S. Balasubramaniam, J. Harvey, & D. Rabin, ASP Conf. Ser., 140, 519 [Google Scholar]
- Newton, H. W., & Milsom, A. S. 1955, MNRAS, 115, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Pulkkinen, P. J., Brooke, J., Pelt, J., & Tuominen, I. 1999, A&A, 341, L43 [NASA ADS] [Google Scholar]
- Sarychev, A. P., & Roshchina, E. M. 2009, Sol. Syst. Res., 43, 151 [Google Scholar]
- Senthamizh Pavai, V., Arlt, R., Dasi-Espuig, M., Krivova, N. A., & Solanki, S. K. 2015, A&A, 584, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I. G., Kovaltsov, G. A., Lockwood, M., et al. 2016, Sol. Phys., 291, 2685 [Google Scholar]
- Zolotova, N. V., Ponyavin, D. I., Arlt, R., & Tuominen, I. 2010, Astron. Nachr., 331, 765 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Latitude parameters (F, H, and L latitudes) as well as wing strength I, listed separately for the two hemispheres (denoted N and S) and the whole Sun.
Linear correlation coefficients between F, H, and L latitudes and the wing strength for cycles 12–23, separately for each hemisphere (N and S), and for the combined hemispheres. p-values for the correlation coefficients are given in parentheses (“ins” means insignificant).
Dates of the start and end of each wing defined as the mean time of the first (last) 1% percentile of sunspot groups in the N and S hemispheres, respectively.
All Figures
 |
Fig. 1 Histograms of the occurrence of the difference Δlat between mean latitudes, as defined from Spörer and other observer’s data for Carrington rotations during the period of the data overlap. Panel a): Spörer vs. RGO (the mean of the distribution is −0.2°, the standard deviation σ = 2.2°). Panel b): Spörer vs. Schwabe (0.25°, σ = 3°). |
| In the text | |
 |
Fig. 2 Butterfly diagram with individual wings indicated by color, constructed for sunspot groups on their first appearance. The green and black wings are for the Schwabe and RGO datasets, and the red and blue wings represent the Spörer data. |
| In the text | |
 |
Fig. 3 Time-latitude diagram of the first 1% (red crosses) and the last 1% groups (blue dots), as well as the highest latitude 1% of groups (black dots) for each wing shown separately. The mean F, H, and L latitudes are shown by filled circles connected by lines of the corresponding color. |
| In the text | |
 |
Fig. 4 Panel a): mean latitude and its standard error of the first 1% spots of each wing (F latitudes). Panel b): mean latitude and its standard error of the highest 1% spots of each wing (H latitudes). Panel c): mean latitude and its standard error of the last 1% spots of each wing (L latitudes). Data for the north and south hemispheres are shown in blue and red (slightly offset horizontally for better visibility), respectively. |
| In the text | |
 |
Fig. 5 Strength of cycle wings separately for N and S hemispheres, as indicated in the legend. The mean of the two hemispheres is shown as the dashed G curve. The asterisks depict the strengths of cycles 12 and 13 corrected for a possible inhomogeneity of the RGO data (see Sect. 2). |
| In the text | |
 |
Fig. 6 Relation between the wing strength (the cumulative sum of the monthly numbers of sunspot groups) and the H, F, and L latitudes in panels a) to c), respectively, separately for the two datasets (RGO and Schwabe) and the two hemispheres, as denoted in the legend of panel a). The blue and red dotted lines depict the best-fit linear trends for the N and S hemispheres, respectively, using the RGO data. |
| In the text | |
 |
Fig. 7 F, H, and L latitudes for the combined hemispheres, with 1σ standard errors. |
| In the text | |
 |
Fig. 8 Total lengths of hemispheric wings separately for northern (blue) and southern (red) hemispheres. The uncertainties are typically within a few months. |
| In the text | |
 |
Fig. 9 Time difference between the end of the wing of one cycle and the start of the next cycle wing. Positive values correspond to overlaps between the wings, negative values correspond to gaps. |
| In the text | |
 |
Fig. 10 Difference between the timing of the start (blue) and end (red) of each wing (see Table 3). |
| In the text | |
 |
Fig. 11 Difference between the mean latitudes of the start (F latitudes, blue) and end (L latitudes, red) of each wing (see Table 1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


