| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 21 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201629659 | |
| Published online | 27 January 2017 | |
Separation and confirmation of showers⋆
1 Astronomical Institute, Slovak Academy of Sciences, 05960 Tatranska Lomnica, Slovak Republic
e-mail: ne@ta3.sk
2 Astronomical Institute, Slovak Academy of Sciences, Dubravska cesta 9, 84504 Bratislava, Slovak Republic
e-mail: astromia@savba.sk
Received: 6 September 2016
Accepted: 30 October 2016
Aims. Using IAU MDC photographic, IAU MDC CAMS video, SonotaCo video, and EDMOND video databases, we aim to separate all provable annual meteor showers from each of these databases. We intend to reveal the problems inherent in this procedure and answer the question whether the databases are complete and the methods of separation used are reliable. We aim to evaluate the statistical significance of each separated shower. In this respect, we intend to give a list of reliably separated showers rather than a list of the maximum possible number of showers.
Methods. To separate the showers, we simultaneously used two methods. The use of two methods enables us to compare their results, and this can indicate the reliability of the methods. To evaluate the statistical significance, we suggest a new method based on the ideas of the break-point method.
Results. We give a compilation of the showers from all four databases using both methods. Using the first (second) method, we separated 107 (133) showers, which are in at least one of the databases used. These relatively low numbers are a consequence of discarding any candidate shower with a poor statistical significance. Most of the separated showers were identified as meteor showers from the IAU MDC list of all showers. Many of them were identified as several of the showers in the list. This proves that many showers have been named multiple times with different names.
Conclusions. At present, a prevailing share of existing annual showers can be found in the data and confirmed when we use a combination of results from large databases. However, to gain a complete list of showers, we need more-complete meteor databases than the most extensive databases currently are. We also still need a more sophisticated method to separate showers and evaluate their statistical significance.
Key words: meteorites, meteors, meteoroids / catalogs / methods: data analysis
Tables A.1 and A.2 are also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/598/A40
© ESO, 2017
1. Introduction
Meteor showers observed in the Earth’s atmosphere are evidence that there are streams of meteoroid particles moving in the vicinity of our planet. At present, there is much human activity in near space. Knowledge of the time of occurrence, the geometry, as well as the sources of meteoroid particles can help us protect both people in space stations and equipment such as artificial satellites from the threat of particles, especially those which are typically more concentrated in streams than those which are sporadic. Prevention, however, can only be reliable if our knowledge of meteoroids in the Earth’s vicinity is complex, and if we know in detail all the significant streams.
Programs such as NASA’s Meteoroid Environment Office, which monitor the flux and the associated risk of meteoroids impacting spacecraft, require constant improvements to the theoretical models for annual meteor showers activity forecasts (Moorhead et al. 2015). This also demands systematic monitoring of the near-Earth space. There are several surveys, such as the NASA All Sky Fireball Network (Cooke & Moser 2012), the Spanish Meteor and Fireball Network (SPMN; Pujols et al. 2013), the All-sky Meteor Orbit System (AMOS; Tóth et al. 2015), the Cameras for Allsky Meteor Surveillance (CAMS; Jenniskens et al. 2011), and others, which provide the basis for the most up-to-date information on the meteoroid environment.
Several lists of meteoroid streams or meteor showers from the first half of twentieth century have been published. Among the first are the well-known Cook’s Working List of Meteor Streams (Cook 1973) and Kronk’s Descriptive Catalog of Meteor Showers (Kronk 1988). Searches for meteor showers have been based on various observational techniques: visual, photographic (e.g., Lindblad 1971; Arlt 1995; Betlem et al. 1998; Ohtsuka & Hidaka 1999), video (e.g., Ueda & Fujiwara 1995; Jopek & Froeschle 1997; de Lignie 1999; Koten et al. 2003), and radio (e.g., Nilsson 1964; Kashcheyev & Lebedinets 1967; Gartrell & Elford 1975; Sekanina 1973, 1976; Galligan & Baggaley 2002). The vast majority of early major surveys measuring meteoroid orbits (overviews to be found in papers by Lindblad 1991; Baggaley 1995) were archived in the Meteor Data Center (MDC) of the International Astronomical Union (IAU; Lindblad 1987, 1991; Lindblad et al. 2003). Due to an increase in reports of the detection of meteor showers (compiled in Jenniskens 2006), a central repository for the efficient collection and designation of meteor showers was established within the IAU MDC (Jenniskens 2008; Jopek & Jenniskens 2011; Jopek & Kaňuchová 2014).
The IAU MDC list of showers, with their mean parameters determined, was considerably expanded by the Canadian Meteor Orbit Radar’s (CMOR) contribution. A meteoroid stream survey using the CMOR was made by Brown et al. (2008) and later repeated with an extended collection time and an enhanced sensitivity of their search for minor showers (Brown et al. 2010).
The next increase in the reporting of meteor showers was caused by the rapid development of video meteor observations, producing a massive number of meteoroid orbits and, therefore, multiplying minor meteor showers identifications (SonotaCo 2009; Jenniskens et al. 2011; Gural et al. 2014; Kornoš et al. 2014b; Rudawska & Jenniskens 2014). A list of meteor showers from observations of the International Meteor Organization (IMO) Video Meteor Network was published by Arlt & Rendtel (2006, 2007), Molau & Rendtel (2009), and the most recent, updated, comprehensive version by Molau (2014). There are many reports confirming individual showers or announcing the detection of a new shower based on observations of national video systems or networks (e.g., Ueda & Okamoto 2008; Jopek et al. 2010; Holman & Jenniskens 2012; Zoladek & Wisniewski 2012; Andreić et al. 2013; Koukal et al. 2014; Šegon et al. 2013). The most recent series of papers by Jenniskens et al. (2016a,c,b), based on the CAMS system, provides exhaustive information on the current status of announced meteor showers. The authors report, in total, 230 meteor showers identified in CAMS data, 177 of them detected in at least two independent surveys. Among them, 60 are newly identified showers, 28 of which are also detected in the independent SonotaCo survey.
Until now, the official list of showers published by the IAU MDC1 (Jopek & Kaňuchová 2014) has grown to more than 700 meteor showers, 112 of which are established and 37 pro tempore (version of the lists from February 2016). However, some of the named showers or published lists of showers were created on the basis of data from a single observational station, which are often biased by observational conditions (local weather) and, possibly, systematic errors. Many meteor showers from these lists have not been independently confirmed.
Independent confirmation of a particular stream faces the problem of the vague nomenclature of meteor showers or streams established in the past. A new shower is named after a bright star which is the nearest star to the mean radiant of the shower. However, as discussed by Jopek2, different authors use star catalogs with different limiting magnitudes of stars; therefore, various “star(s) being nearest to the mean radiant” can be chosen. Moreover, the positions of a mean radiant as determined by several different authors often differ from each other; therefore, the reference star may be different even if the same star catalog is used. Sometimes, the mean radiant is situated at the border of two constellations. One author may determine the radiant in the first, another author in the second constellation. The name of the shower when referred to by two different authors then differs completely. It is possible that some showers were observed by two or more authors and could be regarded as independently confirmed, but this fact could escape our attention if the authors referred the shower by different names.
In our work, we aim to reveal all the meteoroid streams colliding regularly (every, or almost every, year) with our planet. For this purpose, we use four accurate and large photographic and video data sets currently available. Specifically, we use the compilation of several catalogs of the most accurate meteor orbits gained from the photographic observations of meteors, which are collected in the IAU MDC (Lindblad et al. 2003; Neslušan et al. 2014). In addition to the photographic data, we use the extensive video catalogs, which were published by the Cameras for All-sky Meteor Surveillance (CAMS) team (Jenniskens et al. 2011, 2016a), SonotaCo team (SonotaCo 2009, 2016), and EDMOND team (Kornos et al. 2013; Kornoš et al. 2014a).
Rather than recognizing all potential streams in these catalogs, we search for the streams that can be well-proven with the help of the data in a given catalog. As the result, we present the minimum set of the streams, which very probably exist and orbit the Sun along trajectories passing in the immediate vicinity of the Earth’s orbit.
We have attempted to match up all the streams found to the streams given in the IAU MDC list of all showers. The latter should solve the problem of the confusing naming of new showers or identification of unknown showers.
2. Procedure of the separation and confirmation of a shower
In the following, we describe a procedure to find all the annual meteor showers from the given database of the meteor orbits which can be proved, using the database, to really exist. The procedure consisted of two parts: (i) separation of the clusters of meteors, which are regarded as the candidates for the showers; and (ii) proving the candidates to be or not to be the shower.
To separate the clusters, we have used two methods; the method of indices (MoI; Svoreň et al. 2000) and the method suggested and described by Rudawska et al. (2015; MoR&, hereinafter). The two methods are briefly described below.
2.1. Separation of clusters by the method of indices
The procedure was based on dividing the observed ranges of meteor parameters into a number of equidistant intervals and the assignment of indices to a meteor according to the intervals pertinent to its parameters. Meteors with equal indices were regarded as mutually related. A more detailed description follows:
-
1.
Selection of the Perseids using the break point method (Neslušan et al. 1995, 2013), calculation of their mean orbit and determination of errors (σ) of the parameters: q, e, ω, Ω, i, α, δ, and Vg. The errors were regarded as typical errors of the listed parameters in the used database. The Perseids were considered to determine the errors, because they are the most numerous shower in each database and they are a standard, sufficiently compact and well-defined shower.
-
2.
Determination of the ranges for the eight parameters in the whole database. If a meteor, or a few meteors, has a particular parameter considerably higher, or considerably lower, than the vast majority of the set, then this value was ignored; a border of typical values of the vast majority of the meteors was considered to be the limiting value for the range of that particular parameter.
-
3.
The whole range of a particular parameter was divided into a certain number of intervals. The actual range of the ith parameter is divided into ni intervals, according to the equation ni = rangei/σi/K, where K is a constant that is common for all parameters, and that is obtained empirically so that, if possible, all ni (for i = 1, 2, 3, ..., 8) are close to being integers. The σi is the error of determination of a particular parameter in the case of the Perseids (see point 1).
-
4.
Eight indices that correspond to the eight parameters were assigned to each meteor. The value of an index of a particular parameter is the sequential number of the interval matching the value of the particular parameter of the analyzed meteor.
-
5.
The first meteor of a database, with its set of indices, was considered; all other meteors, the indices of which are similar to the corresponding indices of the first, were searched for in the database; the meteors found from this search created a group. The index is considered to be similar when it differs by no more than one from the corresponding index of the first meteor. This tolerance was needed because, in the case of showers, a distribution of a particular quantity can be close to the border of two intervals; thus, the values of this quantity can be found in both of these intervals.
-
6.
Meteors of the selected group were extracted from the database. The procedure was repeated (as in point 5) with the remaining data, considering its first meteor, until the remaining data equals zero.
-
7.
The mean orbit (MO) of each group was calculated as an arithmetic average of its individual elements.
-
8.
The MO of the first group was considered and the Southworth & Hawkins (1963, SH, hereinafter) D-discriminants between this MO and the MO of each other group were determined. If D ≤ 0.20, then a particular group was assigned to the first group; all assigned groups created a cluster. The assigned groups were extracted from the data and the procedure was repeated with the remaining groups.
-
9.
The procedure described in point 8 was repeated until the remaining data equals zero.
-
10.
A mean orbit of each cluster was calculated. A particular parameter y of a cluster was calculated as
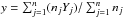 , where n is a number of groups assigned to a particular cluster, Yj is the mean value of the parameter of jth group and nj is the number of meteors in the jth group.
, where n is a number of groups assigned to a particular cluster, Yj is the mean value of the parameter of jth group and nj is the number of meteors in the jth group. -
11.
In the standard MoI, clusters with their mean orbits, were considered to be candidates for meteor showers in the database analyzed. Since we also evaluated the statistical significance of clustering of the shower meteors in the database used, we performed one more step: the mean orbit of given cluster was considered as the initial orbit in the iteration procedure within the break-point method (see Sect. 2.3) and this procedure was performed to select a definive set of meteors of the cluster.
2.2. Separation of clusters by the method of Rudawska et al.
The method was performed in two phases: firstly, searching for a similarity between the orbits of meteoroids; secondly, measuring the similarity based on the geocentric parameters.
PHASE 1
-
1.
The first meteor from the whole database (when starting the process) or from the remnant of the database (when repeating the process) was considered as a reference meteor. The value of the D-discriminant of the SH-criterion for orbital similarity between the orbits of the reference meteor and each next meteor in the database was calculated.
-
2.
Meteors, orbits of which fulfill D ≤ 0.05, were selected from the database and their initial weighted mean orbit (IWMO) was calculated.
-
3.
Step 1 was repeated, with the IWMO as the reference meteor. The D value was calculated for all meteors including the first meteor (i.e., the D value between the first and IWMO must also be calculated).
-
4.
Meteors, orbits of which fulfill D ≤ 0.05, were selected from the database and their new weighted mean orbit (NWMO) was calculated.
-
5.
The given NWMO was compared using the SH D-discriminant, with the value of the previous weighted mean orbit. If the D value between these orbits was found to be more than or equal to 0.001, then Steps 1 to 5 were repeated (the IWMO was always replaced by the last NWMO).
-
6.
If the value of the D-discriminant between the last and the second to last NWMO is less than 0.001, then the last NWMO was considered as the definitive value of the weighted mean orbit of the particular group. Meteors that were used for the calculation of this orbit are extracted from the database (or from the remainder of the database) and the new remnant of the database was used to search for the next groups.
-
Steps 1 to 6 were repeated until the newly-created remnant equals zero. PHASE 2
-
8.
The groups were arranged according to the number of meteors they contain, from the most numerous to the least numerous. In the second phase, only groups that consisted of five or more meteors were considered.
-
9.
The first group was considered as a reference group. The value of the D-discriminant for orbital similarity suggested by Rudawska et al. (2015, hereinafter DR& discriminant) between the weighted mean orbit (WMO) of the reference group and all next groups was calculated. The DR& discriminant was calculated until there was no case with a value equal to or less than 0.15.
-
10.
Meteors of the first and current group (which implicates the value of DR& discriminant ≤0.15) were considered as meteors of a merged group. A new WMO was calculated using orbits of all the meteors from the merged group.
-
11.
Steps 9 and 10 were repeated until the last group is reached. In Step 9, instead of the initial WMO of the first group, the last calculated WMO of this group was considered.
-
12.
The last calculated WMO of the first group was considered as the WMO of a “cluster” of the groups.
-
13.
All groups which were merged with the first group in the previous process (thus, had DR& discriminant ≤0.15), were excluded from the list of groups. Next, we worked only with the remaining groups, among which the most numerous group will be regarded as the first group.
-
14.
Steps 9 to 13 are repeated until the list of groups is exhausted.
-
15.
The clusters found represent candidates for meteor showers in the database.
2.3. On the break-point method
Both MoI and MoR& often produce a set of orbits which are similar to the initial orbit entering the procedure. Such a set can, however, be simply a random clustering of the orbits of sporadic meteors. To prove the existence of a shower, it is necessary to evaluate the statistical significance of the clustering; if it does not occur merely by chance.
In the course of proving whether a given cluster is actually a shower, we analyzed a concentration of cluster meteors in the appropriate phase space of orbital elements. To demonstrate the significance of the concentration, we used the same principle as used in the “method of break-point”, suggested by Neslušan et al. (1995, 2013), to separate the densest part of a given shower from the database. (This method alone cannot be used to find the meteor showers in a database since we need an initial “candidate” orbit to enter the iteration procedure in the break-point method.) In the subsequent part of this sub-section, we give a brief reminder of this method.
The break-point is a critical point in the break-point method. As mentioned above, only meteors of the densest part of the shower are selected from the database using this method, rather than all of the meteors of the particular shower.
The method is based on an analysis of the dependence of the number of the selected meteors of a shower on the limiting value of the SH D discriminant Dlim used for the selection. If a shower is present in a database, then the dependence N = N(Dlim) has convex behavior with a constant or almost constant part – a plateau. Within the plateau, N does not change with increasing Dlim, or increases only very slightly. The value Dlim at the point when the plateau starts is the most suitable limiting value for the D discriminant for the selection of the densest part of a shower. Our task is to find the exact position of this threshold, that is, to find the start of the plateau.
2.4. Description of the search algorithm for the break-point
We assume that we want to perform a selection of meteors of a particular shower which is indicated by a particular cluster of meteors found by MoI or MoR&. The selection of meteors from the database was performed for an ascending series of discrete values of Dlim, generally for Dlim = 0.01, 0.02, 0.03,..., up to the highest value, Dh. We calculated the SH D-discriminant between the initial mean orbit (mean orbit of candidate cluster) and orbit of each meteor in the database. If the resultant D ≤ Dlim, then the meteor was selected as the member of a just separated shower.
It is recommended to choose Dh = 0.6. For the values Dlim>DA (see Fig. 1), the number of selected meteors was non-zero. To find an optimal mean orbit for a particular Dlim, the iteration was used when selecting. If there is another shower in the vicinity of the phase space of orbital elements of the searched shower, the iteration may redirect the search to the other shower, which is often displayed by a decrease in the number N, with increasing Dlim. In such a case, only the non-decreasing part of the dependence N = N(Dlim) was analyzed; thus, for Dh, we consider the last value of Dlim before it starts decreasing.
If the dependence N = N(Dlim) has the expected convex behavior, then in its part after point A, a relatively significant increase in the number of selected meteors has to occur. The proposed algorithm searches for the interval of the maximal increase of the number by calculation of the derivation 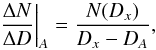 (1)beginning with the value of D discriminant Dx = Dxd = DA + 0.04 and finishing with the value Dx = Dxh = 0.3 (or, if Dh< 0.3, with the value of Dx = Dxh = Dh). If we only suspect there is a shower (hereinafter, such a shower is classified as a shower of the II class), with a number of meteors less than ten, then Dx = Dxh = 0.2. All these limiting values were chosen empirically, based on the experience that a relatively high increase in a number of meteors is observed in an interval Dx with the length of 0.04 and if the plateau occurs within the reasonable values of Dlim, then the increase stops at the values of Dlim less than 0.3, or, in the case of less-numerous showers, at 0.2, respectively.
(1)beginning with the value of D discriminant Dx = Dxd = DA + 0.04 and finishing with the value Dx = Dxh = 0.3 (or, if Dh< 0.3, with the value of Dx = Dxh = Dh). If we only suspect there is a shower (hereinafter, such a shower is classified as a shower of the II class), with a number of meteors less than ten, then Dx = Dxh = 0.2. All these limiting values were chosen empirically, based on the experience that a relatively high increase in a number of meteors is observed in an interval Dx with the length of 0.04 and if the plateau occurs within the reasonable values of Dlim, then the increase stops at the values of Dlim less than 0.3, or, in the case of less-numerous showers, at 0.2, respectively.
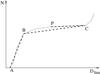 |
Fig. 1 Example of the dependence of the number of selected meteors of a shower from a database on the limiting value of the Southworth-Hawkins D discriminant Dlim, with an illustration of the three fundamental segments of the algorithm of the automated search for the beginning of the plateau. |
The derivation ΔN/ ΔD | A according to Eq. (1) was calculated for all the discrete values of Dlim from the mentioned interval from Dxd to Dxh, and the maximum value ΔN/ ΔD | max is found. A maximum increase in the selected meteors N corresponds to the found maximum; the end of the maximum increase is shown in Fig. 1 as point B. The corresponding value of Dlim will be designated as DB and the corresponding number of selected meteors as NB. The maximum increase in the dependence N = N(Dlim) is followed by a moderate increase and, further, by a plateau in the case of the presence of a meteor shower. In the next step, we found the end of the plateau, designated as point C in Fig. 1, with a corresponding D discriminant DC and a corresponding number of selected meteors NC. The point C was found as follows: starting with the value of the D discriminant Dx = Db = DB + 0.06 and ending with the value Dx = De = Dh, a derivation 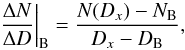 (2)was calculated for all the discrete values of Dx from a given interval, and a minimum of those values will be found. The minimum value corresponds to the actually searched value of DC.
(2)was calculated for all the discrete values of Dx from a given interval, and a minimum of those values will be found. The minimum value corresponds to the actually searched value of DC.
In the last step, the beginning of the plateau was found by calculation of the derivation 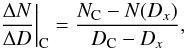 (3)for all the discrete values from the empirically determined interval, from Dbp = DB to Dep = DC−ΔD. The choice of the value ΔD is discussed in the following subsection. The minimum value of the derivation ΔN/ ΔD | C, which is designated as ΔN/ ΔD | min, corresponds to the beginning of the plateau, designated as point P in the figure. This point is the searched break-point, with a corresponding critical value of Dlim equal to DP, and the number of shower meteors is NP.
(3)for all the discrete values from the empirically determined interval, from Dbp = DB to Dep = DC−ΔD. The choice of the value ΔD is discussed in the following subsection. The minimum value of the derivation ΔN/ ΔD | C, which is designated as ΔN/ ΔD | min, corresponds to the beginning of the plateau, designated as point P in the figure. This point is the searched break-point, with a corresponding critical value of Dlim equal to DP, and the number of shower meteors is NP.
There is the theoretical possibility of finding a minimum value of the derivation given by Eq. (3) in a phase space of the orbital elements without the presence of any showers. To make the algorithm work only when the behavior of the dependence N = N(Dlim) is convex, and to be sure we can speak about a plateau, we additionaly require that 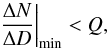 (4)and we find empirically that Q = 0.4 for showers of class I and Q = 0.45 for showers of class II (see below). If the condition is not fulfilled, then the algorithm in the last step fails and the shower does not exist.
(4)and we find empirically that Q = 0.4 for showers of class I and Q = 0.45 for showers of class II (see below). If the condition is not fulfilled, then the algorithm in the last step fails and the shower does not exist.
2.5. Evaluation of the reliability of the real occurence of the selected shower
The above described algorithm finds a break-point and selects a shower, even in some cases when the reality of the shower is questionable. Specifically, we presume that a real shower in a database has to be represented by a minimum of ten meteors; the plateau should not be too short, otherwise, it may occur only due to a statistical fluctuation. Therefore, for a highly probable shower (the reliability class of which we define as class I; see below), we choose ΔD, which delimitates the examined interval, equal to 0.15. This ensures the plateau is within the interval Dlim, with a length of DC−DP ≥ 0.15.
In the dependence N = N(Dlim), a plateau is rarely horizontal. More often, it has a small or greater inclination. We can talk about a plateau if it is inclined up to a certain maximal acceptable rate. This rate is, as mentioned in the previous subsection, set by Eq. (4), with an empirically determined parameter Q. The equation specifies the ratio between the inclination of the plateau and the maximal inclination (corresponding to the maximal increase of the N) in the dependence N = N(Dlim). This ratio is characterized by the parameter Q.
Overall, if the algorithm successfully finds the values of the D discriminant DA, DB, DC, and DP, and the Condition 4 and the demand of the minimum number of meteor in a shower, NP ≥ 10, are fulfilled, then, in the particular phase space of the orbital elements, the shower recorded in the database used exists with a very high probability. We classified such a shower as a shower of the reliability class I (or simply showers of class I).
To distinguish whether a shower with assumed characteristics in the database exists or not is, in practise, difficult, not only when using this algorithm, but also in general. Therefore, we found it useful to also select dubious cases, the existence of which seems to be probable, but which, however, is not provable. Thus, we established a reliability class II (or, simply, shower of class II) for showers that probably need some additional examination. In the case of the showers of the class II, the demand of the minimum number of meteors in the shower is reduced by half, NP ≥ 5. Furthermore, the width of the interval DC−DP, which corresponds to the length of the plateau, is only 0.07; meaning that ΔD in this case is equal to 0.07.
MoI and/or MoR can also find, in a database, a shower with NP ≥ 5, which is not proved (as a shower of class I or class II) by the break-point method, (i.e., by the algorithm described above). It is thus only a selection of a number of meteors clustered by chance in the particular phase space of orbital elements. To distinguish it from an empty phase space, we classified such a meteor cluster as a “shower” of reliability class III (or, simply, shower of class III).
 |
Fig. 2 Dependence of the number of separated meteors on the threshold value of the Southworth-Hawkins D-discriminant in examples of showers of class I (plots a)−c)), II (d)−f)), and III (g)−i)). The break point is shown by an empty circle in plots a)−f). |
Examples of the dependence N = N(Dlim) for the showers of classes I, II, as well as III, are shown in Fig. 2. The examples roughly indicate the differences between the classes. We hope they will demonstrate why some separated candidate clusters can be, and other clusters cannot be, regarded as meteor showers.
An obvious shower of class I are the Geminids, No. 4 in the IAU MDC list. In Fig. 2a, the shower is separated from the photographic database by using the MoI. The algorithm used yields a limiting value of D equal to Dlim = 0.26. However, one could also consider the value of 0.10. This value, in combination with the steep increase to the flat plateau, implies a compact, well defined, and, therefore, well-proven shower.
Another example of a shower of class I are the December Monocerotids, No. 19, separated, again, from the photographic database by MoI (Fig. 2b). Here, the automatic algorithm yields a break point corresponding to Dlim = 0.05. We can see that there is also a second break point at Dlim = 0.22. This point occurs due to the November Orionids, No. 250, which move in orbits not very different from those of the December Monocerotids (Neslušan & Hajduková 2014, Fig. 6). Considering Dlim = 0.22, the December Monocerotids and November Orionids would be separated as a single shower. This is an imperfection of the automatic algorithm, which, however, concerns only a few showers. In the case of a “double shower”, an individual treatment is necessary.
The last example we give of a class-I shower is the October Draconids, No. 9, separated from the EDMOND database by MoR& (Fig. 2c). With respect to the database, the shower is not very numerous. The plateau in the N = N(Dlim) dependence is not very flat, either. In any case, the dependence is clearly different from those for the candidate showers of class III discussed below.
An example of the shower, which cannot be classified as that of class I, but class II, because of a steep increase of the plateau, is shown in Fig. 2d. This shower is the Southern δ-Aquariids, No. 5, separated from the CAMS database by the MoR&. Another shower of class II is the Northern Daytime ω-Cetids, No. 152, separated from the SonotaCo database by the MoI (Fig. 2e). This shower cannot be classified as a class I shower because of an insufficient number (less than ten) of separated meteors. A steep increase in the number of separated meteors at Dlim ~ 0.315 and the non-monotonous behavior of the N = N(Dlim) dependence in the interval of Dlim from 0.37 to 0.40 likely occur due to the presence of another numerous shower in the near orbital phase space.
The third example of a shower of class II is the γ-Eridanids, No. 378 in the list of all showers, separated from the EDMOND database by the MoR& (Fig. 2f). The shower cannot be classified as a class I shower because the plateau in the N = N(Dlim) dependence is too short. One cannot be sure if the increase yielding the break point is not just a statistical fluctuation.
Examples of separated clusters which are candidates to be proven as showers but which are, however, classified as showers of class III are shown in plots g, h, and i of Fig. 2. In plot g, there is a cluster separated from the SonotaCo database by the MoR&. It is the typical – concave – behavior of the N = N(Dlim) dependence of the sporadic background. The case in plot h is a separation in an orbital phase with a low number of meteors. The increase in their number starts at a large value of Dlim. Still, only 14 meteors are separated at Dlim = 0.50. This cluster is separated from the photographic database by the MoR&.
Because of the absence of a plateau, the cluster in the last example in Fig. 2i must also be classified as class III. A steep increase in the number of separated meteors at Dlim ~ 0.40 likely occurs due to the greater density of the sporadic background in the near orbital phase space. The last cluster is separated from the EDMOND database by the MoI.
2.6. Identification of proven showers to the real showers given in the IAU MDC lists of established and all showers
In the past, the name of a newly found meteor shower was derived from the name of a bright star situated in the vicinity of its mean radiant. Since researchers used different star catalogs and/or determined a slightly different mean radiant, which was, however, nearer to another star, the same shower was sometimes called by different names and this circumstance led to misidentification of the shower later.
In the course of a unique identification of each shower, the IAU MDC recently provided a list of known meteor showers. Since many showers were not reliably confirmed, the MDC provided more than a single list of showers3. Showers confirmed by several (at least two) authors, which can be regarded as certain, are given in the list of established showers. The other showers, together with the established showers, are given in the list of all showers. Other partial lists are further provided for some specific purposes. In the following, we consider only the list of all showers and its subset, the list of the established showers.
In the last step of our search for the showers in a given database, we try to identify every shower found with its potential counterpart in the IAU MDC list of all showers. This identification is done with the help of the similarity of mean orbits of the found and MDC-listed showers. The similarity is again evaluated using the SH D criterion. The showers are regarded as identified if the value D ≤ 0.25. Of course, in the identification, we are forced to omit showers without a complete mean orbit from the list. The results, as well as some complications related to this identification, are described and discussed in Sect. 3.
3. Solving some problems
It appears that neither the MoI nor the MoR& yields showers with all shower meteors completely separated from the given database. After the separation, some “relict” members of the shower will always remain, which are separated in a further processing as another shower or (usually) several showers. Thus, the result of the separation is often several clusters related to the same real shower. In Table 1, we illustrate this situation with a set of clusters, separated by the MoI, which can be identified to the c Andromedids, No. 411 in the IAU MDC list of established showers. In this example, two clusters of class I and six clusters of class II were separated.
Mean orbital elements (q, e, ω, Ω, and i), mean radiant coordinates (α and δ), and geocentric velocities (Vg) of the clusters, separated by the method of indices from the CAMS database, which belong to the c Andromedids, No. 411 in the IAU MDC list of established showers.
In principle, we could alleviate the problem of multi-cluster separation by enlarging the values of the threshold of the DSH or the DR& discriminant to separate more, and possibly all, members of the shower. However, such an enlargement necessarily results in a relatively large contamination of the separated shower with the meteors of the sporadic background. In addition, it is risky that an independent shower of few meteors in the orbital phase space in the vicinity of a larger shower is engulfed by this larger shower.
In the MoR&, the weights in the new criterion used, Dc, of the orbital similarity could be tuned. However, while some showers are separated in many clusters using this method, a lot of showers are separated just as a single cluster. In comparison to the MoI, a smaller number of clusters corresponding to the IAU MDC showers is separated. Thus, it is again risky to choose the weights which would reduce the multi-cluster separation because some of the single-cluster showers could be lost.
To keep the quality of the separation and the determination of mean characteristics, we prefer to retain the standard values of the threshold discriminants. Instead, we identify a particular shower, resulting from the multiple separations, with the cluster separated for the lowest value of Dlim. (If there are two or more clusters which have the same lowest Dlim, the lowest-Dlim cluster with the highest number of separated meteors is identified to the shower.) Of course, the clusters of class II are ignored if there is a cluster or clusters of class I.
Mean solar longitude (λ⊙), mean orbital elements (q, e, ω, Ω, and i), mean radiant coordinates (α and δ), and geocentric velocity (Vg) of an example cluster, separated by the method of indices from the SonotaCo database (the first line of the table), and corresponding mean orbital elements of the showers in the IAU MDC list, to which the cluster is identified (from the second to last line).
Furthermore, a given cluster can be identified to more than a single shower in the IAU MDC list of all showers. Of course, in reality, no cluster can belong to two or more showers at the same time. We again use the lowest value of DSH between the mean orbit of a cluster and the mean orbit of its counterpart in the IAU MDC list to make a unique identification. An example of the multiple identification of a given cluster to six IAU MDC showers is demonstrated in Table 2.
In more detail, the cluster with the working serial number 1737 separated from the SonotaCo video database is identified to (i) the established shower α-Capricornids (No. 1 in the IAU MDC list); (ii) candidate showers August ν-Aquariids (No. 467), χ2-Capricornids (No. 623), and ϵ-Aquariids (No. 692); and (iii) to two showers, August β-Capricornids (No. 471) and August θ-Aquilids (No. 472), which are among the “to be removed showers” in the IAU MDC list. In the last column of Table 2, we give the value of the DSH discriminant between the mean orbit of cluster No. 1737 and the mean orbit of a given shower by the various authors. We can see that the values are lower than 0.1 and, thus, the mean orbits are extremely similar for more than a single shower. Again, we use the lowest value of DSH to make a unique identification of a particular cluster to the IAU MDC shower. More detailed information about the multiple identifications is presented in Sect. 4.
4. Results – shower statistics
The lists of showers separated and confirmed from all four databases considered used by the MoI and MoR& are given in Table A.1 and A.2, respectively. Each shower is introduced by its number in the IAU MDC list of all showers (Jopek & Kaňuchová 2014) or by a lower-case roman number if the separated shower is not identified to any IAU MDC shower (the first column of tables).
The names of the non-identified showers are given in Table A.3. Some of these showers found by the MoI correspond to the showers found by the MoR&. The correspondence is given in Table A.3: the shower of given name is numbered as in the first (MoI number) as the second (MoR&) column.
As mentioned in Sect. 3, many showers found and confirmed in this work are identified to more than a single shower in the IAU MDC list of all showers. The complete lists of these multiple identifications are presented in Table A.4, for the found and confirmed showers by the MoI, and in Table A.5, for those by the MoR&. There are 81 (77) multiple identifications when the candidate showers are selected by the MoI (MoR&). Prevailing part of this relatively large number of similar showers can be explained by the confusing naming of the showers, when various authors refer to the shower by different names (the problem mentioned by Jopek; see Sect. 1). Because of this multiplicity, which is not real for the actual showers, we give only a single shower of the multiple identified set in Tables A.1 and A.2.
In some cases, the twice-identified showers are still real. For example, comet 1P/Halley approaches the Earth’s orbit in both pre-perihelion and post-perihelion arcs of its orbit and, hence, it produces two real showers, Orionids and η-Aquariids, with almost the same mean orbit. We devoted extra attention to search for pairs of this kind among the related showers. Using the MoI, we found three such the pairs: Nos. 8 and 31, 206 and 561, and 335 and 520. When using the MoR&, two single real pairs were found: 8 and 31 and 11 and 626. The relationship between showers Nos. 11 and 626 is, however, uncertain because the stream has a very low inclination to the ecliptic (3° to 5.5°), which casuses a large uncertainity in the position of radiant, especially for the shower No. 11, η-Virginids. In the case of real pairs, both showers are listed in Table A.1 and A.2.
Another case of real showers found among the related pairs is that of the December Monocerotids and November Orionids, Nos. 19 and 250, which, however, do not originate from the same parent body (Neslušan & Hajduková 2014). To recognize pairs of this kind requires special treatment of the related showers. In Tables A.1 and A.2, we give both 19 and 250 showers, but other pairs are not recognized in our work.
Statistics of the numbers of showers found and confirmed in the individual databases as well as those found and confirmed in at least one database is presented in Table 3 (Table 4) when the MoI (MoR&) was used. Specifically, we present the partial numbers of the showers of class I (2nd, 4th, 6th, 8th and column) and class II (3rd, 5th, 7th, and 9th column) separated from each of the four databases used, as well as the numbers of showers of class I (10th column) and class II (11th column) separated from at least one of the four databases. In the individual rows, the following numbers are presented:
-
(1)
the total number of the showers;
-
(2)
the number of the showers identified to the showers in the IAU MDC list of all showers;
-
(3)
the number of the showers identified to the showers in the IAU MDC list of established showers;
-
(4)
the number of the showers, which were not identified to any IAU MDC shower (some of these showers may not be newly discovered showers; it is possible that they have already been found by other authors, but are not included in any of the IAU MDC lists).
Various numbers of showers found and confirmed in the photographic IAU MDC (F), CAMS video IAU MDC (C), SonotaCo video (S), EDMOND video (E), and at least one of these databases.
5. Discussion
Using the MoI, we separated 70 showers which are in the IAU MDC list of all showers and 37 other showers. The analogous numbers are 49 and 84, respectively, when the MoR& is used. This documents a different efficiency of the separation of candidate clusters by the methods considered. The showers, which are not present in the IAU MDC list, are almost all of class II, regardless of the method. More than twice the number of these showers are separated by the MoR& in comparison to the MoI. The former method is clearly more capable of separating some diffuse showers and meteor associations.
All large, compact, well-known showers such as the Perseids, Geminids, Orionids and η-Aquariids, Leonids, Southern δ-Aquariids, April Lyrids, Daytime Arietids, α-Capricornids, and October Draconids were separated by both methods, MoI and MoR&. Of the largely dispersed Taurids, the Northern Taurids were not separated by any method and the Southern Taurids were separated only by the MoR& as a class II shower.
In the case of smaller showers, the methods of separation and proof of the meteor showers are, unfortunately, imperfect. Using the same set of meteor-orbit data, the identical list of showers should be separated and proved using any method. However, our result appears to be dependent on the method used. There are 32 showers found and classified as those of class I (numbers: 21, 40, 164, 175, 191, 208, 261, 327, 331, 333, 335, 336, 343, 348, 372, 392, 411, 426, 428, 452, 456, 462, 499, 500, 507, 513, 520, 522, 548, 703, 738, 772) by the MoI, that are not found, even as showers of class II, by the MoR&. And vice versa, there are five showers (numbers: 184, 347, 479, 667, 718) separated with MoR& and classified as those of class I, which are not detected by the MoI.
Using the MoI, 54 (34, 15) showers of class I were separated from at least two (three, all four) databases. The analogous numbers in the case of the class-II showers are 4, 2, and 0. Using the MoR&, 22 (22, 16) showers of class I were separated from at least two (three, all four) databases. The analogous numbers in the case of the class-II showers are 14, 3, and 0. The above mentioned numbers document that the databases used, although they are relatively extensive, still do not contain the sufficient data about all regular showers.
Both methods of separation used, MoI and MoR&, are primarily based on the mean orbital characteristics of meteors. The position of radiant and geocentric velocity are less important. This difference between our methods and those based exclusively on the geophysical or observational characteristics actually has an impact on distiguishing between the showers which seem to be identical by their observational characteristics, but have different mean orbits. An example is the pair of clusters with the first member separated from the photographic and the second member from the SonotaCo video databases by the MoI. Their right ascension and declination of radiant and geocentric velocity are 101.8°, 27.3°, 69.61 km s-1 and 101.0°, 26.2°, 69.67 km s-1, respectively. With respect to these values, the clusters would be regarded as related to the same shower. However, the mean perihelion distance, eccentricity, and especially the argument of perihelion are 0.942 au, 0.881, 186.9° and 0.797 au, 0.975, 233.3°, respectively. The differences are significant enough to regard these clusters as two independent showers.
The numbers of separated and confirmed showers in this work, 107 by the MoI and 133 by the MoR&, are similar to those separated by Brown et al. (2010) (109) using the seven-year survey of the Canadian Meteor Orbit Radar or by Kronk (1988) (112) or to the 112 showers in the IAU MDC list of established showers (Jopek & Kaňuchová 2014). Our numbers are smaller than, for example, the 275 showers identified by Sekanina (1976) in the database of 19 698 radio meteors he used or the 296 showers found by Rudawska et al. (2015) in the collection of the EDMOND database from the period 2001 to 2014, or the 230 meteor showers found by Jenniskens et al. (2016a) searching the CAMS database of about 110 000 meteoroid orbits. Our numbers are also considerably smaller than the number of showers (707) in the considered IAU MDC list of all showers. This is obviously a consequence of the elimination of multiple accounting of a given shower with several names, and due to a reduction in the number of candidate clusters evaluated using the statistical significance of the shower in the given data. In fact, we obtained a much larger number of candidate clusters using both methods than were confirmed as showers, regardless of whether we used the MoI or the MoR&. Specifically, using the MoI, we separated 17, 2639, 2798, and 1805 candidate clusters of class III in the IAU MDC photographic, IAU MDC CAMS video, SonotaCo video, and EDMOND video databases respectively. Using the MoR&, the analogous numbers of candidate clusters of class III were 62, 4997, 7407, and 4351, respectively.
6. Concluding remarks
The data to reliably determine the mean characteristics of annual showers appears to be still insufficient. This can be deduced from the fact that some showers found and well evidenced in one database are not present, often even not as showers of class II, in other databases. All showers of class I should be easily separable as showers of this class in every database. However, only major showers like the Perseids, Geminids, Orionids, Southern Delta Aquariids, Leonids, Quadrantids, or October Draconids are represented with a large enough number of meteors.
Not only the databases but the methods of separation and the proof of the meteor showers are, unfortunately, imperfect. Using the same set of meteor-orbit data, an identical list of showers should be separated and proved using any method. However, our result appears to be dependent on the method used. 32 showers, which have been found and classified as those of class I by the MoI, are not found, even as showers of class II, by the MoR&. And vice versa, there are five showers separated with the help of MoR& and classified as those of class I, which are not detected by the MoI. Certainly, further progress in the theory of separation and proving the shower is strongly desirable.
Despite the problems outlined, we can see a certain convergence of the data in various data sets. A quite large number of showers can be found and proved in two, three, or all four databases considered. Thus, our knowledge of the meteoroid streams crossing the orbit of the Earth is becoming more and more complete. A good and detailed knowledge of meteoroid streams and their structure allows a reliable search for their parent bodies – a search for the sources of most meteoroid particles.
As mentioned in the Introduction, the cosmic space around our planet is increasingly populated by artificial satellites improving our everyday life. Furthermore, it is a place of human-bearing space stations and, we can expect, will in the future contain the stations of space colonists. The meteoroid particles reduce the functionality of the stations and satellites and also threaten the people staying in the cosmos. A good knowledge of the sources of meteoroid streams is the first, necessary condition in an action to remove these sources from the orbits, in which they produce the particles and larger boulders into the space in the Earth’s vicinity. In this sense, the observations and theoretical studies of meteoroid streams have also a potential practical application.
Acknowledgments
This work was supported by VEGA – the Slovak Grant Agency for Science (grants Nos. 2/0225/14 and VEGA 2/0031/14) and by the Slovak Research and Development Agency (contract No. APVV-0517-12). This article was also supported by the realization of the Project ITMS No. 26220120029, based on the supporting operational Research and development program financed from the European Regional Development Fund.
References
- Andreić, Ž., Šegon, D., Korlević, K., et al. 2013, WGN, J. Int. Meteor Org., 41, 103 [Google Scholar]
- Arlt, R. 1995, WGN, J. Int. Meteor Org., 23, 105 [NASA ADS] [Google Scholar]
- Arlt, R., & Rendtel, J. 2006, WGN, J. Int. Meteor Org., 34, 77 [NASA ADS] [Google Scholar]
- Arlt, R., & Rendtel, J. 2007, in Proc. Int. Met. Conf., 25th IMC, Roden, Netherlands, 2006, eds. F. Bettonvil, & J. Kac, 76 [Google Scholar]
- Baggaley, W. J. 1995, Earth Moon and Planets, 68, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Betlem, H., Ter Kuile, C. R., de Lignie, M., et al. 1998, A&AS, 128, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, P., Weryk, R. J., Wong, D. K., & Jones, J. 2008, Icarus, 195, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P., Wong, D. K., Weryk, R. J., & Wiegert, P. 2010, Icarus, 207, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, A. F. 1973, NASA Sp. Publ., 319, 183 [Google Scholar]
- Cooke, W. J., & Moser, D. E. 2012, in Proc. Int. Met. Conf., 30th IMC, Sibiu, Romania, 2011, 9 [Google Scholar]
- de Lignie, M. 1999, in Proc. Int. Met. Conf., 17th IMC, Stara Lesna, Slovakia, 1998, eds. R. Arlt, & A. Knoefel, 5 [Google Scholar]
- Galligan, D. P., & Baggaley, W. J. 2002, in IAU Colloq. 181: Dust in the Solar System and Other Planetary Systems, eds. S. F. Green, I. P. Williams, J. A. M. McDonnell, & N. McBride, 15, 48 [Google Scholar]
- Gartrell, G., & Elford, W. G. 1975, Aust. J. Phys., 28, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Gural, P., Šegon, D., Andreić, Ž., et al. 2014, WGN, J. Int. Meteor Org., 42, 132 [NASA ADS] [Google Scholar]
- Holman, D., & Jenniskens, P. 2012, WGN, J. Int. Meteor Org., 40, 166 [NASA ADS] [Google Scholar]
- Jenniskens, P. 2006, Meteor Showers and their Parent Comets (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Jenniskens, P. 2008, Earth Moon and Planets, 102, 5 [Google Scholar]
- Jenniskens, P., Gural, P. S., Dynneson, L., et al. 2011, Icarus, 216, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Nénon, Q., Albers, J., et al. 2016a, Icarus, 266, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Nénon, Q., Gural, P. S., et al. 2016b, Icarus, 266, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Nénon, Q., Gural, P. S., et al. 2016c, Icarus, 266, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., & Froeschle, C. 1997, A&A, 320, 631 [NASA ADS] [Google Scholar]
- Jopek, T. J., & Jenniskens, P. M. 2011, in Meteoroids: The Smallest Solar System Bodies, eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, 7 [Google Scholar]
- Jopek, T. J., & Kaňuchová, Z. 2014, Meteoroids 2013, 353 [Google Scholar]
- Jopek, T. J., Koten, P., & Pecina, P. 2010, MNRAS, 404, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Kashcheyev, B. L., & Lebedinets, V. N. 1967, Smithsonian Contributions to Astrophysics, 11, 183 [NASA ADS] [Google Scholar]
- Kornos, L., Koukal, J., Piffl, R., & Toth, J. 2013, in Proc. Int. Met. Conf., 31st IMC, La Palma, Canary Islands, Spain, 2012, eds. M. Gyssens, & P. Roggemans, 21 [Google Scholar]
- Kornoš, L., Koukal, J., Piffl, R., & Tóth, J. 2014a, in Proc. Int. Met. Conf., Poznan, Poland, 22–25 August 2013, eds. M. Gyssens, P. Roggemans, & P. Zoladek, 23 [Google Scholar]
- Kornoš, L., Matlovič, P., Rudawska, R., et al. 2014b, Meteoroids 2013, 225 [Google Scholar]
- Koten, P., Spurný, P., Borovička, J., & Stork, R. 2003, Publications of the Astronomical Institute of the Czechoslovak Academy of Sciences, 91, 1 [NASA ADS] [Google Scholar]
- Koukal, J., Tóth, J., Piffl, R., & Kornoš, L. 2014, WGN, J. Int. Meteor Org., 42, 7 [NASA ADS] [Google Scholar]
- Kronk, G. W. 1988, Meteor showers. A descriptive catalog (Enslow Publishers) [Google Scholar]
- Lindblad, B. A. 1971, Smithsonian Contributions to Astrophysics, 12, 14 [Google Scholar]
- Lindblad, B. A. 1987, Publications of the Astronomical Institute of the Czechoslovak Academy of Sciences, 67, 201 [NASA ADS] [Google Scholar]
- Lindblad, B. A. 1991, in IAU Colloq. 126: Origin and Evolution of Interplanetary Dust, eds. A. C. Levasseur-Regoud, & H. Hasegawa, Astrophys. Space Sci. Lib., 173, 311 [Google Scholar]
- Lindblad, B. A., Neslušan, L., Porubčan, V., & Svoreň, J. 2003, Earth Moon and Planets, 93, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Molau, S. 2014, in Proc. Int. Met. Conf., Poznan, Poland, 22–25 August 2013, eds. M. Gyssens, P. Roggemans, & P. Zoladek, 26 [Google Scholar]
- Molau, S., & Rendtel, J. 2009, WGN, J. Int. Meteor Org., 37, 98 [Google Scholar]
- Moorhead, A. V., Sugar, G., Brown, P. G., & Cooke, W. J. 2015, in AAS/Division for Planetary Sciences Meeting Abstracts, 47, 308.18 [Google Scholar]
- Neslušan, L., & Hajduková, M. 2014, A&A, 566, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neslušan, L., Svoreň, J., & Porubčan, V. 1995, Earth Moon and Planets, 68, 427 [Google Scholar]
- Neslušan, L., Svoreň, J., & Porubčan, V. 2013, Earth Moon and Planets, 110, 41 [Google Scholar]
- Neslušan, L., Porubčan, V., & Svoreň, J. 2014, Earth Moon and Planets, 111, 105 [Google Scholar]
- Nilsson, C. S. 1964, Aust. J. Phys., 17, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Ohtsuka, K., & Hidaka, E. 1999, Tokyo Meteor Network Rep., 16, 103 [Google Scholar]
- Pujols, P., Amblàs, M., Trigo-Rodríguez, J. M., et al. 2013, in Lunar and Planetary Science Conference, 44, 2054 [Google Scholar]
- Rudawska, R., & Jenniskens, P. 2014, Meteoroids 2013, 217 [Google Scholar]
- Rudawska, R., Matlovič, P., Tóth, J., & Kornoš, L. 2015, Planet. Space Sci., 118, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z. 1973, Icarus, 18, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z. 1976, Icarus, 27, 265 [NASA ADS] [CrossRef] [Google Scholar]
- SonotaCo. 2009, WGN, J. Int. Meteor Org., 37, 55 [Google Scholar]
- SonotaCo. 2016, WGN, J. Int. Meteor Org., 44, 42 [Google Scholar]
- Southworth, R. B., & Hawkins, G. S. 1963, Smithsonian Contributions to Astrophysics, 7, 261 [NASA ADS] [Google Scholar]
- Svoreň, J., Neslušan, L., & Porubčan, V. 2000, Planet. Space Sci., 48, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Tóth, J., Kornoš, L., Zigo, P., et al. 2015, Planet. Space Sci., 118, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, M., & Fujiwara, Y. 1995, Earth Moon and Planets, 68, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, M., & Okamoto, S. 2008, WGN, J. Int. Meteor Org., 36, 14 [NASA ADS] [Google Scholar]
- Šegon, D., Andreić, Ž., Korlević, K., et al. 2013, WGN, J. Int. Meteor Org., 41, 70 [NASA ADS] [Google Scholar]
- Zoladek, P., & Wisniewski, M. 2012, WGN, J. Int. Meteor Org., 40, 189 [NASA ADS] [Google Scholar]
Appendix A: Tabular results
Characteristics of the showers separated from the used databases by the MoI.
Characteristics of the showers separated from the used databases by the MoR&.
Names of the showers not identified to any shower in the IAU MDC list of all showers.
Identification of the showers in the IAU MDC list of all showers to the showers found and confirmed, using the MoI, in the photographical (F), CAMS-video (C), SonotaCo-video (S), and EDMOND-video (E) databases.
Identification of the showers in the IAU MDC list of all showers to the showers found and confirmed, using the MoR&, in the photographical (F), CAMS-video (C), SonotaCo-video (S), and EDMOND-video (E) databases.
All Tables
Mean orbital elements (q, e, ω, Ω, and i), mean radiant coordinates (α and δ), and geocentric velocities (Vg) of the clusters, separated by the method of indices from the CAMS database, which belong to the c Andromedids, No. 411 in the IAU MDC list of established showers.
Mean solar longitude (λ⊙), mean orbital elements (q, e, ω, Ω, and i), mean radiant coordinates (α and δ), and geocentric velocity (Vg) of an example cluster, separated by the method of indices from the SonotaCo database (the first line of the table), and corresponding mean orbital elements of the showers in the IAU MDC list, to which the cluster is identified (from the second to last line).
Various numbers of showers found and confirmed in the photographic IAU MDC (F), CAMS video IAU MDC (C), SonotaCo video (S), EDMOND video (E), and at least one of these databases.
Names of the showers not identified to any shower in the IAU MDC list of all showers.
Identification of the showers in the IAU MDC list of all showers to the showers found and confirmed, using the MoI, in the photographical (F), CAMS-video (C), SonotaCo-video (S), and EDMOND-video (E) databases.
Identification of the showers in the IAU MDC list of all showers to the showers found and confirmed, using the MoR&, in the photographical (F), CAMS-video (C), SonotaCo-video (S), and EDMOND-video (E) databases.
All Figures
 |
Fig. 1 Example of the dependence of the number of selected meteors of a shower from a database on the limiting value of the Southworth-Hawkins D discriminant Dlim, with an illustration of the three fundamental segments of the algorithm of the automated search for the beginning of the plateau. |
| In the text | |
 |
Fig. 2 Dependence of the number of separated meteors on the threshold value of the Southworth-Hawkins D-discriminant in examples of showers of class I (plots a)−c)), II (d)−f)), and III (g)−i)). The break point is shown by an empty circle in plots a)−f). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


